-
摘要: 采用集合论的方法给出了单位模糊集合和二型模糊集合及其在一点的限制等定义，使得二型模糊集合更易于理解.通过定义嵌入单位模糊集合来描述一般二型模糊集合，并给出离散、半连通二型模糊集合的表达式.根据论域、主隶属度及隶属函数的特性将二型模糊集合分为四种类型：离散、半连通、连通及复合型，并根据连通的特点将连通二型模糊集合分为单连通及多连通两类.利用支集的闭包（Closure of support，CoS）划分法表述主隶属度及区间二型模糊集合.提出了CoS二、三次划分法分别来表述单、复连通二型模糊集合，并使每一个子区域的上下边界及次隶属函数在该子区域上的限制分别具有相同的解析表述式.最后，探讨了二型模糊集合在一点的限制、主隶属度、支集、嵌入单位模糊集合之间的关系.Abstract: New and revised definitions such as unit fuzzy sets, type-2 fuzzy sets (T2 FSs) and their restriction at a point are introduced by the method of set theory to make them easily understandable. All the definitions are uniform and formal, and able to represent type-2 fuzzy sets conveniently. An embedded unit fuzzy set is defined to describe general T2 FSs and the representations of discrete and partially connected T2 FSs are given as well. Based on the universes of discourse, primary membership grade, and membership function, type-2 fuzzy sets are divided into four classes:discrete, partially connected, connected, and compounded. Connected T2 FSs are further classified into two types:single connected and multi-connected. The partition method for closure of support (CoS) is used to represent the primary membership grades and interval type-2 fuzzy sets. A method of second/third partition for CoS is proposed to represent single connected/multi-connected T2 FS, respectively after CoS is divided twice and three times; the upper and lower membership functions, and the restriction of the secondary membership function have same analytic expressions, respectively. Finally, the connections among the restriction of T2 FS at a point, primary membership function, CoS, embedded type-1 fuzzy set are discussed.
-
图 9 单连通三角二型模糊集合CoS的第一次划分
Fig. 9 The first partition for CoS of simply connected triangular T2 FS
图 10 单连通三角二型模糊集合CoS的第二次划分
Fig. 10 The second partition for CoS of simply connected triangular T2 FS
图 12 单连通梯形二型模糊集合CoS的第一次划分
Fig. 12 The first partition for CoS of simply connected trapezoidal T2 FS
图 13 单连通梯形二型模糊集合CoS的第二次划分
Fig. 13 The second partition for CoS of simply connected trapezoidal T2 FS
-
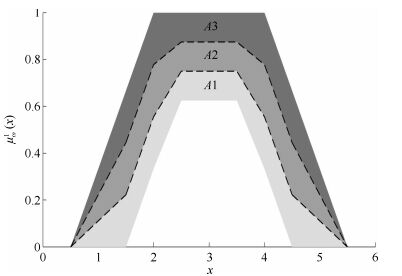
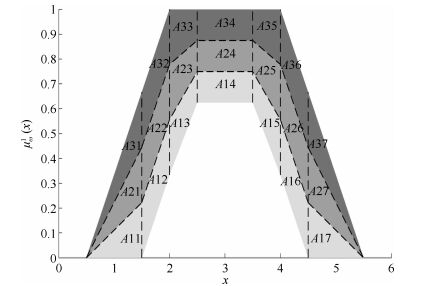
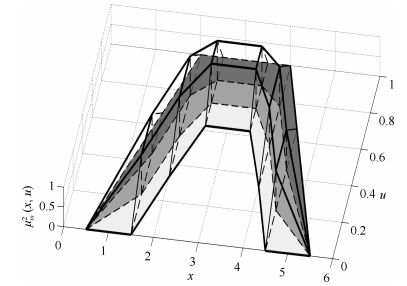
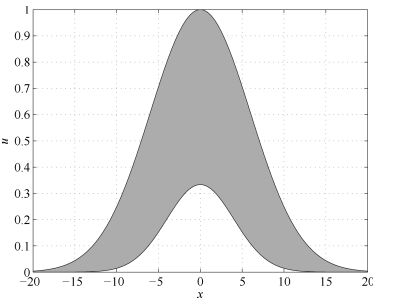
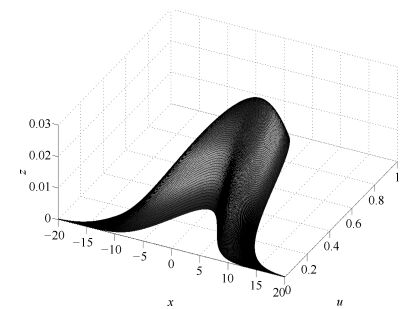
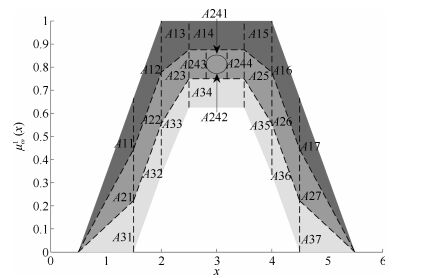
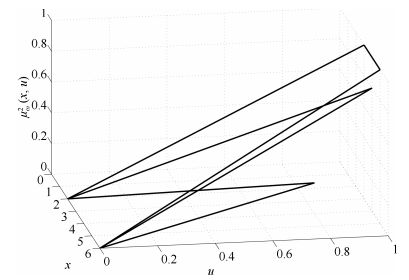
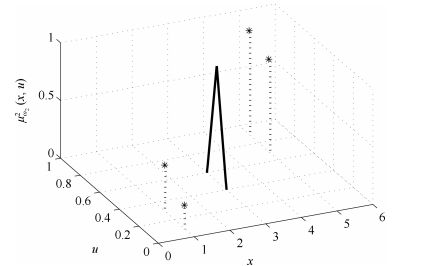
[1] Zadeh L A. The concept of a linguistic variable and its application to approximate reasoning-Ⅰ. Information Sciences, 1975, 8(3):199-249 doi: 10.1016/0020-0255(75)90036-5 [2] Aliev R A, Pedrycz W, Guirimov B G, Aliev R R, Ilhan U, Babagil M, Mammadli S. Type-2 fuzzy neural networks with fuzzy clustering and differential evolution optimization. Information Sciences, 2011, 181(9):1591-1608 doi: 10.1016/j.ins.2010.12.014 [3] Pedrycz W. Granular computing:Analysis and Design of Intelligent Systems. Boca Raton, FL:CRC Press, 2013. [4] 潘永平, 黄道平, 孙宗海. Ⅱ型模糊控制综述.控制理论与应用, 2011, 28(1):13-23 http://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201101003.htmPan Yong-Ping, Huang Dao-Ping, Sun Zong-Hai. Overview of type-2 fuzzy logic control. Control Theory & Applications, 2011, 28(1):13-23 http://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201101003.htm [5] Aisbett J, Rickard J T, Morgenthaler D. Multivariate modeling and type-2 fuzzy sets. Fuzzy sets and Systems, 2011, 163(1):78-95 doi: 10.1016/j.fss.2010.10.001 [6] Uncu O, Turksen I B. Discrete interval type 2 fuzzy system models using uncertainty in learning parameters. IEEE Transactions on Fuzzy Systems, 2007, 15(1):90-106 doi: 10.1109/TFUZZ.2006.889765 [7] Mendel J M, Liu X W. Simplified interval type-2 fuzzy logic systems. IEEE Transactions on Fuzzy Systems, 2013, 21(6):1056-1069 doi: 10.1109/TFUZZ.2013.2241771 [8] Mendel J M, Rajati M R. On computing normalized interval type-2 fuzzy sets. IEEE Transactions on Fuzzy Systems, 2014, 22(5):1335-1340 doi: 10.1109/TFUZZ.2013.2280133 [9] Wu D R, Mendel J M. Aggregation using the linguistic weighted average and interval type-2 fuzzy sets. IEEE Transactions on Fuzzy Systems, 2007, 15(6):1145-1161 doi: 10.1109/TFUZZ.2007.896325 [10] Hagras H. Type-2 FLCs:a new generation of fuzzy controllers. IEEE Computational Intelligence Magazine, 2007, 2(1):30-43 doi: 10.1109/MCI.2007.357192 [11] Mendel J M, Wu H W. New results about the centroid of an interval type-2 fuzzy set, including the centroid of a fuzzy granule. Information Sciences, 2007, 177(2):360-377 doi: 10.1016/j.ins.2006.03.003 [12] Mendel J M, John R I, Liu F L. Interval type-2 fuzzy logic systems made simple. IEEE Transactions on Fuzzy Systems, 2006, 14(6):808-821 doi: 10.1109/TFUZZ.2006.879986 [13] Mendel J M. On a 50% savings in the computation of the centroid of a symmetrical interval type-2 fuzzy set. Information Sciences, 2005, 172(3-4):417-430 doi: 10.1016/j.ins.2004.04.006 [14] Hao M S, Mendel J M. Similarity measures for general type-2 fuzzy sets based on the α-plane representation. Information Sciences, 2014, 277:197-215 doi: 10.1016/j.ins.2014.01.050 [15] Juang C F, Huang R B, Lin Y Y. A recurrent self-evolving interval type-2 fuzzy neural network for dynamic system processing. IEEE Transactions on Fuzzy Systems, 2009, 17(5):1092-1105 doi: 10.1109/TFUZZ.2009.2021953 [16] 莫红, 王飞跃, 赵亮.一一映射下区间二型模糊集合的语言动力学轨迹.模式识别与人工智能, 2010, 23(2):144-147 http://www.cnki.com.cn/Article/CJFDTOTAL-MSSB201002002.htmMo Hong, Wang Fei-Yue, Zhao Liang. LDS trajectories under one-to-one mappings in interval type-2 fuzzy sets. Pattern Recognition and Artificial Intelligence, 2010, 23(2):144-147 http://www.cnki.com.cn/Article/CJFDTOTAL-MSSB201002002.htm [17] 莫红, 王飞跃, 肖志权, 陈茜.基于区间二型模糊集合的语言动力系统稳定性.自动化学报, 2011, 37(8):1018-1024 http://www.aas.net.cn/CN/abstract/abstract17522.shtmlMo Hong, Wang Fei-Yue, Xiao Zhi-Quan, Chen Qian. Stabilities of linguistic dynamic systems based on interval type-2 fuzzy sets. Acta Automatica Sinica, 2011, 37(8):1018-1024 http://www.aas.net.cn/CN/abstract/abstract17522.shtml [18] 张伟斌, 胡怀中, 刘文江.基于二型模糊逻辑的交通流量预测.西安交通大学学报, 2007, 41(10):1160-1164 doi: 10.3321/j.issn:0253-987x.2007.10.008Zhang Wei-Bin, Hu Huai-Zhong, Liu Wen-Jiang. Traffic flow forecast based on type-2 fuzzy logic approach. Journal of Xi'an Jiaotong University, 2007, 41(10):1160-1164 doi: 10.3321/j.issn:0253-987x.2007.10.008 [19] 李成栋, 易建强, 余意, 赵冬斌.柔索驱动并联机构的二型模糊神经逆控制.自动化学报, 2010, 36ć(3):459-464 http://www.aas.net.cn/CN/abstract/abstract13692.shtmlLi Cheng-Dong, Yi Jian-Qiang, Yu Yi, Zhao Dong-Bin. Inverse control of cable-driven parallel mechanism using type-2 fuzzy neural network. Acta Automatica Sinica, 2010, 36(3):459-464 http://www.aas.net.cn/CN/abstract/abstract13692.shtml [20] Zadeh L A. Fuzzy sets. Information and Control, 1965, 8(3):338-353 doi: 10.1016/S0019-9958(65)90241-X [21] Mo H, Wang F Y, Zhou M, Li R M, Xiao Z Q. Footprint of uncertainty for type-2 fuzzy sets. Information Sciences, 2014, 272:96-110 doi: 10.1016/j.ins.2014.02.092 [22] Mo H, Wang J, Li X, Wu Z L. Linguistic Dynamic Modeling and Analysis of Psychological Health State Using Interval Type-2 Fuzzy Sets. IEEE/CAA Journal of Automatica Sinica, 2015, 2(4):366-373 doi: 10.1109/JAS.2015.7296531 [23] Mendel J M. Advances in type-2 fuzzy sets and systems. Information Sciences, 2007, 177(1):84-110 doi: 10.1016/j.ins.2006.05.003 [24] Mendel J M. General type-2 fuzzy logic systems made simple:a tutorial. IEEE Transactions on Fuzzy Systems, 2014, 22(5):1162-1182 doi: 10.1109/TFUZZ.2013.2286414 [25] Mendel J M. Type-2 fuzzy sets and systems:a retrospective. Informatik-Spektrum, 2015, 38(6):523-532 doi: 10.1007/s00287-015-0927-4 [26] Mendel J M, Rajati M R, Sussner P. On clarifying some definitions and notations used for type-2 fuzzy sets as well as some recommended changes. Information Sciences, 2016, 340-341:337-345 doi: 10.1016/j.ins.2016.01.015 [27] 王晓波. 2型Fuzzy集的分解定理.模糊数学, 1:9-13 http://www.cnki.com.cn/Article/CJFDTOTAL-MUTE200101003.htmWang Xiao-Bo. Decomposition theorem of type-2 fuzzy sets, Fuzzy Mathematics, 1983, 1:9-13 http://www.cnki.com.cn/Article/CJFDTOTAL-MUTE200101003.htm [28] Rickard J T, Aisbett J, Gibbon G. Fuzzy subsethood for fuzzy sets of type-2 and generalized type-n. IEEE Transactions on Fuzzy Systems, 2009, 17(1):50-60 doi: 10.1109/TFUZZ.2008.2006369 [29] Mendel J M, John R I B. Type-2 fuzzy sets made simple. IEEE Transactions on Fuzzy Systems, 2002, 10(2):117-127 doi: 10.1109/91.995115 [30] Mendel J M. On KM algorithms for solving type-2 fuzzy set problems. IEEE Transactions on Fuzzy Systems, 2013, 21(3):426-446 doi: 10.1109/TFUZZ.2012.2227488 [31] 黄宣国.空间解析几何与微分几何.上海:复旦大学出版社, 2003.Huang Xuan-Guo. Spatial Analytic Geometry and Differential Geometry. Shanghai:Press of Fudan University, 2003. [32] Wang F Y. Modeling, analysis and synthesis of linguistic dynamic systems:a computational theory. In:Proceedings of the 1995 IEEE International Workshop on Architecture for Semiotic Modeling and Situation Control in Large Complex Systems. Monterey, CA, USA:IEEE, 1995. 173-178 [33] Wang F Y. Outline of a computational theory for linguistic dynamic systems:toward computing with words. International Journal of Intelligent Control and Systems, 1998, 2(2):211-224 https://www.researchgate.net/publication/285014549_Outline_of_a_computational_theory_for_linguistic_dynamic_systems_Toward_computing_with_words [34] 王飞跃.词计算和语言动力学系统的基本问题和研究.自动化学报, 2005, 31(6):844-852 http://www.aas.net.cn/CN/abstract/abstract15941.shtmlWang Fei-Yue. Fundamental issues in research of computing with words and linguistic dynamic systems. Acta Automatica Sinica, 2005, 31(6):844-852 http://www.aas.net.cn/CN/abstract/abstract15941.shtml [35] Mo H, Wang F Y. Linguistic dynamic systems based on computing with words and their stabilities. Science in China Series F:Information Sciences, 2009, 52(5):780-796 doi: 10.1007/s11432-009-0089-6 [36] 莫红, 王飞跃.语言动力系统与二型模糊逻辑.北京:中国科学技术出版社, 2013.Mo Hong, Wang Fei-Yue. Linguistic Dynamic Systems and Type-2 Fuzzy Logic. Beijing:Chinese Press of Science and Technology, 2013. [37] Zhou J, Chen C L P, Chen L, Li H X. A collaborative fuzzy clustering algorithm in distributed network environments. IEEE Transactions on Fuzzy Systems, 2014, 22(6):1443-1456 doi: 10.1109/TFUZZ.2013.2294205 [38] Chen C L P, Wang J, Wang C H, Chen L. A new learning algorithm for a fully connected neuro-fuzzy inference system. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(10):1741-1757 doi: 10.1109/TNNLS.2014.2306915 -
下载:
图(21)
计量
- 文章访问数: 3838
- HTML全文浏览量: 492
- PDF下载量: 1942
- 被引次数: 0
