An Evolutionary Algorithm Through Neighborhood Competition for Multi-objective Optimization
-
摘要: 传统多目标优化算法（Multi-objective evolution algorithms，MOEAs）的基本框架大致分为两部分：首先是收敛性保持，采用Pareto支配方法将种群分成若干非支配层；其次是分布性保持，在临界层中，采用分布性保持机制维持种群的分布性.然而在处理高维优化问题（Many-objective optimization problems，MOPs）（目标维数大于3）时，随着目标维数的增加，种群的收敛性和分布性的冲突加剧，Pareto支配关系比较个体优劣的能力也迅速下降，此时传统的MOEA已不再适用于高维优化问题.鉴于此，本文提出了一种基于邻域竞赛的多目标优化算法（Evolutionary algorithm based on neighborhood competition for multi-objective optimization，NCEA）.NCEA首先将个体的各个目标之和作为个体的收敛性估计；然后，计算当前个体向量与收敛性最好的个体向量之间的夹角，并将其作为当前个体的邻域估计；最后，通过邻域竞赛方法将问题划分为若干个相互关联的子问题并逐步优化.为了验证NCEA的有效性，本文选取5个优秀的算法与NCEA进行对比实验.通过对比实验验证，NCEA具有较强的竞争力，能同时保持良好的收敛性和分布性.
-
关键词:
- 多目标优化算法 /
- Pareto支配关系 /
- 邻域竞赛机制 /
- 高维优化问题
Abstract: The basic framework of traditional multi-objective evolutionary algorithms (MOEAs) can be classified into two parts:one is the convergence holding of the population, for which the fast nondominated sort approach is used to sort the population into certain nondomination layers; the other is the distribution maintenance of the population, for which diversity maintenance mechanisms are adoopted to hold the distribution of the population. However, when dealing with many-objective optimization problems (MOPs) (The number of objective dimensions is greater than 3), with the incease of objective dimensions, the conflicts between convergence and distribution will intensifys, and the Pareto dominance's ability of comparing the individuals will decline. In this case, traditional MOEAs are no longer apt. In this paper, a evolutionary algorithm is proposed based on neighborhood competition for multi-objective optimization (denoted as NCEA). Firstly, the convergence of each individual in the population is estimated by summing its objective values; then the angles between current selected solutions and the best converged solution are calculated and taken as the estimates of the distribution of the selected solutions; lastly, an MOP is divided into a number of mutually correlated sub-problems through neghorhood competition and optimizing, respectively. From the comparative experiments with other five representative MOEAs, NCEA is found to be competitive and successful in finding well-converged and well-distributed solution set.1) 本文责任编委 魏庆来 -
图 2 无分布性保持机制的NSGA-Ⅱ ($A$)与NCEA ($A^*$)的收敛性比较
Fig. 2 Evolutionary trajectories of the average GD for 30 runs of the modified without the diversity maintenance mechanism (denoted as $A$) and the NCEA (denoted as $A^*$) on DTLZ2
图 6 在(0, $\pi$]内, 将$\alpha$等分成100份, 分析NCEA在不同指标下的均值
Fig. 6 Splitting the parameter $\alpha$ into 100 parts in certain ranges, and analyzing the different indicators$'$ mean values NCEA
图 7 各算法在3目标DTLZ3测试问题上的最终解集
Fig. 7 The final solution set of different algorithms on 3-objective DTLZ3 test problem
图 8 各算法在6目标DTLZ3测试问题上的最终解集
Fig. 8 The final solution set of different algorithms on 6-objective DTLZ3 test problem
表 1 6个算法的时间复杂度
Table 1 The time complexity of six algorithms
算法 NCEA $\varepsilon $-MOEA GrEA AR + DMO MSOPS NSGA-Ⅲ 时间复杂度 O$(mn^2)$ O$(mn(n+k))$ O$(mn^2)$ O$(mn^2)$ O$(mnt \cdot {\rm log}(t))$ ($n>t$) O$(mn^2)$ 
下载: 导出CSV
表 2 DTLZ系列测试问题及相关算法参数设置
Table 2 DTLZ series test and related algorithm parameters
问题 目标个数 特性 $\epsilon$参数 GrEA参数 DTLZ1 3, 4, 5, 6, 8, 10 Linear, multimodal 0.033, 0.052, 0.059, 0.0554, 0.0549, 0.0565 10, 10, 10, 10, 10, 11 DTLZ2 3, 4, 5, 6, 8, 10 Concave 0.06, 0.1312, 0.1927, 0.234, 0.29, 0.308 10, 10, 9, 8, 7, 8 DTLZ3 3, 4, 5, 6, 8, 10 Concave, multimodal 0.06, 0.1385, 0.2, 0.227, 0.1567, 0.85 11, 11, 11, 11, 10, 11 DTLZ4 3, 4, 5, 6, 8, 10 Concave, biased 0.06, 0.1312, 0.1927, 0.234, 0.29, 0.308 10, 10, 9, 8, 7, 8 DTLZ5 3, 4, 5, 6, 8, 10 Concave, degenerate 0.0052, 0.042, 0.0785, 0.11, 0.1272, 1.15, 1.45 35, 35, 29, 14, 11, 11 DTLZ6 3, 4, 5, 6, 8, 10 Concave, degenerate, biased 0.0227, 0.12, 0.3552, 0.75, 1.15, 1.45 36, 36, 24, 50, 50, 50 DTLZ7 3, 4, 5, 6, 8, 10 Mixed, disconnected, biased 0.048, 0.105, 0.158, 0.15, 0.225, 0.46 9, 9, 8, 6, 5, 4
下载: 导出CSV
表 3 Metric的网格划分数设置
Table 3 Settings of division for diversity metric
目标数 3 4 5 6 8 10 网格划分数 10 6 4 3 3 3
下载: 导出CSV
表 4 终止条件, 以代数为单位
Table 4 Terminate condition, in generation
问题 DTLZ1 DTLZ2 DTLZ3 DTLZ4 DTLZ5 DTLZ6 DTLZ7 运行代数 1 000 300 1 000 300 300 1 000 300
下载: 导出CSV
表 5 NCEA的参数设置
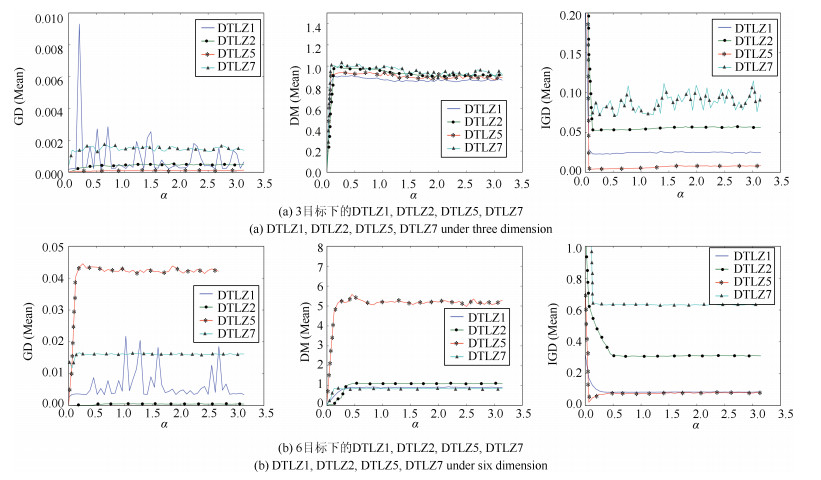
Table 5 Settings of $\alpha$ parameter for NCEA, in degree
目标数 问题 DTLZ1 DTLZ2 DTLZ3 DTLZ4 DTLZ5 DTLZ6 DTLZ7 3 0.128 0.192 0.128 0.256 0.128 0.192 0.064 4 0.256 0.320 0.256 0.512 0.064 0.064 0.128 5 0.385 0.385 0.385 0.385 0.064 0.064 0.064 6 0.385 0.769 0.513 0.833 0.064 0.064 0.128 8 0.385 0.577 0.577 0.577 0.577 0.064 0.192 10 0.513 0.769 0.641 0.641 0.641 0.064 0.256
下载: 导出CSV
表 6 收敛性指标GD的统计数据(均值和方差)
Table 6 Statistical results of the convergence indicator GD (mean and SD)
问题 目标数 均值与方差 NCEA $\varepsilon $-MOEA GrEA AR + DMO MSOPS NSGA-Ⅲ DTLZ1 3 6.5173E-04(2.16738E-03) 2.4240E-04(3.24306E-05) 1.7059E-02(8.29783E-02)$^\dagger$ 1.6188E-02(4.54827E-02) 6.9466E-03(3.67556E-02) 8.3968E-02(3.03360E-01) 4 1.3333E-03(5.87960E-04) 1.5342E-03(1.01728E-04) 5.0108E-02(1.48793E-01) 7.1744E-03(1.27516E-02) 8.0661E-03(3.25514E-02) 2.7705E-02(7.46720E-02) 5 2.3973E-03(3.29058E-04) 2.8019E-03(5.10129E-04) 6.5782E-02(3.16118E-01) 5.9357E-02(1.54993E-01) 2.8872E-02(9.41475E-02) 5.3457E-02(1.27134E-01)$^\dagger$ 6 3.7016E-03(8.14840E-04) 3.5723E-03(4.48798E-04) 4.1469E-02(1.31608E-01) 5.1421E-02(1.02472E-01) 3.8983E-02(1.02165E-01)$^\dagger$ 1.6179E-01(2.49415E-01)$^\dagger$ 8 5.5829E-03(1.27751E-04) 6.1082E-03(9.60869E-04) 8.6450E-02(3.30601E-01)$^\dagger$ 3.6173E-02(9.55063E-02)$^\dagger$ 9.9818E-02(1.48950E-01) $^\dagger$ 9.0905E-01(1.19337E+00)$^\dagger$ 10 8.2959E-03(6.14113E-03) $\underline{3.4608\text{E}-02{{(3.75171\text{E}-02)}^{\dagger }}}$ 4.1050E-02(2.78262E-02)$^\dagger$ 7.8265E-02(1.99814E-01) 1.2987E-01(1.80125E-01)$^\dagger$ 2.0312E-01(4.43355E-01)$^\dagger$ DTLZ2 3 2.4938E-04(7.71848E-05) 7.5429E-04(5.67439E-05)$^\dagger$ 4.4901E-05(4.52089E-05)$^\dagger$ 4.9012E-04(1.50824E-04)$^\dagger$ $\underline{1.1257\text{E}-04{{(1.33222\text{E}-04)}^{\dagger }}}$ 3.0712E-04(2.34867E-04) 4 3.4325E-04(1.07068E-04) 2.1259E-03(1.25929E-04)$^\dagger$ 2.4815E-04(3.10381E-04) 1.1270E-03(3.29167E-04)$^\dagger$ 2.0637E-04(1.21438E-04)$^\dagger$ 7.0224E-04(1.24904E-04)$^\dagger$ 5 2.1616E-04(4.46158E-05) 4.1994E-03(6.61445E-04)$^\dagger$ 4.6204E-04(1.75780E-04)$^\dagger$ 4.1831E-03(1.24812E-03)$^\dagger$ $\underline{3.7035\text{E}-04{{(2.29673\text{E}-04)}^{\dagger }}}$ 1.9392E-03(2.82516E-04) $^\dagger$ 6 5.7860E-04(1.84086E-04) 5.6277E-03(1.97491E-03)$^\dagger$ 6.3318E-04(1.86383E-04) 9.1966E-03(2.34274E-03) $^\dagger$ 5.2284E-04(1.85337E-04) 4.3691E-03(6.82254E-04)$^\dagger$ 8 2.8758E-04(1.06852E-04) 6.8790E-03(8.32033E-04)$^\dagger$ 2.2182E-03(8.86939E-04)$^\dagger$ 1.9660E-02(3.92533E-03)$^\dagger$ $\underline{1.0396\text{E}-03{{(2.79993\text{E}-04)}^{\dagger }}}$ 1.1352E-02(3.21989E-03)$^\dagger$ 10 3.4444E-04(1.40595E-04) 5.5698E-03(4.47660E-04)$^\dagger$ $\underline{1.7998\text{E}-03{{(3.52157\text{E}-04)}^{\dagger }}}$ 3.1090E-02(3.81003E-03)$^\dagger$ 1.6458E-03(3.34714E-04) $^\dagger$ 4.4401E-03(2.74564E-03) $^\dagger$ DTLZ3 3 2.8456E-04(2.41286E-04) 13291E-03(4.28045E-04)$^\dagger$ 1.3041E-01(5.43435E-01)$^\dagger$ 4.0661E-03(8.97266E-03)$^\dagger$ 1.5370E-04(1.11865E-04)$^\dagger$ 8.0032E-03(3.01346E-02) 4 3.9361E-04(2.52161E-04) $\underline{4.8620\text{E}-03{{(2.40060\text{E}-03)}^{\dagger }}}$ 9.6669E-02(4.69495E-01) 1.2016E-01(4.21198E-01) 6.6798E-03(2.22771E-02) 6.3762E-02(1.68358E-01)$^\dagger$ 5 5.6584E-04(3.77953E-04) 8.9207E-03(4.14879E-03) 1.5762E+00(2.65502E+00) 1.7752E-02(4.77234E-02)$^\dagger$ 9.4459E-02(3.57033E-01)$^\dagger$ 6.0880E-01(1.38366E+00) 6 5.6684E-04(3.12144E-04) $\underline{1.7783\text{E}-02{{(1.10904\text{E}-02)}^{\dagger }}}$ 2.9341E+00(4.02971E+00)$^\dagger$ 8.4404E-02(2.22184E-01)$^\dagger$ 2.5392E-01(6.65749E-01)$^\dagger$ 2.7222E+00(2.01272E+00) $^\dagger$ 8 6.8971E-04(3.84881E-04) 1.5738E+00(2.37967E+00)$^\dagger$ 2.1981E+00(2.32611E+00)$^\dagger$ 1.9263E-01(6.19185E-01) 1.3256E+00(1.21451E+00)$^\dagger$ 1.8191E+01(5.70052E+00)$^\dagger$ 10 7.6931E-04(4.06091E-04) 3.1649E+00(2.87679E+00)$^\dagger$ 2.4362E-01(6.95779E-01) $\underline{1.4932\text{E}-01{{(2.98389\text{E}-01)}^{\dagger }}}$ 1.4714E+00(9.55260E-01) $^\dagger$ 1.7709E+01(1.09209E+01)$^\dagger$ DTLZ4 3 2.1106E-04(1.30383E-04) 9.8535E-04(4.16771E-04)$^\dagger$ 1.2073E-04(2.58715E-04) 2.5681E-04(2.91554E-04) 6.5585E-05(1.65279E-04)$^\dagger$ 2.4774E-04(1.30491E-04) 4 5.7399E-04(1.77486E-04) 2.4360E-03(5.77431E-04)$^\dagger$ $\underline{2.0198\text{E}-04{{(3.13694\text{E}-04)}^{\dagger }}}$ 1.5170E-03(3.12700E-03) 1.7653E-04(9.46011E-05)$^\dagger$ 6.7933E-04(2.68225E-04) 5 2.8600E-04(1.56925E-04) 5.3361E-03(1.76792E-03)$^\dagger$ 4.3361E-04(1.76189E-04) $^\dagger$ 2.4495E-03(2.17001E-03) $^\dagger$ 3.5318E-04(9.82127E-05) 1.6399E-03(3.96018E-04)$^\dagger$ 6 5.9198E-04(2.68476E-04) 1.0150E-02(8.10313E-03) $^\dagger$ 8.3766E-04(3.33206E-04) $^\dagger$ 4.8072E-03(3.04760E-03) $^\dagger$ $\underline{8.3145\text{E}-04{{(5.98874\text{E}-04)}^{\dagger }}}$ 3.4386E-03(1.12700E-03) $^\dagger$ 8 4.3000E-04(2.03320E-04) 1.0441E-02(5.13729E-03) $^\dagger$ 2.4109E-03(1.05389E-03) $^\dagger$ 1.4767E-02(2.59938E-03) $^\dagger$ $\underline{1.5980\text{E}-03{{(5.54551\text{E}-04)}^{\dagger }}}$ 5.2812E-03(4.42282E-03) $^\dagger$ 10 3.3791E-04(1.63041E-04) 1.5882E-02(1.24883E-02)$^\dagger$ $\underline{1.6270\text{E}-03{{(2.48190\text{E}-04)}^{\dagger }}}$ 2.8114E-02(4.28606E-03)$^\dagger$ 2.8111E-03(9.12415E-04)$^\dagger$ 1.5193E-02(5.35355E-03)$^\dagger$ DTLZ5 3 8.2379E-05(4.28364E-05) $\underline{6.0527\text{E}-05{{(6.42860\text{E}-06)}^{\dagger }}}$ 5.9233E-05(5.66109E-05) 8.3765E-04(1.13766E-03)$^\dagger$ 1.0821E-01(2.80056E-03)$^\dagger$ 2.0193E-04(4.83885E-05)$^\dagger$ 4 3.4898E-02(2.52789E-03) 5.0231E-02(3.20057E-03)$^\dagger$ 1.9988E-03(1.06200E-03)$^\dagger$ $\underline{1.6314\text{E}-02{{(7.87450\text{E}-03)}^{\dagger }}}$ 1.5362E-01(3.29054E-03)$^\dagger$ 3.3321E-02(1.53968E-02) 5 1.7277E-02(9.20726E-04) 5.1506E-02(1.82190E-03)$^\dagger$ 1.8679E-02(1.93218E-02) 2.4014E-02(6.34334E-03)$^\dagger$ 1.8936E-01(3.08728E-03)$^\dagger$ 5.4787E-02(9.97725E-03)$^\dagger$ 6 1.4070E-02(6.11126E-04) 5.7760E-02(6.23864E-03)$^\dagger$ 5.6970E-02(3.73031E-03)$^\dagger$ $\underline{3.4634\text{E}-02{{(8.44098\text{E}-03)}^{\dagger }}}$ 2.0364E-01(2.87587E-03)$^\dagger$ 7.0914E-02(1.34050E-02)$^\dagger$ 8 4.8683E-02(4.12569E-03) $\underline{5.3952\text{E}-02{{(4.32586\text{E}-03)}^{\dagger }}}$ 1.0139E-01(5.95976E-03) $^\dagger$ 1.3747E-01(3.12555E-02)$^\dagger$ 2.2976E-01(2.27175E-03)$^\dagger$ 1.0419E-01(1.47761E-02) $^\dagger$ 10 5.4205E-02(5.08366E-03) $\underline{6.0848\text{E}-02{{(6.67483\text{E}-03)}^{\dagger }}}$ 1.1183E-01(7.60976E-03)$^\dagger$ 1.7080E-01(2.86372E-02)$^\dagger$ 2.3387E-01(1.92825E-03)$^\dagger$ 1.5273E-01(1.37459E-02)$^\dagger$ DTLZ6 3 3.1665E-03(2.76698E-03) 5.2588E-03(4.90865E-04)$^\dagger$ 3.3264E-03(1.61298E-03) 5.1275E-03(3.55167E-03)$^\dagger$ 2.0425E-01(4.49689E-03)$^\dagger$ 9.8696E-03(7.13856E-03)$^\dagger$ 4 4.2131E-02(5.62475E-03) 1.1064E-01(9.59272E-03)$^\dagger$ 2.5454E-02(9.72852E-03)$^\dagger$ 1.4171E-01(2.38262E-02)$^\dagger$ 3.3404E-01(7.50779E-03) $^\dagger$ 1.6955E-01(2.03052E-02)$^\dagger$ 5 1.5250E-02(1.92197E-03) 1.5048E-01(5.64830E-03)$^\dagger$ $\underline{9.3128\text{E}-02{{(5.99215\text{E}-02)}^{\dagger }}}$ 2.9541E-01(2.07511E-02)$^\dagger$ 4.9366E-01(1.37175E-02)$^\dagger$ 6.8704E-01(2.20882E-02)$^\dagger$ 6 1.3164E-02(1.52962E-03) 2.5553E-01(2.02566E-02)$^\dagger$ $\underline{3.3090\text{E}-02{{(1.30923\text{E}-01)}^{\dagger }}}$ 3.3130E-01(3.18902E-02)$^\dagger$ 5.5517E-01(1.51144E-02) $^\dagger$ 8.7899E-01(1.26348E-03)$^\dagger$ 8 1.3972E-02(1.16462E-03) 2.9568E-01(1.46263E-01)$^\dagger$ $\underline{1.3262\text{E}-01{{(2.81758\text{E}-01)}^{\dagger }}}$ 6.3637E-01(3.31022E-02)$^\dagger$ 7.6863E-01(1.65607E-02)$^\dagger$ 8.8443E-01(6.83775E-02)$^\dagger$ 10 1.6102E-02(9.86460E-04) $\underline{3.4632\text{E}-01{{(2.74054\text{E}-01)}^{\dagger }}}$ 4.0319E-01(3.82174E-01)$^\dagger$ 7.4899E-01(5.44463E-02)$^\dagger$ 8.1216E-01(1.81888E-02) $^\dagger$ 7.6559E-01(3.71012E-02)$^\dagger$ DTLZ7 3 1.4269E-03(6.27153E-04) 6.9496E-04(3.51603E-05)$^\dagger$ $\underline{9.5260\text{E}-04{{(7.14402\text{E}-04)}^{\dagger }}}$ 2.2605E-03(1.09999E-03)$^\dagger$ 4.4358E-03(6.88598E-04)$^\dagger$ 2.6307E-03(9.13444E-04)$^\dagger$ 4 5.6080E-03(4.49695E-04) 2.3024E-03(5.55552E-04)$^\dagger$ $\underline{4.7689\text{E}-03{{(2.24499\text{E}-04)}^{\dagger }}}$ 1.4251E-02(5.16088E-03)$^\dagger$ 6.9670E-03(1.08085E-03)$^\dagger$ 5.4934E-03(1.15755E-03) 5 7.6494E-03(3.39809E-04) 3.3534E-03(1.06828E-03)$^\dagger$ 1.0717E-02(6.69624E-04)$^\dagger$ 8.3798E-02(2.79588E-02)$^\dagger$ 1.0825E-02(3.33610E-03) $^\dagger$ 2.0268E-02(5.51018E-03)$^\dagger$ 6 1.6013E-02(6.62155E-04) 4.6055E-03(1.70038E-03)$^\dagger$ 1.1947E-02(4.76109E-04)$^\dagger$ 1.7956E-01(4.96227E-02)$^\dagger$ 2.4724E-02(1.41937E-02)$^\dagger$ 9.1749E-02(3.63369E-02)$^\dagger$ 8 2.1716E-02(3.75157E-04) 1.4274E-02(1.09412E-02)$^\dagger$ 2.6989E-02(1.56032E-03)$^\dagger$ 3.3977E-01(7.68451E-02)$^\dagger$ 2.0888E-01(1.13986E-01)$^\dagger$ 9.5229E-01(2.31546E-01)$^\dagger$ 10 4.8018E-02(2.56958E-03) 1.5505E-02(1.25040E-02)$^\dagger$ 4.9859E-02(2.27362E-03)$^\dagger$ 6.6739E-01(1.39620E-01)$^\dagger$ 6.5667E-01(2.37870E-01)$^\dagger$ 2.6579E+00(4.98006E-01)$^\dagger$
下载: 导出CSV
表 7 收敛性指标DM的统计数据(均值和方差)
Table 7 Statistical results of the diversity indicator DM (mean and SD)
问题 目标数 均值与方差 NCEA $\varepsilon $-MOEA GrEA AR + DMO MSOPS NSGA-Ⅲ DTLZ1 3 9.0819E-01(2.30021E-02) 1.0026E+00(9.73518E-03)$^\dagger$ 5.9153E-01(1.56974E-01)$^\dagger$ 4.8806E-01(1.41348E-01) $^\dagger$ 7.2868E-01(8.60635E-03)$^\dagger$ 6.5816E-01(1.22945E-01)$^\dagger$ 4 9.3824E-01(3.92344E-02) 9.0282E-01(9.30006E-02) 8.0118E-01(1.90615E-01)$^\dagger$ 2.7235E-01(1.05381E-01)$^\dagger$ 7.5392E-01(1.49390E-02)$^\dagger$ 1.0242E+00(2.41363E-01) 5 8.9325E-01(5.14120E-02) 7.3063E-01(1.26330E-01)$^\dagger$ 7.7569E-01(1.75880E-01)$^\dagger$ 2.4440E-01(8.58044E-02)$^\dagger$ 8.5011E-01(1.34821E-02) $^\dagger$ 1.1297E+00(2.79471E-01)$^\dagger$ 6 9.0806E-01(7.17513E-02) 7.7961E-01(3.00338E-02)$^\dagger$ 8.9749E-01(2.66680E-01) 3.3819E-01(8.43546E-02)$^\dagger$ $\underline{9.9849\text{E}-01{{(1.02165\text{E}-01)}^{\dagger }}}$ 1.0617E+00(4.52105E-01) 8 5.1983E-01(6.96936E-02) 5.5871E+00(1.19030E+01)$^\dagger$ 7.7478E-01(1.97824E-01)$^{\dagger }$ 2.1625E-01(6.57912E-02)$^\dagger$ 9.9818E-02(3.21026E-02)$^\dagger$ 1.3082E-01(3.92564E-01) $^\dagger$ 10 3.7010E-01(6.41427E-02) 6.7953E+00(1.34618E+01)$^\dagger$ 7.3715E-01(3.20770E-01)$^{\dagger }$ 1.5727E-01(4.25823E-02)$^\dagger$ 6.7204E-01(2.40584E-02)$^\dagger$ 3.1103E-02(4.48038E-02) $^\dagger$ DTLZ2 3 9.8798E-01(1.24042E-02) $\underline{8.8260\text{E}-01{{(2.40016\text{E}-02)}^{\dagger }}}$ 6.8468E-01(2.64578E-02) $^\dagger$ 2.7246E-01(6.91272E-02) $^\dagger$ 4.4127E-01(2.73807E-02) $^\dagger$ 6.0373E-01(2.89793E-03)$^\dagger$ 4 1.0198E+00(6.74614E-03) 9.1986E-01(4.11008E-02)$^\dagger$ 8.7220E-01(2.73173E-02)$^\dagger$ 2.3443E-01(7.24373E-02)$^\dagger$ 5.8514E-01(1.84067E-02) $^\dagger$ 1.1324E+00(7.99399E-03)$^\dagger$ 5 1.0296E+00(7.83495E-03) 9.3372E-01(6.11612E-02) $^\dagger$ 9.5388E-01(3.10375E-02) $^\dagger$ 3.5310E-01(9.60867E-02) $^\dagger$ 6.4514E-01(2.30645E-02) $^\dagger$ 1.3012E+00(5.25382E-03)$^\dagger$ 6 1.1161E+00(2.33482E-02) 8.3860E-01(2.37732E-02) $^\dagger$ 9.5260E-01(3.97041E-02) $^\dagger$ 2.9994E-01(5.69157E-02) $^\dagger$ 6.7853E-01(3.23148E-02) $^\dagger$ 1.3499E+00(2.26676E-02)$^\dagger$ 8 9.8795E-01(6.45634E-03) 1.0236E+00(1.25375E-01) 9.1789E-01(2.48723E-02) $^\dagger$ 2.8558E-01(7.24260E-02)$^\dagger$ 6.4368E-01(2.45093E-02)$^\dagger$ 1.0534E+00(2.47743E-01) 10 9.7058E-01(9.77224E-03) 1.1440E+00(1.84157E-01)$^\dagger$ 9.7039E-01(1.69468E-02) 2.6161E-01(5.65284E-02) $^\dagger$ 6.6149E-01(2.40152E-02)$^\dagger$ 2.1640E-01(2.45770E-01)$^\dagger$ DTLZ3 3 9.9727E-01(1.18592E-02) $\underline{8.7523\text{E}-01{{(3.60858\text{E}-02)}^{\dagger }}}$ 5.6777E-01(1.60735E-01) $^\dagger$ 2.5400E-01(1.34175E-01) $^\dagger$ 5.8864E-01(9.58502E-03) $^\dagger$ 5.9554E-01(3.14145E-02) $^\dagger$ 4 9.7707E-01(8.21852E-03) $\underline{8.7997\text{E}-01{{(1.05353\text{E}-01)}^{\dagger }}}$ 6.3245E-01(2.74485E-01) $^\dagger$ 2.6224E-01(8.97735E-02) $^\dagger$ 6.0668E-01(1.93795E-02) $^\dagger$ 9.2399E-01(2.43623E-01) 5 1.0168E+00(6.54401E-03) $\underline{7.4548\text{E}-01{{(1.93596\text{E}-01)}^{\dagger }}}$ 4.1279E-01(3.28220E-01)$^\dagger$ 1.9796E-01(1.09482E-01)$^\dagger$ 6.4776E-01(1.83865E-02)$^\dagger$ 2.2725E-01(3.28181E-01)$^\dagger$ 6 1.1173E+00(1.13113E-02) $\underline{8.7064\text{E}-01{{(4.34695\text{E}-01)}^{\dagger }}}$ 2.8565E-01(3.17094E-01)$^\dagger$ 1.4374E-01(8.15058E-02)$^\dagger$ 6.5772E-01(1.12801E-01)$^\dagger$ 0.0000E+00(0.00000E+00)$^\dagger$ 8 9.7677E-01(9.65714E-03) 6.2783E-01(1.34328E+00) 1.9315E-01(2.84029E-01)$^\dagger$ 1.2406E-01(4.04796E-02)$^\dagger$ 3.9382E-01(2.50102E-01)$^\dagger$ 0.0000E+00(0.00000E+00)$^\dagger$ 10 9.3645E-01(5.16393E-03) 5.7879E-03(1.54484E-02)$^\dagger$ $\underline{6.0733\text{E}-01{{(2.74915\text{E}-01)}^{\dagger }}}$ 1.3581E-01(5.93626E-02)$^\dagger$ 2.6957E-01(2.31341E-01)$^\dagger$ 0.0000E+00(0.00000E+00)$^\dagger$ DTLZ4 3 6.6197E-01(4.27371E-01) 4.6188E-01(3.95122E-01) 6.1770E-01(1.83316E-01) 2.1352E-01(1.48506E-01)$^\dagger$ 5.7741E-01(5.28796E-03) 4.1289E-01(2.54687E-01)$^\dagger$ 4 9.1824E-01(2.05013E-01) 4.4573E-01(3.64057E-01)$^\dagger$ 7.4143E-01(2.48123E-01)$^\dagger$ 2.5653E-01(1.87011E-01)$^\dagger$ 5.7539E-01(1.76688E-02)$^\dagger$ 1.0616E+00(2.37711E-01)$^\dagger$ 5 9.5754E-01(1.68432E-01) 3.9015E-01(2.93544E-01)$^\dagger$ 8.6074E-01(1.58894E-01)$^\dagger$ 2.6176E-01(1.86893E-01)$^\dagger$ 6.3258E-01(3.13921E-02)$^\dagger$ 1.1518E+00(3.40926E-01)$^\dagger$ 6 1.0725E+00(6.38296E-02) 5.1194E-01(2.85566E-01)$^\dagger$ 9.5005E-01(3.82742E-02)$^\dagger$ 3.2241E-01(2.01053E-01)$^\dagger$ 6.8764E-01(2.43298E-02) 9.6736E-01(5.37545E-01) 8 9.4195E-01(1.74009E-02) 7.2219E-01(3.03730E-01)$^\dagger$ $\underline{9.2790\text{E}-01{{(2.26546\text{E}-02)}^{\dagger }}}$ 3.5804E-01(7.20134E-02)$^\dagger$ 6.1996E-01(2.37531E-02)$^\dagger$ 5.2325E-01(5.52567E-01)$^\dagger$ 10 9.1121E-01(2.45957E-02) 9.6665E-01(3.79451E-01) $\underline{9.6638\text{E}-01{{(1.14391\text{E}-02)}^{\dagger }}}$ 3.2112E-01(8.25448E-02)$^\dagger$ 6.9372E-01(3.57074E-02)$^\dagger$ 1.0501E-01(2.40114E-01)$^\dagger$ DTLZ5 3 9.3890E-01(4.68561E-02) 9.4044E-01(1.02859E-02)$^\dagger$ 9.2575E-01(3.86653E-02)$^\dagger$ $\underline{9.5395\text{E}-01{{(6.11423\text{E}-02)}^{\dagger }}}$ $\underline{1.3685\text{E}-00{{(3.30802\text{E}-02)}^{\dagger }}}$ 9.2722E-01(6.44623E-02)$^\dagger$ 4 2.1707E+00(1.27853E-01) $\underline{1.9068\text{E}-00{{(1.34963\text{E}-01)}^{\dagger }}}$ 9.9110E-01(1.54379E-01)$^\dagger$ 1.2684E+00(4.40710E-01)$^\dagger$ 1.3788E+00(8.11361E-02) $^\dagger$ 9.5825E-01(2.91647E-01)$^\dagger$ 5 1.7299E+00(1.43731E-01) $\underline{1.6524\text{E}-00{{(1.18251\text{E}-01)}^{\dagger }}}$ 1.1591E+00(1.75680E-01)$^\dagger$ 1.3607E+00(3.95131E-01)$^\dagger$ 1.2771E+00(1.41335E-01)$^\dagger$ 1.1022E+00(4.99464E-01) 6 2.4580E+00(2.24064E-01) 2.7376E+00(3.75631E-01) 2.6813E+00(2.33371E-01) 1.4756E+00(5.42065E-01) 1.5616E+00(2.20953E-01) 2.1622E+00(9.78533E-01) 8 7.0107E+00(5.94377E-01) $\underline{2.4153\text{E}-00{{(3.37337\text{E}-01)}^{\dagger }}}$ 2.1679E+00(6.84087E-01)$^\dagger$ 5.2367E-02(9.60686E-02)$^\dagger$ 7.2613E-01(2.18209E-01) $^\dagger$ 7.9548E-01(6.32929E-01) $^\dagger$ 10 8.5619E+00(6.27846E-01) 2.3997E+00(3.22199E-01)$^\dagger$ $\underline{2.4172\text{E}-00{{(7.50029\text{E}-01)}^{\dagger }}}$ 4.9863E-03(2.73110E-02)$^\dagger$ 4.0498E-01(1.09439E-01)$^\dagger$ 7.6460E-02(1.46121E-01)$^\dagger$ DTLZ6 3 1.3435E+00(1.34596E-01) 1.3889E+00(8.52688E-02) 1.3396E+00(1.72888E-01) 1.1501E+00(3.41395E-01)$^\dagger$ 1.7816E+00(4.67236E-02)$^\dagger$ $\underline{1.4259\text{E}-00{{(111\text{E}-01)}^{\dagger }}}$ 4 2.4410E+00(1.26378E-01) 3.0357E+00(2.93393E-01)$^\dagger$ 1.5270E+00(4.90222E-01)$^\dagger$ 0.0000E+00(0.00000E+00)$^\dagger$ 1.5699E+00(1.05247E-01)$^\dagger$ 4.5635E-03(1.74166E-02)$^\dagger$ 5 1.7951E+00(1.42279E-01) 3.0859E-03(1.69023E-02)$^\dagger$ $\underline{1.4194\text{E}-00{{(4.09709\text{E}-01)}^{\dagger }}}$ 0.0000E+00(0.00000E+00)$^\dagger$ 1.1870E+00(1.78062E-01)$^\dagger$ 0.0000E+00(0.00000E+00)$^\dagger$ 6 2.8895E+00(3.80171E-01) 0.0000E+00(0.00000E+00)$^\dagger$ 2.5593E-01(8.02479E-02)$^\dagger$ 0.0000E+00(0.00000E+00)$^\dagger$ $\underline{9.4320\text{E}-01{{(4.62978\text{E}-01)}^{\dagger }}}$ 0.0000E+00(0.00000E+00)$^\dagger$ 8 1.9559E+00(2.16270E-01) 6.4114E-02(9.25841E-02)$^\dagger$ $\underline{2.6740\text{E}-01{{(1.18849\text{E}-01)}^{\dagger }}}$ 0.0000E+00(0.00000E+00)$^\dagger$ 0.0000E+00(0.00000E+00) $^\dagger$ 0.0000E+00(0.00000E+00)$^\dagger$ 10 1.8986E+00(2.20235E-01) 3.7771E-02(7.68760E-02)$^\dagger$ $\underline{1.4075\text{E}-01{{(1.32006\text{E}-01)}^{\dagger }}}$ 0.0000E+00(0.00000E+00)$^\dagger$ 0.0000E+00(0.00000E+00)$^\dagger$ 0.0000E+00(0.00000E+00)$^\dagger$ DTLZ7 3 9.7062E-01(1.33304E-01) 9.9912E-01(1.44470E-01)$^\dagger$ 7.1857E-01(4.28577E-02)$^\dagger$ 3.7137E-01(1.72866E-01)$^\dagger$ 7.3749E-01(2.16690E-02)$^\dagger$ 5.6630E-01(5.12711E-02) $^\dagger$ 4 6.6394E-01(5.01756E-02) 3.2074E-01(1.09399E-01)$^\dagger$ $\underline{5.0842\text{E}-01{{(7.85438\text{E}-02)}^{\dagger }}}$ 2.3610E-01(7.93598E-02)$^\dagger$ 4.7106E-01(2.01419E-02)$^\dagger$ 4.0124E-01(1.83707E-01)$^\dagger$ 5 7.1072E-01(6.29801E-02) 1.4714E+00(6.34844E-01)$^\dagger$ $\underline{8.2760\text{E}-01{{(3.84418\text{E}-02)}^{\dagger }}}$ 3.5503E-01(1.60258E-01)$^\dagger$ 4.6132E-01(1.90079E-02) $^\dagger$ 2.4188E-01(9.36043E-02)$^\dagger$ 6 8.7237E-01(3.46582E-02) $\underline{6.5235\text{E}-01{{(4.31959\text{E}-01)}^{\dagger }}}$ 5.4844E-01(4.80601E-02)$^\dagger$ 3.3734E-01(1.55325E-01)$^\dagger$ 2.9776E-01(2.34195E-02)$^\dagger$ 1.0036E-01(6.84524E-02)$^\dagger$ 8 5.9887E-01(1.52663E-02) 2.2230E+00(2.02132E+00)$^\dagger$ $\underline{8.7016\text{E}-01{{(6.50580\text{E}-02)}^{\dagger }}}$ 6.1437E-02(6.25518E-02) $^\dagger$ 1.5046E-01(5.11722E-02)$^\dagger$ 0.0000E+00(0.00000E+00)$^\dagger$ 10 4.4481E-02(1.46695E-02) 3.2024E+00(2.16088E+00)$^\dagger$ $\underline{9.6667\text{E}-01{{(6.04123\text{E}-02)}^{\dagger }}}$ 3.4990E-03(7.53848E-03)$^\dagger$ 1.8454E-02(1.15707E-02)$^\dagger$ 0.0000E+00(0.00000E+00)$^\dagger$
下载: 导出CSV
表 8 综合性指标IGD的统计数据(均值和方差)
Table 8 Statistical results of the integrated indicator IGD (mean and SD)
问题 目标数 均值与方差 NCEA $\varepsilon $-MOEA GrEA AR + DMO MSOPS NSGA-Ⅲ DTLZ1 3 2.2436E-02(1.63962E-03) 2.4240E-04(3.24306E-05)$^\dagger$ 1.7059E-02(8.29783E-02) $^\dagger$ 1.6188E-02(4.54827E-02)$^\dagger$ $\underline{6.9466E\text{E}-03{{(3.67556\text{E}-02)}^{\dagger }}}$ 8.3968E-02(3.03360E-01) 4 4.5368E-02(1.22833E-03) 1.5342E-03(1.01728E-04)$^\dagger$ 5.0108E-02(1.48793E-01) $\underline{7.1744\text{E}-03{{(1.27516\text{E}-02)}^{\dagger }}}$ 8.0661E-03(3.25514E-02)$^\dagger$ 2.7705E-02(7.46720E-02) 5 6.6923E-02(1.51909E-03) 2.8019E-03(5.10129E-04) $^\dagger$ 6.5782E-02(3.16118E-01) $^\dagger$ 5.9357E-02(1.54993E-01) 2.8872E-02(9.41475E-02) 5.3457E-02(1.27134E-01)$^\dagger$ 6 8.5221E-02(2.19744E-03) 3.5723E-03(4.48798E-04) 4.1469E-02(1.31608E-01) 5.1421E-02(1.02472E-01)$^\dagger$ $\underline{3.8983\text{E}-02{{(1.02165\text{E}-01)}^{\dagger }}}$ 1.6179E-01(2.49415E-01)$^\dagger$ 8 5.5829E-03(1.27751E-04) $\underline{6.1082\text{E}-03{{(9.60869\text{E}-04)}^{\dagger }}}$ 8.6450E-02(3.30601E-01) 3.6173E-02(9.55063E-02)$^\dagger$ 9.9818E-02(1.48950E-01) $^\dagger$ 9.0905E-01(1.19337E+00)$^\dagger$ 10 8.2959E-03(6.14113E-03) $\underline{3.4608\text{E}-02{{(3.75171\text{E}-02)}^{\dagger }}}$ 4.1050E-02(2.78262E-02)$^\dagger$ 7.8265E-02(1.99814E-01)$^\dagger$ 1.2987E-01(1.80125E-01) $^\dagger$ 2.0312E-01(4.43355E-01)$^\dagger$ DTLZ2 3 2.4938E-04(7.71848E-05) 7.5429E-04(5.67439E-05)$^\dagger$ 4.4901E-05(4.52089E-05)$^\dagger$ 4.9012E-04(1.50824E-04)$^\dagger$ $\underline{1.1257\text{E}-04{{(1.33222\text{E}-04)}^{\dagger }}}$ 3.0712E-04(2.34867E-04)$^\dagger$ 4 3.4325E-04(1.07068E-04) 2.1259E-03(1.25929E-04)$^\dagger$ $\underline{2.4815\text{E}-04{{(3.10381\text{E}-04)}^{\dagger }}}$ 1.1270E-03(3.29167E-04)$^\dagger$ 2.0637E-04(1.21438E-04)$^\dagger$ 7.0224E-04(1.24904E-04) $^\dagger$ 5 2.1616E-04(4.46158E-05) 4.1994E-03(6.61445E-04)$^\dagger$ 4.6204E-04(1.75780E-04)$^\dagger$ 4.1831E-03(1.24812E-03)$^\dagger$ $\underline{3.7035\text{E}-04{{(2.29673\text{E}-04)}^{\dagger }}}$ 1.9392E-03(2.82516E-04)$^\dagger$ 6 5.7860E-04(1.84086E-04) 5.6277E-03(1.97491E-03) $^\dagger$ 6.3318E-04(1.86383E-04)$^\dagger$ 9.1966E-03(2.34274E-03)$^\dagger$ 5.2284E-04(1.85337E-04)$^\dagger$ 4.3691E-03(6.82254E-04)$^\dagger$ 8 2.8758E-04(1.06852E-04) 6.8790E-03(8.32033E-04)$^\dagger$ 2.2182E-03(8.86939E-04)$^\dagger$ 1.9660E-02(3.92533E-03)$^\dagger$ $\underline{1.0396\text{E}-03{{(2.79993\text{E}-04)}^{\dagger }}}$ 1.1352E-02(3.21989E-03)$^\dagger$ 10 3.4444E-04(1.40595E-04) 5.5698E-03(4.47660E-04)$^\dagger$ 1.7998E-03(3.52157E-04)$^\dagger$ 3.1090E-02(3.81003E-03) $^\dagger$ $\underline{1.6458\text{E}-03{{(3.34714E\text{E}-04)}^{\dagger }}}$ 4.4401E-03(2.74564E-03)$^\dagger$ DTLZ3 3 2.8456E-04(2.41286E-04) 1.3291E-03(4.28045E-04)$^\dagger$ 1.3041E-01(5.43435E-01) $^\dagger$ 4.0661E-03(8.97266E-03)$^\dagger$ 1.5370E-04(1.11865E-04) $^\dagger$ 8.0032E-03(3.01346E-02) $^\dagger$ 4 3.9361E-04(2.52161E-04) $\underline{4.8620\text{E}-03{{(2.40060\text{E}-03)}^{\dagger }}}$ 9.6669E-02(4.69495E-01)$^\dagger$ 1.2016E-01(4.21198E-01)$^\dagger$ 6.6798E-03(2.22771E-02)$^\dagger$ 6.3762E-02(1.68358E-01) 5 5.6584E-04(3.77953E-04) $\underline{8.9207\text{E}-03{{(4.14879\text{E}-03)}^{\dagger }}}$ 1.5762E+00(2.65502E+00)$^\dagger$ 1.7752E-02(4.77234E-02)$^\dagger$ 9.4459E-02(3.57033E-01)$^\dagger$ 6.0880E-01(1.38366E+00)$^\dagger$ 6 5.6684E-04(3.12144E-04) $\underline{1.7783\text{E}-02{{(1.10904\text{E}-02)}^{\dagger }}}$ 2.9341E+00(4.02971E+00)$^\dagger$ 8.4404E-02(2.22184E-01)$^\dagger$ 2.5392E-01(6.65749E-01) 2.7222E+00(2.01272E+00) 8 6.8971E-04(3.84881E-04) 1.5738E+00(2.37967E+00)$^\dagger$ 2.1981E+00(2.32611E+00) $^\dagger$ $\underline{1.9263\text{E}-01{{(6.19185\text{E}-01)}^{\dagger }}}$ 1.3256E+00(1.21451E+00) $^\dagger$ 1.8191E+01(5.70052E+00) $^\dagger$ 10 7.6931E-04(4.06091E-04) 3.1649E+00(2.87679E+00) $^\dagger$ 2.4362E-01(6.95779E-01) $^\dagger$ $\underline{1.4932\text{E}-01{{(2.98389\text{E}-01)}^{\dagger }}}$ 1.4714E+00(9.55260E-01) $^\dagger$ 1.7709E+01(1.09209E+01) $^\dagger$ DTLZ4 3 2.1106E-04(1.30383E-04) 9.8535E-04(4.16771E-04) 1.2073E-04(2.58715E-04) 2.5681E-04(2.91554E-04) $^\dagger$ 6.5585E-05(1.65279E-04)$^\dagger$ 2.4774E-04(1.30491E-04) 4 5.7399E-04(1.77486E-04) 2.4360E-03(5.77431E-04) $^\dagger$ 2.0198E-04(3.13694E-04) 1.5170E-03(3.12700E-03)$^\dagger$ 1.7653E-04(9.46011E-05) 6.7933E-04(2.68225E-04) 5 2.8600E-04(1.56925E-04) 5.3361E-03(1.76792E-03)$^\dagger$ 4.3361E-04(1.76189E-04) 2.4495E-03(2.17001E-03)$^\dagger$ 3.5318E-04(9.82127E-05) 1.6399E-03(3.96018E-04) 6 5.9198E-04(2.68476E-04) 1.0150E-02(8.10313E-03)$^\dagger$ 8.3766E-04(3.33206E-04)$^\dagger$ 4.8072E-03(3.04760E-03)$^\dagger$ $\underline{8.3145\text{E}-04{{(5.98874\text{E}-04)}^{\dagger }}}$ 3.4386E-03(1.12700E-03)$^\dagger$ 8 4.3000E-04(2.03320E-04) 1.0441E-02(5.13729E-03)$^\dagger$ 2.4109E-03(1.05389E-03) $^\dagger$ 1.4767E-02(2.59938E-03)$^\dagger$ $\underline{1.5980\text{E}-03{{(5.54551\text{E}-04)}^{\dagger }}}$ 5.2812E-03(4.42282E-03) $^\dagger$ 10 3.3791E-04(1.63041E-04) 1.5882E-02(1.24883E-02)$^\dagger$ 1.6270E-03(2.48190E-04)$^\dagger$ 2.8114E-02(4.28606E-03)$^\dagger$ $\underline{2.8111\text{E}-03{{(9.12415\text{E}-04)}^{\dagger }}}$ 1.5193E-02(5.35355E-03) $^\dagger$ DTLZ5 3 8.2379E-05(4.28364E-05) $\underline{6.0527\text{E}-05{{(6.42860\text{E}-06)}^{\dagger }}}$ 5.9233E-05(5.66109E-05)$^\dagger$ 8.3765E-04(1.13766E-03) 1.0821E-01(2.80056E-03)$^\dagger$ 2.0193E-04(4.83885E-05) $^\dagger$ 4 3.4898E-02(2.52789E-03) 5.0231E-02(3.20057E-03)$^\dagger$ 1.9988E-03(1.06200E-03) $\underline{1.6314\text{E}-02{{(7.87450\text{E}-03)}^{\dagger }}}$ 1.5362E-01(3.29054E-03)$^\dagger$ 3.3321E-02(1.53968E-02)$^\dagger$ 5 1.7277E-02(9.20726E-04) 5.1506E-02(1.82190E-03)$^\dagger$ $\underline{1.8679\text{E}-02{{(1.93218\text{E}-02)}^{\dagger }}}$ 2.4014E-02(6.34334E-03)$^\dagger$ 1.8936E-01(3.08728E-03)$^\dagger$ 5.4787E-02(9.97725E-03)$^\dagger$ 6 1.4070E-02(6.11126E-04) 5.7760E-02(6.23864E-03)$^\dagger$ 5.6970E-02(3.73031E-03)$^\dagger$ $\underline{3.4634\text{E}-02{{(8.44098\text{E}-03)}^{\dagger }}}$ 2.0364E-01(2.87587E-03)$^\dagger$ 7.0914E-02(1.34050E-02)$^\dagger$ 8 4.8683E-02(4.12569E-03) $\underline{5.3952\text{E}-02{{(4.32586\text{E}-03)}^{\dagger }}}$ 1.0139E-01(5.95976E-03)$^\dagger$ 1.3747E-01(3.12555E-02)$^\dagger$ 2.2976E-01(2.27175E-03) $^\dagger$ 1.0419E-01(1.47761E-02)$^\dagger$ 10 5.4205E-02(5.08366E-03) $\underline{6.0848\text{E}-02{{(6.67483\text{E}-03)}^{\dagger }}}$ 1.1183E-01(7.60976E-03) $^\dagger$ 1.7080E-01(2.86372E-02) $^\dagger$ 2.3387E-01(1.92825E-03)$^\dagger$ 1.5273E-01(1.37459E-02)$^\dagger$ DTLZ6 3 3.1665E-03(2.76698E-03) 5.2588E-03(4.90865E-04) $^\dagger$ $\underline{3.3264\text{E}-03{{(1.61298\text{E}-03)}^{\dagger }}}$ 5.1275E-03(3.55167E-03) $^\dagger$ 2.0425E-01(4.49689E-03) $^\dagger$ 9.8696E-03(7.13856E-03) $^\dagger$ 4 4.2131E-02(5.62475E-03) 1.1064E-01(9.59272E-03) $^\dagger$ 2.5454E-02(9.72852E-03) $^\dagger$ 1.4171E-01(2.38262E-02) $^\dagger$ 3.3404E-01(7.50779E-03) $^\dagger$ 1.6955E-01(2.03052E-02) $^\dagger$ 5 1.5250E-02(1.92197E-03) 1.5048E-01(5.64830E-03) $^\dagger$ $\underline{9.3128\text{E}-02{{(5.99215\text{E}-02)}^{\dagger }}}$ 2.9541E-01(2.07511E-02) $^\dagger$ 4.9366E-01(1.37175E-02) $^\dagger$ 6.8704E-01(2.20882E-02) $^\dagger$ 6 1.3164E-02(1.52962E-03) $\underline{2.5553\text{E}-01{{(2.02566\text{E}-02)}^{\dagger }}}$ 3.3090E-02(1.30923E-01) $^\dagger$ 3.3130E-01(3.18902E-02) $^\dagger$ 5.5517E-01(1.51144E-02) $^\dagger$ 8.7899E-01(1.26348E-03) $^\dagger$ 8 1.3972E-02(1.16462E-03) $\underline{2.9568\text{E}-01{{(1.46263\text{E}-01)}^{\dagger }}}$ 7.6863E-01(1.65607E-02)$^\dagger$ 8.8443E-01(6.83775E-02)$^\dagger$ 3.2865E+00(4.21908E-01)$^\dagger$ 9.6881E+00(9.73209E-01)$^\dagger$ 10 1.6102E-02(9.86460E-04) $\underline{3.4632\text{E}-01{{(2.74054\text{E}-01)}^{\dagger }}}$ 4.0319E-01(3.82174E-01)$^\dagger$ 7.4899E-01(5.44463E-02)$^\dagger$ 8.1216E-01(1.81888E-02)$^\dagger$ 7.6559E-01(3.71012E-02)$^\dagger$ DTLZ7 3 1.4269E-03(6.27153E-04) 6.9496E-04(3.51603E-05) 9.5260E-04(7.14402E-04) 2.2605E-03(1.09999E-03)$^\dagger$ 4.4358E-03(6.88598E-04)$^\dagger$ 2.6307E-03(9.13444E-04)$^\dagger$ 4 5.6080E-03(4.49695E-04) 2.3024E-03(5.55552E-04)$^\dagger$ 4.7689E-03(2.24499E-04) 1.4251E-02(5.16088E-03)$^\dagger$ 6.9670E-03(1.08085E-03)$^\dagger$ 5.4934E-03(1.15755E-03)$^\dagger$ 5 7.6494E-03(3.39809E-04) 3.3534E-03(1.06828E-03)$^\dagger$ 1.0717E-02(6.69624E-04) $^\dagger$ 8.3798E-02(2.79588E-02)$^\dagger$ 1.0825E-02(3.33610E-03)$^\dagger$ 2.0268E-02(5.51018E-03)$^\dagger$ 6 1.6013E-02(6.62155E-04) 4.6055E-03(1.70038E-03) 1.1947E-02(4.76109E-04)$^\dagger$ 1.7956E-01(4.96227E-02)$^\dagger$ 2.4724E-02(1.41937E-02) $^\dagger$ 9.1749E-02(3.63369E-02)$^\dagger$ 8 2.1716E-02(3.75157E-04) 1.4274E-02(1.09412E-02)$^\dagger$ 2.6989E-02(1.56032E-03)$^\dagger$ 3.3977E-01(7.68451E-02)$^\dagger$ 2.0888E-01(1.13986E-01)$^\dagger$ 9.5229E-01(2.31546E-01)$^\dagger$ 10 4.8018E-02(2.56958E-03) 1.5505E-02(1.25040E-02)$^\dagger$ 4.9859E-02(2.27362E-03)$^\dagger$ 6.6739E-01(1.39620E-01)$^\dagger$ 6.5667E-01(2.37870E-01)$^\dagger$ 2.6579E+00(4.98006E-01)$^\dagger$
下载: 导出CSV
-
[1] 郭观七, 尹呈, 曾文静, 李武, 严太山.基于等价分量交叉相似性的Pareto支配性预测.自动化学报, 2014, 40(1):33-40 http://www.aas.net.cn/CN/abstract/abstract18264.shtmlGuo Guan-Qi, Yin Cheng, Zeng Wen-Jing, Li Wu, Yan Tai-Shan. Prediction of Pareto dominance by cross similarity of equivalent components. Acta Automatica Sinica, 2014, 40(1):33-40 http://www.aas.net.cn/CN/abstract/abstract18264.shtml [2] Purshouse R C, Fleming P J. On the evolutionary optimization of many conflicting objectives. IEEE Transactions on Evolutionary Computation, 2007, 11(6):770-784 doi: 10.1109/TEVC.2007.910138 [3] Li M Q, Yang S X, Liu X H. Shift-based density estimation for Pareto-based algorithms in many-objective optimization. IEEE Transactions on Evolutionary Computation, 2014, 18(3):348-365 doi: 10.1109/TEVC.2013.2262178 [4] 陈振兴, 严宣辉, 吴坤安, 白猛.融合张角拥挤控制策略的高维多目标优化.自动化学报, 2015, 41(6):1145-1158 http://www.aas.net.cn/CN/abstract/abstract18689.shtmlChen Zhen-Xing, Yan Xuan-Hui, Wu Kun-An, Bai Meng. Many-objective optimization integrating open angle based congestion control strategy. Acta Automatica Sinica, 2015, 41(6):1145-1158 http://www.aas.net.cn/CN/abstract/abstract18689.shtml [5] Li M Q, Yang S X, Zheng J H, Liu X H. ETEA:a euclidean minimum spanning tree-based evolutionary algorithm for multiobjective optimization. Evolutionary Computation, 2014, 22(2):189-230 doi: 10.1162/EVCO_a_00106 [6] Ikeda K, Kita H, Kobayashi S. Failure of Pareto-based MOEAs: Does non-dominated really mean near to optimal? In: Proceedings of the 2001 IEEE Congress on Evolutionary Computation. Seoul, South Korea: IEEE, 2001. 957-962 [7] Li M Q, Yang S X, Liu X H. Bi-goal evolution for many-objective optimization problems. Artificial Intelligence, 2015, 228:45-65 doi: 10.1016/j.artint.2015.06.007 [8] Deb K, Mohan M, Mishra S. Evaluating the ε-domination based multi-objective evolutionary algorithm for a quick computation of Pareto-optimal solutions. Evolutionary Computation, 2005, 13(4):501-525 doi: 10.1162/106365605774666895 [9] Sato H, Aguirre H E, Tanaka K. Controlling dominance area of solutions and its impact on the performance of MOEAs. In: Proceedings of the 2007 International Conference on Evolutionary Multi-Criterion Optimization. Berlin: Springer, 2007. 5-20 [10] Wang G P, Jiang H W. Fuzzy-dominance and its application in evolutionary many objective optimization. In: Proceedings of the International Conference on Computational Intelligence and Security Workshops (CISW 2007). Washington, D. C., USA: IEEE, 2007. 195-198 [11] Zitzler E, Künzli S. Indicator-based selection in multiobjective search. In: Proceedings of the 8th International Conference on Parallel Problem Solving from Nature. Birmingham, UK: Springer, 2004. 832-842 [12] Beume N, Naujoks B, Emmerich M. SMS-EMOA:multiobjective selection based on dominated hypervolume. European Journal of Operational Research, 2007, 181(3):1653-1669 doi: 10.1016/j.ejor.2006.08.008 [13] Hughes E J. Multiple single objective Pareto sampling. In: Proceedings of the 2003 IEEE Congress on Evolutionary Computation. Canberra, Australia: IEEE, 2003. 2678-2684 [14] Zhang Q F, Li H. MOEA/D:A multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 2007, 11(6):712-731 doi: 10.1109/TEVC.2007.892759 [15] Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach, Part Ⅰ:solving problems with box constraints. IEEE Transactions on Evolutionary Computation, 2014, 18(4):577-601 doi: 10.1109/TEVC.2013.2281535 [16] 巩敦卫, 刘益萍, 孙晓燕, 韩玉艳.基于目标分解的高维多目标并行进化优化方法.自动化学报, 2015, 41(8):1438-1451 http://www.aas.net.cn/CN/abstract/abstract18718.shtmlGong Dun-Wei, Liu Yi-Ping, Sun Xiao-Yan, Han Yu-Yan. Parallel Many-objective evolutionary optimization using objectives decomposition. Acta Automatica Sinica, 2015, 41(8):1438-1451 http://www.aas.net.cn/CN/abstract/abstract18718.shtml [17] Adra S F, Fleming P J. A diversity management operator for evolutionary many-objective optimisation. In: Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization. Nantes, France: Springer, 2009. 81-94 [18] Yang S X, Li M Q, Liu X H, Zheng J H. A grid-based evolutionary algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2013, 17(5):721-736 doi: 10.1109/TEVC.2012.2227145 [19] Deb K, Thiele L, Laumanns M, Zitzler E. Scalable test problems for evolutionary multiobjective optimization. Evolutionary Multiobjective Optimization. In: Proceedings of the Advanced Information and Knowledge Processing. Berlin, Germany: Springer, 2005. 105-145 [20] Deb A, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ. IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197 doi: 10.1109/4235.996017 [21] van Veldhuizen D A, Lamont G B. Evolutionary computation and convergence to a pareto front. In: Proceedings of the Late Breaking Papers at the Genetic Programming 1998 Conference. Stanford University, California, USA: Citeseer, 1998. 221-228 [22] Zheng J H, Li M Q. A diversity metric for MOEAs. In: Proceedings of 7th International Conference on Optimization: Techniques and Applications. Kobe, Japan, 2007. 451-452 [23] Kung H T, Luccio F, Preparata F P. On finding the maxima of a set of vectors. Journal of the ACM (JACM), 1975, 22(4):469-476 doi: 10.1145/321906.321910 [24] Deb K, Jain S. Running performance metrics for evolutionary multi-objective optimization. Technical Report Kangal Report No. 2002004, Indian Institute of Technology, 2002 [25] Bosman P A N, Thierens D. The balance between proximity and diversity in multi-objective evolutionary algorithms. IEEE Transactions on Evolutionary Computation, 2003, 7(2):174-188 doi: 10.1109/TEVC.2003.810761 [26] Shen R M, Zheng J H, Li M Q, Zou J. Many-objective optimization based on information separation and neighbor punishment selection. Soft Computing, 2015, 21(5):1109-1128 [27] Inselberg A. The plane with parallel coordinates. The Visual Computer, 1985, 1(2):69-91 doi: 10.1007/BF01898350 [28] Inselberg A, Dimsdale B. Parallel coordinates: a tool for visualizing multi-dimensional geometry. In: Proceedings of the 1st IEEE Conference on Visualization. San Francisco, California, USA: IEEE, 1990. 361-378 -
图(8) / 表(8)
计量
- 文章访问数: 3697
- HTML全文浏览量: 282
- PDF下载量: 951
- 被引次数: 0
