-
摘要: 目前大部分受限玻尔兹曼机(Restricted Boltzmann machines, RBMs)训练算法都是以多步Gibbs采样为基础的采样算法. 本文针对多步Gibbs采样过程中出现的采样发散和训练速度过慢的问题,首先, 对问题进行实验描述,给出了问题的具体形式; 然后, 从马尔科夫采样的角度对多步Gibbs采样的收敛性质进行了理论分析, 证明了多步Gibbs采样在受限玻尔兹曼机训练初期较差的收敛性质是造成采样发散和训练速度过慢的主要原因; 最后, 提出了动态Gibbs采样算法,给出了对比仿真实验.实验结果表明, 动态Gibbs采样算法可以有效地克服采样发散的问题,并且能够以微小的运行时间为代价获得更高的训练精度.Abstract: Currently, most algorithms for training restricted Boltzmann machines (RBMs) are based on the multi-step Gibbs sampling. This article focuses on the problems of sampling divergence and the low training speed associated with the multi-step Gibbs sampling process. Firstly, these problems are illustrated and described by experiments. Then, the convergence property of the Gibbs sampling procedure is theoretically analyzed from the prospective of the Markov sampling. It is proved that the poor convergence property of the multi-step Gibbs sampling is the main cause of the sampling divergence and the low training speed when training an RBM. Furthermore, a new dynamic Gibbs sampling algorithm is proposed and its simulation results are given. It has been demonstrated that the dynamic Gibbs sampling algorithm can effectively tackle the issue of sampling divergence and can achieve a higher training accuracy at a reasonable expense of computation time.
-
Key words:
- Restricted Boltzmann machine (RBM) /
- Gibbs sampling /
- sampling algorithm /
- Markov theory
-
图 15 采样误差局部放大图
Fig. 15 Local enlarged drawing of reconstruction error in initial phase
图 16 CD_1000 采样误差局部放大图
Fig. 16 Local enlarged drawing of reconstruction error in later stage
图 18 训练初期局部放大图
Fig. 18 Local enlarged drawing of reconstruction error in initial phase
表 1 网络参数初值
Table 1 Initial value of parameters
网络参数 初始值 a zeros(1, 784) b zeros(1, 500) w 0.1 × randn(784, 500) η 0.1 
下载: 导出CSV
表 2 实验分组
Table 2 Experimental grouping
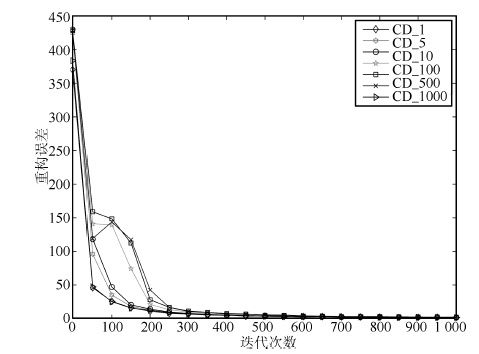
数据集 算法 迭代次数 MNIST CD_1 1000 MNIST CD_5 1000 MNIST CD_10 1000 MNIST CD_100 1000 MNIST CD_500 1000 MNIST CD_1000 1000
下载: 导出CSV
表 3 实验分组
Table 3 Experimental grouping
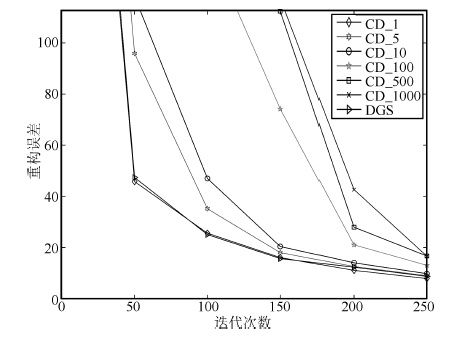
数据集 训练算法 Iter MNIST CD_1 1000 MNIST CD_5 1000 MNIST CD_10 1000 MNIST CD_100 1000 MNIST CD_500 1000 MNIST CD_1000 1000 MNIST DGS 1000
下载: 导出CSV
表 4 网络参数初值
Table 4 Initial values of parameters
算法参数 CD_k DGS a zeros(1,784) zeros(1,784) b zeros(1,500) zeros(1,500) w 0.1 × randn(784,500) 0.1 × randn(784,500) η 0.1 0.1 V 784 784 H 500 500
下载: 导出CSV
表 5 DGS 迭代策略
Table 5 Iterative strategy of DGS
M Gibbs_N (1:m1) = (1:300) Gibbs_N1 = 1 (m1:m2) = (300:900) Gibbs_N2 = 5 (m2:Iter) = (900:1000) Gibbs_N3 = 10
下载: 导出CSV
-
[1] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504-507 [2] Le Roux N, Heess N, Shotton J, Winn J. Learning a generative model of images by factoring appearance and shape. Neural Computation, 2011, 23(3): 593-650 [3] 苏连成,朱枫. 一种新的全向立体视觉系统的设计. 自动化学报, 2006, 32(1): 67-72Su Lian-Cheng, Zhu Feng. Design of a novel omnidirectional stereo vision system. Acta Automatica Sinica, 2006, 32(1): 67-72 [4] Bengio Y. Learning deep architectures for AI. Foundations and Trends® in Machine Learning, 2009, 2(1): 1-127 [5] Deng L, Abdel-Hamid O, Yu D. A deep convolutional neural network using heterogeneous pooling for trading acoustic invariance with phonetic confusion. In: Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Vancouver, BC: IEEE, 2013. 6669-6673 [6] Deng L. Design and learning of output representations for speech recognition. In: Proceedings of the Neural Information Processing Systems (NIPS) Workshop on Learning Output Representations[Online], available: http://research.microsoft.com/apps/pubs/default.aspx?id=204702, July 14, 2015 [7] Chet C C, Eswaran C. Reconstruction and recognition of face and digit images using autoencoders. Neural Computing and Applications, 2010, 19(7): 1069-1079 [8] Deng L, Hinton G, Kingsbury B. New types of deep neural network learning for speech recognition and related applications: an overview. In: Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Vancouver, BC: IEEE, 2013. 8599-8603 [9] Erhan D, Courville A, Bengio Y, Vincent P. Why does unsupervised pre-training help deep learning? In: Proceedings of the 13th International Conference on Artificial Intelligence and Statistics (AISTATS 2010). Sardinia, Italy, 2010. 201-208 [10] Salakhutdinov R, Hinton G. Deep Boltzmann machines. In: Proceedings of the 12th International Conference on Artificial Intelligence and Statistics (AISTATS 2009). Florida, USA, 2009. 448-455 [11] Swersky K, Chen B, Marlin B, de Freitas N. A tutorial on stochastic approximation algorithms for training restricted Boltzmann machines and deep belief nets. In: Proceedings of the 2010 Information Theory and Applications Workshop (ITA). San Diego, CA: IEEE, 2010. 1-10 [12] Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets. Neural Computation, 2006, 18(7): 1527-1554 [13] Fischer A, Igel C. Bounding the bias of contrastive divergence learning. Neural Computation, 2011, 23(3): 664-673 [14] Tieleman T. Training restricted Boltzmann machines using approximations to the likelihood gradient. In: Proceedings of the 25th International Conference on Machine Learning (ICML). New York: ACM, 2008. 1064-1071 [15] Tieleman T, Hinton G E. Using fast weights to improve persistent contrastive divergence. In: Proceedings of the 26th Annual International Conference on Machine Learning (ICML). New York: ACM, 2009. 1033-1040 [16] Sutskever I, Tieleman T. On the convergence properties of contrastive divergence. In: Proceedings of the 13th International Conference on Artificial Intelligence and Statistics (AISTATS 2010). Sardinia, Italy, 2010. 789-795 [17] Fischer A, Igel C. Parallel tempering, importance sampling, and restricted Boltzmann machines. In: Proceedings of 5th Workshop on Theory of Randomized Search Heuristics (ThRaSH),[Online], available: http://www.imm.dtu.dk/projects/thrash-workshop/schedule.php, August 20, 2015 [18] Desjardins G, Courville A, Bengio Y. Adaptive parallel tempering for stochastic maximum likelihood learning of RBMs. In: Proceedings of NIPS 2010 Workshop on Deep Learning and Unsupervised Feature Learning. Granada, Spain, 2010. [19] Cho K, Raiko T, Ilin A. Parallel tempering is efficient for learning restricted Boltzmann machines. In: Proceedings of the WCCI 2010 IEEE World Congress on Computational Intelligence. Barcelona, Spain: IEEE, 2010. 3246-3253 [20] Brakel P, Dieleman S, Schrauwen B. Training restricted Boltzmann machines with multi-tempering: harnessing parallelization. In: Proceedings of the 22nd International Conference on Artificial Neural Networks. Lausanne, Switzerland: Springer, 2012. 92-99 [21] Desjardins G, Courville A, Bengio Y, Vincent P, Delalleau O. Tempered Markov chain Monte Carlo for training of restricted Boltzmann machines. In: Proceedings of the 13th International Conference on Artificial Intelligence and Statistics (AISTATS 2010). Sardinia, Italy, 2010. 145-152 [22] Fischer A, Igel C. Training restricted Boltzmann machines: an introduction. Pattern Recognition, 2014, 47(1): 25-39 [23] Hinton G E. A practical guide to training restricted Boltzmann machines. Neural Networks: Tricks of the Trade (2nd Edition). Berlin Heidelberg: Springer, 2012. 599-619 -
图(29) / 表(5)
计量
- 文章访问数: 2143
- HTML全文浏览量: 409
- PDF下载量: 1546
- 被引次数: 0
