萤火虫算法智能优化粒子滤波

田梦楚; 薄煜明; 陈志敏; 吴盘龙; 赵高鹏

doi:10.16383/j.aas.2016.c150221

萤火虫算法智能优化粒子滤波

doi: 10.16383/j.aas.2016.c150221

田梦楚^1,,
薄煜明^1,,
陈志敏^1,2, ,,
吴盘龙^1,,
赵高鹏^1,

1.
南京理工大学自动化学院南京 210094
2.
中国卫星海上测控部江阴 214431

基金项目:

国防重点预研资助项目 40405070102

国家自然科学基金 61501521, U1330133, 61473153, 61403421, 61203266

详细信息

作者简介:
田梦楚南京理工大学自动化学院博士研究生.主要研究方向为目标跟踪和智能优化算法.E-mail:tianmengchu@163.com

薄煜明南京理工大学自动化学院教授.主要研究方向为控制理论与应用和智能优化算法.E-mail:byming65@126.com

吴盘龙南京理工大学自动化学院副教授.主要研究方向为多传感器信息融合和目标跟踪.E-mail:lxxwpl@hotmail.com

赵高鹏南京理工大学自动化学院讲师.主要研究方向为信息融合和智能控制.E-mail:zhaogaopeng@sina.com

通讯作者:
陈志敏中国卫星海上测控部博士后.主要研究方向为目标跟踪,控制理论与应用,智能优化算法.本文通信作者.E-mail:chenzhimin@188.com

计量
- 文章访问数: 3223
- HTML全文浏览量: 363
- PDF下载量: 1738
- 被引次数: 0
出版历程
- 收稿日期: 2015-04-13
- 录用日期: 2015-09-14
- 刊出日期: 2016-01-01

Firefly Algorithm Intelligence Optimized Particle Filter

1.
School of Automation, Nanjing University of Science and Technology, Nanjing 210094
2.
China Satellite Maritime Tracking and Controlling Department, Jiangyin 214431

Funds:

and Key Defense Advanced Research Project of China 40405070102

Supported by National Natural Science Foundation of China 61501521, U1330133, 61473153, 61403421, 61203266

More Information

Author Bio:
Ph.D. candidate at the School of Automation, Nanjing University of Science and Technology. Her research interest covers target tracking and intelligent optimization algorithm

Professor at the School of Automation, Nanjing University of Science and Technology. His research interest covers control theory and control applications, and intelligent optimization algorithm

Associate professor at the School of Automation, Nanjing University of Science and Technology. His research interest covers multi-sensor information fusion and target tracking

Lecturer at the School of Automation, Nanjing University of Science and Technology. His research interest covers information fusion and intelligent control

Corresponding author: CHEN Zhi-Min Postdoctor at China Satellite Maritime Tracking and Controlling Department. His research interest covers target tracking, control theory and control applications, and intelligent optimization algorithm. Corresponding author of this paper

摘要

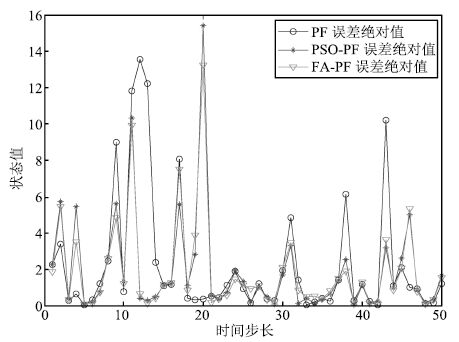
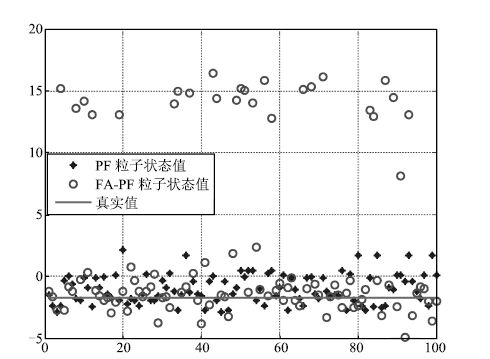
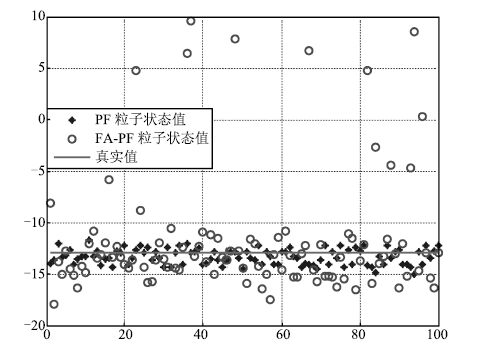
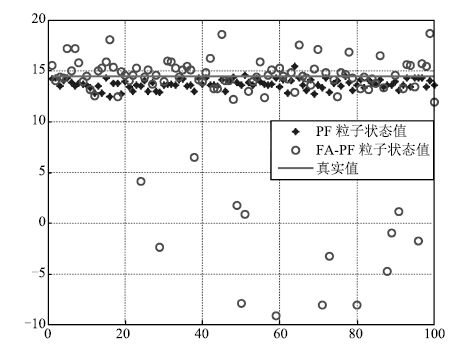
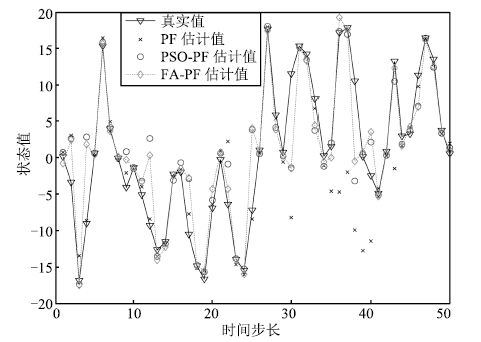
摘要: 针对粒子滤波(Particle filter, PF)重采样导致的粒子贫化以及需要大量粒子才能进行状态估计的问题,本文结合粒子滤波的运行机制,对萤火虫算法的寻优方式进行修正,设计了新的萤火虫位置更新公式和荧光亮度计算公式,并在此基础上提出了萤火虫算法智能优化粒子滤波.该方法引入了萤火虫群体的优胜劣汰机制以及萤火虫个体的吸引和移动的行为,使粒子群智能地向高似然区域移动,提高了粒子群的整体质量.实验表明该方法提高了粒子滤波的预测精度,同时大大降低了状态值预测所需的粒子数量.
- 粒子滤波 /
- 萤火虫算法 /
- 粒子贫化 /
- 状态估计
Abstract: Given the particle impoverishment due to particle filter(PF) resampling and given the need of a large number of particles for state estimate, the optimization mode of firefly algorithm is revised in combination with the operating mechanism of particle filter, and a new update formula of firefly position is designed as well. On this basis, an intelligent optimized particle filter of firefly algorithm is proposed. By means of firefly group's mechanism of survival of the fittest and individual firefly's attraction and movement behaviors, this algorithm enables the particle swarm to move toward the high likelihood region with the purpose of improving the total mass of particle swarm. The experiment has shown that the algorithm has upgraded the prediction accuracy of particle swarm and substantially reduced the quantity of the particles required by the prediction of state value.
- Particle filter(PF) /
- firefly algorithm /
- particle impoverishment /
- state estimation

HTML全文

图 1 滤波状态估计 (${N}=20$,$Q= 1$)

Fig. 1 State estimation of filter ($N= 20$,$Q= 1$)

下载: 全尺寸图片幻灯片

图 2 滤波误差绝对值 ($N= 20$,$Q= 1$)

Fig. 2 Absolute value of filter error ($N= 20$,$Q= 1$)

下载: 全尺寸图片幻灯片

图 3 滤波状态估计 ($N= 50$,$Q= 1$)

Fig. 3 State estimation of filter ($N= 50$,$Q= 1$)

下载: 全尺寸图片幻灯片

图 4 滤波误差绝对值 ($N= 50$,$Q= 1$)

Fig. 4 Absolute value of filter error ($N= 50$,$Q= 1$)

下载: 全尺寸图片幻灯片

图 5 滤波状态估计 ($N= 100$,$Q=1$)

Fig. 5 State estimation of filter ($N= 100$,$Q= 1$)

下载: 全尺寸图片幻灯片

图 6 滤波误差绝对值 ($N= 100$,$Q= 1$)

Fig. 6 Absolute value of filter error ($N= 100$,$Q= 1$)

下载: 全尺寸图片幻灯片

图 7 $k= 10$ 时粒子状态分布情况

Fig. 7 Particle distribution when $k= 10$

下载: 全尺寸图片幻灯片

图 8 $k= 25$ 时粒子状态分布情况

Fig. 8 Particle distribution when $k= 25$

下载: 全尺寸图片幻灯片

图 9 $k=$ 95 时粒子状态分布情况

Fig. 9 Particle distribution when $k=$ 95

下载: 全尺寸图片幻灯片

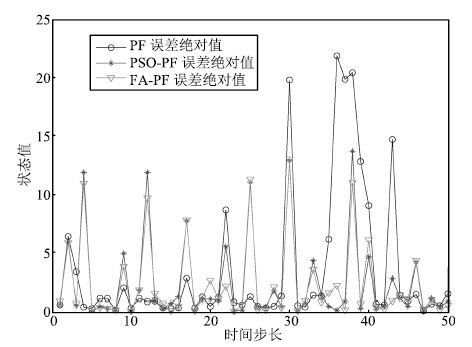
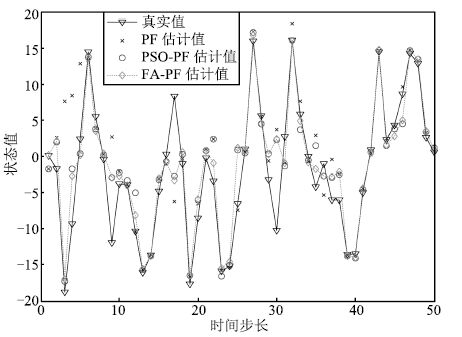
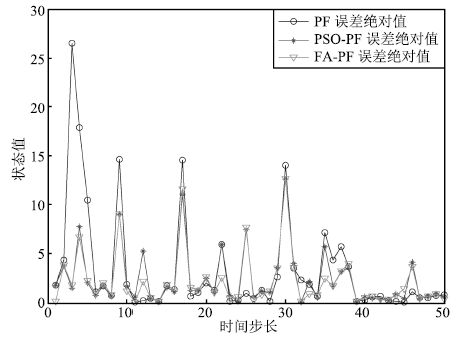
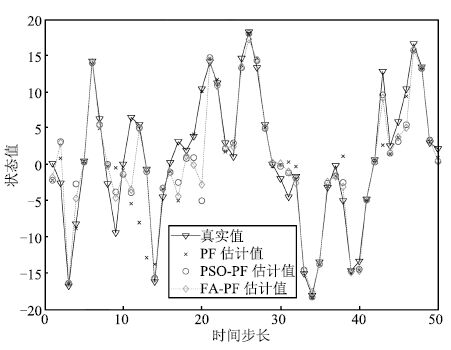
表 1 实验结果对比

Table 1 Comparison of simulation results

参数	PF	RMSE PSO-PF	FA-PF	PF	运算时间(s)PSO-PF	FA-PF
$N= 20,~ Q= 1$	6.5276	4.6309	4.2862	0.0928	0.1259	0.1108
$N= 50,~ Q= 1$	5.5987	4.2807	4.1067	0.1167	0.1492	0.1367
$N = 100,~ Q = 1$	4.7243	4.1109	4.0929	0.1245	0.1977	0.1674
$N = 20,~ Q = 1$0	7.8860	5.3516	5.0235	0.0947	0.1284	0.1162
$N = 50,~ Q = 1$0	6.2733	4.8920	4.7043	0.1150	0.1576	0.1425
$N = 100,~ Q = 1$0	5.3569	4.5583	4.5481	0.1233	0.2031	0.1739

下载: 导出CSV

参考文献(25)

[1]	Niknejad H T, Takeuchi A, Mita S, McAllester D. On-road multivehicle tracking using deformable object model and particle filter with improved likelihood estimation. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2):748-758 doi: 10.1109/TITS.2012.2187894
[2]	Li H W, Wang J. Particle filter for manoeuvring target tracking via passive radar measurements with glint noise. IET Radar, Sonar and Navigation, 2012, 6(3):180-189 doi: 10.1049/iet-rsn.2011.0075
[3]	Vasileios M, Panos S. Improved particle filters for multi-target tracking. Journal of Computational Physics, 2012, 231(2):602-611 doi: 10.1016/j.jcp.2011.09.023
[4]	刘亚雷, 顾晓辉. 确定性核粒子群的粒子滤波跟踪算法及其CRLB推导. 控制与决策, 2012, 27(5):741-746 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201205020.htm Liu Ya-Lei, Gu Xiao-Hui. Deterministic core particle swarm and derivation of CRLB in particle filter tracking algorithm. Control and Decision, 2012, 27(5):741-746 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201205020.htm
[5]	Du M, Nan X M, Guan L. Monocular human motion tracking by using DE-MC particle filter. IEEE Transactions on Image Processing, 2013, 22(10):3852-3865 doi: 10.1109/TIP.2013.2263146
[6]	王伟, 余玉揆. 多点测试的多模型机动目标跟踪算法. 自动化学报, 2015, 41(6):1201-1212 http://www.aas.net.cn/CN/abstract/abstract18694.shtml Wang Wei, Yu Yu-Kui. Multi-try and multi-model particle filter for maneuvering target tracking. Acta Automatica Sinica, 2015, 41(6):1201-1212 http://www.aas.net.cn/CN/abstract/abstract18694.shtml
[7]	Foo P H, Ng G W. Combining the interacting multiple model method with particle filters for manoeuvring target tracking. IET Radar, Sonar and Navigation, 2011, 5(3):234-255 doi: 10.1049/iet-rsn.2009.0093
[8]	王晓, 韩崇昭. 基于混合采样的多模型机动目标跟踪算法. 自动化学报, 2013, 39(7):1152-1156 doi: 10.1016/S1874-1029(13)60069-5 Wang Xiao, Han Chong-Zhao. A multiple model particle filter for maneuvering target tracking based on composite sampling. Acta Automatica Sinica, 2013, 39(7):1152-1156 doi: 10.1016/S1874-1029(13)60069-5
[9]	张琪, 胡昌华, 乔玉坤. 基于权值选择的粒子滤波算法研究. 控制与决策, 2008, 23(1):117-120 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC200801026.htm Zhang Qi, Hu Chang-Hua, Qiao Yu-Kun. Particle filter algorithm based on weight selected. Control and Decision, 2008, 23(1):117-120 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC200801026.htm
[10]	Li T C, Sattar T P, Sun S D. Deterministic resampling:unbiased sampling to avoid sample impoverishment in particle filters. Signal Processing, 2012, 92(7):1637-1645 doi: 10.1016/j.sigpro.2011.12.019
[11]	Stano P M, Lendek Z, Babuška R. Saturated particle filter:almost sure convergence and improved resampling. Automatica, 2013, 49(1):147-159 doi: 10.1016/j.automatica.2012.10.006
[12]	Yu Y H, Zheng X Y. Particle filter with ant colony optimization for frequency offset estimation in OFDM systems with unknown noise distribution. Signal Processing, 2011, 91(5):1339-1342 doi: 10.1016/j.sigpro.2010.12.009
[13]	Zhong J, Fung Y F. Case study and proofs of ant colony optimisation improved particle filter algorithm. IET Control Theory and Applications, 2012, 6(5):689-697 doi: 10.1049/iet-cta.2010.0405
[14]	Xian W M, Long B, Li M, Wang H J. Prognostics of lithium-ion batteries based on the verhulst model, particle swarm optimization and particle filter. IEEE Transactions on Instrumentation and Measurement, 2013, 63(1):2-17 https://www.researchgate.net/publication/260303872_Prognostics_of_Lithium-Ion_Batteries_Based_on_the_Verhulst_Model_Particle_Swarm_Optimization_and_Particle_Filter
[15]	Park S, Hwang J P, Kim E, Kang H J. A new evolutionary particle filter for the prevention of sample impoverishment. IEEE Transactions on Evolutionary Computation, 2009, 13(4):801-809 doi: 10.1109/TEVC.2008.2011729
[16]	宋宇, 李庆玲, 康轶非, 闫德立. 平方根容积Rao-Blackwillised粒子滤波SLAM算法. 自动化学报, 2014, 40(2):357-367 http://www.aas.net.cn/CN/abstract/abstract18297.shtml Song Yu, Li Qing-Ling, Kang Yi-Fei, Yan De-Li. SLAM with square-root cubature Rao-Blackwillised particle filter. Acta Automatica Sinica, 2014, 40(2):357-367 http://www.aas.net.cn/CN/abstract/abstract18297.shtml
[17]	陈志敏, 薄煜明, 吴盘龙, 段文勇, 刘正凡. 基于自适应粒子群优化的新型粒子滤波在目标跟踪中的应用. 控制与决策, 2013, 28(2):193-200 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201302007.htm Chen Zhi-Min, Bo Yu-Ming, Wu Pan-Long, Duan Wen-Yong, Liu Zheng-Fan. Novel particle filter algorithm based on adaptive particle swarm optimization and its application to radar target tracking. Control and Decision, 2013, 28(2):193-200 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201302007.htm
[18]	Yang X S. Firefly algorithm, stochastic test functions and design optimisation. International Journal of Bio-Inspired Computation, 2010, 2(2):78-84 doi: 10.1504/IJBIC.2010.032124
[19]	朱文超, 许德章. 一种基于人工萤火虫群优化的改进粒子滤波算法. 计算机应用研究, 2014, 31(10):2920-2924 http://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ201410009.htm Zhu Wen-Chao, Xu De-Zhang. Improved particle filter algorithm based on artificial glowworm swarm optimization. Application Research of Computers, 2014, 31(10):2920-2924 http://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ201410009.htm
[20]	Lundquist C, Karlsson R, Ozkan E, Gustafsson F. Tire radii estimation using a marginalized particle filter. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(2):663-672 doi: 10.1109/TITS.2013.2284930
[21]	Horng M H. Vector quantization using the firefly algorithm for image compression. Expert Systems with Applications, 2012, 39(1):1078-1091 doi: 10.1016/j.eswa.2011.07.108
[22]	Krishnanand K N, Ghose D. Glowworm swarm based optimization algorithm for multimodal functions with collective robotics applications. Multiagent and Grid Systems, 2006, 2(3):209-222 doi: 10.3233/MGS-2006-2301
[23]	Yang X S, Deb S. Eagle strategy using lévy walk and firefly algorithms for stochastic optimization. Nature Inspired Cooperative Strategies for Optimization(NICSO 2010), Berlin Heidelberg:Springer, 2010. 101-111
[24]	Shan C F, Tan T N, Wei Y C. Real-time hand tracking using a mean shift embedded particle filter. Pattern Recognition, 2007, 40(7):1958-1970 doi: 10.1016/j.patcog.2006.12.012
[25]	方正, 佟国峰, 徐心和. 粒子群优化粒子滤波方法. 控制与决策, 2007, 27(3):273-277 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC200703006.htm Fang Zheng, Tong Guo-Feng, Xu Xin-He. Particle swarm optimized particle filter. Control and Decision, 2007, 22(3):273-277 http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC200703006.htm

施引文献

资源附件(0)

访问统计

图(9) / 表(1)

计量

文章访问数: 3223
HTML全文浏览量: 363
PDF下载量: 1738
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

萤火虫算法智能优化粒子滤波

doi: 10.16383/j.aas.2016.c150221

通讯作者:
陈志敏中国卫星海上测控部博士后.主要研究方向为目标跟踪,控制理论与应用,智能优化算法.本文通信作者.E-mail:chenzhimin@188.com

计量

Firefly Algorithm Intelligence Optimized Particle Filter

Corresponding author: CHEN Zhi-Min Postdoctor at China Satellite Maritime Tracking and Controlling Department. His research interest covers target tracking, control theory and control applications, and intelligent optimization algorithm. Corresponding author of this paper

计量

目录

留言板

萤火虫算法智能优化粒子滤波

doi: 10.16383/j.aas.2016.c150221

通讯作者: 陈志敏 中国卫星海上测控部博士后.主要研究方向为目标跟踪,控制理论与应用,智能优化算法.本文通信作者.E-mail:chenzhimin@188.com

计量

出版历程

Firefly Algorithm Intelligence Optimized Particle Filter

Corresponding author: CHEN Zhi-Min Postdoctor at China Satellite Maritime Tracking and Controlling Department. His research interest covers target tracking, control theory and control applications, and intelligent optimization algorithm. Corresponding author of this paper

计量

出版历程

目录

通讯作者:
陈志敏中国卫星海上测控部博士后.主要研究方向为目标跟踪,控制理论与应用,智能优化算法.本文通信作者.E-mail:chenzhimin@188.com