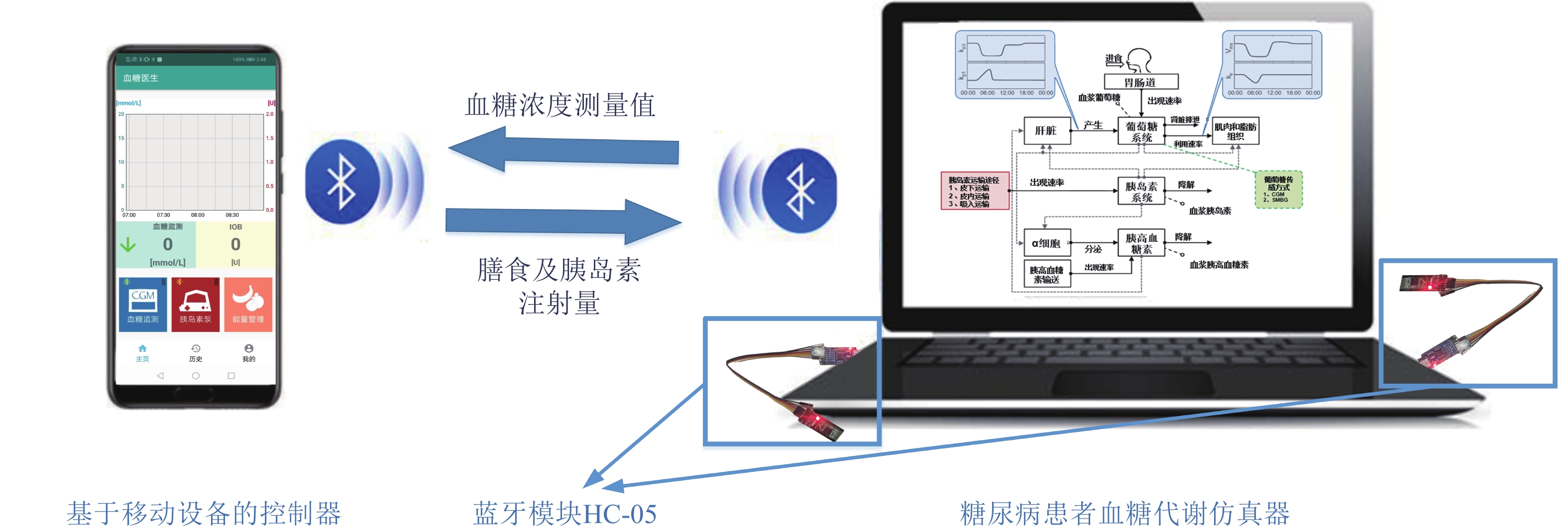
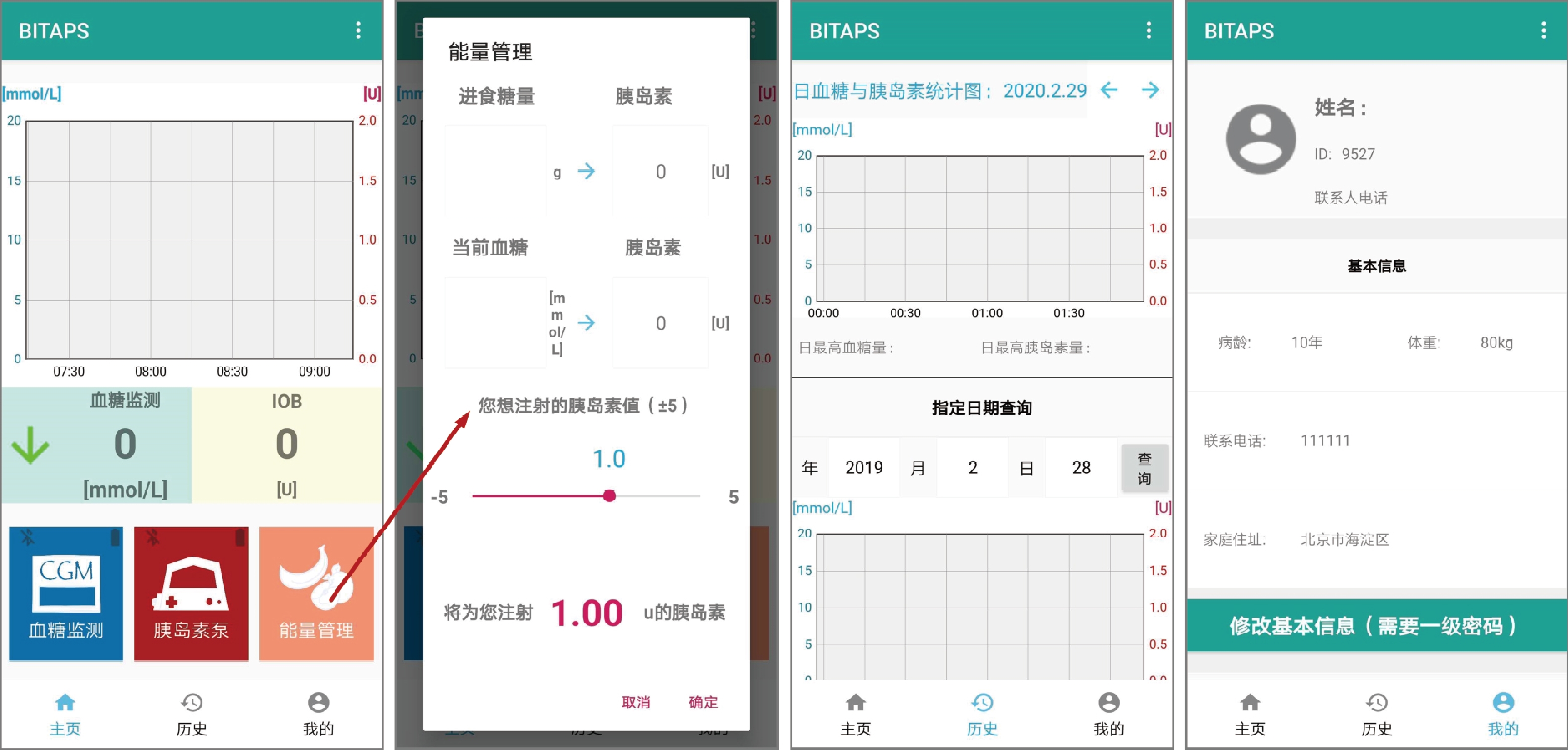
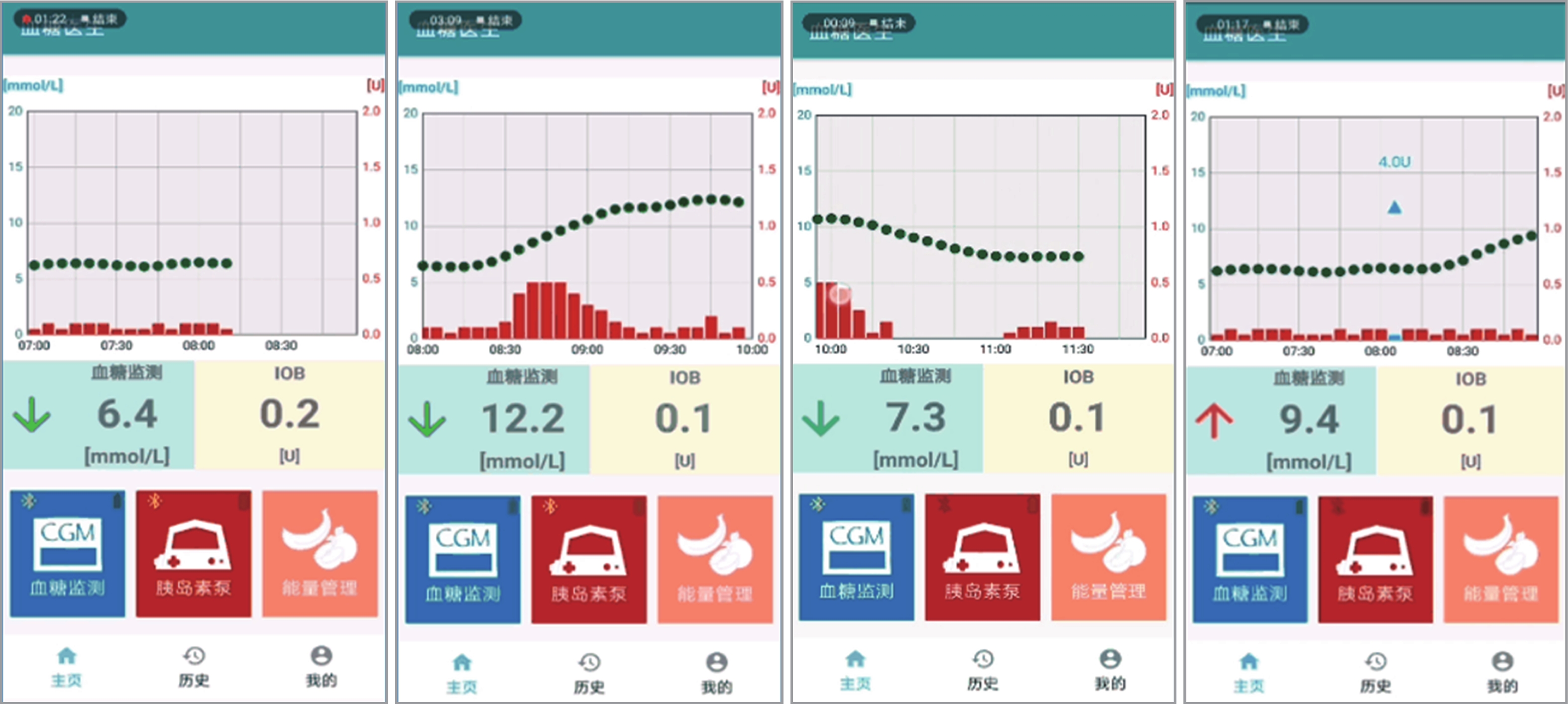
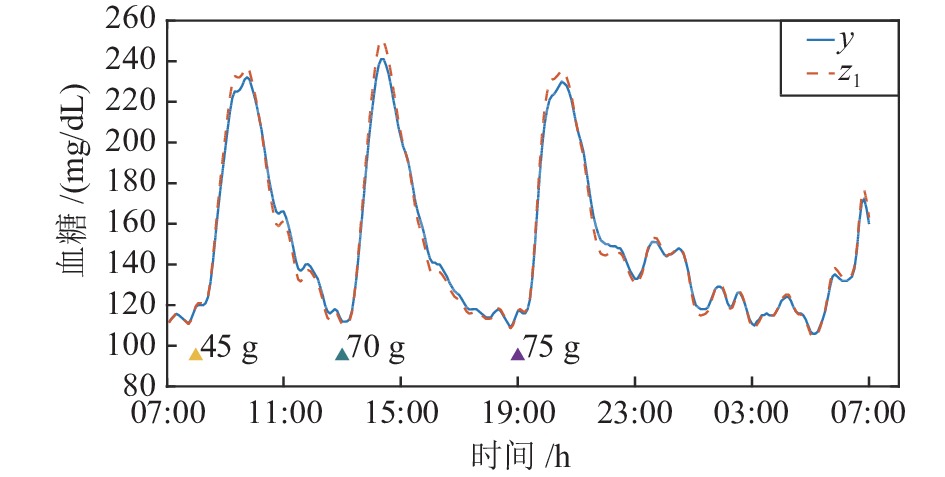
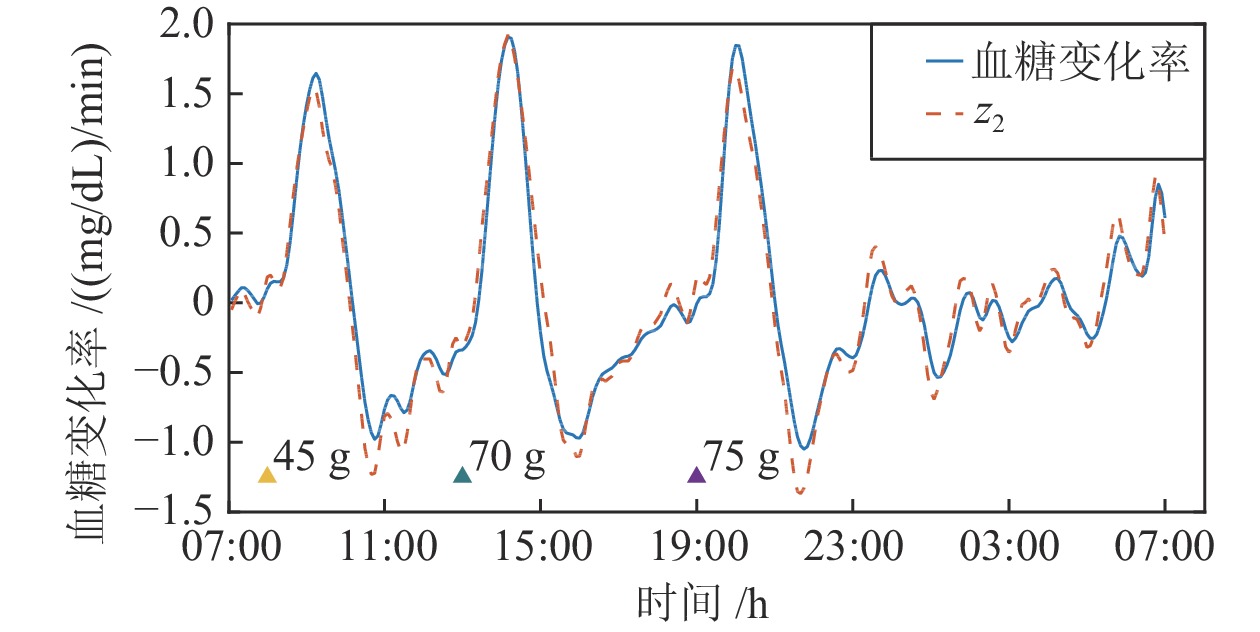
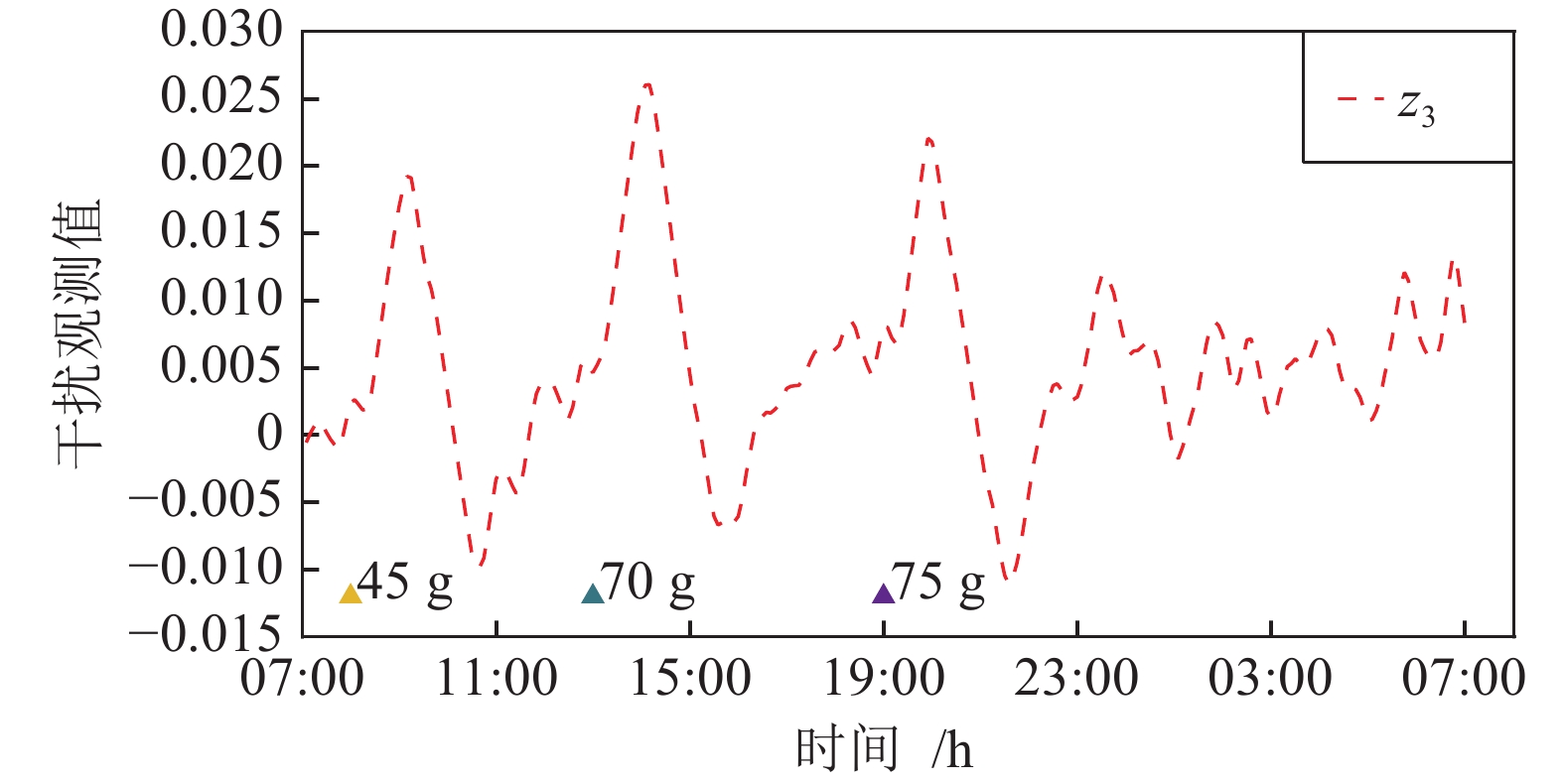
Active Disturbance Rejection Control for Artificial Pancreas System Based on Insulin Basal Rate Estimation
-
摘要:
胰岛素基础率是人工胰腺系统实现人体血糖闭环控制的基准, 但该变量在临床治疗中难以准确确定. 针对这一问题, 本文设计了一种基于胰岛素基础率动态估计的人工胰腺自抗扰控制方法, 通过扩张状态观测器(Extended state observer, ESO)实时估计血糖代谢过程中的内部与外界干扰, 构建具备参数自适应能力的反馈控制律和胰岛素注射安全约束, 实现血糖闭环调控能力的有效改善. 在此基础上, 本文设计了基于移动设备和蓝牙模块的人工胰腺软件系统, 并通过美国食品药品监督管理局(Food and Drug Administration, FDA)接受的UVA/Padova T1DM仿真平台完成算法的比较仿真与功能测试. 本文的工作将为后续人工胰腺临床试验的开展提供方法基础和技术支持, 也为我国糖尿病患者血糖管理的改善提供精准医学治疗手段.
Abstract:Insulin basal rate provides the reference for closed-loop blood glucose regulation using artificial pancreas systems, but this quantity is usually difficult to determine accurately in clinical practice. In this regard, this paper introduces an active disturbance rejection control method for artificial pancreas systems based on dynamic estimation of the basal rate. To enable improved glucose regulation, an extended state observer (ESO) is employed to estimate the internal and external disturbances in the glucose metabolic process, and a feedback control law and insulin infusion safety constraints that both incorporate parameter adaptation are proposed. Based on the proposed method, an artificial pancreas software system is designed for mobile devices with Bluetooth modules. The proposed results are evaluated through comparative simulations and functionality tests by using the US FDA (Food and Drug Administration)-accepted UVA/Padova T1DM simulator. The obtained results provide methodological and technical support for further clinical studies of artificial pancreas systems, and introduce a precision medicine solution to enhanced glucose management for Chinese patients with diabetes mellitus.
-
表 1 线性反馈参数设计
Table 1 Parameter design for linear feedback
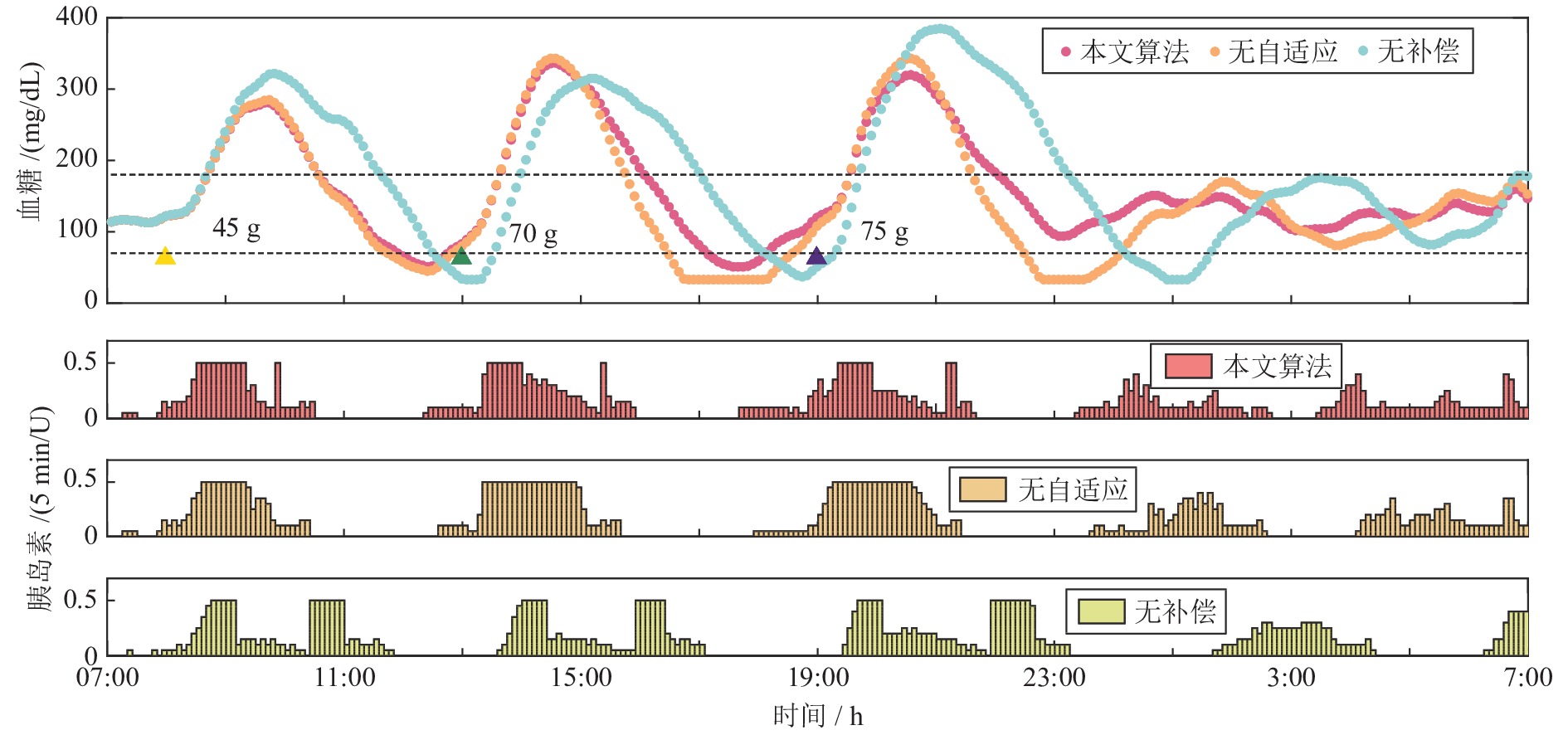
参数 血糖上升阶段 血糖下降阶段 ${y \le 275\;{\rm{mg/dL} } }$ ${ {y > 275}\;{\rm{mg/dL} } }$ k1(y) 0.0001 × exp(h) 0.00001 × exp(−h) 0.00015 × exp(h) k2(y) 0.002 × exp(h) 0.001 × exp(h) 0.002 × exp(h) k3 1 0.15 1 注: $h = (y - {G_r})/y$ 表 2 正常胰岛素基础率下本控制算法与zMPC控制算法的评估结果
Table 2 Evaluation results of the proposed controller and the zMPC controller at normal insulin basal rate
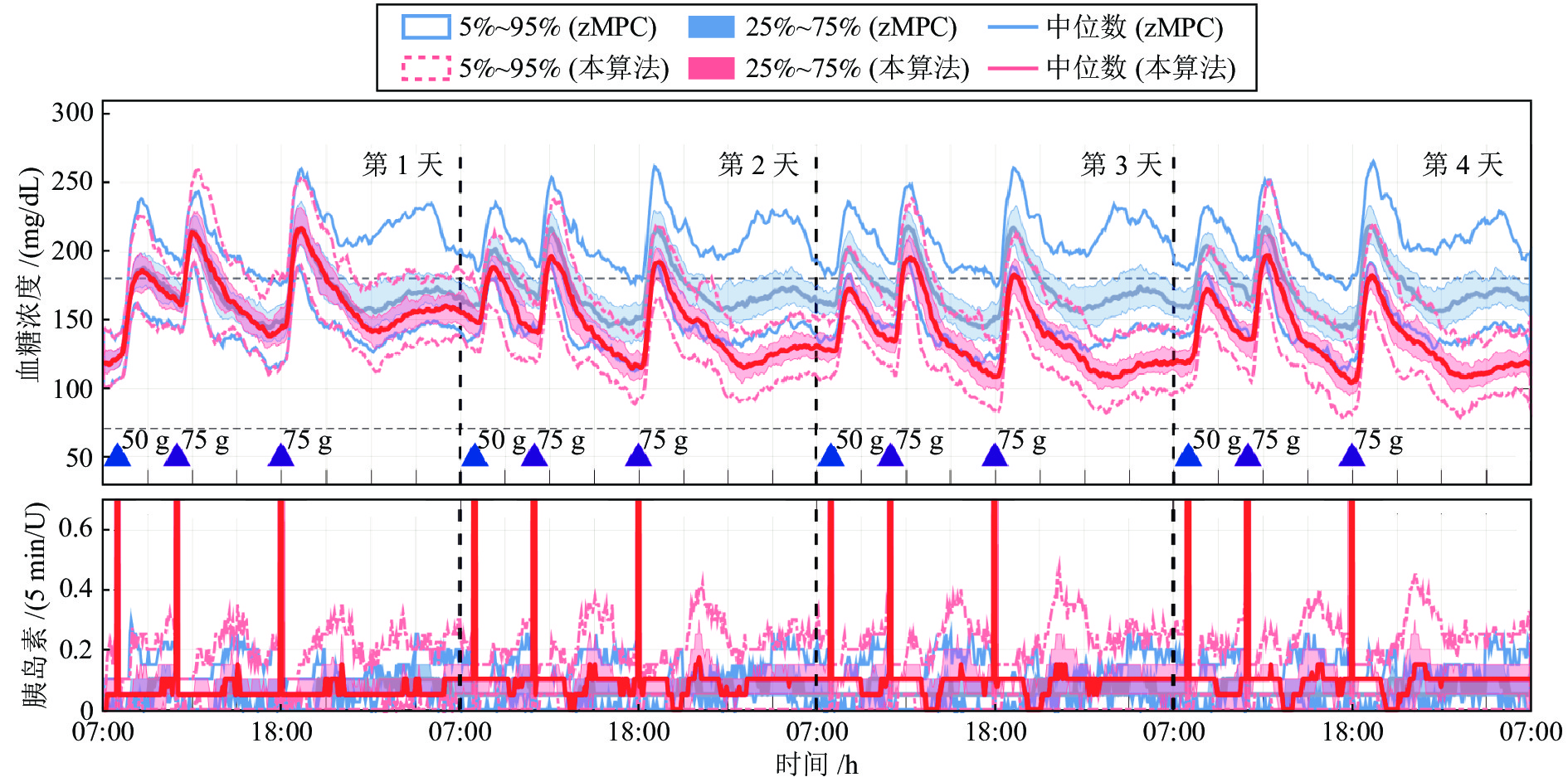
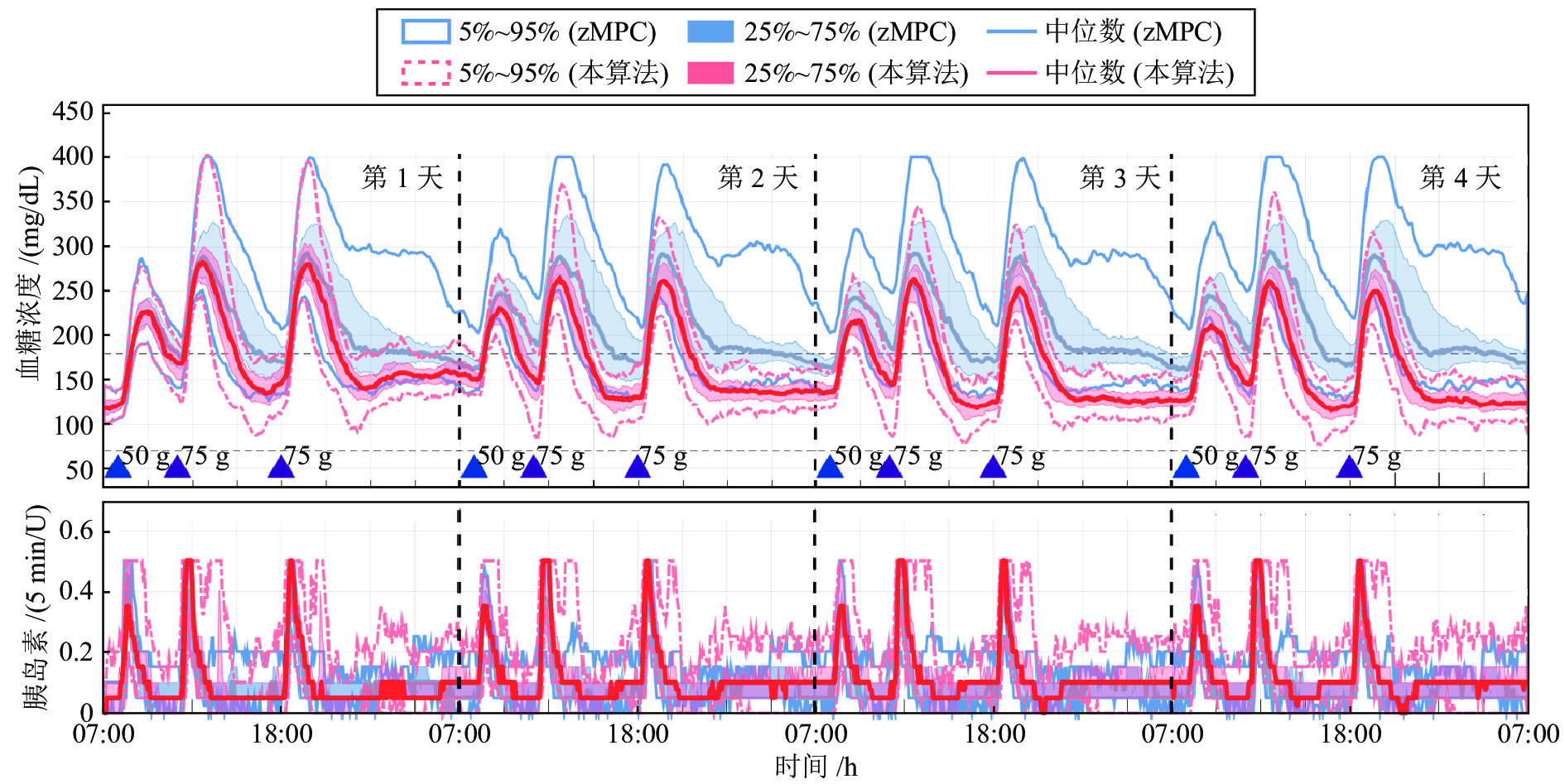
血糖控制性能指标 餐前补充大剂量胰岛素 餐前未补充大剂量胰岛素 zMPC 本算法 zMPC 本算法 < 54 mg/dL 时间比率 (%) 0 (0.0) 0 (0.0) 0 (0.0) 0 (0.0) < 70 mg/dL 时间比率 (%) 0 (0.0) 0 (0.0) 0 (0.0) 0 (0.0) 70 ~ 180 mg/dL 时间比率 (%) 92.4 (10.2) 92.5 (7.8) 72.4 (13.4) 71.8 (9.4) > 250 mg/dL 时间比率 (%) 0 (0.0) 0 (0.0) 1.2 (9.5) 2.5 (9.2) 血糖平均值 (mg/dL) 135.4 (6.1) 133.9 (6.4) 151.7 (19.9) 152.2 (13.9) 标准差 (mg/dL) 28.2 (8.2) 28.0 (4.9) 44.9 (14.1) 45.8 (14.6) 7:00 血糖平均值 (mg/dL) 121.0 (15.2) 116.0 (15.5) 121 (15.5) 118.7 (15.0) 注: 统计数据以中位数 (四分位距) 的形式表示. 表 4 2倍正常胰岛素基础率下本控制算法与zMPC控制算法的评估结果
Table 4 Evaluation results of the proposed controller and the zMPC controller at 2 times of normal insulin basal rate
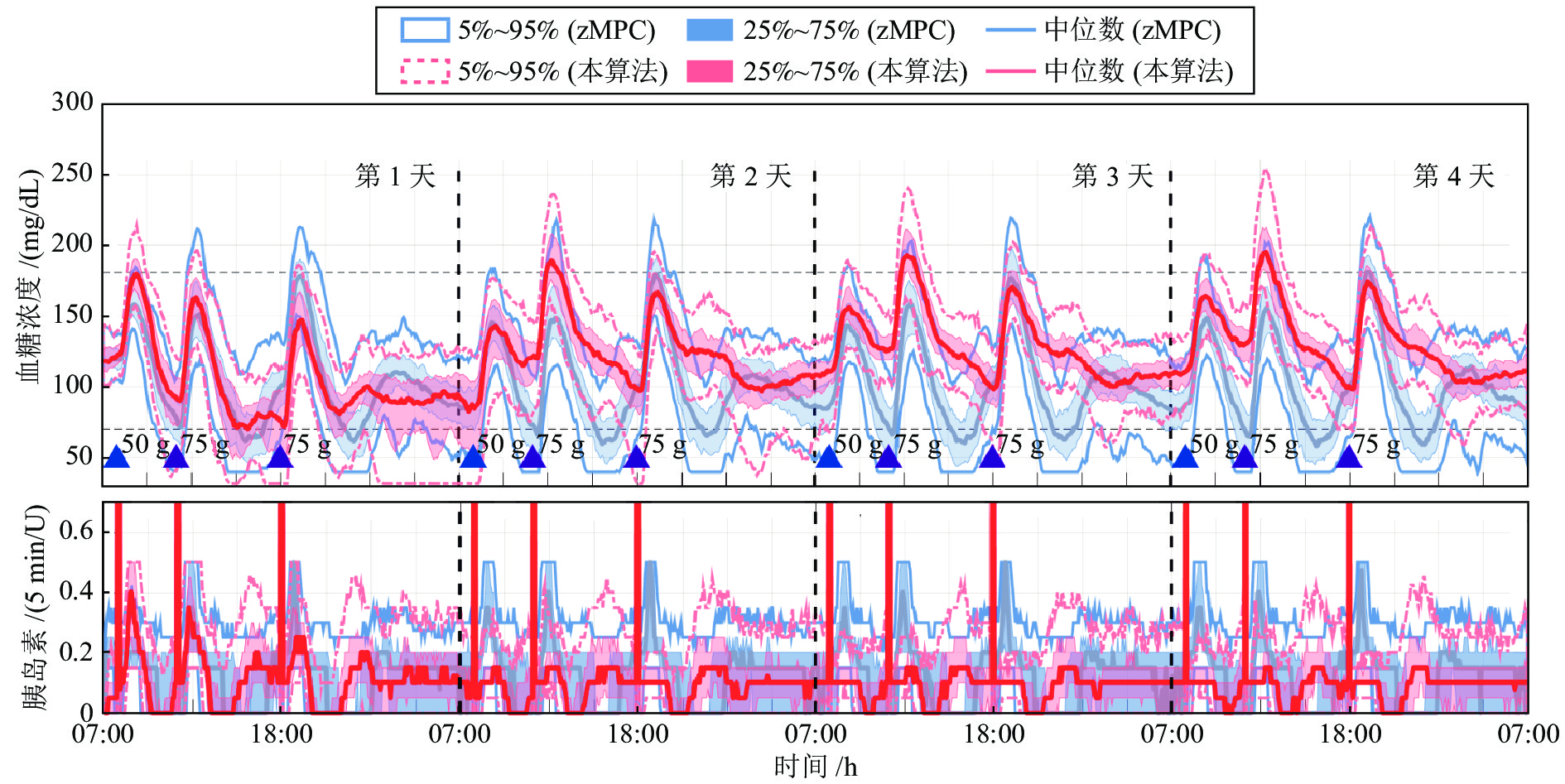
血糖控制性能指标 餐前补充大剂量胰岛素 餐前未补充大剂量胰岛素 zMPC 本算法 zMPC 本算法 < 54 mg/dL 时间比率 (%) 7.9 (10.0) 0 (0.0) 7.8 (10.9) 0 (0.0) < 70 mg/dL 时间比率 (%) 19.9 (9.3) 0 (0.8) 18.4 (9.2) 0 (0.0) 70 ~ 180 mg/dL 时间比率 (%) 77.4 (10.2) 93.4 (6.2) 67.8 (12.8) 74.4 (12.6) > 250 mg/dL 时间比率 (%) 0 (0.0) 0 (0.0) 0 (3.9) 2.2 (9.0) 血糖平均值 (mg/dL) 101.2 (6.2) 130.2 (6.8) 113.5 (14.4) 149.5 (11.9) 标准差 (mg/dL) 35.7 (6.8) 28.3 (5.8) 50.8 (11.0) 45.2 (14.1) 7:00 血糖平均值 (mg/dL) 83.0 (38.0) 111.0 (26.0) 78.5 (35.0) 113.0 (27.0) 注: 统计数据以中位数 (四分位距) 的形式表示. 表 3 0.5倍正常胰岛素基础率下本控制算法与zMPC控制算法的评估结果
Table 3 Evaluation results of the proposed controller and the zMPC controller at 0.5 times of normal insulin basal rate
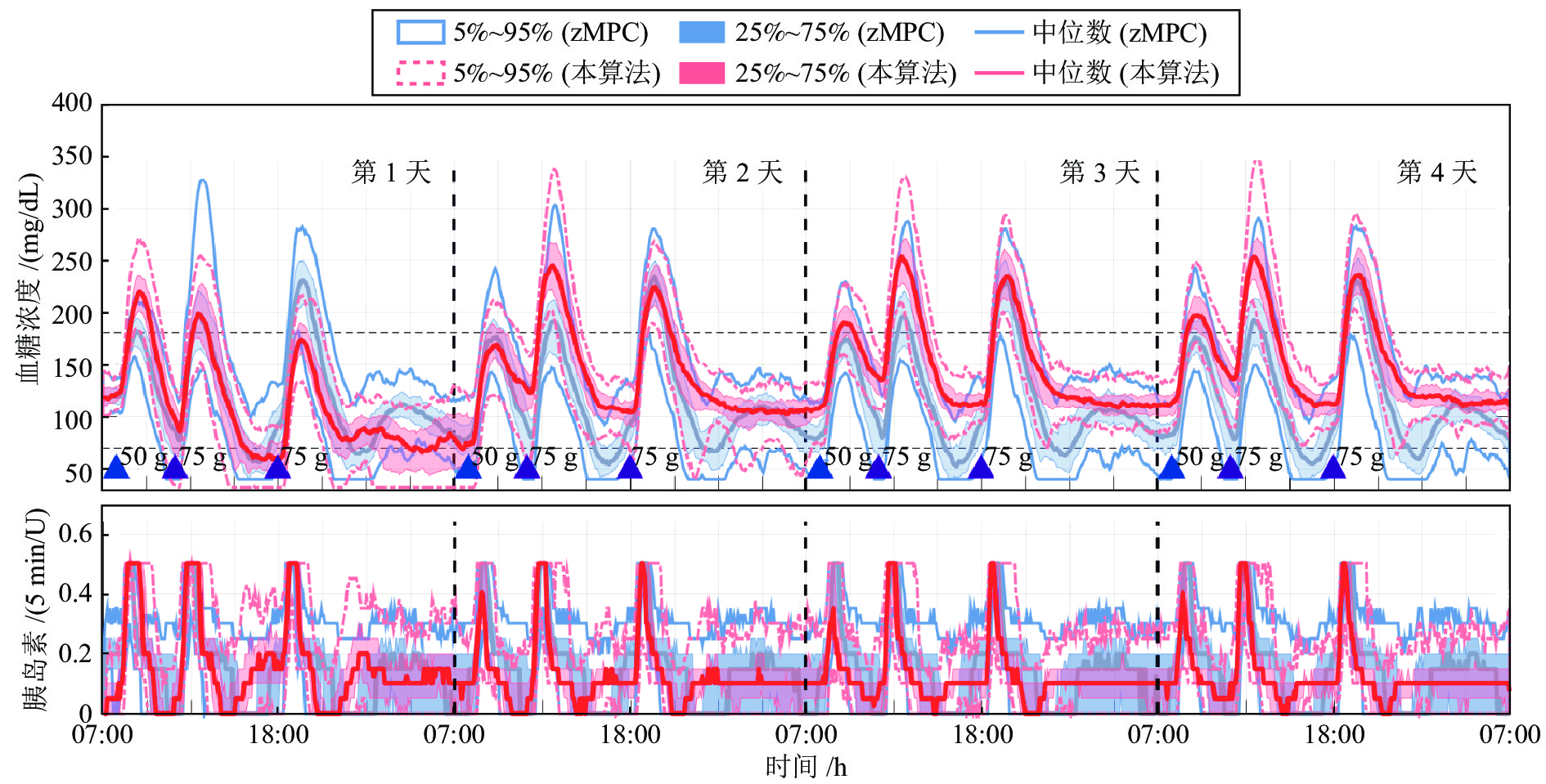
血糖控制性能指标 餐前补充大剂量胰岛素 餐前未补充大剂量胰岛素 zMPC 本算法 zMPC 本算法 < 54 mg/dL 时间比率 (%) 0 (0.0) 0 (0.0) 0 (0.0) 0 (0.0) < 70 mg/dL 时间比率 (%) 0 (0.0) 0 (0.0) 0 (0.0) 0 (0.0) 70 ~ 180 mg/dL 时间比率 (%) 66.6 (9.7) 92.0 (7.4) 38.5 (42.1) 69.6 (9.3) > 250 mg/dL 时间比率 (%) 0 (0.0) 0 (0.0) 18.5 (27.9) 5.0 (11.6) 血糖平均值 (mg/dL) 171.8 (5.9) 135.5 (6.9) 204.9 (49.0) 159.8 (11.7) 标准差 (mg/dL) 24.1 (5.9) 27.7 (5.5) 43.2 (13.5) 45.8 (15.6) 7:00 血糖平均值 (mg/dL) 164.0 (26.5) 117.0 (26.0) 167.5 (28.0) 124.0 (27.0) 注: 统计数据以中位数 (四分位距) 的形式表示. -
[1] 纪立农, 孙子林, 李启富, 秦贵军, 徐海岩. 中国四城市糖尿病患者胰岛素注射相关皮下脂肪增生的横断面研究. 中国糖尿病杂志, 2019, 27(10): 721−727 doi: 10.3969/j.issn.1006-6187.2019.10.001Ji Li-Nong, Sun Zi-Lin, Li Qi-Fu, Qin Gui-Jun, Xu Hai-Yan. Cross-sectional study of insulin injection-related lipohypertrophy in diabetic patients in four cities in China. Chinese Journal of Diabetes, 2019, 27(10): 721−727 doi: 10.3969/j.issn.1006-6187.2019.10.001 [2] 纪立农. 活的更长、活得更好——糖尿病与“健康中国2030”. 中国糖尿病杂志, 2019, 27(1): 1−2 doi: 10.3969/j.issn.1006-6187.2019.01.001Ji Li-Nong. Live longer and live better—diabetes and “Healthy China 2030”. Chinese Journal of Diabetes, 2019, 27(1): 1−2 doi: 10.3969/j.issn.1006-6187.2019.01.001 [3] Liu W, McGuire H C, Kissimova-Skarbek K, Zhou X H, Han X Y, Wang Y N, et al. Factors associated with acute complications among individuals with type 1 diabetes in China: The 3C study. Endocrine Research, 2020, 45(1): 1−8 doi: 10.1080/07435800.2019.1624567 [4] Liu W, Wang Y N, Han X Y, Cai X L, Zhu Y, Zhang M X, et al. Factors associated with resistance to complications in long-standing type 1 diabetes in China. Endocrine Connections, 2020, 9(2): 187−193 doi: 10.1530/EC-19-0521 [5] Beck R W, Bergenstal R M, Laffel P L M, Pickup P J C. Advances in technology for management of type 1 diabetes. The Lancet, 2019, 394(10205): 1265−1273 doi: 10.1016/S0140-6736(19)31142-0 [6] Benhamou P Y, Franc S, Reznik Y, Thivolet C, Schaepelynck P, Renard E, et al. Closed-loop insulin delivery in adults with type 1 diabetes in real-life conditions: A 12-week multicentre, open-label randomised controlled crossover trial. The Lancet Digital Health, 2019, 1(1): e17−e25 doi: 10.1016/S2589-7500(19)30003-2 [7] Weisman A, Bai J W, Cardinez M, Kramer C K, Perkins B A. Effect of artificial pancreas systems on glycaemic control in patients with type 1 diabetes: A systematic review and meta-analysis of outpatient randomised controlled trials. The Lancet Diabetes & Endocrinology, 2017, 5(7): 501−512 [8] Davis G M, Galindo R J, Migdal A L, Umpierrez G E. Diabetes technology in the inpatient setting for management of hyperglycemia. Endocrinology and Metabolism Clinics of North America, 2020, 49(1): 79−93 doi: 10.1016/j.ecl.2019.11.002 [9] Quiroz G. The evolution of control algorithms in artificial pancreas: A historical perspective. Annual Reviews in Control, 2019, 48: 222−232 doi: 10.1016/j.arcontrol.2019.07.004 [10] Kovatchev B. A century of diabetes technology: Signals, models, and artificial pancreas control. Trends in Endocrinology and Metabolism, 2019, 30(7): 432−444 [11] Patra K, Nanda A, Panigrahi S, Mishra A K. The fractional order PID controller design for BG control in type-I diabetes patient. Advances in Intelligent Computing and Communication. Singapore: Springer, 2020. 321−329 [12] Ly T T, Keenan D B, Roy A, Han J, Grosman B, Cantwell M, et al. Automated overnight closed-loop control using a proportional-integral-derivative algorithm with insulin feedback in children and adolescents with type 1 diabetes at diabetes camp. Diabetes Technology & Therapeutics, 2016, 18(6): 377−384 [13] Forlenza G P, Buckingham B A, Christiansen M P, Wadwa R P, Peyser T A, Lee J B, et al. Performance of omnipod personalized model predictive control algorithm with moderate intensity exercise in adults with type 1 diabetes. Diabetes Technology & Therapeutics, 2019, 21(5): 265−272 [14] Villa-Tamayo M F, Rivadeneira P S. Adaptive impulsive offset-free MPC to handle parameter variations for type 1 diabetes treatment. Industrial & Engineering Chemistry Research, 2020, 59(13): 5865−5876 [15] Garcia-Tirado J, Colmegna P, Corbett J P, Ozaslan B, Breton M D. In silico analysis of an exercise-safe artificial pancreas with multistage model predictive control and insulin safety system. Journal of Diabetes Science and Technology, 2019, 13(6): 1054−1064 doi: 10.1177/1932296819879084 [16] Bahremand S, Ko H S, Balouchzadeh R, Lee H F, Park S, Kwon G. Neural network-based model predictive control for type 1 diabetic rats on artificial pancreas system. Medical & Biological Engineering & Computing, 2019, 57(1): 177−191 [17] Huyett L M, Dassau E, Zisser H C, Doyle III F J. Design and evaluation of a robust PID controller for a fully implantable artificial pancreas. Industrial & Engineering Chemistry Research, 2015, 54(42): 10311−10321 [18] 韩月起, 张凯, 宾洋, 秦闯, 徐云霄, 李小川, 等. 基于凸近似的避障原理及无人驾驶车辆路径规划模型预测算法. 自动化学报, 2020, 46(1): 153−167Han Yue-Qi, Zhang Kai, Bin Yang, Qin Chuang, Xu Yun-Xiao, Li Xiao-Chuan, et al. Convex approximation based avoidance theory and path planning MPC for driver-less vehicles. Acta Automatica Sinica, 2020, 46(1): 153−167 [19] 魏永涛, 高原, 孙文义, 王秀蒙. 交通流动态扰动下的区域交通信号协调控制. 自动化学报, 2019, 45(10): 1983−1994Wei Yong-Tao, Gao Yuan, Sun Wen-Yi, Wang Xiu-Meng. Regional traffic signal control considering the dynamic characteristics of traffic flow. Acta Automatica Sinica, 2019, 45(10): 1983−1994 [20] 姜頔, 刘向杰, 孔小兵. 核电站蒸汽发生器水位的软约束预测控制. 自动化学报, 2019, 45(6): 1111−1121Jiang Di, Liu Xiang-Jie, Kong Xiao-Bing. Soft constrained MPC on water level control in steam generator of a nuclear power plant. Acta Automatica Sinica, 2019, 45(6): 1111−1121 [21] Boiroux D, Duun-Henriksen A K, Schmidt S, NΦrgaard K, Poulsen N K, Madsen H, et al. Adaptive control in an artificial pancreas for people with type 1 diabetes. Control Engineering Practice, 2017, 58: 332−342 doi: 10.1016/j.conengprac.2016.01.003 [22] Incremona G P, Messori M, Toffanin C, Cobelli C, Magni L. Artificial pancreas: From control-to-range to control-to-target. IFAC-PapersOnLine, 2017, 50(1): 7737−7742 doi: 10.1016/j.ifacol.2017.08.1152 [23] Shi D W, Dassau E, Doyle III F J. Adaptive zone model predictive control of artificial pancreas based on glucose-and velocity-dependent control penalties. IEEE Transactions on Biomedical Engineering, 2019, 66(4): 1045−1054 doi: 10.1109/TBME.2018.2866392 [24] Palerm C C, Zisser H, Jovanovič L, Doyle III F J. A run-to-run control strategy to adjust basal insulin infusion rates in type 1 diabetes. Journal of Process Control, 2008, 18(3−4): 258−265 doi: 10.1016/j.jprocont.2007.07.010 [25] Toffanin C, Visentin R, Messori M, Di Palma F, Magni L, Cobelli C. Toward a run-to-run adaptive artificial pancreas: In silico results. IEEE Transactions on Biomedical Engineering, 2018, 65(3): 479−488 doi: 10.1109/TBME.2017.2652062 [26] Shi D W, Dassau E, Doyle III F J. Multivariate learning framework for long-term adaptation in the artificial pancreas. Bioengineering & Translational Medicine, 2019, 4(1): 61−74 [27] Wang Y Q, Dassau E, Doyle III F J. Closed-loop control of artificial pancreatic β-cell in type 1 diabetes mellitus using model predictive iterative learning control. IEEE Transactions on Biomedical Engineering, 2010, 57(2): 211−219 doi: 10.1109/TBME.2009.2024409 [28] Wang Y Q, Zhang J P, Zeng F M, Wang N, Chen X P, Zhang B, et al. “Learning” can improve the blood glucose control performance for type 1 diabetes mellitus. Diabetes Technology and Therapeutics, 2017, 19(1): 41−48 [29] Han J P. From PID to active disturbance rejection control. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900−906 doi: 10.1109/TIE.2008.2011621 [30] 杨飞, 谈树萍, 薛文超, 郭金, 赵延龙. 饱和约束测量扩张状态滤波与无拖曳卫星位姿自抗扰控制. 自动化学报, 2020, 46(11): 2337−2349Yang Fei, Tan Shu-Ping, Xue Wen-Chao, Guo Jin, Zhao Yan-Long. Extended state filtering with saturation-constrainted observations and active disturbance rejection control of position and attitude for drag-free satellites. Acta Automatica Sinica, 2020, 46(11): 2337−2349 [31] 刘昊, 魏承, 谭春林, 刘永健, 赵阳. 空间充气展开绳网系统捕获目标自抗扰控制研究. 自动化学报, 2019, 45(9): 1691−1700Liu Hao, Wei Cheng, Tan Chun-Lin, Liu Yong-Jian, Zhao Yang. Research on capturing target of space inflatable net capture system based on active disturbance rejection control. Acta Automatica Sinica, 2019, 45(9): 1691−1700 [32] Huang Y, Xue W C. Active disturbance rejection control: Methodology and theoretical analysis. ISA Transactions, 2014, 53(4): 963−976 doi: 10.1016/j.isatra.2014.03.003 [33] Feng H, Guo Z U. Active disturbance rejection control: Old and new results. Annual Reviews in Control, 2017, 44: 238−248 doi: 10.1016/j.arcontrol.2017.05.003 [34] Guo B Z, Zhao Z L. Active disturbance Rejection Control for Nonlinear Systems: An Introduction. Hoboken, NJ: John Wiley & Sons, 2016. [35] Zhao Z L, Guo B Z. On convergence of nonlinear active disturbance rejection control for SISO nonlinear systems. Journal of Dynamical and Control Systems, 2016, 22(2): 385−412 doi: 10.1007/s10883-015-9304-5 [36] Gao Z Q. Scaling and bandwidth-parameterization based controller tuning. In: Proceedings of the 2003 American Control Conference. Denver, CO, USA: IEEE, 2003. [37] Pu Z Q, Yuan R Y, Yi J Q, Tan X M. A class of adaptive extended state observers for nonlinear disturbed systems. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5858−5869 doi: 10.1109/TIE.2015.2448060 [38] Guo B Z, Zhao Z L. On convergence of the nonlinear active disturbance rejection control for MIMO systems. SIAM Journal on Control and Optimization, 2013, 51(2): 1727−1757 doi: 10.1137/110856824 [39] Keith-Hynes P, Guerlain S, Mize B, Hughes-Karvetski C, Khan M, McElwee-Malloy M, et al. DiAs user interface: A patient-centric interface for mobile artificial pancreas systems. Journal of Diabetes Science and Technology, 2013, 7(6): 1416−1426 doi: 10.1177/193229681300700602 [40] Lazaro C, Oruklu E, Sevil M, Turksoy K, Cinar A. Implementation of an artificial pancreas system on a mobile device. In: Proceedings of the 2016 IEEE International Conference on Electro Information Technology (EIT). Grand Forks, USA: IEEE, 2016. 642−647 [41] Deshpande S, Pinsker J E, Zavitsanou S, Shi D W, Tompot R, Church M M, et al. Design and clinical evaluation of the interoperable artificial pancreas system (iAPS) smartphone app: Interoperable components with modular design for progressive artificial pancreas research and development. Diabetes Technology & Therapeutics, 2019, 21(1): 35−43 [42] Man C D, Micheletto F, Lv D, Breton M, Kovatchev B, Cobelli C. The UVA/PADOVA type 1 diabetes simulator: New features. Journal of Diabetes Science and Technology, 2014, 8(1): 26−34 doi: 10.1177/1932296813514502 [43] Gondhalekar R, Dassau E, Doyle III F J. Periodic zone-MPC with asymmetric costs for outpatient-ready safety of an artificial pancreas to treat type 1 diabetes. Automatica, 2016, 71: 237−246 doi: 10.1016/j.automatica.2016.04.015 [44] Gondhalekar R, Dassau E, Doyle F J. Velocity-weighting and velocity-penalty MPC of an artificial pancreas: Improved safety and performance. Automatica, 2018, 91: 105−117 doi: 10.1016/j.automatica.2018.01.025 [45] Cai D H, Song J L, Wang J Z, Shi D W. Glucose regulation for subjects with type 1 diabetes using active disturbance rejection control. In: Proceedings of the 2019 Chinese Control Conference (CCC). Guangzhou, China: IEEE, 2019. 6970−6975 [46] 韩京清. 自抗扰控制技术——估计补偿不确定因素的控制技术. 北京: 国防工业出版社, 2008.Han Jing-Qing. Active Disturbance Rejection Control Technique: The Technique for Estimating and Compensating the Uncertainties. Beijing: National Defense Industry Press, 2008. [47] Levine W S. The Control Handbook (2nd ed.) Boca Raton, USA: CRC Press, 2011. [48] Huang Y, Wang J Z, Shi D W, Wu J F, Shi L. Event-triggered sampled-data control: An active disturbance rejection approach. IEEE/ASME Transactions on Mechatronics, 2019, 24(5): 2052−2063 doi: 10.1109/TMECH.2019.2933411 [49] Huang Y, Wang J F, Shi D W, Shi L. Toward event-triggered extended state observer. IEEE Transactions on Automatic Control, 2018, 63(6): 1842−1849 doi: 10.1109/TAC.2017.2754340 -




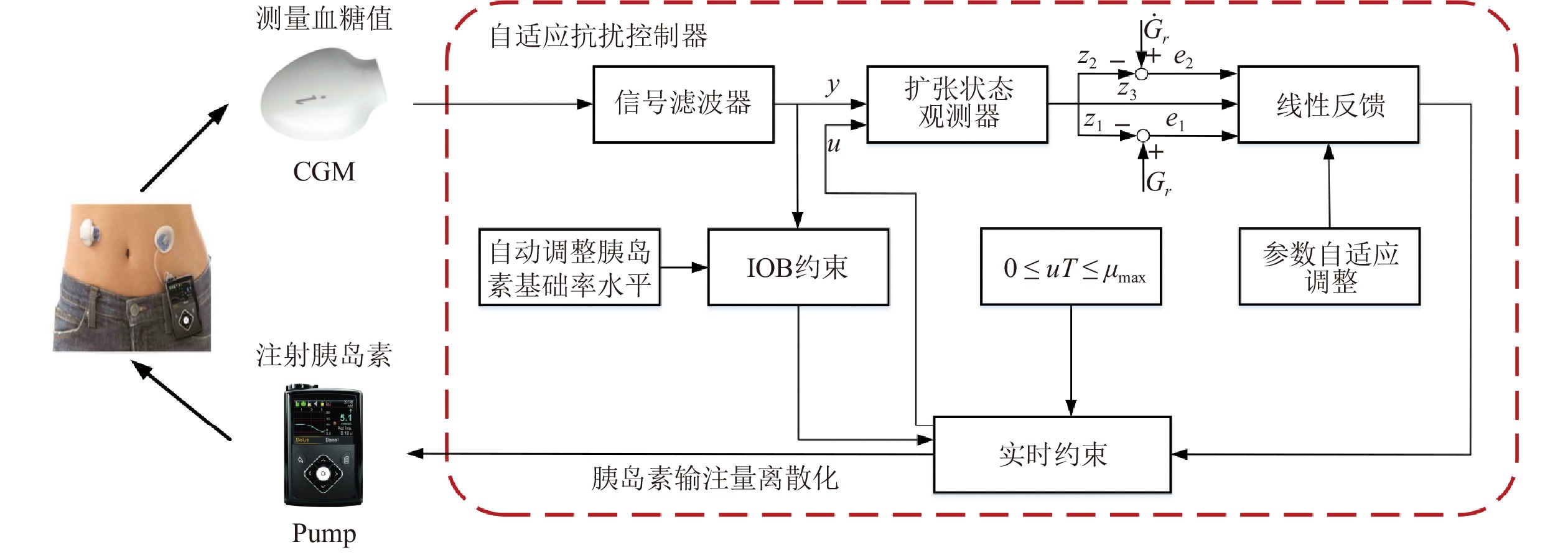
 下载:
下载: