Quality-related Variable Division and Fault Detection Based on Quality-related Virtual Variable
-
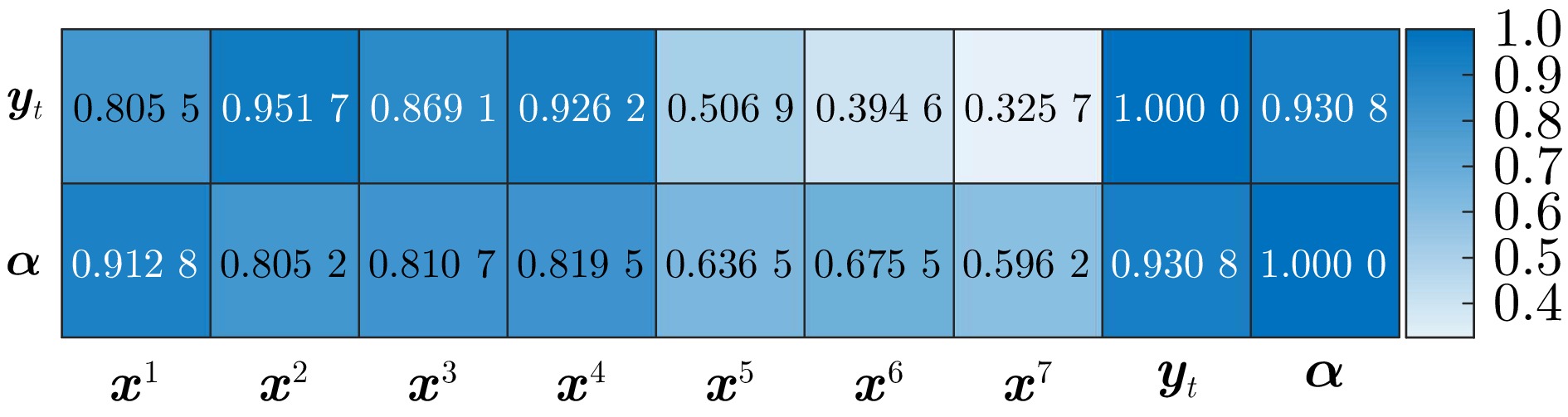
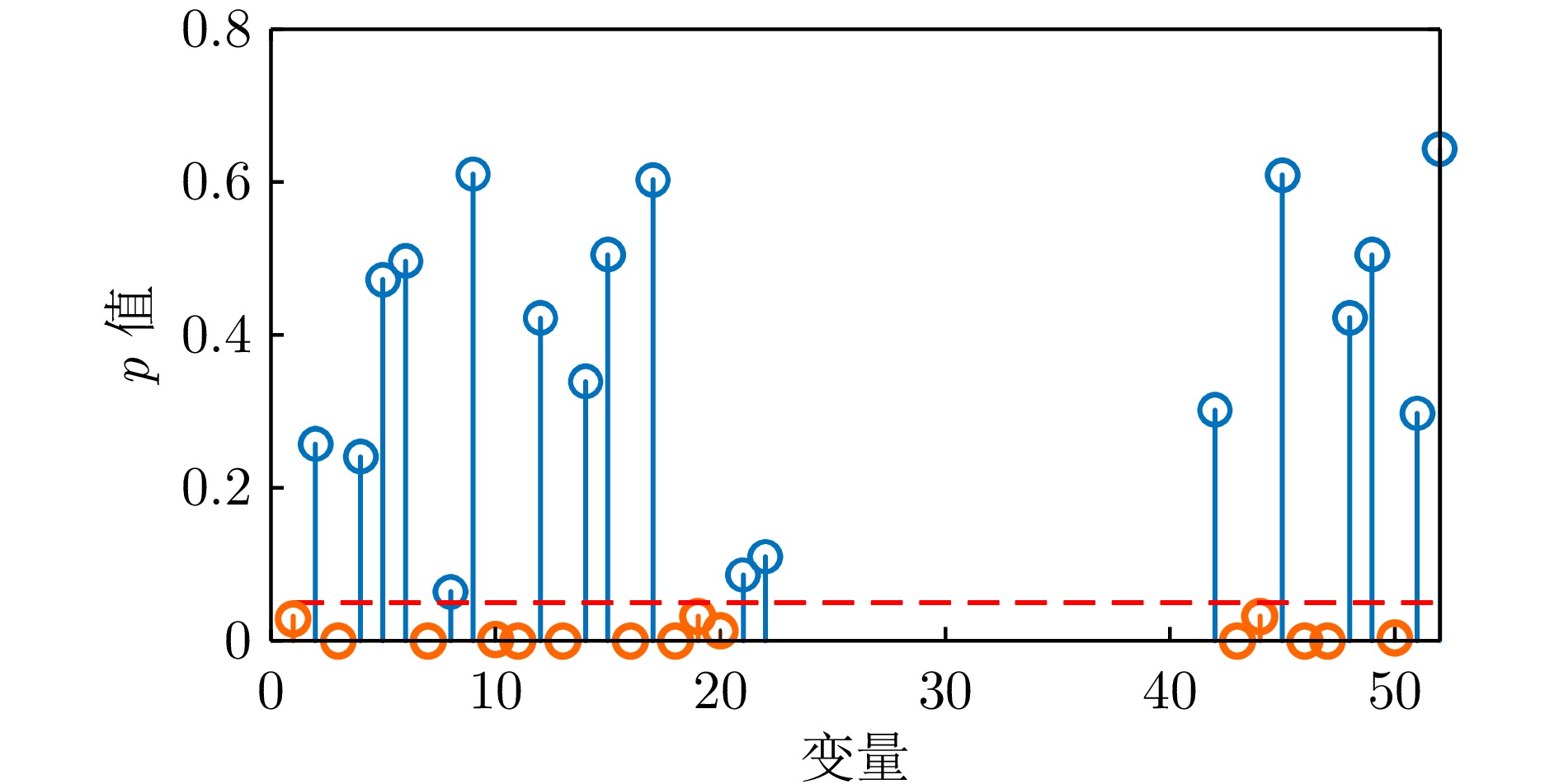
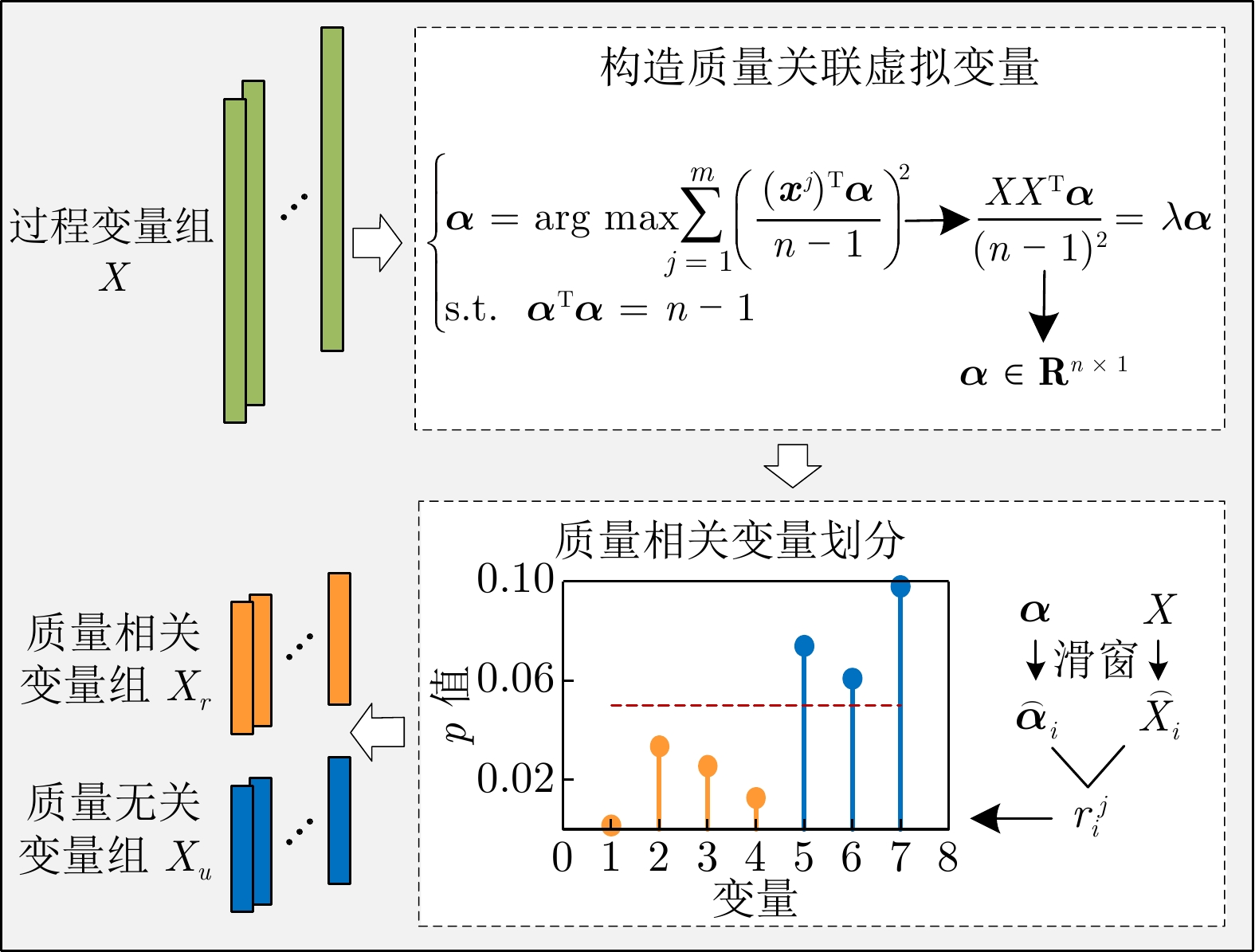
摘要: 质量相关故障检测作为数据驱动的多元统计过程监测的重要研究内容, 是保障复杂装备或工业过程安全高效运行的关键技术, 而确定或划分质量相关变量是该方法的核心环节. 现有质量相关故障检测方法通常高度依赖于质量变量, 一旦质量变量不可测, 其有效性便受到严重挑战. 为解决这一挑战, 本文提出基于质量关联虚拟变量(Quality-related virtual variable, QRV)的质量相关变量划分方法, 基于此建立一种独立成分分析(Independent component analysis, ICA)质量相关故障检测模型, 并开展故障检测应用研究. 首先, 构造一个QRV, 以间接反映系统的质量特性; 其次, 基于该QRV, 利用假设检验将过程变量划分为质量相关和质量无关变量组; 随后, 将该划分结果应用于基于ICA的质量相关故障检测, 利用指数加权移动平均(Exponentially weighted moving average, EWMA)修正统计量, 并构造综合检测指标; 最后, 通过数值仿真和田纳西—伊斯曼过程(Tennessee-Eastman process, TEP)实验验证了所提方法的可行性和有效性.Abstract: Quality-related fault detection, as an important research content in data-driven multivariate statistical process monitoring, is a key technology for ensuring the safe and efficient operation of complex equipments or industrial processes. Determining or dividing quality-related variables is a core aspect of this technology. Existing quality-related fault detection methods typically rely heavily on quality variables, and their effectiveness is severely challenged when quality variables are unmeasurable. To address this challenge, a quality-related variable division method based on a quality-related virtual variable (QRV) is proposed in this paper. An independent component analysis (ICA)-based model for quality-related fault detection is established using this division method, and an application study on fault detection is conducted. First, a QRV is constructed to indirectly reflect the quality characteristics of systems; Second, based on this QRV, process variables are divided into quality-related and quality-unrelated variable groups by hypothesis testing; Subsequently, this division results are applied to the ICA-based quality-related fault detection, utilizing exponentially weighted moving average (EWMA) to modify statistics and construct comprehensive detection indices; Finally, the feasibility and effectiveness of the proposed method are verified through numerical simulations and Tennessee-Eastman process (TEP) experiments.
-
图 1 基于QRV的质量相关变量划分方法的整体框架
Fig. 1 Overall framework of the quality-related variable division method based on QRV
图 3 基于QRVICA的质量相关故障检测流程图
Fig. 3 Flowchart of quality-related fault detection based on QRVICA
图 10 IDV(5)中不同变量组对质量变量的回归结果
Fig. 10 Regression results of the quality variable for different variable groups in IDV(5)
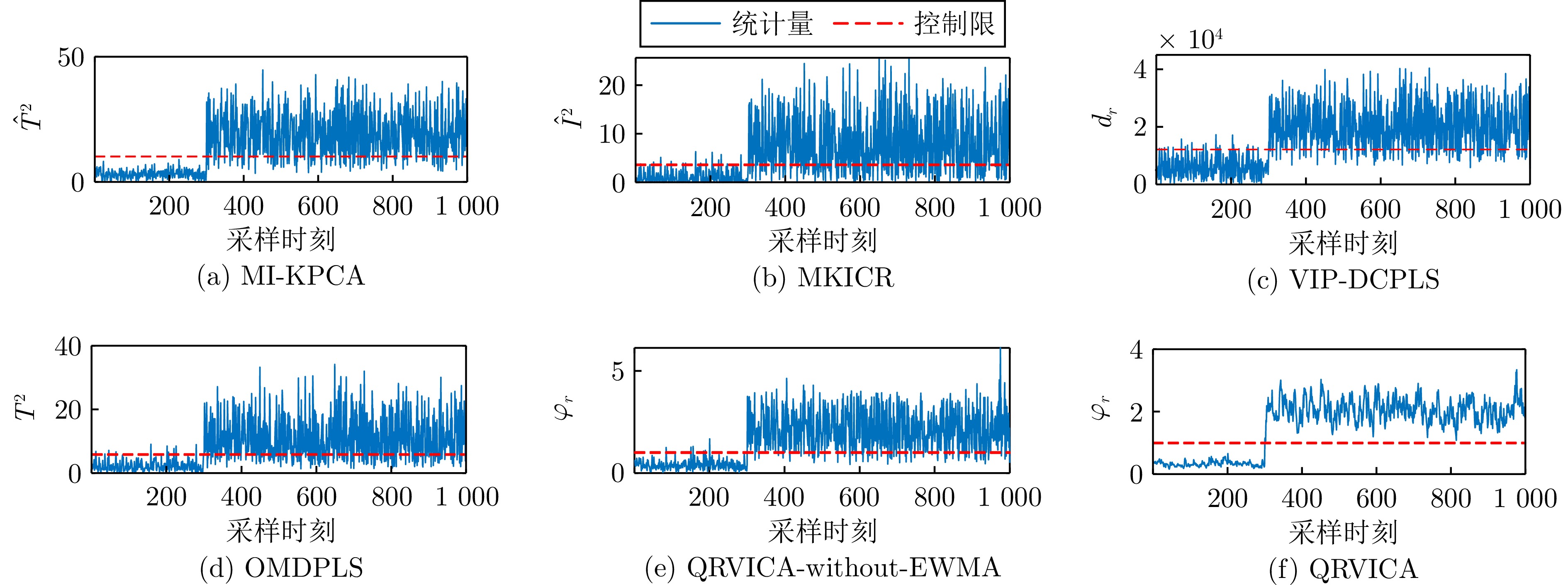
表 1 质量相关故障的FARs和FDRs(%)
Table 1 FARs and FDRs of the quality-related faults (%)
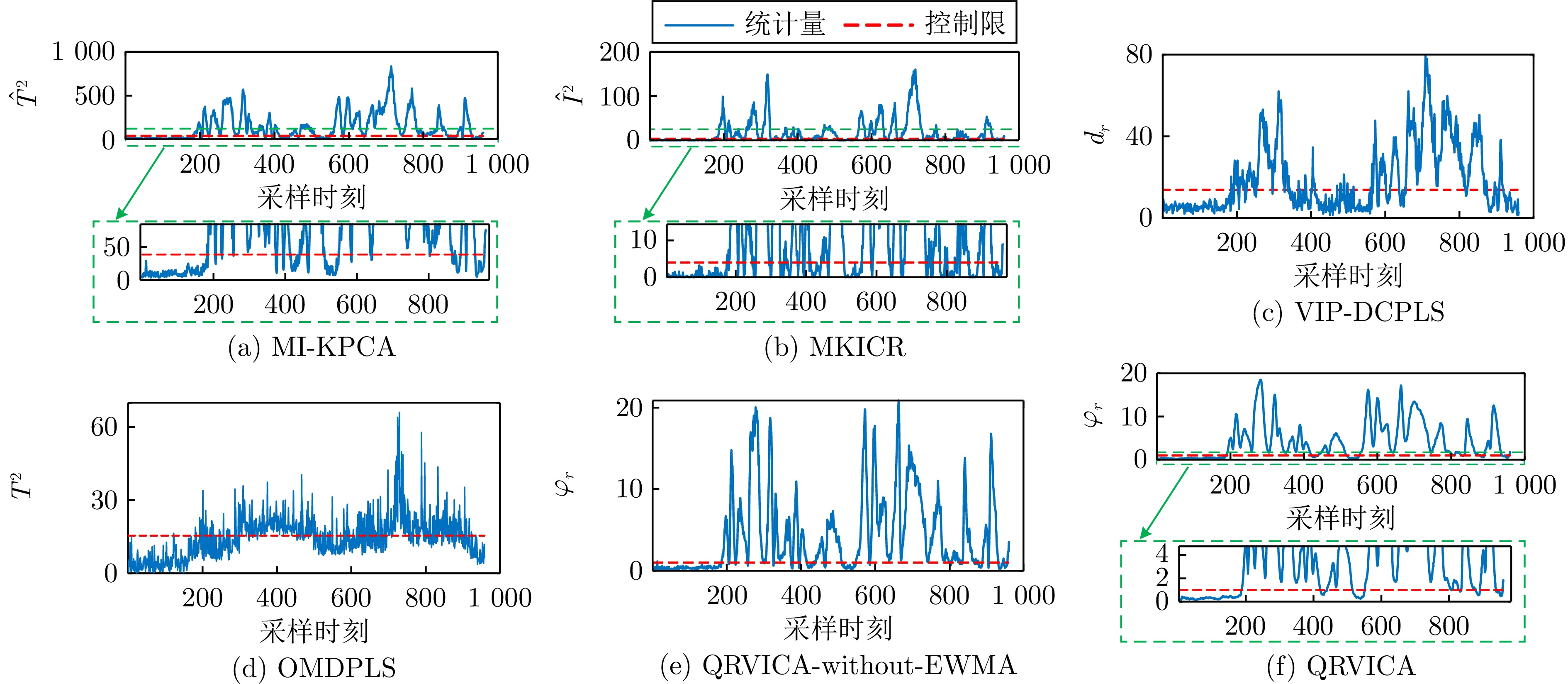
算法故障
编号MI-KPCA MKICR VIP-DCPLS OMDPLS QRVICA-without-EWMA QRVICA FAR ($\hat T^2$) FDR (${{\hat{T}}^{2}}$) FAR ($\hat I^2$) FDR (${{\hat{I}}^{2}}$) FAR (${{d}_{r}}$) FDR (${{d}_{r}}$) FAR ($T^2$) FDR ($T^2$) FAR (${\varphi }_{\text{r}}$) FDR (${\varphi }_{\text{r}}$) FAR (${\varphi }_{\text{r}}$) FDR (${\varphi }_{\text{r}}$) 1 0.30 99.62 0.63 69.13 0.00 99.75 2.50 99.63 0.00 99.75 {0.00} 99.75 2 0.00 98.50 0.63 96.88 0.00 96.50 0.63 97.75 0.00 98.25 0.00 98.50 5 0.00 24.12 0.63 20.62 0.63 24.00 1.25 19.25 0.00 24.13 0.00 25.12 6 0.00 99.75 0.00 100.00 0.00 100.00 3.13 98.75 0.00 100.00 0.00 100.00 7 0.00 40.75 0.63 35.13 0.00 40.88 1.87 64.50 0.00 37.00 0.00 37.62 8 2.40 97.62 3.75 76.00 1.25 97.75 1.25 88.13 0.00 97.63 0.00 97.50 10 0.00 79.87 0.00 63.38 0.00 55.63 0.63 54.00 0.63 80.63 0.00 84.88 12 1.25 98.88 21.88 74.13 0.00 98.75 1.25 83.88 0.00 99.25 0.00 99.62 13 0.00 94.63 1.25 85.38 0.00 95.25 0.63 93.75 0.00 93.75 0.00 94.75 平均 0.44 81.53 3.27 68.96 0.21 78.72 1.46 77.74 0.07 81.15 0.00 81.97 
下载: 导出CSV
表 2 质量无关故障的FARs和FDRs(%)
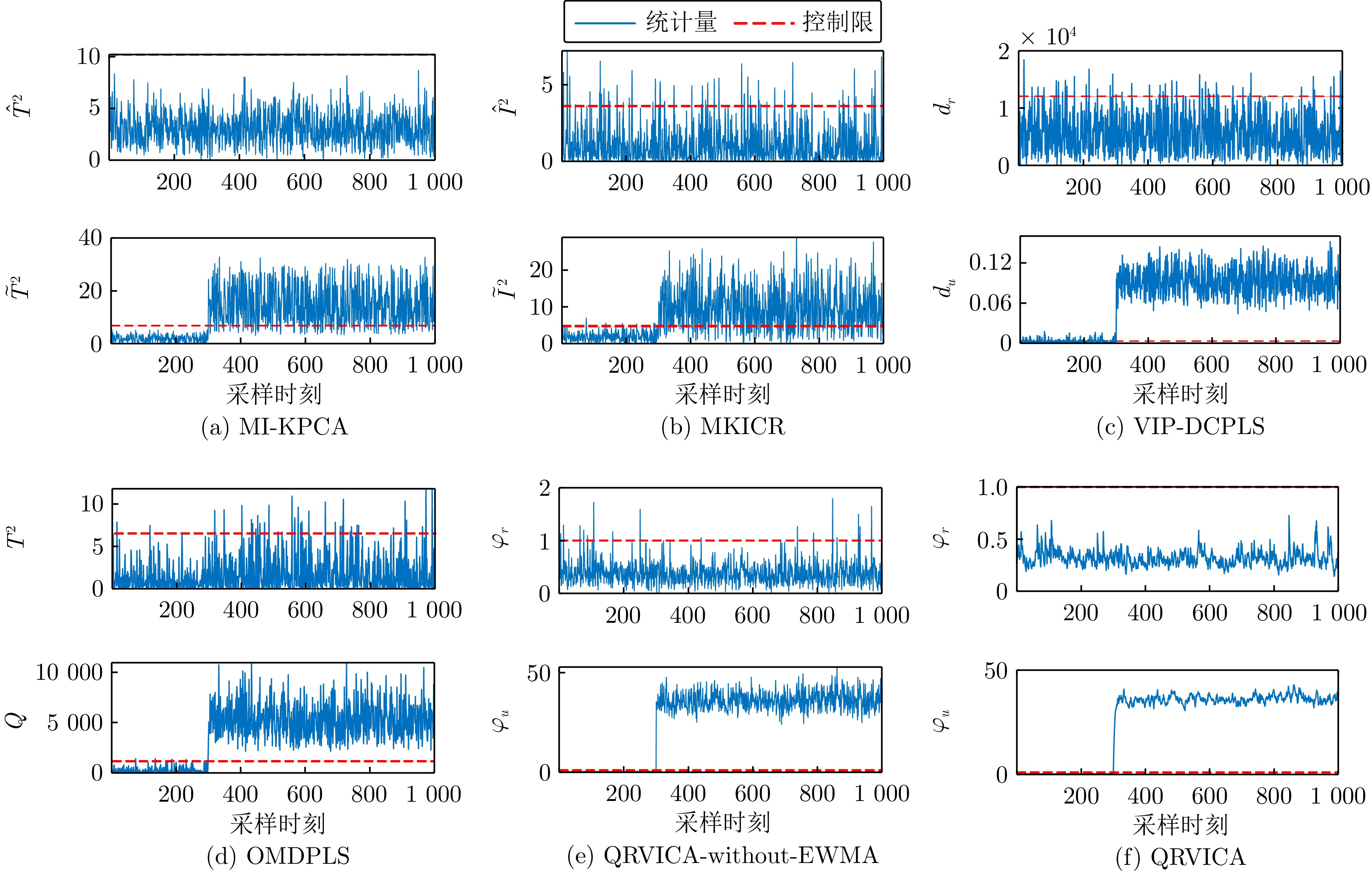
Table 2 FARs and FDRs of the quality-unrelated faults (%)
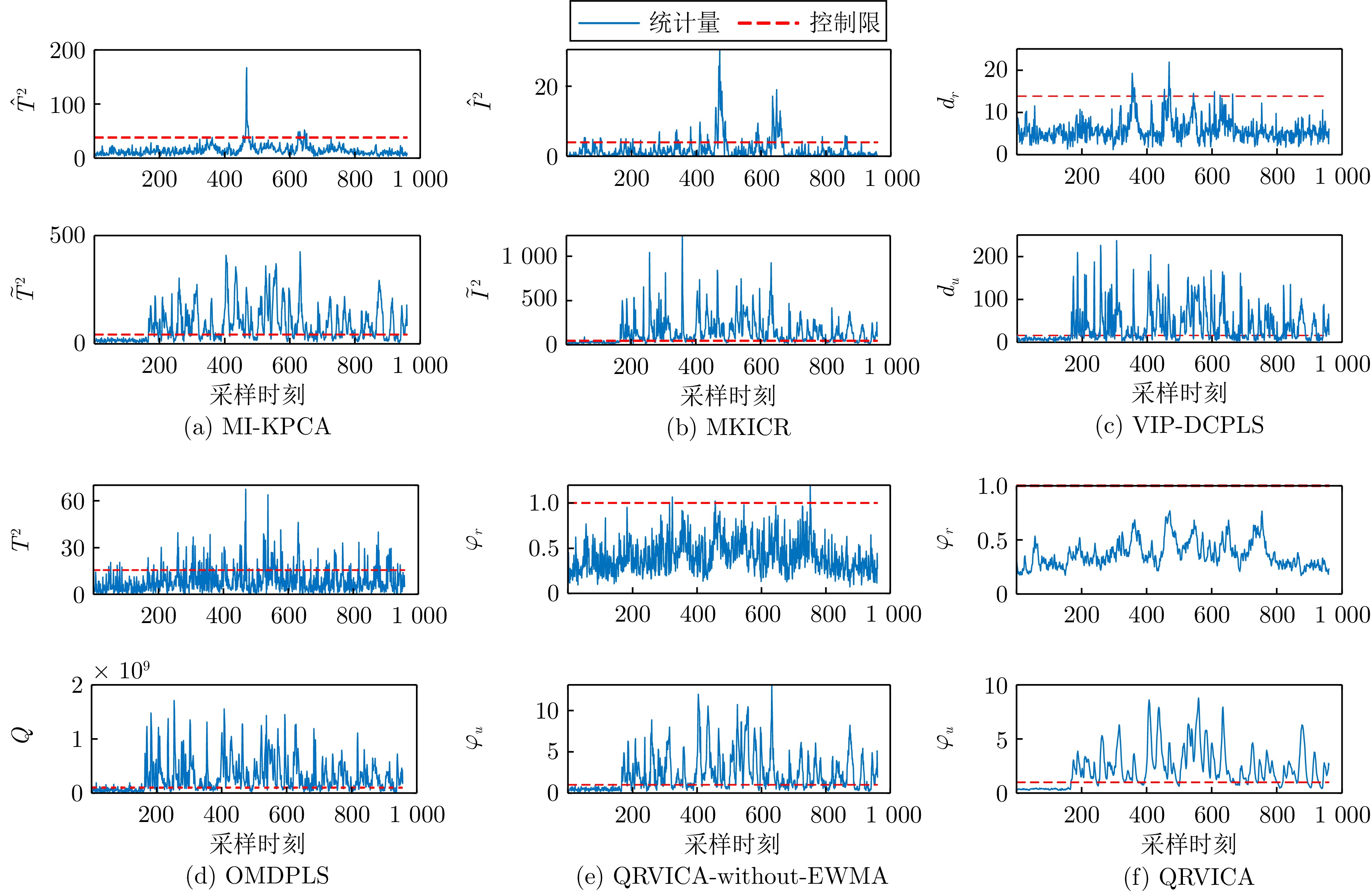
算法故障
编号MI-KPCA MKICR VIP-DCPLS OMDPLS QRVICA-without-EWMA QRVICA FAR ($\hat T^2$) FDR (${{\tilde{T}}^{2}}$) FAR ($\hat I^2$) FDR (${{\tilde{I}}^{2}}$) FAR (${{d}_{r}}$) FDR (${{d}_{u}}$) FAR ($T^2$) FDR ($Q$) FAR (${\varphi }_{\text{r}}$) FDR (${\varphi }_{\text u}$) FAR (${\varphi }_{\text{r}}$) FDR (${\varphi }_{\text u}$) 4 0.10 100.00 3.75 100.00 1.25 99.00 13.00 100.00 0.10 100.00 0.00 100.00 11 2.40 69.87 12.00 83.63 2.62 66.50 17.88 79.50 0.31 73.88 0.00 83.75 14 0.00 100.00 17.88 100.00 0.37 100.00 99.38 99.88 0.21 100.00 0.00 100.00 平均 0.83 89.96 11.21 94.54 1.41 88.50 43.42 93.13 0.21 91.29 0.00 94.58
下载: 导出CSV
-
[1] 董洁, 张伟, 彭开香, 马亮. 一种面向工业过程的质量异常检测与故障量化评估方法. 自动化学报, 2022, 48(10): 2406−2415Dong Jie, Zhang Wei, Peng Kai-Xiang, Ma Liang. A novel method of quality abnormality detection and fault quantitative assessment for industrial processes. Acta Automatica Sinica, 2022, 48(10): 2406−2415 [2] 彭开香, 马亮, 张凯. 复杂工业过程质量相关的故障检测与诊断技术综述. 自动化学报, 2017, 43(3): 349−365Peng Kai-Xiang, Ma Liang, Zhang Kai. Review of quality-related fault detection and diagnosis techniques in complex industrial processes. Acta Automatica Sinica, 2017, 43(3): 349−365 [3] Zhou D H, Li G, Qin S J. Total projection to latent structures for process monitoring. AIChE Journal, 2010, 56(1): 168−178 doi: 10.1002/aic.11977 [4] Ding S X, Yin S, Peng K X, Hao H Y, Shen B. A novel scheme for key performance indicator prediction and diagnosis with application to an industrial hot strip mill. IEEE Transactions on Industrial Informatics, 2013, 9(4): 2239−2247 doi: 10.1109/TII.2012.2214394 [5] Jiao J F, Zhao N, Wang G, Yin S. A nonlinear quality-related fault detection approach based on modified kernel partial least squares. ISA Transactions, 2017, 66: 275−283 doi: 10.1016/j.isatra.2016.10.015 [6] Peng K X, Zhang K, Li G. Quality-related process monitoring based on total kernel PLS model and its industrial application. Mathematical Problems in Engineering, 2013, 2013: Article No. 707953 [7] Hu C H, Luo J Y, Kong X Y, Xu Z Y. Orthogonal multi-block dynamic PLS for quality-related process monitoring. IEEE Transactions on Automation Science and Engineering, 2024, 21(3): 3421−3434 doi: 10.1109/TASE.2023.3279575 [8] Si Y B, Wang Y Q, Zhou D H. Key-performance-indicator-related process monitoring based on improved kernel partial least squares. IEEE Transactions on Industrial Electronics, 2021, 68(3): 2626−2636 doi: 10.1109/TIE.2020.2972472 [9] Wang G, Luo H, Peng K X. Quality-related fault detection using linear and nonlinear principal component regression. Journal of the Franklin Institute, 2016, 353(10): 2159−2177 doi: 10.1016/j.jfranklin.2016.03.021 [10] Chen Q, Wang Y Q. Key-performance-indicator-related state monitoring based on kernel canonical correlation analysis. Control Engineering Practice, 2021, 107: Article No. 104692 doi: 10.1016/j.conengprac.2020.104692 [11] 宋冰, 郑城风, 侍洪波, 陶阳, 谭帅. 基于VAE-OCCA的质量相关故障检测方法研究. 化工学报, 2023, 74(4): 1630−1638Song Bing, Zheng Cheng-feng, Shi Hong-bo. TAO Yang, TAN Shuai. Research on quality-related fault detection method based on VAE OCCA. CIESC Journal, 2023, 74(4): 1630−1638 [12] Du W, Fan Y, Zhang Y, Zhang J. Fault diagnosis of non-Gaussian process based on FKICA. Journal of the Franklin Institute, 2017, 354(6): 2573−2590 doi: 10.1016/j.jfranklin.2016.11.012 [13] Dong J, Wang Y, Peng K. A novel fault detection method based on the extraction of slow features for dynamic nonstationary processes. IEEE Transactions on Instrumentation and Measurement, 2022, 71: Article No. 3500611 [14] Wang G, Yang J H, Qian Y C, Han J S, Jiao J F. KPCA-CCA-based quality-related fault detection and diagnosis method for nonlinear process monitoring. IEEE Transactions on Industrial Informatics, 2023, 19(5): 6492−6501 doi: 10.1109/TII.2022.3204555 [15] Liu M Z, Kong X Y, Luo J Y, Yang L. Fault detection and diagnosis in a non-Gaussian process with modified kernel independent component regression. The Canadian Journal of Chemical Engineering, 2023, 102(2): 781−802 [16] Zhang X Y, Ma L, Peng K X, Zhang C F. A quality-related distributed fault detection method for large-scale sequential processes. Control Engineering Practice, 2022, 127: Article No. 105308 doi: 10.1016/j.conengprac.2022.105308 [17] Huang J P, Yan X F. Quality relevant and independent two block monitoring based on mutual information and KPCA. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6518−6527 doi: 10.1109/TIE.2017.2682012 [18] Huang J, Yang X, Peng K. Double-layer distributed monitoring based on sequential correlation information for large-scale industrial processes in dynamic and static states. IEEE Transactions on Industrial Informatics, 2021, 17(9): 6419−6428 doi: 10.1109/TII.2020.3019499 [19] Fan H P, Lai X Z, Du S, Yu W K, Lu C D, Wu M. Distributed monitoring with integrated probability PCA and mRMR for drilling processes. IEEE Transactions on Instrumentation and Measurement, 2022, 71: Article No. 3516213 [20] Yu W K, Zhao C H, Huang B, Xie M. Intrinsic causality embedded concurrent quality and process monitoring strategy. IEEE Transactions on Industrial Electronics, 2024, 71(11): 15111−15121 doi: 10.1109/TIE.2024.3370955 [21] Jiao J F, Zhen W T, Zhu W X, Wang G. Quality-related root cause diagnosis based on orthogonal kernel principal component regression and transfer entropy. IEEE Transactions on Industrial Informatics, 2021, 17(9): 6347−6356 doi: 10.1109/TII.2020.2989810 [22] Yang J, Wang J Y, Sha J L, Dai H Q, Liu H B. Quality-related monitoring of distributed process systems using dynamic concurrent partial least squares. Computers & Industrial Engineering, 2022, 164: Article No. 107893 [23] Yang J, Wang J Y, Ye Q L, Xiong Z X, Zhang F S, Liu H B. A novel fault detection framework integrated with variable importance analysis for quality-related nonlinear process monitoring. Control Engineering Practice, 2023, 141: Article No. 105733 doi: 10.1016/j.conengprac.2023.105733 [24] Guo L, Shi H B, Tan S, Song B, Tao Y. A knowledge-driven spatial-temporal graph neural network for quality-related fault detection. Process Safety and Environmental Protection, 2024, 184: 1512−1524 doi: 10.1016/j.psep.2024.02.070 [25] Zhu J Z, Shi H B, Song B, Tao Y, Tan S. Convolutional neural network based feature learning for large-scale quality-related process monitoring. IEEE Transactions on Industrial Informatics, 2022, 18(7): 4555−4565 doi: 10.1109/TII.2021.3124578 [26] Lee J-M, Yoo C, Lee I-B. Statistical process monitoring with independent component analysis. Journal of Process Control, 2004, 14(5): 467−485 doi: 10.1016/j.jprocont.2003.09.004 [27] Downs J, Vogel E F. A plant-wide industrial process control problem. Computers and Chemical Engineering, 1993, 17(3): 245−255 doi: 10.1016/0098-1354(93)80018-I -
计量
- 文章访问数: 24
- HTML全文浏览量: 10
- 被引次数: 0
