Time Series Prediction Method Based on Domain Adaptation Physics-informed Neural Network
-
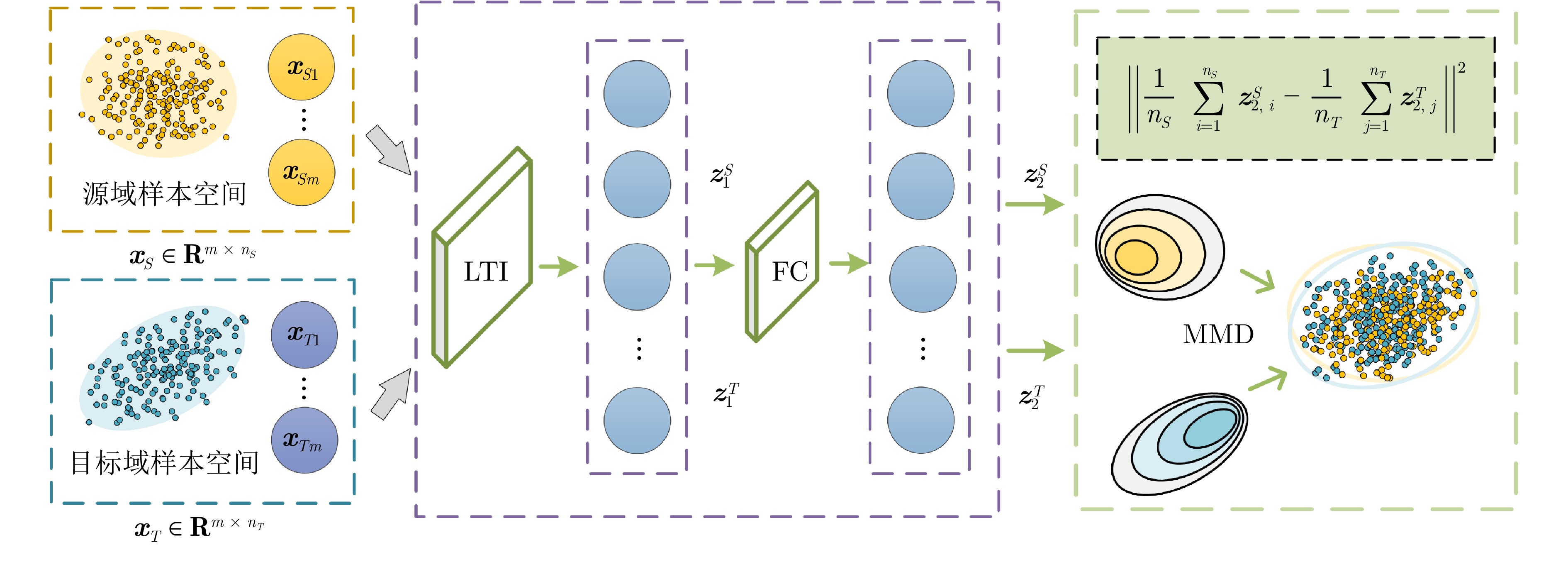
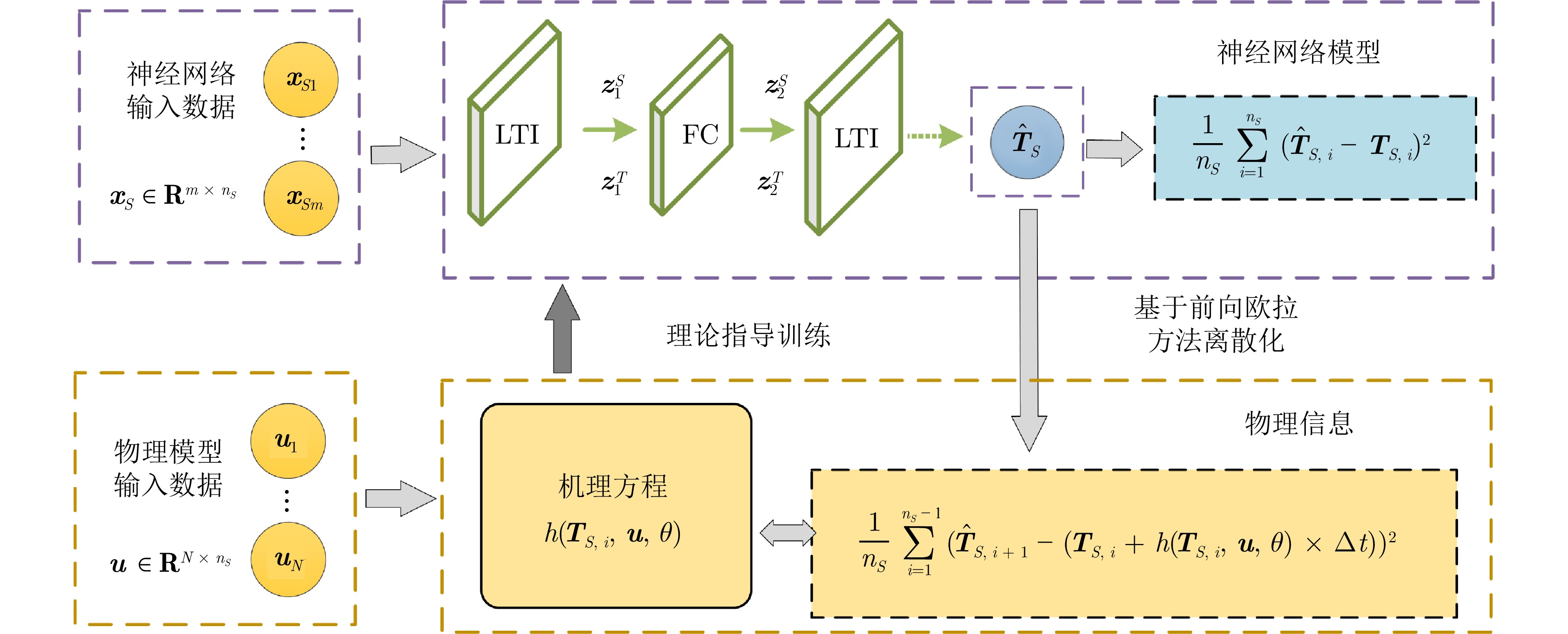
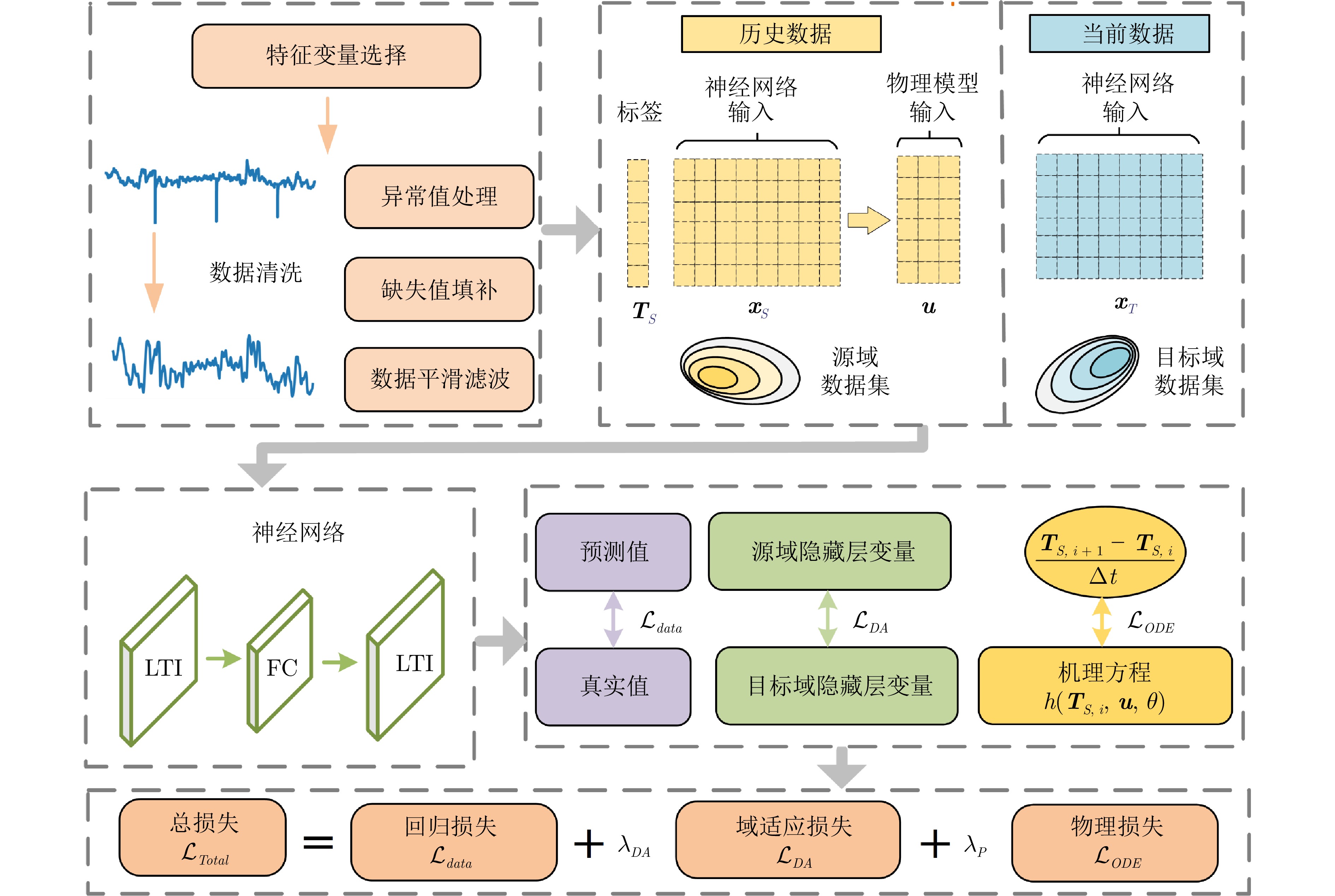
摘要: 基于机器学习的预测方法通常能够实现较高的拟合精度, 但模型可解释性和泛化性能较差. 在工业过程中, 由于概念漂移现象的存在, 这些方法的稳定性受到影响, 使得在复杂工业环境中精确建模成为一项既困难又具挑战性的任务. 为此, 提出一种基于线性动力算子的域适应 (Domain adaptation, DA)物理信息神经网络方法. 首先通过历史工况数据建立线性动力算子神经网络模型, 捕获多变量时间序列数据的动态特性. 然后通过前向欧拉法对机理模型进行离散化, 构造物理信息正则化项, 促使模型服从机理约束. 最后通过最大均值差异 (Maximum mean discrepancy, MMD)对历史工况和当前工况下隐藏层状态变量进行分布对齐, 构建域适应损失, 降低变工况下数据分布变化对模型的影响. 在多个数据集上的实验表明, 该方法可以有效提高模型预测精度和泛化性能.
-
关键词:
- 物理信息机器学习 /
- 概念漂移 /
- 域适应 /
- 线性动力算子神经网络
Abstract: Machine learning-based prediction methods usually achieve high fitting accuracy, but often suffer from limited model interpretability and poor generalization performance. In industrial processes, the stability of these methods is affected by the concept drift phenomenon, which makes accurate modeling in complex industrial environments a difficult and challenging task. To this end, we propose a domain adaptation (DA) Physics-informed neural network method based on Linear Dynamical Operator. A Linear dynamical operator neural network model is built from the historical data, capturing dynamic properties of multivariate time series data. Then the mechanism model is discretized by the forward Euler method to construct the physical information regularization term, so that the model obeys the constraints of the mechanism. Finally, the distribution of hidden layer state variables under historical and current operating conditions is aligned by the maximum mean discrepancy (MMD), and the domain adaptation loss is constructed to reduce the impact of data distribution changes on the model under variable operating conditions. Experiments on several datasets show that the proposed method can effectively improve the model prediction accuracy and generalization performance. -
图 13 各数据集机理模型与LDO-daPInet模型预测结果对比
Fig. 13 Comparison of the prediction results of the mechanism model and LDO-daPInet model for each dataset
图 14 各数据集下不同训练样本量的模型性能
Fig. 14 Model performance with different training sample sizes on various datasets
图 15 各数据集不同域适应方法的比较
Fig. 15 Comparison of different domain adaptation methods across various datasets
图 16 不同数据集$ {n_a} $和$ {n_b} $对RMSE的影响
Fig. 16 The impact of different datasets $ {n_a} $ and $ {n_b} $ on RMSE
图 17 不同数据集$ {\lambda _P} $和$ {\lambda _{DA}} $对RMSE的影响
Fig. 17 The impact of different datasets $ {\lambda _P} $ and $ {\lambda _{DA}} $ on RMSE
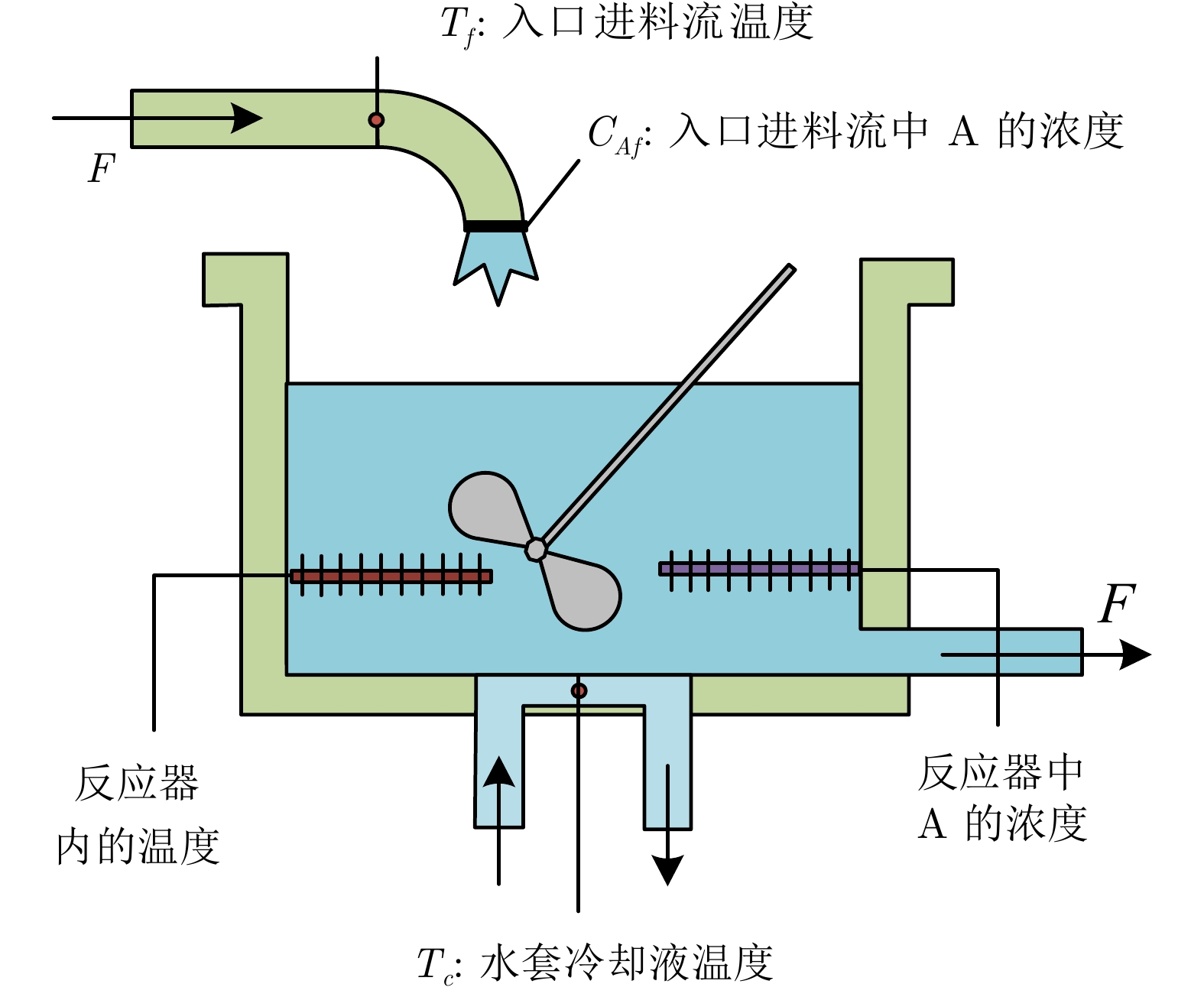
表 1 CSTR模型中的常量值
Table 1 Constant values in the CSTR model
参数 描述 值 单位 $ F $ 体积流量 1 $ {\rm{m^3/h}} $ $ V $ 反应器体积 1 $ {\rm{m^3}} $ $ R $ 玻尔兹曼理想气体常数 8.314 $ {\rm{J/(mol {\cdot} K)}} $ $ \Delta H $ 每摩尔反应热 $ - $24 936.64 $ {\rm{J/mol}} $ $ E $ 每摩尔活化能 49 551.112 $ {\rm{J/mol}} $ $ k_0 $ 指数前非热因子 34 930 800 $ {\rm{1/h}} $ $ \rho {C_p} $ 密度乘以热容 2 092 000 $ {\rm{J/(m^3 {\cdot} K)}} $ $ UA $ 总传热系数乘以储罐面积 174 $ {\rm{W/K}} $ 
下载: 导出CSV
表 2 LDO-daPInet与各方法实验结果对比
Table 2 Comparison of experimental results between LDO-daPInet and various methods
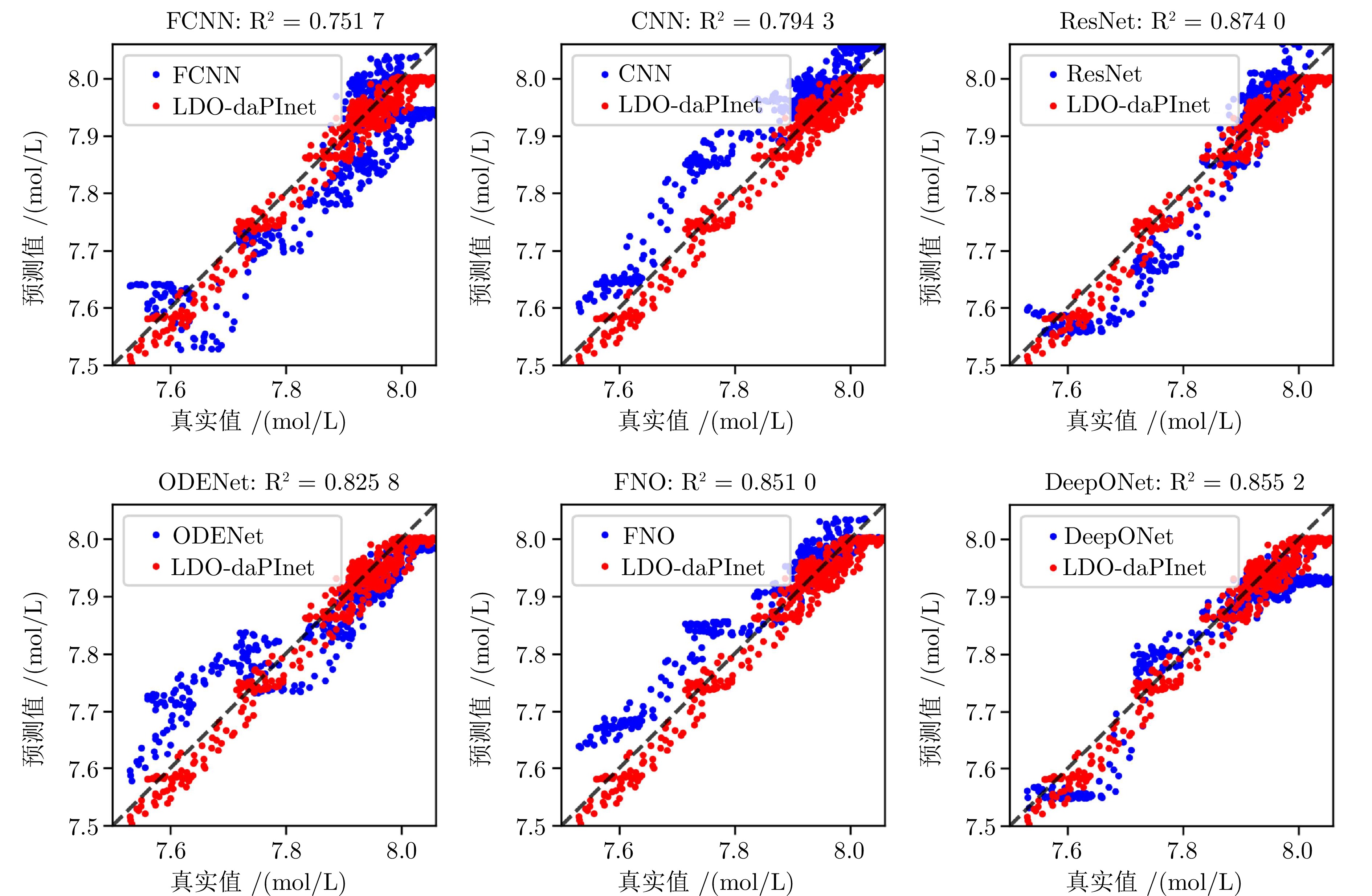
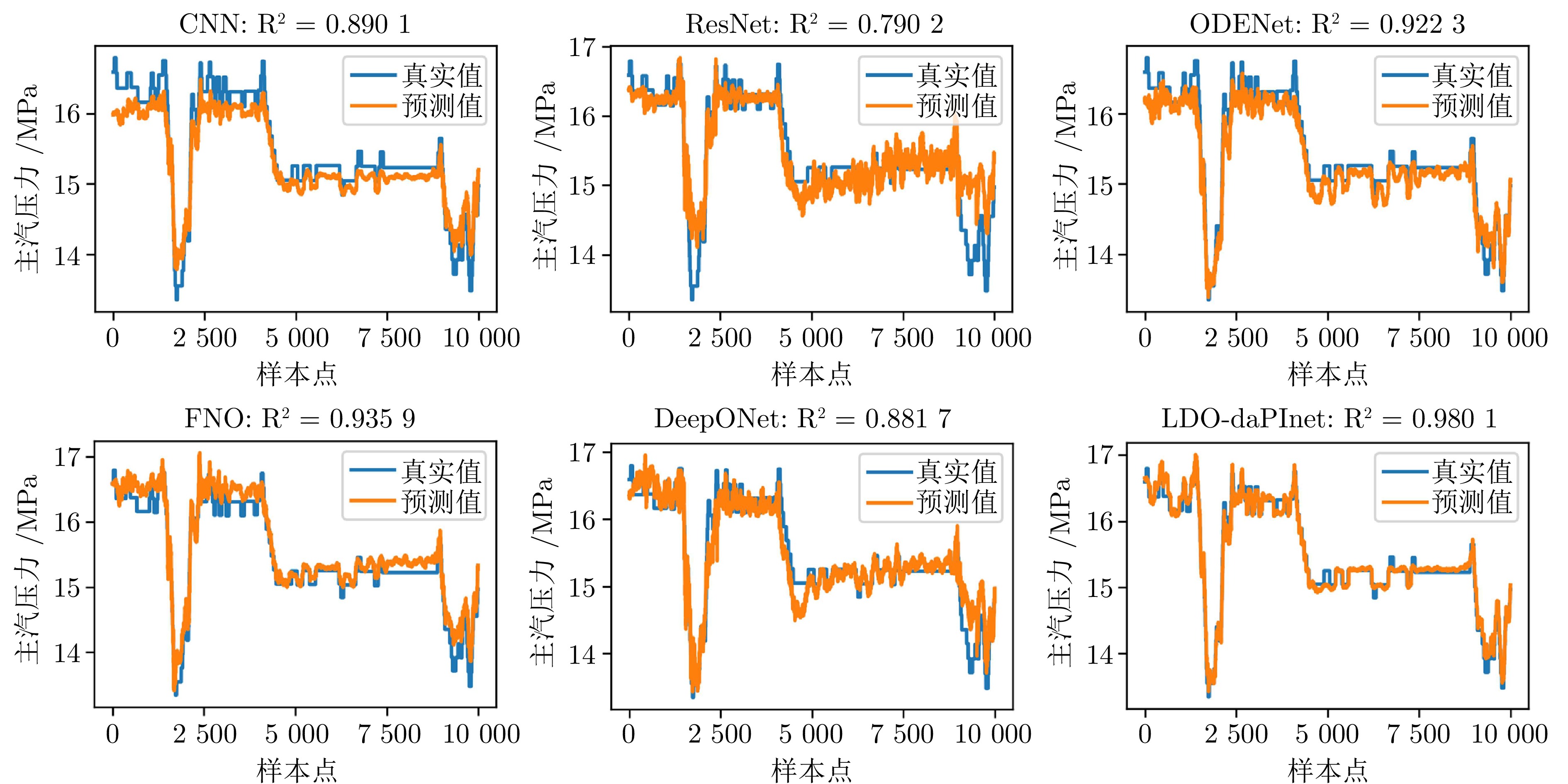
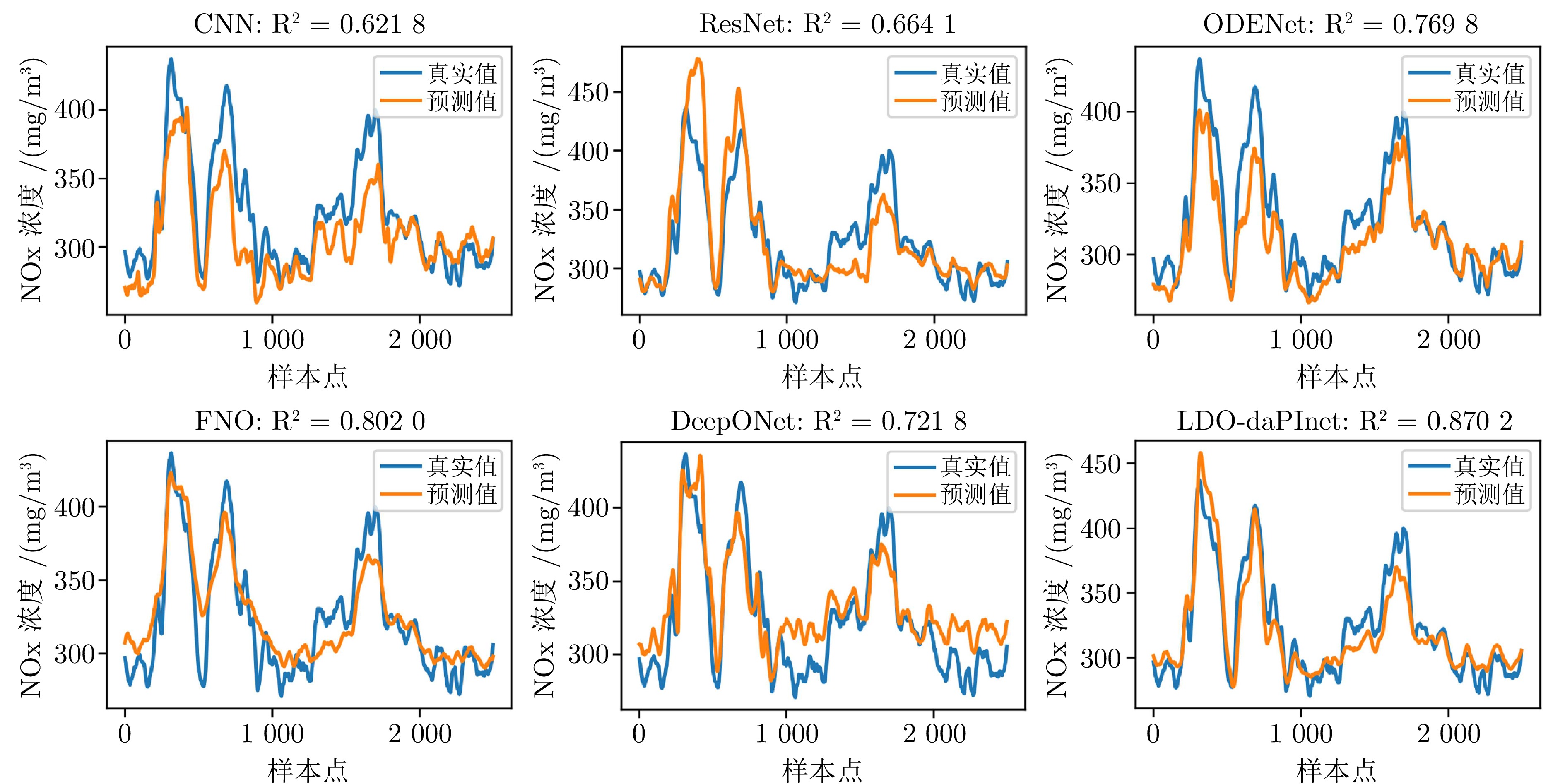
模型 CSTR 主汽压力 NOx RMSE $ {\rm{R}}^2 $ MAE RMSE $ {\rm{R}}^2 $ MAE RMSE $ {\rm{R}}^2 $ MAE FCNN 0.0685 0.7517 0.0587 0.4502 0.6722 0.3497 25.6035 0.6001 20.1770 CNN 0.0623 0.7943 0.0511 0.2607 0.8901 0.2179 24.8983 0.6218 19.4112 ResNet 0.0488 0.8740 0.0402 0.3601 0.7902 0.2525 23.4669 0.6641 16.3799 ODENet 0.0573 0.8258 0.0461 0.2191 0.9223 0.1710 19.4271 0.7698 14.8912 FNO 0.0530 0.8510 0.0420 0.1990 0.9359 0.1616 18.0175 0.8020 14.5429 DeepONet 0.0523 0.8552 0.0416 0.2704 0.8817 0.1972 21.3544 0.7218 17.6638 LDO-daPInet 0.0253 0.9699 0.0214 0.1113 0.9801 0.0824 14.5864 0.8702 11.9644
下载: 导出CSV
表 3 LDO-daPInet消融实验结果
Table 3 Results of LDO-daPInet ablation experiment
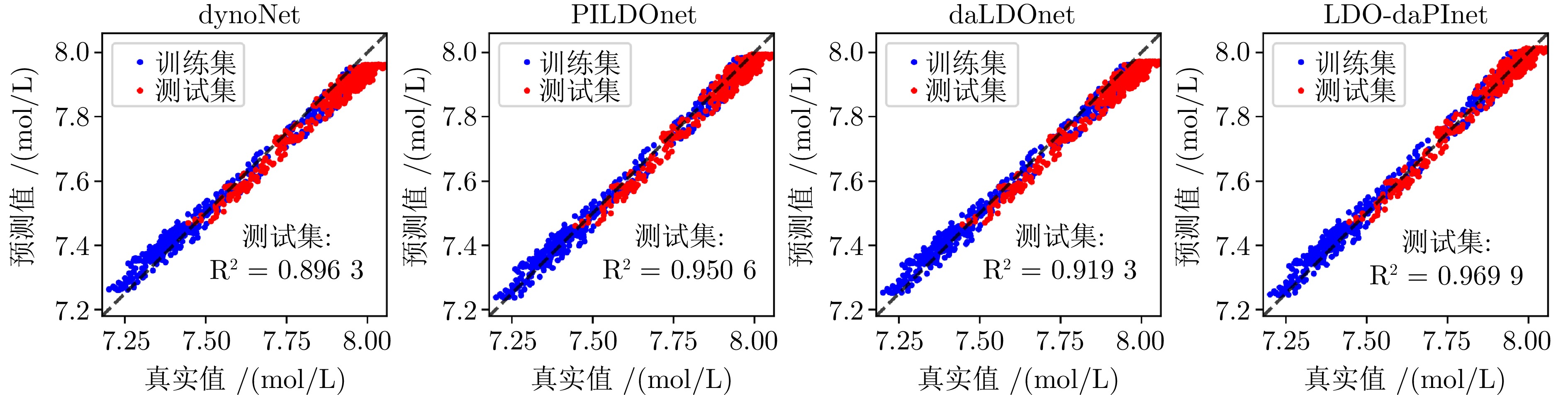
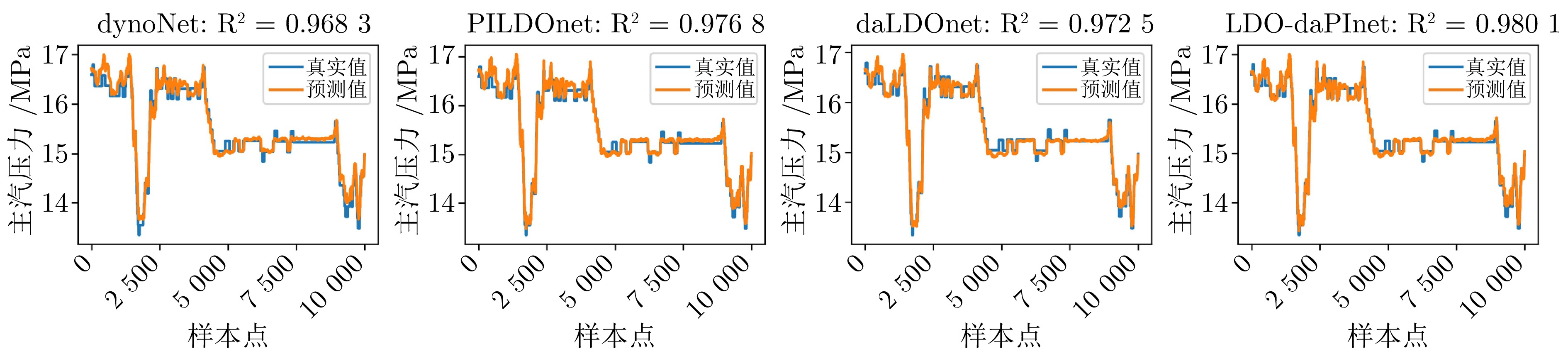
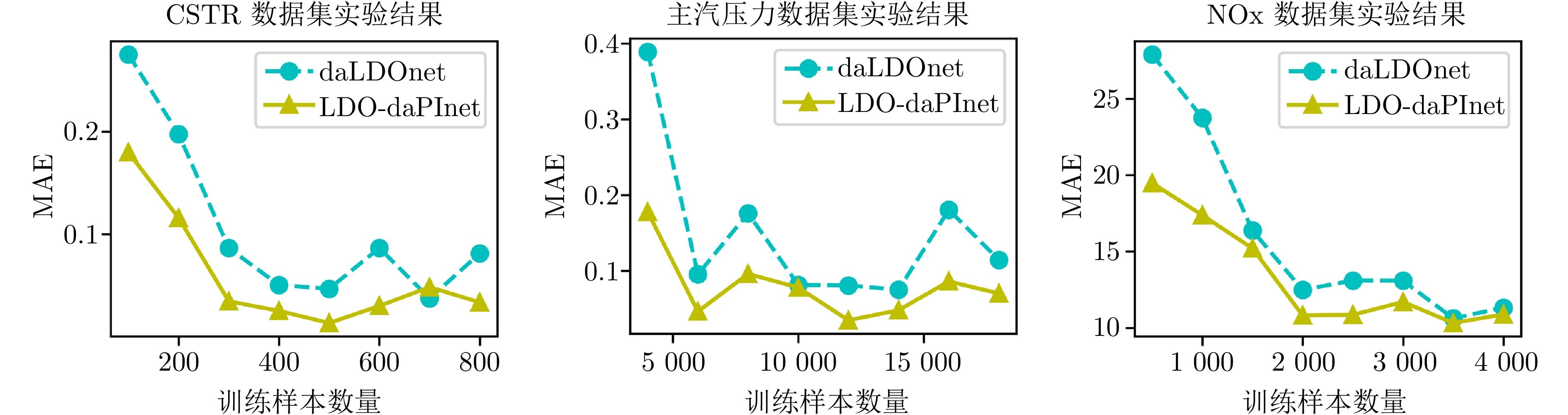
模型 CSTR 主汽压力 NOx RMSE $ {\rm{R}}^2 $ MAE RMSE $ {\rm{R}}^2 $ MAE RMSE $ {\rm{R}}^2 $ MAE dynoNet 0.0470 0.8963 0.0397 0.1400 0.9683 0.1070 16.2558 0.8388 13.3672 PILDOnet 0.0312 0.9506 0.0262 0.1197 0.9768 0.0907 15.6215 0.8511 12.5900 daLDOnet 0.0415 0.9193 0.0346 0.1304 0.9725 0.0984 15.9837 0.8442 12.8131 LDO-daPInet 0.0253 0.9699 0.0214 0.1113 0.9801 0.0824 14.5864 0.8702 11.9644
下载: 导出CSV
表 4 各特征变量与主汽压力的互信息
Table 4 Mutual information between various characteristic variables and main steam pressure
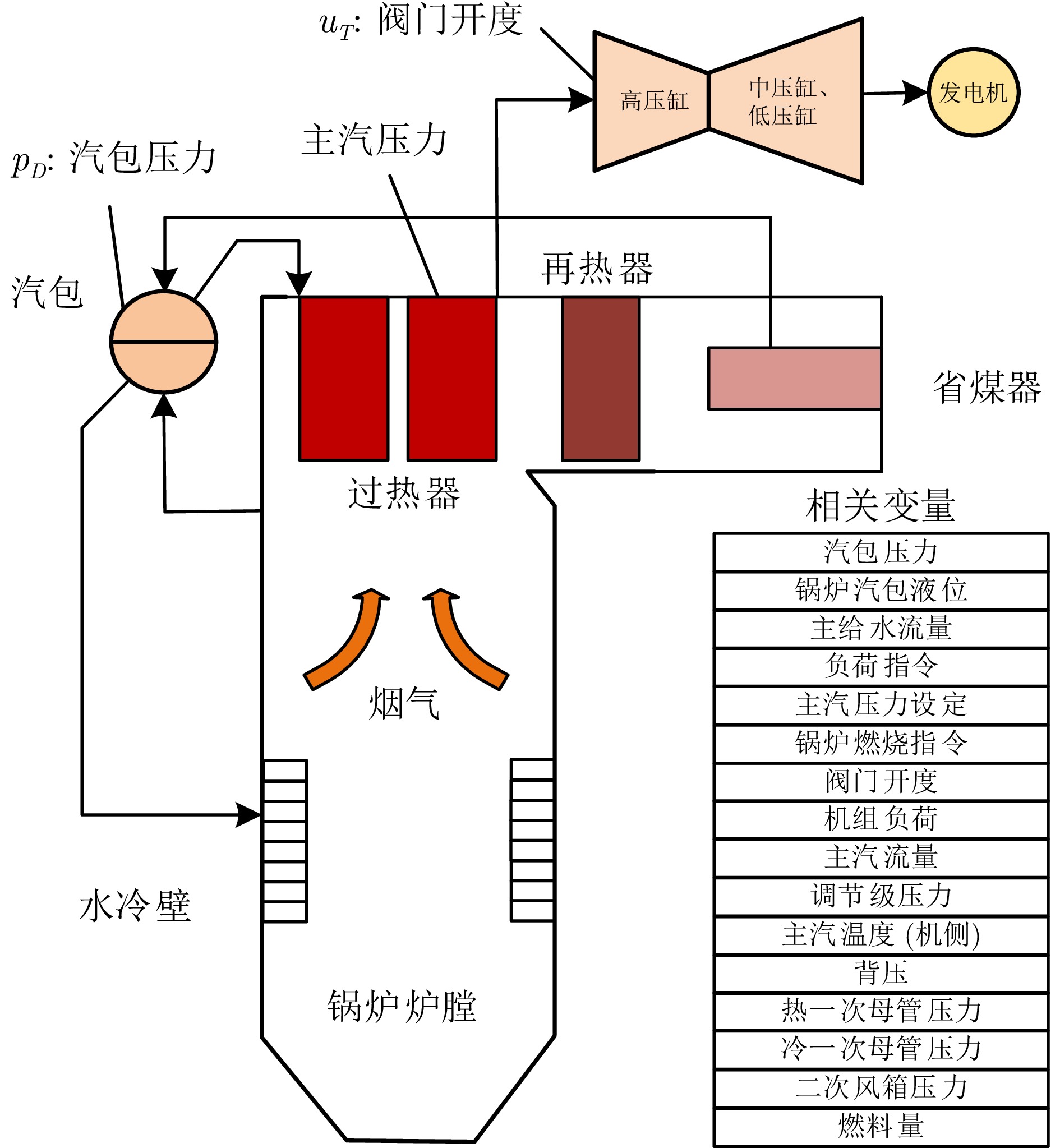
变量 描述 互信息 $ {x_1} $ 主汽温度 (机侧) 4.10 $ {x_2} $ 燃料量 3.99 $ {x_3} $ 锅炉汽包液位 3.90 $ {x_4} $ 阀门开度 3.90 $ {x_5} $ 主汽流量 3.63 $ {x_6} $ 二次风箱压力 3.61 $ {x_7} $ 机组负荷 3.53 $ {x_8} $ 负荷指令 3.41 $ {x_9} $ 锅炉汽包压力 3.38 $ {x_{10}} $ 调节级压力 3.35 $ {x_{11}} $ 冷一次母管压力 3.17 $ {x_{12}} $ 热一次母管压力 3.09 $ {x_{13}} $ 主汽压力设定 2.77 $ {x_{14}} $ 主给水流量 2.67 $ {x_{15}} $ 锅炉燃烧指令 2.65 $ {x_{16}} $ 背压 2.61
下载: 导出CSV
表 5 各特征变量与NOx浓度的互信息
Table 5 Mutual information between each characteristic variable and NOx concentration
变量 描述 互信息 $ {x_1}{\sim}{x_{4}} $ A侧二次风温 (1$ \sim $4) $ 3.82,\; 3.69,\; 3.67,\; 3.17 $ $ {x_5}{\sim}{x_{8}} $ B侧二次风温 (1$ \sim $4) $ 3.78,\; 3.75,\; 3.71,\; 3.65 $ $ {x_9} $ A侧SCR入口烟气氧量 3.06 $ {x_{10}} $ 总风量 3.16 $ {x_{11}}{\sim}{x_{13}} $ SOFA1 (A$ \sim $C) $ 2.91,\; 2.54,\; 1.45 $ $ {x_{14}} $ 机组负荷 2.71 $ {x_{15}} $ 总燃料量 2.69 $ {x_{16}} $ 炉膛温度 1.63 $ {x_{17}}{\sim}{x_{19}} $ A侧二次风流量 (1$ \sim $3) $ 1.32,\; 1.32,\; 1.31 $ $ {x_{20}}{\sim}{x_{22}} $ B侧二次风流量 (1$ \sim $3) $ 1.32,\; 1.31,\; 1.29 $ $ {x_{23}} $ 锅炉热量 0.99 $ {x_{24}} $ 总一次风量 0.91 $ {x_{25}} $ 总二次风量 0.89
下载: 导出CSV
表 6 各数据集机理模型与LDO-daPInet模型对比结果
Table 6 Comparison results of mechanism and LDO-daPInet models across datasets
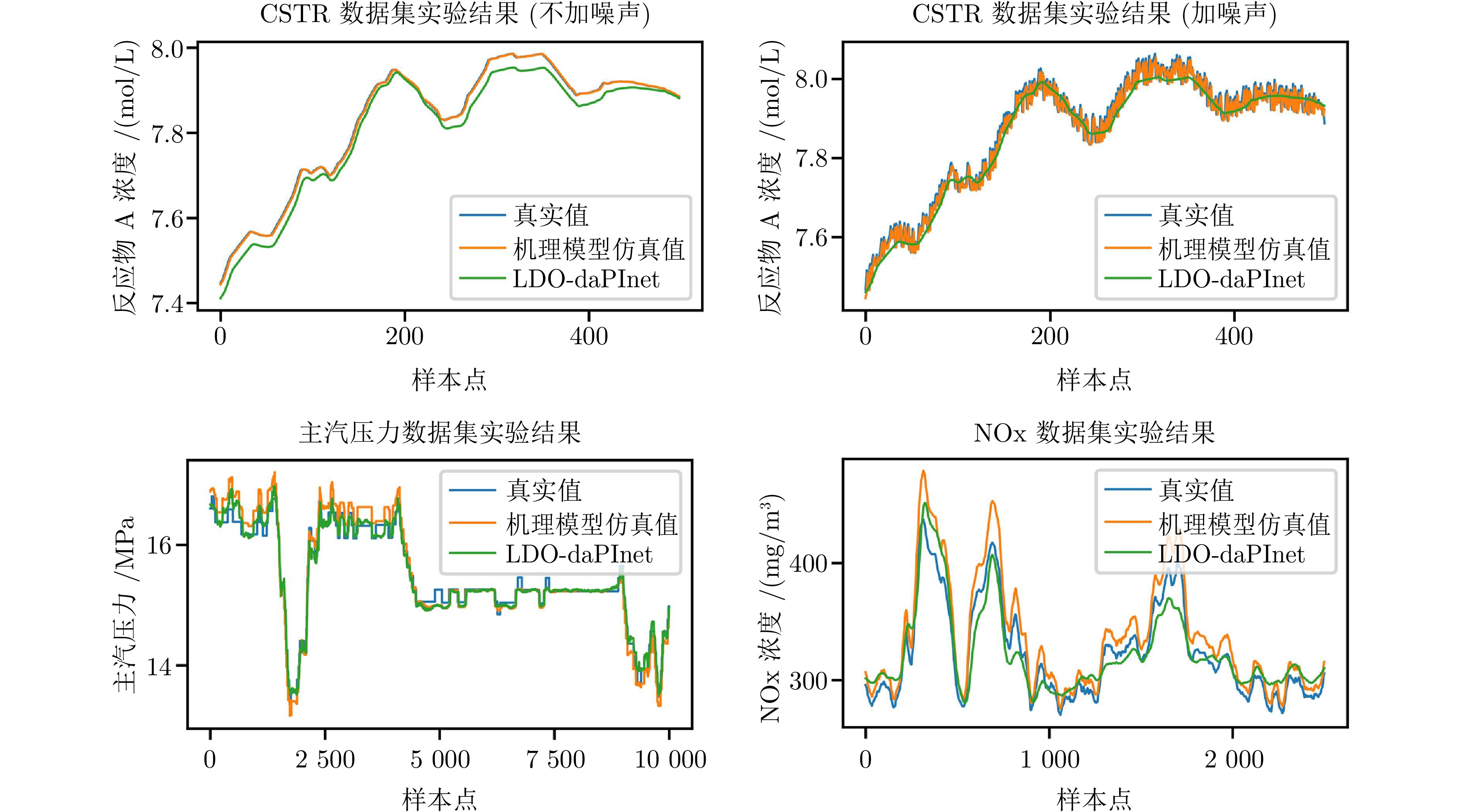
方法 机理模型计算值 LDO-daPInet预测值 RMSE $ {\rm{R}}^2 $ MAE RMSE $ {\rm{R}}^2 $ MAE CSTR (不加噪声) 0.0033 0.9995 0.0025 0.0206 0.9794 0.0177 CSTR (加噪声) 0.0402 0.9232 0.0338 0.0253 0.9699 0.0214 主汽压力 0.1807 0.9472 0.1314 0.1113 0.9801 0.0824 NOx 16.8738 0.8264 14.6142 14.5864 0.8702 11.9644
下载: 导出CSV
表 7 LDO-daPInet与其他域适应方法的比较
Table 7 Comparison of LDO-daPInet with other domain adaptation methods
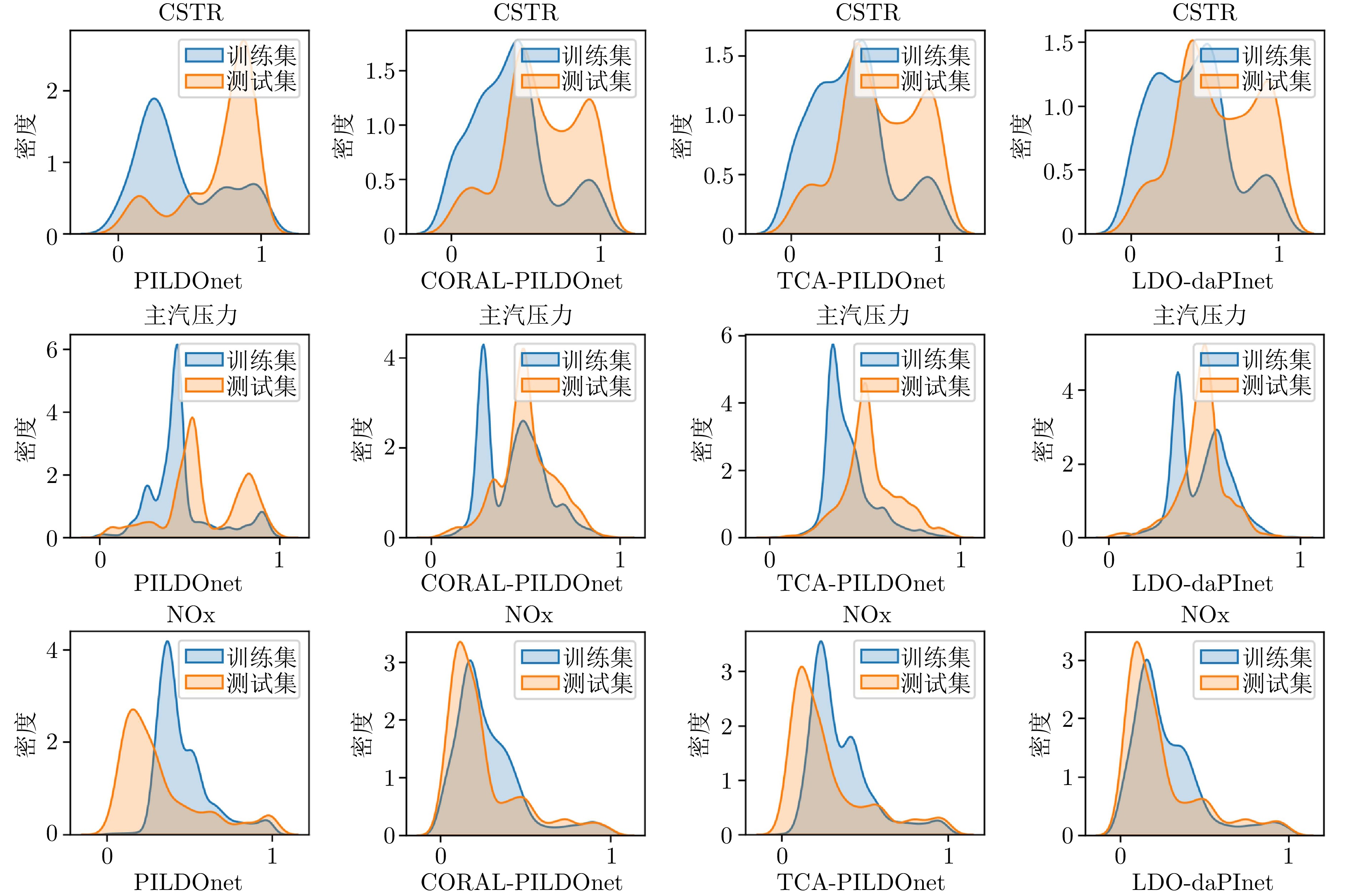
方法 CSTR 主汽压力 NOx RMSE $ {\rm{R}}^2 $ MAE RMSE $ {\rm{R}}^2 $ MAE RMSE $ {\rm{R}}^2 $ MAE PILDOnet 0.0306 0.9460 0.0253 0.1197 0.9768 0.0915 15.6215 0.8511 12.5900 TCA-PILDOnet 0.0289 0.9509 0.0240 0.1165 0.9779 0.0858 15.5895 0.8552 12.5202 CORAL-PILDOnet 0.0299 0.9488 0.0248 0.1218 0.9769 0.0892 15.5729 0.8523 12.8676 LDO-daPInet 0.0253 0.9699 0.0214 0.1133 0.9801 0.0824 14.5864 0.8702 11.9644
下载: 导出CSV
-
[1] Kairm H, Delfin D, Shuvo M A I, Chavez L A, Garcia C R, Barton J H, et al. Concept and model of a metamaterial-based passive wireless temperature sensor for harsh environment applications. IEEE Sensors Journal, 2014, 15 (3): 1445−1452 [2] Peterson L, Bremer J, Sundmacher K. Challenges in data-based reactor modeling: A critical analysis of purely data-driven and hybrid models for a CSTR case study. Computers & Chemical Engineering, 2024, 184: Article No. 108643 [3] Ge Z Q, Song Z H, Gao F R. Review of recent research on data-based process monitoring. Industrial & Engineering Chemistry Research, 2013, 52: 3543−3562 [4] Kadlec P, Gabrys B, Strandt S. Data-Driven Soft Sensors in the Process Industry. Computers & Chemical Engineering, 2009, 33 (4): 795−814 [5] Yuan X F, Huang B, Ge Z Q, Song Z H. Double locally weighted principal component regression for soft sensor with sample selection under supervised latent structure. Chemometrics and Intelligent Laboratory Systems, 2016, 153: 116−125 doi: 10.1016/j.chemolab.2016.02.014 [6] Wang Z X, He Q P, Wang J. Comparison of variable selection methods for PLS-based soft sensor modeling. Journal of Process Control, 2015, 26: 56−72 doi: 10.1016/j.jprocont.2015.01.003 [7] He Z Y, Shao H D, Zhong X, Yang Y, Cheng J S. An intelligent fault diagnosis method for rotor-bearing system using small labeled infrared thermal images and enhanced CNN transferred from CAE. Advanced Engineering Informatics, 2020, 46: Article No. 101150 doi: 10.1016/j.aei.2020.101150 [8] Laubscher R. Time-series forecasting of coal-fired power plant reheater metal temperatures using encoder-decoder recurrent neural networks. Energy, 2019, 189: Article No. 116187 [9] Fan F L, Xiong J J, Li M Z, Wang G. On interpretability of artificial neural networks: A survey. IEEE Transactions on Radiation and Plasma Medical Sciences, 2021, 5 (6): 741−760 doi: 10.1109/TRPMS.2021.3066428 [10] Karpatne A, Atluri G, Faghmous J H, Steinbach M, Banerjee A, Ganguly A. Theory-guided data science: A new paradigm for scientific discovery from data. IEEE Transactions on knowledge and data engineering, 2017, 29 (10): 2318−2331 [11] Liu H, Zhang T, Anoop Krishnan N M, Smedskjaer M M, Ryan J V, Gin S, et al. Predicting the dissolution kinetics of silicate glasses by topology-informed machine learning. Npj Materials Degradation, 2019, 3 (1): Article No. 32 doi: 10.1038/s41529-019-0094-1 [12] Ravinder, Venugopal V, Bishnoi S, Singh S, Zaki M, Grover H S, et al. Artificial intelligence and machine learning in glass science and technology: 21 challenges for the 21st century. International journal of applied glass science, 2021, 12 (3): 277−292 [13] Gülcehre C, Bengio Y. Knowledge matters: Importance of prior information for optimization. The Journal of Machine Learning Research, 2016, 17 (1): 226−257 [14] Jia X, Willard J, Karpatne A, Read J, Zwart J, Steinbach M, et al. Physics guided RNNs for modeling dynamical systems: A case study in simulating lake temperature profiles. IN: Proceedings of the 2019 SIAM international conference on data mining. Calgary, Canada: Society for Industrial and Applied Mathematics, 2019. 558-566 [15] Nam J H, Kim D, Chung D. Sparse linear discriminant analysis using the prior-knowledge-guided block covariance matrix. Chemometrics and Intelligent Laboratory Systems, 2020, 206: Article No. 104142 doi: 10.1016/j.chemolab.2020.104142 [16] Raissi M, Perdikaris P, Karniadakis G E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational physics, 2019, 379: 686−707 [17] Zhu Y, Zabaras N, Koutsourelakis P S, Perdikaris P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantificationwithout labeled data. Journal of Computational physics, 2019, 394: 56−81 doi: 10.1016/j.jcp.2019.05.024 [18] Rao C, Sun H, Liu Y. Physics-informed deep learning for incompressible laminar flows. Theoretical and Applied Mechanics Letters, 2020, 10 (3): 207−212 doi: 10.1016/j.taml.2020.01.039 [19] Jin X, Cai S, Li H, Karniadakis G E. Nsfnets (Navier-Stokes flow nets): physics-informed neural networks for the incompressible Navier-Stokes equations. Journal of Computational physics, 2021, 426: Article No. 109951 [20] Niaki S A, Haghighat E, Campbell T, Poursartip A, Vaziri R. Physics-informed neural network for modelling the thermochemical curing process ofcomposite-tool systems during manufacture. Computer Methods in Applied Mechanics and Engineering, 2021, 384: Article No. 113959 doi: 10.1016/j.cma.2021.113959 [21] Haghighat E, Raissi M, Moure A, Gomez H, Juanes R. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Computer Methods in Applied Mechanics and Engineering, 2021, 379: Article No. 113741 doi: 10.1016/j.cma.2021.113741 [22] Zhang R Y, Liu Y, Sun H. Physics-informed multi-LSTM networks for metamodeling of nonlinear structures. Computer Methods in Applied Mechanics and Engineering, 2020, 369: Article No. 113226 doi: 10.1016/j.cma.2020.113226 [23] Rao C P, Sun H, Liu Y. Physics-informed deep learning for computational elastodynamics without labeled data. Journal of Engineering Mechanics, 2021, 147 (8): Article No. 04021043 [24] Zhu B Y, Ren S J, Weng Q H, Si F Q. A physics-informed neural network that considers monotonic relationships for predicting NOx emissions from coal-fired boilers. Fuel, 2024, 364: Article No. 131026 doi: 10.1016/j.fuel.2024.131026 [25] Zhang Y, Tiňo P, Leonardis A, Tang K. A survey on neural network interpretability. IEEE Transactions on Emerging Topics in Computational Intelligence, 2021, 5 (5): 726−742 doi: 10.1109/TETCI.2021.3100641 [26] Lu L, Jin P Z, Pang G F, Zhang Z Q, Karniadakis G M. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nature machine intelligence, 2021, 3 (3): 218−229 doi: 10.1038/s42256-021-00302-5 [27] Li Z, Kovachki N, Azizzadenesheli K, Liu B, Bhattacharya K, Stuart A, et al. Fourier neural operator for parametric partial differential equations. arXiv preprint arXiv: 2010.08895, 2020 [28] Forgione M, Piga D. dynoNet: A neural network architecture for learning dynamical systems. International Journal of Adaptive Control and Signal Processing, 2021, 35 (4): 612−626 doi: 10.1002/acs.3216 [29] Piga D, Forgione M, Mejari M. Deep learning with transfer functions: new applications in system identification. IFAC-PapersOnLine, 2021, 54 (7): 415−420 doi: 10.1016/j.ifacol.2021.08.395 [30] Zliobaite I. Learning under concept drift: an overview. Computer Science, 2010, 4 (2): 107−194 [31] 乔俊飞, 孙子健, 汤健. 面向工业过程软测量建模的概念漂移检测综述. 控制理论与应用, 2021, 38 (08): 1159−1174 doi: 10.7641/CTA.2021.00334Qiao Jun-Fei, Sun Zi-Jian, Tang Jian. Overview of Conceptual Drift Detection for Industrial Process Soft Sensing Modeling. Control Theory and Application, 2021, 38 (08): 1159−1174 doi: 10.7641/CTA.2021.00334 [32] Sun B, Feng J, Saenko K. Return of frustratingly easy domain adaptation. In: Proceedings of the AAAI Conference on Artificial Intelligence. Phoenix, USA, 2016. 2058-2065 [33] Zhang T M, Yan G W, Ren M F, Cheng L, Li R, et al. Dynamic transfer soft sensor for concept drift adaptation. Journal of Process Control, 2023, 123: 50−63 doi: 10.1016/j.jprocont.2023.01.012 [34] Zhao Z J, Yan G W, Li R, Xiao S Y, Wang F, et al. Instance transfer partial least squares for semi-supervised adaptive soft sensor. Chemometrics and Intelligent Laboratory Systems, 2024, 245: Article No. 105062 doi: 10.1016/j.chemolab.2024.105062 [35] Fernando B, Habrard A, Sebban M, Tuytelaars T. Unsupervised Visual Domain Adaptation Using Subspace Alignment. In: Proceedings of the IEEE International Conference on Computer Vision. Portland, USA: IEEE, 2013. 2960-2967 [36] Sun B C, Feng J S, Saenko K. Correlation alignment for unsupervised domain adaptation. Domain Adaptation in Computer Vision Applications, 2017153−171 [37] Pan S J, Tsang I W, Kwok J T, Yang Q. Domain adaptation via transfer component analysis. IEEE Transactions on Neural Networks, 2011, 22 (2): 199−210 doi: 10.1109/TNN.2010.2091281 [38] Borgwardt K M, Gretton A, Rasch M J, Kriegel H P, Schlkopf B, Smola A J. Integrating structured biological data by kernel maximum mean discrepancy. Bioinformatics, 2006, 22 (14): 49−57 doi: 10.1093/bioinformatics/btl242 [39] Liu Y, Liu W, Yan X, Guo S, Zhang C A. Adaptive transfer learning for PINN. Journal of Computational Physics, 2023, 490: Article No. 112291 doi: 10.1016/j.jcp.2023.112291 [40] Chen R T, Rubanova Y, Bettencourt J, Duvenaud D K. Neural ordinary differential equations. arXiv: 1806.07366, 2018. [41] He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition. Las Vegas, USA: IEEE, 2016, 770-778 [42] Pilario K E S, Cao Y. Canonical variate dissimilarity analysis for process incipient fault detection. IEEE Transactions on Industrial Informatics, 2018, 14 (12): 5308−5315 doi: 10.1109/TII.2018.2810822 [43] Tian Z, Yuan J Q, Xu L. Modeling of drum boiler-turbine unit and the model-based coordinated control strategy. In: Proceedings of the 35th Chinese Control Conference. Chengdu, China: IEEE, 2016. 3327-3332 [44] Li K, Thompson S, Peng J X. Modelling and prediction of NOx emission in a coal-fired power generation plant. Control Engineering Practice, 2004, 12 (6): 707−723 doi: 10.1016/S0967-0661(03)00171-0 -
计量
- 文章访问数: 10
- HTML全文浏览量: 13
- 被引次数: 0
