-
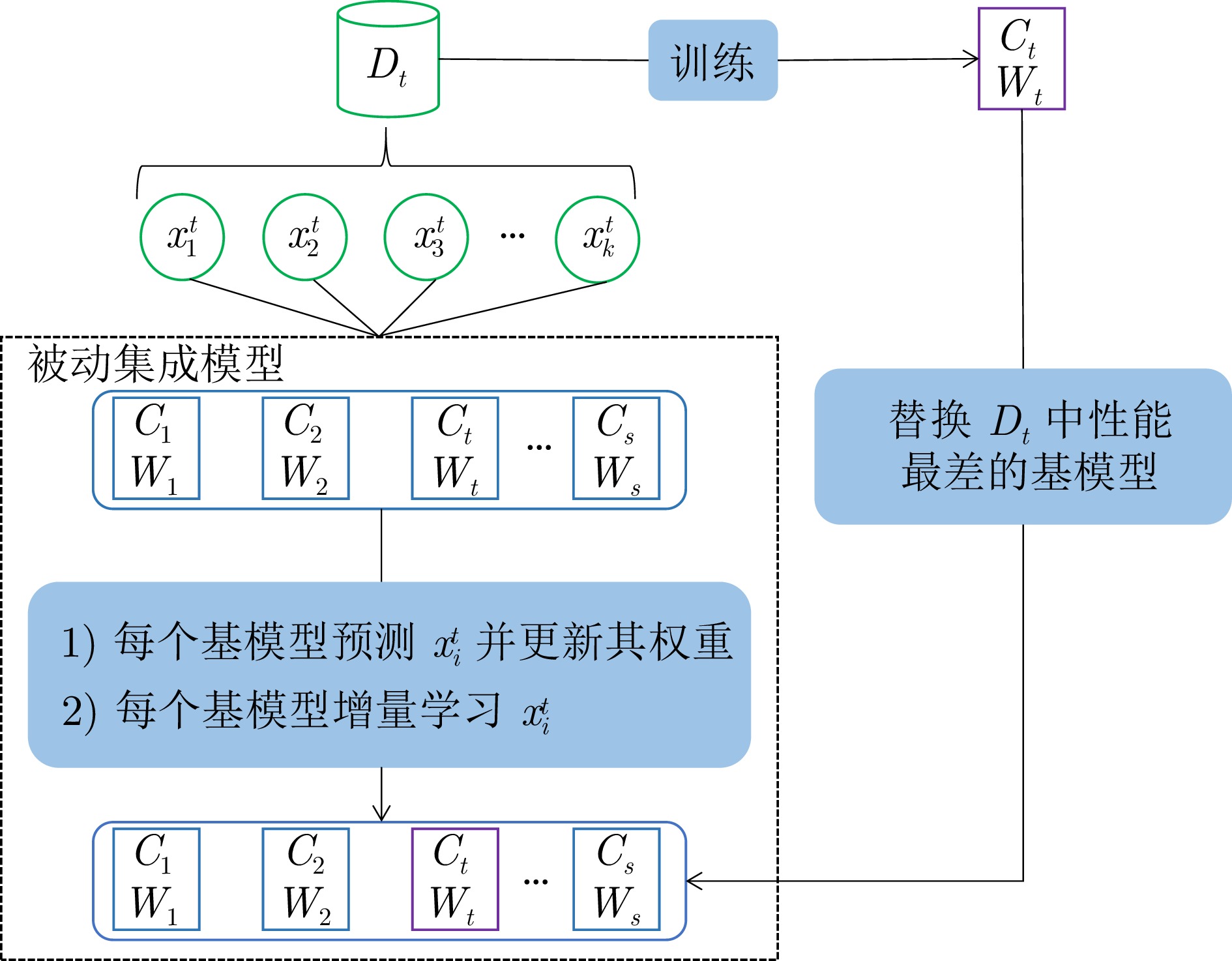
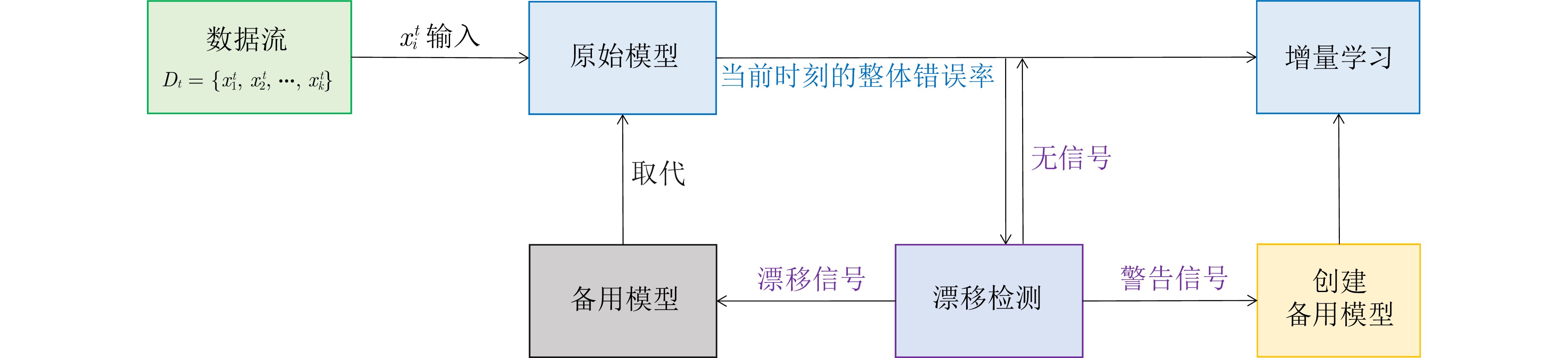
摘要: 数据流是一组随时间连续到来的数据序列, 在数据流不断产生的过程中, 由于各种因素的影响, 数据分布随时间推移可能以不可预测的方式发生变化, 这种现象称为概念漂移. 在漂移发生后, 当前模型需要及时响应数据流中的实时分布变化, 并有效处理不同类型的概念漂移, 从而避免模型泛化性能下降. 针对这一问题, 提出一种基于主动–被动增量集成的概念漂移适应方法(CDAM-APIE). 该方法首先使用在线增量集成策略构建被动集成模型, 对新样本进行实时预测以动态更新基模型权重, 有利于快速响应数据分布的瞬时变化, 并增强模型适应概念漂移的能力. 在此基础上, 利用增量学习和概念漂移检测技术构建主动基模型, 提升模型在平稳数据流状态下的鲁棒性和漂移后的泛化性能. 实验结果表明, CDAM-APIE能够对概念漂移做出及时响应, 同时有效提高模型的泛化性能.Abstract: A data stream refers to a set of data sequences that arrive continuously over time. Due to various influencing factors, the data distribution may change in an unpredictable manner over time during the continuous generation of data streams, a phenomenon known as concept drift. After the drift occurs, the current model needs to respond promptly to the real-time distributional changes in the data stream and handle different types of concept drift efficiently, in order to avoid the degradation of the model generalization performance. Aiming at this problem, we propose a concept drift adaptation method based on the active-passive incremental ensemble (CDAM-APIE). Firstly, CDAM-APIE uses the online incremental ensemble strategy to construct a passive ensemble model, which makes real-time predictions on new samples to dynamically update the weights of the base model. It is beneficial for quickly responding to instantaneous changes in data distribution and enhancing the model's ability to adapt to concept drift. On this basis, an active basis model is constructed with incremental learning and concept drift detection techniques to improve the robustness of the model under steady data stream states and the generalization performance after drift. The experimental results show that CDAM-APIE can respond to concept drift promptly and effectively improve the generalization performance of the model.
-
Key words:
- Concept drift /
- data stream classification /
- incremental learning /
- online ensemble
-
表 1 实验所用数据集
Table 1 Datasets used in experiment
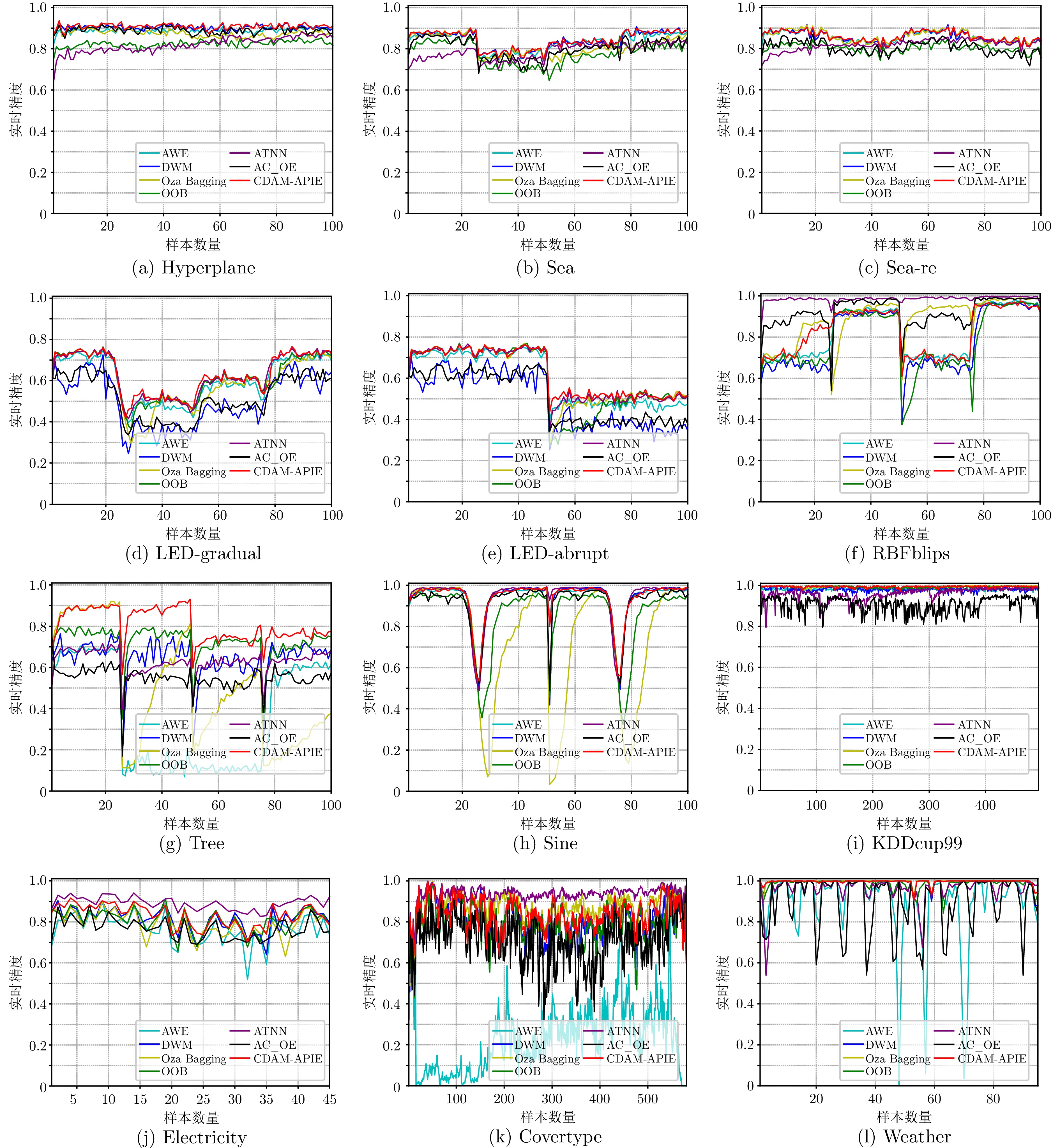
数据集 特征个数 类别个数 样本个数 (k) 漂移类型 漂移次数 漂移位点 (k) Hyperplane 10 2 100 增量 − − Sea 3 2 100 渐变 3 25, 50, 75 Sea-re 3 2 100 重复 3 25, 50, 75 LED-gradual 24 10 100 渐变 3 25, 50, 75 LED-abrupt 24 10 100 突变 1 50 RBFblips 20 4 100 突变 3 25, 50, 75 Tree 30 10 100 突变 3 25, 50, 75 Sine 4 2 100 重复 3 25, 50, 75 KDDcup99 41 23 494 − − − Electricity 6 2 45 − − − Covertype 54 7 581 − − − Weather 9 3 95 − − − 表 2 不同方法在各数据集上的平均实时精度
Table 2 Average real-time accuracy of different methods on each dataset
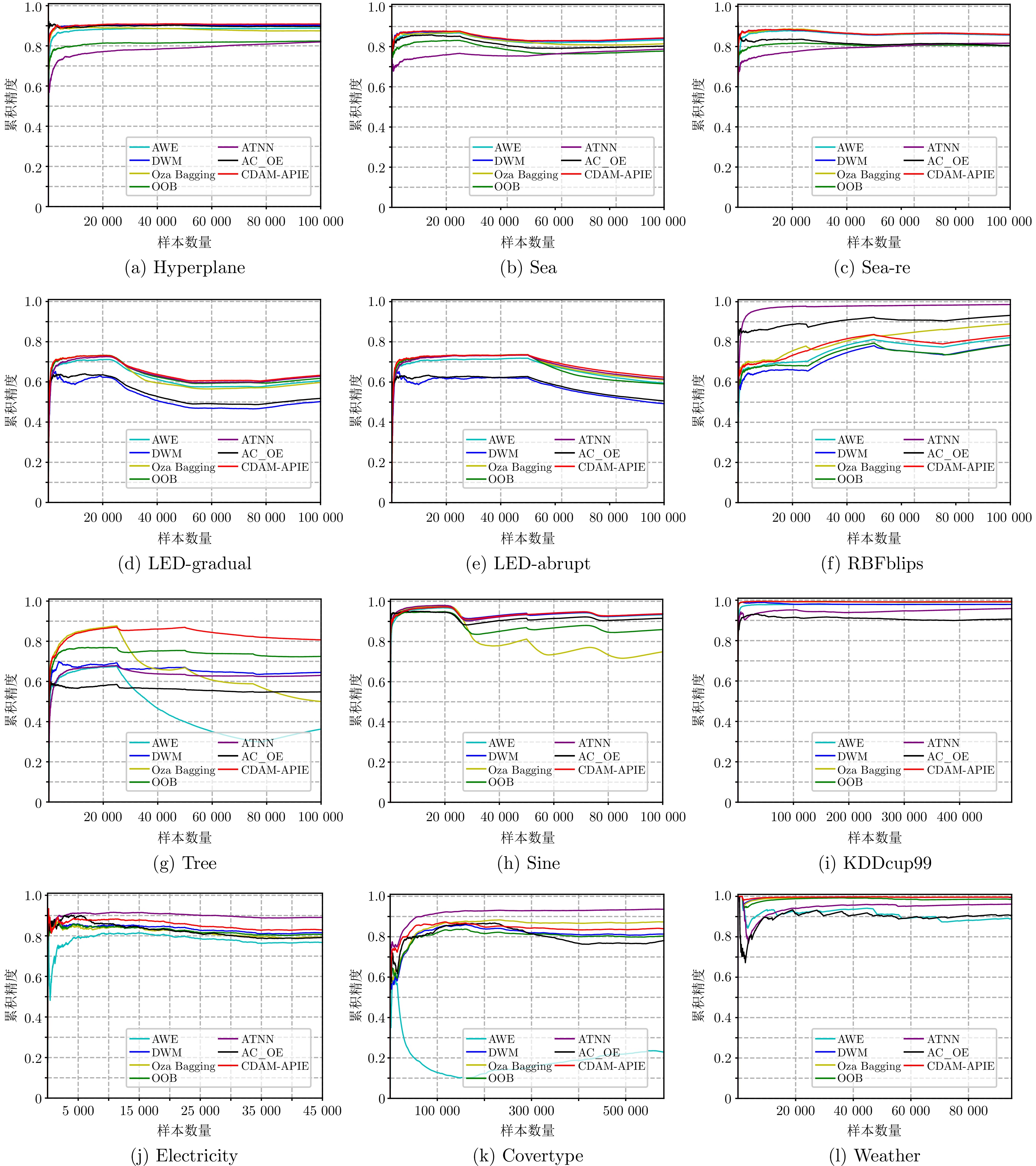
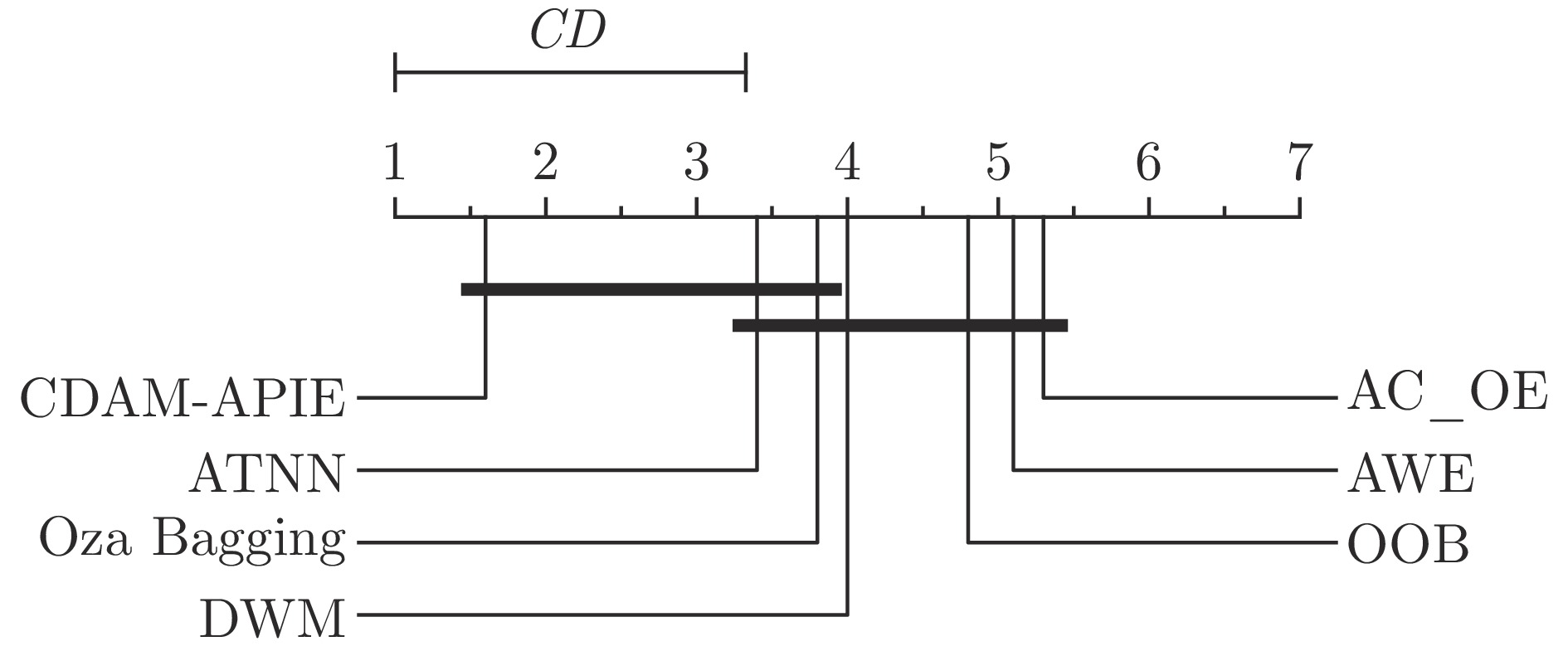
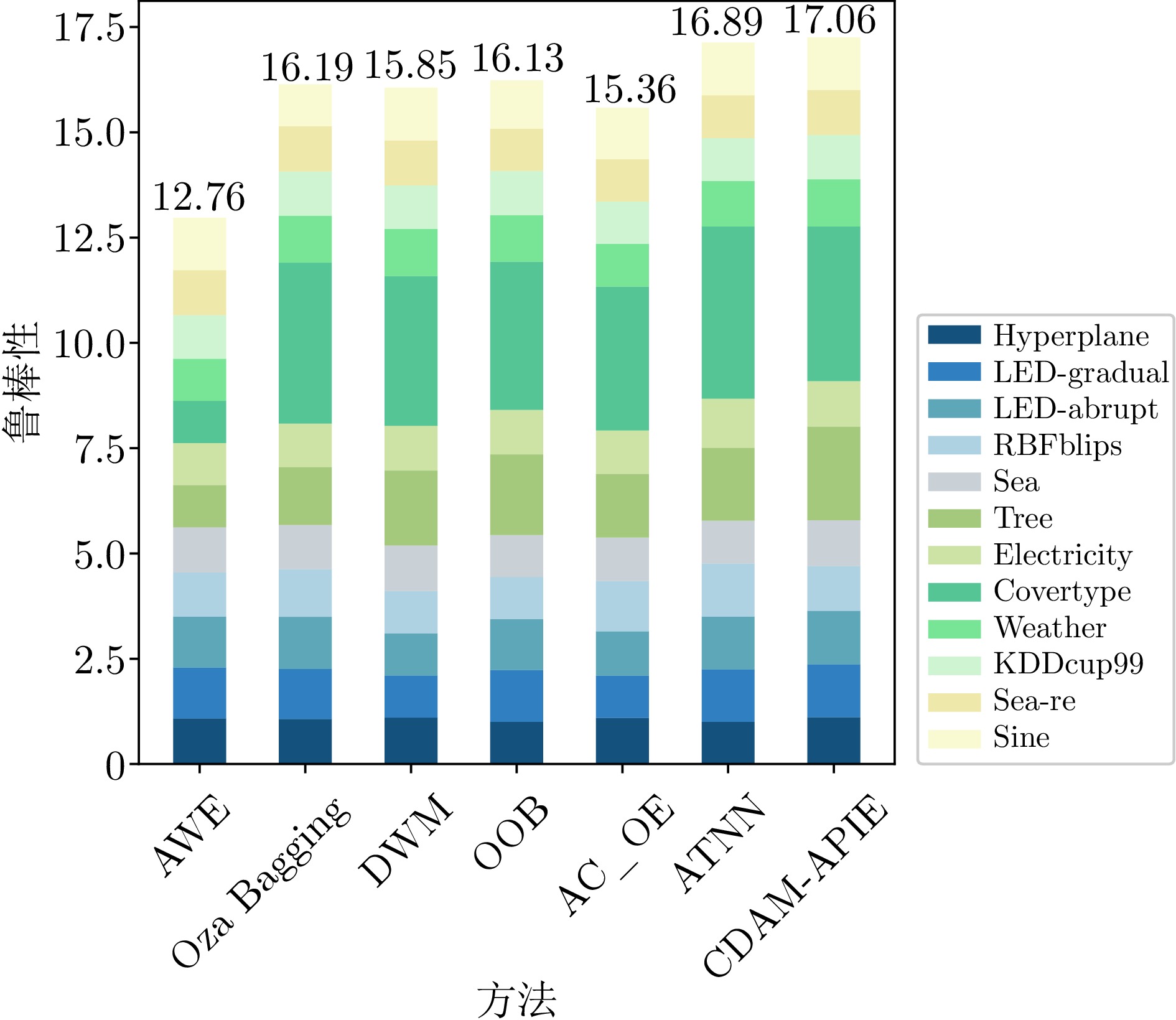
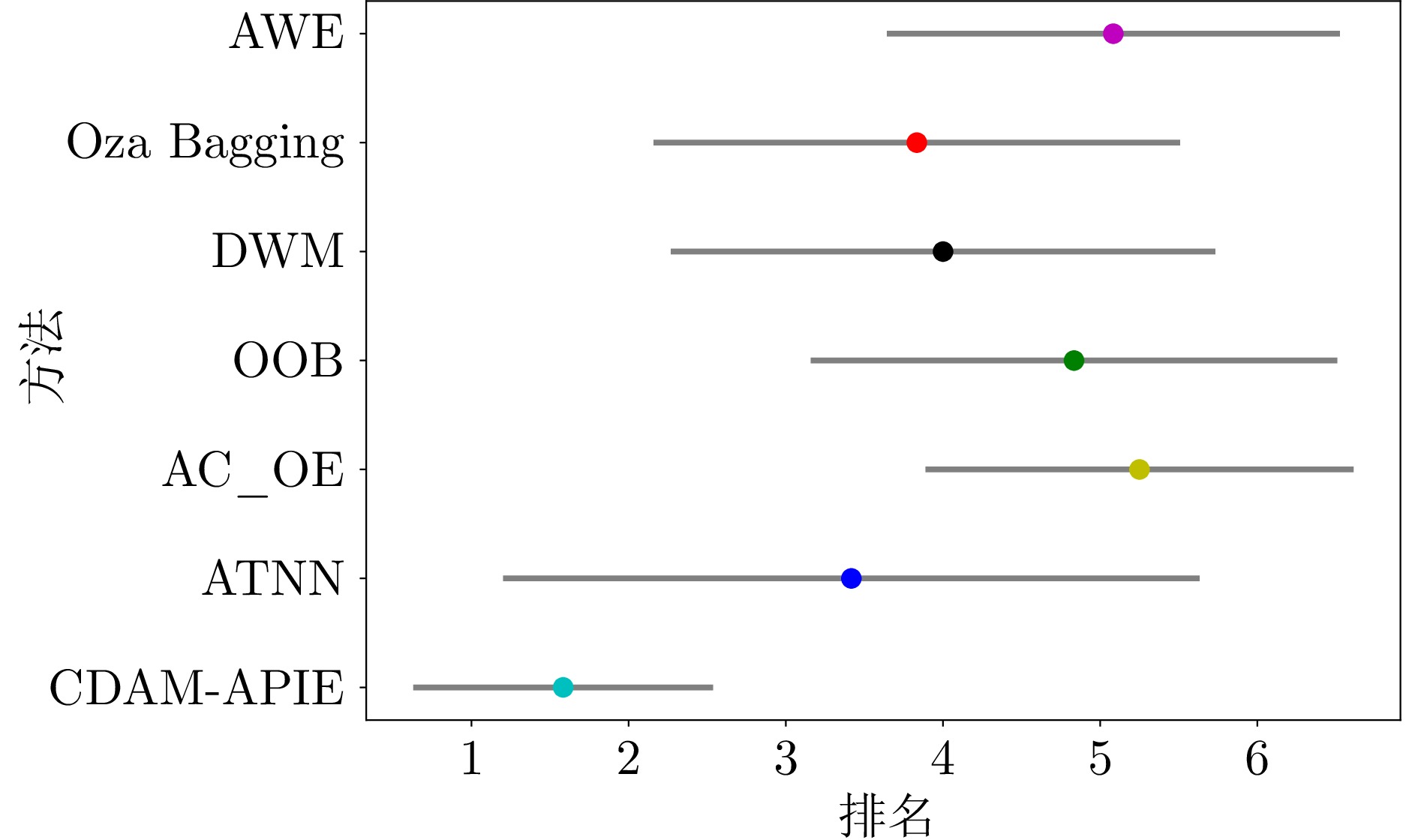
数据集 AWE Oza Bagging DWM OOB AC_OE ATNN CDAM-APIE (本文) Hyperplane 0.8882 (4)0.8758 (5)0.9029 (2)0.8223 (6)0.8966 (3)0.8195 (7)0.9088 (1)Sea 0.8335 (3)0.8159 (4)0.8410 (2)0.7754 (7)0.8027 (5)0.7871 (6)0.8432 (1)Sea-re 0.8564 (4)0.8596 (2)0.8581 (3)0.8030 (7)0.8055 (6)0.8166 (5)0.8605 (1)LED-gradual 0.6055 (4)0.5979 (5)0.5022 (7)0.6163 (3)0.5054 (6)0.6282 (2)0.6330 (1)LED-abrupt 0.5944 (5)0.6075 (3)0.4918 (7)0.5948 (4)0.5178 (6)0.6147 (2)0.6240 (1)RBFblips 0.8208 (5)0.8852 (3)0.7861 (6)0.7811 (7)0.9316 (2)0.9855 (1)0.8309 (4)Tree 0.3630 (7)0.4982 (6)0.6449 (3)0.6938 (2)0.5480 (5)0.6300 (4)0.8072 (1)Sine 0.9331 (4)0.7489 (7)0.9363 (3)0.8595 (6)0.9155 (5)0.9381 (1)0.9374 (2)KDDcup99 0.9796 (4)0.9920 (2)0.9793 (5)0.9913 (3)0.9446 (7)0.9589 (6)0.9926 (1)Electricity 0.7678 (7)0.7928 (5)0.8153 (3)0.8110 (4)0.7919 (6)0.8912 (1)0.8300 (2)Covertype 0.2288 (7)0.8735 (2)0.8135 (4)0.8052 (5)0.7813 (6)0.9362 (1)0.8400 (3)Weather 0.8893 (7)0.9952 (2)0.9941 (3)0.9862 (4)0.9069 (6)0.9616 (5)0.9956 (1)平均排名 5.1 3.8 4.0 4.8 5.3 3.4 1.6 注: 括号内数值表示各方法的排名名次, 加粗字体表示在同一数据集上各方法中的最优结果. 表 3 不同方法的恢复速率
Table 3 Recovery speed of different methods
漂移位点 数据集 AWE Oza Bagging DWM OOB AC_OE ATNN CDAM-APIE (本文) 25 k Sea 0.48 0.52 0.46 0.53 0.76 0.56 0.46 LED-gradual 1.15 1.20 0.72 1.09 1.33 1.12 1.16 RBFblips 0.29 0.38 0.28 0.37 0.17 0.07 0.15 Tree 3.60 1.77 1.39 0.89 1.29 1.33 0.58 平均排名 4.8 5.8 2.8 3.8 5.0 3.5 2.3 50 k Sea 0.20 0.53 0.19 1.17 0.45 0.36 0.17 LED-gradual 0.58 0.57 0.63 0.58 0.61 0.54 0.53 LED-abrupt 1.63 1.36 1.35 1.36 1.28 1.66 1.47 RBFblips 0.86 0.36 1.26 1.17 0.52 0.04 0.87 Tree 0.89 1.55 1.60 1.16 1.44 1.56 0.89 平均排名 3.6 3.8 5.0 4.6 3.8 4.0 2.6 75 k Sea 0.52 0.44 0.33 0.61 0.47 0.20 0.33 LED-gradual 1.09 0.44 0.51 1.06 1.23 0.99 0.47 RBFblips 0.11 0.13 0.24 0.19 0.07 0.02 0.08 Tree 2.20 1.74 1.04 2.62 1.44 1.18 0.76 平均排名 5.5 3.8 3.5 6.3 4.5 2.3 2.0 表 4 消融效果分析
Table 4 Analysis of ablation effect
数据集 基模型 被动集成模型 主动基模型 CDAM-APIE Hyperplane 0.8603 0.8904 0.8716 0.9088 Sea 0.8118 0.8315 0.8333 0.8432 Sea-re 0.8554 0.8505 0.8517 0.8605 LED-gradual 0.5859 0.6266 0.6217 0.6330 LED-abrupt 0.6057 0.6154 0.6197 0.6240 RBFblips 0.8430 0.7825 0.8097 0.8309 Tree 0.4902 0.7873 0.7917 0.8072 Sine 0.6562 0.8941 0.9372 0.9374 KDDcup99 0.9904 0.9786 0.9922 0.9926 Electricity 0.7828 0.8117 0.8092 0.8300 Covertype 0.8247 0.8178 0.8246 0.8400 Weather 0.9953 0.9771 0.9929 0.9956 表 5 CDAM-APIE在不同参数下的平均实时精度
Table 5 Average real-time accuracy of CDAM-APIE under different parameters
固定数据单元$k$ $50$ $100$ $150$ 权重衰退率$\beta$ 权重衰退率$\beta$ 权重衰退率$\beta$ 0.80 0.85 0.90 0.95 0.80 0.85 0.90 0.95 0.80 0.85 0.90 0.95 Hyperplane 0.9005 0.9020 0.9046 0.9076 0.9050 0.9062 0.9076 0.9088 0.9087 0.9099 0.9106 0.9113 Sea 0.8388 0.8400 0.8413 0.8420 0.8417 0.8423 0.8430 0.8432 0.8431 0.8432 0.8431 0.8427 Sea-re 0.8573 0.8584 0.8591 0.8600 0.8596 0.8599 0.8603 0.8605 0.8604 0.8607 0.8609 0.8606 LED-gradual 0.6309 0.6313 0.6317 0.6320 0.6314 0.6319 0.6328 0.6330 0.6348 0.6353 0.6358 0.6362 LED-abrupt 0.6220 0.6223 0.6230 0.6234 0.6229 0.6233 0.6237 0.6240 0.6228 0.6235 0.6241 0.6243 RBFblips 0.8366 0.8369 0.8378 0.8368 0.8308 0.8314 0.8312 0.8309 0.8503 0.8503 0.8505 0.8500 Tree 0.8073 0.8079 0.8086 0.8089 0.8066 0.8068 0.8071 0.8072 0.7960 0.7961 0.7963 0.7970 Sine 0.9372 0.9372 0.9372 0.9372 0.9371 0.9373 0.9371 0.9374 0.9378 0.9379 0.9381 0.9381 KDDcup99 0.9922 0.9922 0.9922 0.9922 0.9922 0.9922 0.9924 0.9926 0.9931 0.9931 0.9931 0.9932 Electricity 0.8548 0.8515 0.8482 0.8416 0.8401 0.8385 0.8358 0.8300 0.8205 0.8205 0.8207 0.8204 Covertype 0.8569 0.8543 0.8510 0.8460 0.8455 0.8444 0.8426 0.8400 0.8451 0.8448 0.8441 0.8415 Weather 0.9946 0.9945 0.9947 0.9956 0.9956 0.9957 0.9956 0.9956 0.9951 0.9952 0.9952 0.9953 总体标准差 $0.121\;0$ 0.120 8 $0.121\;0$ -
[1] Din S, Yang Q, Shao J, Mawuli C, Ullah A, Ali W. Synchronization-based semi-supervised data streams classification with label evolution and extreme verification delay. Information Sciences, 2024, 678: Article No. 120933 doi: 10.1016/j.ins.2024.120933 [2] Liao G, Zhang P, Yin H, Deng X, Li Y, Zhou H, et al. A novel semi-supervised classification approach for evolving data streams. Expert Systems With Applications, 2023, 215: Article No. 119273 doi: 10.1016/j.eswa.2022.119273 [3] Zheng X, Li P, Wu X. Data stream classification based on extreme learning machine: A review. Big Data Research, 2022, 30: Article No. 100356 doi: 10.1016/j.bdr.2022.100356 [4] Agrahari S, Singh A. Concept drift detection in data stream mining: A literature review. Journal of King Saud University-Computer and Information Sciences, 2021, 34(10): 9523−9540 [5] Krempl G, Zliobaite I, Brzezinski D, Hullermeier E, Last M, Lemaire V, et al. Open challenges for data stream mining research. ACM SIGKDD Explorations Newsletter, 2014, 16(1): 1−10 doi: 10.1145/2674026.2674028 [6] Lughofer E, Pratama M. Online active learning in data stream regression using uncertainty sampling based on evolving generalized fuzzy models. IEEE Transactions on Fuzzy Systems, 2018, 26(1): 292−309 doi: 10.1109/TFUZZ.2017.2654504 [7] 翟婷婷, 高阳, 朱俊武. 面向流数据分类的在线学习综述. 软件学报, 2020, 31(4): 912−931Zhai Ting-Ting, Gao Yang, Zhu Jun-Wu. Survey of online learning algorithms for streaming data classification. Journal of Software, 2020, 31(4): 912−931 [8] Li H, Zhao T. A dynamic similarity weighted evolving fuzzy system for concept drift of data streams. Information Sciences, 2024, 659: Article No. 120062 doi: 10.1016/j.ins.2023.120062 [9] 杜航原, 王文剑, 白亮. 一种基于优化模型的演化数据流聚类方法. 中国科学: 信息科学, 2017, 47(11): 1464−1482 doi: 10.1360/N112017-00107Du Hang-Yuan, Wang Wen-Jian, Bai Liang. A novel evolving data stream clustering method based on optimization model. Scientia Sinica: Informationis, 2017, 47(11): 1464−1482 doi: 10.1360/N112017-00107 [10] Wang P, Jin N, Davies D, Woo W. Model-centric transfer learning framework for concept drift detection. Knowledge-Based Systems, 2023, 275: Article No. 110705 doi: 10.1016/j.knosys.2023.110705 [11] 郭虎升, 张爱娟, 王文剑. 基于在线性能测试的概念漂移检测方法. 软件学报, 2020, 31(4): 932−947Guo Hu-Sheng, Zhang Ai-Juan, Wang Wen-Jian. Concept drift detection method based on online performance test. Journal of Software, 2020, 31(4): 932−947 [12] Karimian M, Beigy H. Concept drift handling: A domain adaptation perspective. Expert Systems With Applications, 2023, 224: Article No. 119946 doi: 10.1016/j.eswa.2023.119946 [13] Wozniak M, Zyblewski P, Ksieniewicz P. Active weighted aging ensemble for drifted data stream classification. Information Sciences, 2023, 630: 286−304 doi: 10.1016/j.ins.2023.02.046 [14] Cherif A, Badhib A, Ammar H, Alshehri S, Kalkatawi M, Imine A. Credit card fraud detection in the era of disruptive technologies: A systematic review. Journal of King Saud University-Computer and Information Sciences, 2023, 35(1): 145−174 doi: 10.1016/j.jksuci.2022.11.008 [15] Halstead B, Koh Y, Riddle P, Pears P, Pechenizkiy M, Bifet A, et al. Analyzing and repairing concept drift adaptation in data stream classification. Machine Learning, 2022, 111(10): 3489−3523 doi: 10.1007/s10994-021-05993-w [16] Jiao B, Guo Y, Gong D, Chen Q. Dynamic ensemble selection for imbalanced data streams with concept drift. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(1): 1278−1291 doi: 10.1109/TNNLS.2022.3183120 [17] Liu N, Zhao J. Streaming data classification based on hierarchical concept drift and online ensemble. IEEE Access, 2023, 11: 126040−126051 doi: 10.1109/ACCESS.2023.3327637 [18] Wilson J, Chaudhury S, Lall B. Homogeneous-heterogeneous hybrid ensemble for concept-drift adaptation. Neurocomputing, 2023, 557: Article No. 126741 doi: 10.1016/j.neucom.2023.126741 [19] Gama J, Medas P, Castillo G, Rodrigues P. Learning with drift detection. In: Proceedings of the 17th Brazilian Symposium on Artificial Intelligence. Maranhao, Brazil: Springer, 2004. 286−295 [20] Hinder F, Artelt A, Hammer B. Towards non-parametric drift detection via dynamic adapting window independence drift detection (DAWIDD). In: Proceedings of the 37th International Conference on Machine Learning. New York, USA: PMLR, 2020. 4249−4259 [21] Wen Y, Liu X, Yu H. Adaptive tree-like neural network: Overcoming catastrophic forgetting to classify streaming data with concept drifts. Knowledge-Based Systems, 2024, 293: Article No. 111636 doi: 10.1016/j.knosys.2024.111636 [22] Pratama M, Pedrycz W, Lughofer E. Evolving ensemble fuzzy classifier. IEEE Transactions on Fuzzy Systems, 2018, 26(5): 2552−2567 [23] Street W, Kim Y. A streaming ensemble algorithm (SEA) for large-scale classification. In: Proceedings of the 7th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2001. 377−382 [24] Wang H, Fan W, Yu P, Han J. Mining concept-drifting and noisy data streams using ensemble classifiers. In: Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2003. 226−235 [25] Weinberg A, Last M. EnHAT-Synergy of a tree-based ensemble with Hoeffding adaptive tree for dynamic data streams mining. Information Fusion, 2023, 89: 397−404 doi: 10.1016/j.inffus.2022.08.026 [26] Oza N, Russell S. Experimental comparisons of online and batch versions of bagging and boosting. In: Proceedings of the 7 ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2001. 359−364 [27] Kolter J, Maloof M. Dynamic weighted majority: An ensemble method for drifting concepts. Journal of Machine Learning Research, 2007, 8(12): 2755−2790 [28] 郭虎升, 丛璐, 高淑花, 王文剑. 基于在线集成的概念漂移自适应分类方法. 计算机研究与发展, 2023, 60(7): 1592−1602Guo Hu-Sheng, Cong Lu, Gao Shu-Hua, Wang Wen-Jian. Adaptive classification method for concept drift based on online ensemble. Journal of Computer Research and Development, 2023, 60(7): 1592−1602 [29] Gama J, Zliobaite I, Bifet A, Pechenizkiy M, Bouchachia A. A survey on concept drift adaptation. ACM Computing Surveys, 2014, 46(4): 1−37 [30] Wang B, Pineau J. Online bagging and boosting for imbalanced data streams. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(12): 3353−3366 doi: 10.1109/TKDE.2016.2609424 [31] 赵鹏, 周志华. 基于决策树模型重用的分布变化流数据学习. 中国科学: 信息科学, 2021, 51(1): 1−12 doi: 10.1360/SSI-2020-0170Zhao Peng, Zhou Zhi-Hua. Learning from distribution-changing data streams via decision tree model reuse. Scientia Sinica: Informationis, 2021, 51(1): 1−12 doi: 10.1360/SSI-2020-0170 [32] Pereira D, Afonso A, Medeiros F. Overview of Friedman's test and post-hoc analysis. Communications in Statistics-Simulation and Computation, 2015, 44(10): 2636−2653 doi: 10.1080/03610918.2014.931971 [33] Demsar J. Statistical comparisons of classifiers over multiple data sets. The Journal of Machine Learning Research, 2006, 7: 1−30 -




 下载:
下载: