在线优化广泛应用于目标跟踪^[1]、在线广告投放^[2]等各个领域, 其主要特点是学习者在动态或对抗环境中根据历史信息做出决策, 然后获得当前时刻的代价函数信息^[3]. 目前为止, 研究者已经提出许多在线优化算法^[4−7], 并分析它们对应的收敛性. 然而, 传统在线算法以轮流顺序的方式处理目标函数, 这会导致多核中央处理器或图形处理器的资源浪费. 为解决这一问题, 出现分布式在线算法, 其将大型问题分配给具有网络拓扑结构的各个代理或智能体, 或者每个代理天然地具有自己的私有信息, 其中, 每个代理都有自己的处理器和内存. 通过并行计算和相邻智能体之间的协作, 可以有效解决大规模复杂优化问题, 如编队跟踪^[8]、智能电网^[9]、智能建筑^[10]等. 相关的工作包括解决分布式一致问题^{[7, 11]}, 并将其拓展到更多复杂场景中, 同时也考虑了时变有向通讯图^[12]、不等式约束和Bandit反馈^[13]、随机梯度或噪声梯度反馈^[14]等情况.

在分布式在线场景中, 常常会出现每个智能体的局部目标函数由不同性质的函数组成, 例如包含一个非光滑正则项, 将这样的问题称为分布式在线复合优化问题, 如电网资源分配中每个区域的目标函数中包含电压约束的投影算子^[15]; 在水下信道识别中, 每个传感器的局部目标函数是其识别信息的均方误差1范数^[16]. 这种目标函数是复合函数的优化问题广泛出现于电网资源分配^[15]、压缩感知^[16]等问题中. 为解决分布式在线复合优化问题, 目前已经提出的相关算法有分布式近似镜像下降法^[5]、分布式近端梯度下降法^[6]、分布式前向后向分裂法^[7]等.

然而, 在实际应用中, 如多卫星协调^[17]、无线传感器网络^[16]以及可再生能源分配^[15]等问题, 由于昂贵的梯度计算、网络不稳定性、磁盘吞吐量、带宽、硬件、距离等因素, 智能体在更新状态时不得不使用过时的信息, 这就造成分布式计算过程中的延迟现象. 目前的工作主要考虑两种延迟: 反馈延迟和通讯延迟. 反馈延迟是由于智能体获取或计算自身信息 (例如函数信息或梯度信息) 需要花费额外时间, 从而导致更新状态时使用延迟的信息; 而通讯延迟是由于智能体将信息传输给其他智能体时需要额外时间, 从而导致接收到延迟的邻居信息. 事实上, 不仅硬件条件会导致反馈延迟, 某些问题的设置也不得不使用带有延迟的反馈信息. 例如, 在在线广告推广算法中, 从推广某广告到用户决定点击该广告之间必然存在一定的时间间隔; 在军事应用中, 在线算法给出干扰策略后并不能立即得知干扰是否成功, 需要等待接收端做出反应后才能确定是否干扰成功; 在云计算中, 在线算法给出资源分配策略到批处理任务未完成前, 并不能知道该分配策略的效果; 投资组合在线学习算法受到市场信息和交易延迟的影响也无法立刻知道投资策略所获得的收益. Quanrud等^[18]在梯度下降算法和follow-the-perturbed-leader算法中考虑使用延迟反馈得到与没有延迟情况下相同的静态遗憾度, 表明在线学习算法在延迟反馈下不影响其静态遗憾上界, 并从理论上证明在延迟反馈下运行一般在线算法的合理性. 目前已经有大量的工作考虑了在线凸优化^[18−21]中的延迟现象. 如, Wang等^[19]在带有长期和短期约束的在线凸优化问题中考虑反馈延迟并基于路径长度和函数变化度分析动态遗憾上界. Bedi等^[22]利用非线性邻近函数作为约束保证智能体之间的状态相近, 并提出梯度延迟下的分布式异步在线鞍点算法, 然后以牺牲遗憾度为代价, 改进算法使得智能体之间的状态一致. Inoue等^[23]针对有向通信网络上的通讯延迟和动态不等式约束提出一种分布式原始对偶算法. 在近期相关的工作中, Liu等^[24]研究具有时变延迟反馈的分布式分簇博弈问题, 其中, 每个集群智能体的决策在不同的局部可行约束集内, 且所有智能体的决策满足不等式耦合约束. 他们提出的分布式在线延迟容忍广义纳什均衡学习算法在给定条件下建立动态遗憾和约束违反的次线性增长界. 与他们的工作相比, 本文研究了多智能体合作下的分布式在线优化问题.

另外, 在一些实际问题中, 智能体由于未知函数具体表达式或求解梯度信息需要花费巨大的计算资源, 从而导致无法获得梯度信息, 但可以获得函数在有限点处的取值. 例如, 在实践中, 大规模神经网络中的损失函数参数众多且涉及隐藏参数, 因此, 不易得到解析表达式和梯度信息, 但可以利用数值计算方式估计函数值信息^[25]. 类似的情况还出现在数据网络在线路由、黑盒对抗性攻击等问题中^[26]. 此时基于梯度信息的算法将不再适用, 需要使用一些无梯度优化算法来解决, 例如利用Bandit反馈技术设计算法, 利用函数在有限点处的取值对梯度进行估计来解决梯度未知的困难. 一些文献考虑没有延迟的Bandit反馈^{[5, 13, 25]}, 也有一些文献考虑具有延迟的Bandit反馈. Wan等^[20]研究在线有约束凸优化中的不确定延迟, 即延迟随时间发生变化, 当目标函数强凸时, 设计并分析所提出延迟在线梯度下降算法的静态遗憾上界, 然后又将其扩展为两点和$ n+1 $点Bandit反馈的情况. 针对完全信息反馈和Bandit反馈中的延迟, Cao等^[27]分别设计两种在线分布式梯度下降算法, 并证明只要平均延迟是次线性的, 静态遗憾就是次线性的. 基于时变耦合不等式约束, Wang等^[28]在时变有向图上提出分布式在线延迟原始对偶Bandit push-sum算法. Xiong等^[29]利用事件触发机制缓解网络带宽有限问题, 并提出具有延迟单点和延迟两点Bandit反馈的事件触发分布式在线凸优化算法.

事实上, 许多分布式在线复合优化问题都存在延迟反馈现象. 以现实水下无线通信信道识别 (经典的分布式在线复合优化问题) 为例, 由于许多海洋信道的混响时间很长, 该信道具有很大的延迟^[30]. 然而, 很少有研究讨论分布式在线复合优化中的时变延迟问题. 虽然20世纪初期研究人员就发现针对复合函数的不同项进行不同处理所设计的算法的表现效果要优于将函数整体一起处理的表现效果^[5−7], 但考虑分布式在线场景的研究是近些年才发展起来的, 目前已有的针对分布式在线复合优化的研究包括设计不同的分布式复合优化算法、考虑不等式约束、考虑动态图下算法的设计和分析等^{[5−7, 15, 31]}, 迫切需要理论研究考虑更多复杂且真实的场景, 为分布式在线复合优化应用于更多复杂真实场景做理论保证. 另外, 分布式在线场景中考虑延迟也需要一定的理论突破, 集中式场景下的延迟大都是时变的^{[18, 20]}, 而在分布式场景下每个智能体的延迟往往都是时不变的^{[27−29, 32−33]}, 少数工作研究了时变的延迟^{[21, 34]}. 设置时变的延迟会导致接收到的函数序列发生变化, 此时需要估计接收函数序列与真实函数序列的差距, 再加上每个智能体具有不同的延迟, 这样的设置会对分析带来困难.

以下是近期基于延迟反馈的分布式在线优化研究. Wang等^[21]设计时变有向图上的时变延迟梯度反馈和时变延迟通讯反馈算法, 并获得次线性的静态遗憾上界. Cao等^[27]针对分布式环境下凸的局部目标函数设计具有延迟梯度反馈和延迟两点Bandit反馈的算法, 考虑到每个智能体有不同的固定延迟, 获得$ {\rm O}(\sqrt{\bar{\tau}T}) $的静态遗憾上界, $ \bar{\tau} $为所有智能体延迟的均值. Wang等^[28]设计有向动态图上每个智能体的状态受时变不等式耦合约束的固定延迟两点Bandit反馈的分布式在线算法, 并对静态遗憾进行分析. Xiong等^[29]考虑事件触发机制下的固定延迟单点Bandit反馈和两点Bandit反馈算法, 分别获得$ {\rm O}(\bar{\tau}T^{\frac{3}{4}}) $和$ {\rm O}(\bar{\tau}\sqrt{T}) $的静态遗憾上界. 而后, Xiong等^[32]研究具有有限带宽和反馈延迟的分布式在线多智能体凸优化问题, 设计延迟次梯度的事件触发分布式在线镜像下降算法, 并获得次线性的静态遗憾和动态遗憾, 其中, 在合适的参数选择下获得$ {\rm O}(\tau(\sqrt{T(1+C_T)}+C_T)) $的动态遗憾上界, $ \tau $为每个智能体固定的延迟. Meng等^[33]研究具有单点Bandit反馈延迟的分布式在线博弈问题, 其中, 每个智能体的局部时变代价函数和时变耦合约束均有共同的延迟, 设计一种基于镜像梯度下降和单点Bandit延迟反馈的分布式在线算法. Nguyen等^[34]研究集中式和分布式中的时变反馈延迟, 并获得$ {\rm O}(\sqrt{d_{\max}T}) $的静态遗憾上界, 其中, $ d_{\max} $是每个智能体在各时刻延迟之和的最大值. 总体而言, 大部分工作对静态遗憾上界进行分析^{[21, 27−29, 34]}, 且延迟大都为固定延迟^{[27−29, 32−34]}. 与已有工作相比, 本文考虑更加复杂的复合优化问题, 目标函数由强凸光滑函数与非光滑凸正则项复合而成, 且考虑更一般的延迟情况, 即每个智能体具有不同的时变延迟, 并对算法的动态遗憾进行分析, 相较静态遗憾中固定的比较序列来说, 将时变的最优序列作为比较序列更能评估算法的动态决策效果. 另外, 分布式在线工作中有关复合目标函数的讨论较少, 仅在早期的工作中针对复合目标函数研究分布式一致问题带有固定反馈延迟的影响^[35], 且这项工作仅考虑一般凸函数与非光滑正则项复合的情况, 并未研究本文讨论的由强凸光滑函数与非光滑正则项组成的复合情形.

基于上述事实, 本文分析带有时变反馈延迟的分布式在线复合优化问题的动态遗憾上界, 为分布式在线复合优化算法应用于更多反馈延迟场景奠定理论基础, 针对分布式复合优化问题中的梯度反馈、单点和两点Bandit反馈考虑时变延迟现象, 设计三种算法并分析它们的动态遗憾上界. 本文主要的贡献如下:

1) 首次考虑分布式在线复合优化问题中具有时变反馈延迟的现象, 同时, 每个智能体的局部目标函数由一个强凸函数与凸的非光滑正则项组成. 具体地, 每个智能体具有不同且时变的反馈延迟, 分别考虑了梯度反馈、单点Bandit反馈和两点Bandit反馈三种情况.

2) 基于这三种反馈延迟设计分布式复合优化算法, 并分析它们的动态遗憾上界. 梯度反馈延迟与两点Bandit反馈延迟在期望意义下获得相同阶数的动态遗憾上界$ {\rm O}(\bar{\tau} (D_T+1)+C_T+1) $, 单点Bandit反馈延迟下的动态遗憾上界在期望意义下稍差于前面两种, 为$ {\rm O}(\sqrt{T\log T}+\bar{\tau} (D_T+1)+C_T\,+ 1) $, 其中, $ \bar{\tau} $为所有智能体的平均延迟, $ T $为总迭代次数, $ C_T $为路径长度.

本文内容安排如下. 第1节给出相关符号定义; 第2节描述所研究的问题和评价指标, 并给出需要的假设条件; 第3节针对梯度反馈延迟设计算法并分析动态遗憾; 第4节针对单点和两点Bandit反馈延迟设计算法并分析动态遗憾; 第5节描述仿真实验与仿真结果; 最后一节对全文进行总结并提出未来的研究方向.

1.   符号

下面简要介绍本文所使用的相关数学符号. 符号$ {\bf{R}} $和$ {\bf{R}}^n $分别表示实数集和$ n $维欧氏空间. $ \lVert \cdot\rVert $默认为$ 2 $范数, $ \lVert \cdot\rVert_1 $表示$ 1 $范数. $ \lVert \cdot\rVert_\infty $为矩阵的无穷范数. $ \partial f(x) $表示为函数$ f $在$ x $点处的次微分集合, $ \tilde{\partial} f(x) $表示这个次微分集合中任意一个次梯度. $ {\bf{1}} $代表一个所有元素都为$ 1 $的$ N $维向量. $ [N] $代表集合$ \{1, 2,\;\cdots,\;N\} $. 矩阵$ A $和矩阵$ B $的克罗内克积定义为$ A \otimes B $. $ \langle \cdot,\; \cdot \rangle $是$ {\bf{R}}^n $空间中的欧氏内积. 令$ {\rm col}(x_1, x_2,\;\ldots,\;x_N) $表示各分量$ x_i\in {\bf{R}}^n $的串联列向量. 对于任意标量$ x\in{\bf{R}} $, 定义如下符号函数:

对于向量$ x\in{\bf{R}}^n $的符号函数$ {\rm sgn}(x) $是一个向量, 其中, 每个分量是对$ x $的相应分量做式(1)计算. 函数$ f(x):X\rightarrow {\bf{R}} $的近端算子定义为$ {\rm prox}_{\eta f}(x)= \arg\min_{u\in X} f(u)+\frac{1}{2\eta}\|u-x\|^2 $, 其中, $ X $表示函数$ f $的定义域.

2.   问题描述及假设

本文研究带有反馈延迟的分布式在线复合优化问题. 下面对这一问题进行数学化描述并给出研究所需要的假设条件.

首先, 一个由$ N $个智能体组成的无向连通网络可以表示为图$ {\cal{G}}=(V,\;E,\;A) $. 其中, $ V=[N] $表示顶点集合, $ E\subseteq V \times V $表示边集合, $ A\in{\bf{R}}^{N\times N} $表示加权邻接矩阵. 矩阵$ A $中的元素$ a_{ij} $代表智能体$ j $到$ i $的权重. 若$ a_{ij}>0 $, 说明$ j $可以向$ i $发送消息, 即$ (j,\;i) \in E $; 若$ a_{ij}=0 $, 则反之, 即$ (j,\;i) \notin E $. 令$ a_{\min}= \min_{(j,\;i) \in E}a_{ij} $代表最小非零权重.

在每个时刻$ t $, 具有$ N $个智能体的分布式在线复合优化问题的全局目标是每个智能体局部目标函数之和, 可以表示为

其中, $ X\subset{\bf{R}}^n $是优化约束集合, $ f_{i,\;t}(x),\;r_{i}(x):X\rightarrow {\bf{R}} $是智能体$ i $的局部目标函数, 而$ r_{i}(x) $是非光滑正则项. 由于局部目标函数是由光滑函数与非光滑函数组成的复合结构且随时间变化, 因此, 这样的问题称为分布式在线复合优化问题. 常见的正则项有$ 1 $范数、$ 2 $范数及投影算子等. 在整个优化过程中, 每个智能体只能利用自己与邻居的信息来更新自身的状态, 最终的目标是优化全局目标函数$ F_t(x) $.

在此问题的基础上, 考虑反馈延迟现象, 也就是说每个智能体无法实时获得它的局部目标函数信息. 造成反馈延迟的原因有很多, 例如网络拥塞、带宽限制、代理计算能力有限、传输速度等^[22]. 对于智能体$ i $来说, 在时刻$ t $, 它得到$ t-\tau_{i,\;t} $时刻的梯度信息或函数信息. 在此设置下, 每个智能体的延迟时间可以不相同, 并且由于延迟随时间变化, 智能体接收到的函数顺序也会发生变化.

2.1   评价指标

遗憾度是一种广泛认可的在线算法性能评估指标, 它表示一段时间内算法选择行动下的目标函数与比较序列下的目标函数之间的差异. 有效的在线算法可以使得遗憾上界达到次线性, 并且遗憾上界越小, 说明在线算法的表现效果越好. 静态遗憾是一种广泛使用的评估指标, 定义为$ \sum_{t=1}^{T}F_t(x_{j,\;t})\;- \sum_{t=1}^{T}F_t(x^*) $, 其中的比较序列为目标函数在$ T $时段内总和的固定最优变量$ x^*\in \arg\min_{x\in X}\sum_{t=1}^{T}F_t(x) $. 而在动态场景中, 时变目标函数的最优值在每个时刻往往并不相同, 动态遗憾更能体现出算法在动态场景下的表现效果. 本文选择任意智能体$ j $的动态遗憾作为评估所提出算法的性能指标, 定义为

其中, $ x_{j,\;t}\in X $是第$ j $个智能体在第$ t $次迭代的状态, $ x^*_t $是函数在$ t $时刻的最优解, $ T $是总迭代次数. 需要注意, 由于比较序列随时间变化, 动态遗憾上界除与时间$ T $有关以外, 还与问题的复杂度度量有关, 否则将无法实现次线性上界^[36], 例如路径长度$ C_T=\sum_{t=1}^{T}\rVert x^*_{t+1}-x^*_t\rVert $, 函数变化度$ F_T= \sum_{i=1}^{N} \sum_{t=1}^{T}\max_{x\in X}| f_{i,\;t+1}(x)-f_{i,\;t}(x)| $, 梯度变化度 $ D_T= \sum_{i=1}^{N}\sum_{t=1}^{T}\max_{x\in X}\rVert \nabla f_{i,\;t+1}(x) - \nabla f_{i,\;t}(x)\rVert $等^{[4, 37]}.

2.2   假设条件

下面给出本文所需要的假设条件.

假设1. 对于任意$ t\in [T] $和$ i\in [N] $, $ f_{i,\;t} $是$ \mu $-强凸函数, 即对于任意$ x,\;y\in X $, $ f_{i,\;t}(y)\geq f_{i,\;t}(x)\,+ \langle \nabla f_{i,\;t}(x),\;y-x \rangle+\frac{\mu}{2}\rVert x-y\rVert^2 $.

假设2. 对于任意$ t\in [T] $和$ i\in [N] $, $ f_{i,\;t} $是$ \alpha $-光滑函数, 即对于任意$ x,\;y\in X $, 有$ \rVert \nabla f_{i,\;t}(x)\;- \nabla f_{i,\;t}(y)\rVert\leq \alpha\rVert x-y\rVert $.

假设3. 对于任意$ t\in [T] $和$ i\in [N] $, $ r_{i} $是闭凸函数.

假设4. 约束集合$ X $是凸紧集, 于是, 存在一个正实数$ R $, 对于任意$ x\in X $, 有$ \rVert x\rVert\leq R $.

假设5. 对于任意$ t\in [T] $和$ i\in [N] $, $ f_{i,\;t},\;r_{i} $是$ G $-利普希茨连续函数, 即, 对于任意$ x,\;y\in X $, 有$ \rVert f_{i,\;t}(x)-f_{i,\;t}(y)\rVert\leq G\rVert x-y\rVert $ 和 $ \rVert r_{i}(x)-r_{i}(y)\rVert\leq G\rVert x-y\rVert $.

假设6. 对于任意$ t\in [T] $, 每个智能体$ i $的延迟时间$ \tau_{i,\;t} $有不同的上界, 即$ \tau_{i,\;t}\leq\tau_i $.

假设1保证最优解存在且唯一. 假设2是研究复合优化常见的假设条件^[6]. 为便于理论分析, 假设3 ~ 5是凸优化的标准假设^{[5, 13, 38]}. 注意: 假设5表示函数$ f_{i,\;t},\;r_{i} $具有有界梯度(或次梯度), 且界为$ G $.

3.   梯度反馈延迟情况

下面设计具有延迟梯度反馈的分布式在线近端梯度下降法 (Distributed online proximal gradient algorithm with gradient delays, DOPG-GD), 用于处理分布式在线复合优化问题并对动态遗憾上界进行分析.

3.1   预备知识

首先, 对任意$ {\boldsymbol x}={\rm col}(x_1,\;x_2,\;\cdots,\;x_N)\in X^N $, 定义如下目标函数:

其中, $ L_{\delta}(x)=\sum_{i=1}^{n}l_{\delta}(x^i) $, $ x^i $是$ x\in X\subset{\bf{R}}^n $的第$ i $个分量. $ l_{\delta} $是Huber函数, 它是绝对值函数的一种光滑化处理, 定义如下:

当$ \delta>0 $时, $l_\delta $是$ 1/\delta $光滑函数; 当$ \delta=0 $时, $ l_\delta $恢复为绝对值函数. 根据Huber函数的定义, 可得到$ L_{\delta}(x) $的相关性质(见附录A). 令$ l_t({\boldsymbol x})= \frac{\lambda}{2}\sum_{i=1}^{N}\sum_{j=1}^{N} a_{ij}\times L_{\delta_t}(x_i-x_j) $, 可以证明当$ \delta_t>0 $时, $ l_t({\boldsymbol x}) $为光滑函数.

引理1. 对任意$ \delta_t>0 $, 函数$ l_t({\boldsymbol x}) $为$ \tilde{\alpha} $光滑函数, 其中, $ \tilde{\alpha}=\lambda \|A\|_{\infty}/\delta_t $, $ A $为网络通讯图的加权邻接矩阵.

引理1的详细证明见附录B. 以往利用求解等价问题来求解原问题的方法^[25]仅考虑非光滑惩罚项, 即$ \delta_t=0 $时, 所设计的算法在处理强凸光滑$ f_{i,\;t} $时没有优势. 下面通过引入Huber函数得到光滑的一致性惩罚项$ l_t $, 这样的优势是更好地利用$ f_{i,\;t} $的光滑性, 使得$ f_t({\boldsymbol x})+\gamma_t l_t({\boldsymbol x}) $整体具有光滑性, 于是才能保证引理6的成立, 从而得到其他主要结论.

可以观察到$ \widetilde{F}_t({\boldsymbol x}) $的第1项与$ F_t(x) $的区别在于$ \widetilde{F}_t({\boldsymbol x}) $的每个局部目标函数具有独立的状态$ x_i $, 其中, $ l_t({\boldsymbol x}) $是保证一致性的惩罚项, 当每个分量$ x_i $达到一致时, 两个目标函数相等. 当$ \delta_t=0 $时, 根据文献[39]中的定理1可以得出, 若惩罚项系数$ \lambda $足够大, 可推出问题(P)与问题(P')是等价问题, 具体等价性见引理2.

引理2. 基于假设3 ~ 5, 并假设函数$ f_{i,\;t} $为凸函数, 当$ \lambda>NG/a_{\min} $, $ \delta_t=0 $时, 对任意时间$ t $, $ \widetilde{F}_t({\boldsymbol x}) $与$ F_t(x) $是等价问题, 体现在$ \widetilde{F}_t({\boldsymbol x}) $的最优解为$ {\bf{1}}\otimes x^*_t $, 其中, $ x^*_t $为$ F_t(x) $的最优解.

对任意$ x\in X $, 都有$ \widetilde{F}_t({\bf{1}}\otimes x)=F_t(x) $, 于是在一般情况下, 问题(P)与问题(P')有如下关系: $ \min_{{\boldsymbol x}\in X^N} \widetilde{F}_t({\boldsymbol x}) \leq \min_{x\in X} F_t(x) $. 但如果取$ \lambda >4NG/ a_{\min},\; \delta_t=2a_{\min}V({\boldsymbol x}_t)/na_{\max}N^2,\; $其中,

式中, $ {\boldsymbol x}_t={\rm col}(x_{1,\;t},\;x_{2,\;t},\;\cdots,\;x_{N,\;t}) $, $ x_i^l $是第$ i $个智能体状态的第$ l $个分量, 那么, 对任意$ s\in[N] $而言, $ \widetilde{F}_t({\boldsymbol x}_t) $都是$ F_t(x_{s,\;t}) $的一个上界, 详细证明见引理7. 这里的$ \frac{\lambda}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}a_{ij}L_{\delta_t}(x_i-x_j) $就是使得各分量相等的一致性惩罚项, 要求$ \lambda $大于给定常数可以让分量不相等时惩罚项占问题(P')主体, 迫使各分量趋于一致. 注意这里只对每个时刻算法给出的状态$ {\boldsymbol x}_t $和$ x_{s,\;t} $成立. 事实上, 对任意的$ {\boldsymbol x} $和$ x_{s} $来说, $ \widetilde{F}_t({\boldsymbol x}) $并不是$ F_t(x_{s}) $的上界. 在所选参数下, 引理7表明所提出的算法会趋于选择各分量一致的更新, 因为只有这样的更新才能使得$ \widetilde{F}_t({\boldsymbol x}) $更小.

接下来可以通过求解新的问题(P'), 进而间接求解原问题(P). 与原问题相比, 新问题(P')的局部目标函数仅与每个智能体自身的状态相关, 一致性通过惩罚项$ l_t({\boldsymbol x}) $保证, 不需要额外考虑一致性.

3.2   梯度反馈延迟下的分布式复合优化算法

由于参数$ \lambda $和步长$ \eta $仅与全局变量有关, 在算法的开始选择

其中, $ \Delta=\lambda a_{\max}N^2\lVert A\lVert_\infty/2a_{\min} $. 然后, 在每个时刻$ t $时, 利用分布式最大最小一致算法^[40]计算$ V({\boldsymbol x}_t) $. 接着选择$ \gamma_t=V({\boldsymbol x}_t) $以及$ \delta_t=2a_{\min}V({\boldsymbol x}_t)/na_{\max}N^2 $, 由于在时刻$ t $智能体$ i $只能使用延迟的梯度信息$ \nabla f_{i,\;t-\tau_{i,\;t}}(x_{i,\;t-\tau_{i,\;t}}) $, 于是智能体$ i $根据式(4)更新自身状态:

其中, $ \eta $为每次迭代的步长, 近端算子定义为$ {\rm prox}_{\eta r_{i}}(x)=\arg\min_{u\in X} r_i(u)+\frac{1}{2\eta}\|u-x\|^2 $. 另外, 若当前时刻获取不到函数信息, 则有

详细的算法描述如算法1所示.

　 算法1. 具有延迟梯度反馈的分布式近端梯度下降法 (DOPG-GD)

输入. 初始化向量 $ {\boldsymbol x}_1={\rm col}(x_{1,\,1},\,x_{2,\,1},\,\ldots,\, x_{N,\,1}) $, $ \lambda $, $ \eta $

输出. $ {\boldsymbol x}(2),\;{\boldsymbol x}(3),\;\cdots,\;{\boldsymbol x}(T) $

1) 对$ t=1,\; \cdots,\; T $执行:

2) 计算$ V({\boldsymbol x}_t) $, 令$ \delta_t=2a_{\min}V({\boldsymbol x}_t)/na_{\max}N^2 $, $ \gamma_t= V({\boldsymbol x}_t) $;

3) 每个智能体$ i $收到邻居发送的状态$ x_{j,\;t} $, 并获取自身的延迟梯度信息$ \nabla f_{i,\;t-\tau_{i,\;t}}(x_{i,\;t-\tau_{i,\;t}}) $;

4) 每个智能体$ i $根据式(4)更新自身状态.

3.3   梯度反馈下关于动态遗憾的结果

定理1给出了具有延迟梯度反馈的分布式近端梯度下降法的动态遗憾上界.

定理1. 基于假设1 ~ 6, 设置算法1中$ \lambda>4NG/ a_{\min},\; \gamma_t=V({\boldsymbol x}_t) $, 且

则有

其中, $ \Delta=\lambda a_{\max}N^2\lVert A\lVert_\infty/2a_{\min} $, $ \bar{\tau}=\sum_{i=1}^{N}\tau_i/N $.

证明见附录C. 根据定理1, 算法1的动态遗憾上界与延迟上界$ \tau $、迭代时间$ T $、路径长度$ C_T $和梯度变化度$ D_T $均有关.

由于延迟会导致接收到的函数序列发生变化, 因此, 上界与函数序列的复杂度度量有关是合理的, 即梯度变化度$ D_T $. 若梯度变化度过于剧烈, 必然导致延迟后的梯度与真实梯度相差过大, 最终影响算法的表现效果. 反之, 若梯度变化度$ D_T $随时间呈次线性增长, 则动态遗憾也随时间呈次线性增长. 定理1从理论上给出了梯度变化度与动态遗憾上界的关系.

根据算法1, 每个智能体的延迟可以不相同, 这区别于每个智能体具有相同延迟的设置^{[27, 29]}, 另外, 本文所考虑的延迟是时变的, 在大部分分布式设置中都只考虑时不变延迟^[27−29], 而时变延迟更一般, 在分析上更复杂, 需要评估每个智能体由不同的时变延迟导致的误差, 且函数序列会发生变化, 需要评估原序列与变化后序列的差距. 本文通过分析将函数序列的变化转化到梯度变化度$ D_T $上, 即若梯度变化度越小, 由时变延迟导致接收到的函数序列与原序列的变化也相应越小, 那么算法的表现效果也越好. Bedi等^[22]考虑时变延迟, 选择延迟动态遗憾$ \sum_{t=1}^{T}\sum_{i=1}^N (f_{t-\tau_{i,\;t}}(x_{i,\;t})- f_{t-\tau_{i,\;t}}(x_i^*)) $作为评估指标, 延迟动态遗憾使用时延后的函数序列, 虽然这样可避免估计接收到的函数序列与原序列的差距, 但由于不适合用于评估原问题(P), 因此, 本文依然选择普通动态遗憾作为评估指标进行分析.

Wang等^[19]研究受到长短期约束的在线凸优化问题, 且损失函数和长期约束函数均有固定反馈延迟. 若长期约束固定不变, 选择合适的参数, 当损失函数是强凸光滑时, 动态遗憾上界为$ {\rm O}(\tau^2T^\delta) $, 其中, $ \sum_{t=1}^{T}\|\nabla f_t(x^*_t)\|^2 $, $ \sum_{t=1}^{T}\|x_t^{st}-x_t^*\|^2={\rm O}(T^\delta) $, $ x_t^{st} $仅受短期约束控制, $ \delta\in(0,\;1) $. 在固定延迟且不考虑约束的情况下, 算法1的动态遗憾上界中关于延迟时间的阶数小于它们的阶数.

事实上, 目前, 已有文献很少研究分布式在线复合优化中的延迟影响, 并且大部分对于时延现象的研究都是以静态遗憾作为度量指标^{[22, 27−29]}. 在分析上, 以静态遗憾为度量时考虑固定的比较序列$ x^*_t={\rm arg}\min_{x\in X}F_t(x) $, 而以动态遗憾为度量需要考虑时变的比较序列, 分析过程会更复杂. 由于引理5和引理6的分析不可直接将$ x^*_t $替换为$ x^* $, 因此定理1的结论不适用于静态遗憾, 对静态遗憾的分析可以作为未来的研究方向之一.

当延迟消失时, 即$ \tau=0 $时, 取$ \eta<1/(\alpha+\Delta) $, 得到动态遗憾上界为$ {\rm O}(C_T+1) $. 这一结论与不考虑延迟的工作中的结论相匹配^[37]. Ajalloeian等^[37]考虑集中式场景下的不准确信息, 若信息是准确的(与本文设定相同), 定理1的结论与文献[37]的结论是相同的, 而本文考虑的则是更加复杂的分布式场景.

4.   Bandit反馈延迟

在一些情形下, 每个智能体只能知道目标函数在一个或几个点处的函数取值, 而非梯度信息. 在这种情况下, 第3节基于梯度反馈的方式不再适用. 为解决这一问题, 本节讨论Bandit反馈下的延迟, 并提出基于单点Bandit反馈和两点Bandit反馈下的分布式在线近端梯度下降算法 (Distributed online proximal gradient algorithm with one-point (two-point) bandit delays, DOPG-BD). 其中, 单点Bandit反馈指智能体能获取函数在一点处的信息, 两点Bandit反馈指智能体能获取函数在两点处的信息. 最终分别对这两种算法在期望意义上的动态遗憾$ {\rm E}({\boldsymbol{Reg}}_j^T) $进行分析.

4.1   预备知识

首先, 给出函数估计的基本知识. 一般地, 函数$ \psi: {\bf{R}}^n\rightarrow {\bf{R}} $的估计函数为

其中, $ \xi $是大于0的实数, $ {\boldsymbol{B}}=\{x\in{\bf{R}}^n|\|x\|\leq 1\} $是单位球体, $ {\rm U}({\boldsymbol{B}}) $是单位球上的均匀分布. 那么$ \hat{\psi}(x) $就是由函数$ \psi $在以$ x $为圆心$ \xi $为半径的球体上的点确定. 对任意$ x\in{\bf{R}}^n $, $ \hat{\psi}(x) $的梯度为

其中, $ {\boldsymbol{S}}=\{x\in{\bf{R}}^n|\|x\|= 1\} $是单位球面^[26]. 于是, $ \nabla\hat{\psi}(x) $由函数$ \psi $在以$ x $为圆心$ \xi $为半径的球面上的点决定. 除此之外, $ \hat{\psi} $与$ \psi $还有如下关系^[41].

引理3. 如果$ \psi $是凸的, 那么$ \hat{\psi} $也是凸的. 如果$ \psi $是$ G $-利普希茨连续, 那么$ \hat{\psi} $也是$ G $-利普希茨连续.

事实上, 由于$ \nabla\hat{\psi}(x)={\rm E}[\nabla\psi(x)] $^[41], 若$ \psi $是$ \mu $-强凸的, 那么$ \hat{\psi} $也是$ \mu $-强凸的. 于是, 根据假设1和假设5, 对任意的$ i\in[N] $和$ t\in[T] $, $ \hat{f}_{i,\;t}(x)= {\rm E}_{v\sim{\rm U}({\boldsymbol{B}})} [f_{i,\;t}(x+\xi v)] $是 $ \mu $-强凸和 $ G $-利普希茨连续函数.

由于$ f_{i,\;t} $的定义域为$ {X} $, 为了保证$ \hat{f}_{i,\;t} $是良好定义的, 基于Bandit反馈的研究往往都需要引入下面的假设^{[25, 27, 41]}. 令$ { B}(x,\;r)=\{u\in{\bf{R}}^n|\|u-x\|\leq r\} $代表以$ x $为圆心$ r $为半径的单位球.

假设7. 定义域$ {X} $有内点, 即存在$ y_0\in{X} $和$ r> 0 $, 使得$ {\rm B}(y_0,\;r)\subset {X} $.

引理4. 基于假设7, 对于任意$ \beta\in(0,\;1) $以及$ x\in{X} $, 令$ \widetilde{{X}}={B}((1-\beta)x+\beta y_0,\;\beta r) $, 则有$ \widetilde{{X}}\subset{X} $.

引理4的证明详见文献[26]. 于是, 假设7可保证估计函数$ \hat{f}_{i,\;t}(x) $在$ \widetilde{{X}} $上是良好定义的.

除此之外, 在单点Bandit反馈时还需要引入假设8, 它是处理单点Bandit反馈的常见假设^{[13, 26, 29, 42]}.

假设8. 对于任意$ t\in [T] $和$ i\in [N] $, $ f_{i,\;t} $是有界的, 即存在正实数$ C $, 对任意$ x\in X $, 有$ \rVert f_{i,\;t}(x)\rVert\leq C $.

4.2   Bandit反馈延迟下的分布式复合优化算法

在单点Bandit反馈下, 智能体能够获得局部目标函数在状态$ x_{i,\;t} $周围1点处的函数值, 即$ f_{i,\;t}(x_{i,\;t} +\;\xi u_{i,\;t}) $, 其中, $ u_{i,\;t} $是单位向量. 根据式(5), 设

则$ q_{i,\;t} $ 是$ \nabla \hat{f}_{i,\;t}(x_{i,\;t}) $ 的一个无偏估计, 即$ \nabla \hat{f}_{i,\;t}(x_{i,\;t})= {\rm E}[q_{i,\;t}|x_{i,\;t}] $. 在单点Bandit反馈下, $ q_{i,\;t} $用于估计函数的梯度信息. 另外, 本文考虑了反馈延迟现象, 因此, 在$ t $时刻, 智能体只能获得$ q_{i,\;t-\tau_{i,\;t}} $, 然后利用式(7)进行状态更新:

为保证更新的状态在$ \widetilde{{X}} $中, 这里新的近端算子定义为$ {\rm prox}^{\widetilde{{X}}}_{\eta r_{i}}(x)=\arg\min_{{u}\in\widetilde{{X}}}r_{i}({u})\;+ \frac{1}{2\eta}\rVert u-x\rVert^2 $.

在两点Bandit反馈下, 智能体能够获得局部目标函数在状态$ x_{i,\;t} $周围两点处的函数值, 即$ f_{i,\;t}(x_{i,\;t}+\xi u_{i,\;t}) $和$ f_{i,\;t}(x_{i,\;t}-\xi u_{i,\;t}) $. 此时, 可以用$ p_{i,\;t} $来估计函数的梯度信息, 定义为

根据式(5)知, $ p_{i,\;t} $也是$ \nabla \hat{f}_{i,\;t}(x_{i,\;t}) $的一个无偏估计, 即$ \nabla\hat{f}_{i,\;t}(x_{i,\;t})={\rm E}[p_{i,\;t}|x_{i,\;t}] $. 详细的算法过程见算法2和算法3.

　 算法2 (3). 具有单点(两点) Bandit反馈延迟的分布式近端梯度下降法(DOPG-BD)

输入. 初始化向量 $ {\boldsymbol x}_1={\rm col}(x_{1,\;1},\;x_{2,\;1},\;\ldots,\; x_{N,\;1}) $, $ \lambda $, $ \eta $

输出. $ {\boldsymbol x}(2),\;{\boldsymbol x}(3),\;\cdots,\;{\boldsymbol x}(T) $

1) 对$ t=1,\; \cdots,\; T $执行:

2) 计算$ V({\boldsymbol x}_t) $, 令$ \delta_t=2a_{\min}V({\boldsymbol x}_t)/na_{\max}N^2 $, $ \gamma_t= V({\boldsymbol x}_t) $;

3) 每个智能体$ i $收到邻居发送的状态$ x_{j,\;t} $, 获取延迟Bandit反馈信息$ g_{i,\;t-\tau_{i,\;t}} $, 其中

其中, $ u_{i,\;t-\tau_{i,\;t}} $由智能体$ i $根据单位球面上的均匀分布选取.

4) 每个智能体$ i\in[N] $更新自身状态:

与梯度反馈的分析类似, 在Bandit反馈下, 也可以通过分析类似问题$ \hat{F}_t({\boldsymbol x}) $(见附录D)的动态遗憾来分析$ {\rm E}({\boldsymbol{Reg}}_j^T) $.

4.3   Bandit反馈下关于动态遗憾的结果

定理2给出了延迟单点Bandit反馈的分布式近端梯度下降法的动态遗憾上界.

定理2. 对于单点Bandit反馈下的算法2, 基于假设1 ~ 8, 对于任意$ j\in[N] $和$ \xi\in(0,\;r) $, 其中, $ r $由假设7确定, 取

则有

其中, $ \bar{\tau}=\sum_{i=1}^{N}\tau_i/N $, $ \Delta $的定义与定理1相同.

定理2的证明见附录D. 与第3节基于梯度反馈的算法相比, 单点Bandit反馈情况下的动态遗憾在期望意义下多出$ \sqrt{T\log T} $这一项, 虽然此时算法的表现效果较梯度反馈稍差, 但单点Bandit反馈下的算法只需要函数一点处的信息即可, 从而扩展了算法在更多复杂场景中的应用.

在不考虑延迟时, 即$ \bar{\tau}=0 $, 可取

此时的动态遗憾上界为$ {\rm O}(\sqrt{T\log T}+C_T+1) $. 已有的针对强凸光滑目标函数的单点Bandit反馈研究得到无延迟下的静态遗憾上界$ {\rm O}(\sqrt{T\log T}) $^[43−45]. 本文对更复杂的动态遗憾进行分析, 且不需要函数的整体光滑性, 只需要$ f_{i,\;t} $是光滑的, $ r_{i} $可以是非光滑的, 且考虑了分布式场景.

定理3给出延迟两点Bandit反馈的分布式近端梯度下降法的动态遗憾上界.

定理3. 对于两点Bandit反馈下的算法3, 基于假设1 ~ 7, 对于任意$ j\in[N] $和$ \xi\in(0,\;r) $, 其中, $ r $由假设7确定, 取

则有

其中, $ \bar{\tau}=\sum_{i=1}^{N}\tau_i/N $, $ \Delta $的定义与定理1相同.

定理3的证明见附录D. 定理3表明若使用函数在两点处的信息, 则可以在期望意义下获得与梯度反馈相同的结果. 这是由于两点Bandit反馈下可得$ \rVert p_{i,\;t}\rVert\leq nG $, 与梯度反馈下得到的$ \rVert\nabla f_{i,\;t}(x_{i,\;t})\rVert \leq G $仅相差$ n $倍, 因此不影响动态遗憾上界中关于迭代总次数$ T $的阶数. 注意, 由于两点Bandit反馈与梯度反馈相比多出与$ n $的关系, 因此随着智能体状态的维度增大, 梯度反馈与两点Bandit反馈的差别会表现出来, 因此两者的上界并不相等, 但在期望意义下与迭代总次数$ T $的阶数相同. 由于定理2和定理3所选取的参数是使得它们的遗憾上界最小的参数, 在证明中不能通过调整参数大小使得它们的动态遗憾上界更小, 从这个角度来说, 两点Bandit反馈较单点Bandit反馈的动态遗憾上界更小.

另外, 值得注意的是, 梯度反馈和单点与两点Bandit反馈下的动态遗憾界在期望意义下关于平均时延$ \bar{\tau} $是一致的, 这表明三种反馈类型不会影响延迟与动态遗憾上界的关系.

5.   仿真实验

下面通过对具有延迟反馈的分布式在线回归问题进行仿真验证, 验证所提出算法的有效性. 仿真实验分别验证了算法在不同网络规模、不同网络拓扑、不同数据集、不同延迟分布以及不同延迟上界情形下三种算法的表现效果.

考虑分布式场景下的逻辑回归问题, 每个智能体的局部目标函数由下面两部分组成:

其中, $ X\subset{\bf{R}}^n $, $ b_{i,\;t}\in{\bf{R}} $, $ a_{i,\;t}\in{\bf{R}}^n $. $ r_{i} $是常见的稀疏惩罚项, 适用于处理各种稀疏数据问题, 例如稀疏信号识别、稀疏矩阵分析等问题^[16].

每个实验均在梯度反馈、单点Bandit反馈和两点Bandit反馈下进行, 并画出最大平均遗憾(Maximum average regret) $ \max_{j\in[N]}{\boldsymbol{Reg}}_j^T/T= \max_{j\in[N]} (\sum_{t=1}^{T}F_t(x_{j,\;t})-\sum_{t=1}^{T}F_t(x_t^*))/T $与迭代次数$ T $的关系, 其中, $ x_t^* $是$ F_t $的最优解. 若不特殊说明, 实验中的基本设置如下: 最大延迟$ \tau_{\max} $为10, $ \tau_{i,\;t} $服从0到10上的均匀分布, 参数$ \lambda=0.5 $, $ \rho=0.1 $, 特征维度$ n=10 $, 智能体数量$ N=20 $, 网络连通度为$ d_c=0.4 $, 在Python的sklearn库生成的数据集上进行实验, 步长$ \eta $在梯度反馈、单点Bandit反馈和两点Bandit反馈下分别根据定理1 ~ 3进行设置.

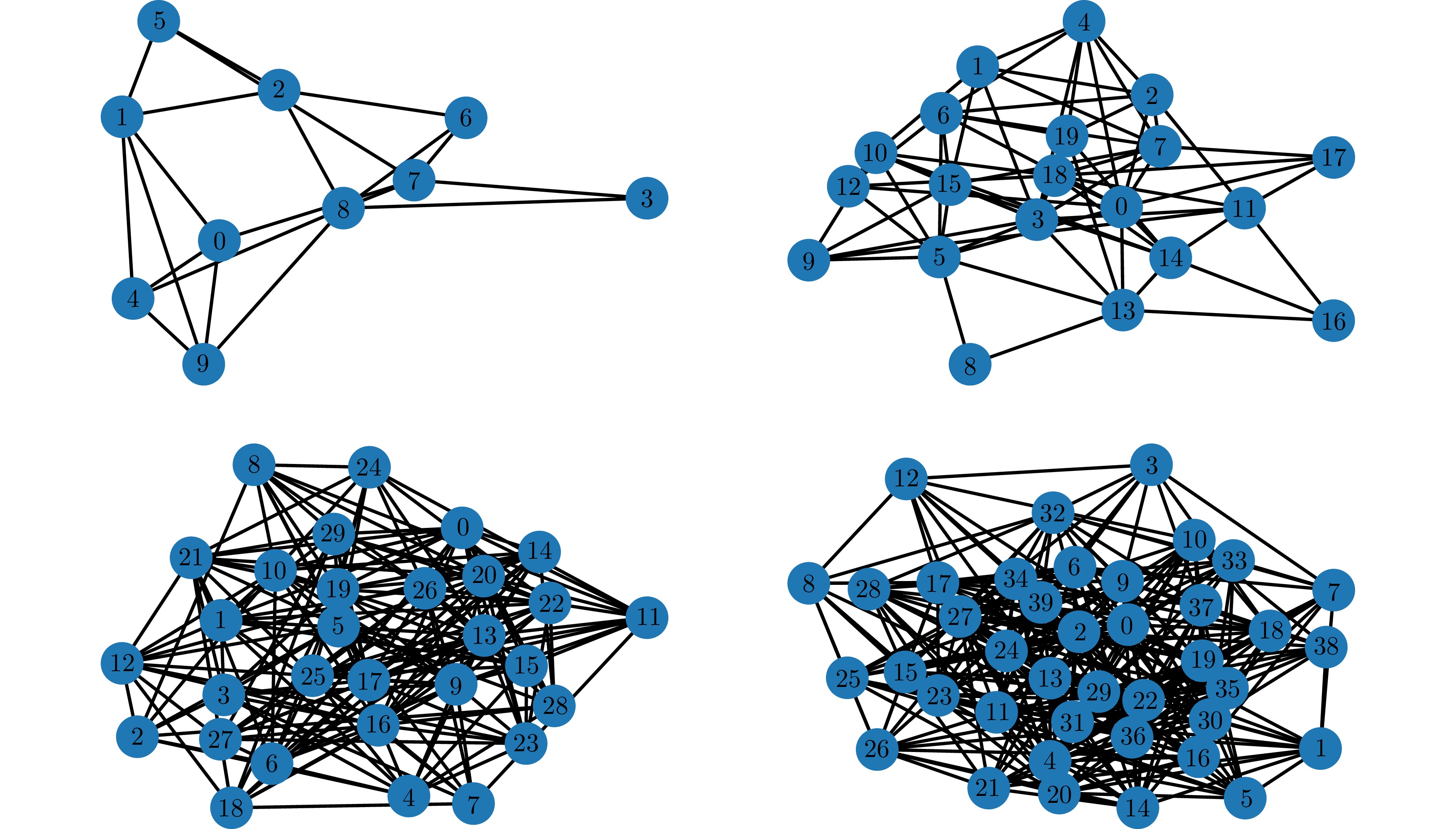
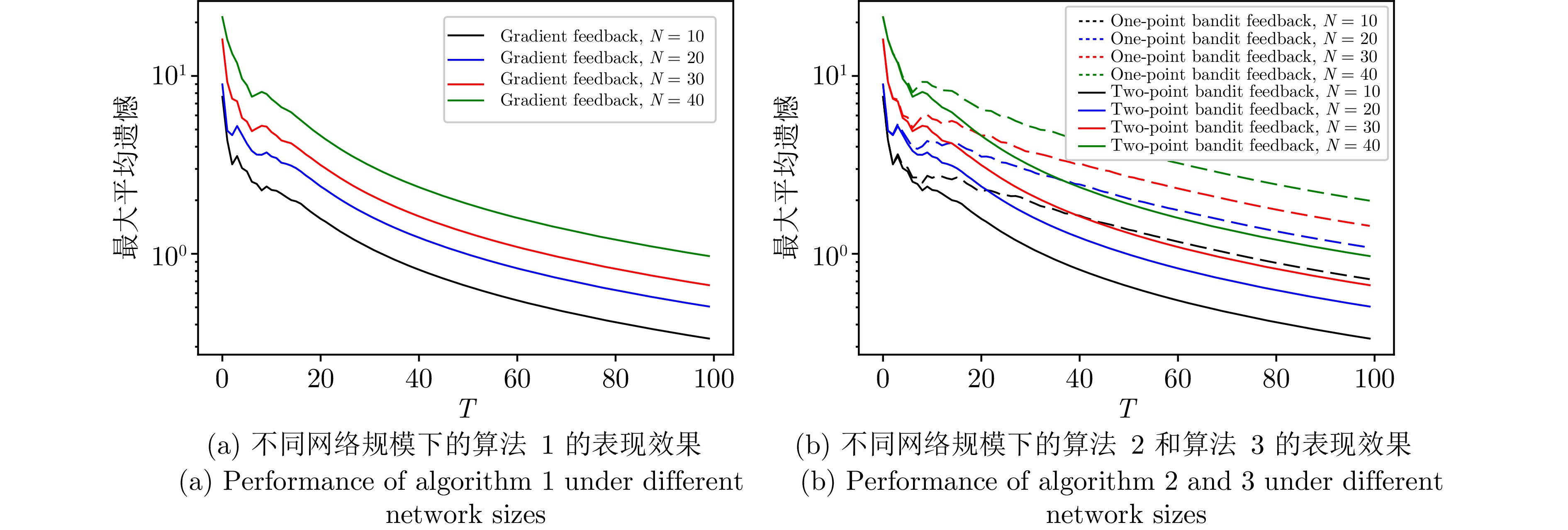
5.1   在不同网络规模和不同网络拓扑下的表现效果

为验证所提出算法在不同网络规模下的表现效果, 本节实验分别在图1中的4种不同网络下进行, 其中, 智能体数量$ N $分别为10, 20, 30, 40, 各个智能体之间的拓扑关系如图1所示. 梯度反馈延迟(算法1)、单点Bandit反馈延迟(算法2)和两点Bandit反馈延迟(算法3)的表现效果如图2所示. 可以发现, 随着网络规模的增大, 三种算法的最大平均遗憾也在增大, 且单点Bandit反馈的最大平均遗憾较两点Bandit反馈更大, 这与定理1 ~ 3中给出的动态遗憾上界和$ N $成正比(见证明中的详细上界), 以及定理2中的界较定理3更高是一致的. 在实际应用中, 较大的网络规模一般会影响算法的表现效果, 而它对两点Bandit反馈算法的性能影响较单点Bandit反馈算法的性能影响更小.

图 1  4种不同规模的网络

Fig. 1  Four networks with different sizes

下载: 全尺寸图片 幻灯片

图 2  不同网络规模下本文所提出算法的性能表现

Fig. 2  Performance of the proposed algorithms under different network sizes

下载: 全尺寸图片 幻灯片

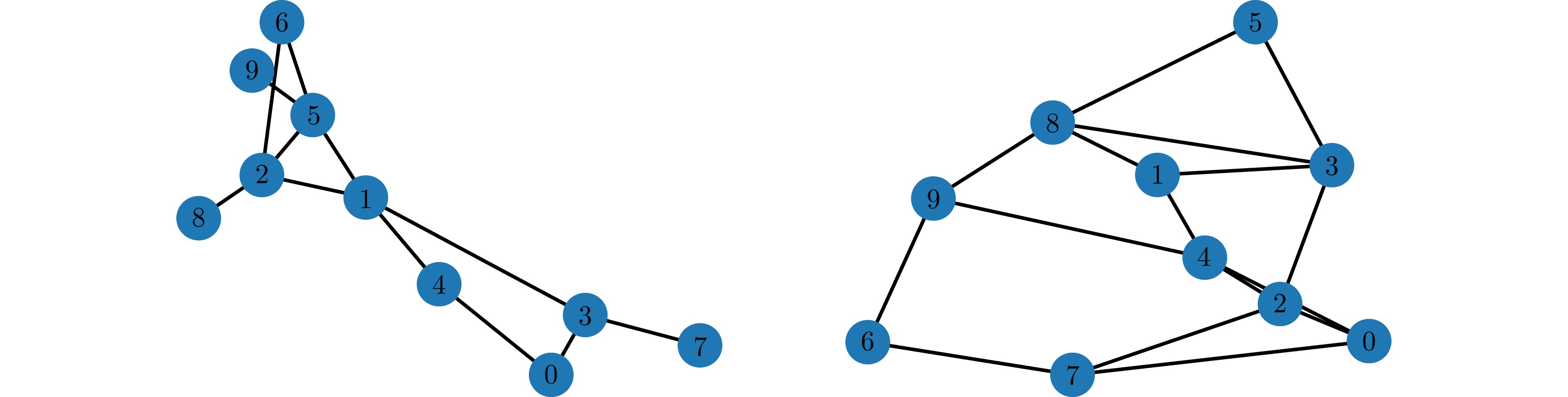
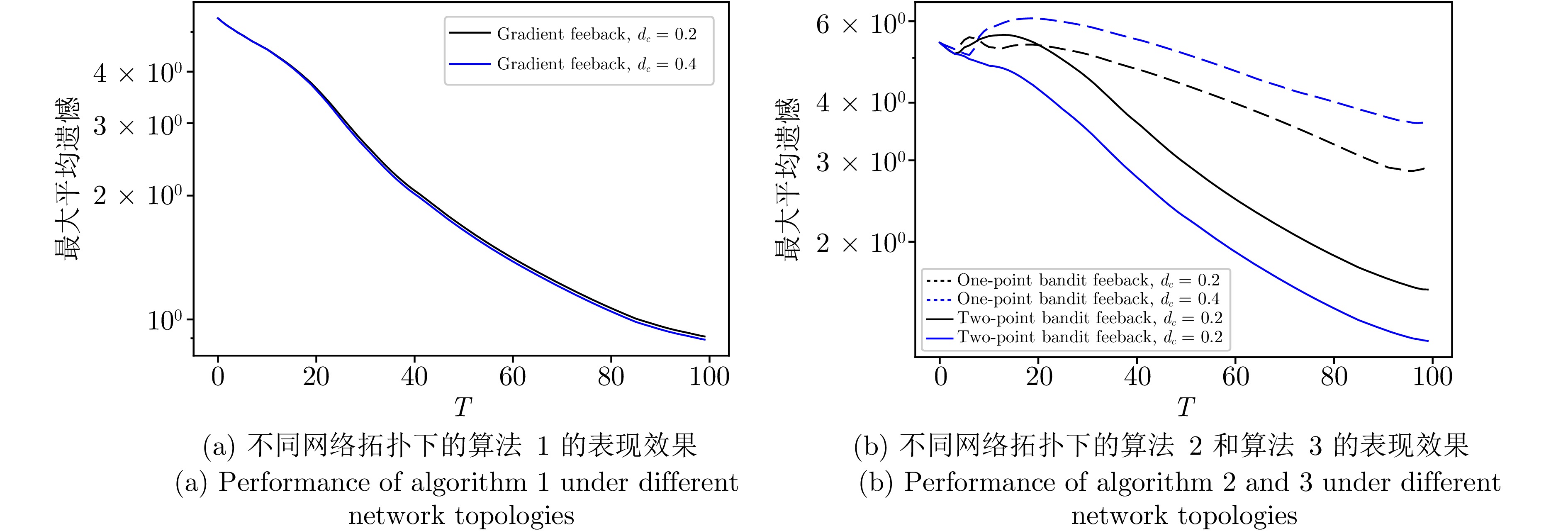
而后, 为验证所提出算法在不同网络拓扑下的表现效果, 在真实数据集TwitterDate下, 本节实验分别在图3中具有10个智能体的两种不同连通度的网络下进行, 连通度$ d_c $分别为0.2和0.4. 梯度反馈延迟(算法1)、单点Bandit反馈延迟(算法2)和两点Bandit反馈延迟(算法3)的表现效果如图4所示. 可以发现, 随着网络连通度的增大, 三种算法的最大平均遗憾在减小, 且单点Bandit反馈的最大平均遗憾较两点Bandit反馈更大, 这意味着在实际应用中, 网络的连通程度会影响算法的表现效果, 算法在高连通度网络下的表现效果通常会更好, 且两点Bandit反馈比单点Bandit反馈的算法效果更好.

图 3  2种不同的网络拓扑

Fig. 3  Two different network topologies

下载: 全尺寸图片 幻灯片

图 4  不同网络拓扑下本文所提出算法的性能表现

Fig. 4  Performance of the proposed algorithms under different network topologies

下载: 全尺寸图片 幻灯片

5.2   在不同数据集下的表现效果

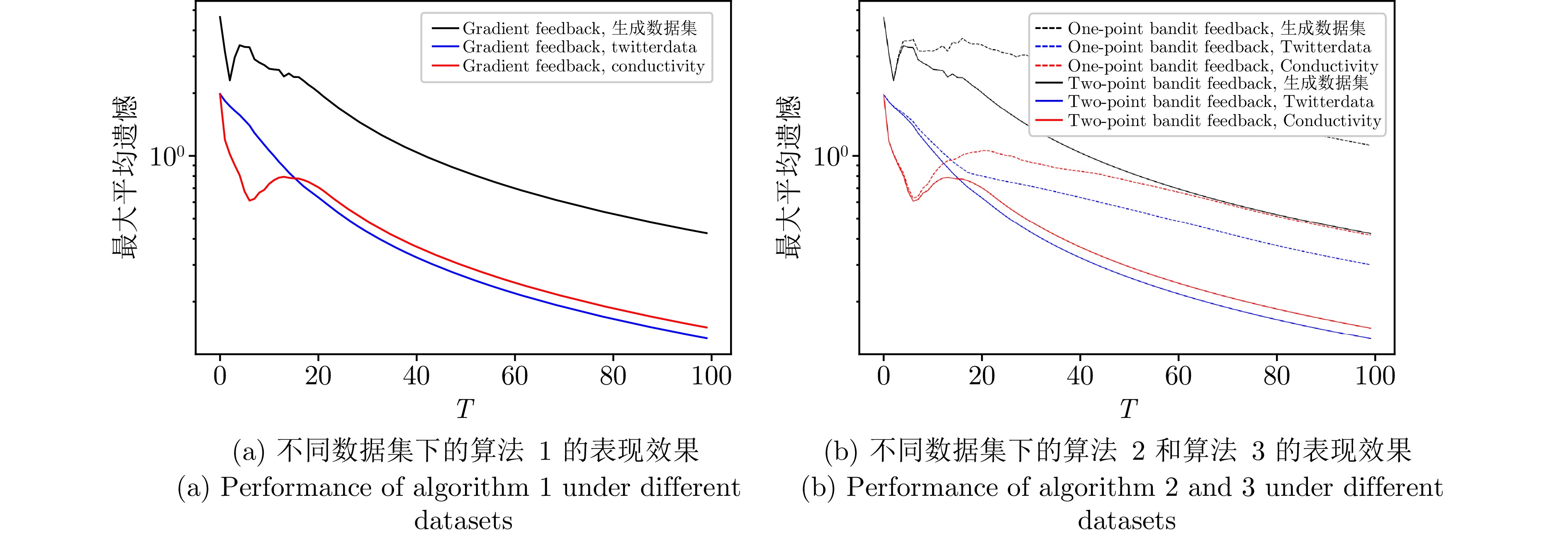
为验证所提出算法在不同数据集下的表现效果, 本节实验分别在Python的sklearn库生成的数据集和两个真实数据集(Conductivity和TwitterDate)上进行. 梯度反馈延迟(算法1)、单点Bandit反馈延迟(算法2)和两点Bandit反馈延迟(算法3)的表现效果如图5所示. 随着迭代的增加, 最大平均遗憾在三种数据集上均减小, 这说明算法在三种数据集上是有效的. 与两个真实数据集相比, 算法在生成数据集上的效果稍差, 这是由于生成数据集上数据的稀疏性不如前两者高造成的, 而本文算法基于近端梯度下降法设计, 近端梯度下降法在处理稀疏数据时具有更好的表现效果^[46], 因此这一结果并不意外. 另外, 在Conductivity数据集上前期不太稳定, 这是由于不同数据集内部数据分布不同造成的, TwitterDate数据较Conductivity更集中, 因此算法运行更平稳. 在实际应用中, 本文提出的算法针对不同的数据集可能会有不同的表现效果, 但均得到令人满意的动态遗憾性能.

图 5  不同数据集下本文所提出算法的性能表现

Fig. 5  Performance of the proposed algorithms under different datasets

下载: 全尺寸图片 幻灯片

5.3   在不同延迟分布下的表现效果

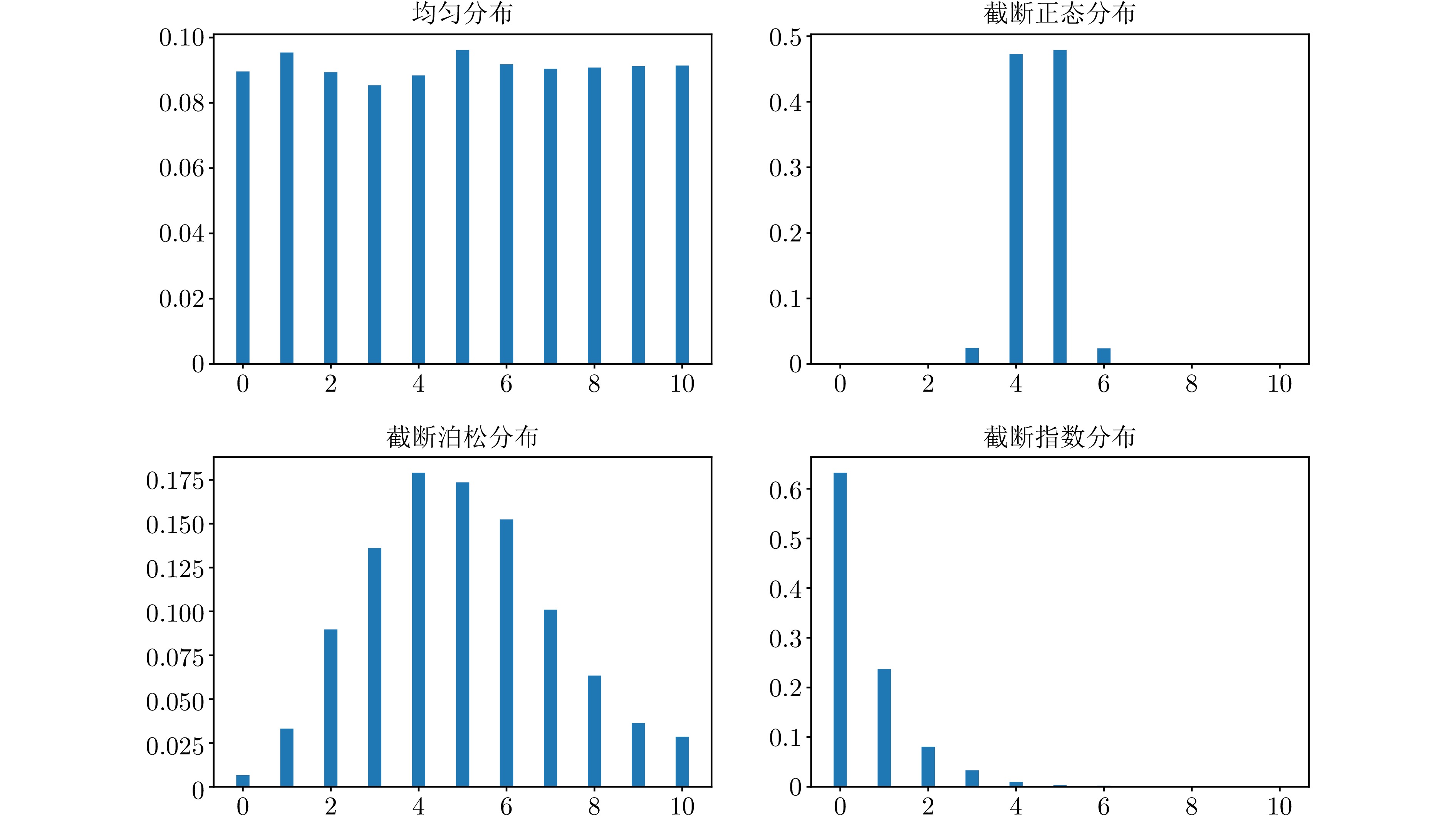
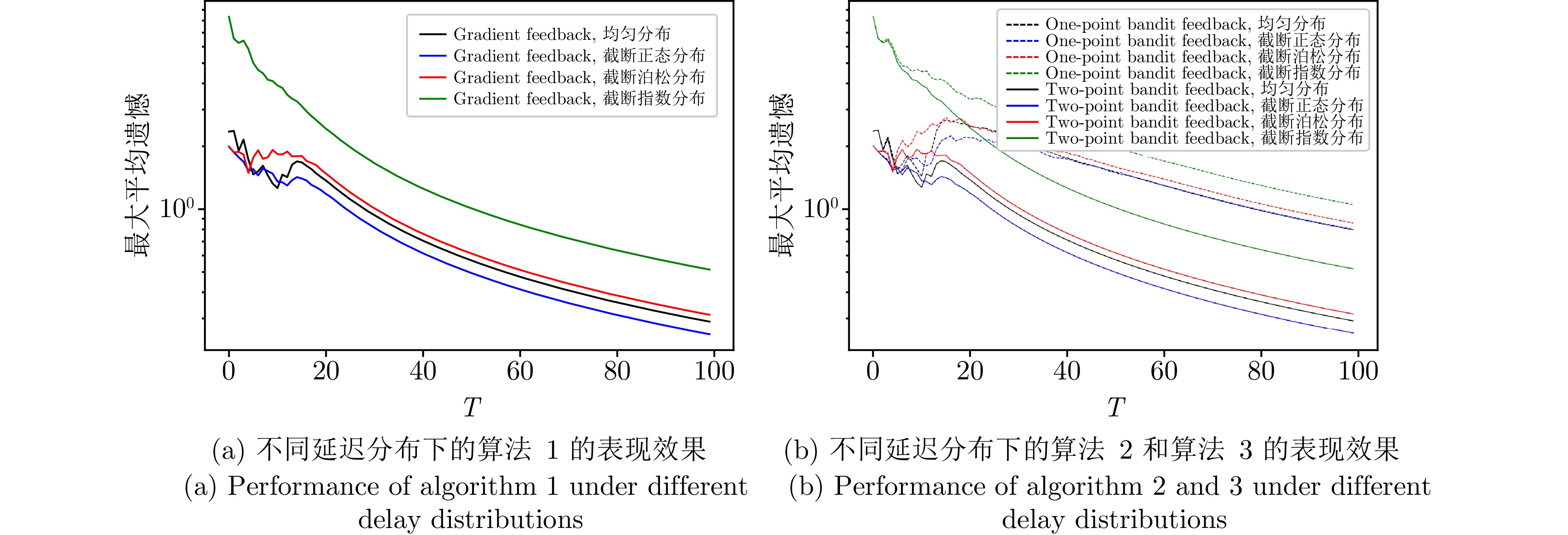
为验证所提出算法在不同延迟分布下的表现效果, 本节实验在4种常见的延迟分布下进行, 分别为$ [0,\;1] $之间的均匀分布、截断正态分布、截断泊松分布和截断指数分布, 它们的截断区间为$ [0,\;10] $, 因此所有延迟上界为10, 相应的概率分布图如图6所示. 梯度反馈延迟(算法1)、单点Bandit反馈延迟(算法2)和两点Bandit反馈延迟(算法3)的表现效果如图7所示. 随着迭代的进行, 算法在不同的延迟分布上表现稍有差异, 但它们的最大平均遗憾都在减小, 这说明所提出算法能够有效处理不同类型的延迟分布.

图 6  4种不同延迟分布

Fig. 6  Four different delay distributions

下载: 全尺寸图片 幻灯片

图 7  不同延迟分布下本文所提出算法的性能表现

Fig. 7  Performance of the proposed algorithms under different delay distributions

下载: 全尺寸图片 幻灯片

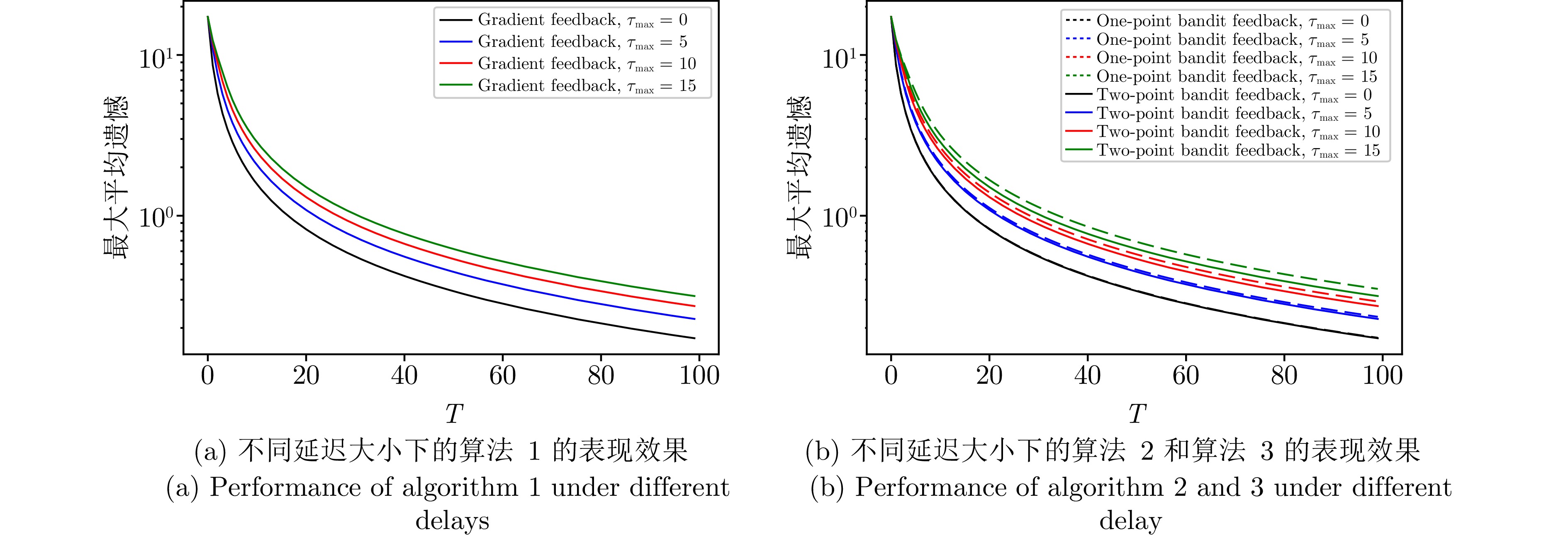
5.4   在不同延迟大小下的表现效果

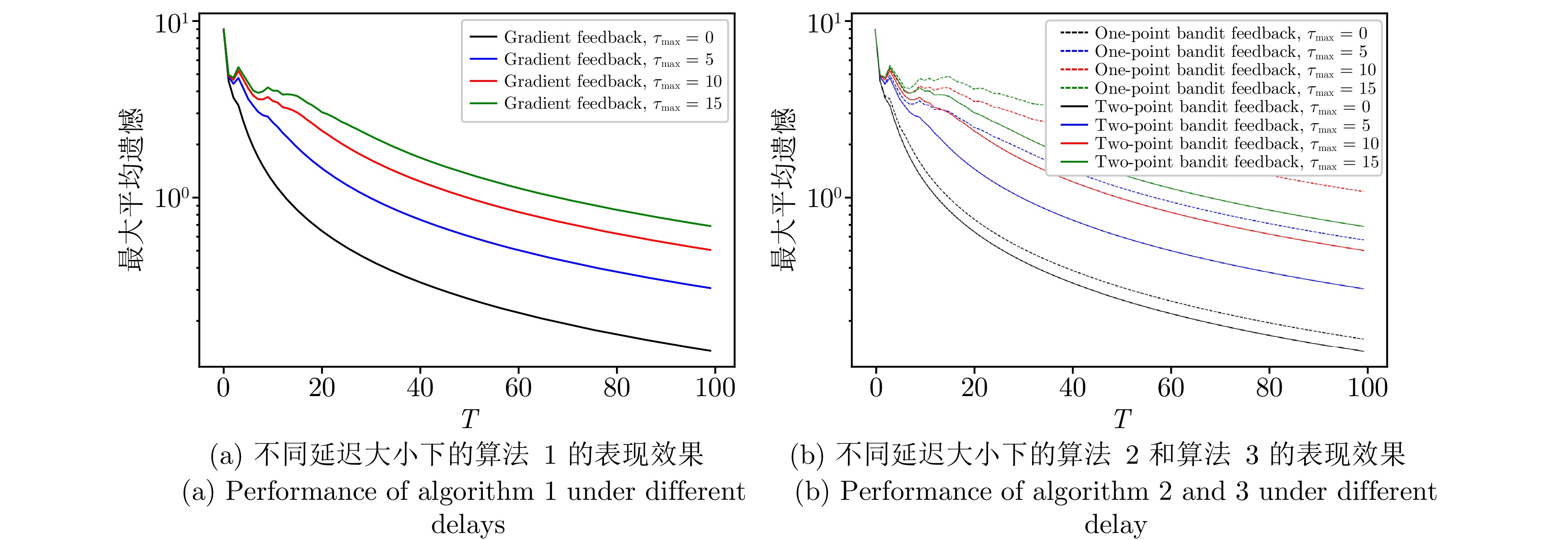
为探究所提出算法在不同延迟大小下的表现效果, 本节分别在小网络 (包含20个智能体) 和大网络 (包含100个智能体) 下对不同延迟上界 (分别为0, 5, 10, 15) 进行仿真实验. 梯度反馈延迟(算法1)、单点Bandit反馈延迟(算法2)和两点Bandit反馈延迟(算法3)的表现效果如图8和图9所示. 从图8和图9可知, 延迟越小算法的表现效果越好, 且与单点Bandit反馈相比, 获得更多信息的两点Bandit反馈效果更好. 从定理1 ~ 3可知, 算法的动态遗憾上界与平均延迟成正比, 而延迟上界会直接影响由均匀分布产生的延迟均值, 因此这一表现与本文理论相一致. 另外, 两点Bandit反馈的表现在不同延迟下均优于单点Bandit反馈, 这与定理2中的界大于定理3也一致. 在实际应用中, 过大的延迟和较少的信息都会影响算法的表现效果, 当延迟较大时尽量使用更多的信息来更新算法, 例如梯度反馈或两点Bandit反馈; 而在进行单点Bandit反馈时尽量选择延迟更小的智能体.

图 8  在小网络的不同延迟大小下本文所提出算法的性能表现 (小网络: N = 20)

Fig. 8  Performance of the proposed algorithms under different delays (small network: N = 20)

下载: 全尺寸图片 幻灯片

图 9  在大网络的不同延迟大小下本文所提出算法的性能表现 (大网络: N = 100)

Fig. 9  Performance of the proposed algorithms under different delays of large networks (large network: N = 100)

下载: 全尺寸图片 幻灯片

以上的仿真实验分别从不同网络规模、不同网络拓扑、不同数据集、不同延迟分布和不同延迟大小这些角度验证了所提出的三种算法在实际中的广泛应用性, 同时这些实验结果也进一步支撑理论分析结果.

6.   结束语

本文研究带有时变反馈延迟的分布式在线复合优化问题, 分别考虑梯度反馈、单点Bandit反馈和两点Bandit反馈三种反馈类型中存在延迟的情况, 其中, 每个智能体可以有不同的时变延迟. 针对这三种情况分别设计相应的算法, 理论分析表明延迟梯度反馈和延迟两点Bandit反馈的动态遗憾上界的阶数在期望意义下相同, 而延迟单点Bandit反馈的动态遗憾上界在期望意义下会稍差于前两种反馈情形, 但在期望意义下动态遗憾上界与平均延迟的关系相同, 这表明不同反馈类型不会影响延迟与动态遗憾上界的关系. 最后通过仿真实验验证算法的性能和理论分析结果. 未来的研究方向包括将其扩展到动态图中、考虑时变非光滑项下的Bandit反馈、考虑函数仅为凸的情况、探索静态遗憾性能或设计算法达到最优动态遗憾界等.

附录 A.   $ L_\delta(x) $函数的相关性质

对任意$ x\in{\bf{R}} $, 根据$ l_\delta(x) $的定义:

当$ \delta>0 $时, $ l_\delta $是$ 1/\delta $-光滑函数; 当 $ \delta=0 $时, $ l_\delta $就恢复为绝对值函数. 另外, $ l_\delta(x) $的梯度为

对任意$ x\in{\bf{R}} $, 都有$ \|\nabla l_\delta(x)\|\leq 1 $以及$ \nabla l_\delta(x)= -\nabla l_\delta(-x) $. 利用$ l_\delta $的性质容易得到, 对任意$ x= (x^1,\;\cdots,\;x^n)\in{\bf{R}}^n $, 函数$ L_{\delta}(x)=\sum_{i=1}^{n}l_{\delta}(x^i) $有如下性质:

性质1. 对任意$ x\in{\bf{R}}^n $, 有$ L_{\delta}(x)\geq0 $, 等号成立当且仅当$ x $为零向量.

性质2. $ L_{\delta}(x) $是梯度有界的, 即有$ \|\nabla L_{\delta}(x)\|\leq \sqrt{n}$.

性质3. 当$ \delta>0 $时, $ L_{\delta}(x) $是$ 1/\delta $-光滑函数; 当$ \delta=0 $时, $ L_{\delta}(x)=\|x\|_1 $.

性质4. 对任意$ x\in{\bf{R}}^n $, 有$ \nabla L_{\delta}(x)= -\nabla L_{\delta}(-x) $.

性质5. 对任意$ x\in{\bf{R}}^n $, 有$ L_{\delta}(x)\geq \|x\|_1-{n\delta}/{2} $.

附录 B.   引理1的证明

根据光滑性的定义, 需要证明, 对任意的$ {\boldsymbol x}= (x_1,\;\cdots,\;x_N),\;{\boldsymbol y}=(y_1,\;\cdots,\;y_N)\in{\bf{R}}^{N\times n} $, 都有下式成立

根据$ L_\delta(x) $的性质3, 对任意$ \delta_t>0 $和$ x,\;y\in {\bf{R}}^{n} $, 都有下式成立$ L_{\delta_t}(y)\leq L_{\delta_t}(x)+\langle \nabla L_{\delta_t}(x),\; y-x\rangle\;+ \frac{1}{2\delta_t}\|y-x\|^2 $. 取$ x=x_i-x_j $, $ y=y_i-y_j $, 于是有

由于智能体之间由无向连通网络连接, 因此, 有$ a_{ij}=a_{ji} $. 根据$ L_\delta(x) $的性质4, 有$ \nabla L_{\delta_t}(x_j-x_i)= -\nabla L_{\delta_t}(x_i-x_j) $, 然后通过交换式(B1)最后一个不等式中的第2项和第3项的下标, 可以证明这两项相等, 详细的证明如下:

用相同的方法也可以证明式(B1)最后一个不等式中的第4项与第5项也是相等的. 于是得到

□

附录 C.   定理1的证明

为简化符号, 令

另外, 前文设置了$ l_t({\boldsymbol x}) = \frac{\lambda}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}a_{ij} \times L_{\delta_t} (x_i\,- x_j) .$ 于是, 梯度反馈延迟下的状态更新过程(式(4))等价于$ {\boldsymbol x}_{t+1} ={\rm prox}_{\eta r}\{{\boldsymbol x}_{t} - \eta[\nabla f_{t-\tau}({\boldsymbol x}_{t-\tau})\,+ \gamma_t \nabla l_t({\boldsymbol x}_{t})]\} $.

引理5. 基于假设3 ~ 5, 并假设函数$ f_{i,\;t} $为凸函数, 令$ \lambda>NG/a_{\min} $, 有$ {\bf{1}}\otimes x_t^*= {\rm prox}_{\eta r}\{{\bf{1}}\otimes x_t^*\;- \eta\nabla f_t({\bf{1}}\otimes x_t^*)\} $.

证明. 由于满足引理2的假设条件, 有$ {\bf{1}}\otimes x_t^*\in \arg\min_{{\boldsymbol x}\in {\cal{X}}^N}\widetilde{F}_t({\boldsymbol x}) $. 根据近端算子在最优点处的性质^[46], $ \widetilde{F}_t $在最优值点满足如下等式:

由于$ \nabla l_t({\bf{1}}\otimes x_t^*)=0 $, 即得. □

引理6. 基于假设1 ~ 5, 令$ \Delta= \lambda a_{\max}N^2\times \lVert A\lVert_\infty/2a_{\min} $, 设置算法1中

则有

其中, $ \rho=1-\eta\mu $.

证明. 基于引理5, 有

式(C1)的第二个不等式是由于近端算子的不可伸缩性^[46]得到: 对任意$ {\boldsymbol u},\;{\boldsymbol v}\in{\cal{X}}^N $, 都有$ \|{\rm prox}_{\eta r}({\boldsymbol u})-{\rm prox}_{\eta r}({\boldsymbol v})\|\leq \|{\boldsymbol u}-{\boldsymbol v}\| $. 式(C1)的最后一个不等式利用与文献[37]中的引理1相同的步骤得到, 其中, $ \mu $和$ \alpha+\gamma_t\tilde{\alpha} $分别是$ f_t+\gamma_tl_t $函数的强凸系数和光滑系数, $ \rho=\max\{|1-\eta\mu|, |1- \eta(\alpha+ \gamma_t\tilde{\alpha})|\} $. 式(C1)最后一个不等式的最后一项由$ f_{i,\;t} $的光滑性得到.

选择$ \gamma_t=V({\boldsymbol x}_t) $, $ \delta_t=2a_{\min}V({\boldsymbol x}_t)/na_{\max}N^2 $, 令$ \Delta=\lambda a_{\max}N^2\lVert A\lVert_\infty/2a_{\min} $, 则有

由于

所以$ \rho=1-\eta\mu $. □

引理7. 基于假设3 ~ 5, 并假设函数$ f_{i,\;t} $为凸函数, 取$ \lambda>4NG/a_{\min} $, $ \delta_t= 2a_{\min}V({\boldsymbol x}_t)/ na_{\max}N^2 $, 对任意的$ s\in[N] $, 都有$ \widetilde{F}_t({\boldsymbol x}_t)\geq F_t(x_{s,\;t}) $. 具体而言, 若$ {\boldsymbol x}_t\neq {\bf{1}}\otimes x_{s,\;t} $, 则$ \widetilde{F}_t({\boldsymbol x}_t)> F_t(x_{s,\;t}) $, 若$ {\boldsymbol x}_t= {\bf{1}}\otimes x_{s,\;t} $, 则$ \widetilde{F}_t({\boldsymbol x}_t)= F_t(x_{s,\;t}) $.

证明. 对任意的$ s\in[N] $, 根据$ f_{i,\;t} $和$ r_{i} $的凸性, 有

其中, 式(C2)的第二个不等式成立源于$ L_\delta(x) $的性质5, 式(C2)的第三个不等号成立源于假设5和$ \lVert x\lVert\leq\lVert x\lVert_1 $.

又根据如下事实:

于是有$ 2G\sum_{i=1}^{N}\lVert x_{i,\;t}-x_{s,\;t}\lVert_1\leq 2GNV({\boldsymbol x}_t) $. 另外, 与文献[39]中式(15)的获取类似, 可以得到:

取$ \delta_t= 2a_{\min}V({\boldsymbol x}_t)/na_{\max}N^2 $, 将上述两个事实代入式(C5)中得到

由于$ \lambda>4NG/a_{\min} $, 所以对任意$ s\in[N] $, $ \widetilde{F}_t({\boldsymbol x}_t)\geq F_t(x_{s,\;t}) $. 特别地, 如果$ {\boldsymbol x}_t\neq{\bf{1}}\otimes x_{s,\;t} $, 则有$ V({\boldsymbol x}_t)= \sum_{l=1}^{n}[\max_{i}(x_i^l(t))-\min_{i}(x_i^l(t))]>0 $, 于是$ \widetilde{F}_t({\boldsymbol x}_t)> F_t(x_{s,\;t}) $. 而当$ {\boldsymbol x}_t= {\bf{1}}\otimes x_{s,\;t} $时, 根据$ \widetilde{F}_t({\boldsymbol x}) $的定义, 有$ \widetilde{F}_t({\boldsymbol x}_t)=F_t(x_{s,\;t}) $. □

定理1的证明. 首先根据引理7, 对任意的$ j\in [N] $, 都有$ F_t(x_{j,\;t})\leq\widetilde{F}_t({\boldsymbol x}_t) $, 于是有

接下来将对$ \widetilde{F}_t $进行分析.

在此之前, 对于任意的$ {\boldsymbol x}=(x_1,\;\cdots, \; x_N)\in X^N $, 给出$ \nabla \widetilde{F}_t({\boldsymbol x}) $的上界如下

其中, 最后一个不等式由假设5和$ L_{\delta}(x) $的性质2得到.

然后估计由延迟造成的误差上界,

其中, $ D_i=\sum_{t=1}^{T}\max_{u \in X}\|\nabla f_{i,\;t+1}(u)-\nabla f_{i,\;t}(u)\| $. 式(C6)的第四个不等式是由于

中的每个$ \max_{u \in X} \|\;\nabla \;f_{i,\;t-k+1}(u)\;- \nabla f_{i,\;t-k}(u)\| $最多会被计算$ \tau_i $次. 使用相似的分析方法, 还可以得到

式(C6)的第五个不等式由柯西不等式得出, 式(C6)的第六个不等式由2范数小于1范数且$ \tau_i,\; D_i\geq 0 $得到. 然后, 根据式(4)近端算子$ {\rm prox}_{\eta r} $的定义, 可以得到$ {x}_{i,\,t+1}-{x}_{i,\,t}\in\eta (\tilde{\partial}r_i({x}_{i,\,t+1})\;+ \nabla f_{i,\,t-\tau_{i,\,t}}(x_{i,\,t-\tau_{i,\,t}}) + \gamma_t\lambda\sum_{j=1}^{N}a_{ij}\nabla L_{\delta_t}(x_{i,\,t}-x_{j,\,t})), $于是有

其中, 最后一个不等号是由$ \|\gamma_t\|=\|V({\boldsymbol x}_t)\|\;= \|\sum_{l=1}^{n}(\max_{i\in[N]}x_i^l-\min_{i\in[N]}x_i^l)\|\leq nR $得到. 结合前面对$ \sum_{t=1}^{T}\|{\boldsymbol x}_t-{\boldsymbol x}_{t-\tau}\| $的分析, 于是有

利用引理6的结论, 结合式(C6)和式(C8), 有如下结论

其中, 最后一个不等号成立由

得到. 令$ M=N(2G+\lambda\|A\|_\infty\sqrt{n}) $, 结合式(C4), 式(C5)和式(C9), 问题P的动态遗憾有如下上界:

□

附录D.   定理2和定理3的证明

在给出证明之前, 首先定义如下目标函数

其中,

由于$ \hat{f}_{i,\;t} $是$ \mu $-强凸函数, 这里的$ h_{i,\;t}(x) $也是$ \mu $-强凸函数. 特别地, 在单点Bandit反馈时, 有$ \nabla h_{i,\;t}(x_{i,\;t})=q_{i,\;t} $; 在两点Bandit点反馈时, 有$ \nabla h_{i,\;t}(x_{i,\;t})=p_{i,\;t} $.

引理8. 基于假设3 ~ 5和假设7, 并假设函数$ f_{i,\;t} $为凸函数, 对任意$ j\in[N] $和$ \xi<r $, $ \lambda>4NG/ a_{\min} $, $ \delta_t=2a_{\min}V({\boldsymbol x}_t)/na_{\max}N^2 $, 令$ \hat{x}_t^*:=(1-\frac{\xi}{r})x_t^*\;+ \frac{\xi}{r}y_0,\; $则有

其中, $ r $和$ y_0 $由假设7给出.

证明. 根据假设5, $ f_{i,\;t} $是$ G $-利普希茨连续函数, 则有$ \rVert f_{i,\;t}(x_{i,\;t}+\xi v_i)-f_{i,\;t}(x_{i,\;t})\rVert\leq G\rVert\xi v_i\rVert= G\xi $, 其中, 随机变量$ v_i $是单位向量. 于是, 对下式加上并减去$ \sum_{i=1}^{N}f_{i,\;t}(x_{i,\;t}) $, 得到

其中, 最后一个不等号式根据引理7, 对任意的$ j\in [N] $, 都有$ F_t(x_{j,\;t})\leq\widetilde{F}_t({\boldsymbol x}_t) $得到. 对(D3)求全期望, 可得

首先, 给出单点Bandit反馈下的结论, 此时$ h_{i,\;t}(x)=\hat{f}_{i,\;t}(x)+\langle q_{i,\;t}-\nabla\hat{f}_{i,\;t}(x_{i,\;t}),\;x\rangle $, 其中, $ x\in \widetilde{{X}} $. 根据期望的可加性, $ {\rm E}[\hat{F}_t({\boldsymbol x}_t)] $等价于

由于$ q_{i,\;t} $是$ \hat{f}_{i,\;t}(x_{i,\;t}) $的无偏估计, 于是

将式(D6)和式(D4)代入式(D5)中, 有

令$ \hat{x}_t^*:=(1-\frac{\xi}{r})x_t^*+\frac{\xi}{r}y_0 $, 根据假设5, 有

对下式加上并减去$ \sum_{i=1}^{N}f_{i,\;t}(x_t^*) $, 代入式(D8)得到

由于$ \hat{F}_t({\bf{1}}\otimes \hat{x}_t^*)\;=\;\sum_{i=1}^{N}(\hat{f}_{i,\;t}(\hat{x}_t^*)\;+\;r_{i}(\hat{x}_t^*))\;+ \sum_{i=1}^{N}\langle q_{i,\;t}- \nabla\hat{f}_{i,\;t}(x_{i,\;t}),\;\hat{x}_t^*\rangle $, 根据式(D9), 得到

其中, 式(D10)的第二个不等式由$ {\rm E}[\langle q_{i,\;t}\;- \nabla\hat{f}_{i,\;t}(x_{i,\;t}),\;\hat{x}_t^*\rangle]=0 $得到, 证明与式(D6)类似.

将式(D10)代入式(D7)中, 有

这意味着有

对于两点Bandit反馈来说, 由于$ p_{i,\;t} $也是$ \nabla \hat{f}_{i,\;t}(x_{i,\;t}) $的无偏估计, 于是有$ {\rm E}[\langle p_{i,\;t}-\nabla\hat{f}_{i,\;t}(x_{i,\;t}), \hat{x}_t^*\rangle]=0 $. 将$ q_{i,\;t} $由$ p_{i,\;t} $替换后, 也有与式(D12)一样的结论. □

为简化符号, 延用附录C中对$ r({\boldsymbol x}) $, $ {\boldsymbol x}_{t-{{\tau}}} $, $ l_t({\boldsymbol x}) $的定义, 另外, 令

此时, Bandit 反馈延迟下的状态更新过程(9)等价于$ {\boldsymbol x}_{t+1}=\;{\rm prox}^{\widetilde{{X}}}_{\eta r}\;\{{\boldsymbol x}_{t}-\eta\;[\nabla h_{t-\tau}\;({\boldsymbol x}_{t-\tau})\;+ \gamma_t \nabla l_t({\boldsymbol x}_{t})]\} $. 根据$ h_{i,\;t}(x) $的定义(式(D2)), 有

引理9. 若$ h_{i,\;t}(x_{i,\;t}) $是$ H $-梯度有界的, 基于假设1 ~ 5, 令$ \Delta=\lambda a_{\max}N^2\lVert A\lVert_\infty/2a_{\min} $, 设置算法1中

有

其中, $ \rho=1-\eta\mu $.

证明. 若$ h_{i,\;t}(x_{i,\;t}) $是有界梯度的, 界为$ H $, 则有

利用引理6的结论, 可以得到

由于$ h_{i,\;t}(x_{i,\;t}) $是有界梯度的, 界为$ H $, 与定理1中式(C8)的证明类似, 可得

结合式(C6)和上式, 有

□

定理2的证明. 在单点Bandit反馈下, $ h_{i,\;t}(x)= \hat{f}_{i,\;t}(x)+\langle q_{i,\;t}-\nabla\hat{f}_{i,\;t}(x_{i,\;t}),\;x\rangle $. 根据假设8, 此时有

合并引理8和引理9的结论, 其中, 引理9中的$ H $为$ nC/\xi $, 得到

其中, 最后一个不等式由单点反馈时引理9中$ H= nC/\xi $得到. 取

于是有

最后的等式根据$ \lim_{T\rightarrow \infty}(\log T)^\frac{3}{2}/\sqrt{T}=0 $得到. $ M $的定义与定理1的相同, 为$ N(2G+\lambda\|A\|_\infty\sqrt{n}) $. □

定理3的证明. 在两点Bandit反馈下, $ h_{i,\;t}(x)= \hat{f}_{i,\;t}(x)+\langle p_{i,\;t}-\nabla\hat{f}_{i,\;t}(x_{i,\;t}),\;x\rangle $. 根据假设5, 有

结合引理8和引理9的结论, 此时引理9中的$ H $为$ nG $, 与定理2的证明类似, 可以得到

取

于是有

其中, $ M $的定义与定理1的相同, 为$ N(2G\;+ \lambda\|A\|_\infty\sqrt{n}) $.□