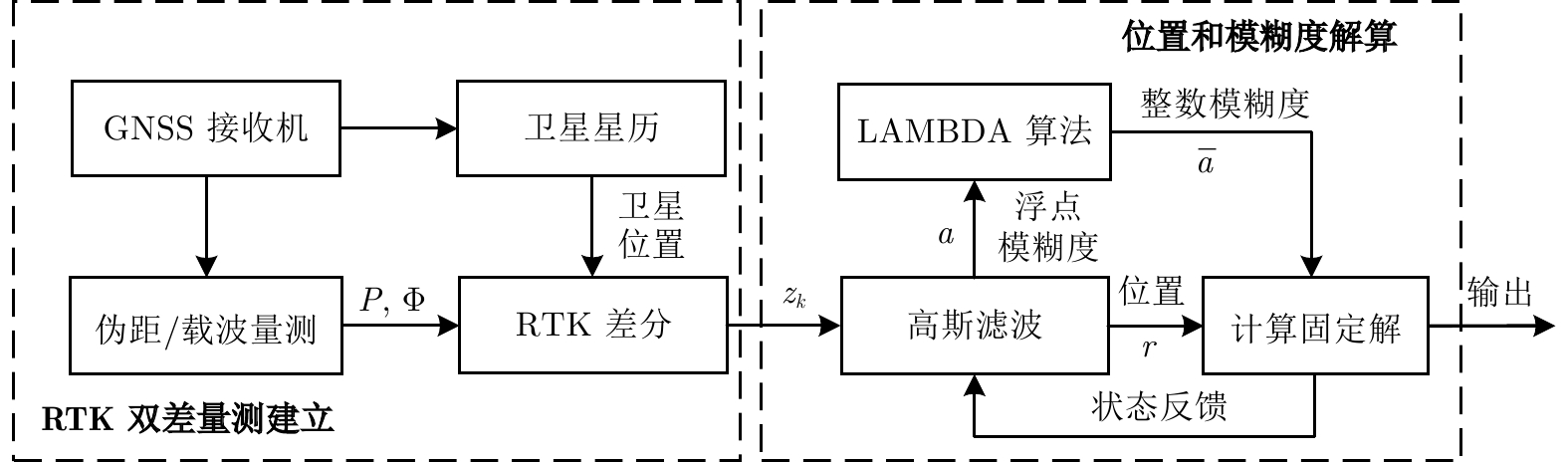
-
摘要: 本文研究了卫星信号干扰下 RTK (Real-time kinematic)整周模糊度固定问题, 提出一种基于整数约束型渐进高斯滤波的 RTK 定位方法. 首先, 结合贝叶斯推理与同伦方法优势, 导出一种兼容整数、浮点状态的渐进高斯滤波框架. 其次, 构造从先验分布到后验分布的同伦路径, 以目标浮点状态与模糊度固定的迭代求解来提高信号干扰情形下的整周模糊度固定率. 特别地, 通过渐进地融合卫星双差信息来降低线性化误差, 进而提升对目标状态后验分布的逼近精度. 最后, 通过车载 RTK 实验及后处理分析, 验证了所提方法的有效性和优越性.Abstract: This paper investigates the issue of real-time kinematic (RTK) integer ambiguity resolution under satellite signal interference and proposes an RTK positioning method based on integer-constrained progressive Gaussian filtering. Firstly, by combining the advantages of Bayesian inference and homotopy methods, a progressive Gaussian filtering framework that is compatible with both integer and floating-point states is derived. Secondly, a homotopic path is constructed from the prior distribution to the posterior distribution, and the target floating-point state and ambiguity resolution is solved iteratively for improving the integer ambiguity fixed rate under signal interference conditions. Specifically, the linearization error is reduced by progressively fusing satellite double-difference information, thus enhancing the approximation accuracy of the posterior distribution of the target state. Finally, the effectiveness and superiority of the proposed method are validated through vehicle-mounted RTK experiments and post-processing analysis.
-
图 9 卫星失锁后定位误差收敛速度
Fig. 9 Positioning error convergence speed after satellite signal loss
表 1 RMSE和固定率对比
Table 1 Comparison of RMSE and fixed rate
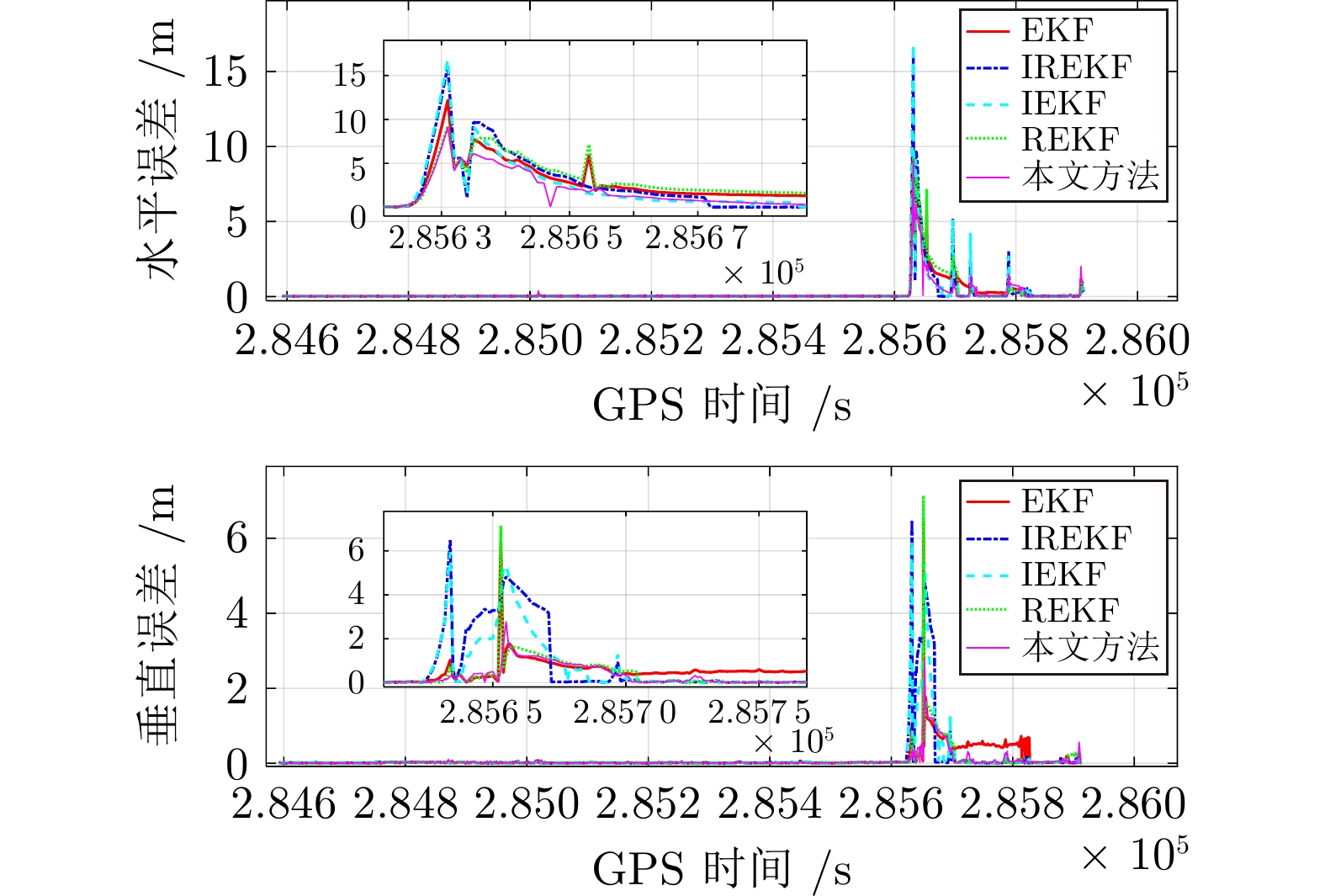
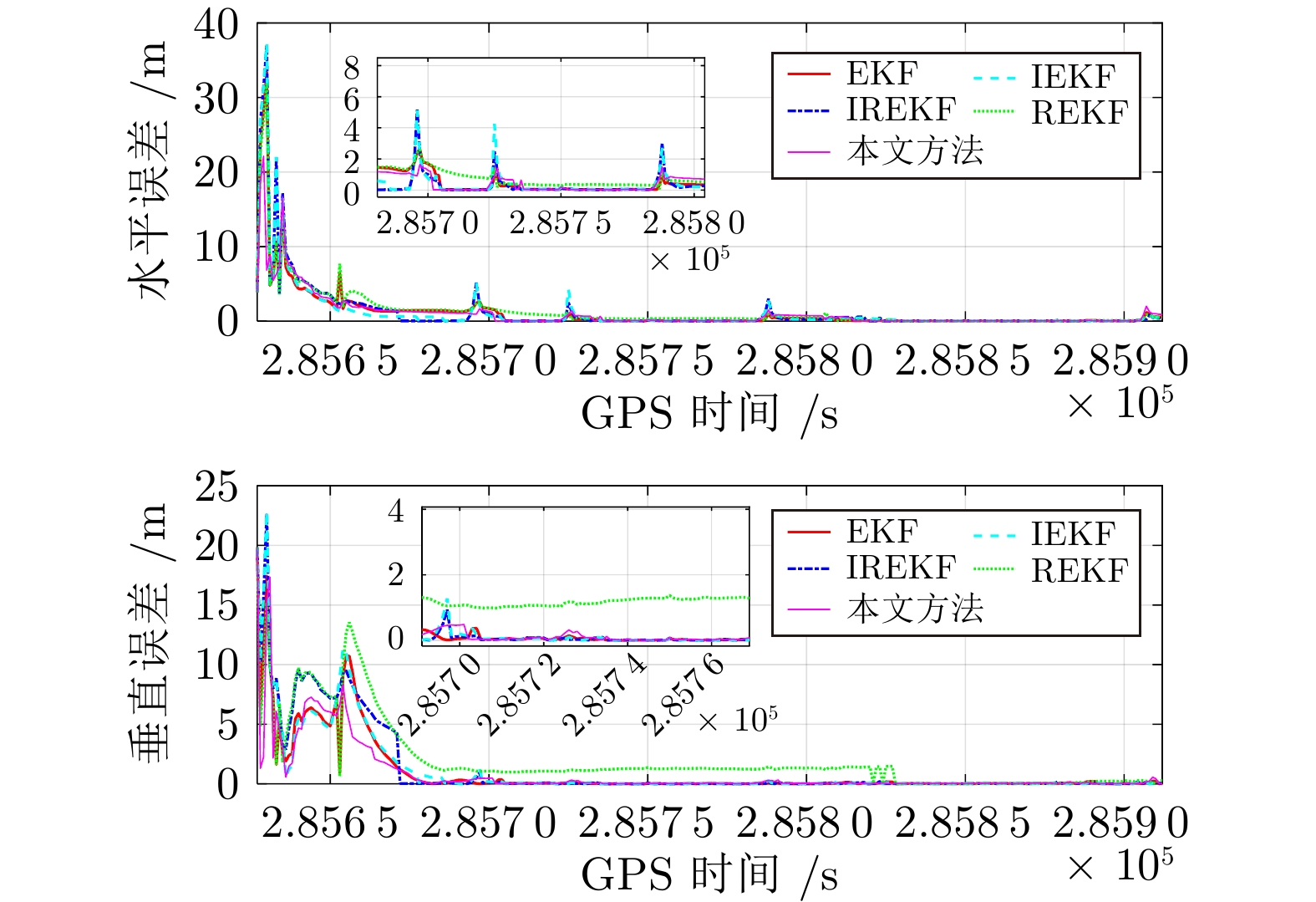
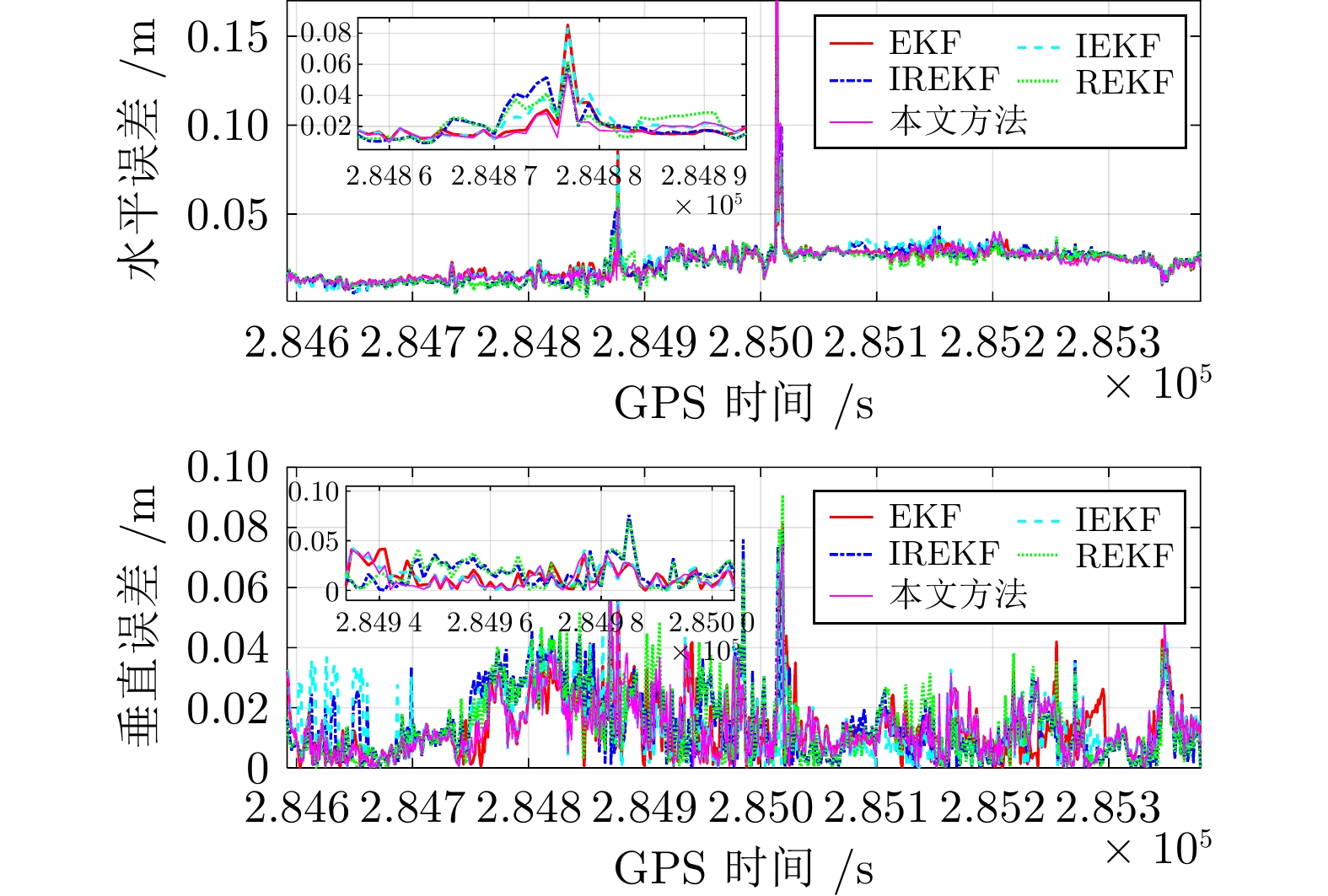
方法 EKF IREKF IEKF REKF 所提方法 提升 RMSE-水平 (m) 0.8718 1.0223 0.9600 0.9075 0.6696 23.19% RMSE-垂直 (m) 0.2959 0.6174 0.5150 0.2871 0.2062 28.18% 固定率 (%) 50.3300 61.5800 58.4800 71.1300 90.3800 19.25% 
下载: 导出CSV
表 2 单个历元平均解算时间
Table 2 The average calculation time of each epoch
方法 EKF IREKF IEKF REKF 所提方法 时间 (s) 0.0821 0.1506 0.1490 0.0863 0.0899
下载: 导出CSV
-
[1] Ji R, Jiang X, Chen X, Zhu H, Ge M, Neitzel F. Quality monitoring of real-time GNSS precise positioning service system. Geo-Spatial Information Science, 2023, 26(1): 1−15 doi: 10.1080/10095020.2022.2070554 [2] Chen Q, Lin H, Kuang J, Luo Y, Niu X. Rapid initial heading alignment for MEMS land vehicular GNSS/INS navigation system. IEEE Sensors Journal, 2023, 23(7): 7656−7666 doi: 10.1109/JSEN.2023.3247587 [3] 王婷娴, 贾克斌, 姚萌. 面向轻轨的高精度实时视觉定位方法. 自动化学报, 2021, 47(9): 2194−2204Wang Ting-Xian, Jia Ke-Bin, Yao Meng. Real-time visual localization method for light-rail with high accuracy. Acta Automatica Sinica, 2021, 47(9): 2194−2204 [4] Medina D, Calatrava H, Castro-Arvizu J M, Closas P, Vila-Valls J. A collaborative RTK approach to precise positioning for vehicle swarms in urban scenarios. In: Proceedings of IEEE/ION Position, Location and Navigation Symposium (PLANS). Monterey, USA: IEEE, 2023. 254−259 [5] Tao X, Liu W, Wang Y, Li L, Zhu F, Zhang X. Smartphone RTK positioning with multi-frequency and multi-constellation raw observations: GPS L1/L5, Galileo E1/E5a, BDS B1I/B1C/B2a. Journal of Geodesy, 2023, 97(5): Article No. 43 doi: 10.1007/s00190-023-01731-3 [6] Gao Y, Jiang Y, Gao Y, Huang G, Yue Z. Solution separation-based integrity monitoring for RTK positioning with faulty ambiguity detection and protection level. GPS Solutions, 2023, 27(3): Article No. 140 doi: 10.1007/s10291-023-01472-y [7] 陈杰, 程兰, 甘明刚. 基于高斯和近似的扩展切片高斯混合滤波器及其在多径估计中的应用. 自动化学报, 2013, 39(1): 1−10 doi: 10.1016/S1874-1029(13)60001-4Chen Jie, Cheng Lan, Gan Ming-Gang. Extension of SGMF using Gaussian sum approximation for nonlinear/non-Gaussian model and its application in multipath estimation. Acta Automatica Sinica, 2013, 39(1): 1−10 doi: 10.1016/S1874-1029(13)60001-4 [8] Teunissen P. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. Journal of Geodesy, 1995, 70(1): 65−82 [9] Chang X W, Yang X, Zhou T. MLAMBDA: A modified LAMBDA method for integer ambiguity determination. In: Proceedings of the 61st Annual Meeting of the Institute of Navigation. Cambridge, USA: 2005. 1086−1097 [10] Takasu T, Yasuda A. Kalman-filter-based integer ambiguity resolution strategy for long-baseline RTK with ionosphere and troposphere estimation. In: Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, USA: 2010. 161−171 [11] Gao Y, Jiang Y, Liu B, Gao Y. Integrity monitoring of multi-constellation GNSS-based precise velocity determination in urban environments. Measurement, 2023, 222: Article No. 113676 doi: 10.1016/j.measurement.2023.113676 [12] Giorgi G, Teunissen P. Carrier phase GNSS attitude determination with the multivariate constrained LAMBDA method. In: Proceedings of 2010 IEEE Aerospace Conference. Big Sky, USA: IEEE, 2010. 1−12 [13] 张文安, 林安迪, 杨旭升, 俞立, 杨小牛. 融合深度学习的贝叶斯滤波综述. 自动化学报, 2024, 50(8): 1502−1516Zhang Wen-An, Lin An-Di, Yang Xu-Sheng, Yu Li, Yang Xiao-Niu. A survey on bayesian filtering with deep learning. Acta Automatica Sinica, 2024, 50(8): 1502−1516 [14] Fang H, Tian N, Wang Y, Zhou M C, Haile M. Nonlinear Bayesian estimation: From Kalman filtering to a broader horizon. IEEE/CAA Journal of Automatica Sinica, 2018, 5(2): 401−417 doi: 10.1109/JAS.2017.7510808 [15] 杨旭升, 王雪儿, 汪鹏君, 张文安. 基于渐进无迹卡尔曼滤波网络的人体肢体运动估计. 自动化学报, 2023, 49(8): 1723−1731Yang Xu-Sheng, Wang Xue-Er, Wang Peng-Jun, Zhang Wen-An. Estimation of human limb motion based on progressive unscented Kalman filter network. Acta Automatica Sinica, 2023, 49(8): 1723−1731 [16] Katriniok A, Abel D. Adaptive EKF-based vehicle state estimation with online assessment of local observability. IEEE Transactions on Control Systems Technology, 2016, 24(4): 1368−1381 doi: 10.1109/TCST.2015.2488597 [17] Chen X, Wang X, Xu Y. Performance enhancement for a GPS vector-tracking loop utilizing an adaptive iterated extended Kalman filter. Sensors, 2014, 14(12): 23630−23649 doi: 10.3390/s141223630 [18] Li H, Medina D, Vilà-Valls J, Closas P. Robust Kalman filter for RTK positioning under signal-degraded scenarios. In: Proceedings of the 32nd International Technical Meeting of the Satellite Division of the Institute of Navigation. Miami, USA: 2019. 3717−3729 [19] Medina D, Li H, Vilà-Valls J, Closas P. Robust filtering techniques for RTK positioning in harsh propagation environments. Sensors, 2021, 21(4): Article No. 1250 doi: 10.3390/s21041250 [20] Yuan H, Zhang Z, He X, Wen Y, Zeng J. An extended robust estimation method considering the multipath effects in GNSS real-time kinematic positioning. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 1−9 [21] Huang Y, Zhang Y, Li N, Zhao L. Gaussian approximate filter with progressive measurement update. In: Proceedings of 54th IEEE Conference on Decision and Control (CDC). Osaka, Japan: IEEE, 2015. 4344−4349 [22] 郑婷婷, 杨旭升, 张文安, 俞立. 一种高斯渐进滤波框架下的目标跟踪方法. 自动化学报, 2018, 44(12): 2250−2258Zheng Ting-Ting, Yang Xu-Sheng, Zhang Wen-An, Yu Li. A target tracking method in Gaussian progressive filtering framework. Acta Automatica Sinica, 2018, 44(12): 2250−2258 [23] Yang X, Zhao C, Chen B. Progressive Gaussian approximation filter with adaptive measurement update. Measurement, 2019, 148: Article No. 106898 doi: 10.1016/j.measurement.2019.106898 [24] 杨旭升, 吴江宇, 胡佛, 张文安. 基于渐进高斯滤波融合的多视角人体姿态估计. 自动化学报, 2024, 50(3): 607−616Yang Xu-Sheng, Wu Jiang-Yu, Hu Fo, Zhang Wen-An. Multi-view human pose estimation based on progressive Gaussian filtering fusion. Acta Automatica Sinica, 2024, 50(3): 607−616 [25] Verhagen S, Teunissen P. The ratio test for future GNSS ambiguity resolution. GPS Solutions, 2013, 17: 535−548 doi: 10.1007/s10291-012-0299-z -
图(10) / 表(2)
计量
- 文章访问数: 192
- HTML全文浏览量: 62
- PDF下载量: 44
- 被引次数: 0
