Online Learning Control of Uncertain Nonlinear Systems Using Gaussian Processes and Its Application
-
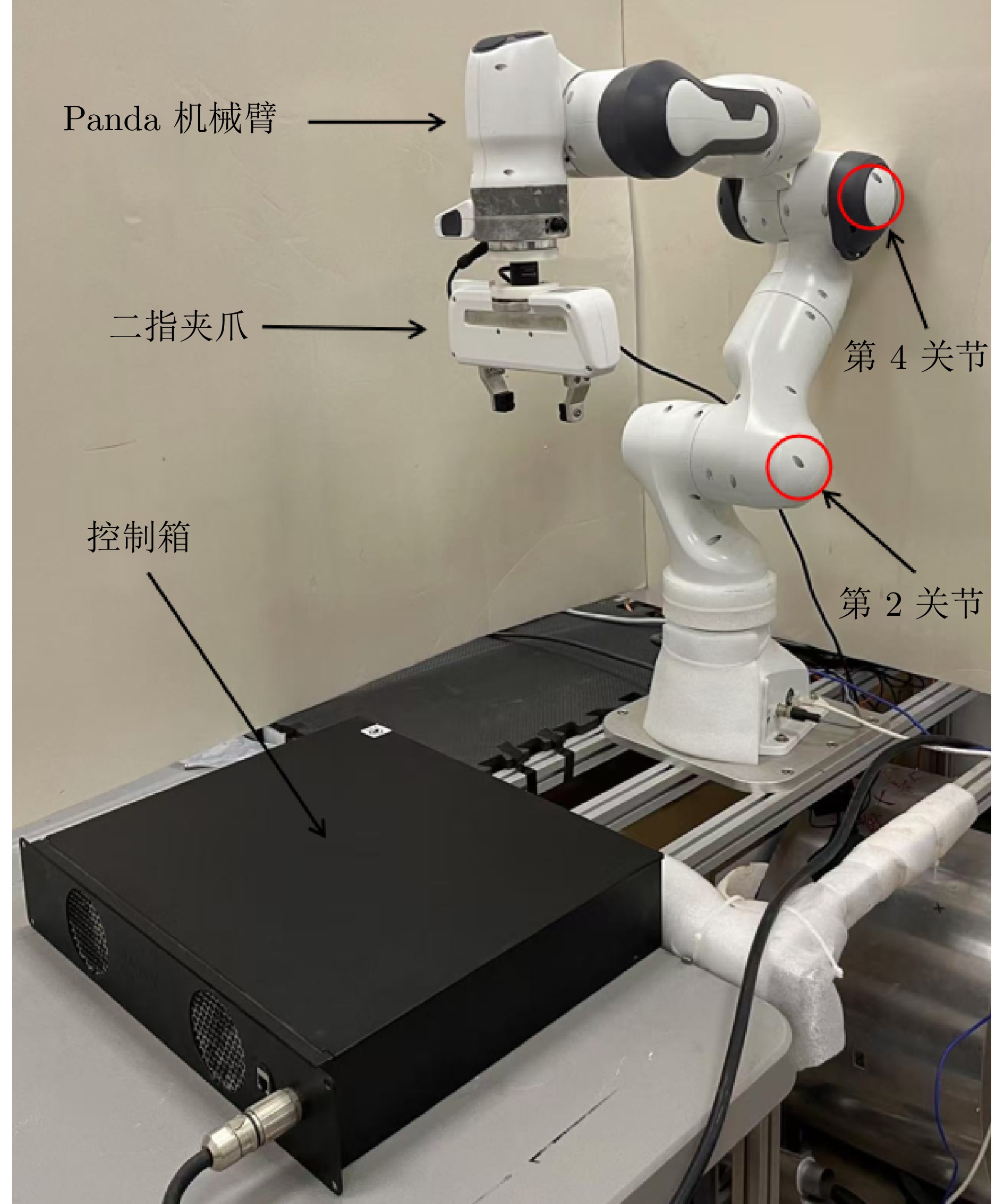
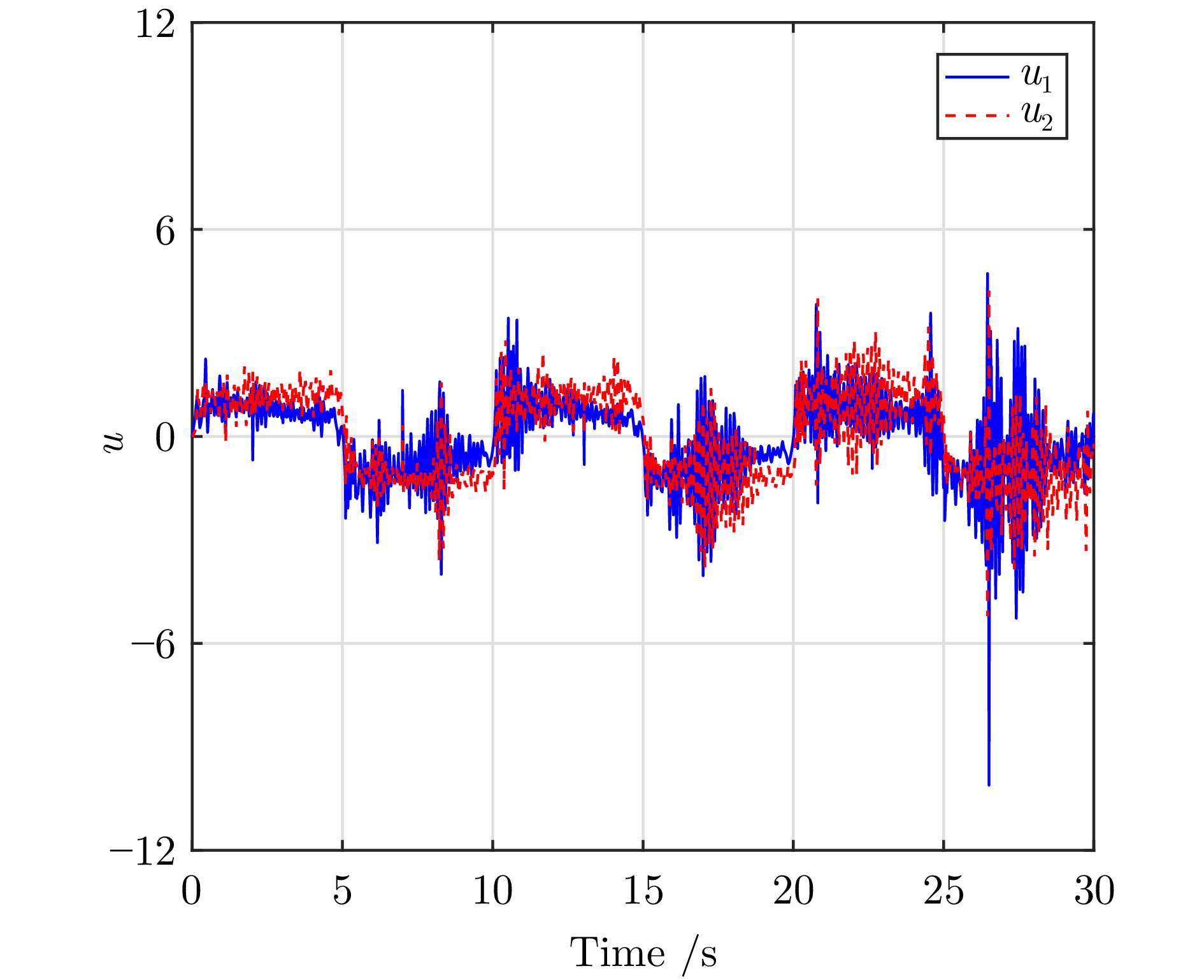
摘要: 针对一类不确定非线性系统, 提出了一种基于高斯过程的在线学习控制方法. 该方法首先通过障碍函数间接设定系统状态的运行区域. 其次, 在该区域内在线采集量测数据, 利用高斯过程回归对系统中未知非线性动态进行学习. 然后通过Lyapunov稳定理论, 证明了所提在线学习控制算法可保证闭环系统所有信号的有界性. 与基于径向基神经网络(Radial basis function neural networks, RBFNNs) 的自适应控制方案相比, 所提控制算法无需精确给出系统状态的运行区域及预先分配径向基函数中心值. 最后, 通过数值仿真与Franka Emika Panda 协作机械臂关节控制实验, 验证了控制算法的有效性与先进性.Abstract: This paper presents a Gaussian process-based online learning control (GP-OLC) approach for a class of uncertain nonlinear systems. Initially, a barrier function is introduced to indirectly define the operating domain of the system states. Subsequently, a Gaussian process regression is employed to learn the unknown system dynamics utilizing measurement data collected online within this domain. Through Lyapunov stability theory, we prove that the proposed GP-OLC algorithm ensures the boundedness of all signals in the closed-loop system. Compared to adaptive control schemes using radial basis function neural networks (RBFNNs), the developed controller does not necessitate precise specification of the system states' operating domain nor preallocation of radial basis function (RBF) center values. Finally, the effectiveness and superiority of the proposed approach are validated through numerical simulations and joint control experiments on a Franka Emika Panda collaborative robot.
-
Key words:
- Nonlinear systems /
- uncertain systems /
- Gaussian processes /
- online learning control /
- manipulators
-
图 7 由Franka Emika Panda机械臂本体和控制箱组成的实验平台
Fig. 7 The experimental platform consisted of the Franka Emika Panda robot body和control box
图 8 位置状态$q_1$, 参考轨迹$q_{d1}$和跟踪误差$e_{11}=q_1-q_{d1}$
Fig. 8 Position state $q_1$, desired trajectory $q_{d1}$ and tracking error $e_{11}=q_1-q_{d1}$
图 9 位置状态$q_2$, 参考轨迹$q_{d2}$和跟踪误差$e_{12}=q_2-q_{d2}$
Fig. 9 Position state $q_2$, desired trajectory $q_{d2}$ and tracking error $e_{12}=q_2-q_{d2}$
图 11 文中GP-OLC和PD控制作用下关节位置跟踪误差$e_{11}=q_1-q_{d1}$
Fig. 11 Position tracking error $e_{11}=q_1-q_{d1}$ under the proposed GP-OLC in this paper and PD control
图 12 文中GP-OLC和PD控制作用下关节位置跟踪误差$e_{12}=q_2-q_{d2}$
Fig. 12 Position tracking error $e_{12}=q_2-q_{d2}$ the proposed GP-OLC in this paper and PD control
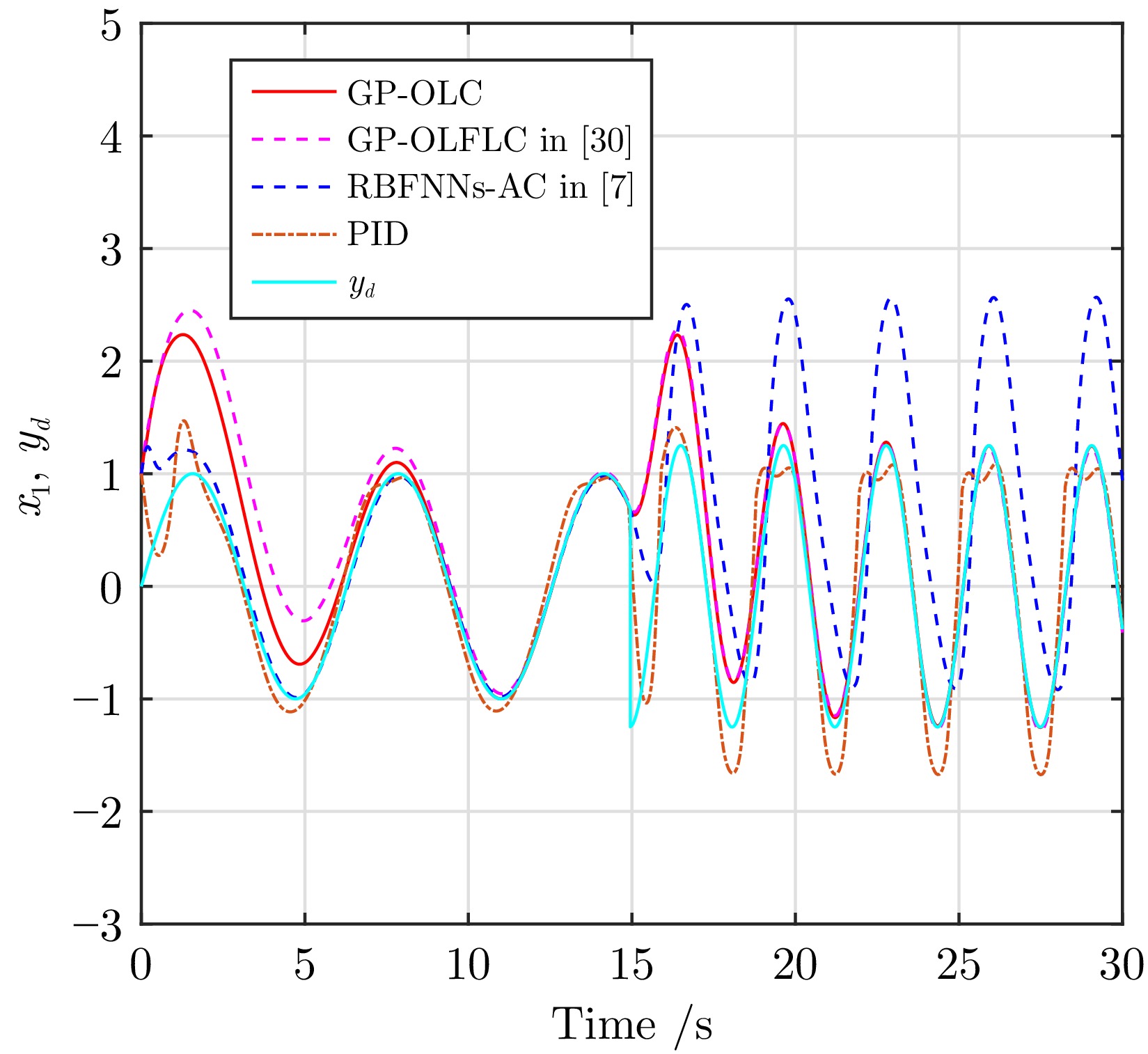
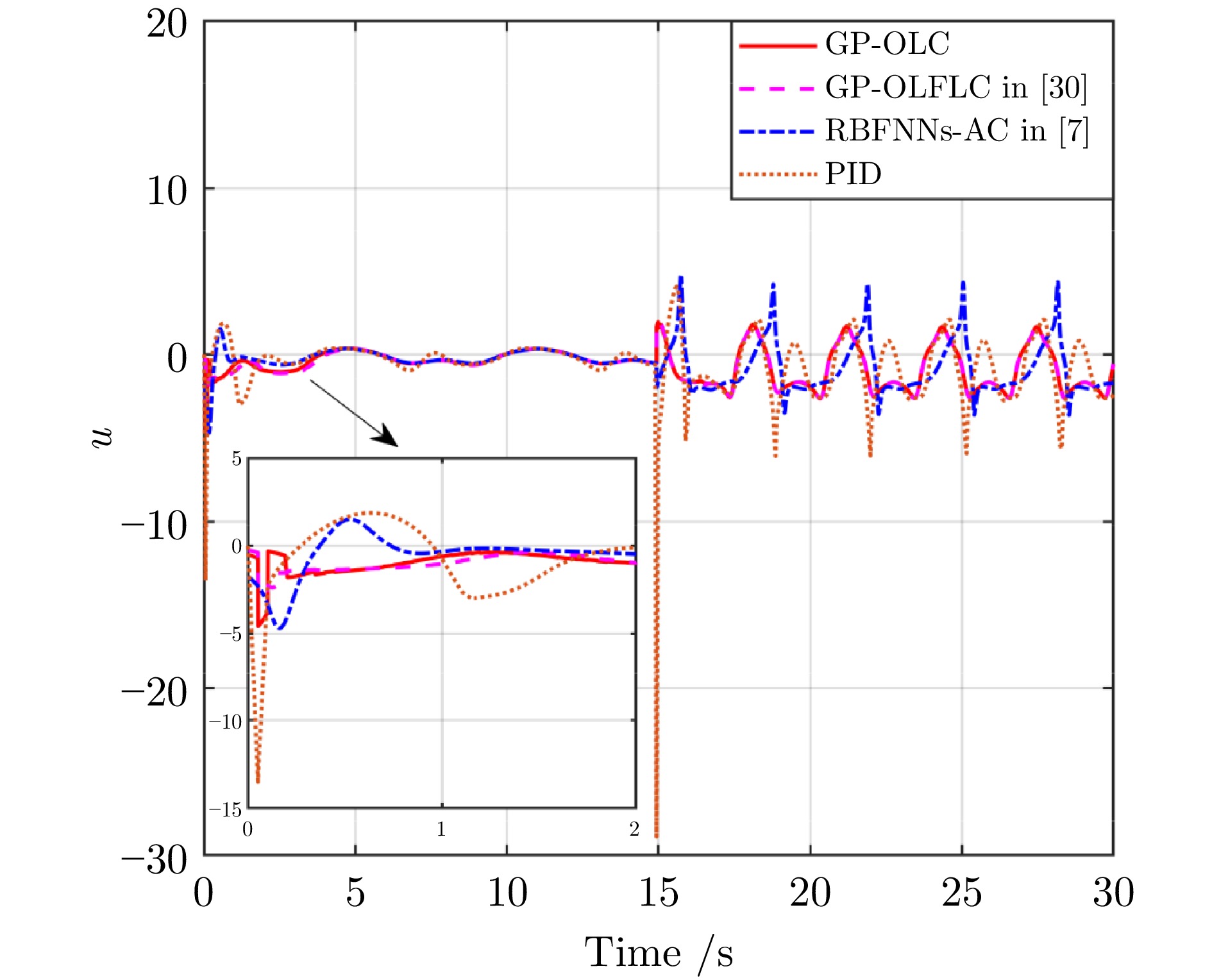
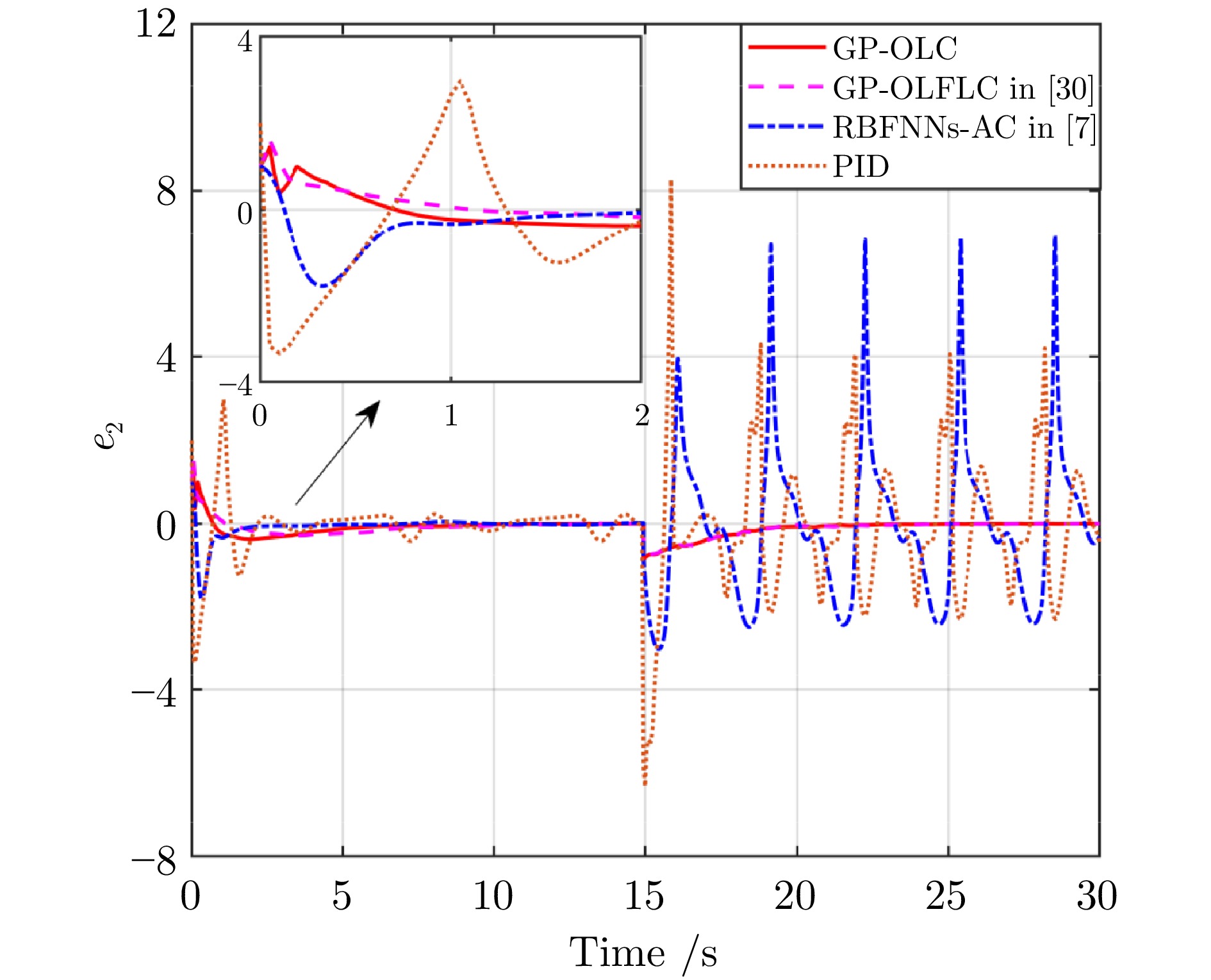
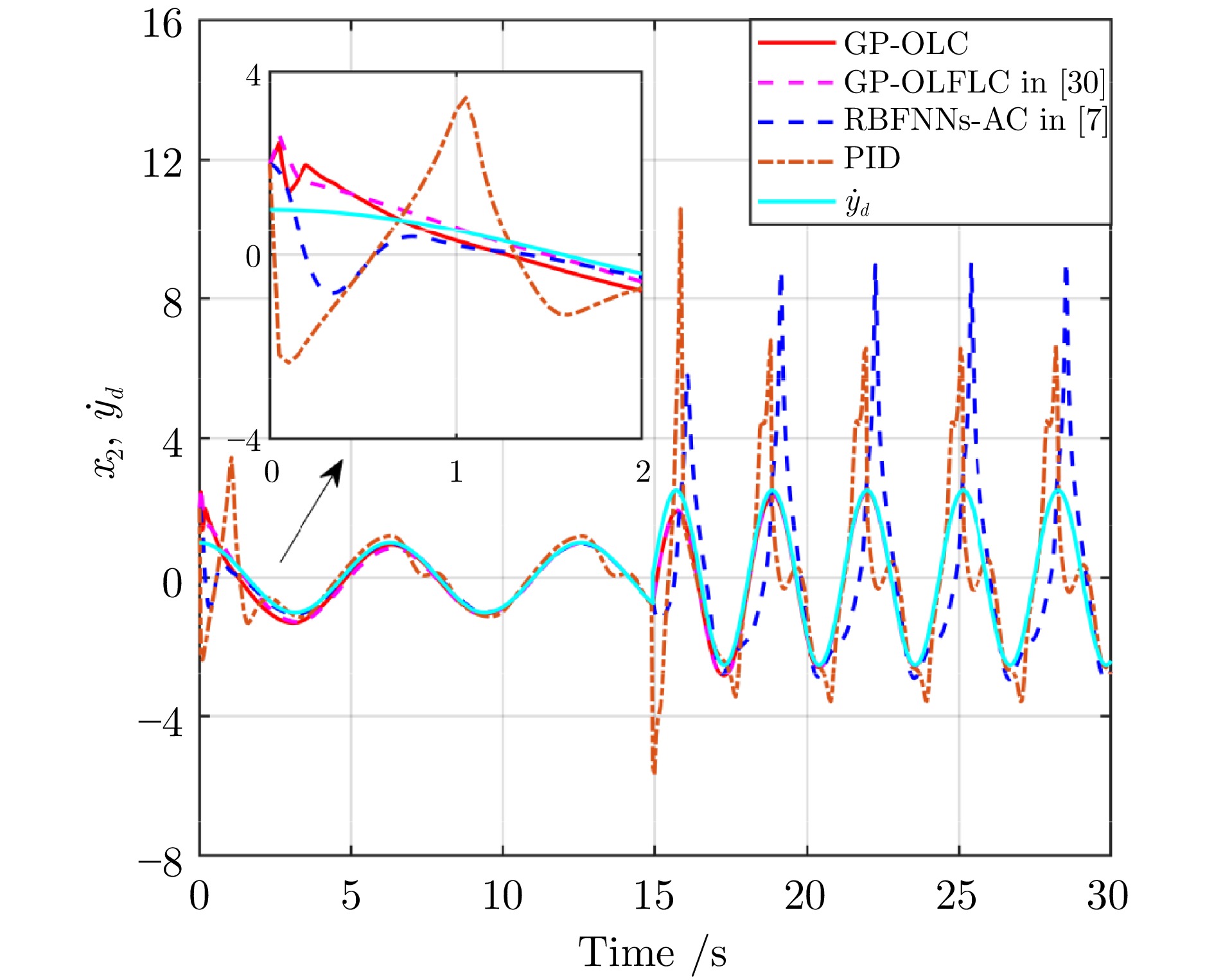
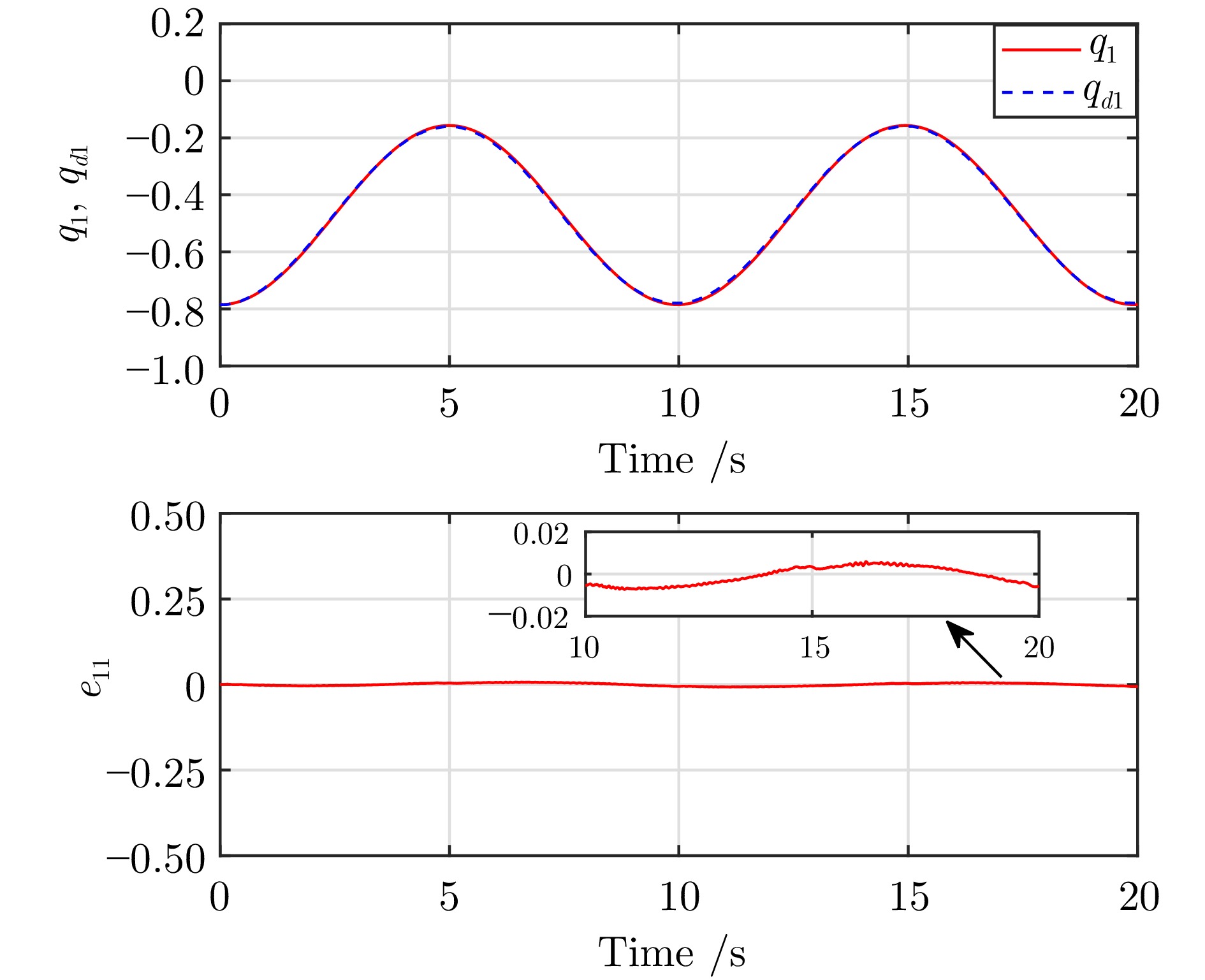
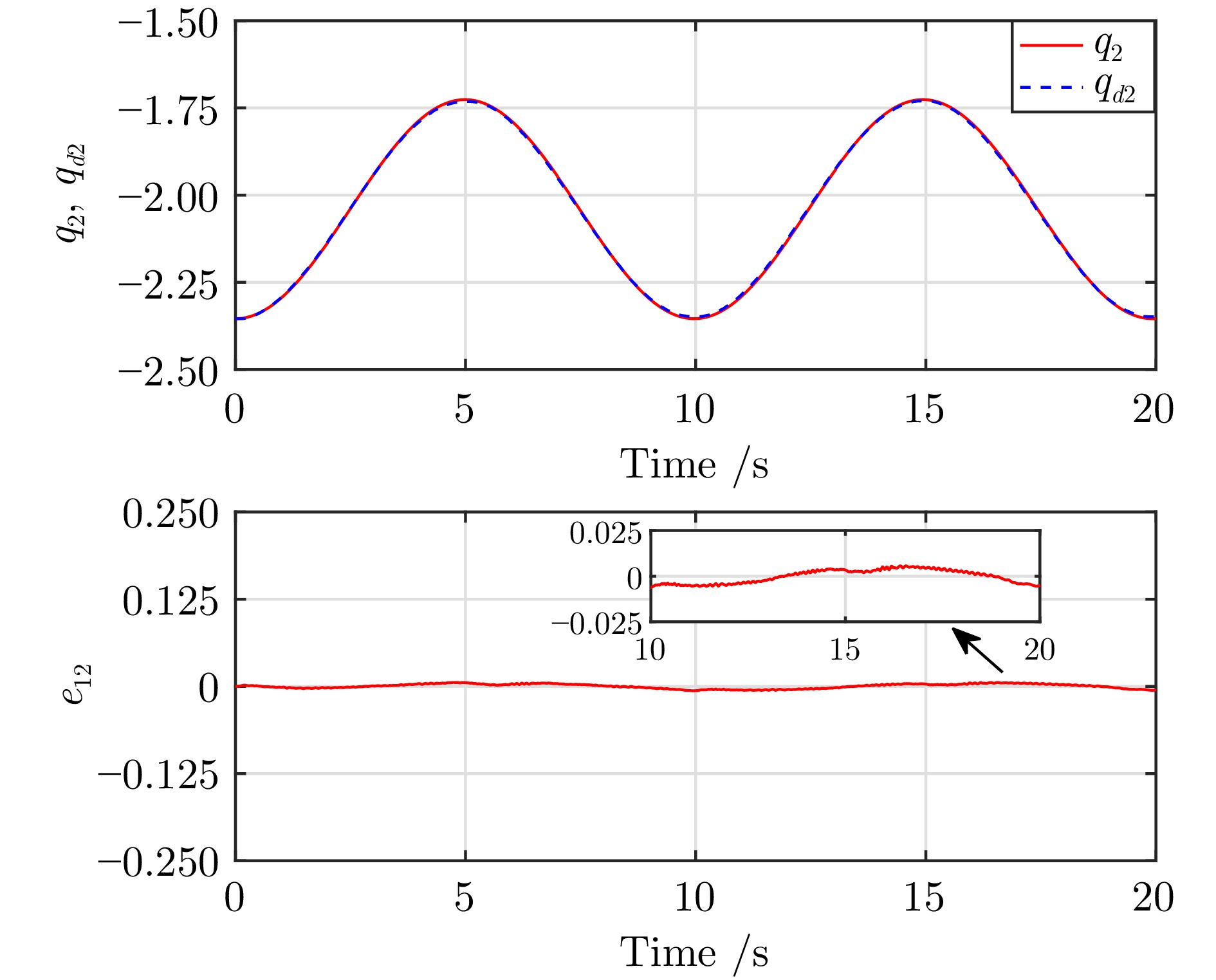
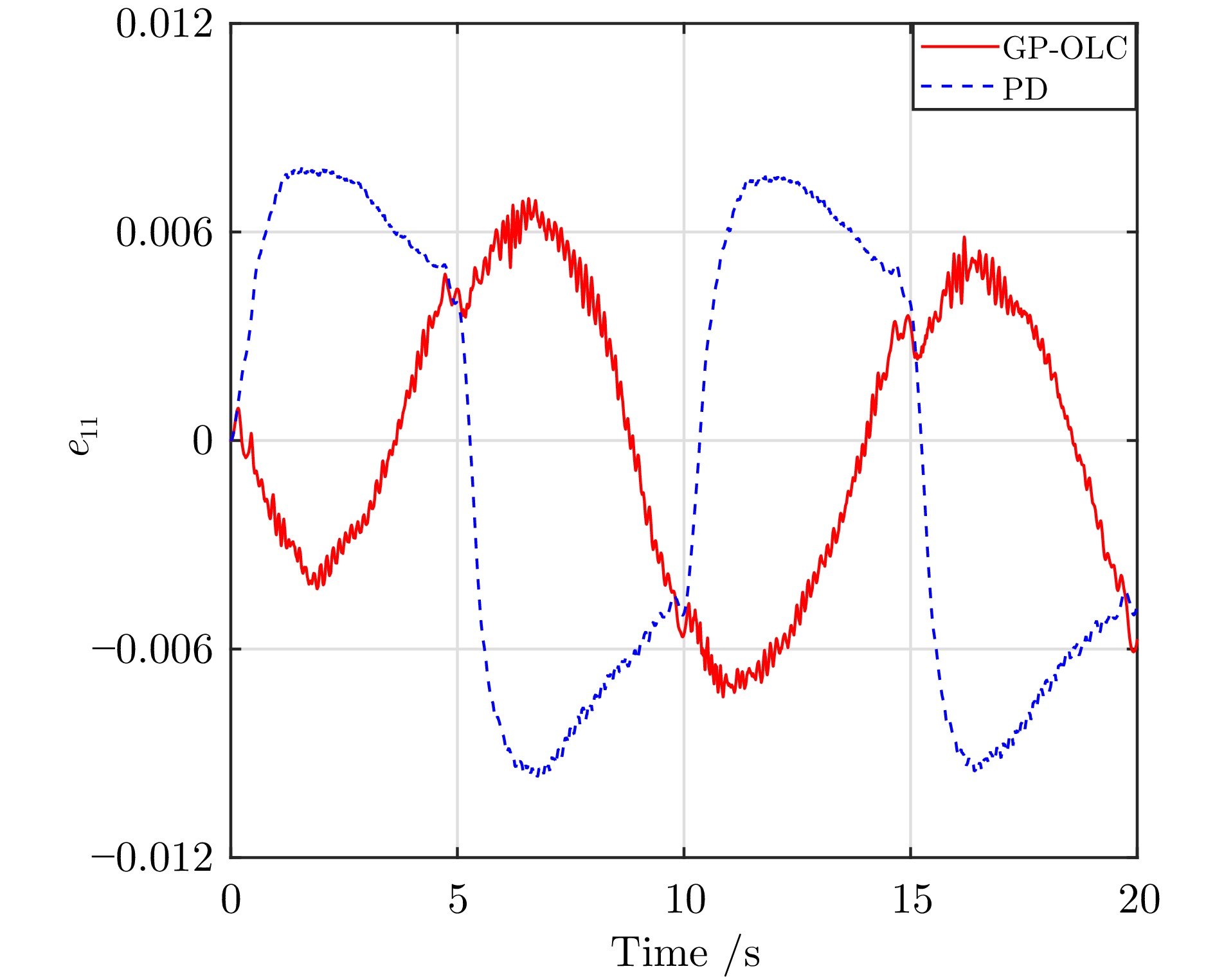
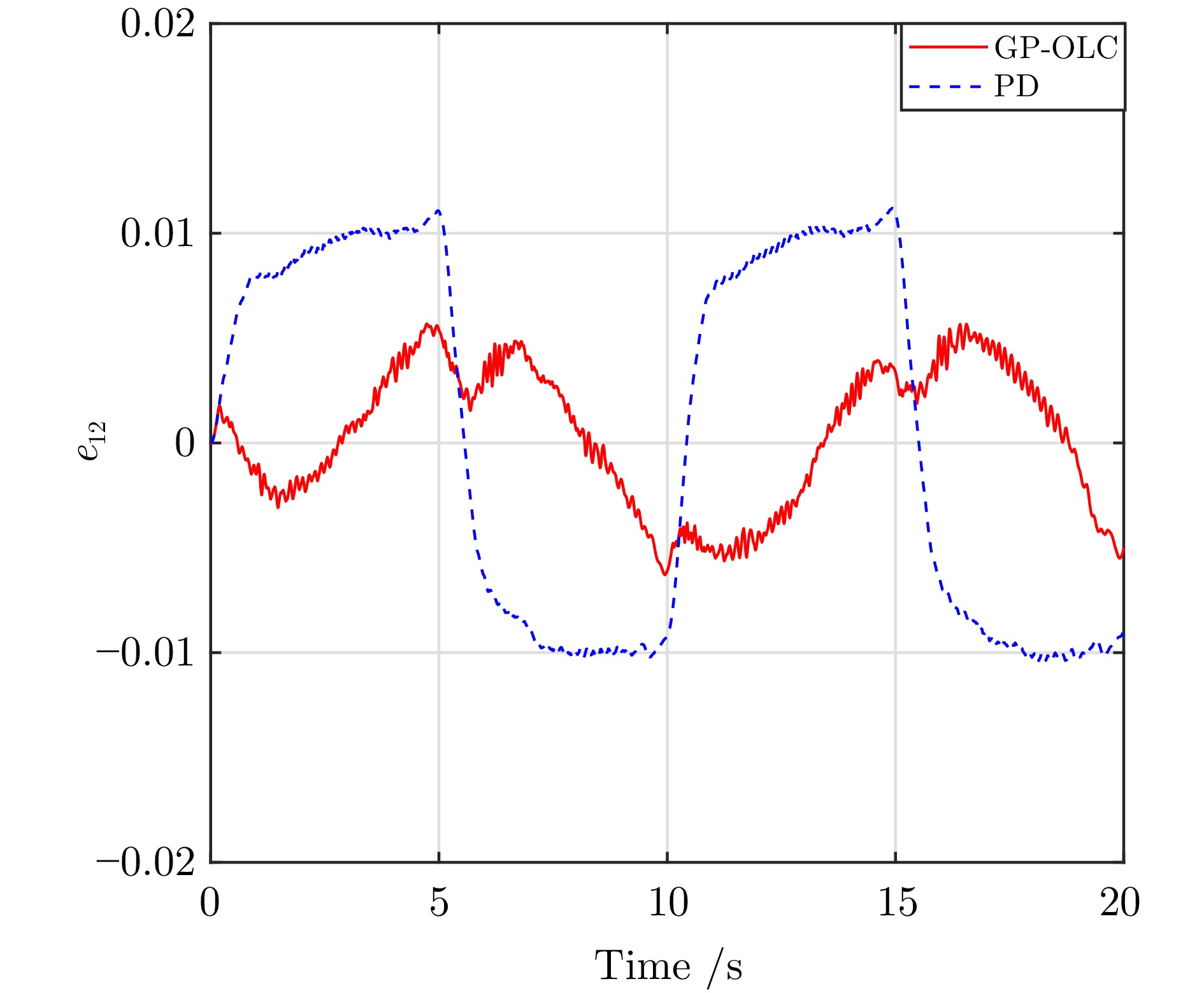
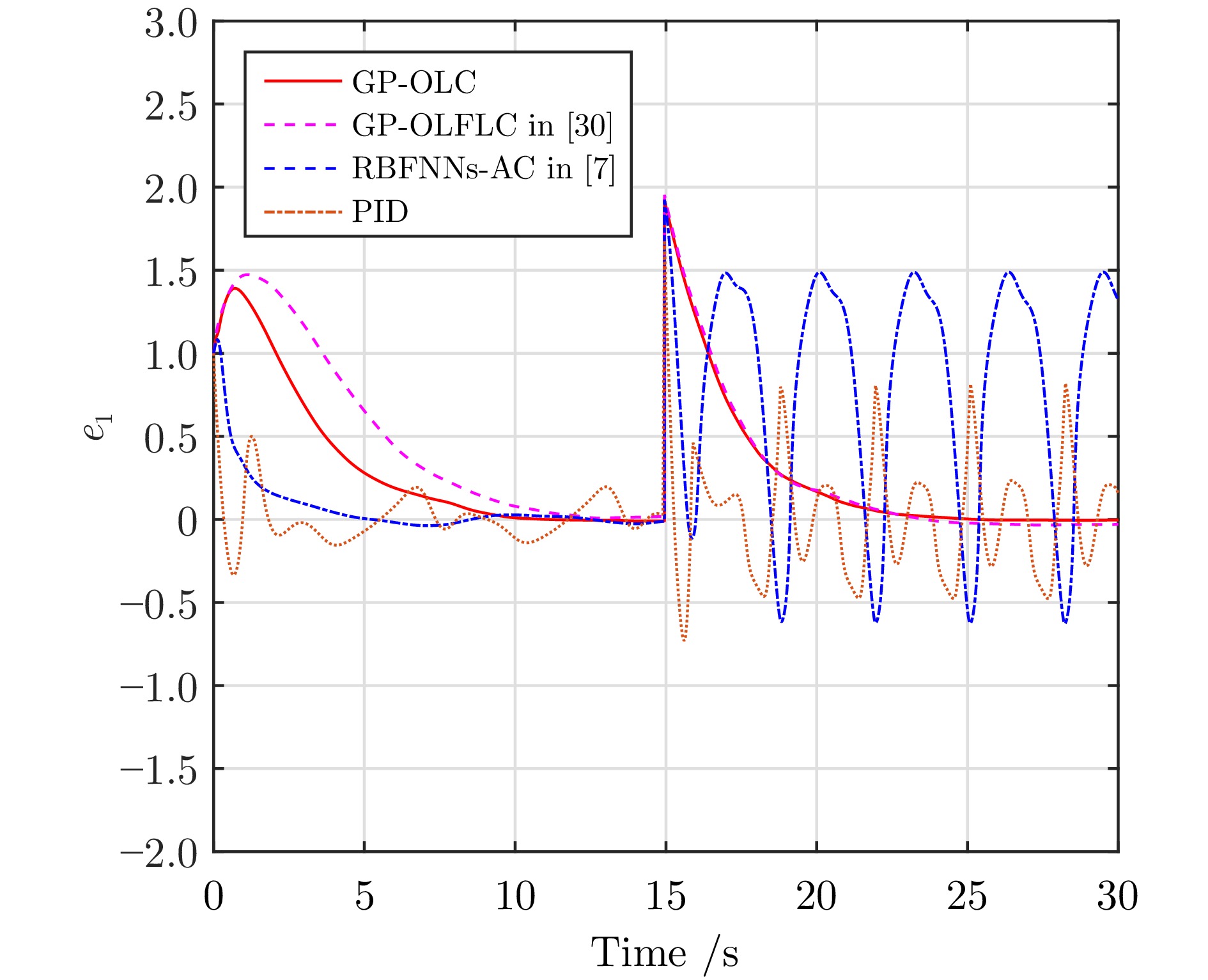
表 1 在时间间隔$ [20,\;30] $上跟踪误差$ e_1 $和$ e_2 $的$ L_2 $范数
Table 1 $ L_2 $ norm of tracking errors $ e_1 $ and $ e_2 $ over time interval $ [20,\;30] $
GP-OLC GP-OLFLC PID RBFNNs-AC $ ||e_1||_{L_2} $ 4.46 5.41 6.76 97.22 $ ||e_2||_{L_2} $ 2.61 2.82 32.41 161.17 
下载: 导出CSV
表 2 Franka Emika Panda机械臂的运动学参数
Table 2 Kinematic parameters of Franka Emika Panda robot
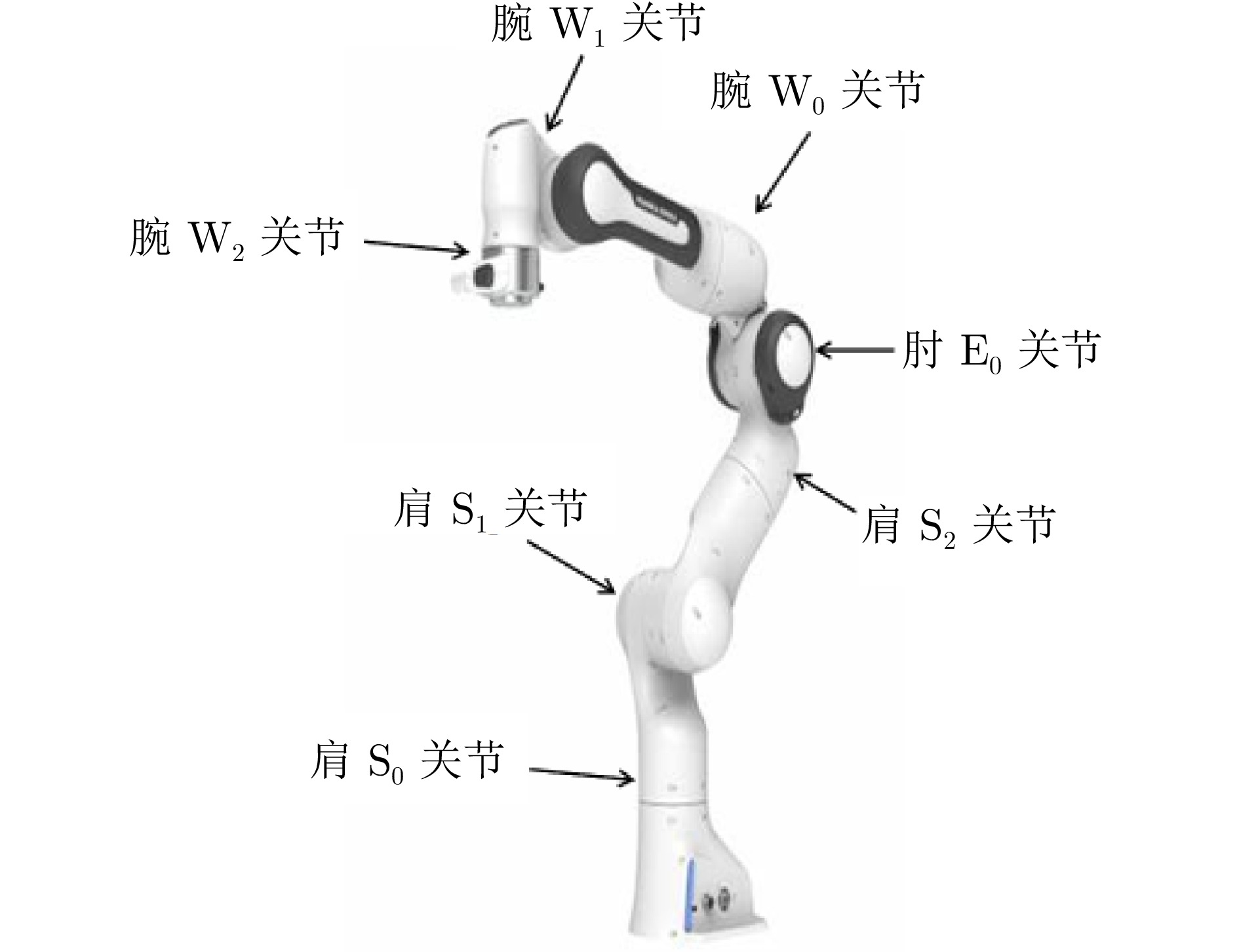
关节 $ j $ $ d_j $[m] $ a_j $[rad] $ b_j $[m] $ q_j $[rad] 关节1 0.333 0 0 $ q_1 $ 关节2 0 $ -\dfrac{\pi}{2} $ 0 $ q_2 $ 关节3 0.316 $ \dfrac{\pi}{2} $ 0 $ q_3 $ 关节4 0 $ \dfrac{\pi}{2} $ 0.0825 $ q_4 $ 关节5 0.384 $ -\dfrac{\pi}{2} $ − 0.0825 $ q_5 $ 关节6 0 $ \dfrac{\pi}{2} $ 0 $ q_6 $ 关节7 0 $ \dfrac{\pi}{2} $ 0.088 $ q_7 $
下载: 导出CSV
-
[1] Wu Chengxi, Karimi Hamid Reza, Shan Liang, Dai Yuewei. Data-driven iterative learning cooperative trajectory tracking control for multiple autonomous underwater vehicles with input saturation constraints. Journal of Field Robotics, 2024, DOI: 10.1002/ROB.22343 [2] Zhang M, Zhang Z, Sun M. Adaptive tracking control of uncertain robotic m anipulators. IEEE Transactions on Circuits and Systems II: Express Briefs, 2024, 71(5): 2734−2738 [3] 王浩亮, 柴亚星, 王丹, 刘陆, 王安青, 彭周华. 基于事件触发机制的多自主水下航行器协同路径跟踪控制. 自动化学报, 2024, 50(5): 1001−1011Wang Hao-Liang, Chai Ya-Xing, Wang Dan, Liu Lu, Wang An-Qing, Peng Zhou-Hua. Event-triggered cooperative path following of multiple autonomous underwater vehicles. Acta Automatica Sinica, 2024, 50(5): 1001−1011 [4] 路遥. 一种非仿射高超声速飞行器输出反馈控制方法. 自动化学报, 2022, 48(6): 1530−1542Lu Yao. A method of output feedback control for non-affine hypersonic vehicles. Acta Automatica Sinica, 2022, 48(6): 1530−1542 [5] Ma J, Wang H, QiaoJ. Adaptive neural fixed-time tracking control for high-order nonlinear systems. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(1): 708−717 [6] Bai W, Liu P X, Wang H. Neural-network-based adaptive fixed-time control for nonlinear multiagent non-affine systems. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(1): 570−583 doi: 10.1109/TNNLS.2022.3175929 [7] Wang C. Deterministic Learning Theory for Identification, Recognition, and Control. Boca Raton: CRC Press, 2017 [8] Zheng S, Shi P, Wang S, Shi Y. Adaptive neural control for a class of nonlinear multiagent systems. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(2): 763−776 [9] 吴锦娃, 刘勇华, 苏春翌, 鲁仁全. 具有不确定控制增益严格反馈系统的自适应命令滤波控制. 自动化学报, 2024, 50(5): 1−10Wu Jin-Wa, Liu Yong-Hua, Su Chun-Yi, Lu Ren-Quan. Adaptive command filtered control of strict feedback systems with uncertain control gains. Acta Automatica Sinica, 2024, 50(5): 1−10 [10] Zhang J, Niu B, Wang D, Wang H, Zong G. Time-/event-triggered adaptive neural asymptotic tracking control for nonlinear systems with full-state constraints and application to a single-link robot. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(11): 3390−6700 [11] Zhang F, Wu W, Wang C. Dynamic learning from neural network-based control for sampled-data strict-feedback nonlinear systems. International Journal of Robust and Nonlinear Control, 2022, 32(15): 8397−8420 doi: 10.1002/rnc.6292 [12] Wang M, Shi H, Wang C, Fu J. Dynamic learning from adaptive neural control for discrete-time strict-feedback systems. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(8): 3700−3712 [13] Sanner R M, Slotine J. Gaussian networks for direct adaptive control. IEEE Transactions on Neural Networks, 1992, 3(6): 837−863 doi: 10.1109/72.165588 [14] Chen W, Ge S S, Wu J, Gong M. Globally stable adaptive backstepping neural network control for uncertain strict-feedback systems with tracking accuracy known a priori. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(9): 1842−1854 doi: 10.1109/TNNLS.2014.2357451 [15] Liu Y H, Su C Y, Li H, Lu R. Barrier function-based adaptive control for uncertain strict-feedback systems within predefined neural network approximation sets. IEEE Transactions on Neural Networks and Learing Systems, 2020, 31(8): 2942−2954 doi: 10.1109/TNNLS.2019.2934403 [16] Liu Y H, Liu Y, Liu Y F, Su C Y, Zhou Q, Lu R. Adaptive approximation-based tracking control for a class of unknown high-order nonlinear systems with unknown powers. IEEE Transactions on Cybernetics, 2022, 52(6): 4559−4573 doi: 10.1109/TCYB.2020.3030310 [17] Liu Y H, Liu Y, Liu Y F, Su C Y. Adaptive fuzzy control with global stability guarantees for unknown strict-feedback systems using novel integral barrier Lyapunov functions. IEEE Transactions on Systems, Man and Cybernetics: Systems, 2022, 52(7): 4336−4348 doi: 10.1109/TSMC.2021.3094975 [18] Liu Y H, Liu Y F, Su C Y, Liu Y, Zhou Q, Lu R. Guaranteeing global stability for neuro-adaptive control of unknown pure-feedback nonaffine systems via barrier functions. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(9): 5869−5881 doi: 10.1109/TNNLS.2021.3131364 [19] Nardi F. Neural Network Based Adaptive Algorithms for Nonlinear Control[Ph. D. dissertation], Georgia Institute of Technology, US, 2000 [20] Shankar P. Self-organizing Radial Basis Function Networks for Adaptive Flight Control and Aircraft Engine State Estimation [Ph. D. dissertation], The Ohio State University, US, 2007 [21] Sundararajan N, Saratchandran P, Yan L. Fully Tuned Radial Basis Function Neural Networks for Flight Control. New York, US: Springer, 2002 [22] Deisenroth M P, Turner R D, Huber M F, Hanebeck U D, Rasmussen C E. Robust filtering and smoothing with Gaussian processes. IEEE Transactions on Automatic Control, 2012, 57(7): 1865−1871 doi: 10.1109/TAC.2011.2179426 [23] Rasmussen C E, Williams C. Gaussian Processes for Machine Learning. Cambridge, MA: MIT Press, 2006 [24] Kocijan J. Modelling and Control of Dynamic Systems using Gaussian Process Models. New York, US: Springer, 2016 [25] Duvenaud D. Automatic Model Construction with Gaussian Processes[Ph. D. dissertation], University of Cambridge, UK, 2014 [26] Umlauft J M. Safe Learning Control for Gaussian Process[Ph. D. dissertation], Technical University of Munich, Germany, 2020 [27] Umlauft J, Beckers T, Kimmel M, Hirche S. Feedback linearization using Gaussian processes. In: Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC). Melbourne, VIC, Australia: 2017. 5249−5255 [28] Capone A, Hirche S. Backstepping for partially unknown nonlinear systems using Gaussian processes. IEEE Control Systems Letters, 2019, 3(2): 416−421 doi: 10.1109/LCSYS.2018.2890467 [29] Chowdhary G, Kingravi H A, How J P, Vela P A. Bayesian nonparametric adaptive control using Gaussian processes. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(3): 537−550 doi: 10.1109/TNNLS.2014.2319052 [30] Umlauft J, Hirche S. Feedback linearization based on Gaussian Processes with event-triggered online learning. IEEE Transactions on Automatic Control, 2020, 65(10): 4154−4169 doi: 10.1109/TAC.2019.2958840 [31] Jiao J J, Capone A, Hirche S. Backstepping tracking control using Gaussian processes with event-triggered online learning. IEEE Control Systems Letters, 2022, 6: 3176−3181 doi: 10.1109/LCSYS.2022.3183530 [32] Lederer A, Yang Z, Jiao J, Hirche S. Cooperative control of uncertain multiagent systems via distributed Gaussian processes. IEEE Transactions on Automatic Control, 2023, 68(5): 3091−3098 doi: 10.1109/TAC.2022.3205424 [33] Beckers T, D Kulic, Hirche S. Stable Gaussian process based tracking control of Euler-Lagrange systems. Automatica, 2019, 103: 390−397 doi: 10.1016/j.automatica.2019.01.023 [34] Lederer A, Capone A, Umlauft J, Hirche S. How training data impacts performance in learning-based control. IEEE Control Systems Letters, 2021, 5(3): 905−910 doi: 10.1109/LCSYS.2020.3006725 [35] Beckers T, Hirche S, Colombo L. Online learning-based formation control of multi-agent systems with Gaussian processes. In: Proceedings of the 60th IEEE Conference on Decision and Control (CDC). Austin, TX, USA: IEEE, 2021. 2197−2022 [36] Beckers T, Hirche S. Prediction with approximated Gaussian process dynamical models. IEEE Transactions on Automatic Control, 2022, 67(12): 6460−6473 doi: 10.1109/TAC.2021.3131988 [37] Beckers T, Colombo L, Hirche S, Pappas G J. Online learning-based trajectory tracking for underactuated vehicles with uncertain dynamics. IEEE Control Systems Letters, 2022, 6: 2090−2095 doi: 10.1109/LCSYS.2021.3138546 [38] Khalil H K. Nonlinear Systems, 3rd Edition. Englewood Cliffs: Prentice-Hall, 2002 [39] Seeger M W, Kakade S M, Foster D P. Information consistency of nonparametric Gaussian process methods. IEEE Transactions on Information Theory, 2008, 54(5): 2376−2382 doi: 10.1109/TIT.2007.915707 [40] Song Y, Wang Y, Wen C. Adaptive fault-tolerant pi tracking control with guaranteed transient and steady-state performance. IEEE Transactions on Automatic Control, 2017, 62(1): 481−487 [41] Logemann M, Ryan E P. Ordinary Differential Equations: Analysis, Qualitative Theory and Control. London, UK: Springer, 2014 [42] Gaz C, Cognetti M, Oliva A, Giordano P Robuffo, Luca A De. Dynamic identification of the franka emika panda robot with retrieval of feasible parameters using penalty-based optimization. IEEE Robotics and Automation Letters, 2019, 4(4): 4147−4154 -
计量
- 文章访问数: 18
- HTML全文浏览量: 28
- 被引次数: 0
