Distributed Collision Avoidance Tracking Control for Quadrotor Cooperative Suspension System Under Performance Constraints
-
摘要: 针对存在未知扰动的多四旋翼无人机协同吊挂系统(Multi-quadrotor cooperative supension system, MQCSS), 提出一种具有避碰和性能约束的分布式自适应积分反步跟踪控制(Distributed adaptive integral backstepping tracking control, DAIBC)方法. 首先, 设计新型的有限时间性能函数(Finite time performance function, FTPF)和人工势函数分别用于处理负载的跟踪约束和四旋翼无人机(Quadrotor unmanned aerial vehicle, QUAV)之间的避碰问题. 然后, 构造一种积分型的辅助变量并结合动态面技术设计反步控制器, 实现四旋翼无人机的分布式编队运输负载. 同时, 将动态面技术与自适应调节机制相结合, 对系统存在的未知干扰进行抑制. 接着, 给出严格的Lyapunov稳定性分析, 证明闭环系统所有信号的最终一致有界. 最后, 通过数值对比仿真和实飞实验结果验证了所提方法的有效性.Abstract: This paper presents a distributed adaptive integral backstepping tracking control (DAIBC) method for a multi-quadrotor cooperative suspension system (MQCSS) under unknown disturbances. The proposed approach addresses both collision avoidance and performance constraints. Initially, a novel finite-time performance function (FTPF) and an artificial potential function are formulated to manage load tracking constraints and prevent collisions among quadrotor unmanned aerial vehicle (QUAV). An integral auxiliary variable is then introduced, and a backstepping controller is designed using dynamic surface technology to facilitate the distributed formation transport of quadrotors. Additionally, the dynamic surface technique is integrated with an adaptive adjustment mechanism to mitigate unknown disturbances within the system. A rigorous Lyapunov stability analysis demonstrates the ultimate uniform boundedness of all signals in the closed-loop system. Finally, the effectiveness of the proposed method is validated through numerical comparative simulations and real flight experiments.
-
图 4 数值仿真: 负载跟踪误差的性能约束
Fig. 4 Numerical simulation: Performance constraint for load tracking error
图 5 数值仿真: QUAV分布式编队跟踪误差的2范数和QUAV之间的欧氏距离 $ ||d_{ij}|| $
Fig. 5 Numerical simulation: The 2-morm for QUAV distributed formation tracking errors and Euclidean distance $ ||d_{ij}|| $ between QUAVs
图 9 实验验证: 负载跟踪误差的性能约束
Fig. 9 Experimental verification: Performance constraint for load tracking error
图 10 实验验证: QUAV分布式编队跟踪误差的2范数
Fig. 10 Experimental verification: The 2-norm for QUAV distributed formation tracking errors
图 11 实验验证: QUAV之间的欧氏距离 $||d_{ij}||$
Fig. 11 Experimental verification: Euclidean distance $||d_{ij}||$ between QUAVs
图 12 实验验证: MQCSS的控制信号 $u_i$
Fig. 12 Experimental verification: Control signals $u_i$ for MQCSS
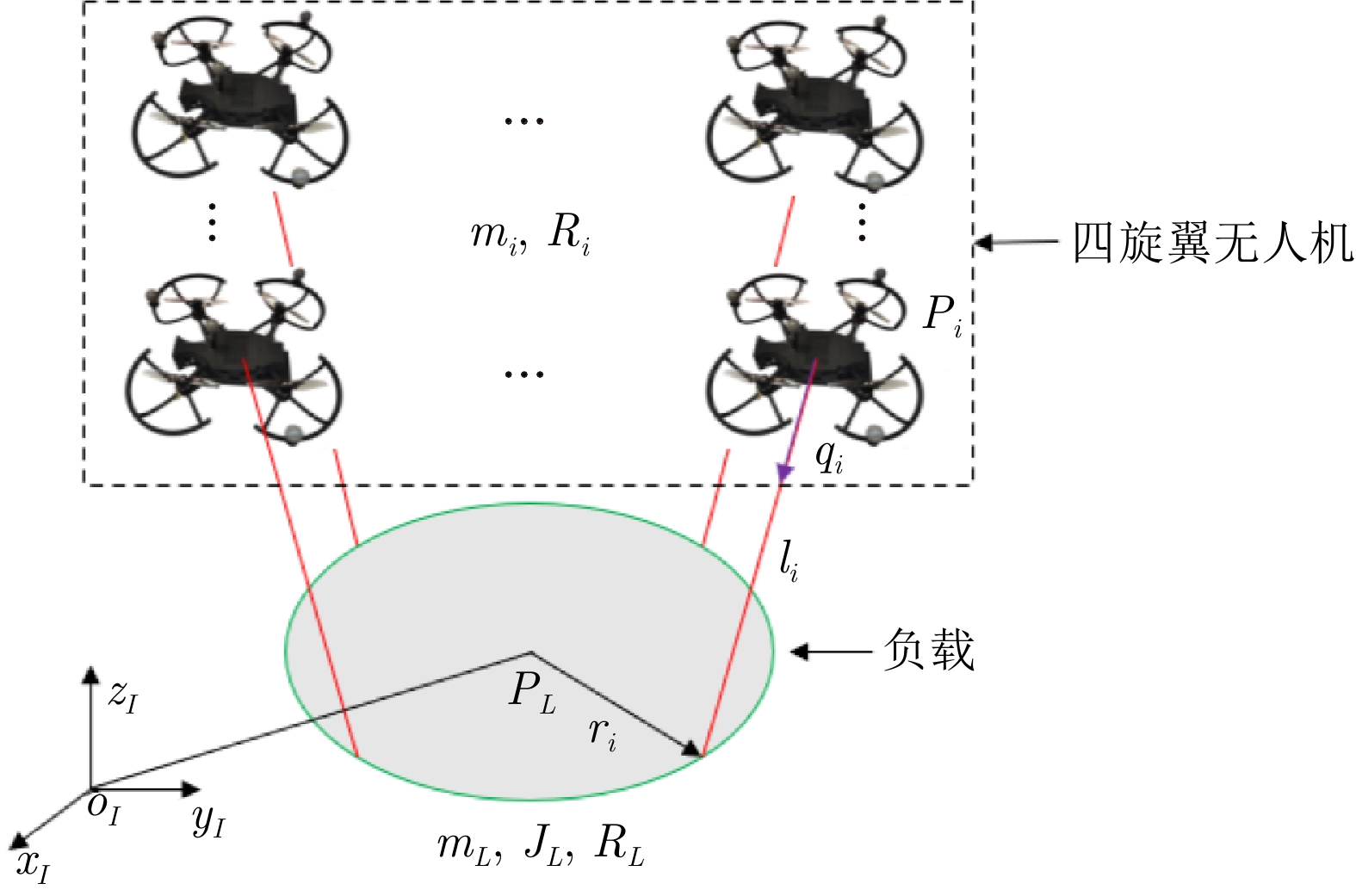
符号 定义 $ {{{P}}_i} = {\left[ {x_i,\;y_i,\;z_i} \right]^{\rm T}} $ 第$ i $架QUAV的位置 $ {{{P}}_L} = {\left[ {x_L,\;y_L,\;z_L} \right]^{\rm T}} $ 负载的位置 $ R_i $, $ R_L $ 第$ i $架QUAV和负载的旋转矩阵 $ q_i $ 第$ i $根连接杆的单位方向向量 $ r_i $ 负载质心到第$ i $个连接点的向量 $ m_{i} $, $ m_L $ 第$ i $架QUAV和负载的质量 $ J_L $ 负载的惯性矩阵 $ l_i $ 第$ i $根连接杆的长度 
下载: 导出CSV
表 2 数值仿真结果的定量分析
Table 2 Quantitative analysis of numerical simulation results
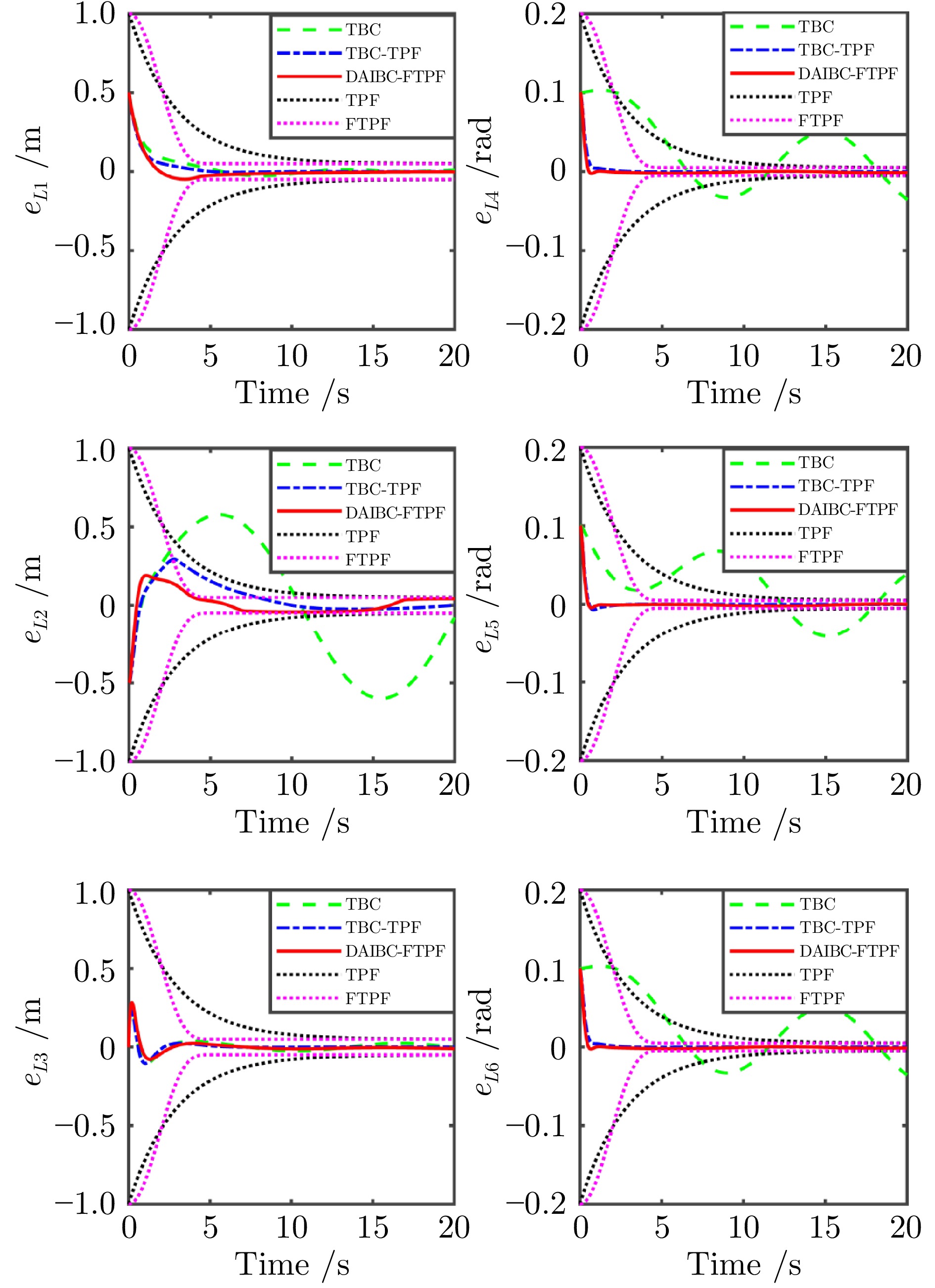
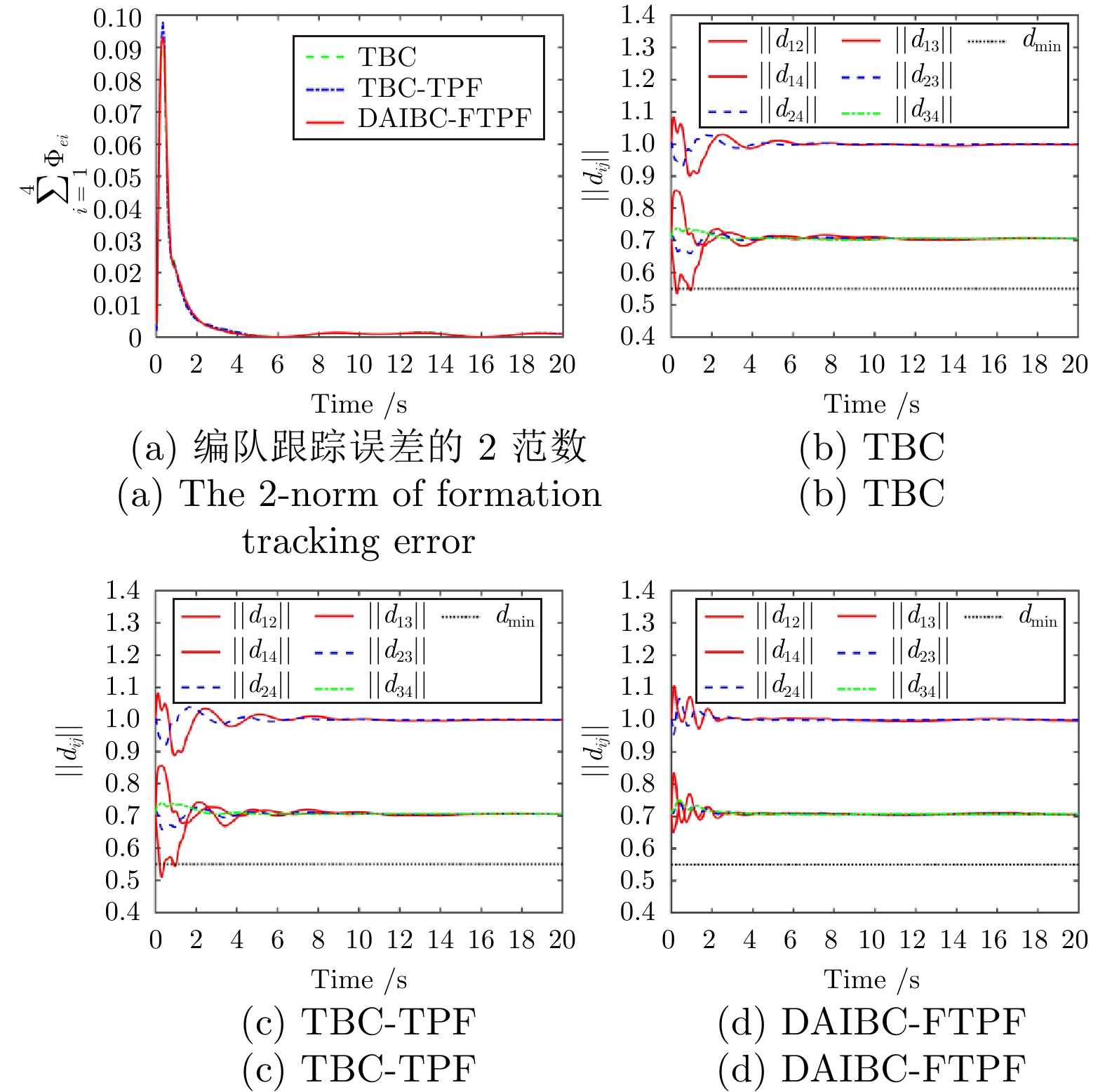
控制方法 TBC TBC-TPF DAIBC-FTPF $ \Upsilon_{e_{L}} $ 0.1602 0.1136 0.0912 $ E $ $ 1.528\;3\times10^5 $ $ 1.527\;9\times10^5 $ $ 1.502\;9\times10^5 $
下载: 导出CSV
表 3 模型参数、控制器参数、初始条件以及参考轨迹
Table 3 Model parameters, controller parameters, initial conditions, and reference trajectories
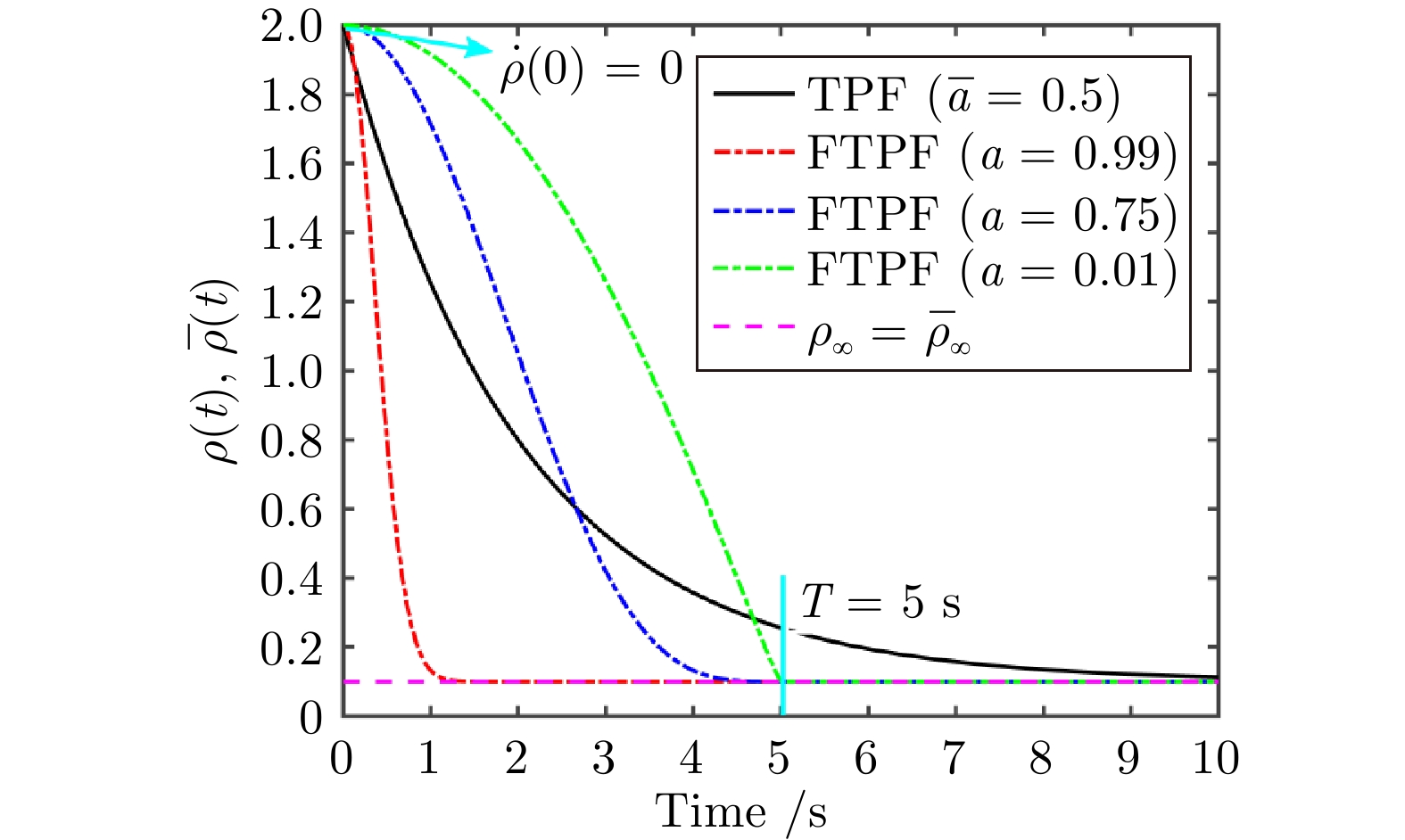
参数项 数值 模型参数 $ m_i=0.285\;({\rm kg}) $, $ m_L=0.245\;({\rm kg}), \;l_i=0.75\;({\rm m}) $, $ r_1=[0.75, \;0, \;0.1]^{\rm T}\;({\rm m}) $, $ r_2=[0, \;-0.75, \;0.1]^{\rm T}\;({\rm m}) $ $ r_3=[-0.75, \;0, \;0.1]^{\rm T}\;({\rm m}) $, $ r_4=[0, \;0.75.0.1]^{\rm T}\;({\rm m}) $, $ J_L={\rm diag}\{1.5, \;4.6, \;0.08\}10^{-2}\;({\rm kg\cdot m^2}) $ 控制器参数 $ T=5 $, $ a=[0.75, \;0.75, \;0.75, \;0.75, \;0.75, \;0.75]^{\rm T} $, $ \rho_{L0}=[0.5, \;0.5, \;0.5, \;0.25, \;0.25, \;0.25]^{\rm T} $ $ \rho_{L_\infty}=[0.1, \;0.1, \;0.1, \;0.1, \;0.1, \;0.1]^{\rm T} $, $ \Xi_{{\rm max}}=0.6 $, $ \Xi_{{\rm min}}=0.3 $, $ \sigma_{ij}=1 $, $ \beta_{id}^*=1 $ $ k_L={\rm diag}\{1, \;1, \;1, \;1, \;1, \;1\} $, $ \beta_L={\rm diag}\{1, \;1, \;1, \;1, \;1, \;1\} $, $ K_1={\rm diag}\{5, \;5, \;5, \;5, \;5, \;5\} $, $ K_2={\rm diag}\{10, \;10, \;10, \;10, \;10, \;10\} $ $ \gamma_{L}={\rm diag}\{0.1, \;0.1, \;0.1, \;0.1, \;0.1, \;0.1\} $, $ \gamma_{1i}=\gamma_{2i}={\rm diag}\{0.1, \;0.1, \;0.1\} $, $ \ell=0.01 $, $ \Upsilon_{L}=\Upsilon_{i}=1 $, $ \zeta_L=\zeta_i=2 $ $ k_i={\rm diag}\{1, \;1, \;1\} $, $ \beta_i={\rm diag}\{1, \;1, \;1\} $, $ K_{1i}={\rm diag}\{5, \;5, \;5\} $, $ K_{2i}={\rm diag}\{10, \;10, \;10\} $ 初始条件 $ P_{L}(0)=[1.25, \;0.25, \;0.25]^{\rm T}\;({\rm m}) $, $ \Theta_{L}(0)=[0, \;0, \;0]^{\rm T}\;({\rm rad}) $, $ P_{i}(0)=P_L(0)+r_i-l_i[0, \;0, \;-1]^{\rm T}\;({\rm m}) $ 参考轨迹 $ P_{Ldx}=1.5-0.15t\; ({\rm m}) $, $ P_{Ldy}=0\; ({\rm m}) $, $ P_{Ldz}=0.5\; ({\rm m}) $, $ \Theta_{Ld}=[0, \;0, \;0]^{\rm T}\;({\rm rad}) $
下载: 导出CSV
-
[1] Sebastian W, Wang S, Zheng C H, Sun X Q. AERIAL: A meta review and discussion of challenges toward unmanned aerial vehicle operations in logistics, mobility, and monitoring. IEEE Transactions on Intelligent Transportation Systems, 2024, 25(7): 6276−6289 doi: 10.1109/TITS.2023.3343713 [2] Estevez J, Garate G, Lopez-Guede J M, Larrea M. Review of aerial transportation of suspended-cable payloads with quadrotors. Drones, 2024, 8(2): 1−21 [3] Gu X, Xian B, Wang Y X. Geometry-based adaptive tracking control for an underactuated small-size unmanned helicopter. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2023, 53(12): 7489−7500 doi: 10.1109/TSMC.2023.3298034 [4] Li G F, Huang J, William S, Christopher A. Cooperative-transportation dynamics of two helicopters transporting a rocket booster undergoing planar motions. Aerospace Science and Technology, 2024, 145: 1−13 [5] 梁晓, 胡欲立. 四旋翼吊挂运输系统动态反馈线性化轨迹控制. 自动化学报, 2020, 46(9): 1993−2002 doi: 10.16383/j.aas.c180857Liang Xiao, Hu Yu-Li. Trajectory control of quadrotor with cable-suspended load via dynamic feedback linearization. Acta Automatica Sinica, 2020, 46(9): 1993−2002 doi: 10.16383/j.aas.c180857 [6] Liu W, Chen M, Shi P. Fixed-time disturbance observer-based control for quadcopter suspension transportation system. IEEE Transactions on Circuits and Systems I: Regular Papers, 2022, 69(11): 4632−4642 doi: 10.1109/TCSI.2022.3193878 [7] Cardona G A, Tellez-Castro D, Mojica-Nava E. Cooperative transportation of a cable-suspended load by multiple quadrotors. IFAC-PapersOnLine, 2019, 52(20): 145−150 doi: 10.1016/j.ifacol.2019.12.149 [8] Lee T, Sreenath K, Kumar V. Geometric control of cooperating multiple quadrotor UAVs with a suspended payload. In: Proceedings of the 52nd IEEE Conference on Decision and Control. Firenze, Italy: IEEE, 2013. 5510−5515 [9] Zhao K, Zhang J. Composite disturbance rejection control strategy for multi-quadrotor transportation system. IEEE Robotics and Automation Letters, 2023, 8(8): 4697−4704 doi: 10.1109/LRA.2023.3288374 [10] Jin X, Hu Z. Adaptive cooperative load transportation by a team of quadrotors with multiple constraint requirements. IEEE Transactions on Intelligent Transportation Systems, 2022, 24(1): 801−814 [11] 曹承钰, 李繁飙, 廖宇新, 殷泽阳, 桂卫华. 高超声速变外形飞行器建模与固定时间预设性能控制. 自动化学报, 2024, 50(3): 486−504 doi: 10.16383/j.aas.c230240Cao Cheng-Yu, Li Fan-Biao, Liao Yu-Xin, Yin Ze-Yang, Gui Wei-Hua. Modeling and fixed-time prescribed performance control for hypersonic morphing vehicle. Acta Automatica Sinica, 2024, 50(3): 486−504 doi: 10.16383/j.aas.c230240 [12] Bechlioulis C P, Rovithakis G A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance. IEEE Transactions on Automatic Control, 2008, 53(9): 2090−2099 doi: 10.1109/TAC.2008.929402 [13] Liu Y, Liu X, Jing Y. Adaptive fuzzy finite-time stability of uncertain nonlinear systems based on prescribed performance. Fuzzy Sets and Systems, 2019, 374: 23−39 doi: 10.1016/j.fss.2018.12.015 [14] Jiang T, Huang J, Li B. Composite adaptive finite-time control for quadrotors via prescribed performance. Journal of the Franklin Institute, 2020, 357(10): 5878−5901 doi: 10.1016/j.jfranklin.2020.03.021 [15] 高力, 陆丽萍, 褚端峰, 张勇, 吴超仲. 基于图与势场法的多车道编队控制. 自动化学报, 2020, 46(1): 117−126 doi: 10.16383/j.aas.c190052Gao Li, Lu Li-Ping, Chu Duan-Feng, Zhang Yong, Wu Chao-Zhong. Multi-lane convoy control based on graph and potential field. Acta Automatica Sinica, 2020, 46(1): 117−126 doi: 10.16383/j.aas.c190052 [16] Pan Z H, Zhang C, Xia Y Q, Xiong H, Shao X D. An improved artificial potential field method for path planning and formation control of the multi-UAV systems. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2021, 69(3): 1129−1133 [17] Wen G, Chen C L P, Liu Y J. Formation control with obstacle avoidance for a class of stochastic multiagent systems. IEEE Transactions on Industrial Electronics, 2017, 65(7): 5847−5855 [18] Liu Y, Huang P F, Zhang F, Zhao Y K. Distributed formation control using artificial potentials and neural network for constrained multiagent systems. IEEE Transactions on Control Systems Technology, 2018, 28(2): 697−704 [19] Liu W, Chen M, Yong K. Flexible performance constraint-based control of a quadrotor UAV-suspended payload system under input saturation. International Journal of Systems Science, 2024, 55(1): 130−146 doi: 10.1080/00207721.2023.2268772 [20] Xian B, Yang S. Robust tracking control of a quadrotor unmanned aerial vehicle-suspended payload system. IEEE/ASME Transactions on Mechatronics, 2020, 26(5): 2653−2663 [21] Wang J, Ma X, Li H C, Tian B L. Self-triggered sliding mode control for distributed formation of multiple quadrotors. Journal of the Franklin Institute, 2020, 357(17): 12223−12240 doi: 10.1016/j.jfranklin.2020.09.008 [22] Shao X, Yue X, Liu J. Distributed adaptive formation control for underactuated quadrotors with guaranteed performances. Nonlinear Dynamics, 2021, 105(4): 3167−3189 doi: 10.1007/s11071-021-06757-w [23] Miao Q Y, Zhang K, Jiang B. Fixed-time collision-free fault-tolerant formation control of multi-UAVs under actuator faults. IEEE Transactions on Cybernetics, 2014, 54 (6): 3679−3691 doi: 10.1109/TCYB.2024.3352251 [24] Chen M, Tao G, Jiang B. Dynamic surface control using neural networks for a class of uncertain nonlinear systems with input saturation. IEEE Transactions on Neural Networks and Learning Systems, 2014, 26(9): 2086−2097 -
图(13) / 表(3)
计量
- 文章访问数: 158
- HTML全文浏览量: 70
- PDF下载量: 40
- 被引次数: 0
