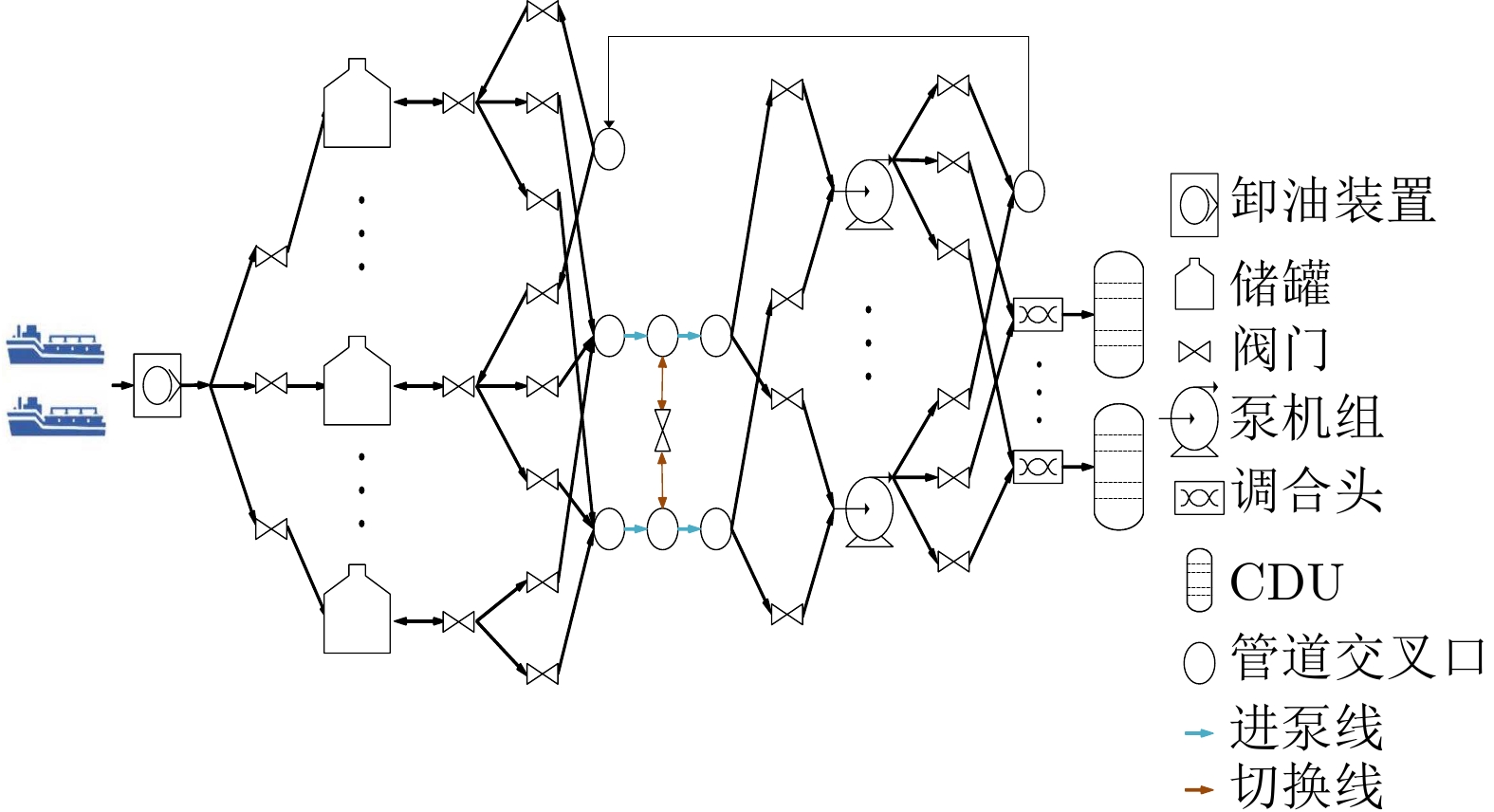
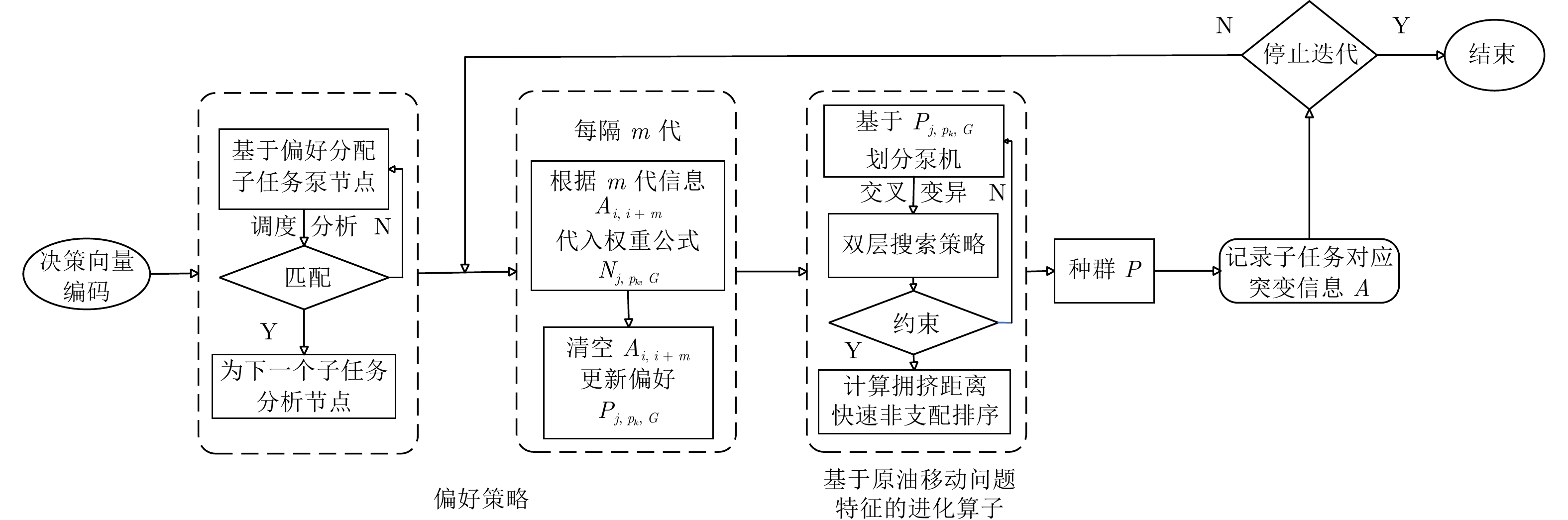
-
摘要: 原油移动路径规划是原油调度中至关重要的子任务, 直接影响到生产过程中原油供给的稳定性和付油的高效性. 由于此任务需要考虑大规模罐区内复杂的设备条件, 并受到严格的工业生产约束, 同时需要兼顾途径阀门数量与泵机组运力, 导致目前依然倚重调度人员的人工经验来制定路径规划方案, 对传统算法和进化算法的应用提出了挑战. 据此, 本研究基于有向图结构对大规模原油罐区进行细致数学建模, 并提出一种基于偏好的原油移动路径多目标优化(Preference-based multi-objective optimization for crude oil movement path，PB-MOO)算法, 突破了过去高度依赖人工方法的局限性, 为原油移动路径规划提供智能化解决方案. 实验证明该算法能够在满足实际约束的条件下, 找到复杂任务的高质量候选解, 验证了其在此领域的可行性和有效性.Abstract: The planning of crude oil movement path is a crucial subtask within crude oil scheduling, directly impacting the stability of crude oil supply and the efficiency of oil delivery in the production process. Given the need to consider complex equipment conditions within large-scale tank areas and strict industrial production constraints, while also balancing the number of valves along the route with pump unit capacity, the current reliance on manual experience of schedulers for developing path planning schemes poses a challenge to the application of traditional algorithms and evolutionary algorithms. Therefore, this study undertakes a meticulous mathematical modeling of large-scale crude oil tank areas based on directed graph structures. It proposes a preference-based multi-objective optimization algorithm for crude oil movement path (PB-MOO), overcoming the limitations associated with past heavily manual methods and providing an intelligent solution for crude oil movement path planning. Experimental results demonstrate that the algorithm can identify high-quality candidate solutions for complex tasks while meeting practical constraints. This validates its feasibility and effectiveness in this field.
-
图 2 简化的原储罐区管道运输流程图模型
Fig. 2 Simplified pipeline transportation flowchart model for crude oil tank areas
图 4 从罐T05和罐T13出发的2个子任务各自偏好泵机权重
Fig. 4 Preference pump weights of two subtasksstarting from tank T05 and T13
表 1 参数说明
Table 1 Parameter descriptions
符号 描述 $BH_b$ 第$b $个调合头 $d_{k_1,\;k_2}$ 节点$v_{k_1}$与节点$v_{k_2}$ 之间的路径长度 $IL_l$ 第$l $条进泵线 K 节点总数 L 进泵线个数 J 罐底阀个数 N 原油类型总数 NB 调合头节点个数 $ND_{k,\;r}$ 第$k $个个体中第$r $条路径包含的节点个数 NP 泵节点个数 NT 罐节点个数 $Q_{n,\;r}$ 原油移动路径$R_{n,\;r}$中泵能提供的最大流量 $H_{n,\;r}$ 原油移动路径$R_{n,\;r}$中泵的额定扬程 $\eta_{n,\;r}$ 原油移动路径$R_{n,\;r}$中泵的运行效率 $P_{n,\;r}$ 原油移动路径$R_{n,\;r}$中泵的功率 $PP_o$ 第$o $个泵 $Q_{n,\;r}^{dmand}$ 原油移动路径$R_{n,\;r}$中的需求流量 $Q_{n,\;r}^{pump}$ 原油移动路径$R_{n,\;r}$中泵的流量 R 路径$R_{n,\;r}$的节点个数 $TK_t$ 第$t $个罐 $VL_j^{TK_t}$ 罐$TK_t$的第$j $个罐底阀 $p_k$ 表示$v_k$是否为泵节点 $x^k_{n,\;r,\;i}$ 第$k $个个体中第$n $个子任务的第$r $个节点为$v_i$ $y_{k,\;IL_l,\;PP_o}$ $v_k$为进泵线$IL_l$与泵$PP_o$之间的阀门 $y_{k,\;PP_o,\;BH_b}$ $v_k$为泵$PP_o$与调合头$BH_b$之间的阀门 $y_{j,\;IN\_TK_t}^k$ $v_k$为连接罐$TK_t$的罐底阀$VL_j^{TK_t}$的进罐阀门 $y_{j,\;OUT\_TK_t,\;IL_l}^k$ $v_k$为罐底阀$VL_j^{TK_t}$与进泵线$IL_l$之间的阀门 $z_{k,\;IL_l}$ $v_k$是否处于进泵线$IL_l$中 
下载: 导出CSV
表 2 部分储罐节点信息
Table 2 Information of partial storage tank nodes
罐节点 罐底阀节点 罐容量下限 (t) 罐容量上限 (t) T01 E-T01-1 4 000 16 000 E-T01-2 T02 E-T02-1 4 000 35 000 E-T02-2 T03 E-T03 12 000 45 000 T04 E-T04 10 000 16 000 T05 E-T05-1-1 12 000 45 000 E-T05-1-2 E-T05-2-1 E-T05-2-2
下载: 导出CSV
表 4 部分管道节点信息
Table 4 Information of partial pipline nodes
管道名 连接节点 双向边 阀门 8-E-104/T06 T06, N6 否 16 001 10-E-022/T06 4toE-T06, N5 否 11 602 10-E-023/T06 4toE-T06, N1 否 11 603 7-E-102/T06 4toE-T06, N4 否 11 605 E-T06-1 T06, 4toE-T06 是 11 607
下载: 导出CSV
表 3 部分泵节点信息
Table 3 Information of partial pump nodes
泵节点 流量 (m3/h) 扬程 (m) 额定功率 (KW) P01 47 175 8 P02 100 120 12 P03 200 160 32 P04 500 150 75 P07 800 150 120
下载: 导出CSV
表 5 实验任务设置
Table 5 Experimental task settings
子任务数 起始节点 目标节点 需求流量(m3/h) 2 T03 CDU-B 500 T11 CDU-A# 1 100 4 T01 CDU-B 300 T05 CDU-C 500 T08 CDU-A 1 300 T20 E-14去CDU-A# 300 6 T01 CDU-D 300 T05 CDU-B 500 T08 CDU-A 1 300 T13 CDU-A# 1 100 T20 E-14去CDU-A# 300 T17 E-12去CDU-A# 500
下载: 导出CSV
表 6 每个任务通过不同算法得到HV值的均值与标准差
Table 6 Each task obtains the mean and standard deviation of HV values through different algorithms
NSGA-III RVEA MOEAD-LWS PB-MOO 2子任务 9.287e + 2 (6.1e + 1) 8.124e + 2 (1.5e + 0) 8.176e + 2 (9.5e + 1) 1.061e + 3 (3.5e + 1) 4子任务 2.772e + 3 (1.9e + 2) 2.021e + 3 (2.4e + 2) 2.732e + 3 (1.3e + 3) 3.632e + 3 (3.8e + 2) 6子任务 4.275e + 3 (9.5e + 2) 3.726e + 3 (1.9e + 3) — 5.499e + 3 (1.9e + 2)
下载: 导出CSV
表 7 每个任务通过不同算法得到IGD值的均值与标准差
Table 7 Each task obtains the mean and standard deviation of IGD values through different algorithms
NSGA-III RVEA MOEAD-LWS PB-MOO 2子任务 7.461e + 0 (3.8e + 0) 9.123e + 0 (5.2e + 0) 1.865e + 1 (6.1e + 0) 3.543e + 0 (3.2e + 0) 4子任务 4.448e + 1 (3.7e + 1) 7.841e + 1 (4.6e + 1) 9.247e + 1 (1.1e + 1) 6.765e + 0 (2.1e + 0) 6子任务 5.167e + 1 (2.3e + 1) 1.054e + 2 (1.5e + 1) — 4.313e + 0 (1.5e + 0)
下载: 导出CSV
表 8 每个任务通过不同算法获得的最终解
Table 8 The final solution of each task obtained by different algorithms
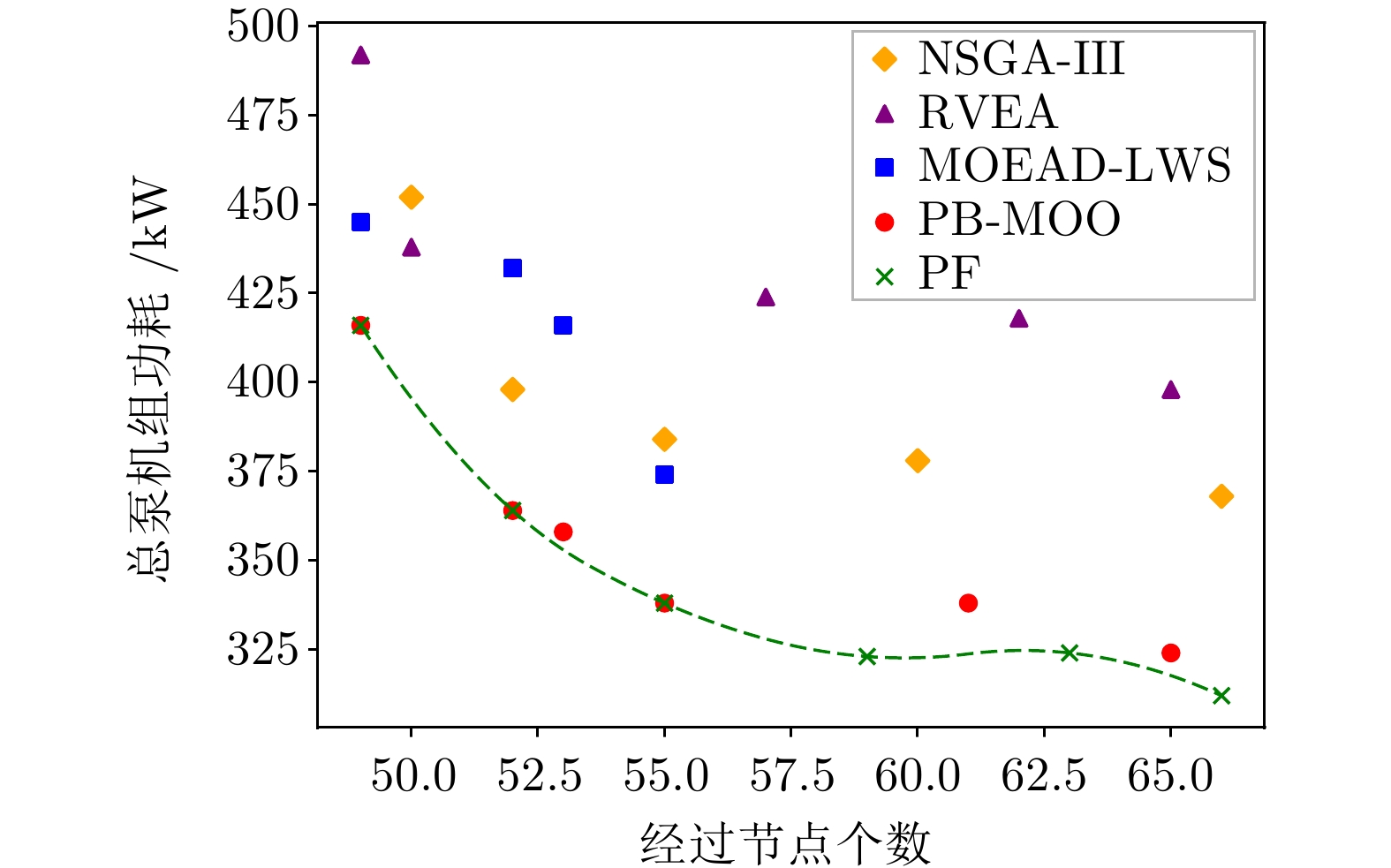
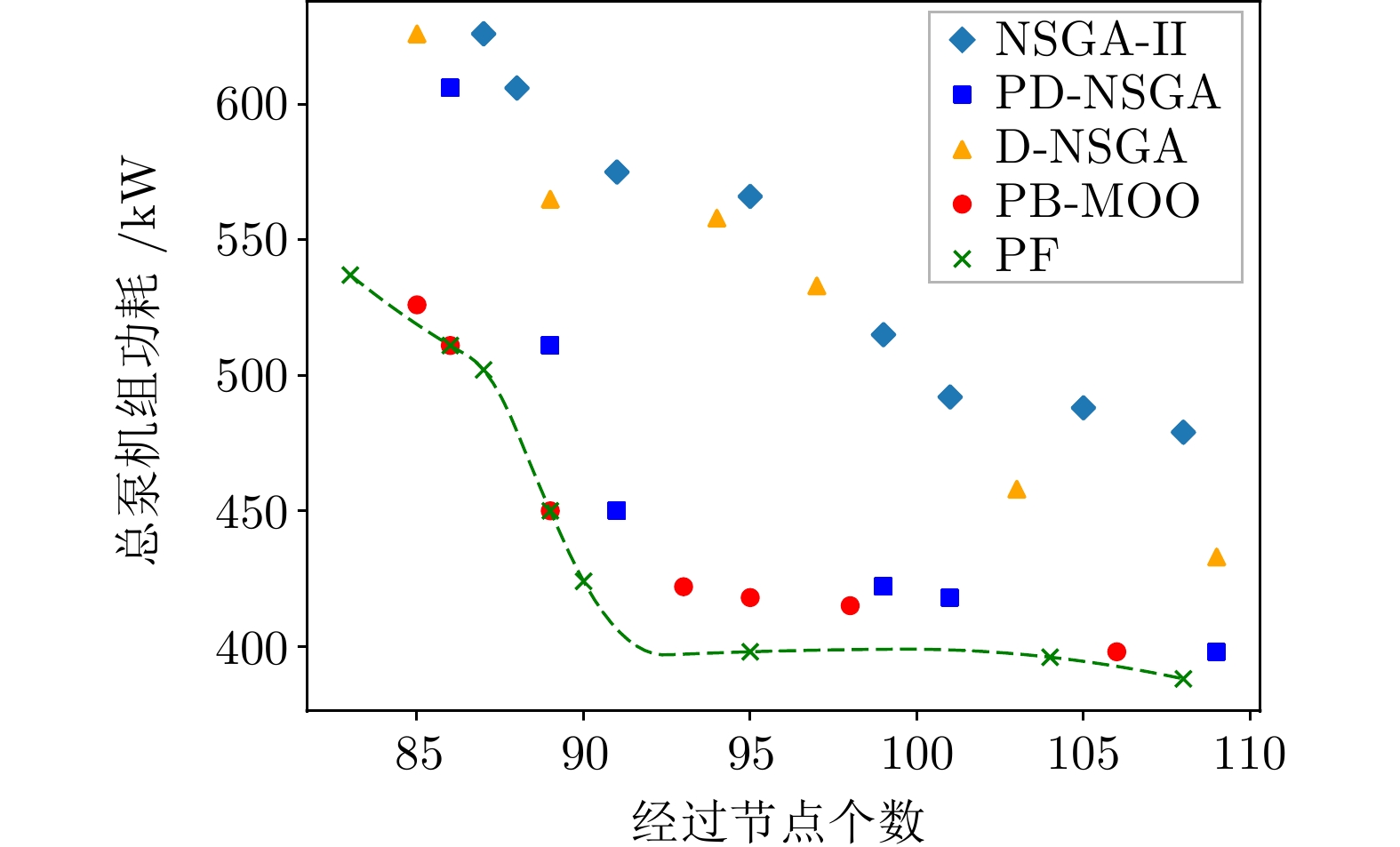
NSGA-III RVEA MOEAD-LWS PB-MOO 2子任务 (25, 190.4) (26, 195.6) (26, 215.7) (24, 190.1) 4子任务 (60, 378.2) (57, 424.5) (52, 432.7) (52, 364.3) 6子任务 (90, 500.1) (93, 522.1) (91, 522.3) (89, 450.8)
下载: 导出CSV
-
[1] 黄德先, 江永亨, 金以慧. 炼油工业过程控制的研究现状、问题与展望. 自动化学报, 2017, 43(6): 902−916Huang De-Xian, Jiang Yong-Heng, Jin Yi-Hui. Present research situation, major bottlenecks, and prospect of refinery industry process control. Acta Automatica Sinica, 2017, 43(6): 902−916 [2] Zhang W T, Du W, Yu G, He R C, Du W L. Large-scale crude oil scheduling: A framework of hybrid optimization based on plan decomposition. In: Proceedings of 2022 IEEE Congress on Evolutionary Computation. Padua, Italy: IEEE, 2022. 1−8 [3] Zhang W T, Du W, Yu G, He R C, Jin Y C. Knowledge-assisted dual-stage evolutionary optimization of large-scale crude oil scheduling. IEEE Transactions on Emerging Topics in Computational Intelligence, 2024, 8(2): 1567−1581 doi: 10.1109/TETCI.2024.3353590 [4] Hou Y, Zhang Y X, Wu N Q, Zhu Q H. Constrained multi-objective optimization of short-term crude oil scheduling with dual pipelines and charging tank maintenance requirement. Information Sciences, 2022, 588: 381−404 doi: 10.1016/j.ins.2021.12.067 [5] Hou Y, Wu N Q, Zhou M C, Li Z W. Pareto-optimization for scheduling of crude oil operations in refinery via genetic algorithm. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 47(3): 517−530 doi: 10.1109/TSMC.2015.2507161 [6] Yin J, Huang R, Sun H, Cai S Y. Multi-objective optimization for coordinated production and transportation in prefabricated construction with on-site lifting requirements. Computers & Industrial Engineering, DOI: 10.1016/j.cie.2024.110017 [7] He C L, Zhang Y, Gong D W, Song X F, Sun X Y. A multitask bee colony band selection algorithm with variable-size clustering for hyperspectral images. IEEE Transactions on Evolutionary Computation, 2022, 26(6): 1566−1580 doi: 10.1109/TEVC.2022.3159253 [8] Fang Y L, Li Z Y, Wang S W, Lu X W. Multi-objective multi-fidelity optimisation for position-constrained human-robot collaborative disassembly planning. International Journal of Production Research, 2024, 62(11): 3872−3889 doi: 10.1080/00207543.2023.2251064 [9] Wang R Q, Zhang D M, Kang Z J, Zhou R C, Hui G. Study on deep reinforcement learning-based multi-objective path planning algorithm for inter-well connected-channels. Applied Soft Computing, DOI: 10.1016/j.asoc.2023.110761 [10] Zhu Z X, Wang F X, He S, Sun Y W. Global path planning of mobile robots using a memetic algorithm. International Journal of Systems Science, 2015, 46(11): 1982−1993 doi: 10.1080/00207721.2013.843735 [11] Suresh K S, Venkatesan R, Venugopal S. Mobile robot path planning using multi-objective genetic algorithm in industrial automation. Soft Computing, 2022, 26(15): 7387−7400 doi: 10.1007/s00500-022-07300-8 [12] Zhang W T, Du W L, Du W, He R C, Jin Y C. Large-scale continuous-time crude oil scheduling: A variable-length evolutionary optimization approach. IEEE Transactions on Automation Science and Engineering, DOI: 10.1109/TASE.2024.3380744 [13] Ramteke M, Srinivasan R. Large-scale refinery crude oil scheduling by integrating graph representation and genetic algorithm. Industrial & Engineering Chemistry Research, 2012, 51(14): 5256−5272 [14] Panda D, Ramteke M. Reactive scheduling of crude oil using structure adapted genetic algorithm under multiple uncertainties. Computers & Chemical Engineering, 2018, 116: 333−351 [15] Hou Y, Wu N Q, Li Z W. A genetic algorithm approach to short term scheduling of crude oil operations in refinery. IEEJ Transactions on Electrical and Electronic Engineering, 2016, 11(5): 593−603 doi: 10.1002/tee.22277 [16] Palakonda V, Kang J M. Pre-DEMO: Preference-inspired differential evolution for multi/many-objective optimization. IEEE Transactions on Systems, Man, and Cybernetics-Systems, 2023, 53(12): 7618−7630 doi: 10.1109/TSMC.2023.3298690 [17] Deb K, Sundar J. Reference point based multi-objective optimization using evolutionary algorithms. In: Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation. Seattle, USA: ACM SIGEVO, 2006. 635−642 [18] Zheng J H, Lai N, Guo G Q. $ \epsilon $-pareto dominance strategy based on angle preference in MOEA. Pattern Recognition and Artificial Intelligence, 2014, 27(6): 569−575 [19] Chaudhuri S, Deb K. An interactive evolutionary multi-objective optimization and decision making procedure. Applied Soft Computing, 2010, 10(2): 496−511 doi: 10.1016/j.asoc.2009.08.019 [20] Wang C, Jiao L C, Zhao J X, Li L L, Liu X, Liu F, et al. Bi-level multiobjective evolutionary learning: A case study on multitask graph neural topology search. IEEE Transactions on Evolutionary Computation, 2024, 28(1): 208−222 doi: 10.1109/TEVC.2023.3255263 [21] Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective geneticalgorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182−197 doi: 10.1109/4235.996017 [22] Yao Y, Peng Z, Xiao B. Parallel hyper-heuristic algorithm for multi-objective route planning in a smart city. IEEE Transactions on Vehicular Technology, 2018, 67(11): 10307−10318 doi: 10.1109/TVT.2018.2868942 [23] While L, Hingston P, Barone L, Huband S. A faster algorithm for calculating hypervolume. IEEE Transactions on Evolutionary Computation, 2006, 10(1): 29−38 doi: 10.1109/TEVC.2005.851275 [24] Zitzler E, Thiele L, Laumanns M, Fonseca C M, Fonseca V G. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Transactions on Evolutionary Computation, 2003, 7(2): 117−132 doi: 10.1109/TEVC.2003.810758 [25] Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577−601 doi: 10.1109/TEVC.2013.2281535 [26] Wang R, Zhou Z B, Ishibuchi H, Liao T J, Zhang T. Localized weighted sum method for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2018, 22(1): 3−18 doi: 10.1109/TEVC.2016.2611642 [27] Cheng R, Jin Y C, Olhofer M, Sendhoff B. A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 773−791 doi: 10.1109/TEVC.2016.2519378 -
计量
- 文章访问数: 134
- HTML全文浏览量: 49
- 被引次数: 0
