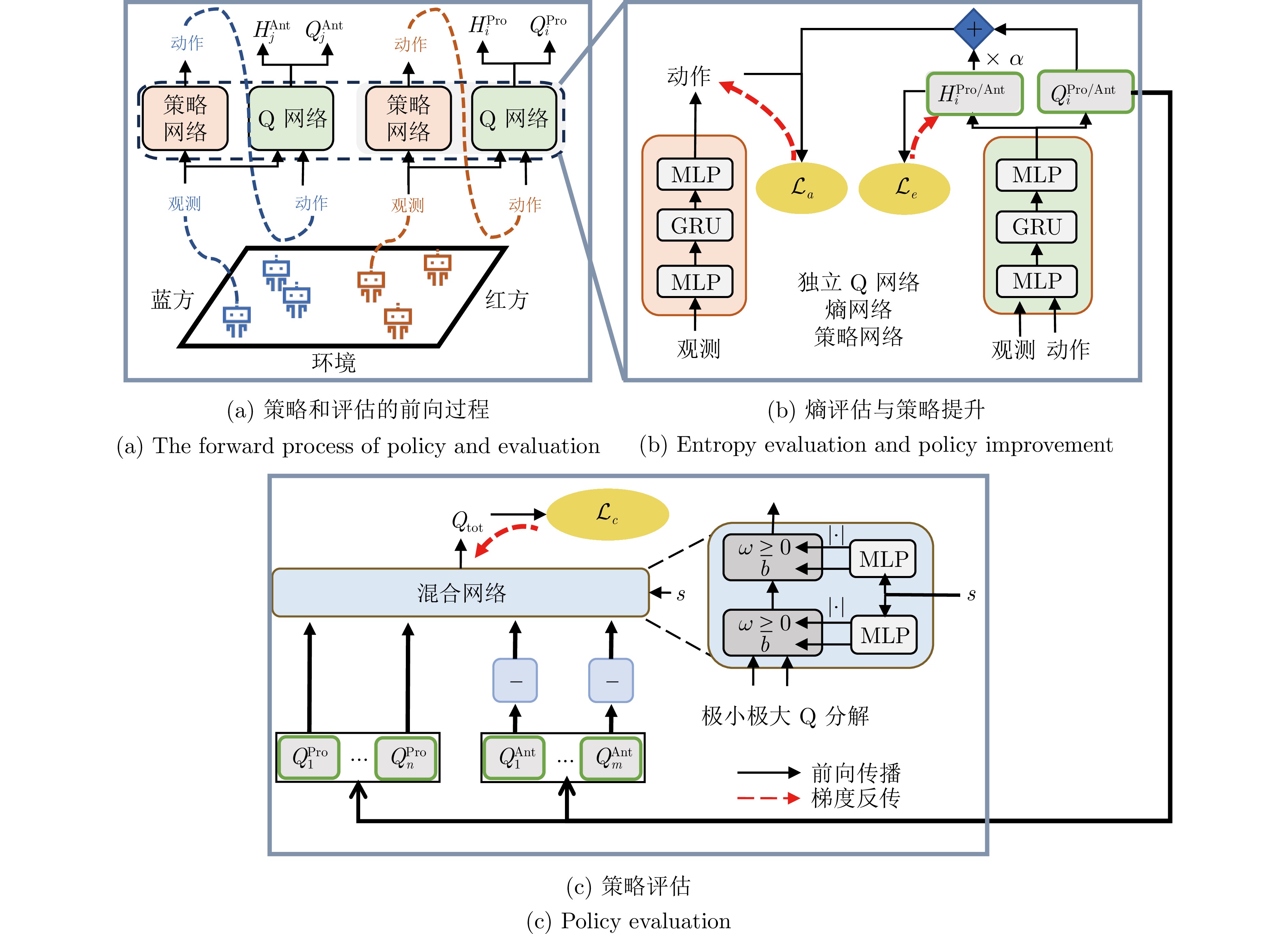
Entropy-guided Minimax Factorization for Reinforcement Learning in Two-team Zero-sum Games
-
摘要: 在两团队零和马尔科夫博弈中, 一组玩家通过合作与另一组玩家进行对抗. 由于对手行为的不确定性和复杂的团队内部合作关系, 在高采样成本的任务中快速识别优势的分布式策略仍然具有挑战性. 鉴于此, 提出一种熵引导的极小极大值分解(Entropy-guided minimax factorization, EGMF)强化学习方法, 在线学习队内合作和队间对抗的策略. 首先, 提出基于极小极大值分解的多智能体执行器−评估器框架, 在高采样成本的、不限动作空间的任务中, 提升优化效率和博弈性能; 其次, 引入最大熵使智能体可以更充分地探索状态空间, 避免在线学习过程收敛到局部最优; 此外, 策略在时间域累加的熵值用于评估策略的熵, 并将其与分解的个体独立Q函数结合用于策略改进; 最后, 在多种博弈仿真场景和一个实体机器人任务平台上进行方法验证, 并与其他基线方法进行比较. 结果显示EGMF可以在更少样本下学到更具有对抗性能的两团队博弈策略.
-
关键词:
- 多智能体深度强化学习 /
- 两团队零和马尔科夫博弈 /
- 最大熵 /
- 值分解
Abstract: In two-team zero-sum Markov games, a group of players collaborates and confronts a team of adversaries. Due to the uncertainty of opponent behavior and the complex cooperation within teams, quickly identifying advantageous distributed policies in high-sampling-cost tasks remains challenging. This paper introduces the entropy-guided minimax factorization (EGMF) reinforcement learning method, which enables online learning of cooperative policies within teams and competitive policies between teams. Firstly, a multi-agent actor-critic framework based on minimax factorization is proposed to enhance optimization efficiency and game performance in tasks with high sampling costs and unrestricted action spaces. Secondly, maximum entropy is introduced to allow agents to explore the state space more comprehensively, preventing the online learning process from converging to local optima. In addition, the entropy of the strategy is also summed along the time domain for evaluation, which is combined with the decomposed individual independent Q function for policy improvement. Finally, experiments are conducted in some game simulated scenarios and a real-robot platform, comparing EGMF with other baseline methods. The results demonstrate that EGMF can learn more adversarial two-team game strategies with relatively fewer samples.1)1 1 红方(Proponents, Pros), 蓝方(Antagonists, Ants) -
图 1 EGMF的方法架构(EGMF通过联合极小极大Q函数分解框架进行策略评估, 分解的个体独立Q函数与熵评估函数结合用于策略改进)
Fig. 1 The architecture of EGMF (EGMF evaluates policies through the joint minimax Q function decomposition framework, and combines the factorized individual Q function with the entropy evaluation function for policy improvement)
图 2 实验验证平台(包括Wimblepong 2v2、MPE 3v3、RoboMaster 2v2和现实世界的RoboMaster 2v2)
Fig. 2 Experimental verification platform (including Wimblepong 2v2, MPE 3v3, RoboMaster 2v2 and real-world RoboMaster 2v2)
图 3 训练过程中与基于脚本的智能体进行对抗的结果
Fig. 3 The results of playing against the scripted-based agents during the training process
图 4 训练过程中多种算法交叉对抗的循环赛回报
Fig. 4 The cross-play results of RR returns throughout the training process
图 5 训练期间EGMF和基线方法的近似NashConv结果
Fig. 5 The results of the approximate NashConv of EGMF and baselines during the training process
图 6 EGMF方法在六种场景中的收益矩阵
Fig. 6 Illustration of the payoff values of EGMF modules in the six scenarios
图 7 最大熵消融实验过程中与基于脚本的智能体对抗的结果
Fig. 7 The results with respect to the ablation of maximum entropy by playing against the scripted-based agents
图 9 基于EGMF模型部署在实体机器人连续任务中的演示
Fig. 9 Demonstration of the continuous real-world robot task based on the EGMF model
表 1 实验中所有方法的重要超参数
Table 1 Important hyperparameters of all methods in experiments
算法 超参数 名称 Wimblepong 2v2 MPE 3v3 RoboMaster 2v2 共用超参数 n_episodes 回合数 13000 13000 80000 n_seeds 种子数 8 8 8 $\gamma$ 折扣因子 0.99 0.98 0.99 hidden_layers 隐藏层 [64, 64] [64, 64] [128, 128] mix_hidden_dim 混合网络隐藏层 32 32 32 learning_rate 学习率 0.0005 0.0005 0.0005 EGMF (本文) buffer_size 经验池大小 400 000 40 000 400 000 RADAR[15]/Team-PSRO[16]/NXDO[46] n_genes 迭代数 13 13 10 ep_per_gene 单次迭代回合 1000 1000 80000 batch_size 批大小 1000 1000 2000 buffer_size 经验池大小 200000 20000 200000 
下载: 导出CSV
表 2 训练结束后各个算法与基于脚本的智能体对抗的结果和循环赛交叉对抗的结果
Table 2 Performance of all methods at the end of training by playing against the scripted-based agents, and the cross-play results of round-robin returns
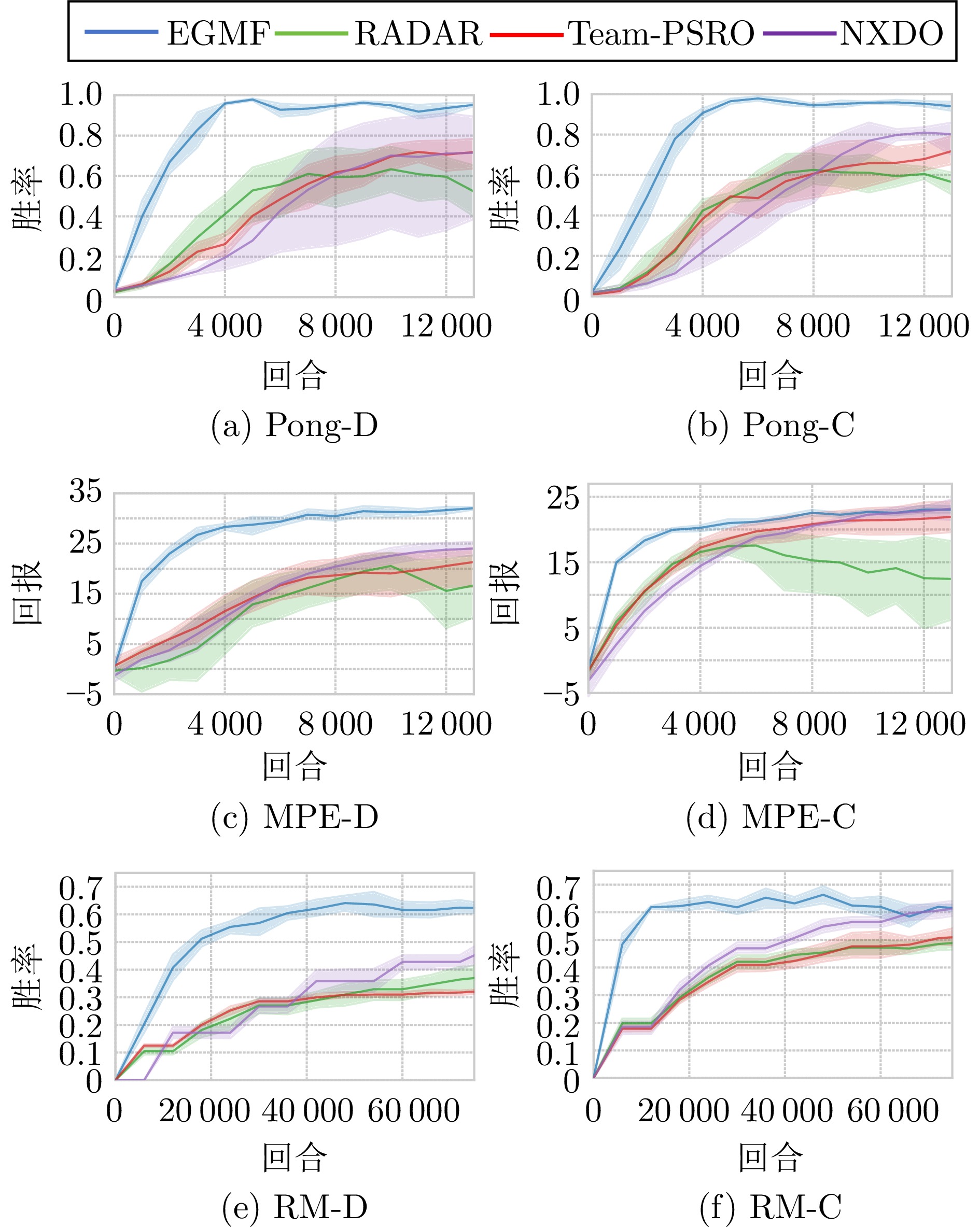
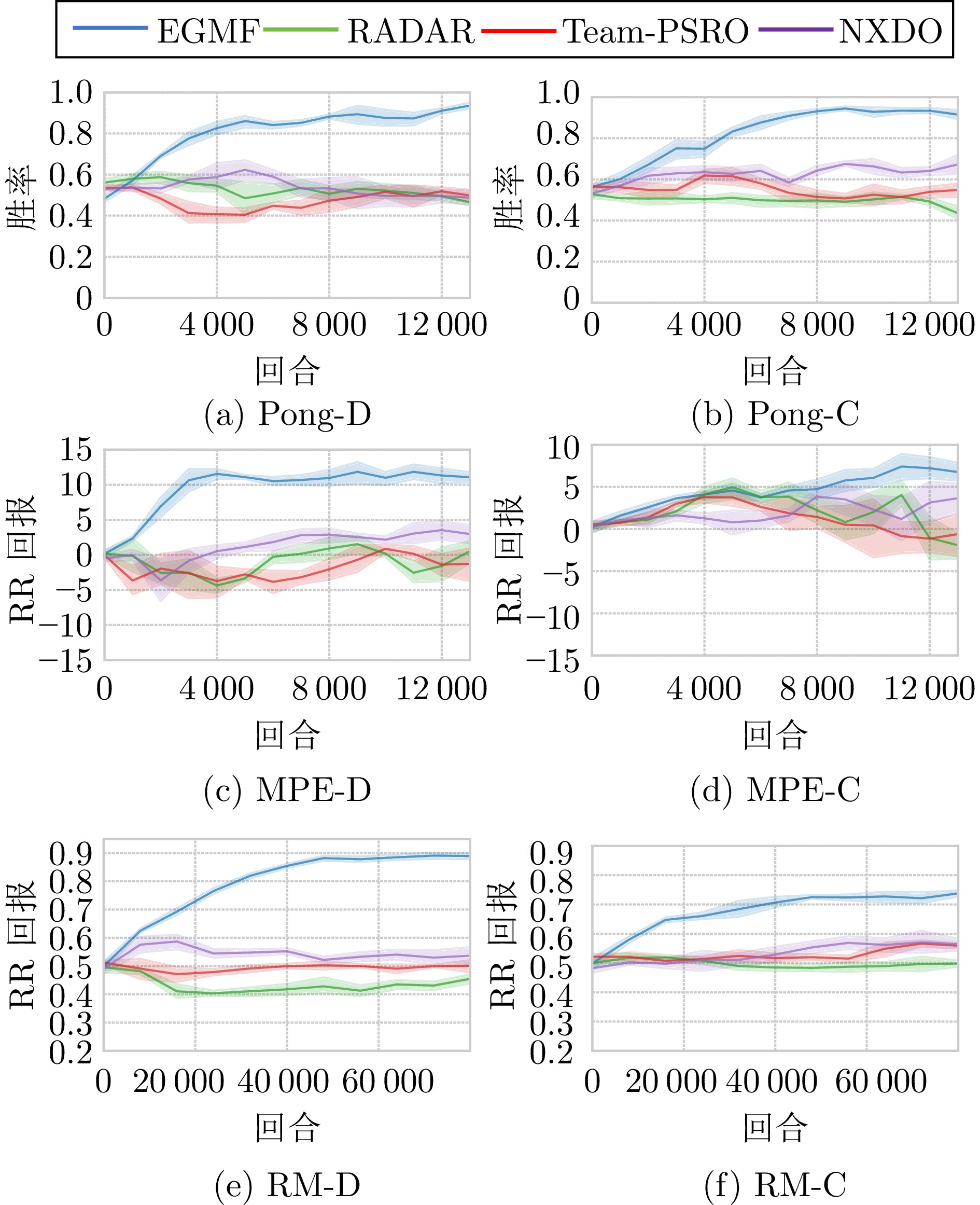
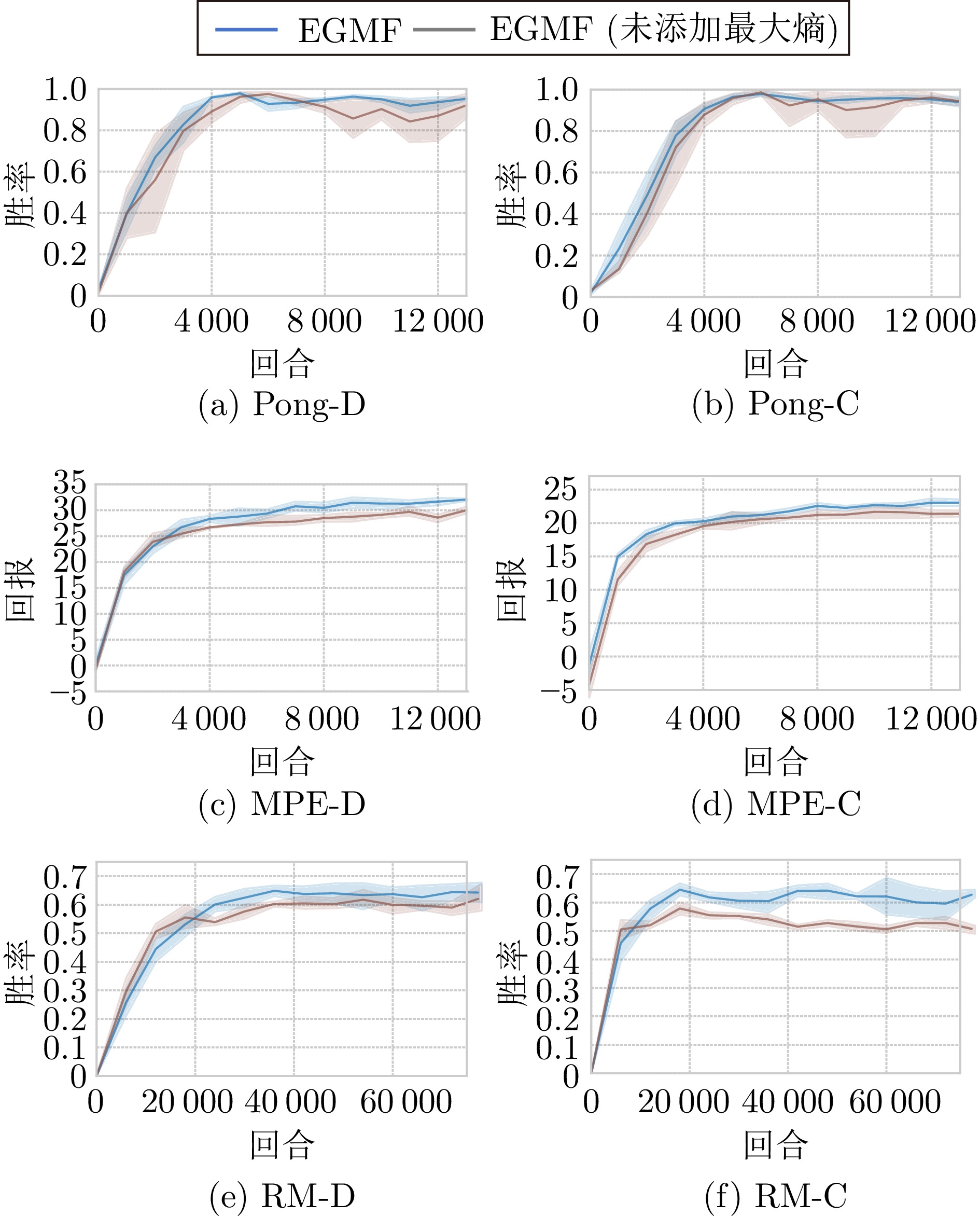
指标 算法 场景 Pong-D MPE-D RM-D Pong-C MPE-C RM-C 与固定脚本对抗 EGMF (本文) 0.95±0.01 32.3±1.0 0.63±0.03 0.95±0.02 23.0±0.5 0.62±0.03 RADAR[15] 0.52±0.11 16.3±5.2 0.35±0.02 0.58±0.03 12.5±5.1 0.52±0.02 Team-PSRO[16] 0.71±0.04 21.2±3.4 0.33±0.01 0.71±0.06 22.1±2.9 0.54±0.03 NXDO[46] 0.71±0.10 24.1±1.6 0.45±0.02 0.80±0.05 23.0±0.4 0.61±0.01 循环赛结果 EGMF (本文) 0.92±0.01 12.1±0.3 0.90±0.02 0.91±0.02 7.8±2.2 0.72±0.01 RADAR[15] 0.45±0.02 −2.4±2.5 0.45±0.04 0.43±0.02 −1.8±1.9 0.50±0.01 Team-PSRO[16] 0.53±0.02 1.9±1.9 0.49±0.01 0.56±0.04 −3.7±2.8 0.55±0.01 NXDO[46] 0.51±0.02 2.5±1.2 0.51±0.02 0.63±0.02 2.9±1.9 0.58±0.02 注: 粗体表示各算法在不同场景下的最优结果.
下载: 导出CSV
表 3 EGMF和FM3Q与基于脚本的智能体对抗的结果
Table 3 Performance of EGMF and FM3Q by playing against the scripted-based agents
算法 Pong-D MPE-D RM-D 回合(0.8) 性能 回合(25) 性能 回合(0.6) 性能 EGMF (本文) 3.0 k 0.95±0.01 2.8 k 32.3±1.0 35 k 0.63±0.03 FM3Q[17] 3.1 k 0.96±0.03 3.6 k 29.9±1.2 19 k 0.68±0.03 注: 粗体表示各方法在不同场景下的最优结果.
下载: 导出CSV
-
[1] Silver D, Huang A, Maddison C J, Guez A, Sifre L, van den Driessche G, et al. Mastering the game of Go with deep neural networks and tree search. Nature, 2016, 529(7587): 484−489 doi: 10.1038/nature16961 [2] 唐振韬, 邵坤, 赵冬斌, 朱圆恒. 深度强化学习进展: 从AlphaGo到AlphaGo Zero. 控制理论与应用, 2017, 34(12): 1529−1546 doi: 10.7641/CTA.2017.70808Tang Zhen-Tao, Shao Kun, Zhao Dong-Bin, Zhu Yuan-Heng. Recent progress of deep reinforcement learning: From AlphaGo to AlphaGo Zero. Control Theory and Applications, 2017, 34(12): 1529−1546 doi: 10.7641/CTA.2017.70808 [3] Sandholm T. Solving imperfect-information games. Science, 2015, 347(6218): 122−123 doi: 10.1126/science.aaa4614 [4] Tang Z T, Zhu Y H, Zhao D B, Lucas S M. Enhanced rolling horizon evolution algorithm with opponent model learning: Results for the fighting game AI competition. IEEE Transactions on Games, 2023, 15(1): 5−15 doi: 10.1109/TG.2020.3022698 [5] Guan Y, Afshari M, Tsiotras P. Zero-sum games between mean-field teams: Reachability-based analysis under mean-field sharing. In: Proceedings of the 38th AAAI Conference on Artificial Intelligence. Vancouver, Canada: AAAI, 2024. 9731−9739 [6] Mathieu M, Ozair S, Srinivasan S, Gulcehre C, Zhang S T, Jiang R, et al. Starcraft II unplugged: Large scale offline reinforcement learning. In: Proceedings of the 35th Conference on Neural Information Processing Systems. Sydney, Australia: NeurIPS, 2021. [7] Ye D H, Liu Z, Sun M F, Shi B, Zhao P L, Wu H, et al. Mastering complex control in MOBA games with deep reinforcement learning. In: Proceedings of the 34th AAAI Conference on Artificial Intelligence. New York, USA: AAAI, 2020. 6672−6679 [8] Littman M L. Markov games as a framework for multi-agent reinforcement learning. In: Proceedings of the 7th International Conference on International Conference on Machine Learning. San Francisco, USA: ACM, 1994. 157−163 [9] Hu J L, Wellman M P. Nash Q-learning for general-sum stochastic games. The Journal of Machine Learning Research, 2003, 4: 1039−1069 [10] Zhu Y H, Zhao D B. Online minimax Q network learning for two-player zero-sum Markov games. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(3): 1228−1241 doi: 10.1109/TNNLS.2020.3041469 [11] Lanctot M, Zambaldi V, Gruslys A, Lazaridou A, Tuyls K, Pérolat J, et al. A unified game-theoretic approach to multiagent reinforcement learning. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: ACM, 2017. 4193−4206 [12] Chai J J, Chen W Z, Zhu Y H, Yao Z X, Zhao D B. A hierarchical deep reinforcement learning framework for 6-DOF UCAV air-to-air combat. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2023, 53(9): 5417−5429 doi: 10.1109/TSMC.2023.3270444 [13] Li W F, Zhu Y H, Zhao D B. Missile guidance with assisted deep reinforcement learning for head-on interception of maneuvering target. Complex and Intelligent Systems, 2022, 8(2): 1205−1216 [14] Haarnoja T, Moran B, Lever G, Huang S H, Tirumala D, Humplik J, et al. Learning agile soccer skills for a bipedal robot with deep reinforcement learning. Science Robotics, 2024, 9(89): Article No. eadi8022 doi: 10.1126/scirobotics.adi8022 [15] Phan T, Belzner L, Gabor T, Sedlmeier A, Ritz F, Linnhoff-Popien C. Resilient multi-agent reinforcement learning with adversarial value decomposition. In: Proceedings of the 35th AAAI Conference on Artificial Intelligence. AAAI, 2021. 11308−11316 [16] McAleer S, Farina G, Zhou G, Wang M Z, Yang Y D, Sandholm T. Team-PSRO for learning approximate TMECor in large team games via cooperative reinforcement learning. In: Proceedings of the 37th Conference on Neural Information Processing Systems. NeurIPS, 2023. [17] Hu G Z, Zhu Y H, Li H R, Zhao D B. FM3Q: Factorized multi-agent MiniMax Q-learning for two-team zero-sum Markov game. IEEE Transactions on Emerging Topics in Computational Intelligence, 2024, 8(6): 4033−4045 doi: 10.1109/TETCI.2024.3383454 [18] Bai Y, Jin C. Provable self-play algorithms for competitive reinforcement learning. In: Proceedings of the 37th International Conference on Machine Learning. PMLR, 2020. Article No. 52 [19] Perez-Nieves N, Yang Y D, Slumbers O, Mguni D H, Wen Y, Wang J. Modelling behavioural diversity for learning in open-ended games. In: Proceedings of the 38th International Conference on Machine Learning. PMLR, 2021. 8514−8524 [20] Balduzzi D, Garnelo M, Bachrach Y, Czarnecki W, Pérolat J, Jaderberg M, et al. Open-ended learning in symmetric zero-sum games. In: Proceedings of the 36th International Conference on Machine Learning. Long Beach, USA: ICML, 2019. 434−443 [21] McAleer S, Lanier J B, Fox R, Baldi P. Pipeline PSRO: A scalable approach for finding approximate Nash equilibria in large games. In: Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver, Canada: ACM, 2020. Article No. 1699 [22] Muller P, Omidshafiei S, Rowland M, Tuyls K, Pérolat J, Liu S Q, et al. A generalized training approach for multiagent learning. In: Proceedings of the 8th International Conference on Learning Representations. Addis Ababa, Ethiopia: ICLR, 2020. [23] Marris L, Muller P, Lanctot M, Tuyls K, Graepel T. Multi-agent training beyond zero-sum with correlated equilibrium meta-solvers. In: Proceedings of the 38th International Conference on Machine Learning. PMLR, 2021. 7480−7491 [24] Feng X D, Slumbers O, Wan Z Y, Liu B, McAleer S, Wen Y, et al. Neural auto-curricula in two-player zero-sum games. In: Proceedings of the 35th International Conference on Neural Information Processing Systems. NeurIPS, 2021. Article No. 268 [25] Anagnostides I, Kalogiannis F, Panageas I, Vlatakis-Gkaragkounis E V, Mcaleer S. Algorithms and complexity for computing Nash equilibria in adversarial team games. In: Proceedings of the 24th ACM Conference on Economics and Computation. London, UK: ACM, 2023. Article No. 89 [26] Zhu Y H, Li W F, Zhao M C, Hao J Y, Zhao D B. Empirical policy optimization for $n$ -player Markov games. IEEE Transactions on Cybernetics, 2023, 53(10): 6443−6455 doi: 10.1109/TCYB.2022.3179775 [27] Luo G Y, Zhang H, He H B, Li J L, Wang F Y. Multiagent adversarial collaborative learning via mean-field theory. IEEE Transactions on Cybernetics, 2021, 51(10): 4994−5007 doi: 10.1109/TCYB.2020.3025491 [28] Lowe R, Wu Y, Tamar A, Harb J, Abbeel P, Mordatch I. Multi-agent actor-critic for mixed cooperative-competitive environments. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: ACM, 2017. 6382−6393 [29] Sunehag P, Lever G, Gruslys A, Czarnecki W M, Zambaldi V, Jaderberg M, et al. Value-decomposition networks for cooperative multi-agent learning based on team reward. In: Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems. Stockholm, Sweden: ACM, 2018. 2085−2087 [30] Rashid T, Samvelyan M, de Witt C S, Farquhar G, Foerster J, Whiteson S. Monotonic value function factorisation for deep multi-agent reinforcement learning. The Journal of Machine Learning Research, 2020, 21(1): Article No. 178 [31] Chai J J, Li W F, Zhu Y H, Zhao D B, Ma Z, Sun K W, et al. UNMAS: Multiagent reinforcement learning for unshaped cooperative scenarios. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(4): 2093−2104 doi: 10.1109/TNNLS.2021.3105869 [32] Peng B, Rashid T, de Witt C A S, Kamienny P A, Torr P H S, Böhmer W, et al. FACMAC: Factored multi-agent centralised policy gradients. In: Proceedings of the 35th International Conference on Neural Information Processing Systems. NeurIPS, 2021. Article No. 934 [33] Zhang T H, Li Y H, Wang C, Xie G M, Lu Z Q. FOP: Factorizing optimal joint policy of maximum-entropy multi-agent reinforcement learning. In: Proceedings of the 38th International Conference on Machine Learning. PMLR, 2021. 12491−12500 [34] Haarnoja T, Tang H R, Abbeel P, Levine S. Reinforcement learning with deep energy-based policies. In: Proceedings of the 34th International Conference on Machine Learning. Sydney, Australia: PMLR, 2017. 1352−1361 [35] Haarnoja T, Zhou A, Abbeel P, Levine S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In: Proceedings of the 35th International Conference on Machine Learning. Stockholm, Sweden: PMLR, 2018. 1856−1865 [36] Duan J L, Guan Y, Li S E, Ren Y G, Sun Q, Cheng B. Distributional soft actor-critic: Off-policy reinforcement learning for addressing value estimation errors. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(11): 6584−6598 doi: 10.1109/TNNLS.2021.3082568 [37] Kalogiannis F, Panageas I, Vlatakis-Gkaragkounis E V. Towards convergence to Nash equilibria in two-team zero-sum games. In: Proceedings of the 11th International Conference on Learning Representations. Kigali, Rwanda: ICLR, 2023. [38] Wang J H, Ren Z Z, Liu T, Yu Y, Zhang C J. QPLEX: Duplex dueling multi-agent Q-learning. In: Proceedings of the 9th International Conference on Learning Representations. ICLR, 2021. [39] Condon A. On algorithms for simple stochastic games. Advances in Computational Complexity Theory, 1990, 13: 51−72 [40] Zhou M, Liu Z Y, Sui P W, Li Y X, Chung Y Y. Learning implicit credit assignment for cooperative multi-agent reinforcement learning. In: Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver, Canada: NeurIPS, 2020. Article No. 994 [41] Ziebart B D, Maas A, Bagnell J A, Dey A K. Maximum entropy inverse reinforcement learning. In: Proceedings of the 23rd AAAI Conference on Artificial Intelligence. Chicago, USA: AAAI, 2008. 1433−1438 [42] Bellman R. On the theory of dynamic programming. Proceedings of the National Academy of Sciences of the United States of America, 1952, 38(8): 716−719 [43] Mnih V, Kavukcuoglu K, Silver D, Rusu A A, Veness J, Bellemare M G, et al. Human-level control through deep reinforcement learning. Nature, 2015, 518(7540): 529−533 doi: 10.1038/nature14236 [44] Terry J K, Black B, Grammel N, Mario Jayakumar M, Ananth Hari A, Sullivan R, et al. PettingZoo: A standard API for multi-agent reinforcement learning. In: Proceedings of the 35th International Conference on Neural Information Processing Systems. NeurIPS, 2021. Article No. 1152 [45] Hu G Z, Li H R, Liu S S, Zhu Y H, Zhao D B. NeuronsMAE: A novel multi-agent reinforcement learning environment for cooperative and competitive multi-robot tasks. In: Proceedings of the International Joint Conference on Neural Networks (IJCNN). Gold Coast, Australia: IEEE, 2023. 1−8 [46] McAleer S, Lanier J, Wang K A, Baldi P, Fox R. XDO: A double oracle algorithm for extensive-form games. In: Proceedings of the 35th International Conference on Neural Information Processing Systems. NeurIPS, 2021. Article No. 1771 [47] Samvelyan M, Khan A, Dennis M, Jiang M Q, Parker-Holder J, Foerster J N, et al. MAESTRO: Open-ended environment design for multi-agent reinforcement learning. In: Proceedings of the 11th International Conference on Learning Representations. Kigali, Rwanda: ICLR, 2023. [48] Timbers F, Bard N, Lockhart E, Lanctot M, Schmid M, Burch N, et al. Approximate exploitability: Learning a best response. In: Proceedings of the 31st International Joint Conference on Artificial Intelligence. Vienna, Austria: IJCAI, 2022. 3487−3493 [49] Cohen A, Yu L, Wright R. Diverse exploration for fast and safe policy improvement. In: Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans, USA: AAAI, 2018. Article No. 351 [50] Tsai Y Y, Xu H, Ding Z H, Zhang C, Johns E, Huang B D. DROID: Minimizing the reality gap using single-shot human demonstration. IEEE Robotics and Automation Letters, 2021, 6(2): 3168−3175 doi: 10.1109/LRA.2021.3062311 -
图(9) / 表(3)
计量
- 文章访问数: 109
- HTML全文浏览量: 80
- PDF下载量: 41
- 被引次数: 0
