Security Customization Consensus of Multi-agent Systems Based on Saturation Impulse Under DOS Attacks
-
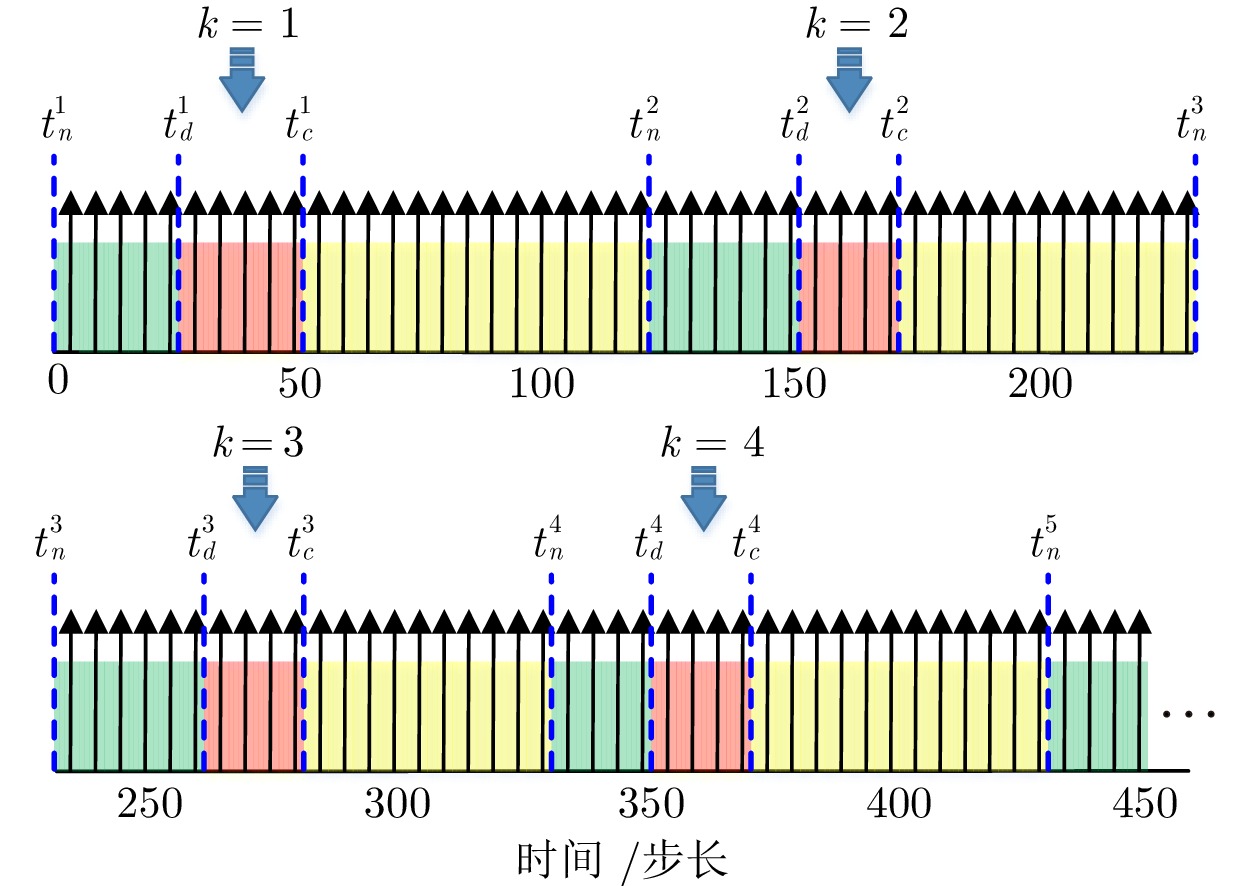
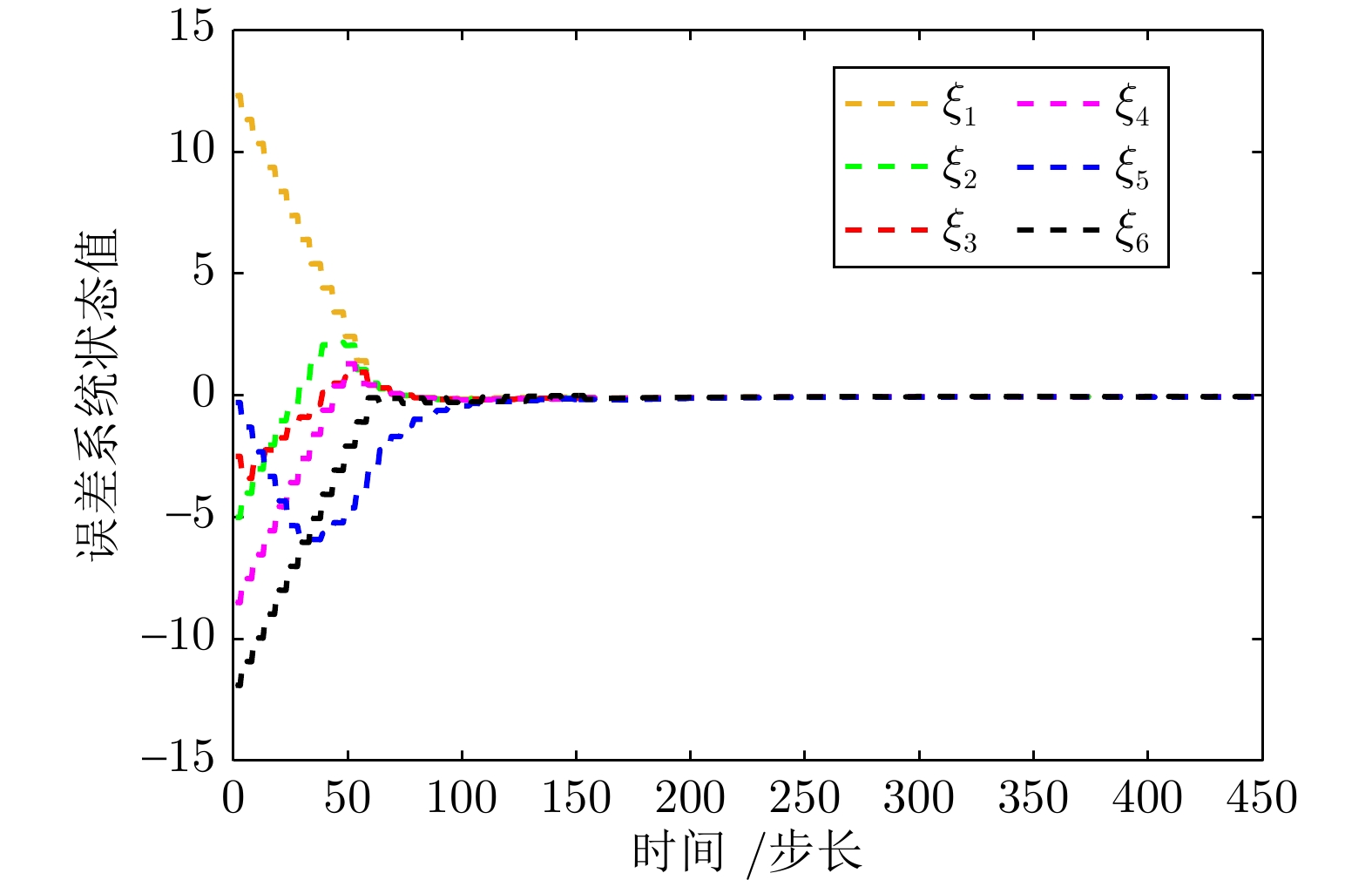
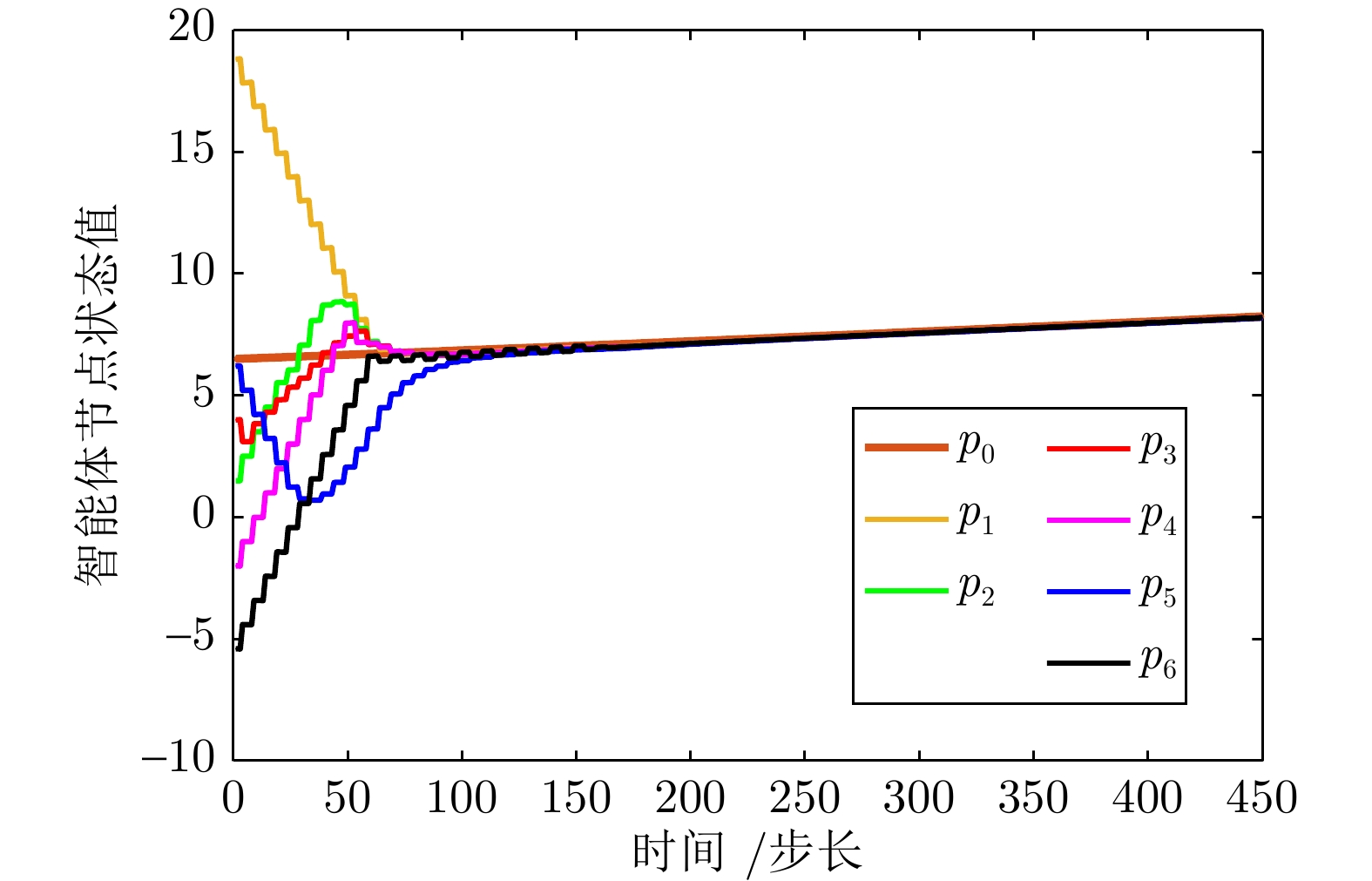
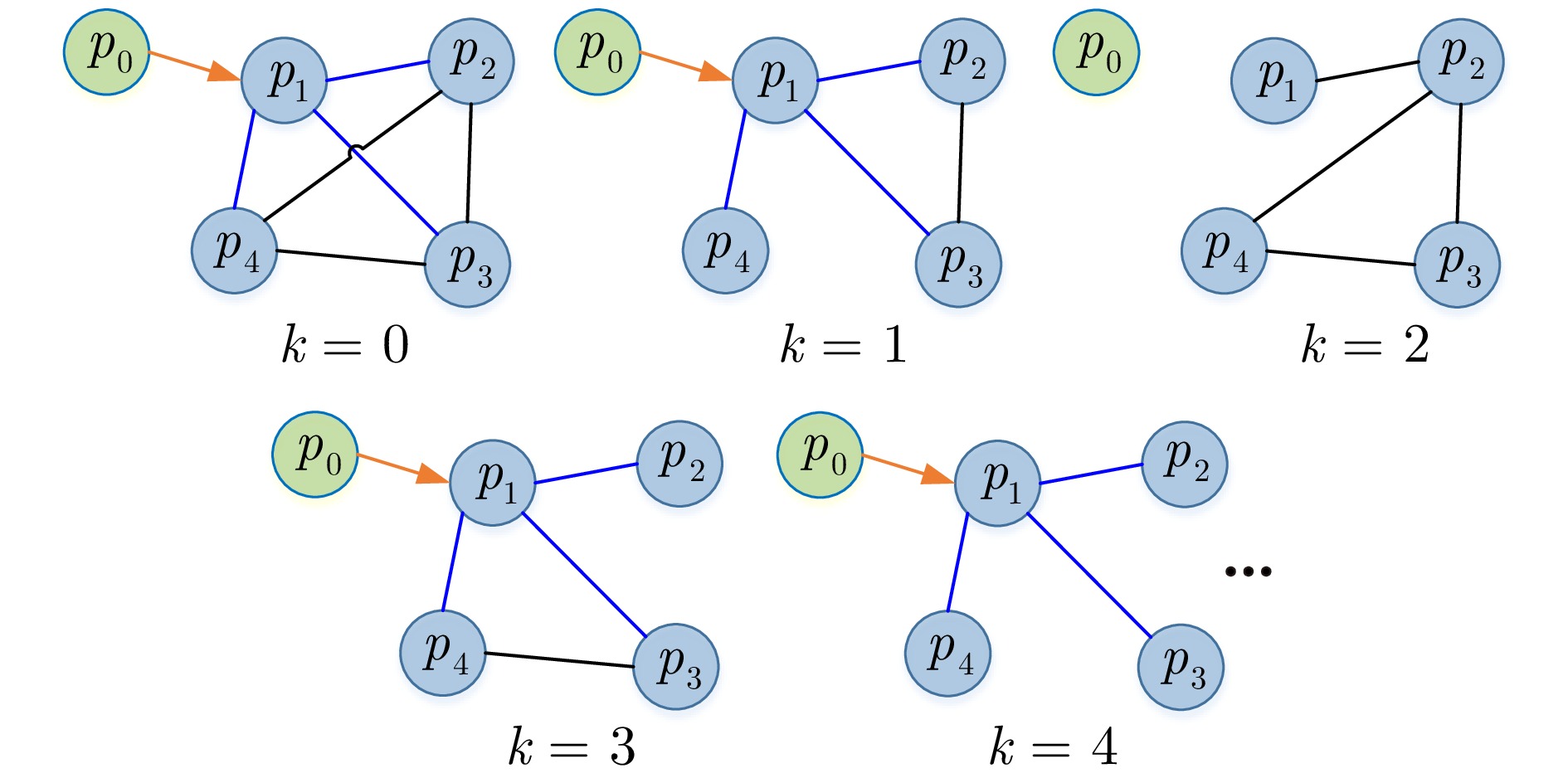
摘要: 提出并解决一种饱和脉冲多智能体系统在拒绝服务(Denial of service, DOS)攻击环境中的安全定制化一致性控制问题. 首先引入微分机制和加权策略, 构建一种带可调参数一致性模式项的系统模型, 以满足复杂场景对一致性的定制化需求. 其次结合饱和效应和脉冲机制, 为系统设计一种满足执行器功率受限约束的饱和脉冲控制协议. 再次采用切换拓扑分析DOS攻击下系统的网络拓扑结构, 并采用李雅普洛夫稳定性和矩阵测度理论, 得到系统实现安全定制化一致性的充分条件. 最后通过仿真实验和对比分析, 验证了所提理论的有效性和优越性.Abstract: This paper proposes and solves the problem of security customization consensus control for multi-agent systems based on saturation impulse in denial of service (DOS) attack environment. Firstly, the differential mechanism and weighting strategy are introduced to construct a system model that contains a consensus schema item with adjustable parameters, so as to meet the customization requirements for consensus in some complex scenarios. Secondly, combined with saturation effect and impulse mechanism, a saturation impulse control protocol is designed for the system, which satisfies the constraint of actuators power. Thirdly, some switching topologies are used to analyze the network topologies of the system under DOS attacks, and the sufficient conditions for the system to achieve security customization consensus are obtained by using Lyapunov stability and matrix measure theories. Finally, through some simulation experiments and comparative analysis, the validity and superiority of the proposed theories are verified.
-
表 1 定制化一致性模式
Table 1 Customization consensus schemes
序号 参数取值 一致性模式种类 1 $({{\varepsilon _1} = 1}) \land ({{\varepsilon _2} = 0})$ 平均一致性模式 2 $({{\varepsilon _1} = 0}) \land ({{\varepsilon _2} = 1})$ 领导跟随一致性模式 3 $({1 > {\varepsilon _1} > 0}) \land ({{\varepsilon _2} > 0})$ 混合一致性模式 -
[1] Lu K L, Xu H, Zheng Y S. Distributed resource allocation via multi-agent systems under time-varying networks. Automatica, 2022, 136: Article No. 110059 doi: 10.1016/j.automatica.2021.110059 [2] Zheng Y L, Liu Q S. A review of distributed optimization: Problems, models and algorithms. Neurocomputing, 2022, 483: 446−459 doi: 10.1016/j.neucom.2021.06.097 [3] 柴天佑. 工业人工智能发展方向. 自动化学报, 2020, 46(10): 2005−2012Chai Tian-You. Development directions of industrial artificial intelligence. Acta Automatica Sinica, 2020, 46(10): 2005−2012 [4] Gong Z, Nie Z G, Liu Q, Liu X J. Design and control of a multi-mobile-robot cooperative transport system based on a novel six degree-of-freedom connector. ISA Transactions, 2023, 139: 606−620 doi: 10.1016/j.isatra.2023.04.006 [5] Li K Q, Wang J W, Zheng Y. Cooperative formation of autonomous vehicles in mixed traffic flow: Beyond platooning. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(9): 15951−15966 doi: 10.1109/TITS.2022.3146612 [6] Yu K T, Li Y M, Peng Z H, Tong S C. Distributed event-triggered formation control of planar vehicles without velocity sensors. IEEE Transactions on Vehicular Technology, 2023, 72(3): 2988−3000 doi: 10.1109/TVT.2022.3218706 [7] Mohammad H, Mohammad B. Adaptive output stationary average consensus for heterogeneous unknown linear multi-agent systems. IET Control Theory and Applications, 2018, 12(7): 847−856 doi: 10.1049/iet-cta.2017.0877 [8] Tian Y, Li H Q, Han Q. Finite-time average consensus of directed second-order multi-agent systems with Markovian switching topology and impulsive disturbance. Neural Computing and Applications, 2023, 35: 8575−8588 doi: 10.1007/s00521-022-08131-2 [9] Hu W F, Cheng Y, Yang C H. Leader-following consensus of linear multi-agent systems via reset control: A time-varying systems approach. Automatica, 2023, 149: Article No. 110824 doi: 10.1016/j.automatica.2022.110824 [10] Wang K P, Ding D, Tang Z, Feng J W. Leader-following consensus of nonlinear multi-agent systems with hybrid delays: Distributed impulsive pinning strategy. Applied Mathematics and Computation, 2022, 424: Article No. 127031 doi: 10.1016/j.amc.2022.127031 [11] Huang W C, Tian B B, Liu T T, Wang J H, Liu Z Q. Event-triggered leader-following consensus of multi-agent systems under semi-Markov switching topology with partially unknown rates. Journal of the Franklin Institute, 2022, 359(7): 3103−3125 doi: 10.1016/j.jfranklin.2022.02.024 [12] Lui D, Petrillo A, Santini S. Bipartite tracking consensus for high-order heterogeneous uncertain nonlinear multi-agent systems with unknown leader dynamics via adaptive fully-distributed PID control. IEEE Transactions on Network Science and Engineering, 2023, 10(2): 1131−1142 doi: 10.1109/TNSE.2022.3229752 [13] Wu Y H, Wang Z P, Zhang H, Huang C. Output-based event-triggered consensus of general linear multi-agent systems with communication delay under directed graphs. Journal of the Franklin Institute, 2020, 357(6): 3702−3720 doi: 10.1016/j.jfranklin.2020.02.036 [14] Qu M H, Wang Q D, Wei C L. Event-triggered consensus for second-order multi-agent systems with sampled position data via impulsive control. Journal of the Franklin Institute, 2022, 359(17): 9989−10016 doi: 10.1016/j.jfranklin.2022.09.023 [15] Wang K P, Tang Z, Park J H, Feng J W. Impulsive time window based quasi-consensus on stochastic nonlinear multi-agent systems. IEEE Transactions on Network Science and Engineering, 2022, 9(5): 3602−3613 doi: 10.1109/TNSE.2022.3185307 [16] Hu Z H, Mu X W. Impulsive consensus of stochastic multi-agent systems under semi-Markovian switching topologies and application. Automatica, 2023, 150: Article No. 110871 doi: 10.1016/j.automatica.2023.110871 [17] He W L, Chen G R, Han Q L, Feng Q. Network-based leader-following consensus of nonlinear multi-agent systems via distributed impulsive control. Information Sciences, 2017, 380: 145−158 doi: 10.1016/j.ins.2015.06.005 [18] Ma L, Wang Y L, Fei M R, Pan Q K. Cross-dimensional formation control of second-order heterogeneous multi-agent systems. ISA Transactions, 2022, 127: 188−196 doi: 10.1016/j.isatra.2022.02.036 [19] Yang R, Liu S, Tan Y Y, Zhang Y J, Jiang W. Consensus analysis of fractional-order nonlinear multi-agent systems with distributed and input delays. Neurocomputing, 2019, 329: 46−52 doi: 10.1016/j.neucom.2018.10.045 [20] 晋守博, 魏章志, 李耀红. 基于大通讯时滞的二阶多智能体系统的一致性分析. 电子与信息学报, 2021, 43(4): 1029−1034 doi: 10.11999/JEIT191009Jin Shou-Bo, Wei Zhang-Zhi, Li Yao-Hong. Consensus analysis of the second order multi-agent systems based on large communication delay. Journal of Electronics and Information Technology, 2021, 43(4): 1029−1034 doi: 10.11999/JEIT191009 [21] Wang X, Mou S S, Anderson B. Consensus-based distributed optimization enhanced by integral feedback. IEEE Transactions on Automatic Control, 2023, 68(3): 1894−1901 doi: 10.1109/TAC.2022.3169179 [22] Zhang T Y, Xu Y, Sun J. Dynamic event-triggered strategies for tracking control of directed multi-agent systems with Lipschitz nonlinear dynamics. International Journal of Robust and Nonlinear Control, 2022, 32(14): 8147−8162 doi: 10.1002/rnc.6280 [23] Hu T S, Lin Z L. Control Systems With Actuator Saturation: Analysis and Design. Berlin: Springer Science and Business Media, 2001. 56−92 [24] Desoer C, Vidyasagar M. Feedback Systems: Input-output Properties. New York: Academic Press, 1975. 85−116 -




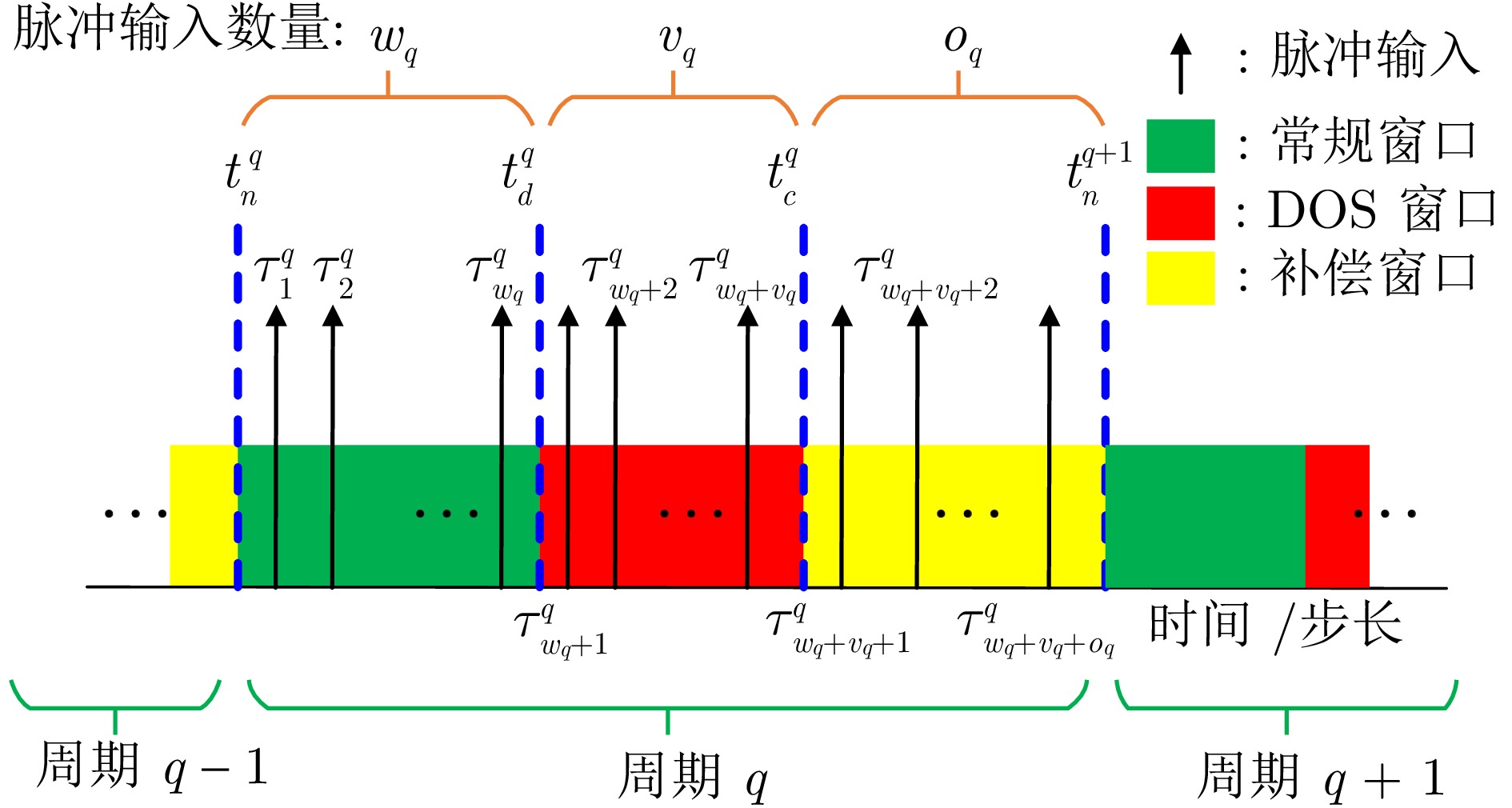
 下载:
下载: