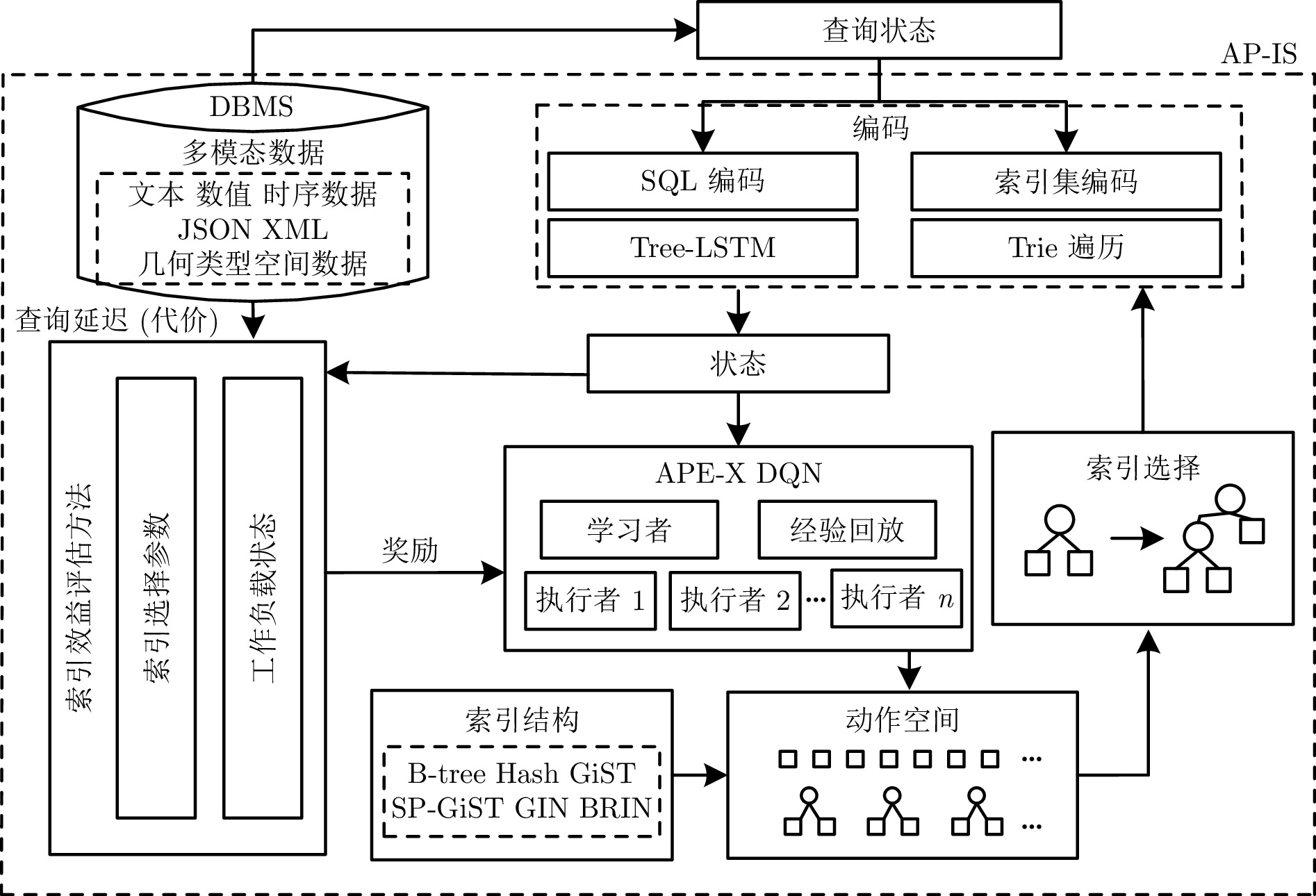
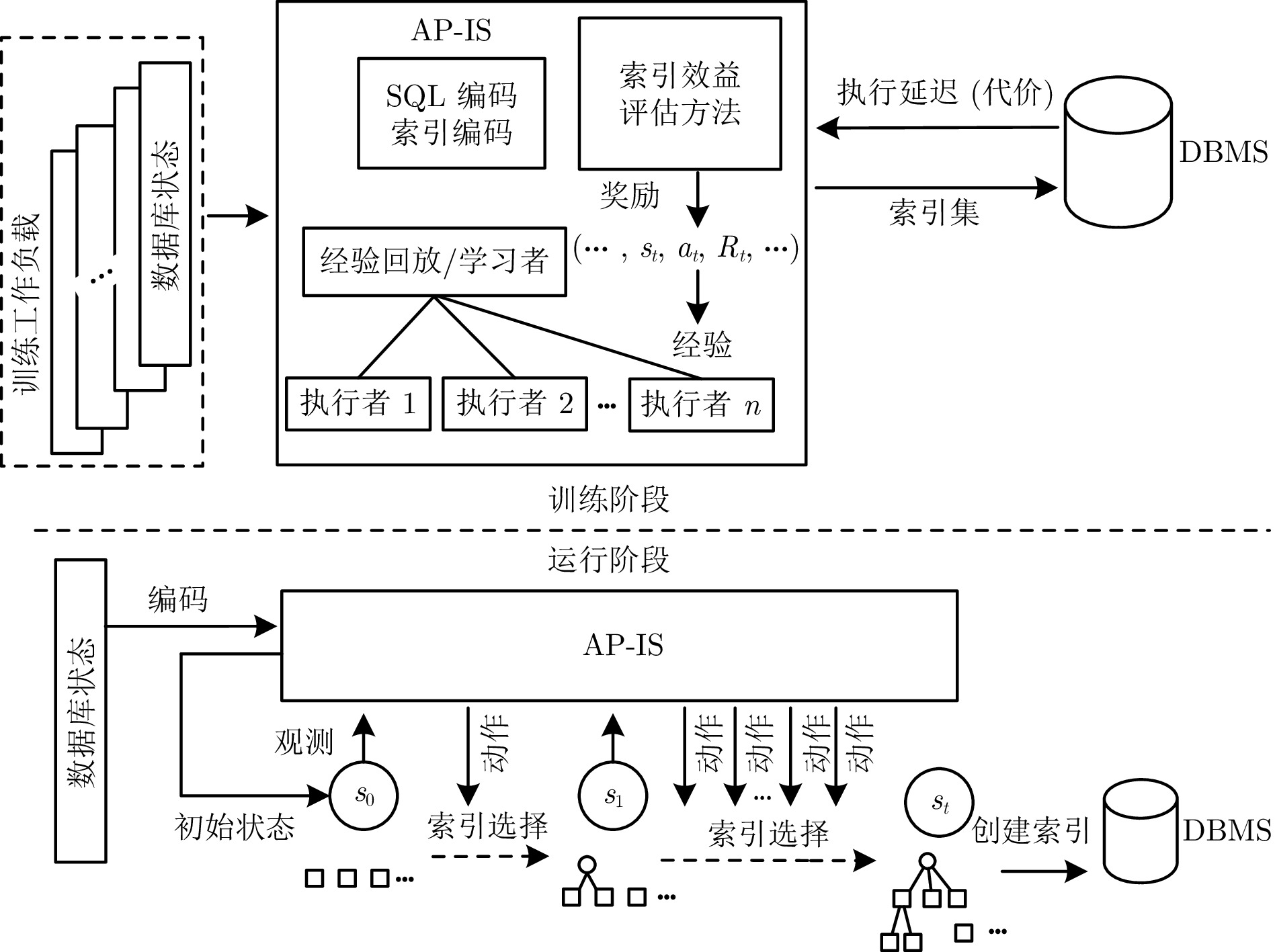
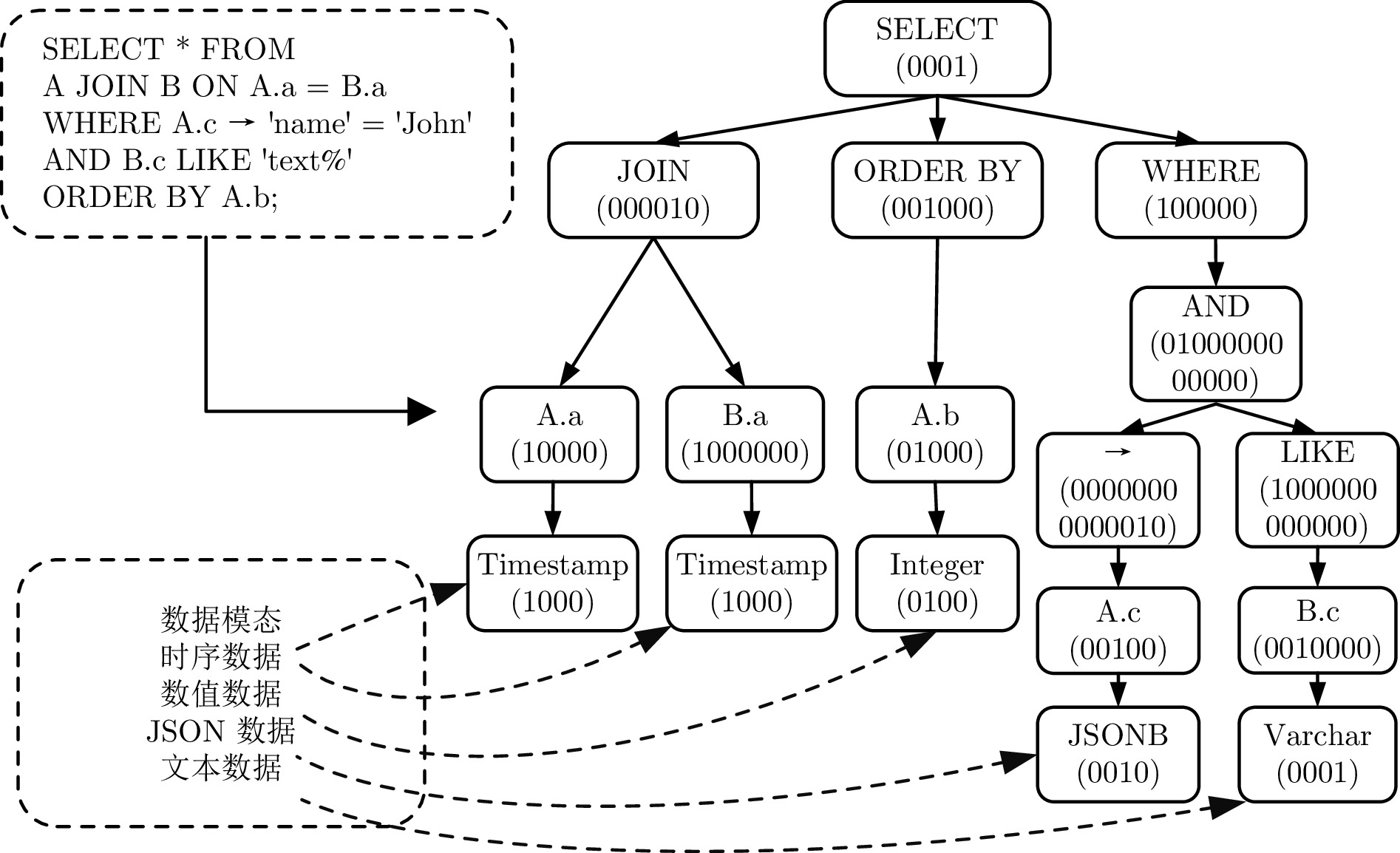
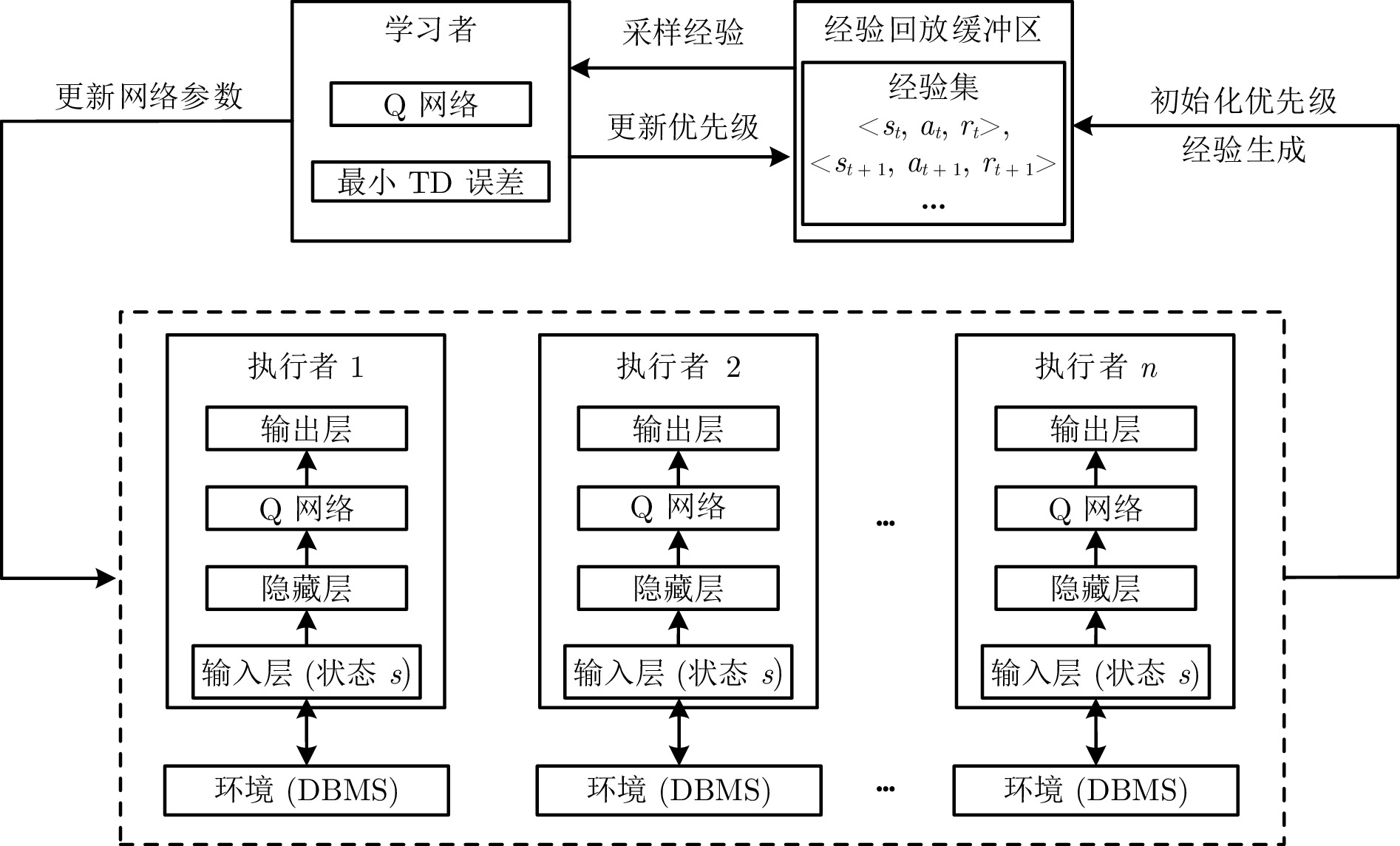
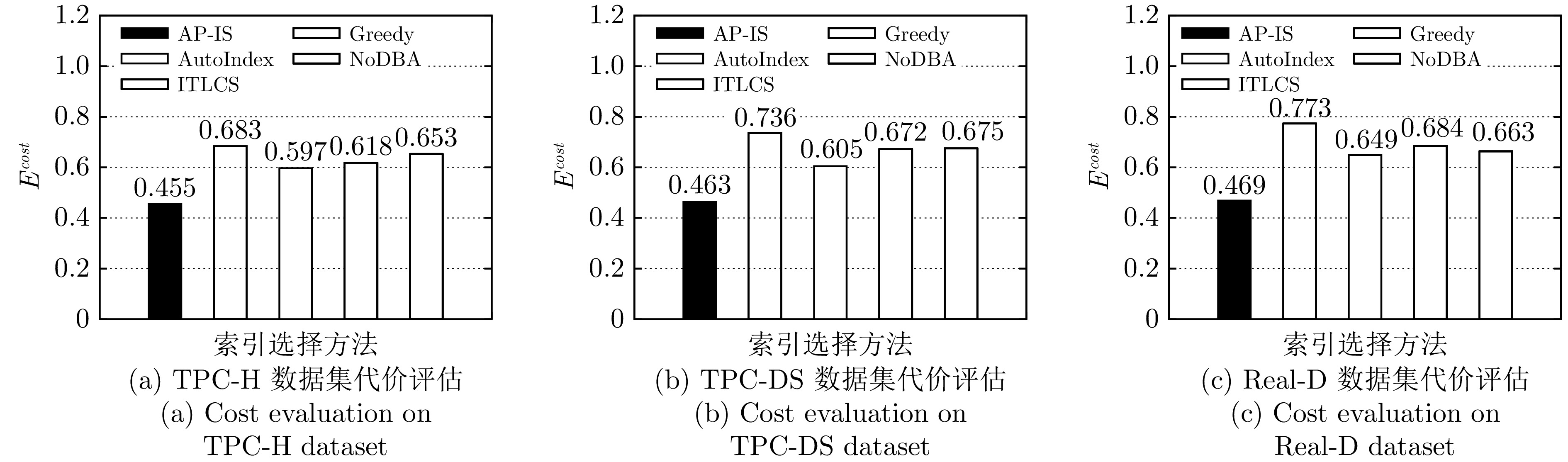
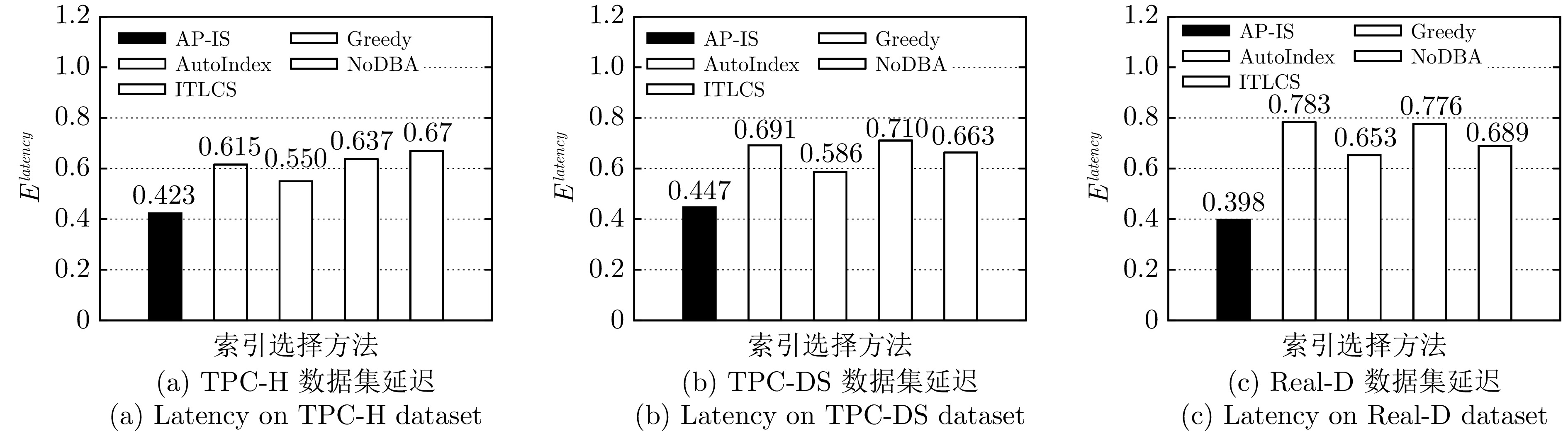
-
摘要: 现有的索引选择方法存在诸多局限性. 首先, 大多数方法考虑场景较为单一, 不能针对特定数据模态选择合适的索引结构, 进而无法有效应对海量多模态数据; 其次, 现有方法未考虑索引选择时索引构建的代价, 无法有效应对动态的工作负载. 针对上述问题, 提出一种面向多模态数据的智能高效索引选择模型 APE-X DQN (Distributed prioritized experience replay in deep Q-network), 称为 AP-IS (APE-X DQN for index selection). AP-IS 设计了新型索引集编码和 SQL 语句编码方法, 该方法使 AP-IS 在感知多模态数据的同时兼顾索引结构本身的特性, 极大地降低了索引的存储代价. AP-IS 集成新型索引效益评估方法, 在优化强化学习奖励机制的同时, 监控数据库工作负载的执行状态, 保证动态工作负载下 AP-IS 在时间和空间上的优化效果. 在真实多模态数据集上进行大量实验, 验证了 AP-IS 在工作负载的延迟、存储代价和训练效率等方面的性能, 结果均明显优于最新索引选择方法.Abstract: Existing index selection methods have several limitations. Firstly, most methods only consider a single scenario and cannot select an appropriate index structure for a specific data modal, thus being unable to effectively cope with massive multimodal data; Secondly, these methods do not take into consideration the cost of constructing indexes when selecting indexes, making them be unable to effectively handle dynamic workloads. Aiming to cope with these issues, an intelligent and efficient index selection model for multimodal data based on the APE-X DQN (distributed prioritized experience replay in deep Q-network) model, called AP-IS (APE-X DQN for index selection). AP-IS designs a new index set encoding and a new SQL statement encoding method, allowing AP-IS to perceive multimodal data while considering the characteristics of the index structure itself, significantly reducing the storage cost of indexes. AP-IS integrates a novel index benefit evaluation method. While optimizing the reward mechanism of reinforcement learning, it can monitor the execution state of database workloads, guaranteeing the effect of time and space optimization of AP-IS under dynamic workloads. Extensive experiments are conducted on real multimodal datasets to evaluate the performance of AP-IS under workloads including latency, storage cost, training efficiency, and the results of AP-IS significantly outperforms the state-of-the-art index selection methods.
-
Key words:
- Intelligent database /
- multimodal data /
- index selection /
- reinforcement learning /
- execution plan
-
图 1 时序数据模态下BRIN索引和B-tree索引的性能对比
Fig. 1 Performance comparison of BRIN index and B-tree index in temporal data modal
图 11 动态工作负载下不同强化学习算法延迟
Fig. 11 Latency of different reinforcement learning algorithms under dynamic workloads
图 14 AP-IS在动态工作负载下的编码方法评估
Fig. 14 Evaluation of encoding methods for AP-IS under dynamic workloads
表 1 索引选择方法对比分析
Table 1 Comparison analysis of index selection methods
方法策略 方法名称 优点 不足 传统的数据库索引选择方法 Drop[19] 通过启发式方法, 针对工作负载创建索引, 减轻DBA的工作负担 没有充分利用DBA经验, 无法适应动态的工作负载, 无法创建复合索引 AutoAdmin[20] 每轮迭代通过增加索引宽度支持多列索引选择 无法处理动态变化的工作负载, 加重DBA的负担 DB2Advis[21] 采用随机替换法适应动态的工作负载 随机的索引替换造成大量磁盘开销, 索引方案的不断变化影响系统的稳定性 基于学习的
数据库索引
选择方法NoDBA[22] 首次采用深度强化学习进行数据库索引自动选择, 降低工作负载的执行延迟 无法适应动态的工作负载, 也无法创建复合索引 ITLCS[23] 将遗传算法和强化学习相结合, 能够适应动态的工作负载和表结构较复杂的场景 依赖遗传算法索引选择策略, 未将基于学习的方法应用到问题的求解过程中 AutoIndex[10] 利用蒙特卡罗树搜索根据候选索引优化现有索引, 支持复合索引和动态的工作负载 无法适应多模态数据场景, 不支持多种索引类型的选择 
下载: 导出CSV
表 2 不同索引类型在多模态数据场景的适用性和局限性
Table 2 Applicability and limitations of different index types in multimodal data scenarios
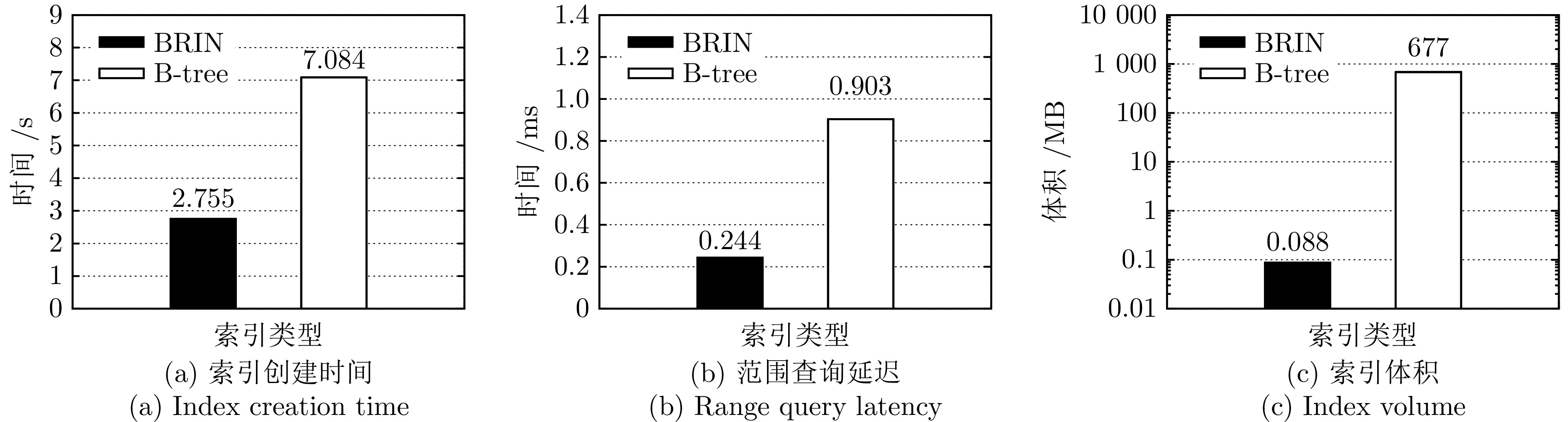
索引类型 适用数据模态及场景 不适用数据模态及场景 B-tree 整型、浮点型的等值、范围查询、排序等 文本类型的全文搜索, JSON等半结构化数据 Hash 等值查询 数据分布不均匀或更新频繁的场景 GiST 空间数据、文本数据的全文搜索、模糊查询 精确匹配、排序、去重等场景 SP-GiST 空间数据、文本数据的全文搜索 去重、排序, 不支持复合索引 GIN JSON等半结构化数据更新频繁的场景 大型二进制对象数据, 精确匹配等场景 BRIN 时序数据, 顺序访问模式 随机访问、精确匹配等场景
下载: 导出CSV
表 3 Real-D数据集描述
Table 3 Description of Real-D dataset
数据类型 数据来源 数据规模(GB) 时序数据 滴滴轨迹日志数据 22.1 JSON数据 HTTP请求数据 5.4 字符串数据 图片特征数据 6.8 数值数据 Kaggle 0.7
下载: 导出CSV
表 4 TPC-H、TPC-DS数据集描述
Table 4 Description of TPC-H and TPC-DS datasets
数据集名称 数据类型 数据规模(GB) TPC-H 数值、字符串等 1 TPC-DS 数值、字符串等 10
下载: 导出CSV
表 5 实验超参数设置
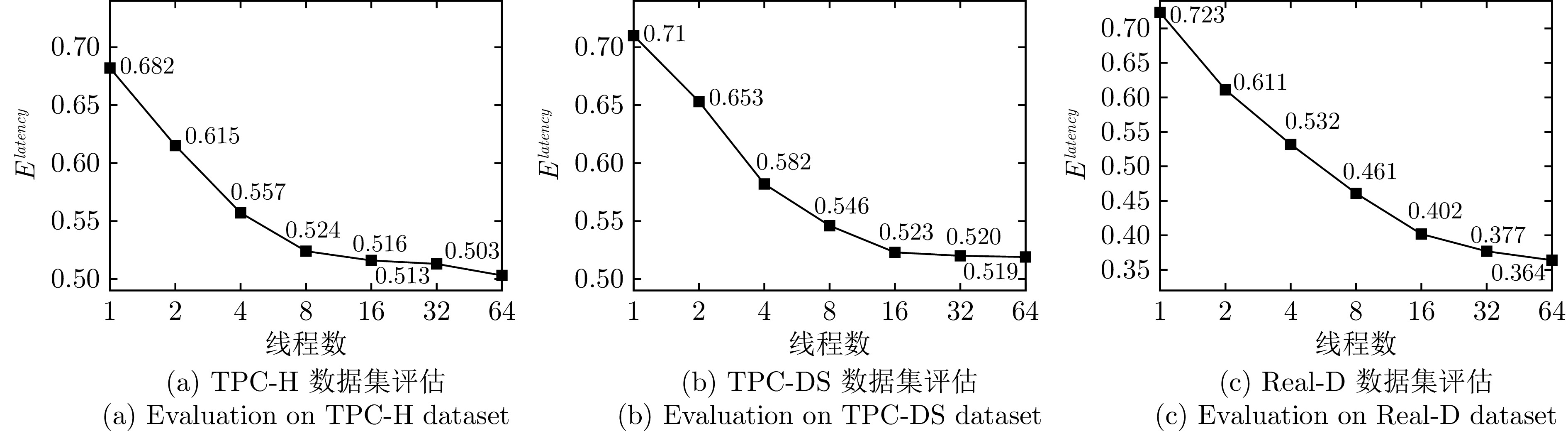
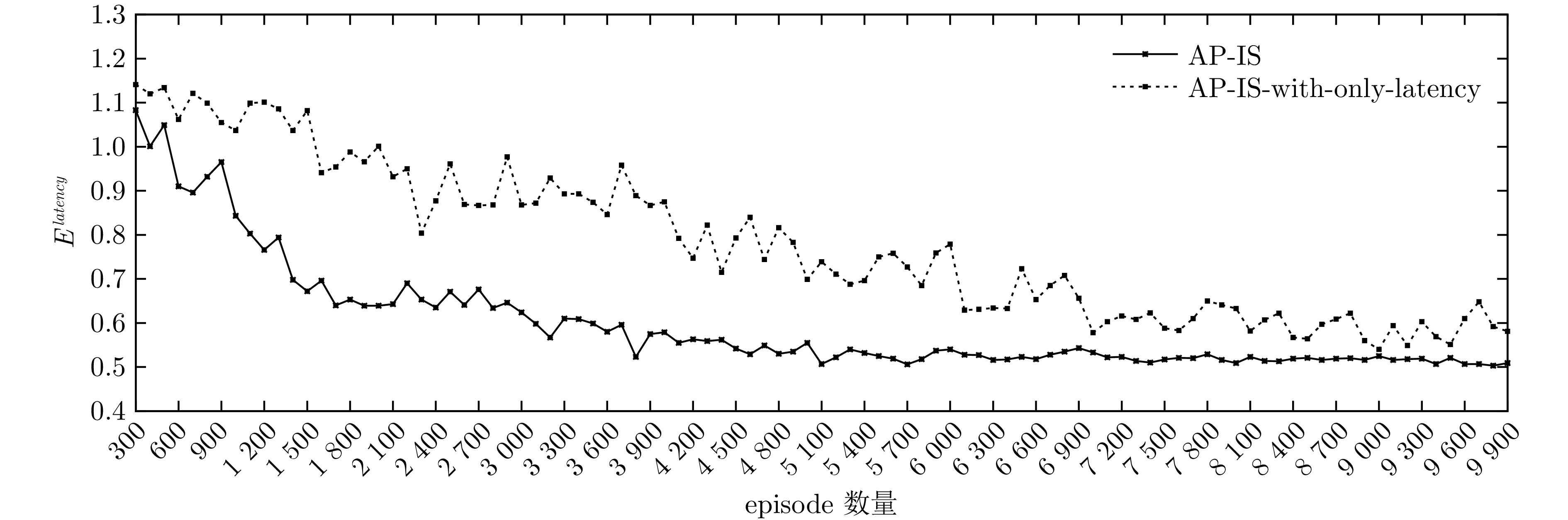
Table 5 Experimental setup of hyperparameters
参数名 参数值 参数说明 $ N $ 10000 训练中episode数量 $ K $ 64 单次采样经验条数 $ lr $ 0.01 学习率 $ \gamma $ 0.95 折扣因子 $ S_D $ 30000 经验回放缓冲区大小
下载: 导出CSV
表 6 AP-IS不同状态表示方法的延迟对比
Table 6 Latency comparison of different state representation methods of AP-IS
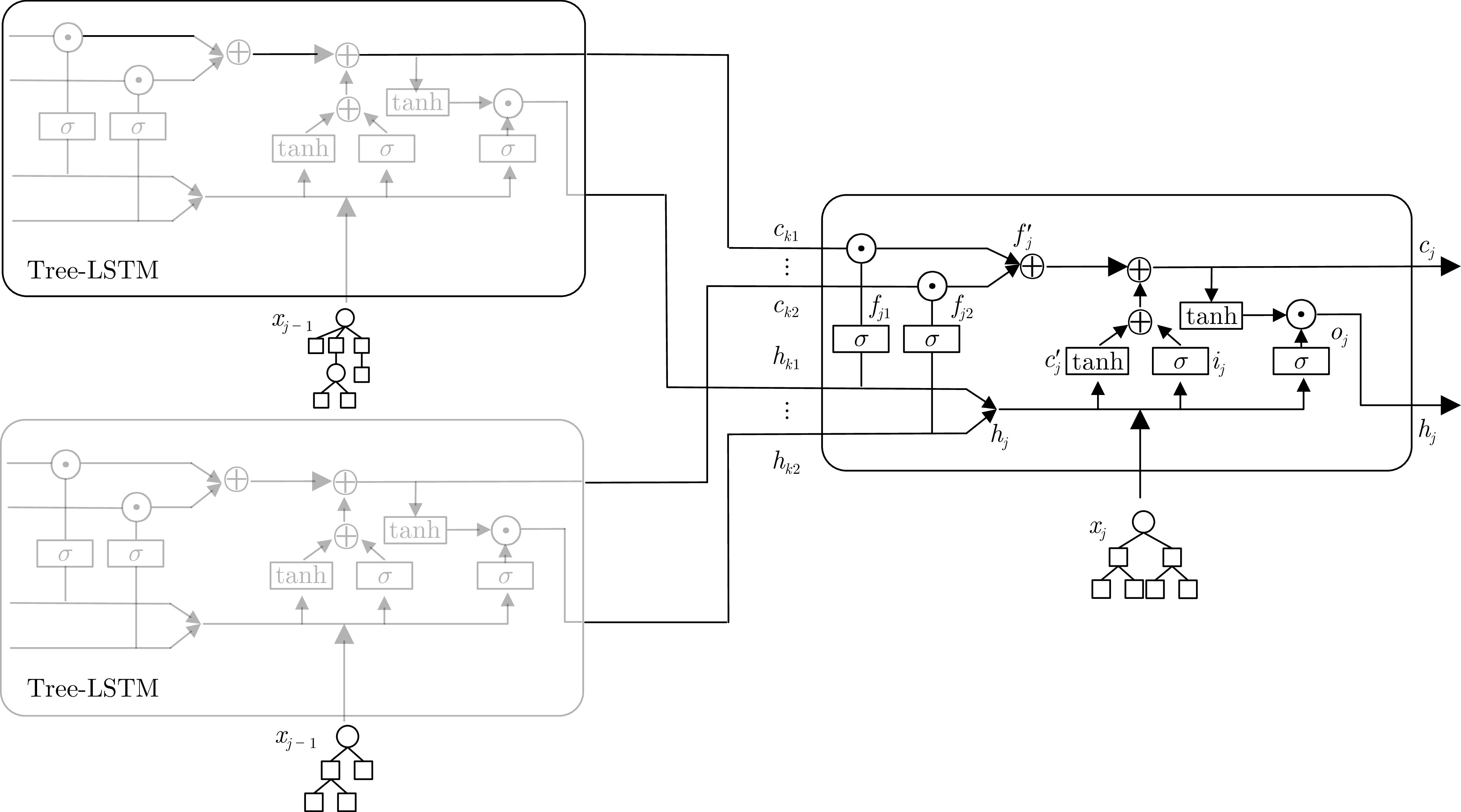
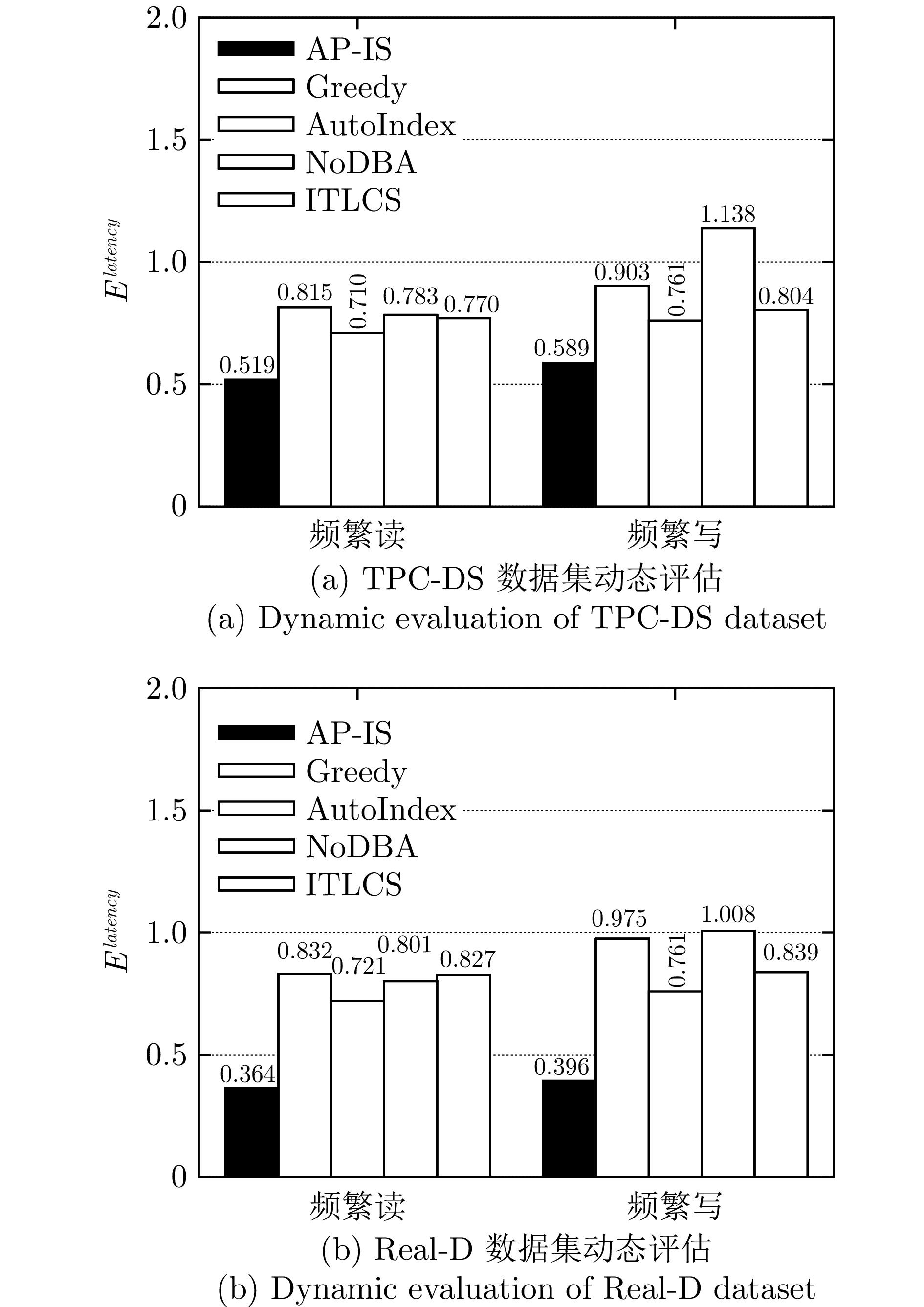
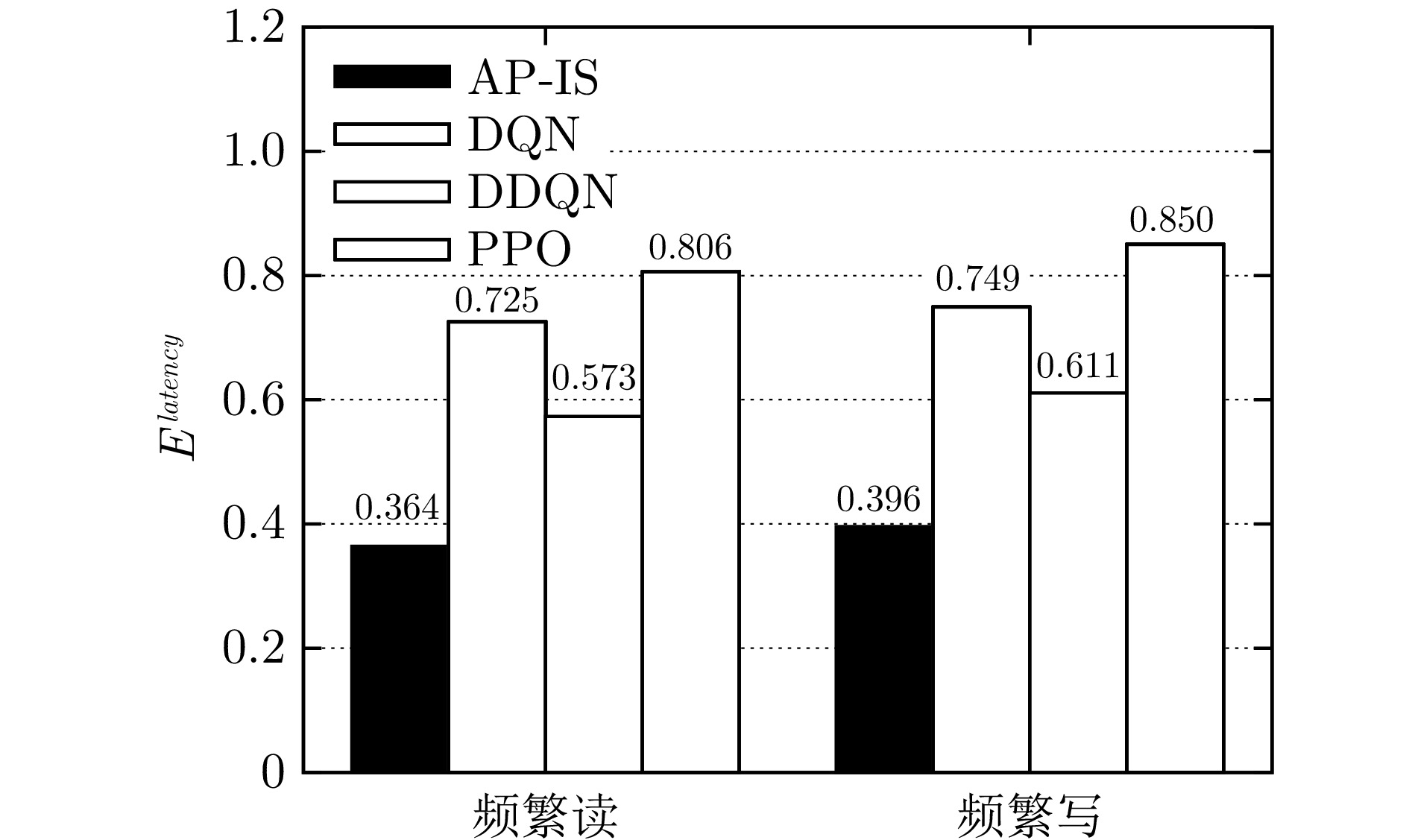
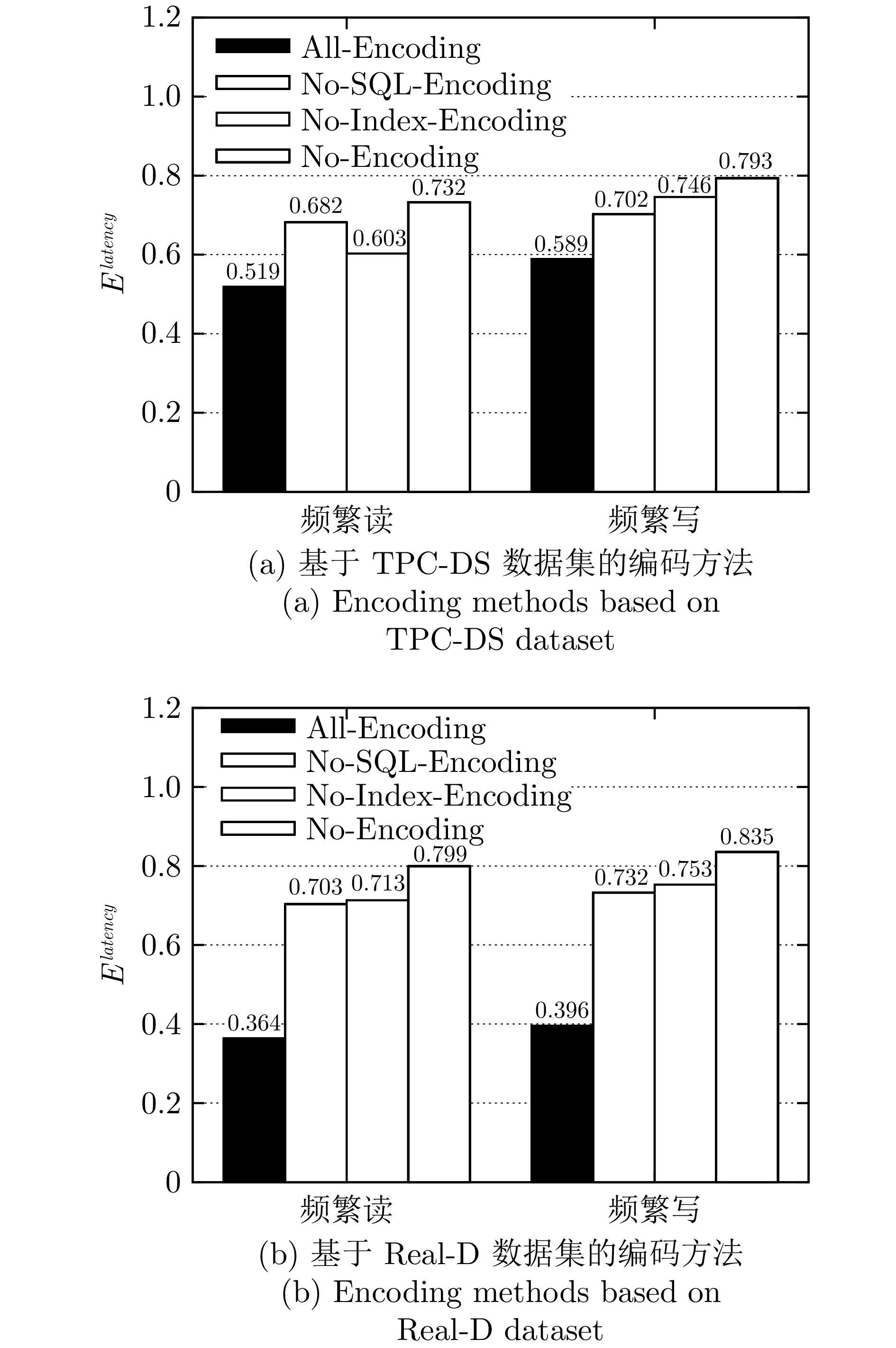
方法 频繁读 频繁写 只读 TPC-H TPC-DS Real-D TPC-H TPC-DS Real-D TPC-H TPC-DS Real-D RNN 0.550 0.604 0.548 0.616 0.695 0.599 0.569 0.618 0.657 BiRNN 0.549 0.591 0.522 0.546 0.633 0.534 0.576 0.570 0.599 LSTM 0.506 0.563 0.496 0.523 0.629 0.513 0.513 0.537 0.539 BiLSTM 0.452 0.549 0.430 0.472 0.603 0.530 0.468 0.459 0.456 GRU 0.459 0.552 0.427 0.486 0.593 0.429 0.436 0.447 0.428 Tree-LSTM 0.433 0.519 0.364 0.460 0.589 0.396 0.423 0.447 0.398
下载: 导出CSV
表 7 AP-IS在Real-D数据集上不同索引类型的选择数量
Table 7 Selection number of different index types on the Real-D dataset of AP-IS
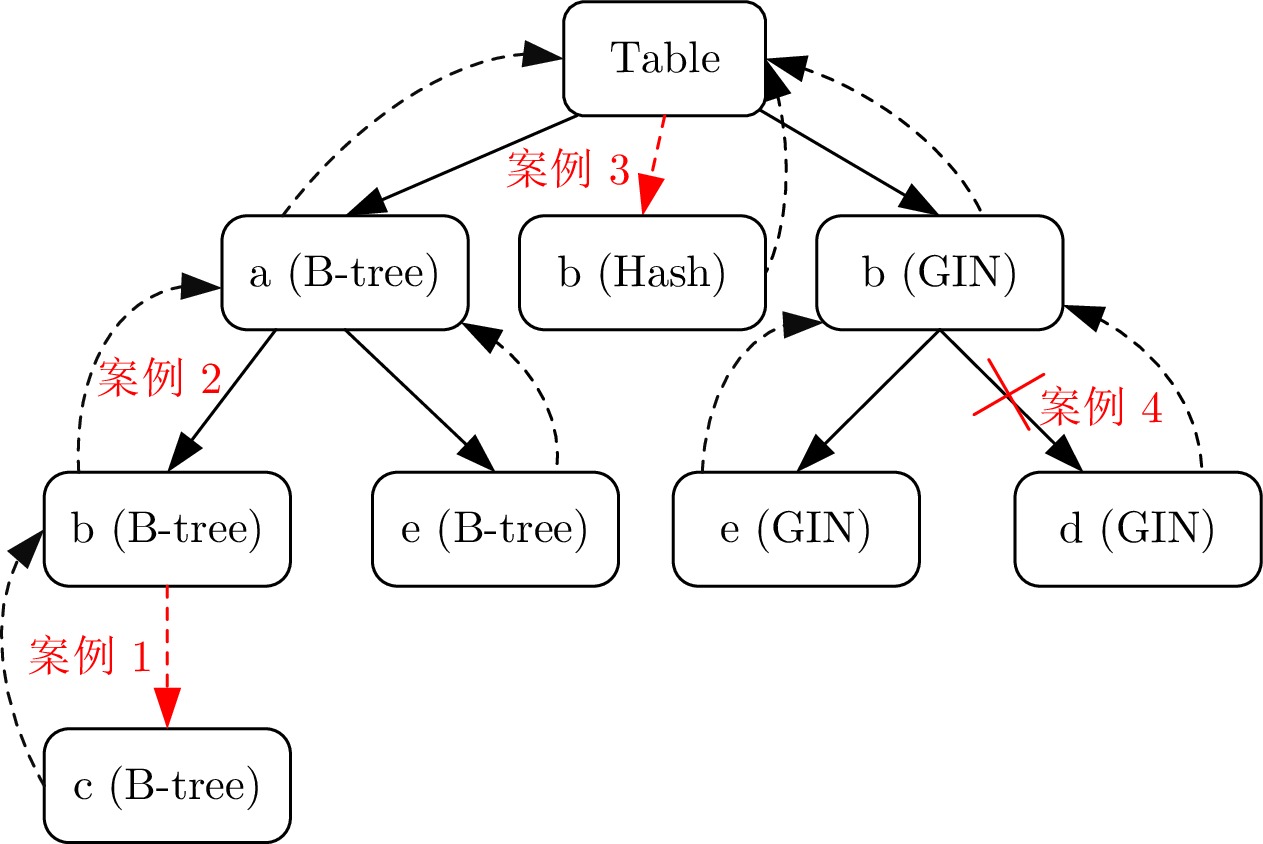
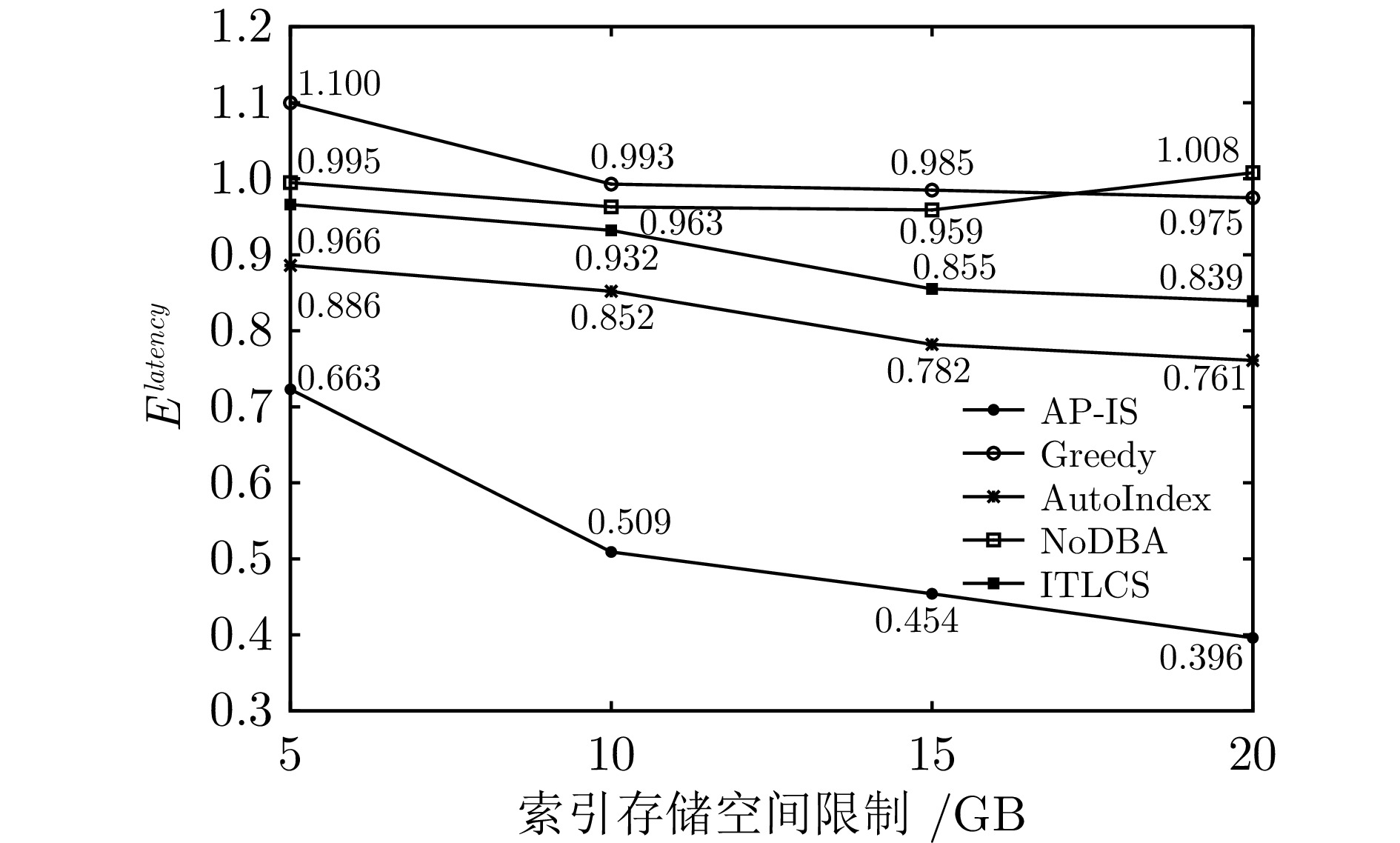
索引类型 选择数量(10 GB) 选择数量(20 GB) B-tree 13 19 Hash 7 9 GiST 5 4 SP-GiST 3 7 GIN 1 4 BRIN 8 10
下载: 导出CSV
-
[1] Zhang C, Yang Z, He X, Deng L. Multimodal intelligence: Representation learning, information fusion, and applications. IEEE Journal of Selected Topics in Signal Processing, 2020, 14(3): 478−493 doi: 10.1109/JSTSP.2020.2987728 [2] Lu J, Holubová I. Multi-model databases: A new journey to handle the variety of data. ACM Computing Surveys, 2019, 52(3): 1−38 [3] Li G, Zhou X, Cao L. AI meets database: AI4DB and DB4AI. In: Proceedings of the 2021 ACM SIGMOD International Conference on Management of Data. New York, USA: ACM, 2021. 2859−2866 [4] Chaudhuri S, Datar M, Narasayya V. Index selection for databases: A hardness study and a principled heuristic solution. IEEE Transactions on Knowledge and Data Engineering, 2004, 16(11): 1313−1323 doi: 10.1109/TKDE.2004.75 [5] Sun Z, Zhou X, Li G. Learned index: A comprehensive experimental evaluation. Proceedings of the VLDB Endowment, 2023, 16(8): 1992−2004 doi: 10.14778/3594512.3594528 [6] AlMahamid F, Grolinger K. Reinforcement learning algorithms: An overview and classification. In: Proceedings of the 2021 IEEE Canadian Conference on Electrical and Computer Engineering. Washington, USA: IEEE, 2021. 1−7 [7] Huang S, Wang Y, Li G. ACR-Tree: Constructing r-trees using deep reinforcement learning. In: Proceedings of the 28th International Conference of Database Systems for Advanced Applications. Berlin, Germany: Springer, 2023. 80−96 [8] 孙长银, 穆朝絮. 多智能体深度强化学习的若干关键科学问题. 自动化学报, 2020, 46(7): 1301−1312Sun Chang-Yin, Mu Chao-Xu. Important scientific problems of multi-agent deep reinforcement learning. Acta Automatica Sinica, 2020, 46(7): 1301−1312 [9] 胡子剑, 高晓光, 万开方, 张乐天, 汪强龙, Neretin Evgeny. 异策略深度强化学习中的经验回放研究综述. 自动化学报, 2023, 49(11): 2237−2256Hu Zi-Jian, Gao Xiao-Guang, Wan Kai-Fang, Zhang Le-Tian, Wang Qiang-Long, Neretin Evgeny. Research on experience replay of off-policy deep reinforcement learning: A review. Acta Automatica Sinica, 2023, 49(11): 2237−2256 [10] Zhou X, Liu L, Li W, Jin L, Li S, Wang T. AutoIndex: An incremental index management system for dynamic workloads. In: Proceedings of the 2022 IEEE 38th International Conference on Data Engineering. Washington, USA: IEEE, 2022. 2196−2208 [11] 蒲志强, 易建强, 刘振, 丘腾海, 孙金林, 李非墨. 知识和数据协同驱动的群体智能决策方法研究综述. 自动化学报, 2022, 48(3): 627−643Pu Zhi-Qiang, Yi Jian-Qiang, Liu Zhen, Qiu Teng-Hai, Sun Jin-Lin, Li Fei-Mo. Knowledge-based and data-driven integrating methodologies for collective intelligence decision making: A survey. Acta Automatica Sinica, 2022, 48(3): 627−643 [12] Horgan D, Quan J, Budden D, Barth-Maron G, Hessel M, Hasselt H. Distributed prioritized experience replay. In: Proceedings of the 6th International Conference on Learning Representations. Appleton, USA: ICLR Press, 2018. 1−19 [13] Boncz P, Neumann T, Erling O. TPC-H analyzed: Hidden messages and lessons learned from an influential benchmark. In: Proceedings of the Performance Characterization and Benchmarking. Berlin, Germany: Springer, 2014. 61−76 [14] Tardío R, Maté A, Trujillo J. Beyond TPC-DS, a benchmark for big data OLAP systems (BDOLAP-Bench). Future Generation Computer Systems, 2022, 132(5): 136−151 [15] Chaudhuri S, Narasayya V R. AutoAdmin “what-if” index analysis utility. In: Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data. New York, USA: ACM, 1998. 367−378 [16] Valentin G, Zuliani M, Zilio D C, Lohman G M, Skelley A. DB2 advisor: An optimizer smart enough to recommend its own indexes. In: Proceedings of the 16th International Conference on Data Engineering. Washington, USA: IEEE, 2000. 101−110 [17] Sharma V, Dyreson C, Flann N. MANTIS: Multiple type and attribute index selection using deep reinforcement learning. In: Proceedings of the 25th International Database Engineering & Applications Symposium. New York, USA: ACM, 2021. 56−64 [18] Perera R, Oetomo B, Rubinstein B, Borovica-Gajic R. DBA bandits: Self-driving index tuning under ad-hoc, analytical workloads with safety guarantees. In: Proceedings of the IEEE 37th International Conference on Data Engineering. Washington, USA: IEEE, 2021. 600−611 [19] Kossmann J, Halfpap S, Jankrift M, Schlosser R. Magic mirror in my hand, which is the best in the land? An experimental evaluation of index selection algorithms. Proceedings of the VLDB Endowment, 2020, 13(12): 2382−2395 doi: 10.14778/3407790.3407832 [20] Chaudhuri S, Narasayya V. An efficient cost-driven index selection tool for microsoft SQL server. In: Proceedings of the 23rd International Conference on Very Large Data Bases. San Francisco, USA: Morgan Kaufmann Publishers Inc., 1997. 146−155 [21] Valentin G, Zuliani M, Zilio D, Lohman G, Skelley A. DB2 advisor: An optimizer smart enough to recommend its own indexes. In: Proceedings of the 16th International Conference on Data Engineering. Washington, USA: IEEE, 2000. 101−110 [22] Sharma A, Schuhknecht F M, Dittrich J. The case for automatic database administration using deep reinforcement learning. arXiv preprint arXiv: 1801.05643, 2018. [23] Pedrozo W, Nievola J, Carvalho D. An adaptive approach for index tuning with learning classifier systems on hybrid storage environments. In: Proceedings of the Hybrid Artificial Intelligent Systems. Berlin, Germany: Springer, 2018. 716−729 [24] Wang X, Wang S, Liang X, Zhao D, Huang J, Xu X. Deep reinforcement learning: A survey. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(4): 5064−5078 doi: 10.1109/TNNLS.2022.3207346 [25] Mnih V, Kavukcuoglu K, Silver D, Rusu A, Veness J, Bellemare M. Human-level control through deep reinforcement learning. Nature, 2015, 518(7540): 529−533 doi: 10.1038/nature14236 [26] Katoch S, Chauhan S, Kumar V. A review on genetic algorithm: Past, present, and future. Multimedia Tools and Applications, 2021, 80(5): 8091−8126 doi: 10.1007/s11042-020-10139-6 [27] Swiechowski M, Godlewski K, Sawicki B, Mandziuk J. Monte carlo tree search: A review of recent modifications and applications. Artificial Intelligence Review, 2023, 56(3): 2497−2562 doi: 10.1007/s10462-022-10228-y [28] Tai K, Socher R, Manning C. Improved semantic representations from tree-structured long short-term memory networks. In: Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing. Stroudsburg, USA: Association for Computational Linguistics, 2015. 1556−1566 [29] Lindemann B, Müller T, Vietz H, Jazdi N, Weyrich M. A survey on long short-term memory networks for time series prediction. In: Proceedings of the 14th CIRP Conference on Intelligent Computation in Manufacturing Engineering. Amsterdam, Netherlands: Elsevier, 2021. 650−655 [30] Yao Y, He J, Li T, Wang Y, Lan X, Li Y. An automatic xss attack vector generation method based on the improved dueling DDQN algorithm. IEEE Transactions on Dependable and Secure Computing, 2024, 21(4): 2852−2868 doi: 10.1109/TDSC.2023.3319352 [31] Chen Y, Shih W, Lai H, Chang H, Huang J. Pairs trading strategy optimization using proximal policy optimization algorithms. In: Proceedings of the International Conference on Big Data and Smart Computing. Washington, USA: IEEE, 2023. 40−47 [32] Han Y, Li G, Yuan H, Sun J. AutoView: An autonomous materialized view management system with encoder-reducer. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(6): 5626−5639 [33] Holzer S, Stockinger K. Detecting errors in databases with bidirectional recurrent neural networks. In: Proceedings of the 25th International Conference on Extending Database Technology. Edinburgh, UK: EDBT Association, 2022. 364−367 [34] Zheng Y, Gao Z, Shen J, Zhai X. Optimizing automatic text classification approach in adaptive online collaborative discussion——A perspective of attention mechanism-based Bi-LSTM. IEEE Transactions on Learning Technologies, 2023, 16(5): 591−602 doi: 10.1109/TLT.2022.3192116 [35] Yao D, Cong G, Zhang C, Meng X, Duan R, Bi J. A linear time approach to computing time series similarity based on deep metric learning. IEEE Transactions on Knowledge Data Engineering, 2022, 34(10): 4554−4571 doi: 10.1109/TKDE.2020.3047070 -
图(15) / 表(7)
计量
- 文章访问数: 235
- HTML全文浏览量: 107
- PDF下载量: 46
- 被引次数: 0
