基于决策变量时域变化特征分类的动态多目标进化算法

闵芬; 董文波; 丁炜超

doi:10.16383/j.aas.c230741

基于决策变量时域变化特征分类的动态多目标进化算法

doi: 10.16383/j.aas.c230741

闵芬^{1, 2,},
董文波^1,,
丁炜超^{1, 2,}

1.
华东理工大学信息科学与工程学院上海 200237
2.
上海市计算机软件评测重点实验室上海 201112

基金项目: 上海市基础研究特区计划(22TQ1400100-16), 上海市自然科学基金(23ZR1414900), 上海市计算机软件评测重点实验室开放课题(SSTL2023_03)资助

详细信息

作者简介:
闵芬：华东理工大学信息科学与工程学院硕士研究生. 2018年获得安徽大学学士学位. 主要研究方向为多目标优化及其应用. E-mail: minfen@mail.ecust.edu.cn

董文波：华东理工大学信息科学与工程学院讲师. 主要研究方向为多视图机器学习, 深度高斯过程和多目标优化. E-mail: wbdong@ecust.edu.cn

丁炜超：华东理工大学信息科学与工程学院副教授. 2019年获得华东理工大学计算机应用技术博士学位. 主要研究方向为群体智能与演化计算, 多目标优化算法和模式识别. 本文通信作者. E-mail: weich@ecust.edu.cn

中图分类号: Y
计量
- 文章访问数: 125
- HTML全文浏览量: 79
- PDF下载量: 12
- 被引次数: 0
出版历程
- 收稿日期: 2023-11-27
- 录用日期: 2024-05-30
- 网络出版日期: 2024-08-01

Dynamic Multi-objective Evolutionary Algorithm Based on Classification of Decision Variable Temporal Change Characteristics

MIN Fen^{1, 2
,},
DONG Wen-Bo^1
,,
DING Wei-Chao^{1, 2
,}

1.
School of Information Science and Engineering, East China University of Science and Technology, Shanghai 200237
2.
Shanghai Key Laboratory of Computer Software Evaluating and Testing, Shanghai 201112

Funds: Supported by Shanghai Basic Research Special Zone Plan (22TQ1400100-16), Shanghai Natural Science Foundation (23ZR1414900), Shanghai Key Laboratory of Computer Software Evaluating and Testing Open Topics (SSTL2023_03)

More Information

Author Bio:
MIN Fen　Master student at the School of Information Science and Engineering, East China University of Science and Technology. She received her bachelor degree from Anhui University in 2018. Her research interest covers multi-objective optimization and applications

DONG Wen-Bo　Lecturer at the School of Information Science and Engineering, East China University of Science and Technology. His research interest covers multi-view machine learning, deep Gaussian processes, and multi-objective optimization

DING Wei-Chao　Associate professor at the School of Information Science and Engineering, East China University of Science and Technology. He received his Ph.D. degree in computer application technology from East China University of Science and Technology in 2019. His research interest covers swarm intelligence and evolutionary computation, multi-objective optimization algorithm, and pattern classification. Corresponding author of this paper

摘要

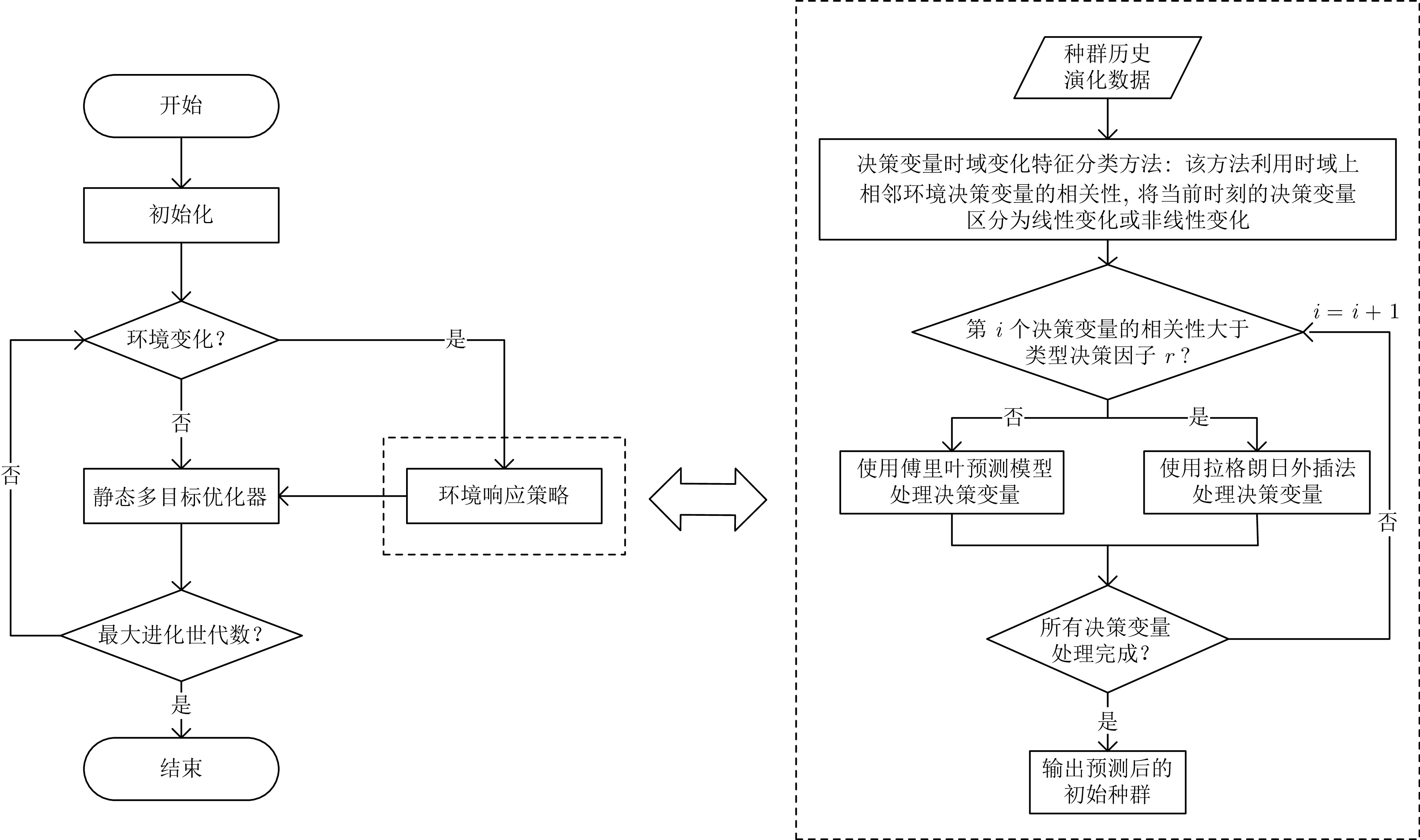
摘要: 动态多目标优化问题(Dynamic multi-objective optimization problems, DMOPs) 广泛存在于科学研究和工程实践中, 其主要考虑在动态环境下同时联合优化多个冲突目标. 现有方法往往关注于目标空间的时域特征, 忽视了对单个决策变量变化特性的探索与利用, 从而在处理更复杂的问题时不能有效引导种群收敛. 为此, 提出一种基于决策变量时域变化特征分类的动态多目标进化算法(Dynamic multi-objective evolutionary algorithm based on classification of decision variable temporal change characteristics, FT-DMOEA). 所提算法在环境动态变化时, 首先基于决策变量时域变化特征分类方法将当前时刻决策变量划分为线性变化和非线性变化两种类型; 然后分别采用拉格朗日外插法和傅里叶预测模型对线性和非线性变化决策变量进行下一时刻的初始化操作. 为了更有效地识别非线性决策变量变化模式, 傅里叶预测模型通过傅里叶变换将历史种群数据从时域转换到频域, 在分析周期性频率特征后, 使用自回归模型进行频谱估计后再反变换至时域. 在多个基准数据集上和其他算法进行对比, 实验结果表明, 所提算法是有效的.
- 傅里叶变换 /
- 动态多目标优化问题 /
- 决策变量分类 /
- 动态多目标进化算法 /
- 预测策略
Abstract: Dynamic multi-objective optimization problems (DMOPs) are widely encountered in scientific research and engineering practice, where the main focus is on jointly optimizing multiple conflicting objectives in dynamic environments. Existing methods often emphasize the temporal characteristics of the objective space, neglecting the exploration and utilization of the characteristics of individual decision variable changes, thus failing to effectively guide population convergence when dealing with more complex problems. To address this issue, a dynamic multi-objective evolutionary algorithm based on classification of decision variable temporal change characteristics (FT-DMOEA) is proposed. When the environment undergoes dynamic changes, the algorithm first classifies the decision variables at the current time into two types: Linear change and nonlinear change, based on the decision variable temporal change feature classification method. Subsequently, the algorithm uses Lagrange interpolation and Fourier prediction models to initialize the linear and nonlinear change decision variables for the next time step, respectively. In order to more effectively identify patterns of nonlinear decision variable changes, the Fourier prediction model transforms historical population data from the time domain to the frequency domain using Fourier transformation. After analyzing the periodic frequency features, an autoregressive model is used for spectral estimation before transforming back to the time domain. The experimental results indicate that the proposed algorithm is effective when compared with other algorithms on multiple benchmark datasets.

HTML全文

图 1 FT-DMOEA的流程图

Fig. 1 Flowchart of FT-DMOEA

下载: 全尺寸图片幻灯片

图 2 FT-DMOEA与其他算法在测试函数集上的表现性能显著性差异(越接近白色表示均值差异越明显)

Fig. 2 The performance significant differences obtained by FT-DMOEA and other algorithms on the benchmark suite (The closer the region color is to white, the greater the difference in the mean)

下载: 全尺寸图片幻灯片

图 3 DMOA、SGEA和FTMOA在FDA1、FDA2和FDA3上获得的POF

Fig. 3 POFs obtained by DMOA, SGEA, and FTMOA on FDA1, FDA2, and FDA3

下载: 全尺寸图片幻灯片

图 4 DMOA、SGEA和FTMOA在FDA测试函数集上获得的平均IGD演化曲线

Fig. 4 Average IGD evolution curves obtained by DMOA, SGEA, and FTMOA on FDA benchmark suite

下载: 全尺寸图片幻灯片

图 5 使用不同$r$的FT-DMOEA在DF测试函数集上获得的平均MIGD值

Fig. 5 Mean MIGD values obtained by FT-DMOEA with different parameters r on DF benchmark suite

下载: 全尺寸图片幻灯片

表 1 FDA测试函数集与DF测试函数集的问题特征与变化类型

Table 1 The problem features and types of variations in the FDA benchmark suite and the DF benchmark suite

问题名	目标数	变化类型	问题特征
FDA1	2	类型1	POS随时间改变
FDA2	2	类型3	POF凹凸变化
FDA3	2	类型2	POF中解的分布随时间变化
FDA4	3	类型1	POS随时间改变
FDA5	3	类型2	POF中解的分布随时间变化
DF1	2	类型2	POF凹凸变化
DF2	2	类型1	POS随时间改变
DF3	2	类型2	决策变量相关, POF凹凸变化
DF4	2	类型2	决策变量相关, POF范围和POS边界随时间变化
DF5	2	类型2	拐点的数量随时间改变, POF形状随时间变化
DF6	2	类型2	多模态, POF形状具有拐点区域和长尾特征
DF7	2	类型2	POS改变但质心不变, POF范围随时间变化
DF8	2	类型2	POS改变但质心不变, 决策变量相关
DF9	2	类型2	决策变量相关, POF的连续性随时间变化
DF10	3	类型2	POS改变但质心不变, 决策变量相关, POF凹凸变化
DF11	3	类型2	决策变量相关, POF的区域范围随时间变化
DF12	3	类型1	决策变量相关, POF存在随时间变化的孔洞
DF13	3	类型2	不连续性, 断开的POF段数量随时间变化
DF14	3	类型2	决策变量相关, POF退化性, 拐点的数量随时间变化

下载: 导出CSV

表 2 FT-DMOEA与四种对比算法在DF测试函数集上获得的MIGD指标的平均值和标准差值的统计结果

Table 2 Statistical results of mean and standard deviation values of MIGD metric obtained by FT-DMOEA and four comparative algorithms on the DF benchmark suite

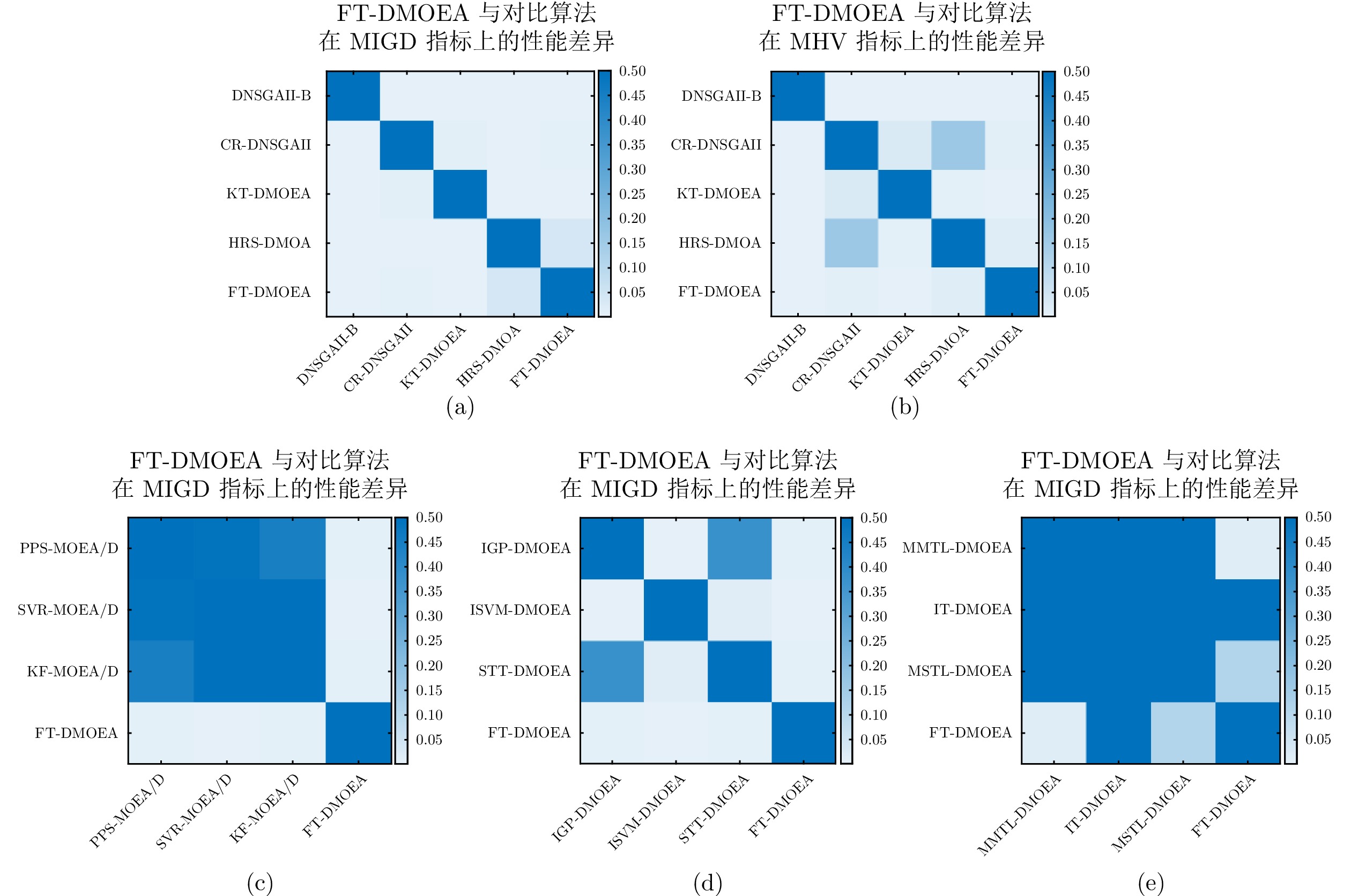
测试问题	$n_{t}$, $\tau_{t}$	DNSGAII-B	CR-DNSGAII	KT-DMOEA	HRS-DMOA	FT-DMOEA
DF1	5, 10	0.430 5 ± 1.18 ×$10^{-1}$	0.084 9 ± 1.22 ×$10^{-2}$	0.142 7 ± 2.17 ×$10^{-2}$	0.074 0 ± 1.62 ×$10^{-2}$	0.024 8 ± 3.94 ×$10^{-3}$
	10, 5	2.323 2 ± 7.40 ×$10^{-1}$	0.110 2 ± 5.41 ×$10^{-2}$	0.132 6 ± 2.27 ×$10^{-2}$	0.085 9 ± 1.94 ×$10^{-2}$	0.016 6 ± 2.10 ×$10^{-3}$
	10, 10	2.092 3 ± 6.29 ×$10^{-1}$	0.103 8 ± 2.54 ×$10^{-2}$	0.126 1 ± 1.94 ×$10^{-2}$	0.088 4 ± 1.80 ×$10^{-2}$	0.016 7 ± 3.11 ×$10^{-3}$
DF2	5, 10	0.266 7 ± 7.12 ×$10^{-2}$	0.024 2 ± 4.11 ×$10^{-3}$	0.109 3 ± 1.29 ×$10^{-2}$	0.050 5 ± 1.68 ×$10^{-2}$	0.047 2 ± 9.43 ×$10^{-3}$
	10, 5	1.233 8 ± 5.04 ×$10^{-1}$	0.034 7 ± 1.87 ×$10^{-2}$	0.119 6 ± 1.04 ×$10^{-2}$	0.041 9 ± 1.31 ×$10^{-2}$	0.036 8 ± 8.36 ×$10^{-3}$
	10, 10	1.345 8 ± 5.50 ×$10^{-1}$	0.040 2 ± 1.66 ×$10^{-2}$	0.109 5 ± 1.09 ×$10^{-2}$	0.048 2 ± 1.37 ×$10^{-2}$	0.037 5 ± 6.50 ×$10^{-3}$
DF3	5, 10	0.834 4 ± 1.86 ×$10^{-1}$	0.639 3 ± 3.50 ×$10^{-1}$	0.836 6 ± 8.29 ×$10^{-2}$	0.518 2 ± 1.33 ×$10^{-1}$	0.050 1 ± 1.12 ×$10^{-2}$
	10, 5	2.444 3 ± 8.07 ×$10^{-1}$	0.380 7 ± 7.25 ×$10^{-2}$	0.735 0 ± 1.24 ×$10^{-1}$	0.568 0 ± 1.44 ×$10^{-1}$	0.039 1 ± 7.27 ×$10^{-3}$
	10, 10	2.717 8 ± 7.92 ×$10^{-1}$	0.394 3 ± 1.18 ×$10^{-1}$	0.712 8 ± 9.16 ×$10^{-2}$	0.591 6 ± 1.57 ×$10^{-1}$	0.040 6 ± 7.75 ×$10^{-3}$
DF4	5, 10	1.636 0 ± 2.44 ×$10^{-1}$	1.274 2 ± 1.41 ×$10^{-1}$	1.623 1 ± 1.43 ×$10^{-1}$	0.362 0 ± 7.49 ×$10^{-2}$	0.111 0 ± 1.07 ×$10^{-2}$
	10, 5	1.860 1 ± 3.52 ×$10^{-1}$	1.329 6 ± 1.47 ×$10^{-1}$	1.710 9 ± 9.97 ×$10^{-2}$	0.429 6 ± 6.97 ×$10^{-2}$	0.108 3 ± 8.49 ×$10^{-3}$
	10, 10	1.713 3 ± 3.27 ×$10^{-1}$	1.368 4 ± 1.81 ×$10^{-1}$	1.708 9 ± 1.14 ×$10^{-1}$	0.431 0 ± 7.83 ×$10^{-2}$	0.114 4 ± 8.83 ×$10^{-3}$
DF5	5, 10	0.330 9 ± 5.93 ×$10^{-2}$	0.069 8 ± 5.30 ×$10^{-2}$	0.406 0 ± 4.98 ×$10^{-2}$	0.036 1 ± 7.22 ×$10^{-3}$	0.016 9 ± 2.47 ×$10^{-3}$
	10, 5	1.510 3 ± 5.20 ×$10^{-1}$	0.059 4 ± 2.09 ×$10^{-2}$	0.362 3 ± 6.79 ×$10^{-2}$	0.036 7 ± 9.04 ×$10^{-3}$	0.015 5 ± 2.54 ×$10^{-3}$
	10, 10	1.496 0 ± 4.17 ×$10^{-1}$	0.065 5 ± 4.32 ×$10^{-2}$	0.350 1 ± 6.63 ×$10^{-2}$	0.036 6 ± 5.65 ×$10^{-3}$	0.015 5 ± 3.10 ×$10^{-3}$
DF6	5, 10	6.276 0 ± 1.45 ×$10^{0}$	2.780 8 ± 2.50 ×$10^{0}$	3.269 4 ± 3.06 ×$10^{-1}$	1.530 2 ± 6.95 ×$10^{-1}$	0.677 7 ± 2.68 ×$10^{-1}$
	10, 5	1.825 8 ± 6.45 ×$10^{-1}$	5.904 6 ± 4.39 ×$10^{0}$	3.791 6 ± 4.24 ×$10^{-1}$	1.778 4 ± 6.44 ×$10^{-1}$	0.935 7 ± 5.40 ×$10^{-1}$
	10, 10	1.876 8 ± 1.04 ×$10^{0}$	6.877 3 ± 3.12 ×$10^{0}$	3.917 2 ± 3.90 ×$10^{-1}$	1.206 6 ± 6.06 ×$10^{-1}$	0.751 4 ± 3.15 ×$10^{-1}$
DF7	5, 10	2.857 8 ± 5.82 ×$10^{-1}$	2.355 3 ± 7.25 ×$10^{-1}$	2.938 0 ± 7.64 ×$10^{-1}$	0.909 4 ± 2.12 ×$10^{-1}$	37.663 0 ± 4.45 ×$10^{1}$
	10, 5	1.120 9 ± 1.35 ×$10^{-1}$	9.100 2 ± 7.34 ×$10^{0}$	4.445 3 ± 7.07 ×$10^{-1}$	1.228 6 ± 1.74 ×$10^{-1}$	13.374 3 ± 1.84 ×$10^{1}$
	10, 10	1.115 4 ± 1.53 ×$10^{-1}$	5.756 8 ± 2.25 ×$10^{0}$	2.967 1 ± 4.29 ×$10^{-1}$	1.129 8 ± 1.53 ×$10^{-1}$	105.840 0 ± 1.19 ×$10^{2}$
DF8	5, 10	0.302 3 ± 5.64 ×$10^{-2}$	0.958 2 ± 1.32 ×$10^{-1}$	1.093 7 ± 1.53 ×$10^{-2}$	0.137 3 ± 6.89 ×$10^{-2}$	0.075 9 ± 5.27 ×$10^{-3}$
	10, 5	0.278 3 ± 5.55 ×$10^{-2}$	1.082 2 ± 1.38 ×$10^{-1}$	1.073 6 ± 2.32 ×$10^{-2}$	0.123 2 ± 3.16 ×$10^{-2}$	0.070 0 ± 1.39$\times10^{-2}$
	10, 10	0.274 9 ± 5.93 ×$10^{-2}$	1.035 3 ± 1.20 ×$10^{-1}$	1.090 4 ± 1.78 ×$10^{-2}$	0.110 8 ± 3.15 ×$10^{-2}$	0.072 7 ± 4.83 ×$10^{-3}$
DF9	5, 10	1.164 3 ± 2.73 ×$10^{-1}$	0.269 9 ± 1.11 ×$10^{-1}$	0.677 8 ± 7.75 ×$10^{-2}$	0.218 9 ± 3.09 ×$10^{-2}$	0.584 4 ± 6.38 ×$10^{-2}$
	10, 5	1.146 7 ± 2.80 ×$10^{-1}$	0.279 7 ± 1.12 ×$10^{-1}$	0.642 7 ± 1.09 ×$10^{-1}$	0.199 3 ± 3.56 ×$10^{-2}$	0.795 7 ± 2.47 ×$10^{-1}$
	10, 10	1.089 1 ± 2.99 ×$10^{-1}$	0.295 3 ± 1.40 ×$10^{-1}$	0.656 7 ± 8.32 ×$10^{-2}$	0.196 5 ± 2.64 ×$10^{-2}$	0.497 2 ± 1.71 ×$10^{-2}$
DF10	5, 10	0.870 8 ± 1.70 ×$10^{-1}$	0.434 5 ± 8.85 ×$10^{-2}$	0.308 6 ± 1.91 ×$10^{-2}$	0.266 1 ± 7.70 ×$10^{-2}$	0.246 2 ± 2.48 ×$10^{-2}$
	10, 5	1.281 6 ± 3.47 ×$10^{-1}$	0.393 3 ± 7.34 ×$10^{-2}$	0.283 6 ± 2.15 ×$10^{-2}$	0.328 3 ± 2.28 ×$10^{-2}$	0.239 0 ± 1.84 ×$10^{-2}$
	10, 10	1.234 8 ± 3.28 ×$10^{-1}$	0.350 4 ± 6.57 ×$10^{-2}$	0.294 6 ± 1.33 ×$10^{-2}$	0.323 0 ± 2.76 ×$10^{-2}$	0.302 8 ± 2.62 ×$10^{-2}$
DF11	5, 10	0.771 7 ± 1.56 ×$10^{-1}$	0.386 8 ± 5.11 ×$10^{-3}$	0.163 6 ± 5.54 ×$10^{-3}$	0.149 2 ± 3.68 ×$10^{-3}$	0.111 7 ± 1.89 ×$10^{-3}$
	10, 5	0.873 0 ± 1.55 ×$10^{-1}$	0.484 7 ± 8.07 ×$10^{-3}$	0.163 4 ± 8.18 ×$10^{-3}$	0.367 7 ± 2.78 ×$10^{-3}$	0.111 4 ± 2.36 ×$10^{-3}$
	10, 10	0.903 9 ± 9.84 ×$10^{-2}$	0.477 6 ± 1.52 ×$10^{-2}$	0.164 3 ± 8.74 ×$10^{-3}$	0.366 6 ± 2.20 ×$10^{-3}$	0.111 3 ± 1.36 ×$10^{-3}$
DF12	5, 10	0.820 8 ± 6.17 ×$10^{-2}$	0.307 6 ± 1.14 ×$10^{-2}$	0.609 3 ± 5.28 ×$10^{-2}$	0.510 8 ± 1.78 ×$10^{-1}$	4.967 4 ± 4.42 ×$10^{0}$
	10, 5	0.865 6 ± 7.23 ×$10^{-2}$	0.305 1 ± 3.42 ×$10^{-3}$	0.632 1 ± 5.39 ×$10^{-2}$	0.464 3 ± 1.81 ×$10^{-1}$	2.445 5 ± 2.05 ×$10^{0}$
	10, 10	0.903 6 ± 7.61 ×$10^{-2}$	0.307 4 ± 3.26 ×$10^{-3}$	0.635 8 ± 7.12 ×$10^{-2}$	0.623 6 ± 1.69 ×$10^{-1}$	4.977 7 ± 4.31 ×$10^{0}$
DF13	5, 10	0.505 7 ± 1.04 ×$10^{-1}$	0.255 4 ± 1.82 ×$10^{-2}$	0.406 7 ± 4.16 ×$10^{-2}$	0.240 9 ± 7.86 ×$10^{-3}$	0.270 9 ± 7.57 ×$10^{-3}$
	10, 5	1.674 7 ± 4.90 ×$10^{-1}$	0.305 2 ± 1.93 ×$10^{-2}$	0.378 9 ± 3.80 ×$10^{-2}$	0.255 6 ± 1.20 ×$10^{-2}$	0.280 0 ± 5.47 ×$10^{-3}$
	10, 10	1.645 0 ± 6.22 ×$10^{-1}$	0.303 1 ± 9.74 ×$10^{-3}$	0.374 1 ± 3.30 ×$10^{-2}$	0.252 7 ± 1.26 ×$10^{-2}$	0.280 4 ± 3.85 ×$10^{-3}$
DF14	5, 10	0.412 6 ± 1.07 ×$10^{-1}$	0.124 6 ± 2.11 ×$10^{-2}$	0.131 0 ± 1.44 ×$10^{-2}$	0.097 2 ± 4.35 ×$10^{-3}$	0.116 9 ± 1.25 ×$10^{-2}$
	10, 5	3.002 8 ± 8.52 ×$10^{-1}$	0.157 0 ± 2.06 ×$10^{-2}$	0.125 3 ± 1.16 ×$10^{-2}$	0.121 6 ± 3.71 ×$10^{-3}$	0.079 9 ± 2.87 ×$10^{-3}$
	10, 10	3.082 5 ± 1.14 ×$10^{0}$	0.161 4 ± 2.42 ×$10^{-2}$	0.121 0 ± 1.32 ×$10^{-2}$	0.123 1 ± 3.97 ×$10^{-3}$	0.081 2 ± 3.78 ×$10^{-3}$

下载: 导出CSV

表 3 FT-DMOEA与四种对比算法在DF测试函数集上获得的MHV指标的平均值和标准差值的统计结果

Table 3 Statistical results of mean and standard deviation values of MHV metric obtained by FT-DMOEA and four comparative algorithms on the DF benchmark suite

测试问题	$n_{t}$, $\tau_{t}$	DNSGAII-B	CR-DNSGAII	KT-DMOEA	HRS-DMOA	FT-DMOEA
DF1	5, 10	0.183 8 ± 5.31 ×$10^{-2}$	0.450 0 ± 1.54 ×$10^{-2}$	0.381 1 ± 1.63 ×$10^{-2}$	0.458 7 ± 3.15 ×$10^{-2}$	0.507 2 ± 5.70 ×$10^{-3}$
	10, 5	0.008 9 ± 3.60 ×$10^{-2}$	0.424 1 ± 6.92 ×$10^{-2}$	0.390 9 ± 1.69 ×$10^{-2}$	0.463 3 ± 3.03 ×$10^{-2}$	0.521 4 ± 3.11 ×$10^{-3}$
	10, 10	0.010 8 ± 3.39 ×$10^{-2}$	0.423 6 ± 3.82 ×$10^{-2}$	0.394 0 ± 1.57 ×$10^{-2}$	0.469 7 ± 4.19 ×$10^{-2}$	0.521 4 ± 4.19 ×$10^{-3}$
DF2	5, 10	0.231 7 ± 7.41 ×$10^{-2}$	0.687 2 ± 8.42 ×$10^{-3}$	0.586 2 ± 1.04 ×$10^{-2}$	0.699 0 ± 2.31 ×$10^{-2}$	0.631 3 ± 1.43 ×$10^{-2}$
	10, 5	0.051 6 ± 1.14 ×$10^{-1}$	0.674 3 ± 2.50 ×$10^{-2}$	0.589 5 ± 9.76 ×$10^{-3}$	0.659 5 ± 2.02 ×$10^{-2}$	0.657 2 ± 5.78 ×$10^{-3}$
	10, 10	0.046 5 ± 8.94 ×$10^{-2}$	0.666 1 ± 1.66 ×$10^{-2}$	0.597 6 ± 1.28 ×$10^{-2}$	0.681 8 ± 1.76 ×$10^{-2}$	0.660 5 ± 6.43 ×$10^{-3}$
DF3	5, 10	0.030 5 ± 4.37 ×$10^{-2}$	0.087 8 ± 7.50 ×$10^{-2}$	0.149 5 ± 1.06 ×$10^{-2}$	0.119 6 ± 8.54 ×$10^{-2}$	0.444 5 ± 1.12 ×$10^{-2}$
	10, 5	0.008 7 ± 3.91 ×$10^{-2}$	0.162 8 ± 5.45 ×$10^{-2}$	0.165 5 ± 1.40 ×$10^{-2}$	0.106 9 ± 6.22 ×$10^{-2}$	0.456 2 ± 8.62 ×$10^{-3}$
	10, 10	0.005 0 ± 2.33 ×$10^{-3}$	0.160 9 ± 7.74 ×$10^{-2}$	0.163 4 ± 7.47 ×$10^{-3}$	0.130 4 ± 5.94 ×$10^{-2}$	0.455 4 ± 9.13 ×$10^{-3}$
DF4	5, 10	0.162 5 ± 3.79 ×$10^{-2}$	0.601 3 ± 5.63 ×$10^{-2}$	0.496 0 ± 3.08 ×$10^{-2}$	0.521 8 ± 3.35 ×$10^{-2}$	0.697 1 ± 4.72 ×$10^{-3}$
	10, 5	0.148 9 ± 6.04 ×$10^{-2}$	0.518 5 ± 5.31 ×$10^{-2}$	0.484 0 ± 3.13 ×$10^{-2}$	0.519 3 ± 2.72 ×$10^{-2}$	0.698 1 ± 3.55 ×$10^{-3}$
	10, 10	0.181 3 ± 5.76 ×$10^{-2}$	0.570 9 ± 5.39 ×$10^{-2}$	0.470 5 ± 3.54 ×$10^{-2}$	0.521 6 ± 2.87 ×$10^{-2}$	0.697 4 ± 3.46 ×$10^{-3}$
DF5	5, 10	0.253 8 ± 4.22 ×$10^{-2}$	0.497 1 ± 5.73 ×$10^{-2}$	0.233 5 ± 2.46 ×$10^{-2}$	0.529 3 ± 1.22 ×$10^{-2}$	0.559 7 ± 3.16 ×$10^{-3}$
	10, 5	0.028 2 ± 6.65 ×$10^{-2}$	0.499 9 ± 3.00 ×$10^{-2}$	0.271 9 ± 2.37 ×$10^{-2}$	0.530 6 ± 1.69 ×$10^{-2}$	0.562 9 ± 3.25 ×$10^{-3}$
	10, 10	0.016 6 ± 4.68 ×$10^{-2}$	0.493 2 ± 5.37 ×$10^{-2}$	0.277 7 ± 2.35 ×$10^{-2}$	0.528 4 ± 1.08 ×$10^{-2}$	0.562 5 ± 3.68 ×$10^{-3}$
DF6	5, 10	0.001 2 ± 3.19 ×$10^{-3}$	0.247 1 ± 4.22 ×$10^{-2}$	0.027 1 ± 1.19 ×$10^{-2}$	0.026 8 ± 1.13 ×$10^{-2}$	0.393 7 ± 7.44 ×$10^{-2}$
	10, 5	0.063 5 ± 9.28 ×$10^{-2}$	0.174 5 ± 4.44 ×$10^{-2}$	0.029 9 ± 1.34 ×$10^{-2}$	0.026 0 ± 9.25 ×$10^{-3}$	0.381 0 ± 8.23 ×$10^{-2}$
	10, 10	0.078 5 ± 6.97 ×$10^{-2}$	0.241 2 ± 2.41 ×$10^{-2}$	0.028 9 ± 1.22 ×$10^{-2}$	0.027 5 ± 1.22 ×$10^{-2}$	0.414 9 ± 8.27 ×$10^{-2}$
DF7	5, 10	0.128 5 ± 3.17 ×$10^{-2}$	0.012 4 ± 1.25 ×$10^{-2}$	0.233 4 ± 2.03 ×$10^{-2}$	0.126 9 ± 1.62 ×$10^{-2}$	0.420 2 ± 1.60 ×$10^{-1}$
	10, 5	0.140 0 ± 3.17 ×$10^{-2}$	0.031 5 ± 2.15 ×$10^{-2}$	0.269 2 ± 3.50 ×$10^{-2}$	0.134 7 ± 3.30 ×$10^{-2}$	0.422 4 ± 2.31 ×$10^{-2}$
	10, 10	0.139 8 ± 2.99 ×$10^{-2}$	0.037 9 ± 1.78 ×$10^{-2}$	0.247 1 ± 2.12 ×$10^{-2}$	0.138 2 ± 2.96 ×$10^{-2}$	0.534 8 ± 1.14 ×$10^{-1}$
DF8	5, 10	0.690 9 ± 3.88 ×$10^{-2}$	0.934 0 ± 1.51 ×$10^{-2}$	0.911 5 ± 6.78 ×$10^{-3}$	0.953 2 ± 1.28 ×$10^{-2}$	0.592 1 ± 2.18 ×$10^{-3}$
	10, 5	0.648 4 ± 5.18 ×$10^{-2}$	0.943 9 ± 1.84 ×$10^{-2}$	0.913 3 ± 5.97 ×$10^{-3}$	0.944 2 ± 1.69 ×$10^{-2}$	0.604 6 ± 2.60 ×$10^{-3}$
	10, 10	0.644 5 ± 3.04 ×$10^{-2}$	0.940 2 ± 1.69 ×$10^{-2}$	0.912 3 ± 7.45 ×$10^{-3}$	0.925 5 ± 1.82 ×$10^{-2}$	0.604 7 ± 3.06 ×$10^{-3}$
DF9	5, 10	0.055 5 ± 3.79 ×$10^{-2}$	0.323 2 ± 9.77 ×$10^{-2}$	0.169 8 ± 1.88 ×$10^{-2}$	0.316 1 ± 3.47 ×$10^{-2}$	0.163 9 ± 1.81 ×$10^{-2}$
	10, 5	0.049 5 ± 3.63 ×$10^{-2}$	0.302 0 ± 9.94 ×$10^{-2}$	0.195 8 ± 2.34 ×$10^{-2}$	0.339 1 ± 4.16 ×$10^{-2}$	0.195 4 ± 4.46 ×$10^{-2}$
	10, 10	0.063 4 ± 4.50 ×$10^{-2}$	0.275 3 ± 1.20 ×$10^{-1}$	0.184 2 ± 1.53 ×$10^{-2}$	0.344 3 ± 3.07 ×$10^{-2}$	0.250 1 ± 3.04 ×$10^{-2}$
DF10	5, 10	0.037 1 ± 1.37 ×$10^{-1}$	0.911 5 ± 3.26 ×$10^{-2}$	0.614 2 ± 2.17 ×$10^{-2}$	0.879 1 ± 1.36 ×$10^{-1}$	0.600 0 ± 8.01 ×$10^{-3}$
	10, 5	0.053 0 ± 1.75 ×$10^{-1}$	0.906 6 ± 1.73 ×$10^{-2}$	0.660 5 ± 1.57 ×$10^{-2}$	0.915 0 ± 1.83 ×$10^{-2}$	0.653 3 ± 8.56 ×$10^{-3}$
	10, 10	0.040 7 ± 1.40 ×$10^{-1}$	0.916 1 ± 1.81 ×$10^{-2}$	0.658 1 ± 1.26 ×$10^{-2}$	0.924 7 ± 1.76 ×$10^{-2}$	0.637 3 ± 2.43 ×$10^{-2}$
DF11	5, 10	0.109 3 ± 2.03 ×$10^{-1}$	0.487 5 ± 8.77 ×$10^{-3}$	0.219 3 ± 2.94 ×$10^{-3}$	0.767 0 ± 1.62 ×$10^{-2}$	0.260 1 ± 4.43 ×$10^{-4}$
	10, 5	0.056 1 ± 1.91 ×$10^{-1}$	0.635 0 ± 1.03 ×$10^{-2}$	0.222 4 ± 3.19 ×$10^{-3}$	0.777 5 ± 9.94 ×$10^{-3}$	0.263 9 ± 1.52 ×$10^{-3}$
	10, 10	0.054 8 ± 1.90 ×$10^{-1}$	0.630 7 ± 2.01 ×$10^{-2}$	0.223 1 ± 2.20 ×$10^{-3}$	0.772 8 ± 1.65 ×$10^{-2}$	0.265 5 ± 1.18 ×$10^{-3}$
DF12	5, 10	0.980 0 ± 1.55 ×$10^{-2}$	0.896 0 ± 8.09 ×$10^{-3}$	0.778 4 ± 1.38 ×$10^{-2}$	0.837 5 ± 3.47 ×$10^{-2}$	0.377 3 ± 8.04 ×$10^{-2}$
	10, 5	0.948 6 ± 3.99 ×$10^{-2}$	0.908 9 ± 3.54 ×$10^{-3}$	0.798 8 ± 6.90 ×$10^{-3}$	0.837 1 ± 5.48 ×$10^{-2}$	0.334 8 ± 7.32 ×$10^{-2}$
	10, 10	0.964 9 ± 2.56 ×$10^{-2}$	0.907 5 ± 6.50 ×$10^{-3}$	0.795 7 ± 8.83 ×$10^{-3}$	0.814 1 ± 6.23 ×$10^{-2}$	0.425 1 ± 1.30 ×$10^{-1}$
DF13	5, 10	0.464 3 ± 1.16 ×$10^{-1}$	0.513 5 ± 2.02 ×$10^{-2}$	0.404 4 ± 2.37 ×$10^{-2}$	0.454 9 ± 1.63 ×$10^{-2}$	0.576 2 ± 1.33 ×$10^{-2}$
	10, 5	0.093 3 ± 1.08 ×$10^{-1}$	0.302 0 ± 2.54 ×$10^{-2}$	0.422 3 ± 2.17 ×$10^{-2}$	0.450 6 ± 1.17 ×$10^{-2}$	0.571 7 ± 6.93 ×$10^{-3}$
	10, 10	0.104 5 ± 1.08 ×$10^{-1}$	0.295 3 ± 1.99 ×$10^{-2}$	0.423 2 ± 2.11 ×$10^{-2}$	0.454 4 ± 6.67 ×$10^{-3}$	0.576 6 ± 3.31 ×$10^{-3}$
DF14	5, 10	0.028 1 ± 1.39 ×$10^{-2}$	0.422 6 ± 3.28 ×$10^{-2}$	0.406 3 ± 1.91 ×$10^{-2}$	0.488 4 ± 1.03 ×$10^{-2}$	0.475 5 ± 1.94 ×$10^{-2}$
	10, 5	0.002 7 ± 1.22 ×$10^{-2}$	0.411 6 ± 1.59 ×$10^{-2}$	0.427 6 ± 1.65 ×$10^{-2}$	0.480 1 ± 9.70 ×$10^{-3}$	0.569 1 ± 4.24 ×$10^{-3}$
	10, 10	0.001 8 ± 8.25 ×$10^{-3}$	0.409 6 ± 1.58 ×$10^{-2}$	0.432 6 ± 1.38 ×$10^{-2}$	0.479 1 ± 1.01 ×$10^{-2}$	0.567 6 ± 9.03 ×$10^{-3}$

下载: 导出CSV

表 4 FT-DMOEA与三种预测算法在DF测试函数集上获得的MIGD指标的平均值和标准差值的统计结果

Table 4 Statistical results of mean and standard deviation values of MIGD metric obtained by FT-DMOEA and three prediction algorithms on the DF benchmark suite

测试问题	$\tau_{t}$, $n_{t}$	PPS-MOEA/D	SVR-MOEA/D	KF-MOEA/D	FT-DMOEA
DF1	10, 10	0.100 2 ± 6.67 ×$10^{-2}$	0.092 0 ± 7.72 ×$10^{-2}$	0.159 4 ± 8.61 ×$10^{-2}$	0.016 7 ± 3.11 ×$10^{-3}$
	10, 5	0.157 3 ± 1.43 ×$10^{-1}$	0.099 6 ± 9.21 ×$10^{-2}$	0.185 9 ± 1.35 ×$10^{-1}$	0.024 8 ± 3.94 ×$10^{-3}$
	5, 10	0.182 0 ± 1.38 ×$10^{-1}$	0.141 2 ± 9.07 ×$10^{-2}$	0.201 9 ± 9.91 ×$10^{-2}$	0.031 2 ± 4.02 ×$10^{-3}$
DF2	10, 10	0.075 8 ± 7.61 ×$10^{-2}$	0.084 6 ± 6.28 ×$10^{-2}$	0.105 2 ± 5.76 ×$10^{-2}$	0.037 5 ± 6.50 ×$10^{-3}$
	10, 5	0.119 4 ± 9.53 ×$10^{-2}$	0.083 7 ± 6.97 ×$10^{-2}$	0.122 5 ± 9.97 ×$10^{-2}$	0.047 2 ± 9.43 ×$10^{-3}$
	5, 10	0.122 2 ± 5.90 ×$10^{-2}$	0.133 5 ± 7.36 ×$10^{-2}$	0.146 7 ± 7.13 ×$10^{-2}$	0.087 8 ± 9.36 ×$10^{-3}$
DF3	10, 10	0.423 3 ± 2.61 ×$10^{-1}$	0.393 4 ± 2.19 ×$10^{-1}$	0.366 3 ± 1.64 ×$10^{-1}$	0.040 6 ± 7.75 ×$10^{-3}$
	10, 5	0.419 4 ± 2.37 ×$10^{-1}$	251 917.360 1 ± 1.78 ×$10^{6}$	0.383 2 ± 2.24 ×$10^{-1}$	0.050 1 ± 1.12 ×$10^{-2}$
	5, 10	0.476 6 ± 2.83 ×$10^{-1}$	0.415 3 ± 1.66 ×$10^{-1}$	0.361 5 ± 1.50 ×$10^{-1}$	0.065 2 ± 1.28 ×$10^{-2}$
DF4	10, 10	0.956 7 ± 5.86 ×$10^{-1}$	1.087 1 ± 6.54 ×$10^{-1}$	1.299 5 ± 8.17 ×$10^{-1}$	0.114 4 ± 8.83 ×$10^{-3}$
	10, 5	1.012 5 ± 5.70 ×$10^{-1}$	1.113 3 ± 7.08 ×$10^{-1}$	1.201 9 ± 6.09 ×$10^{-1}$	0.111 0 ± 1.07 ×$10^{-2}$
	5, 10	0.996 2 ± 5.71 ×$10^{-1}$	1.048 8 ± 6.32 ×$10^{-1}$	1.289 2 ± 7.78 ×$10^{-1}$	0.127 7 ± 1.15 ×$10^{-2}$
DF5	10, 10	1.305 9 ± 2.04 ×$10^{0}$	1 615.366 0 ± 5.92 ×$10^{3}$	1.303 2 ± 2.04 ×$10^{0}$	0.015 5 ± 3.10 ×$10^{-3}$
	10, 5	1.358 9 ± 2.01 ×$10^{0}$	1 427.275 3 ± 9.29 ×$10^{3}$	1.350 9 ± 2.23 ×$10^{0}$	0.016 9 ± 2.47 ×$10^{-3}$
	5, 10	1.364 1 ± 2.25 ×$10^{0}$	52.096 5 ± 3.61 ×$10^{2}$	1.363 0 ± 1.96 ×$10^{0}$	0.023 1 ± 2.68 ×$10^{-3}$
DF6	10, 10	4.057 9 ± 4.60 ×$10^{0}$	2.938 5 ± 4.38 ×$10^{0}$	3.148 8 ± 3.41 ×$10^{0}$	0.751 4 ± 3.15 ×$10^{-1}$
	10, 5	2.907 7 ± 3.33 ×$10^{0}$	2.788 8 ± 4.77 ×$10^{0}$	2.989 9 ± 3.28 ×$10^{0}$	0.677 7 ± 2.68 ×$10^{-1}$
	5, 10	5.411 3 ± 6.42 ×$10^{0}$	4.153 2 ± 4.82 ×$10^{0}$	3.765 0 ± 4.81 ×$10^{0}$	0.988 9 ± 1.46 ×$10^{-1}$
DF7	10, 10	4.174 4 ± 5.18 ×$10^{0}$	2.752 9 ± 3.77 ×$10^{0}$	4.005 4 ± 4.94 ×$10^{0}$	105.840 0 ± 1.19 ×$10^{2}$
	10, 5	3.601 3 ± 5.32 ×$10^{0}$	2.627 7 ± 4.30 ×$10^{0}$	3.349 1 ± 4.19 ×$10^{0}$	37.663 0 ± 4.45 ×$10^{1}$
	5, 10	5.488 4 ± 6.69 ×$10^{0}$	3.376 0 ± 4.15 ×$10^{0}$	3.978 8 ± 4.79 ×$10^{0}$	47.097 5 ± 6.81 ×$10^{1}$
DF8	10, 10	1.094 3 ± 5.98 ×$10^{-1}$	0.977 4 ± 5.21 ×$10^{-1}$	1.148 6 ± 5.44 ×$10^{-1}$	0.072 7 ± 4.83 ×$10^{-3}$
	10, 5	1.070 4 ± 4.75 ×$10^{-1}$	0.981 0 ± 5.19 ×$10^{-1}$	1.109 5 ± 5.46 ×$10^{-1}$	0.075 9 ± 5.27 ×$10^{-3}$
	5, 10	1.018 7 ± 5.63 ×$10^{-1}$	0.907 0 ± 4.97 ×$10^{-1}$	1.017 4 ± 4.98 ×$10^{-1}$	0.086 4 ± 8.08 ×$10^{-3}$
DF9	10, 10	1.754 6 ± 1.75 ×$10^{0}$	551.812 2 ± 3.83 ×$10^{3}$	1.684 6 ± 1.62 ×$10^{0}$	0.497 2 ± 1.71 ×$10^{-2}$
	10, 5	1.468 3 ± 1.41 ×$10^{0}$	128.944 1 ± 8.88 ×$10^{2}$	1.430 5 ± 1.38 ×$10^{0}$	0.584 4 ± 6.38 ×$10^{-2}$
	5, 10	1.770 8 ± 1.85 ×$10^{0}$	2.656 3 ± 1.94 ×$10^{0}$	1.681 1 ± 1.49 ×$10^{0}$	0.842 6 ± 1.42 ×$10^{-1}$
DF10	10, 10	0.189 1 ± 8.50 ×$10^{-2}$	64.903 7 ± 2.84 ×$10^{2}$	0.214 4 ± 1.51 ×$10^{-1}$	0.302 8 ± 2.62 ×$10^{-2}$
	10, 5	0.251 5 ± 1.37 ×$10^{-1}$	11.104 9 ± 6.54 ×$10^{1}$	0.236 6 ± 9.22 ×$10^{-2}$	0.246 2 ± 2.48 ×$10^{-2}$
	5, 10	0.243 9 ± 1.42 ×$10^{-1}$	10.869 8 ± 5.26 ×$10^{1}$	0.241 9 ± 8.71 ×$10^{-2}$	0.251 4 ± 3.57 ×$10^{-2}$
DF11	10, 10	0.194 8 ± 7.28 ×$10^{-2}$	237.626 9 ± 4.57 ×$10^{2}$	0.185 1 ± 3.45 ×$10^{-2}$	0.111 3 ± 1.36 ×$10^{-3}$
	10, 5	0.274 3 ± 1.07 ×$10^{-1}$	372.452 2 ± 8.32 ×$10^{2}$	0.262 4 ± 7.94 ×$10^{-2}$	0.111 7 ± 1.89 ×$10^{-3}$
	5, 10	0.214 2 ± 9.17 ×$10^{-2}$	287.159 9 ± 6.83 ×$10^{2}$	0.197 5 ± 4.46 ×$10^{-2}$	0.132 1 ± 2.66 ×$10^{-3}$
DF12	10, 10	1.177 1 ± 1.13 ×$10^{-1}$	252.611 5 ± 6.25 ×$10^{2}$	0.989 0 ± 2.71 ×$10^{-1}$	4.977 7 ± 4.31 ×$10^{0}$
	10, 5	1.189 1 ± 3.31 ×$10^{-2}$	288.469 9 ± 6.96 ×$10^{2}$	0.912 1 ± 3.19 ×$10^{-1}$	4.967 4 ± 4.42 ×$10^{0}$
	5, 10	1.184 7 ± 5.55 ×$10^{-2}$	336.943 1 ± 7.04 ×$10^{2}$	0.959 1 ± 3.05 ×$10^{-1}$	1.117 5 ± 7.59 ×$10^{-1}$
DF13	10, 10	1.395 8 ± 1.70 ×$10^{0}$	1.378 5 ± 1.77 ×$10^{0}$	1.441 3 ± 1.80 ×$10^{0}$	0.280 4 ± 3.85 ×$10^{-3}$
	10, 5	1.412 4 ± 1.83 ×$10^{0}$	1.466 1 ± 1.20 ×$10^{0}$	1.478 2 ± 1.96 ×$10^{0}$	0.270 9 ± 7.57 ×$10^{-3}$
	5, 10	1.423 5 ± 1.84 ×$10^{0}$	1.536 1 ± 1.94 ×$10^{0}$	1.555 2 ± 2.02 ×$10^{0}$	0.299 5 ± 5.82 ×$10^{-3}$
DF14	10, 10	0.865 7 ± 1.31 ×$10^{0}$	4.188 3 ± 5.27 ×$10^{0}$	0.906 5 ± 1.37 ×$10^{0}$	0.081 2 ± 3.78 ×$10^{-3}$
	10, 5	0.873 5 ± 1.30 ×$10^{0}$	4.440 2 ± 5.48 ×$10^{0}$	0.919 4 ± 1.32 ×$10^{0}$	0.116 9 ± 1.25 ×$10^{-2}$
	5, 10	0.886 4 ± 1.35 ×$10^{0}$	3.694 4 ± 4.41 ×$10^{0}$	0.978 4 ± 1.46 ×$10^{0}$	0.091 2 ± 3.26 ×$10^{-3}$

下载: 导出CSV

表 5 FT-DMOEA与其他先进对比算法在双目标函数DF1 ~ DF5上获得的MIGD指标的平均值和标准差值的统计结果

Table 5 Statistical results of mean and standard deviation values of MIGD metric obtained by FT-DMOEA and other advanced algorithms on biobjective functions DF1 ~ DF5

测试问题	$\tau_{t}$, $n_{t}$	IGP-DMOEA	ISVM-DMOEA	STT-DMOEA	FT-DMOEA
DF1	10, 5	0.008 8 ± 6.51 ×$10^{-3}$	0.013 6 ± 1.19 ×$10^{-2}$	0.010 8 ± 9.08 ×$10^{-3}$	0.004 3 ± 1.09 ×$10^{-4}$
DF1	5, 10	0.016 7 ± 8.78 ×$10^{-3}$	0.068 7 ± 1.21 ×$10^{-2}$	0.014 6 ± 1.81 ×$10^{-3}$	0.004 2 ± 8.40 ×$10^{-5}$
DF2	10, 5	0.011 5 ± 1.05 ×$10^{-2}$	0.013 6 ± 1.57 ×$10^{-3}$	0.033 6 ± 1.39 ×$10^{-2}$	0.005 2 ± 1.48 ×$10^{-4}$
DF2	5, 10	0.031 8 ± 1.89 ×$10^{-3}$	0.098 5 ± 1.16 ×$10^{-2}$	0.045 5 ± 1.62 ×$10^{-2}$	0.005 3 ± 1.55 ×$10^{-4}$
DF3	10, 5	0.021 1 ± 4.24 ×$10^{-3}$	0.228 8 ± 1.80 ×$10^{-2}$	0.057 7 ± 1.83 ×$10^{-2}$	0.007 6 ± 3.46 ×$10^{-4}$
DF3	5, 10	0.040 4 ± 6.65 ×$10^{-3}$	0.227 6 ± 4.14 ×$10^{-2}$	0.096 4 ± 8.01 ×$10^{-2}$	0.006 9 ± 1.61 ×$10^{-4}$
DF4	10, 5	0.106 7 ± 4.68 ×$10^{-4}$	0.116 2 ± 2.22 ×$10^{-3}$	0.103 0 ± 1.16 ×$10^{-3}$	0.082 2 ± 1.50 ×$10^{-3}$
DF4	5, 10	0.112 3 ± 5.22 ×$10^{-3}$	0.341 8 ± 3.86 ×$10^{-2}$	0.105 4 ± 5.62 ×$10^{-3}$	0.083 2 ± 2.66 ×$10^{-3}$
DF5	10, 5	0.004 4 ± 2.65 ×$10^{-4}$	0.005 8 ± 5.69 ×$10^{-4}$	0.004 1 ± 1.11 ×$10^{-4}$	0.004 5 ± 4.98 ×$10^{-5}$
DF5	5, 10	0.007 9 ± 1.89 ×$10^{-3}$	0.085 7 ± 4.17 ×$10^{-2}$	0.006 4 ± 1.56 ×$10^{-3}$	0.004 5 ± 9.01 ×$10^{-5}$

下载: 导出CSV

表 6 FT-DMOEA与其他先进对比算法在三目标函数DF11 ~ DF14上获得的MIGD指标的平均值和标准差值的统计结果

Table 6 Statistical results of mean and standard deviation values of MIGD metric obtained by FT-DMOEA and other advanced algorithms on triobjective functions DF11 ~ DF14

测试问题	$n_{t}$, $\tau_{t}$	MMTL-DMOEA	IT-DMOEA	MSTL-DMOEA	FT-DMOEA
DF11	10, 5	0.152 3 ± 6.36 ×$10^{-3}$	0.143 5 ± 5.72 ×$10^{-3}$	0.155 1 ± 1.05 ×$10^{-2}$	0.142 8 ± 2.17 ×$10^{-3}$
DF11	10, 10	0.115 1 ± 3.60 ×$10^{-3}$	0.115 2 ± 3.60 ×$10^{-3}$	0.116 8 ± 3.42 ×$10^{-3}$	0.112 1 ± 1.57 ×$10^{-3}$
DF12	10, 5	0.318 7 ± 4.21 ×$10^{-2}$	0.209 0 ± 1.06 ×$10^{-2}$	0.198 5 ± 1.97 ×$10^{-2}$	1.182 2 ± 1.44 ×$10^{0}$
DF12	10, 10	0.255 6 ± 2.37 ×$10^{-2}$	0.158 9 ± 1.29 ×$10^{-2}$	0.138 4 ± 8.06 ×$10^{-3}$	0.320 4 ± 1.21 ×$10^{-1}$
DF13	10, 5	0.269 7 ± 1.39 ×$10^{-2}$	0.249 1 ± 5.09 ×$10^{-3}$	0.268 0 ± 1.32 ×$10^{-2}$	0.298 0 ± 2.29 ×$10^{-2}$
DF13	10, 10	0.264 4 ± 1.34 ×$10^{-2}$	0.253 2 ± 7.29 ×$10^{-3}$	0.260 4 ± 1.51 ×$10^{-2}$	0.252 9 ± 1.24 ×$10^{-2}$
DF14	10, 5	0.104 2 ± 3.53 ×$10^{-3}$	0.090 7 ± 2.42 ×$10^{-3}$	0.111 7 ± 1.02 ×$10^{-2}$	0.088 4 ± 4.62 ×$10^{-3}$
DF14	10, 10	0.081 7 ± 2.81 ×$10^{-3}$	0.078 5 ± 1.40 ×$10^{-3}$	0.084 6 ± 5.06 ×$10^{-3}$	0.077 1 ± 2.50 ×$10^{-3}$

下载: 导出CSV

表 7 FT-DMOEA与KTS-DMOEA在DF问题上获得的MIGD指标的平均值和标准差值的统计结果

Table 7 Statistical results of mean and standard deviation values of MIGD metric obtained by FT-DMOEA and KTS-DMOEA on the DF problems

测试问题	$\tau_{t} $, $n_{t} $	KTS-DMOEA	FT-DMOEA
DF3	10, 5	0.262 4 ± 2.87 ×$10^{-2}$	0.070 8 ± 1.56 ×$10^{-2}$
	10, 10	0.250 4 ± 3.39 ×$10^{-2}$	0.044 0 ± 1.42 ×$10^{-2}$
	10, 20	0.269 2 ± 2.88 ×$10^{-2}$	0.040 3 ± 1.22 ×$10^{-2}$
DF4	10, 5	0.111 0 ± 3.55 ×$10^{-3}$	0.100 3 ± 1.54 ×$10^{-2}$
	10, 10	0.101 5 ± 2.55 ×$10^{-3}$	0.110 7 ± 1.01 ×$10^{-2}$
	10, 20	0.090 4 ± 2.81 ×$10^{-3}$	0.113 3 ± 1.49 ×$10^{-2}$
DF5	10, 5	0.0453 ± 2.86 ×$10^{-3}$	0.020 0 ± 4.51 ×$10^{-3}$
	10, 10	0.025 3 ± 1.20 ×$10^{-3}$	0.015 1 ± 4.01 ×$10^{-3}$
	10, 20	0.017 0 ± 4.34 ×$10^{-4}$	0.014 0 ± 4.04 ×$10^{-3}$
DF10	10, 5	0.105 5 ± 6.54 ×$10^{-3}$	0.284 6 ± 1.08 ×$10^{-2}$
	10, 10	0.110 0 ± 6.72 ×$10^{-3}$	0.282 9 ± 3.48 ×$10^{-2}$
	10, 20	0.091 1 ± 4.17 ×$10^{-3}$	0.284 2 ± 2.72 ×$10^{-2}$
DF11	10, 5	0.216 6 ± 8.03 ×$10^{-4}$	0.113 7 ± 1.72 ×$10^{-3}$
	10, 10	0.214 6 ± 5.19 ×$10^{-4}$	0.112 8 ± 1.54 ×$10^{-3}$
	10, 20	0.214 3 ± 2.82 ×$10^{-4}$	0.113 5 ± 2.99 ×$10^{-3}$

下载: 导出CSV

表 8 DMOA、SGEA和FTMOA在FDA测试函数集上获得的MIGD的各项统计结果

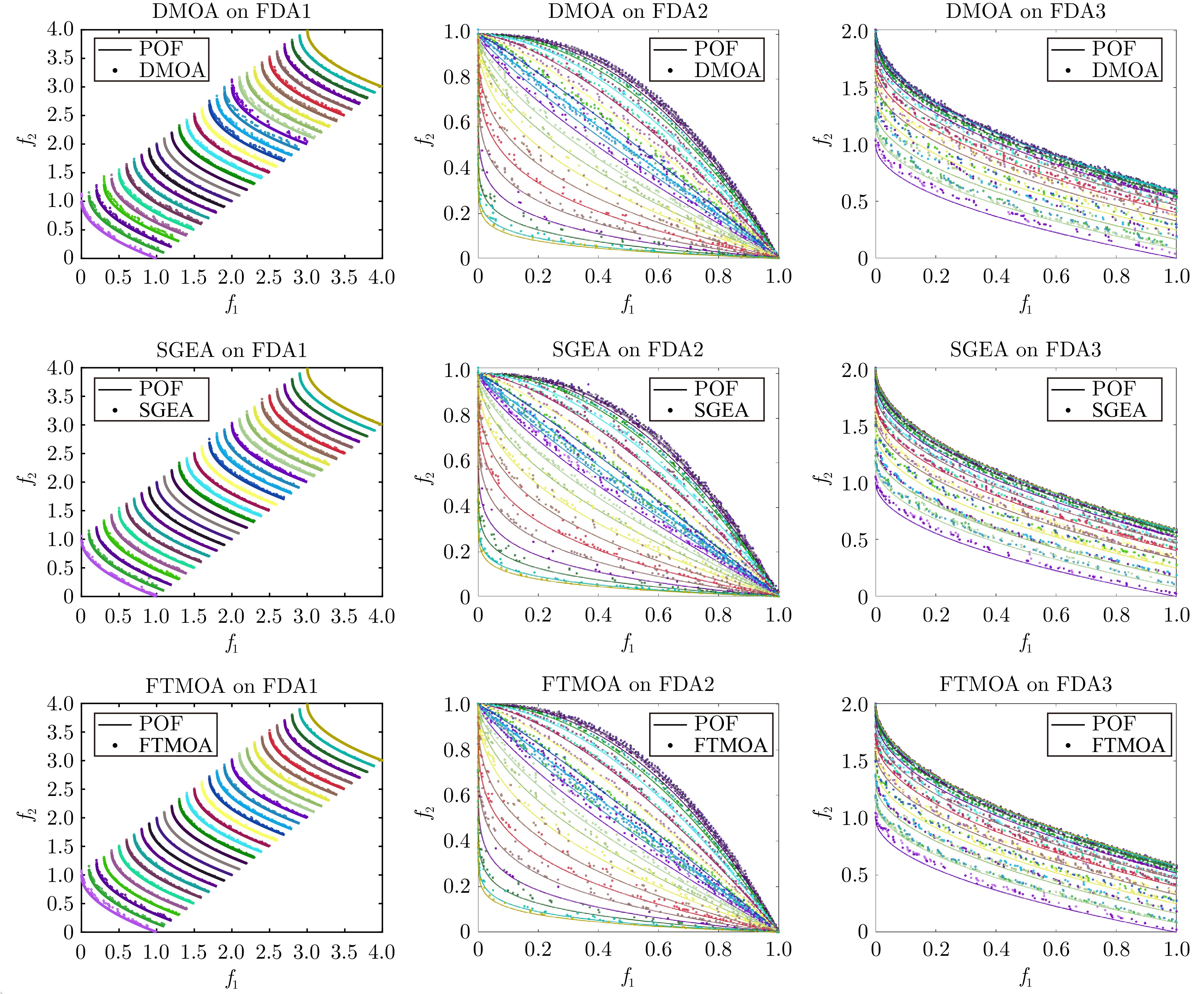
Table 8 Statistical results of MIGD obtained by DMOA, SGEA, and FTMOA on the FDA benchmark suite

		$1 \leq T \leq 30$					$31 \leq T \leq 100$
测试问题	算法	平均值	中位数	上四分位数	下四分位数	t检验	平均值	中位数	上四分位数	下四分位数	t检验
FDA1	DMOA	0.024 6	0.023 8	0.016 6	0.031 8	＋	0.023 4	0.024 8	0.014 3	0.031 8	＋
	SGEA	0.015 4	0.016 9	0.010 7	0.018 8	$-$	0.014 7	0.016 8	0.010 4	0.018 3	$-$
	FTMOA	0.017 2	0.017 2	0.010 7	0.021 1		0.015 3	0.016 9	0.009 7	0.020 0
FDA2	DMOA	0.017 4	0.012 4	0.009 6	0.021 5	＋	0.014 0	0.012 1	0.008 9	0.013 5	＋
	SGEA	0.016 4	0.011 7	0.008 5	0.019 2	＋	0.013 7	0.011 3	0.008 8	0.013 2	＋
	FTMOA	0.016 2	0.013 5	0.010 8	0.017 1		0.011 5	0.009 3	0.007 7	0.011 2
FDA3	DMOA	0.050 5	0.032 9	0.022 3	0.044 0	$-$	0.078 4	0.039 2	0.024 1	0.126 7	$-$
	SGEA	0.045 9	0.0218	0.016 7	0.030 3	$-$	0.059 8	0.022 6	0.018 3	0.041 9	$-$
	FTMOA	0.067 2	0.020 5	0.017 5	0.046 2		0.093 2	0.024 5	0.016 7	0.109 4
FDA4	DMOA	0.157 5	0.147 1	0.095 7	0.194 6	＋	0.138 5	0.130 9	0.083 8	0.179 4	＋
	SGEA	0.117 6	0.117 3	0.077 1	0.153 1	＋	0.117 3	0.121 8	0.072 6	0.155 2	＋
	FTMOA	0.109 7	0.102 2	0.079 3	0.135 6		0.105 8	0.108 6	0.072 3	0.130 4
FDA5	DMOA	0.203 8	0.214 8	0.167 9	0.243 3	＋	0.205 5	0.204 4	0.143 5	0.260 2	＋
	SGEA	0.191 7	0.197 3	0.152 4	0.220 0	＋	0.177 0	0.176 2	0.146 0	0.208 0	＋
	FTMOA	0.149 9	0.146 4	0.133 0	0.162 5		0.150 8	0.150 8	0.131 4	0.165 7

下载: 导出CSV

表 9 使用不同参数的FT-DMOEA在DF问题上获得的平均MIGD值

Table 9 Mean MIGD values obtained by FT-DMOEA with different parameters on DF problems

$\eta_c,\; p_c$	DF1	DF2	DF3	DF10	DF11
10, 0.7	0.052 8	0.113 6	0.172 0	0.250 1	0.167 3
10, 0.8	0.041 3	0.087 1	0.081 2	0.254 2	0.140 0
10, 0.9	0.035 9	0.084 8	0.082 5	0.244 2	0.134 6
20, 0.7	0.048 3	0.101 6	0.136 8	0.270 2	0.142 5
20, 0.8	0.044 1	0.080 3	0.120 6	0.230 9	0.142 2
20, 0.9	0.038 0	0.089 7	0.089 0	0.235 7	0.140 8
$\eta_m,\;p_m$	DF1	DF2	DF3	DF10	DF11
10, 0.1	0.034 6	0.064 2	0.099 6	0.236 4	0.129 8
10, 0.05	0.052 6	0.096 6	0.122 4	0.272 9	0.143 0
20, 0.1	0.044 1	0.090 3	0.090 6	0.230 9	0.122 2
20, 0.05	0.064 6	0.127 9	0.113 7	0.246 6	0.163 9

下载: 导出CSV

参考文献(55)

[1]	Li J, Sun T, Lin Q Z, Jiang M, Tan K C. Reducing negative transfer learning via clustering for dynamic multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2022, 26(5): 1102−1116 doi: 10.1109/TEVC.2022.3144180
[2]	Jiang M, Wang Z Z, Guo S H, Gao X, Tan K C. Individual-based transfer learning for dynamic multiobjective optimization. IEEE Transactions on Cybernetics, 2021, 51(10): 4968−4981 doi: 10.1109/TCYB.2020.3017049
[3]	Deb K, Udaya B R N, Karthik S. Dynamic multi-objective optimization and decision-making using modified NSGA-II: A case study on hydro-thermal power scheduling. In: Proceedings of the 4th International Conference on Evolutionary Multi-criterion Optimization. Berlin, Germany: Springer-Verlag, 2007. 803−817
[4]	Jiang S L, Liu Q, Bogle I D L, Zheng Z. A self-learning based dynamic multi-objective evolutionary algorithm for resilient scheduling problems in steelmaking plants. IEEE Transactions on Automation Science and Engineering, 2023, 20(2): 832−845 doi: 10.1109/TASE.2022.3168385
[5]	Ren Z Q, Rathinam S, Likhachev M, Choset H. Multi-objective safe-interval path planning with dynamic obstacles. IEEE Robotics and Automation Letters, 2022, 7(3): 8154−8161 doi: 10.1109/LRA.2022.3187270
[6]	Zhang L Y, Bienkowski A, Macesker M, Pattipati K R, Sidoti D, Hansen J A. Many-objective maritime path planning for dynamic and uncertain environments. In: Proceedings of the IEEE Aerospace Conference. Big Sky, USA: IEEE, 2021. 1−10
[7]	李文桦, 明梦君, 张涛, 王锐, 黄生俊, 王凌. 考虑全局和局部帕累托前沿的多模态多目标优化算法. 自动化学报, 2023, 49(1): 148−160 Li Wen-Hua, Ming Meng-Jun, Zhang Tao, Wang Rui, Huang Sheng-Jun, Wang Ling. Multimodal multi-objective evolutionary algorithm considering global and local pareto fronts. Acta Automatica Sinica, 2023, 49(1): 148−160
[8]	余伟伟, 谢承旺, 闭应洲, 夏学文, 李雄, 任柯燕, 等. 一种基于自适应模糊支配的高维多目标粒子群算法. 自动化学报, 2018, 44(12): 2278−2289 Yu Wei-Wei, Xie Cheng-Wang, Bi Ying-Zhou, Xia Xue-Wen, Li Xiong, Ren Ke-Yan, et al. Many-objective particle swarm optimization based on adaptive fuzzy dominance. Acta Automatica Sinica, 2018, 44(12): 2278−2289
[9]	孙超利, 李贞, 金耀初. 模型辅助的计算费时进化高维多目标优化. 自动化学报, 2022, 48(4): 1119−1128 Sun Chao-Li, Li Zhen, Jin Yao-Chu. Surrogate-assisted expensive evolutionary many-objective optimization. Acta Automatica Sinica, 2022, 48(4): 1119−1128
[10]	陈美蓉, 郭一楠, 巩敦卫, 杨振. 一类新型动态多目标鲁棒进化优化方法. 自动化学报, 2017, 43(11): 2014−2032 Chen Mei-Rong, Guo Yi-Nan, Gong Dun-Wei, Yang Zhen. A novel dynamic multi-objective robust evolutionary optimization method. Acta Automatica Sinica, 2017, 43(11): 2014−2032
[11]	Jiang S Y, Yang S X. A steady-state and generational evolutionary algorithm for dynamic multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2017, 21(1): 65−82 doi: 10.1109/TEVC.2016.2574621
[12]	丁进良, 杨翠娥, 陈立鹏, 柴天佑. 基于参考点预测的动态多目标优化算法. 自动化学报, 2017, 43(2): 313−320 Ding Jin-Liang, Yang Cui-E, Chen Li-Peng, Chai Tian-You. Dynamic multi-objective optimization algorithm based on reference point prediction. Acta Automatica Sinica, 2017, 43(2): 313−320
[13]	范勤勤, 李盟, 黄文焘, 姜庆超. 时空视角下的动态多目标进化算法研究综述. 控制与决策, 2024, 39(1):1−16 Fan Qin-Qin, Li Meng, Huang Wen-Tao, Jiang Qing-Chao. A research survey of dynamic multi-objective evolutionary algorithms from spatiotemporal perspective. Control and Decision, 2024, 39(1):1−16
[14]	郭一楠, 汤万宝, 陈国玉, 巩敦卫. 动态多目标进化优化研究进展. 信息与控制, 2021, 50(2): 162−173 Guo Yi-Nan, Tang Wan-Bao, Chen Guo-Yu, Gong Dun-Wei. Research progress on dynamic multi-objective evolutionary optimization. Information and Control, 2021, 50(2): 162−173
[15]	Hatzakis I, Wallace D. Dynamic multi-objective optimization with evolutionary algorithms: A forward-looking approach. In: Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation. New York, USA: Association for Computing Machinery, 2006. 1201−1208
[16]	Koo W T, Goh C K, Tan K C. A predictive gradient strategy for multiobjective evolutionary algorithms in a fast changing environment. Memetic Computing, 2010, 2: 87−110 doi: 10.1007/s12293-009-0026-7
[17]	Zhou A M, Jin Y C, Zhang Q F. A population prediction strategy for evolutionary dynamic multiobjective optimization. IEEE Transactions on Cybernetics, 2014, 44(1): 40−53 doi: 10.1109/TCYB.2013.2245892
[18]	Zou J, Li Q Y, Yang S X, Bai H, Zheng J H. A prediction strategy based on center points and knee points for evolutionary dynamic multi-objective optimization. Applied Soft Computing, 2017, 61: 806−818 doi: 10.1016/j.asoc.2017.08.004
[19]	Wang F, Li Y X, Liao F S, Yan H Y. An ensemble learning based prediction strategy for dynamic multi-objective optimization. Applied Soft Computing, 2020, 96: Article No. 106592
[20]	Rambabu R, Vadakkepat P, Tan K C, Jiang M. A mixture-of--experts prediction framework for evolutionary dynamic multiobjective optimization. IEEE Transactions on Cybernetics, 2020, 50(12): 5099−5112 doi: 10.1109/TCYB.2019.2909806
[21]	Xu P, Wu X M, Guo M, Wang S, Li Q Y, Huang W P, et al. A hybrid predictive strategy carried through simultaneously from decision space and objective space for evolutionary dynamic multiobjective optimization. Wireless Communications and Mobile Computing, 2019, 2019(1): 1−17
[22]	Guo Y N, Huang M Y, Chen G Y, Gong D W, Liang J, Yu Z K. A dynamic constrained multiobjective evolutionary algorithm based on decision variable classification. Swarm and Evolutionary Computation, 2023, 83: Article No. 101420 doi: 10.1016/j.swevo.2023.101420
[23]	Cao L L, Xu L H, Goodman E D, Bao C T, Zhu S W. Evolutionary dynamic multiobjective optimization assisted by a support vector regression predictor. IEEE Transactions on Evolutionary Computation, 2020, 24(2): 305−319 doi: 10.1109/TEVC.2019.2925722
[24]	Zou F, Yen G G, Tang L X, Wang C F. A reinforcement learning approach for dynamic multi-objective optimization. Information Sciences, 2021, 546: 815−834 doi: 10.1016/j.ins.2020.08.101
[25]	Liu X F, Xu X X, Zhan Z H, Fang Y C, Zhang J. Interaction-based prediction for dynamic multiobjective optimization. IEEE Transactions on Evolutionary Computation, DOI: 10.1109/TEVC.2023.3234113
[26]	Lu K S, Ortega A. Fast graph fourier transforms based on graph symmetry and bipartition. IEEE Transactions on Signal Processing, 2019, 67(18): 4855−4869 doi: 10.1109/TSP.2019.2932882
[27]	Chaudhary S, Taran S, Bajaj V, Sengur A. Convolutional neural network based approach towards motor imagery tasks eeg signals classification. IEEE Sensors Journal, 2019, 19(12): 4494−4500 doi: 10.1109/JSEN.2019.2899645
[28]	Wen C K, Shih W T, Jin T. Deep learning for massive mimo csi feedback. IEEE Wireless Communications Letters, 2018, 7(5): 748−751 doi: 10.1109/LWC.2018.2818160
[29]	Bolinder E F. The relationship of physical applications of fourier transforms in various fields of wave theory and circuitry. IRE Transactions on Microwave Theory and Techniques, 1957, 5(2): 153−158 doi: 10.1109/TMTT.1957.1125115
[30]	Al-Ani M, Belmont M, Christmas J, Tarczynski A, Ahmad B I. On random sampling and fourier transform estimation in sea waves prediction. In: Proceedings of the 6th International Conference on Event-Based Control, Communication, and Signal Processing. Krakow, Poland: 2020. 1−4
[31]	Raets C, Aisati C E, Rifi A L, Barbé K, Ridder M D. Predicting the response to chemoradiotherapy in rectal cancer patients using bayesian evolutionary random forest and three-dimensional discrete fourier transform. In: Proceedings of the 2023 IEEE International Symposium on Medical Measurements and Applications. Jeju, Korea: 2023. 1−5
[32]	Nakatani T, Yoshioka T, Kinoshita K, Miyoshi M, Juang B H. Blind speech dereverberation with multi-channel linear prediction based on short time fourier transform representation. In: Proceedings of 2008 IEEE International Conference on Acoustics, Speech and Signal Processing. Las Vegas, USA: 2008. 85−88
[33]	Farina M, Deb K, Amato P. Dynamic multiobjective optimization problems: Test cases, approximations, and applications. IEEE Transactions on Evolutionary Computation, 2004, 8(5): 425−442 doi: 10.1109/TEVC.2004.831456
[34]	杨庆, 任超. 大坝变形的去噪傅里叶模型预测. 测绘科学, 2019, 44(2): 158−163 Yang Qing, Ren Chao. Prediction of dam deformation based on de-noising Fourier model. Science of Surveying and Mapping, 2019, 44(2): 158−163
[35]	王志刚. 自回归模型的定阶方法选择及弱信号探测 [硕士学位论文], 武汉理工大学, 中国, 2020. Wang Zhi-Gang. Selection of Order Determination Method and Weak Signal Detection of Autoregressive Model [Master thesis], Wuhan University of Technology, China, 2020.
[36]	Chen J, Shao H, Liu C. An improved deadbeat control strategy based on repetitive prediction against grid frequency fluctuation for active power filter. IEEE Access, 2021, 9: 24646−24657 doi: 10.1109/ACCESS.2021.3057386
[37]	Li Y, Chen W C, Yang L. Multistage linear gauss pseudospectral method for piecewise continuous nonlinear optimal control problems. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(4): 2298−2310 doi: 10.1109/TAES.2021.3054074
[38]	Qiang G, You W. Ship trajectory prediction based on ST-LSTM. In: Proceedings of 14th International Conference on Signal Processing Systems. Jiangsu, China: 2022. 730−735
[39]	Yan Y Z, Tian Z J, Hou S W, Cai Z Q. Prediction of gear bending fatigue life based on grey gm (1, 1) prediction. In: Proceedings of IEEE International Conference on Industrial Engineering and Engineering Management. Kuala Lumpur, Malaysia: 2022. 492−496
[40]	Zhang Q, Li H. Moea/d: A multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712−731 doi: 10.1109/TEVC.2007.892759
[41]	Jiang S Y, Yang S X, Yao X, Tan K C, Kaiser M, Krasnogor N. Benchmark problems for cec2018 competition on dynamic multiobjective optimisation. In: Proceedings of CEC Competition. 2018. 1−18
[42]	Van Veldhuizen D A, Lamont G B. On measuring multiobjective evolutionary algorithm performance. In: Proceedings of the 2000 Congress on Evolutionary Computation. La Jolla, USA: 2000. 204−211
[43]	Schutze O, Esquivel X, Lara A, Coello C A C. Using the averaged hausdorff distance as a performance measure in evolutionary multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2012, 16(4): 504−522 doi: 10.1109/TEVC.2011.2161872
[44]	Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182−197 doi: 10.1109/4235.996017
[45]	Sahmoud S, Topcuoglu H R. Exploiting characterization of dynamism for enhancing dynamic multi-objective evolutionary algorithms. Applied Soft Computing, 2019, 85: Article No. 105783
[46]	Li H, Wang Z D, Lan C B, Wu P S, Zeng N Y. A novel dynamic multiobjective optimization algorithm with hierarchical response system. IEEE Transactions on Computational Social Systems, DOI: 10.1109/TCSS.2023.3293331
[47]	Jiang M, Wang Z Z, Hong H K, Yen G G. Knee point-based imbalanced transfer learning for dynamic multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2021, 25(1): 117−129 doi: 10.1109/TEVC.2020.3004027
[48]	Muruganantham A, Tan K C, Vadakkepat P. Evolutionary dynamic multiobjective optimization via kalman filter prediction. IEEE Transactions on Cybernetics, 2016, 46(12): 2862−2873 doi: 10.1109/TCYB.2015.2490738
[49]	Zhang H, Ding J L, Jiang M, Tan K C, Chai T Y. Inverse gaussian process modeling for evolutionary dynamic multiobjective optimization. IEEE Transactions on Cybernetics, 2022, 52(10): 11240−11253 doi: 10.1109/TCYB.2021.3070434
[50]	Xu D, Jiang M, Hu W, Li S Z, Pan R H, Yen G G. An online prediction approach based on incremental support vector machine for dynamic multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2022, 26(4): 690−703 doi: 10.1109/TEVC.2021.3115036
[51]	Wang X P, Zhao Y M, Tang L X, Yao X. Moea/d with spatial-temporal topological tensor prediction for evolutionary dynamic multiobjective optimization. IEEE Transactions on Evolutionary Computation, DOI: 10.1109/TEVC.2024.3367747
[52]	Ye Y L, Lin Q Z, Ma L J, Wong K C, Gong M G, Coello C C A. Multiple source transfer learning for dynamic multiobjective optimization. Information Sciences, 2022, 607: 739−757 doi: 10.1016/j.ins.2022.05.114
[53]	Jiang M, Wang Z Z, Qiu L M, Guo S H, Gao X, Tan K C. A fast dynamic evolutionary multiobjective algorithm via manifold transfer learning. IEEE Transactions on Cybernetics, 2021, 51(7): 3417−3428 doi: 10.1109/TCYB.2020.2989465
[54]	Guo Y N, Chen G Y, Jiang M, Gong D W, Liang J. A knowledge guided transfer strategy for evolutionary dynamic multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2023, 27(6): 1750−1764 doi: 10.1109/TEVC.2022.3222844
[55]	Wilcoxon F, Bulletin S B, Dec N. Individual comparisons by ranking methods. Springer New York, DOI: 10.1007/978-1-4612-4380-916