-
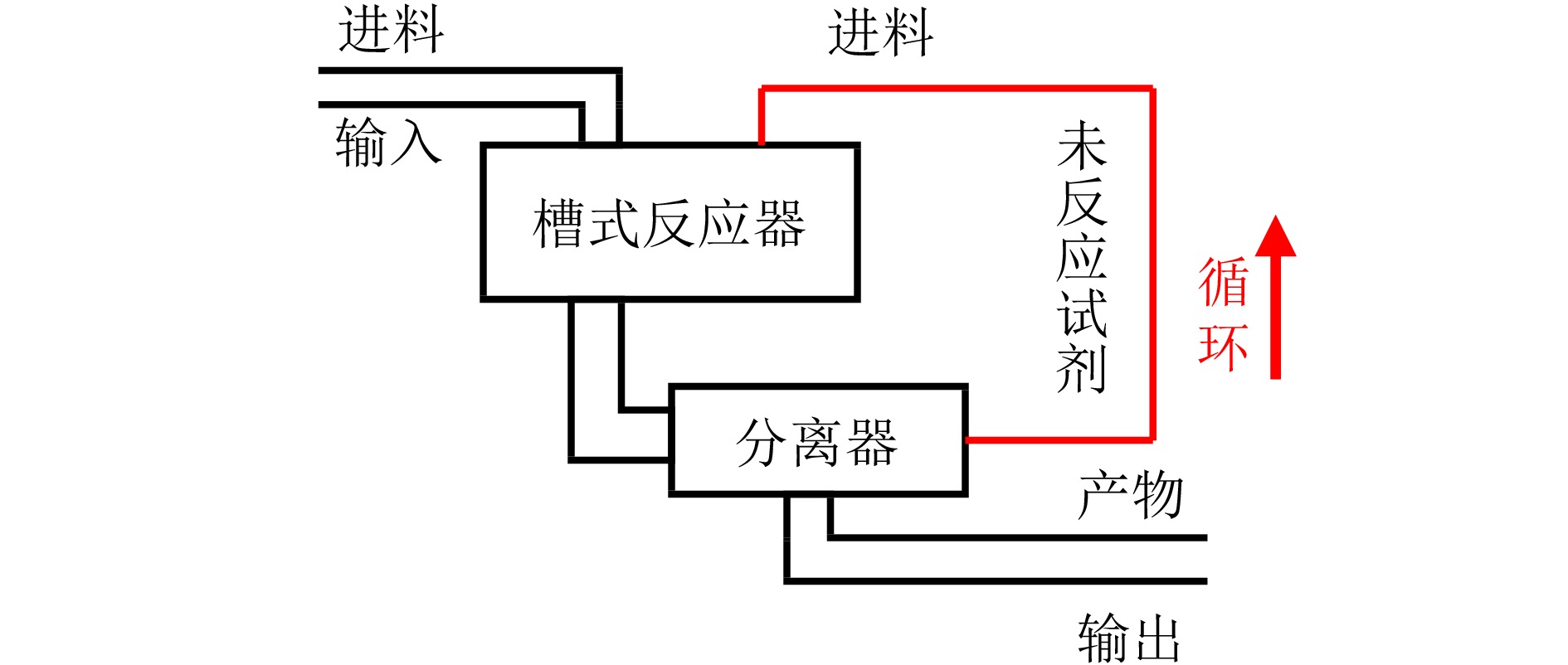
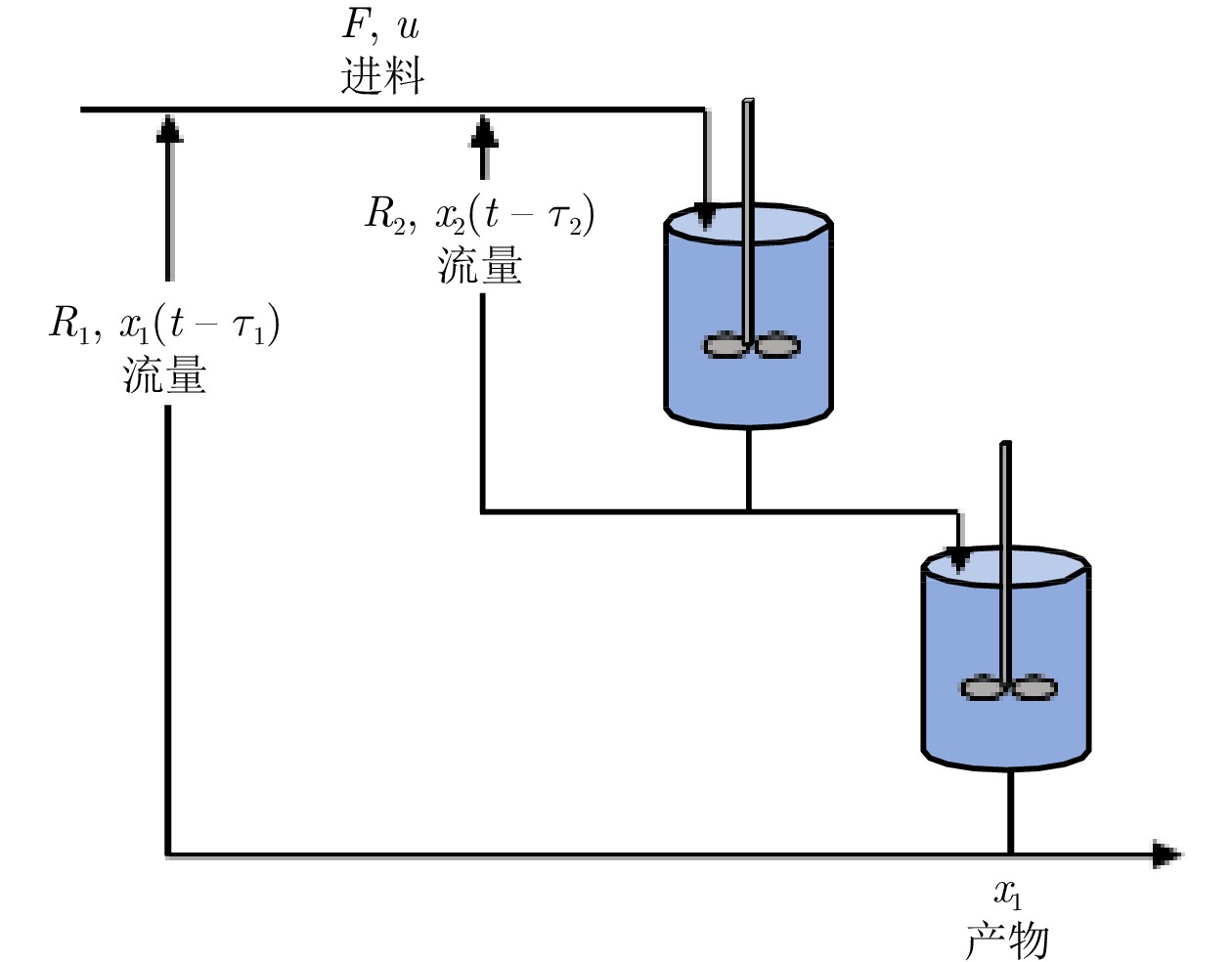
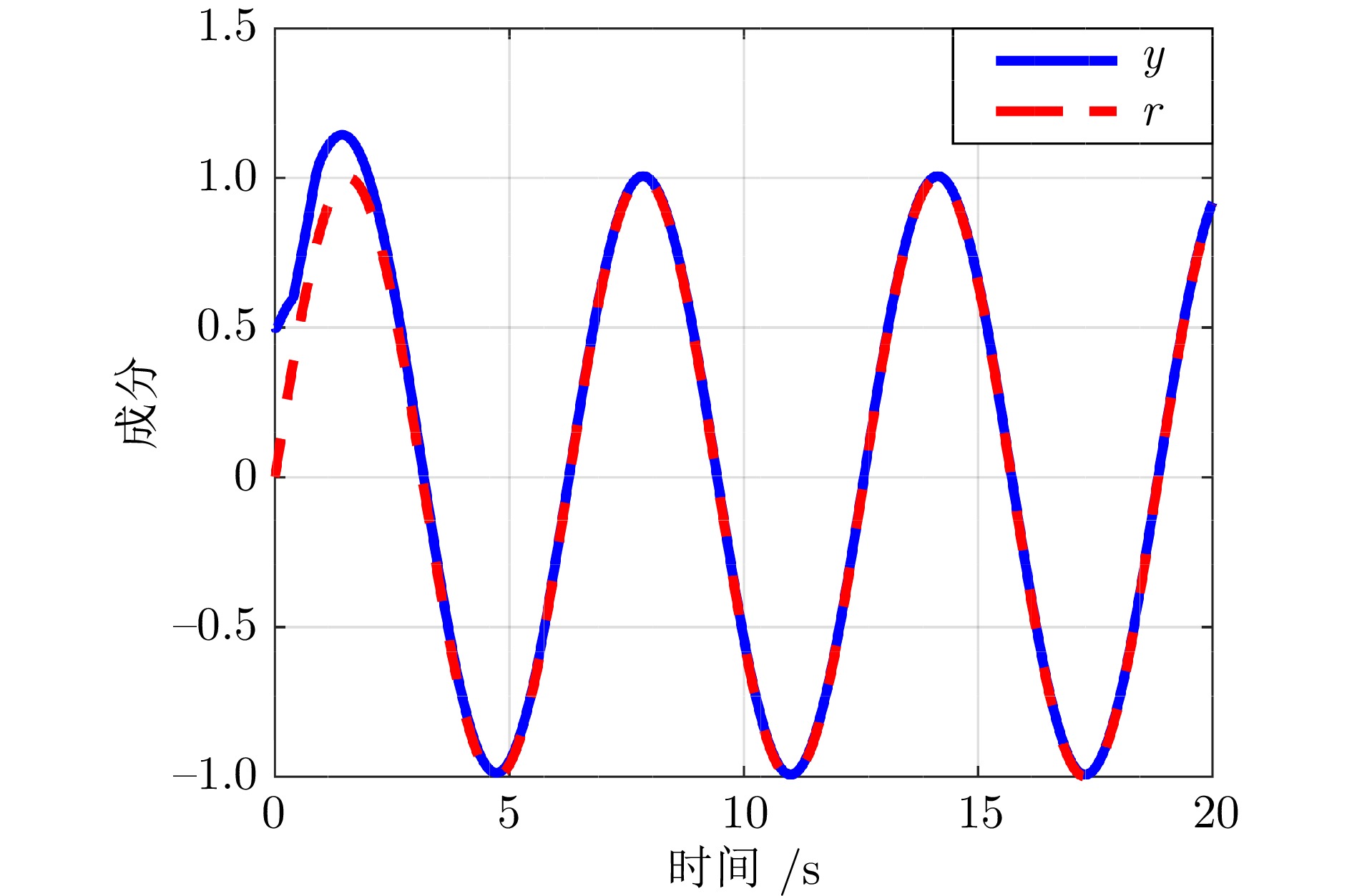
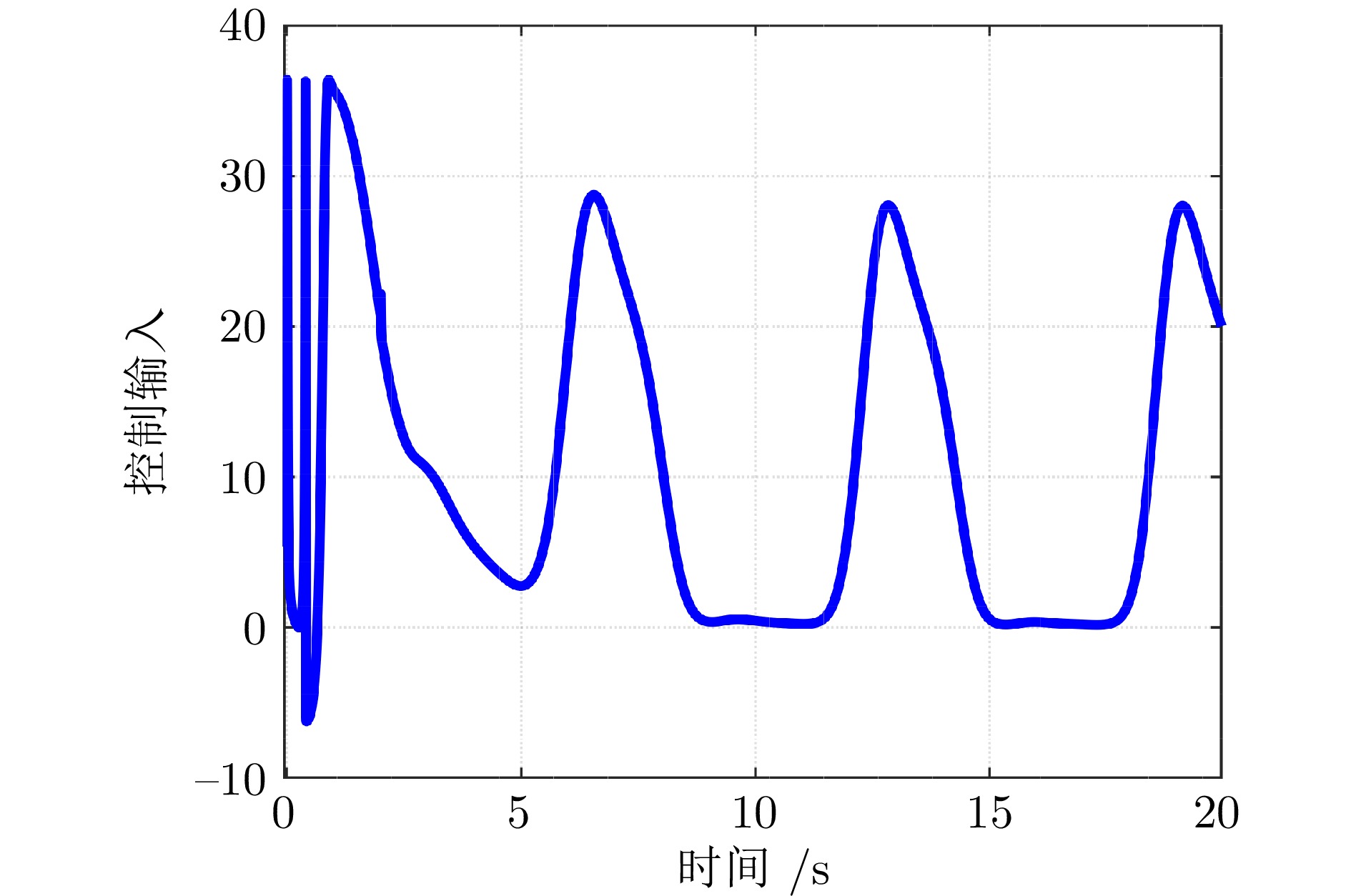
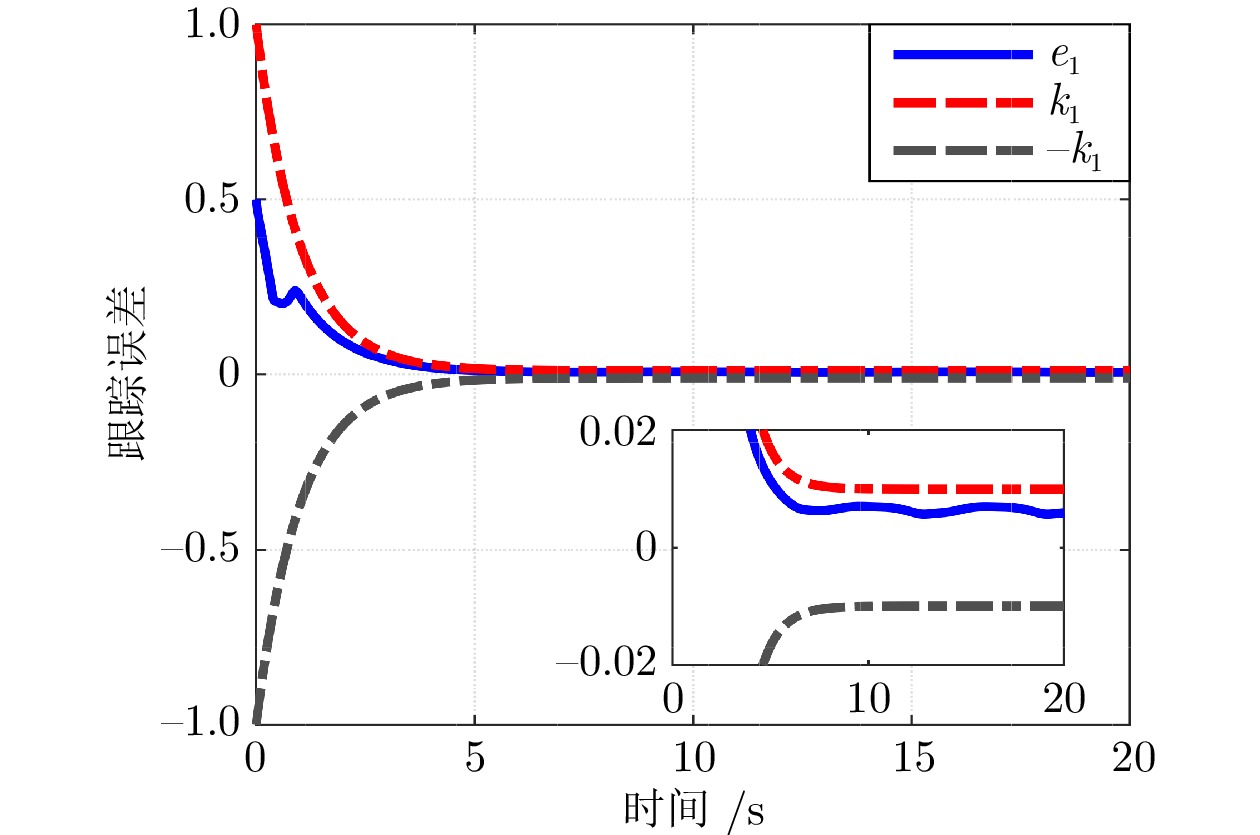
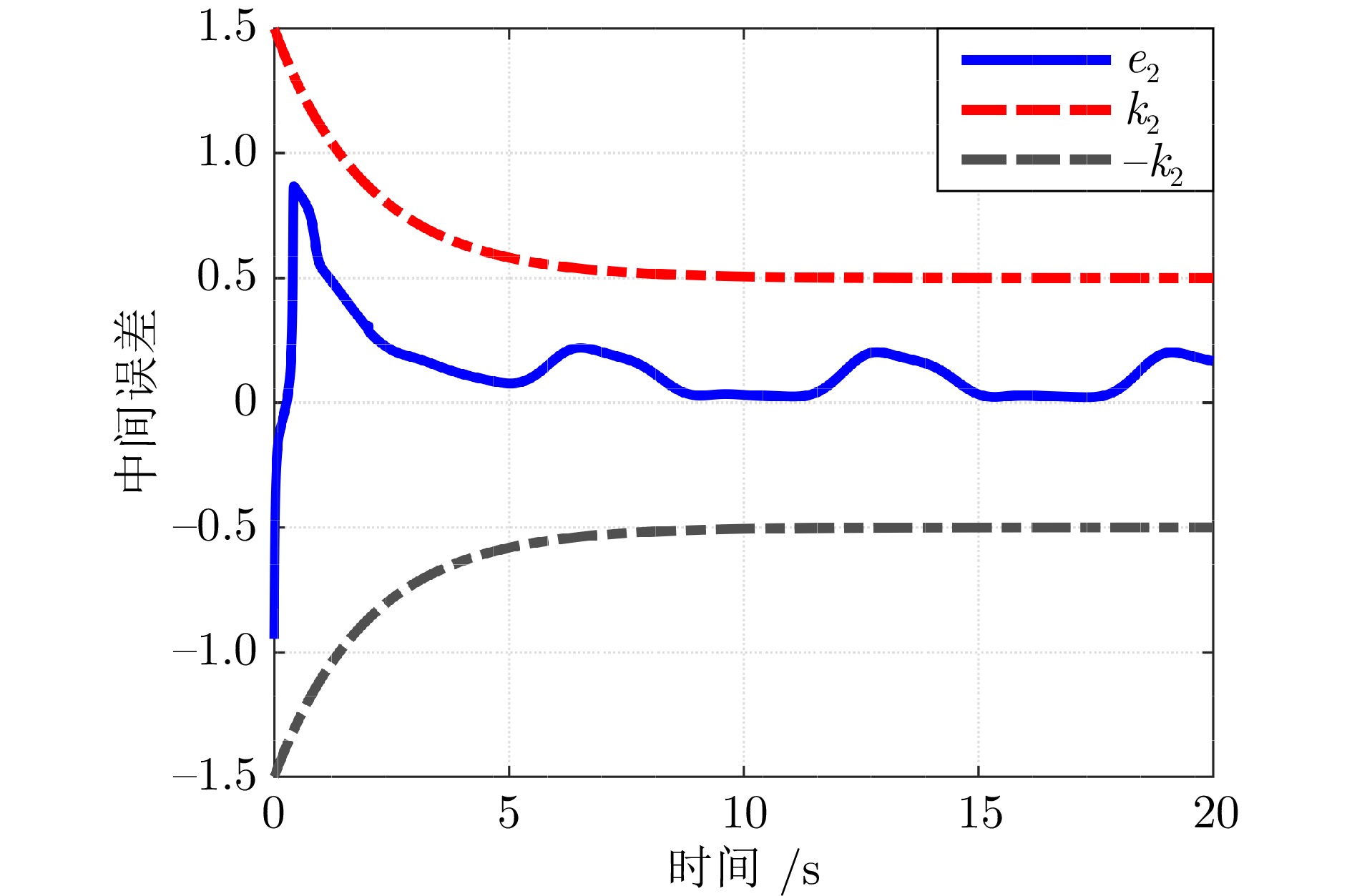
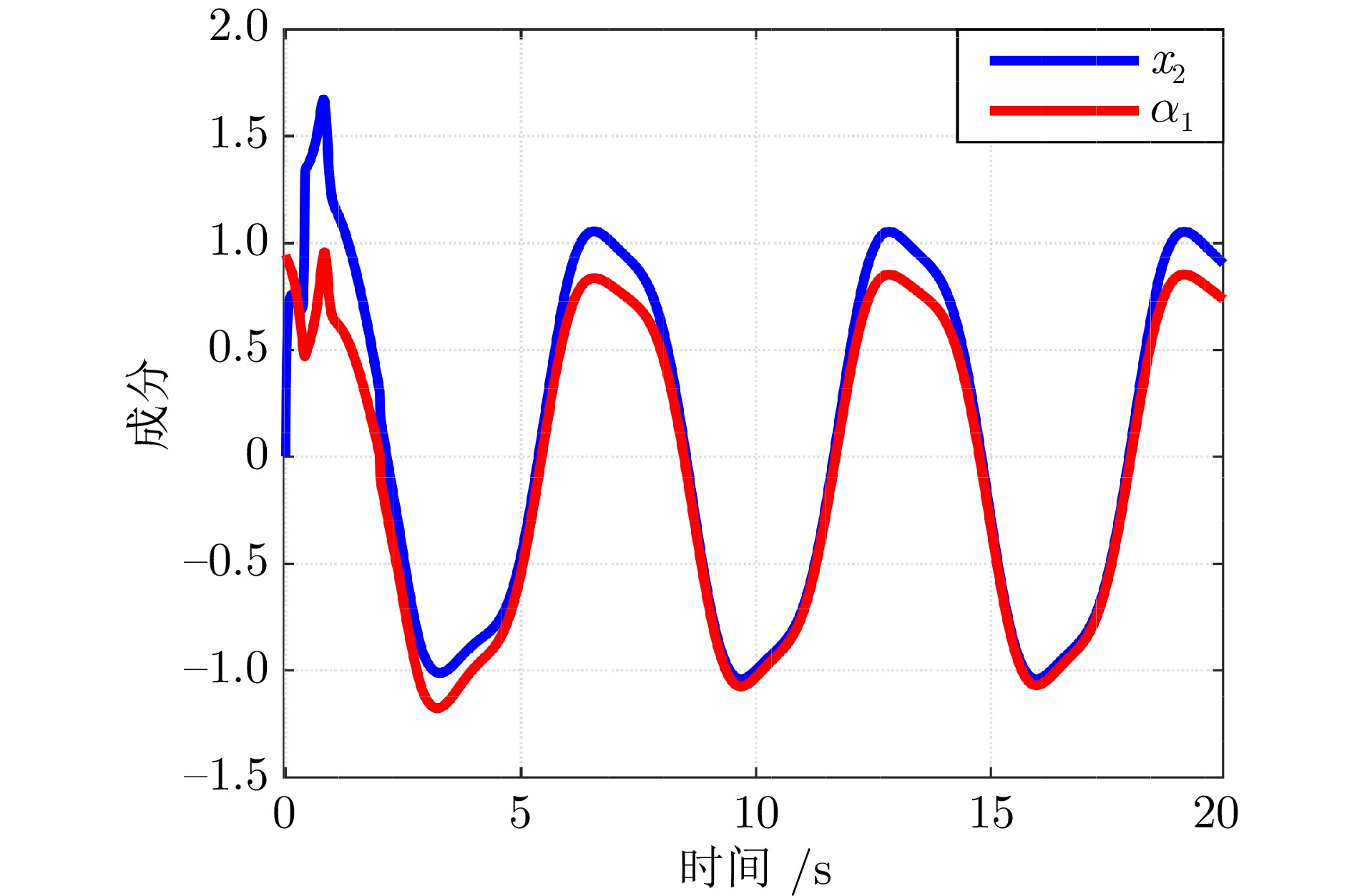
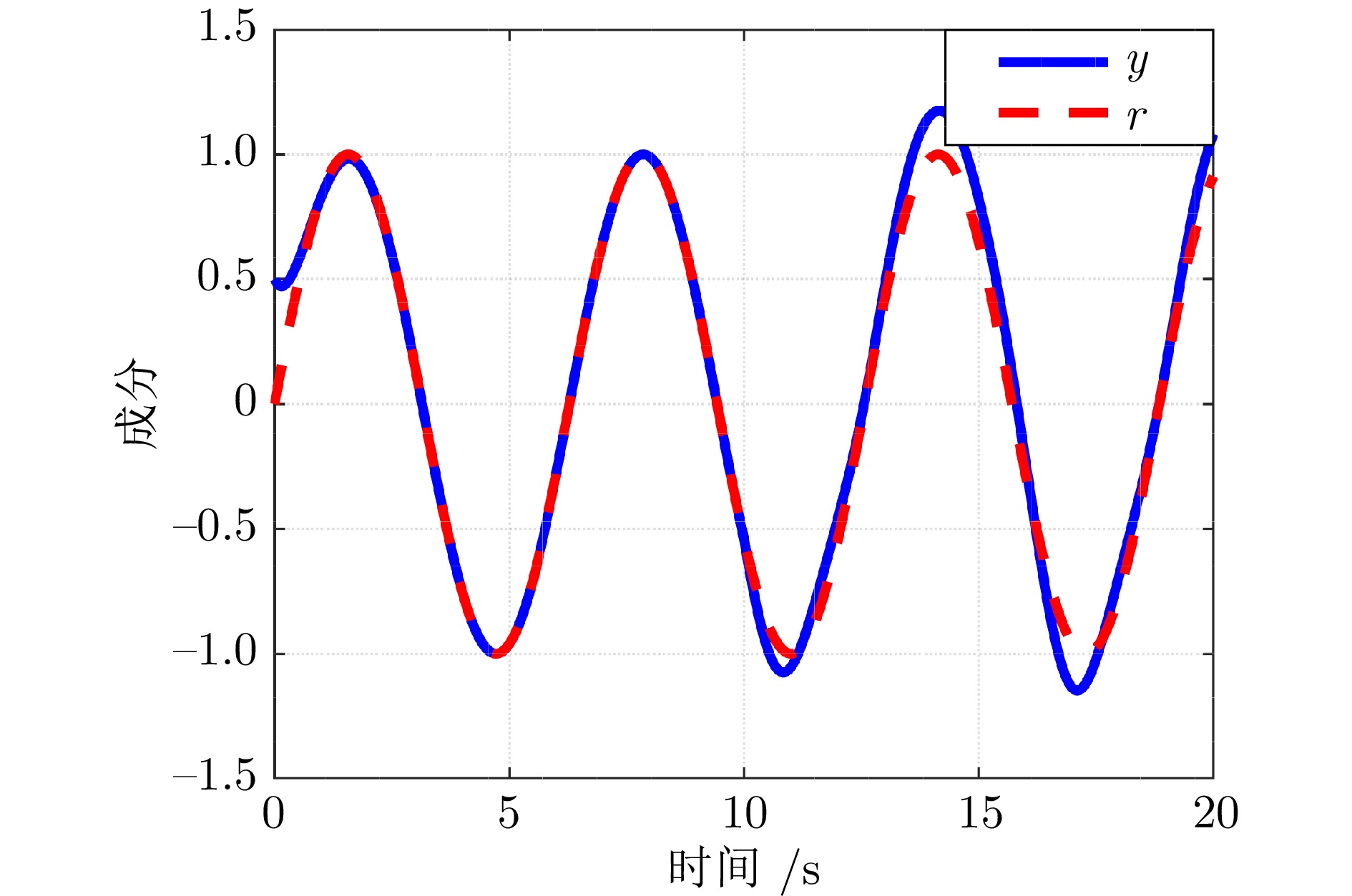
摘要: 研究含有状态时延的严反馈非线性系统的跟踪控制问题, 充分考虑时延的时变性和任意性以及系统的未知动力学特性. 为解决该问题, 取代参数辨识、函数逼近、增益调节、指令滤波等常规技术, 提出基于导向函数的预设性能控制方法, 移除了控制器设计对于系统非线性、控制方向和虚拟控制信号导数等信息的依赖. 并且, 摆脱基于李雅普诺夫−克拉索夫斯基泛函或拉祖米欣函数的稳定性分析框架, 采用基于反证法的受限分析理论, 移除性能分析对于已知的时延上界、部分已知的时延非线性函数和时延导数小于1等常见约束. 因此, 形成无模型、低复杂度、高性能控制方法, 将跟踪误差限制于设计者预先选取的性能包络线内, 确保系统输出以预先设定的速度和精度跟踪上时变的设定值. 最后, 以具有延迟回收流的两级化学反应器为对象开展对比仿真, 实验结果验证了所提方法的有效性和优越性.Abstract: This paper is concerned with the tracking control problem for time-delay strict-feedback nonlinear systems, in which the time-varying arbitrary state delays and the completely unknown system dynamics are taken into full consideration. To address this problem, instead of parameter identification, function approximation, gain adaption and command filtering, an orientation function-based prescribed performance control approach is put forward. It eliminates the dependence of the control design on the system nonlinearities, the control directions and the virtual control signal derivatives. Moreover, in lieu of the stability analysis based on Lyapunov-Krasovskii functionals or Razumikhin functions, a framework for constraint analysis by contradiction is adopted. It excludes the commonly adopted assumptions on the known bounds of time-delays, the partially known time-delay nonlinearities and the time-delay derivatives less than 1. Therefore, a model-free low-complexity high-performance control scheme is obtained, which confines the tracking error inside the predefined performance envelop. In this way, it is achieved that the system output tracks the time-varying reference with the prescribed rate and accuracy. Finally, a comparative simulation on the two-stage chemical reactor with delayed recycle streams is conducted, and the simulation results substantiate the effectiveness and the superiority of the proposed approach.
-
Key words:
- Model-free control /
- prescribed performance /
- reference tracking /
- time-delay /
- nonlinear systems
-
表 1 模型参数
Table 1 Model parameters
$a_1$ $a_2$ $b_1$ $b_2$ $R_1$ $R_2$ $V_1$ $V_2$ $F$ 2 2 0.3 0.3 0.5 0.5 0.5 0.5 0.5 -
[1] Niculescu S I. Delay Effects on Stability: A Robust Control Approach. London: Springer, 2001. [2] Nguang S K. Robust stabilization of a class of time-delay nonlinear systems. IEEE Transactions on Automatic Control, 2000, 45(4): 756−762 doi: 10.1109/9.847117 [3] Mahmoud M S. Robust Control and Filtering for Time-Delay Systems. Boca Raton: CRC Press, 2000. [4] Lehman B. Stability of chemical reactions in a CSTR with delayed recycle stream. In: Proceedings of the American Control Conference. Baltimore, USA: IEEE, 1994. 3521−3522 [5] Zhang J X, Xu K D, Wang Q G. Prescribed performance tracking control of time-delay nonlinear systems with output constraints. IEEE/CAA Journal of Automatica Sinica, DOI: 10.1109/JAS.2023.123831 [6] Zhang Z Q, Xu B, Tan C, Ge S S. Adaptive control of uncertain nonlinear time-delay systems with external disturbance. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(2): 1288−1295 doi: 10.1109/TSMC.2020.3017801 [7] Niu B, Wang D, Liu M, Song X M, Wang H Q, Duan P Y. Adaptive neural output-feedback controller design of switched nonlower triangular nonlinear systems with time delays. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(10): 4084−4093 doi: 10.1109/TNNLS.2019.2952108 [8] Sun W W, Wu Y, Lv X Y. Adaptive neural network control for full-state constrained robotic manipulator with actuator saturation and time-varying delays. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(8): 3331−3342 doi: 10.1109/TNNLS.2021.3051946 [9] Li H F, Liu Q R, Feng G, Zhang X F. Leader-follower consensus of nonlinear time-delay multiagent systems: A time-varying gain approach. Automatica, 2021, 126: Article No. 109444 doi: 10.1016/j.automatica.2020.109444 [10] Xie Y K, Ma Q. Adaptive event-triggered neural network control for switching nonlinear systems with time delays. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(2): 729−738 doi: 10.1109/TNNLS.2021.3100533 [11] Liu Z G, Xue L R, Zhang W H. Universal adaptive control strategies for stochastic nonlinear time-delay systems with odd rational powers. Automatica, 2021, 125: Article No. 109419 doi: 10.1016/j.automatica.2020.109419 [12] Liu Z G, Xue L R, Sun Z Y. A new robust adaptive tracking strategy to uncertain time-delay nonlinear systems with a general form. Automatica, 2022, 146: Article No. 110560 doi: 10.1016/j.automatica.2022.110560 [13] Zhang Z Q, Yang C, Ge S S. Decentralized adaptive control of large-scale nonlinear systems with time-delay interconnections and asymmetric dead-zone input. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2023, 53(4): 2259−2270 doi: 10.1109/TSMC.2022.3212882 [14] Hua C C, Wang Q G, Guan X P. Adaptive tracking controller design of nonlinear systems with time delays and unknown dead-zone input. IEEE Transactions on Automatic Control, 2008, 53(7): 1753−1759 doi: 10.1109/TAC.2008.928324 [15] Sun H B, Hou L L, Zong G D, Yu X H. Adaptive decentralized neural network tracking control for uncertain interconnected nonlinear systems with input quantization and time delay. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(4): 1401−1409 doi: 10.1109/TNNLS.2019.2919697 [16] Li D P, Liu L, Liu Y J, Tong S C, Chen C L P. Fuzzy approximation-based adaptive control of nonlinear uncertain state constrained systems with time-varying delays. IEEE Transactions on Fuzzy Systems, 2020, 28(8): 1620−1630 doi: 10.1109/TFUZZ.2019.2919490 [17] Li M, Li S, Ahn C K, Xiang Z R. Adaptive fuzzy event-triggered command-filtered control for nonlinear time-delay systems. IEEE Transactions on Fuzzy Systems, 2022, 30(4): 1025−1035 doi: 10.1109/TFUZZ.2021.3052095 [18] Ji R H, Li D Y, Ge S S. Saturation-tolerant prescribed control for nonlinear time-delay systems. IEEE Transactions on Fuzzy Systems, 2023, 31(8): 2495−2508 doi: 10.1109/TFUZZ.2022.3227984 [19] Liu G P, Park J H, Xu H S, Hua C C. Reduced-order observer-based output-feedback tracking control for nonlinear time-delay systems with global prescribed performance. IEEE Transactions on Cybernetics, 2023, 53(9): 5560−5571 doi: 10.1109/TCYB.2022.3158932 [20] 方玫. 不确定广义时滞系统的时滞依赖鲁棒H∞ 控制. 自动化学报, 2009, 35(1): 65−70Fang Mei. Delay-dependent robust H∞ control for uncertain singular systems with state delay. Acta Automatica Sinica, 2009, 35(1): 65−70 [21] 陈为胜, 王元亮, 李俊民. 周期时变时滞非线性参数化系统的自适应学习控制. 自动化学报, 2008, 34(12): 1556−1560Chen Wei-Sheng, Wang Yuan-Liang, Li Jun-Min. Adaptive learning control for nonlinearly parameterized systems with periodically time-varying delays. Acta Automatica Sinica, 2008, 34(12): 1556−1560 [22] 高金凤, 潘海鹏, 嵇小辅. 具有时变时滞的Lurie系统时滞依赖绝对稳定性新判据. 自动化学报, 2010, 36(6): 845−850Gao Jin-Feng, Pan Hai-Peng, Ji Xiao-Fu. A new delay-dependent absolute stability criterion for Lurie systems with time-varying delay. Acta Automatica Sinica, 2010, 36(6): 845−850 [23] Zhang J F, Raïssi T, Deng X J. Indefinite Krasovskii and Razumikhin stability for nonlinear positive time-varying systems. IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, 69(4): 2321−2325 [24] Yan X G, Spurgeon S K, Edwards C. Decentralised stabilisation for nonlinear time delay interconnected systems using static output feedback. Automatica, 2013, 49(2): 633−641 doi: 10.1016/j.automatica.2012.11.040 [25] Zhang X F, Baron L, Liu Q R, Boukas E K. Design of stabilizing controllers with a dynamic gain for feedforward nonlinear time-delay systems. IEEE Transactions on Automatic Control, 2011, 56(3): 692−697 doi: 10.1109/TAC.2010.2097150 [26] Wang T C, Luo X X, Li W Q. Razumikhin-type approach on state feedback of stochastic high-order nonlinear systems with time-varying delay. International Journal of Robust and Nonlinear Control, 2017, 27(16): 3124−3134 doi: 10.1002/rnc.3730 [27] Dimanidis I S, Bechlioulis C P, Rovithakis G A. Output feedback approximation-free prescribed performance tracking control for uncertain MIMO nonlinear systems. IEEE Transactions on Automatic Control, 2020, 65(12): 5058−5069 doi: 10.1109/TAC.2020.2970003 [28] Zhang J X, Chai T Y. Proportional-integral funnel control of unknown lower-triangular nonlinear systems. IEEE Transactions on Automatic Control, 2024, 69(3): 1921−1927 doi: 10.1109/TAC.2023.3330900 [29] Bu X W, Jiang B X, Lei H M. Performance guaranteed finite-time non-affine control of waverider vehicles without function-approximation. IEEE Transactions on Intelligent Transportation Systems, 2023, 24(3): 3252−3262 doi: 10.1109/TITS.2022.3224424 [30] Bu X W, Jiang B X. Fragility-free prescribed performance control without approximation applied to waverider aerocraft. IEEE Journal on Miniaturization for Air and Space Systems, 2023, 4(2): 146−156 doi: 10.1109/JMASS.2023.3242304 [31] Karayiannidis Y, Papageorgiou D, Doulgeri Z. A model-free controller for guaranteed prescribed performance tracking of both robot joint positions and velocities. IEEE Robotics and Automation Letters, 2016, 1(1): 267−273 doi: 10.1109/LRA.2016.2516245 [32] Hu Y B, Geng Y H, Wu B L, Wang D W. Model-free prescribed performance control for spacecraft attitude tracking. IEEE Transactions on Control Systems Technology, 2021, 29(1): 165−179 doi: 10.1109/TCST.2020.2968868 [33] Wang N, Gao Y, Zhang X F. Data-driven performance-prescribed reinforcement learning control of an unmanned surface vehicle. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(12): 5456−5467 doi: 10.1109/TNNLS.2021.3056444 [34] Hao L Y, Zhang H, Li T S, Lin B, Chen C L P. Fault tolerant control for dynamic positioning of unmanned marine vehicles based on T-S fuzzy model with unknown membership functions. IEEE Transactions on Vehicular Technology, 2021, 70(1): 146−157 doi: 10.1109/TVT.2021.3050044 [35] Hao L Y, Zhang H, Guo G, Li H. Quantized sliding mode control of unmanned marine vehicles: Various thruster faults tolerated with a unified model. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(3): 2012−2026 [36] Hao L Y, Dong G G, Li T S, Peng Z H. Path-following control with obstacle avoidance of autonomous surface vehicles subject to actuator faults. IEEE/CAA Journal of Automatica Sinica, 2024, 11(4): 956−964 doi: 10.1109/JAS.2023.123675 [37] Zhang J X, Yang T, Chai T Y. Neural network control of underactuated surface vehicles with prescribed trajectory tracking performance. IEEE Transactions on Neural Networks and Learning Systems, DOI: 10.1109/TNNLS.2022.3223666 [38] Liu D, Yang G H. Prescribed performance model-free adaptive integral sliding mode control for discrete-time nonlinear systems. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(7): 2222−2230 doi: 10.1109/TNNLS.2018.2881205 [39] Zhang J X, Yang G H. Prescribed performance fault-tolerant control of uncertain nonlinear systems with unknown control directions. IEEE Transactions on Automatic Control, 2017, 62(12): 6529−6535 doi: 10.1109/TAC.2017.2705033 [40] Zhang J X, Yang G H. Adaptive prescribed performance control of nonlinear output-feedback systems with unknown control direction. International Journal of Robust and Nonlinear Control, 2018, 28(16): 4696−4712 doi: 10.1002/rnc.4277 [41] Zhang J X, Yang G H. Low-complexity adaptive tracking control of MIMO nonlinear systems with unknown control directions. International Journal of Robust and Nonlinear Control, 2019, 29(7): 2203−2222 doi: 10.1002/rnc.4486 [42] Hsu L, Oliveira T R, Cunha J P V S, Yan L. Adaptive unit vector control of multivariable systems using monitoring functions. International Journal of Robust and Nonlinear Control, 2019, 29(3): 583−600 doi: 10.1002/rnc.4253 [43] Zhang J X, Yang G H. Low-complexity tracking control of strict-feedback systems with unknown control directions. IEEE Transactions on Automatic Control, 2019, 64(12): 5175−5182 doi: 10.1109/TAC.2019.2910738 [44] Zhang J X, Wang Q G, Ding W. Global output-feedback prescribed performance control of nonlinear systems with unknown virtual control coefficients. IEEE Transactions on Automatic Control, 2022, 67(12): 6904−6911 doi: 10.1109/TAC.2021.3137103 [45] Cao L F, Fan X G, Li D W, Kong W B, Qu R H, Liu Z R. Improved LPTN-based online temperature prediction of permanent magnet machines by global parameter identification. IEEE Transactions on Industrial Electronics, 2023, 70(9): 8830−8841 doi: 10.1109/TIE.2022.3208600 [46] Wang Y J, Wang T, Yang X B, Yang J E. Gradient descent-barzilai borwein-based neural network tracking control for nonlinear systems with unknown dynamics. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(1): 305−315 doi: 10.1109/TNNLS.2021.3093877 [47] Tang F H, Niu B, Wang H Q, Zhang L, Zhao X D. Adaptive fuzzy tracking control of switched MIMO nonlinear systems with full state constraints and unknown control directions. IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, 69(6): 2912−2916 [48] Wang H Q, Kang S J, Zhao X D, Xu N, Li T S. Command filter-based adaptive neural control design for nonstrict-feedback nonlinear systems with multiple actuator constraints. IEEE Transactions on Cybernetics, 2022, 52(11): 12561−12570 doi: 10.1109/TCYB.2021.3079129 [49] Cui G Z, Yu J P, Wang Q G. Finite-time adaptive fuzzy control for MIMO nonlinear systems with input saturation via improved command-filtered backstepping. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(2): 980−989 doi: 10.1109/TSMC.2020.3010642 -





 下载:
下载: