Sensor Management Method Based on Deep Reinforcement Learning in Extended Target Tracking
-
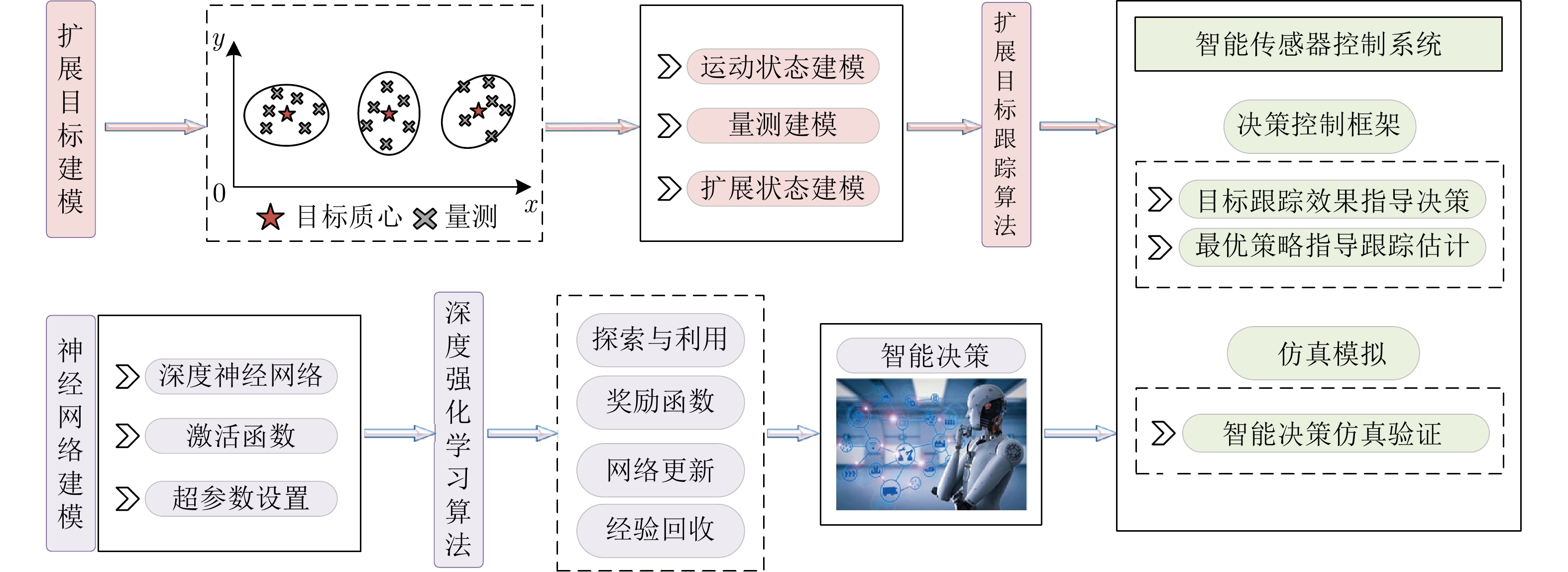
摘要: 针对扩展目标跟踪(Extended target tracking, ETT)优化中的传感器管理问题, 基于随机矩阵模型(Random matrices model, RMM)建模扩展目标, 提出一种基于深度强化学习(Deep reinforcement learning, DRL)的传感器管理方法. 首先, 在部分可观测马尔科夫决策过程(Partially observed Markov decision process, POMDP)理论框架下, 给出基于双延迟深度确定性策略梯度(Twin delayed deep deterministic policy gradient, TD3)算法的扩展目标跟踪传感器管理的基本方法; 其次, 利用高斯瓦瑟斯坦距离(Gaussian Wasserstein distance, GWD)求解扩展目标先验概率密度与后验概率密度之间的信息增益, 对扩展目标多特征估计信息进行综合评价, 进而以信息增益作为TD3算法奖励函数的构建; 然后, 通过推导出的奖励函数, 进行基于深度强化学习的传感器管理方法的最优决策; 最后, 通过构造扩展目标跟踪优化仿真实验, 验证了所提方法的有效性.
-
关键词:
- 传感器管理 /
- 扩展目标跟踪 /
- 深度强化学习 /
- 双延迟深度确定性策略梯度 /
- 信息增益
Abstract: To solve the problem of sensor management in the optimization of extended target tracking (ETT), this paper proposes a sensor management method based on deep reinforcement learning (DRL) by modeling the extended target based on random matrices model (RMM). First, in the theoretical framework of partially observed Markov decision process (POMDP), a elementary method of sensor management for extended target tracking based on twin delayed deep deterministic policy gradient (TD3) algorithm is presented. After that, the Gaussian Wasserstein distance (GWD) is used to calculate the information gain between the prior probability density and the posterior probability density of the extended target, which is used to comprehensively evaluate the multi-feature estimation information of the extended target, and then the information gain is used as the reward function of TD3 algorithm. Furthermore, the optimal sensor management scheme based on deep reinforcement learning is decided by the derived reward function. Finally, the effectiveness of the proposed algorithm is verified by constructing an elliptical extended target tracking optimization simulation experiment. -
图 1 扩展目标跟踪中传感器管理方法的研究框架
Fig. 1 Research framework of sensor management method in extended target tracking
图 4 基于TD3的扩展目标跟踪算法伪代码流程图
Fig. 4 Pseudocode flow chart of elliptical extended target tracking algorithm based on TD3
图 5 传感器控制智能决策训练曲线
Fig. 5 Training curve of intelligent decision-making for sensor control
图 16 群目标轨迹跟踪估计细节放大图
Fig. 16 Estimate detail enlarge image of group target trajectory tracking
图 17 群目标跟踪场景中的传感器控制轨迹对比
Fig. 17 Comparison of sensor control trajectory in group target tracking scenarios
图 18 群目标编队第1次变换跟踪细节放大图
Fig. 18 Group target formation the 1st transformation tracking detail enlarge image
图 19 群目标编队第2次变换跟踪细节放大图
Fig. 19 Group target formation the 2nd transformation tracking detail enlarge image
图 21 基于6种方法的群目标跟踪估计的GWD
Fig. 21 GWD of group target tracking estimation based on 6 methods
表 1 智能体训练参数
Table 1 TD3 agent training parameters
超参数名称 参数值 评论家网络学习率${\alpha _Q}$ 0.001 演员网络学习率${\beta _\mu }$ 0.0001 训练批次大小$N$ 128 经验回放单元${\cal{D}} $容量 $1 \times {10^4}$ 每幕最大时间步 $1 \times {10^3}$ 惯性更新率$\tau $ 0.002 更新频率比$m$ 2 折扣因子$\gamma $ 0.9 
下载: 导出CSV
表 2 6种方法下质心误差的统计均值
Table 2 Statistical average of centroid error under 6 methods
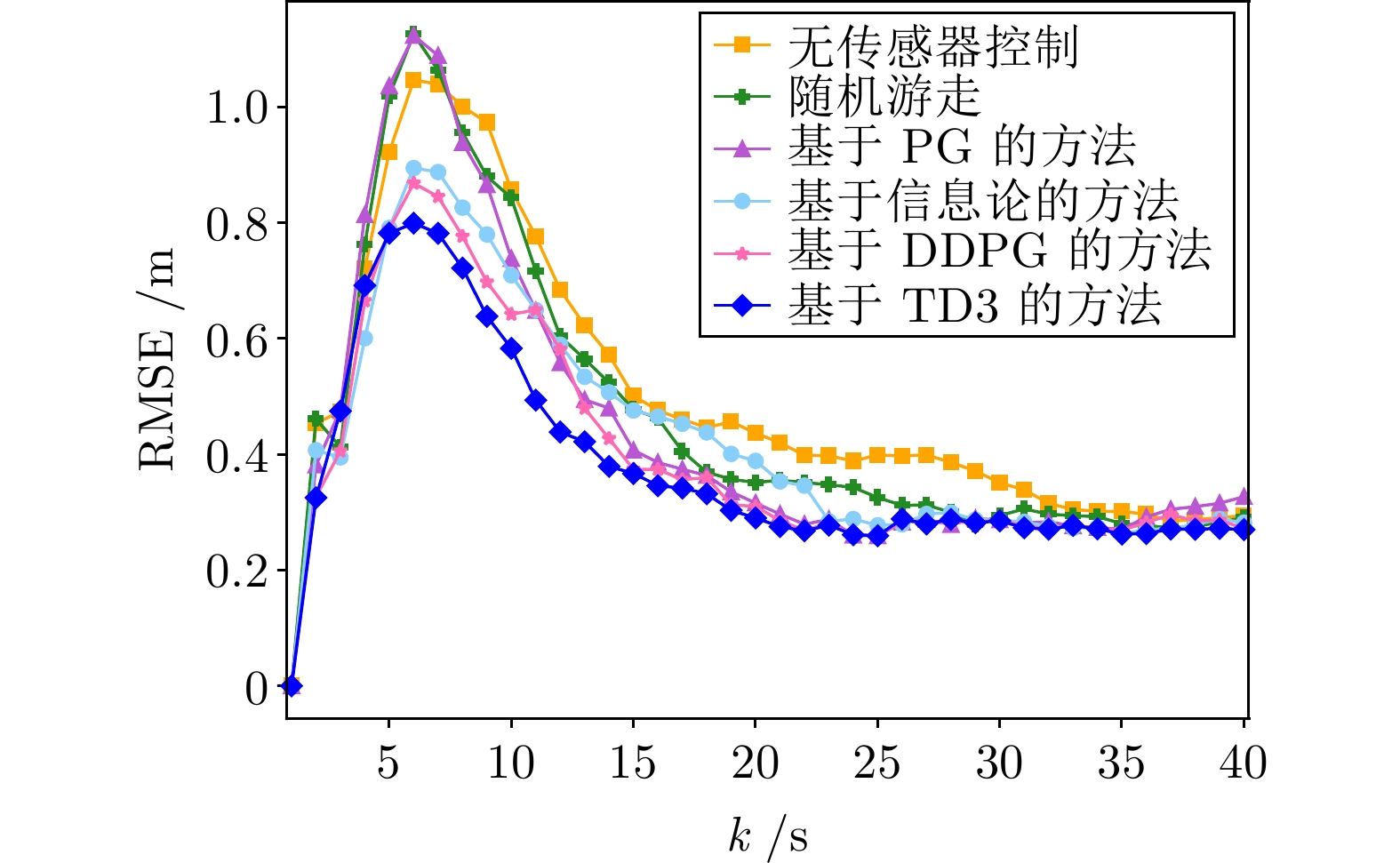
实验方法 质心误差统计均值(m) 对比方法1提升率(%) 方法1 0.5091 — 方法2 0.4732 7 方法3 0.4507 11 方法4 0.4349 15 方法5 0.3974 22 方法6 0.3842 25
下载: 导出CSV
表 3 6种方法下GWD的统计均值
Table 3 Statistical average of GWD under 6 methods
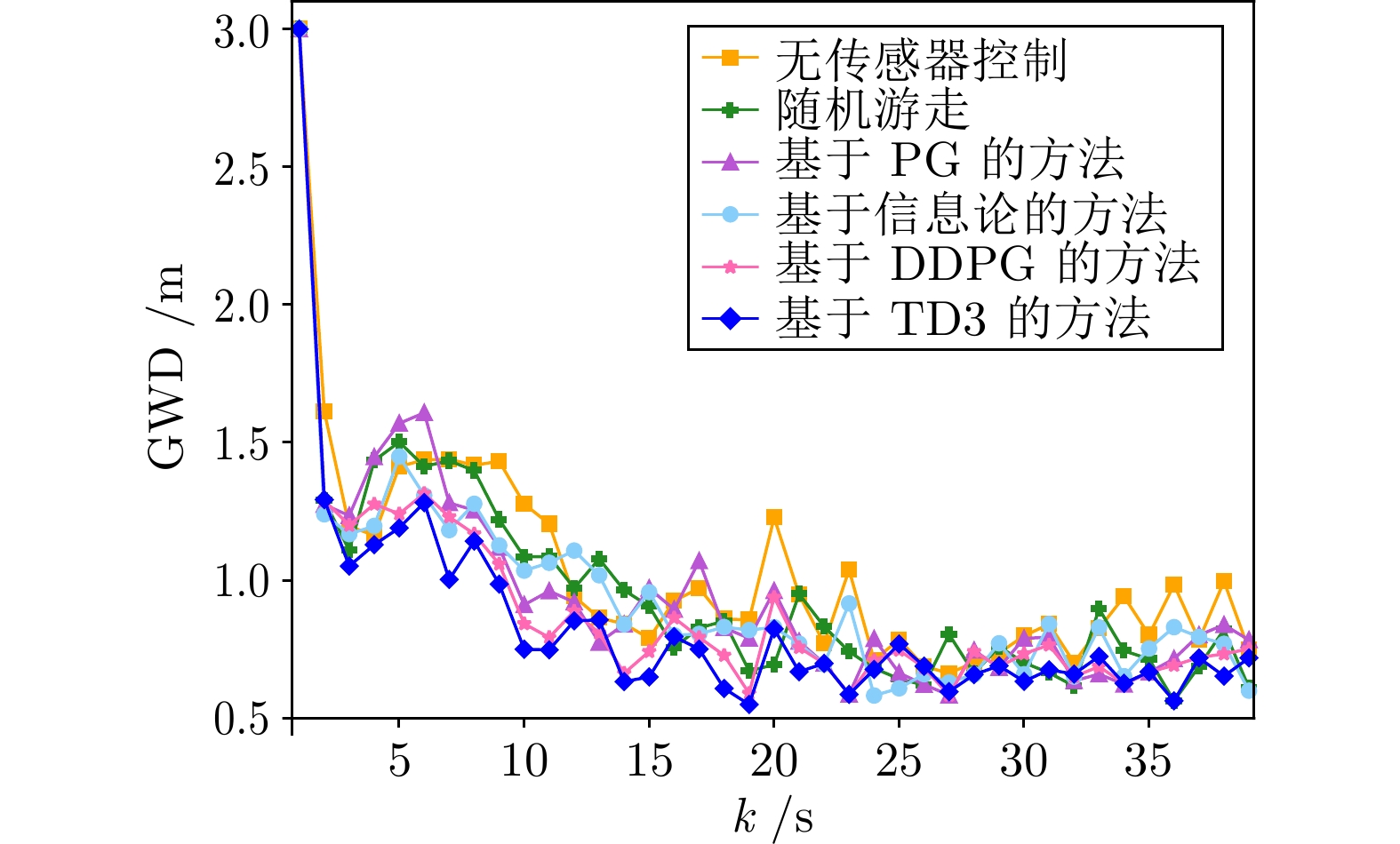
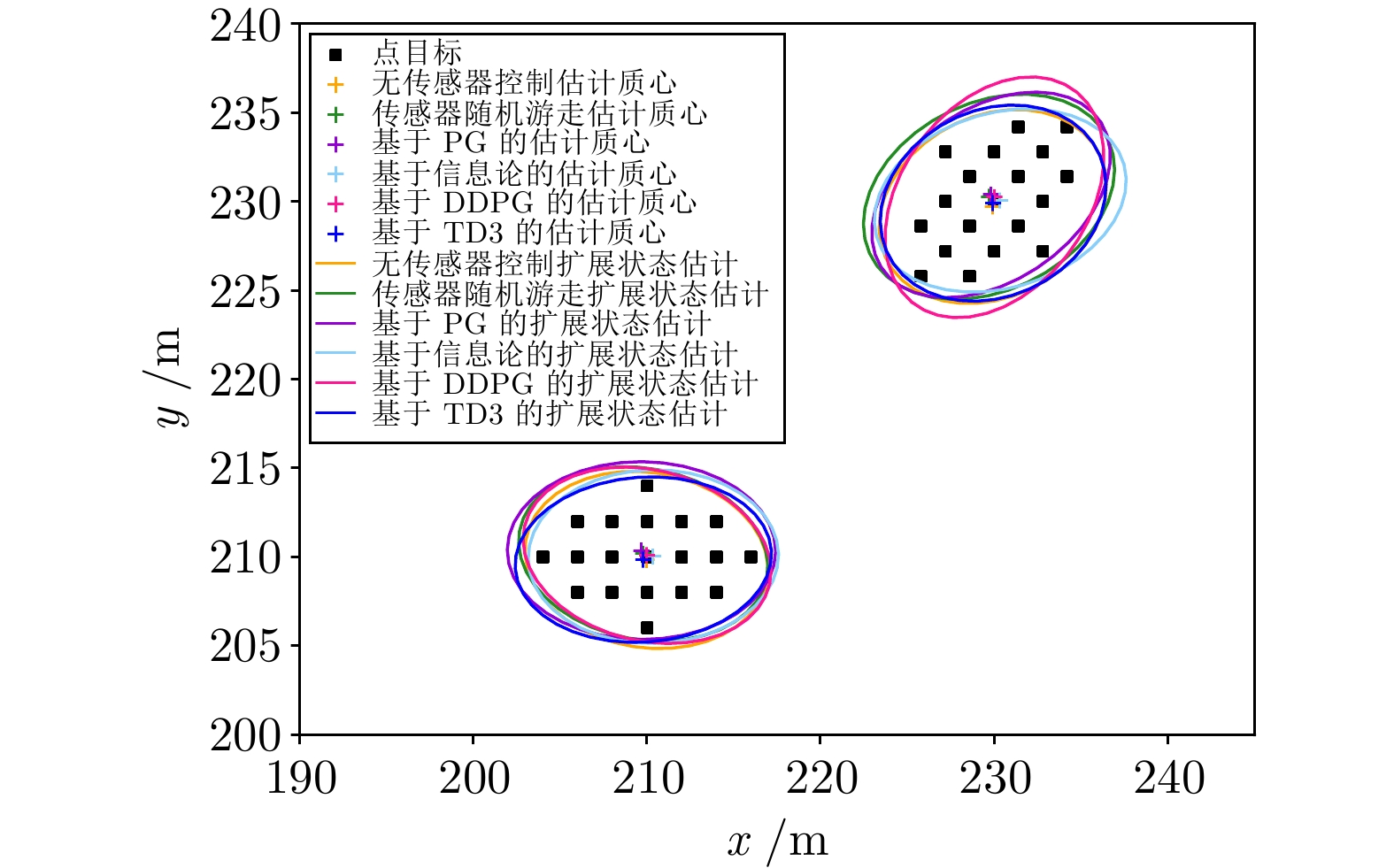
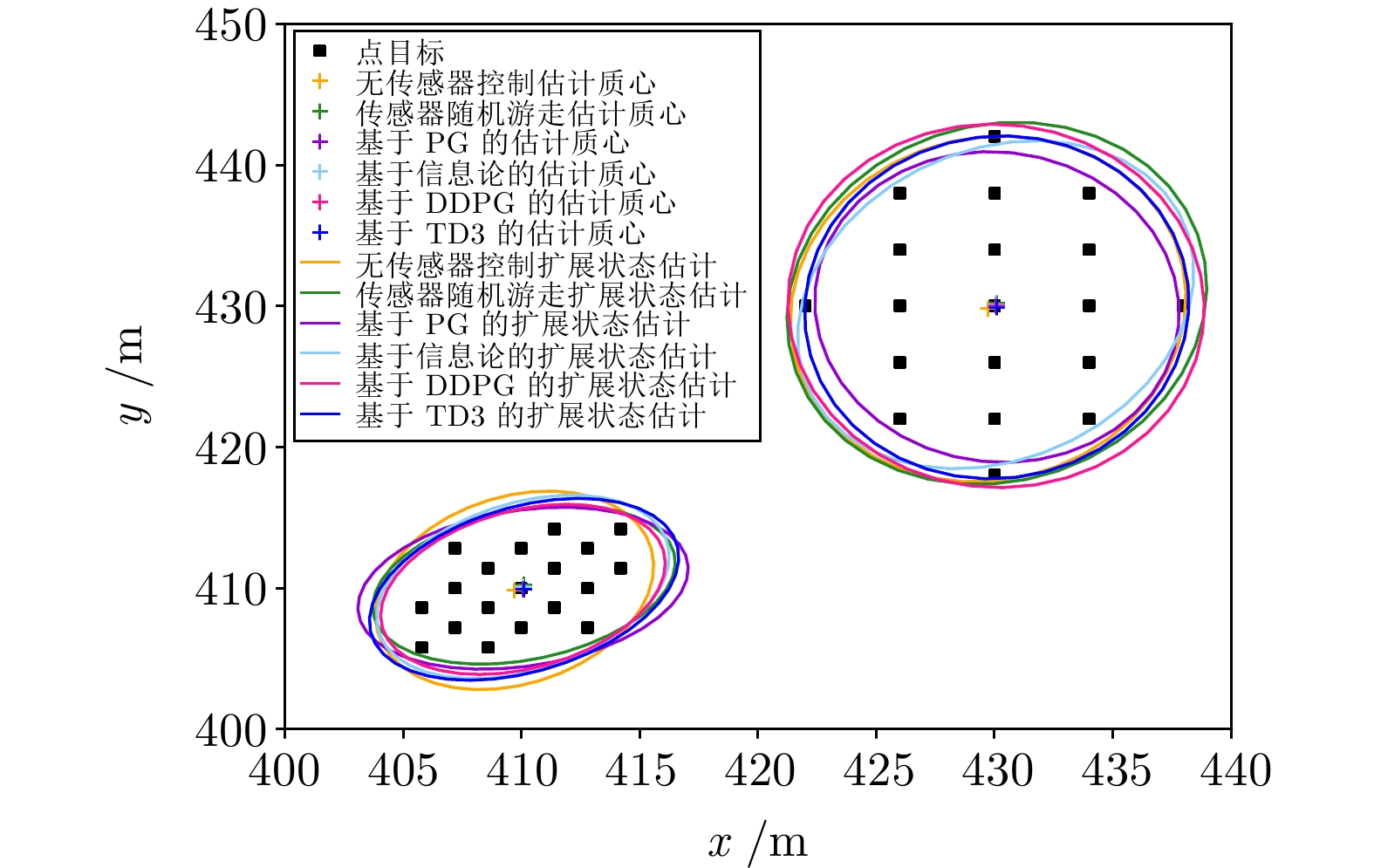
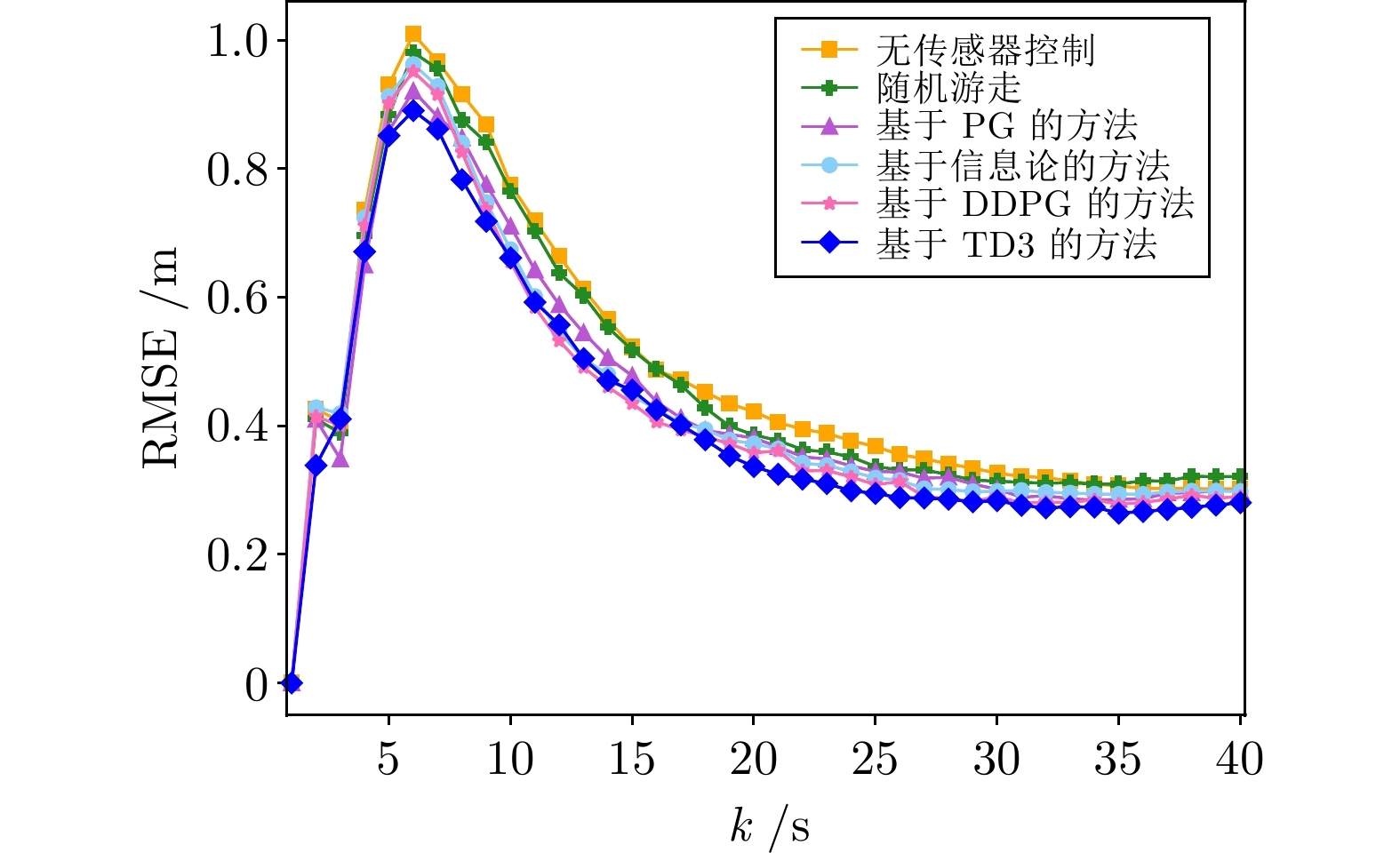
实验方法 GWD统计均值(m) 对比方法1提升率(%) 方法1 1.2848 — 方法2 1.2373 4 方法3 1.1751 9 方法4 1.2042 6 方法5 1.1565 10 方法6 1.0612 17
下载: 导出CSV
表 4 6种方法下质心误差的统计均值
Table 4 Statistical average of centroid error under 6 methods
实验方法 质心误差统计均值(m) 对比方法1的提升率(%) 方法1 0.4902 — 方法2 0.4753 3 方法3 0.4463 9 方法4 0.4455 9 方法5 0.4353 11 方法6 0.4197 14
下载: 导出CSV
表 5 6种方法下GWD的统计均值
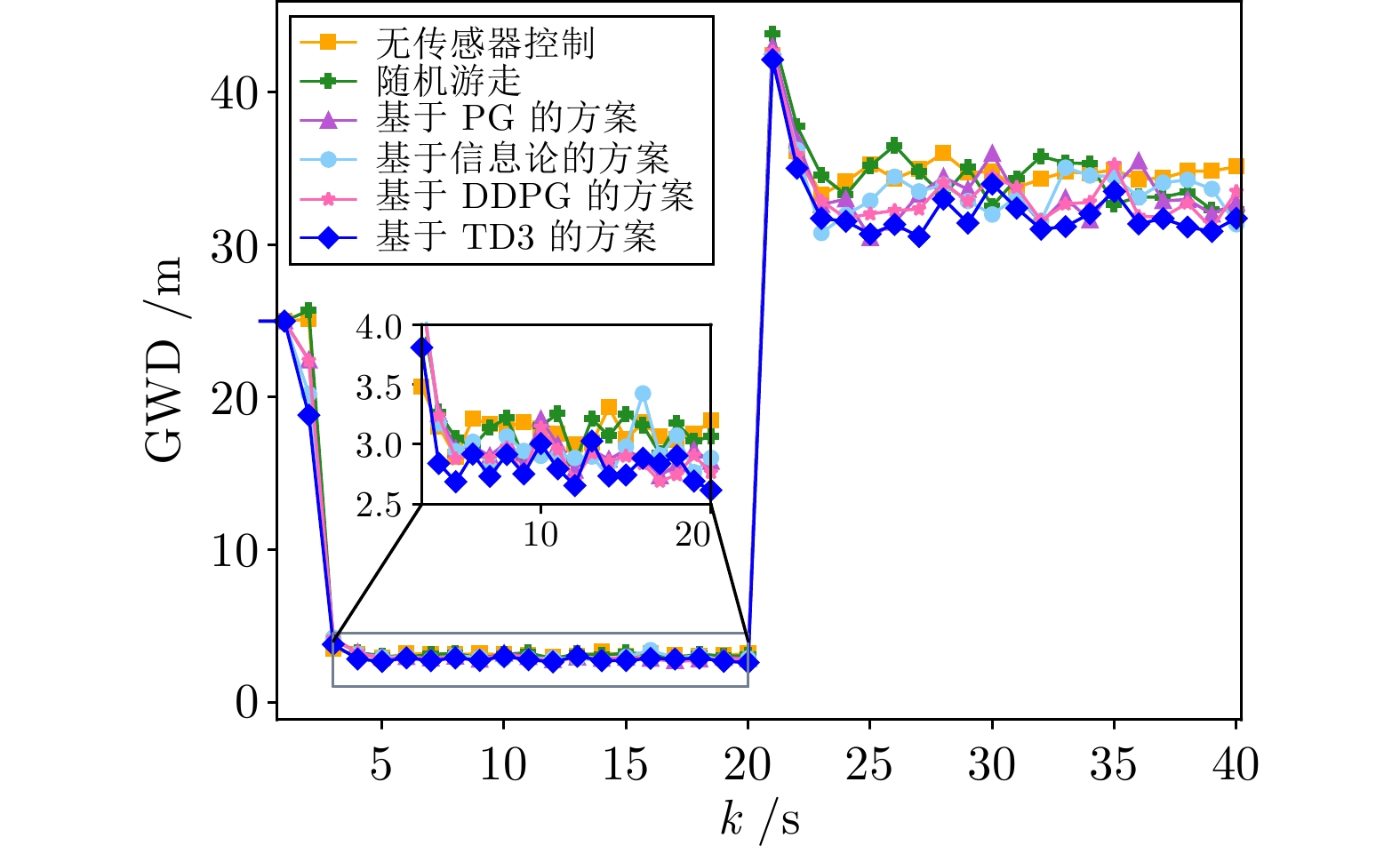
Table 5 Statistical average of GWD under 6 methods
实验方法 GWD的统计均值(m) 对比方法1提升率(%) 方法1 20.8413 — 方法2 20.6772 1 方法3 20.0186 4 方法4 20.0284 4 方法5 19.7976 5 方法6 19.2237 8
下载: 导出CSV
-
[1] Misra S, Singh A, Chatterjee S, Mandal A K. QoS-aware sensor allocation for target tracking in sensor-cloud. Ad Hoc Networks, 2015, 33: 140−153 doi: 10.1016/j.adhoc.2015.04.009 [2] Song H, Xiao M, Xiao J, Liang Y, Yang Z. A POMDP approach for scheduling the usage of airborne electronic countermeasures in air operations. Aerospace Science and Technology, 2016, 48: 86−93 doi: 10.1016/j.ast.2015.11.001 [3] Yan J, Jiao H, Pu W, Shi C, Dai J, Liu H. Radar sensor network resource allocation for fused target tracking: A brief review. Information Fusion, 2022, 86: 104−115 [4] Hero A O, Cochran D. Sensor management: Past, present, and future. IEEE Sensors Journal, 2011, 11(12): 3064−3075 doi: 10.1109/JSEN.2011.2167964 [5] Bello L L, Lombardo A, Milardo S, Patti G, Reno M. Experimental assessments and analysis of an SDN framework to integrate mobility management in industrial wireless sensor networks. IEEE Transactions on Industrial Informatics, 2020, 16(8): 5586−5595 doi: 10.1109/TII.2020.2963846 [6] Newell D, Duffy M. Review of power conversion and energy management for low-power, low-voltage energy harvesting powered wireless sensors. IEEE Transactions on Power Electronics, 2019, 34(10): 9794−9805 doi: 10.1109/TPEL.2019.2894465 [7] Shi C, Dai X, Wang Y, Zhou J, Salous S. Joint route optimization and multidimensional resource management scheme for airborne radar network in target tracking application. IEEE Systems Journal, 2021, 16(4): 6669−6680 [8] Dai J, Pu W, Yan J, Shi Q, Liu H. Multi-UAV collaborative trajectory optimization for asynchronous 3D passive multitarget tracking. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 1−16 [9] Zuo L, Hu J, Sun H, Gao Y. Resource allocation for target tracking in multiple radar architectures over lossy networks. Signal Processing, 2023, 208: 108973−108984 doi: 10.1016/j.sigpro.2023.108973 [10] Han D, Wu J, Zhang H, Shi L. Optimal sensor scheduling for multiple linear dynamical systems. Automatica, 2017, 75: 260−270 doi: 10.1016/j.automatica.2016.09.015 [11] Ross S M, Cobb R G, Baker W P. Stochastic real-time optimal control for bearing-only trajectory planning. International Journal of Micro Air Vehicles, 2014, 6(1): 1−27 doi: 10.1260/1756-8293.6.1.1 [12] Singh S S, Kantas N, Vo B N, Doucet A, Evans R J. Simulation-based optimal sensor scheduling with application to observer trajectory planning. Automatica, 2007, 43(5): 817−830 doi: 10.1016/j.automatica.2006.11.019 [13] Panicker S, Gostar A K, Bab-Haidashar A, Hoseinnezhad R. Sensor control for selective object tracking using labeled multi-Bernoulli filter. In: Proceedings of the 21st International Conference on Information Fusion. Cambridge, UK: IEEE, 2018. 2218−2224 [14] Song C, Zhang C, Shafieezadeh A, Xiao R. Value of information analysis in non-stationary stochastic decision environments: A reliability-assisted POMDP approach. Reliability Engineering & System Safety, 2022, 217 : Article No. 108034 [15] Gostar A K, Hoseinnezhad R, Bab-Hadiashar A. Sensor control for multi-object tracking using labeled multi-Bernoulli filter. In: Proceedings of the 17th International Conference on Information Fusion. Salamanca, Spain: IEEE, 2014. 1−8 [16] Gostar A K, Hoseinnezhad R, Bab-Hadiashar A. Multi-Bernoulli sensor control via minimization of expected estimation errors. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 1762−1773 doi: 10.1109/TAES.2015.140211 [17] Gostar A K, Hoseinnezhad R, Bab-Hadiashar A, Liu W. Sensor-management for multitarget filters via minimization of posterior dispersion. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(6): 2877−2884 doi: 10.1109/TAES.2017.2718280 [18] Aughenbaugh J M, La Cour B R. Metric selection for information theoretic sensor management. In: Proceedings of the 11th International Conference on Information Fusion. Cologne, Germany: IEEE. 2008. 1−8 [19] Ristic B, Vo B N, Clark D. A note on the reward function for PHD filters with sensor control. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1521−1529 doi: 10.1109/TAES.2011.5751278 [20] Hoang H G, Vo B N, Vo B T, Mahler R. The Cauchy–Schwarz divergence for Poisson point processes. IEEE Transactions on Information Theory, 2015, 61(8): 4475−4485 doi: 10.1109/TIT.2015.2441709 [21] Gostar A K, Hoseinnezhad R, Rathnayake T, Wang X, Bab-Hadiashar A. Constrained sensor control for labeled multi-Bernoulli filter using Cauchy-Schwarz divergence. IEEE Signal Processing Letters, 2017, 24(9): 1313−1317 doi: 10.1109/LSP.2017.2723924 [22] Matsuo Y, LeCun Y, Sahani M, Precup D, Silver D, Sugiyama M, et al. Deep learning, reinforcement learning, and world models. Neural Networks, 2022, 152: 267−275 doi: 10.1016/j.neunet.2022.03.037 [23] Wurman P R, Barrett S, Kawamoto K, MacGlashan J, Subramanian K, Walsh T J, et al. Outracing champion Gran Turismo drivers with deep reinforcement learning. Nature, 2022, 602(7896): 223−228 doi: 10.1038/s41586-021-04357-7 [24] Liu D, Wang Z, Lu B, Cong M, Yu H, Zou Q. A reinforcement learning-based framework for robot manipulation skill acquisition. IEEE Access, 2020, 8: 108429−108437 doi: 10.1109/ACCESS.2020.3001130 [25] Berscheid L, Meißner P, Kröger T. Self-supervised learning for precise pick-and-place without object model. IEEE Robotics and Automation Letters, 2020, 5(3): 4828−4835 doi: 10.1109/LRA.2020.3003865 [26] Luong N C, Hoang D T, Gong S, Niyato D, Wang P, Liang Y C, et al. Applications of deep reinforcement learning in communications and networking: A survey. IEEE Communications Surveys & Tutorials, 2019, 21(4): 3133−3174 [27] Oakes B, Richards D, Barr J, Ralph J. Double deep Q networks for sensor management in space situational awareness. In: Proceeding of the 25th International Conference on Information Fusion. Linköping, Sweden: IEEE, 2022. 1−6 [28] Zheng L, Liu M, Zhang S. An end-to-end sensor scheduling method based on D3QN for underwater passive tracking in UWSNs. Journal of Network and Computer Applications, 2023, 219 : Article No. 103730 [29] Schulman J, Levine S, Abbeel P, Jordan M, Moritz P. Trust region policy optimization. In: Proceedings of the International Conference on Machine Learning. Lille, France: PMLR, 2015. 1889−1897 [30] Schulman J, Wolski F, Dhariwal P, Radford A, Klimov O. Proximal policy optimization algorithms. arXiv preprint arXiv: 1707. 06347, 2017. [31] Lillicrap T P, Hunt J J, Pritzel A, Heess N, Erez T, Tassa Y, et al. Continuous control with deep reinforcement learning. arXiv preprint arXiv: 1509.02971, 2015. [32] Fujimoto S, Hoof H, Meger D. Addressing function approximation error in actor-critic methods. In: Proceedings of the International Conference on Machine Learning. Stockholm, Sweden: PMLR, 2018. 1587−1596 [33] Mosali N A, Shamsudin S S, Alfandi O, Omar R, Al-Fadhali N. Twin delayed deep deterministic policy gradient-based target tracking for unmanned aerial vehicle with achievement rewarding and multistage training. IEEE Access, 2022, 10: 23545−23559 doi: 10.1109/ACCESS.2022.3154388 [34] Li B, Wu Y. Path planning for UAV ground target tracking via deep reinforcement learning. IEEE Access, 2020, 8: 29064−29074 doi: 10.1109/ACCESS.2020.2971780 [35] Tuncer B, Ozkan E. Random matrix based extended target tracking with orientation: A new model and inference. IEEE Transactions on Signal Processing, 2021, 69: 1910−1923 doi: 10.1109/TSP.2021.3065136 [36] Wahlstrom N, Ozkan E. Extended target tracking using Gaussian processes. IEEE Transactions on Signal Processing, 2015, 63(16): 4165−4178 doi: 10.1109/TSP.2015.2424194 [37] Daniyan A, Lambotharan S, Deligiannis A, Gong Y, Chen W H. Bayesian multiple extended target tracking using labeled random finite sets and splines. IEEE Transactions on Signal Processing, 2018, 66(22): 6076−6091 doi: 10.1109/TSP.2018.2873537 [38] Koch J W. Bayesian approach to extended object and cluster tracking using random matrices. IEEE Transactions on Aeros pace and Electronic Systems, 2008, 44(3): 1042−1059 doi: 10.1109/TAES.2008.4655362 [39] Yang S, Baum M, Granström K. Metrics for performance evaluation of elliptic extended object tracking methods. In: Proceedings of the IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems. Baden-Baden, Germany: IEEE, 2016. 523−528 -
点击查看大图
计量
- 文章访问数: 46
- HTML全文浏览量: 25
- 被引次数: 0
