基于PCA和ICA模式融合的非高斯特征检测识别

葛泉波; 程惠茹; 张明川; 郑瑞娟; 朱军龙; 吴庆涛

doi:10.16383/j.aas.c230326

基于PCA和ICA模式融合的非高斯特征检测识别

doi: 10.16383/j.aas.c230326

葛泉波^{1, 2, 3,},
程惠茹^4,,
张明川^4,,
郑瑞娟^4,,
朱军龙^4,,
吴庆涛^4,

1.
南京信息工程大学自动化学院南京 210044
2.
江苏省大气环境与装备技术协同创新中心南京 210044
3.
江苏省大数据分析技术重点实验室南京 210044
4.
河南科技大学信息工程学院洛阳 471023

基金项目: 国家自然科学基金(62033010, U23B2061), 中原科技创新领军人才(224200510004), 江苏高校青蓝工程(R2023Q07), 龙门实验室重大项目(231100220600), 河南省高校科技创新团队(24IRTSTHN022)资助

详细信息

作者简介:
葛泉波：南京信息工程大学教授. 主要研究方向为状态估计与信息融合, 自主智能无人系统, 飞行器测试数据分析和电力IOT技术. E-mail: 003535@nuist.edu.cn

程惠茹：河南科技大学信息工程学院硕士研究生. 主要研究方向为状态估计与信息融合. E-mail: 210321050404@stu.haust.edu.cn

张明川：河南科技大学信息工程学院教授. 主要研究方向为新型网络, 智能信息处理, 医疗辅助诊断和机器学习. 本文通信作者. E-mail: zhang_mch@haust.edu.cn

郑瑞娟：河南科技大学信息工程学院教授. 主要研究方向为移动云计算, 生物启发的网络安全, 物联网安全和智能电网. E-mail: zhengruijuan@haust.edu.cn

朱军龙：河南科技大学信息工程学院副教授. 主要研究方向为大规模优化, 分布式多智能体优化, 随机优化及其在机器学习中的应用. E-mail: jlzhu@haust.edu.cn

吴庆涛：河南科技大学信息工程学院教授. 主要研究方向为工业互联网, 智能系统, 模式识别和机器学习. E-mail: wqt8921@hauet.edu.cn

计量
- 文章访问数: 451
- HTML全文浏览量: 139
- PDF下载量: 167
- 被引次数: 0
出版历程
- 收稿日期: 2023-06-02
- 录用日期: 2023-10-27
- 网络出版日期: 2023-12-18
- 刊出日期: 2024-01-29

Non-Gaussian Feature Detection and Recognition Based on PCA and ICA Pattern Fusion

1.
School of Automation, Nanjing University of Information Science & Technology, Nanjing 210044
2.
Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology, Nanjing 210044
3.
Jiangsu Key Laboratory of Big Data Analysis Technology, Nanjing 210044
4.
School of Information Engineering, Henan University of Science and Technology, Luoyang 471023

Funds: Supported by National Natural Science Foundation of China (62033010, U23B2061), Leading Talents of Science and Technology in the Central Plain of China (224200510004), Qing Lan Project of Jiangsu Province (R2023Q07), Major Project of Longmen Laboratory (231100220600), and Scientific and Technological Innovation Team of Colleges and Universities in Henan Province (24IRTSTHN022)

More Information

Author Bio:
GE Quan-Bo　Professor at Nanjing University of Information Science & Technology. His research interest covers state estimation and information fusion, autonomous intelligent unmanned system, aircraft test data analysis, and power IOT technology

CHENG Hui-Ru　Master student at the School of Information Engineering, Henan University of Science and Technology. Her research interest covers state estimation and information fusion

ZHANG Ming-Chuan　Professor at the School of Information Engineering, Henan University of Science and Technology. His research interest covers new generation network, intelligent information processing, medical aided diagnosis, and machine learning. Corresponding author of this paper

ZHENG Rui-Juan　Professor at the School of Information Engineering, Henan University of Science and Technology. Her research interest covers mobile cloud computing, biologically network security, internet of things security, and smart grid

ZHU Jun-Long　Associate professor at the School of Information Engineering, Henan University of Science and Technology. His research interest covers large-scale optimization, distributed multi-agent optimization, stochastic optimization, and their applications to machine learning

WU Qing-Tao　Professor at the School of Information Engineering, Henan University of Science and Technology. His research interest covers industrial internet, intelligent system, pattern recognition, and machine learning

摘要

摘要: 针对无人船(Unmanned surface vehicle, USV)航行位姿观测数据的非高斯性/高斯性判别问题, 提出一种基于主成分分析(Principal component analysis, PCA)和独立成分分析(Independent component analysis, ICA) 模式融合的非高斯特征检测识别方法. 首先, 采用基于标准化加权平均和信息熵的数据预处理方法. 其次, 引入混合加权核函数并使用灰狼优化(Grey wolf optimization, GWO)算法进行参数优化, 以提高PCA方法的准确性. 同时, 该算法采用一种新的非线性控制因子策略, 提高全局和局部搜索能力. 最后, 建立了一种基于ICA和PCA联合的相关性分析方法来实现多维数据的降维, 在降维数据的基础上综合T型多维偏度峰度检验法和KS (Kolmogorov-Smirnov)检验法进行非高斯性/高斯性特征检测识别. 该方法考虑了非线性非高斯的噪声对降维结果精确度的影响, 有效降低了多维数据非高斯检测的复杂度, 同时也为后续在实际USV位姿估计等应用中提供了保障. 实验表明, 该方法具有较高的准确性和稳定性, 可为 USV 航行位姿观测数据处理提供支持.
- 主成分分析 /
- 混合核函数 /
- 灰狼优化算法 /
- 高维降维 /
- 非高斯
Abstract: A non-Gaussian feature detection and recognition method based on principal component analysis (PCA) and independent component analysis (ICA) pattern fusion is proposed for the non-Gaussian/Gaussian discrimination problem of unmanned surface vehicle (USV) navigation pose observation data. Firstly, a data preprocessing approach based on standardization weighted average and information entropy is adopted. Secondly, a mixed weighted kernel function is introduced and the grey wolf optimization (GWO) algorithm is used for parameter optimization to enhance the accuracy of the PCA method. Moreover, a new non-linear control factor strategy is applied in the algorithm to improve both global and local search abilities. Finally, a correlation analysis method based on ICA and PCA joint is established to realize the dimensionality reduction of multidimensional data, and the non-Gaussian/Gaussian feature detection and recognition is carried out based on the comprehensive T-type multidimensional skewness kurtosis test and KS (Kolmogorov-Smirnov) test method on the basis of dimensionality reduction data. The proposed method takes into account the influence of nonlinear non-Gaussian noise on the accuracy of dimensionality reduction results, which can effectively reduce the complexity of non-Gaussian detection of multidimensional data, and also provide guarantee for the subsequent applications such as actual USV attitude estimation. Experimental results show high accuracy and stability, supporting the processing of USV navigation attitude observation data.
- Principal component analysis (PCA) /
- mixed kernel function /
- grey wolf optimization (GWO) algorithm /
- high-dimensional dimensionality reduction /
- non-Gaussian

HTML全文

图 1 主成分分析改进方案过程

Fig. 1 Principal component analysis improvement plan process

下载: 全尺寸图片幻灯片

图 2 变量$ {A} $与算法搜索的关系

Fig. 2 The relationship between variable ${A} $ and algorithm search

下载: 全尺寸图片幻灯片

图 3 不同控制因子策略的迭代结果

Fig. 3 Iterative results of different control factor strategies

下载: 全尺寸图片幻灯片

图 4 GWO参数优化流程图

Fig. 4 GWO parameter optimization flowchart

下载: 全尺寸图片幻灯片

图 5 ICA-PCA融合过程图

Fig. 5 ICA-PCA fusion process diagram

下载: 全尺寸图片幻灯片

图 6 实际数据采集环境

Fig. 6 Actual data collection environment

下载: 全尺寸图片幻灯片

图 7 单峰函数结果对比图

Fig. 7 Comparison chart of unimodal function results

下载: 全尺寸图片幻灯片

图 8 多峰函数结果对比图

Fig. 8 Comparison chart of multimodal function results

下载: 全尺寸图片幻灯片

图 9 固定维数多峰函数结果对比图

Fig. 9 Comparison chart of fixed dimension multimodal function results

下载: 全尺寸图片幻灯片

图 10 降维主成分结果

Fig. 10 Dimensionality reduction principal component results

下载: 全尺寸图片幻灯片

图 11 三个方向的速度图

Fig. 11 Chart of speed in three directions

下载: 全尺寸图片幻灯片

图 12 降维结果

Fig. 12 Dimensionality reduction results

下载: 全尺寸图片幻灯片

图 13 检测结果1

Fig. 13 Test result 1

下载: 全尺寸图片幻灯片

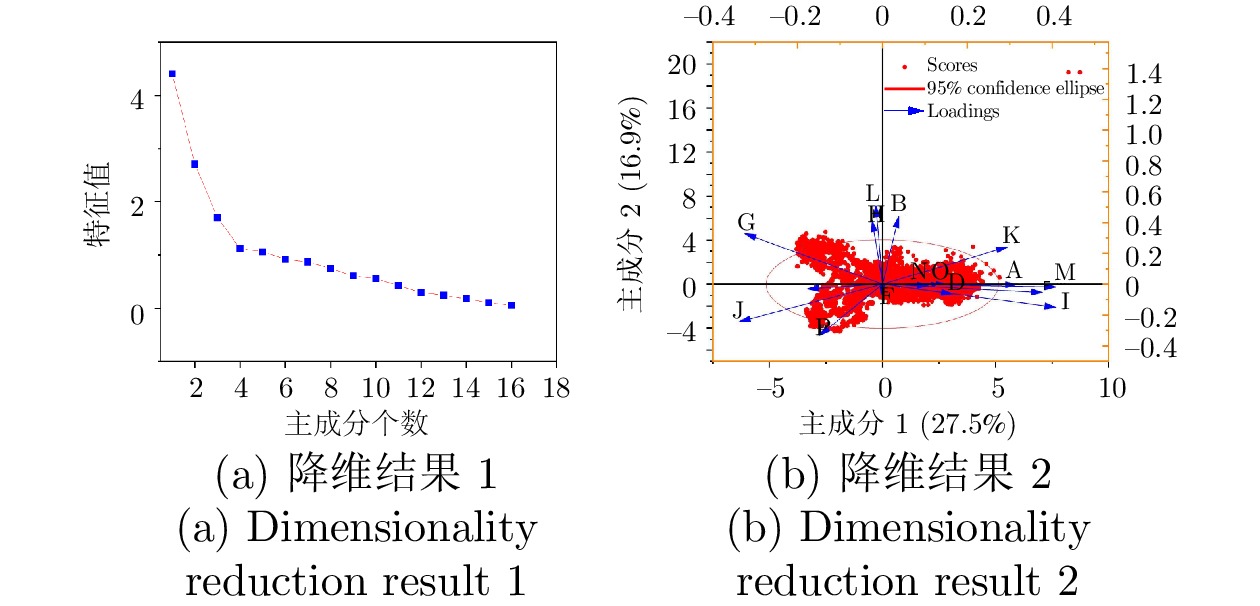
表 1 降维结果对比表

Table 1 Comparison table of dimensionality reduction results

方法名称	累计方差贡献率 (%)
方法名称	80	85	90	95	99
原PCA方法	57	69	70	110	155
EW-PCA方法	6	7	11	45	78
本文改进的PCA方法	5	6	9	36	59

下载: 导出CSV

表 2 ICA-PCA方法对比结果

Table 2 ICA-PCA method comparison results

评价指标	ICA-PCA方法	本文改进方法
主成分个数	53	48
累计贡献率	95%	95%
运行时间(s)	6	4

下载: 导出CSV

表 3 降维结果

Table 3 Dimensionality reduction results

序数	特征值	方差百分比 (%)	累计贡献率 (%)
1	542214.889	38.965	38.965
2	401455.508	28.849	67.814
3	69059.859	4.963	72.777
4	49084.360	3.527	76.304
5	29370.855	2.111	78.414
$ \vdots$	$ \vdots$	$ \vdots$	$ \vdots$
14	8118.445	0.583	87.186
15	7161.289	0.515	87.701

下载: 导出CSV

表 4 正态性检验结果

Table 4 Normality test results

名称	样本量	平均值	标准差	偏度	峰度	Kolmogorov-Smirnov检验		Shapiro-Wilk检验
名称	样本量	平均值	标准差	偏度	峰度	统计量D值	P	统计量W值	P
$x_{1}$	100	34.82	52.531	1.528	1.228	0.254	**	0.712	**
$x_{2}$	100	42.16	38.881	0.936	1.063	0.139	**	0.902	**
$x_{3}$	100	70.18	67.337	0.493	−1.039	0.166	**	0.881	**
$x_{4}$	100	311.51	179.214	0.138	−1.173	0.083	0.086	0.954	**
$ \vdots$	$ \vdots$	$ \vdots$	$ \vdots$	$ \vdots$	$ \vdots$	$ \vdots$	$ \vdots$	$ \vdots$	$ \vdots$
$x_{148}$	100	91.01	62.455	−0.092	−0.807	0.157	**	0.924	**
$x_{149}$	100	3.80	13.206	5.688	40.094	0.473	**	0.321	**
$x_{150}$	100	25.89	28.440	1.015	0.290	0.181	**	0.852	**
* 表示P < 0.05, ** 表示P < 0.01

下载: 导出CSV

表 5 非高斯检测结果

Table 5 Non-Gaussian detection results

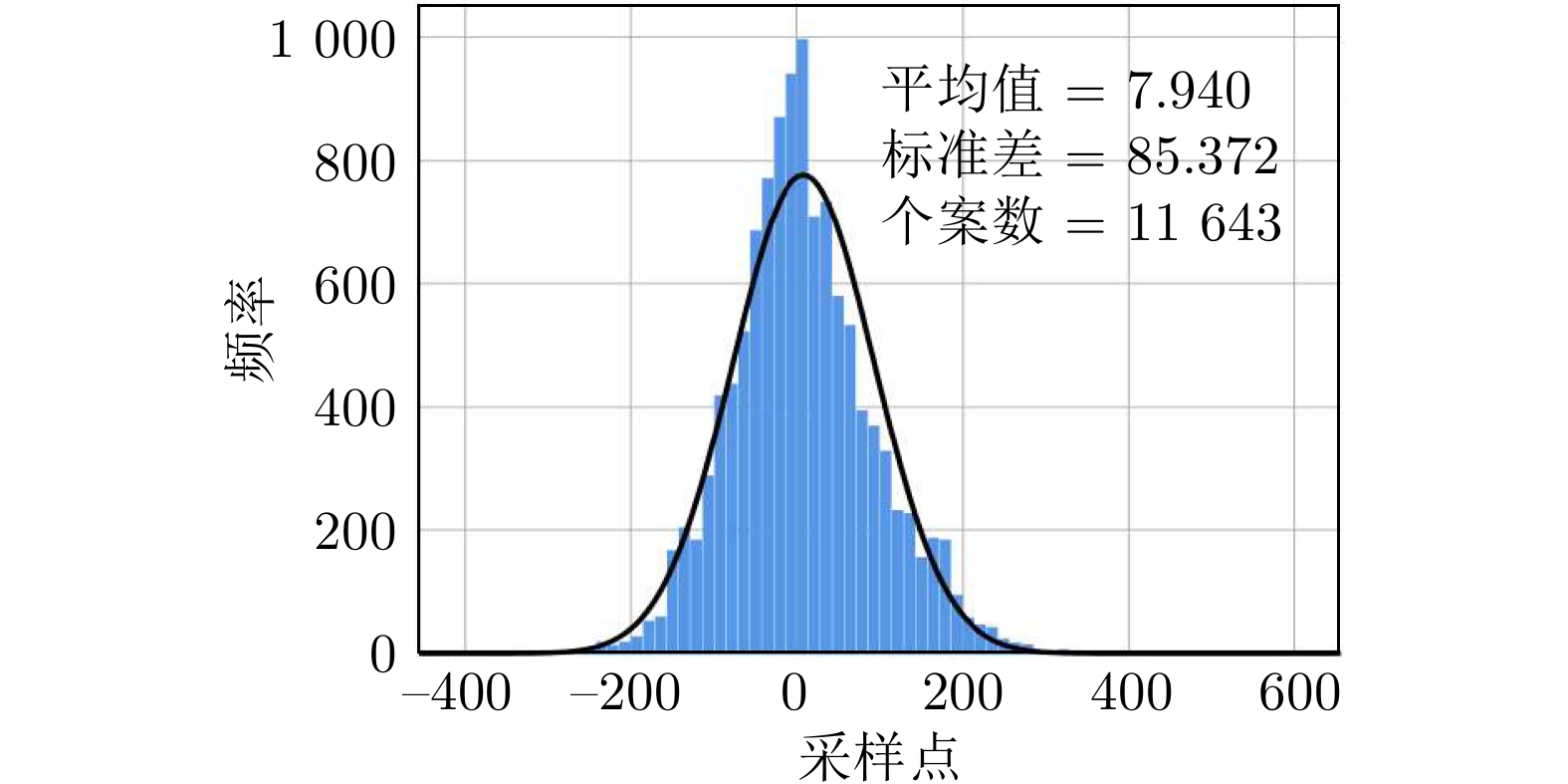
检验结果
总计N		11643
最大极差	绝对	0.049
	正	0.049
	负	−0.020
检验统计量		0.049
渐进显著性(双边检验)		0

下载: 导出CSV

参考文献(34)

[1]	葛泉波, 李文斌, 孙若愚, 徐姿. 基于EKF的集中式融合估计研究[J]. 自动化学报, 2013, 39(6): 816-825 Ge Quan-Bo, Li Wen-Bin, Sun Ruo-Yu, Xu Zi. Centralized fusion algorithms based on EKF for multisensor non-linear systems. Acta Automatica Sinica, 2013, 39(6): 816-825
[2]	Fu H P, Cheng Y M. An enhanced adaptive Kalman filtering for linear systems with inaccurate noise statistics. Asian Journal of Control, 2023, 25(4): 3269-3281 doi: 10.1002/asjc.2964
[3]	Gao Y, Gao Z, Zong H, Gao S S, Hong G Y. Adaptive weighted federated Kalman filtering based on Mahalanobis distance and its application in navigation. IET Communications, 2023, 17(17): 1962-1973 doi: 10.1049/cmu2.12664
[4]	徐小良, 汤显峰, 葛泉波, 管冰蕾. 基于量化新息的容积粒子滤波融合目标跟踪算法. 自动化学报, 2014, 40(9): 1867-1874 Xu Xiao-Liang, Tang Xian-Feng, Ge Quan-Bo, Guan Bing-Lei. Target tracking algorithm based on cubature particle filtering fusion with quantized innovation. Acta Automatica Sinica, 2014, 40(9): 1867-1874
[5]	Mardia K V. Measures of multivariate skewness and kurtosis with applications. Biometrika, 1970, 57(3): 519-530 doi: 10.1093/biomet/57.3.519
[6]	Srivastava M S. A measure of skewness and kurtosis and a graphical method for assessing multivariate normality. Statistics Probability Letters, 1984, 2(5): 263-267 doi: 10.1016/0167-7152(84)90062-2
[7]	Mardia K V. Applications of some measures of multivariate skewness and kurtosis in testing normality and robustness studies. Sankhyā: The Indian Journal of Statistics, Series B, 1974: 115-128
[8]	田禹. 基于偏度和峰度的正态性检验 [硕士学位论文], 上海交通大学, 中国, 2012. Tian Yu. Tests for Normality Based on Skewness and Kurtosis [Master thesis], Shanghai Jiao Tong University, China, 2012.
[9]	梁少军, 张世荣, 孙澜琼. 基于最优密度方向的等距映射降维算法. 控制理论与应用, 2021, 38(4): 467-478 Liang Shao-Jun, Zhang Shi-Rong, Sun Lan-Qiong. Optimal density direction based isometric mapping dimensionality reduction algorithm. Control Theory & Applications, 2021, 38(4): 467-478
[10]	王继奎, 杨正国, 刘学文, 易纪海, 李冰, 聂飞平. 一种基于极大熵的快速无监督线性降维方法. 软件学报, 2023, 34(4): 1779-1795 Wang Ji-Kui, Yang Zheng-Guo, Liu Xue-Wen, Yi Ji-Hai, Li Bing, Nie Fei-Ping. Fast unsupervised dimension reduction method based on maximum entropy. Journal of Software, 2023, 34(4): 1779-1795
[11]	高月, 宿翀, 李宏光. 一类基于非线性PCA和深度置信网络的混合分类器及其在PM2.5浓度预测和影响因素诊断中的应用. 自动化学报, 2018, 44(2): 318-329 Gao Yue, Su Chong, Li Hong-Guang. A kind of deep belief networks based on nonlinear features extraction with application to PM2.5 concentration prediction and diagnosis. ACTA AUTOMATICA SINICA, 2018, 44(2): 318-329
[12]	Yang Z L, Shi Y Q, Li P L, Pan K H, Li G Q, Li X Q, et al. Application of principal component analysis(PCA) to the evaluation and screening of multiactivity fungi.Journal of Ocean University of China, 2022, 21(3): 763-772 doi: 10.1007/s11802-022-5096-x
[13]	孙平安, 王备战. 机器学习中的PCA降维方法研究及其应用. 湖南工业大学学报, 2019, 33(1): 80-85 Sun Ping-An, Wang Bei-Zhan. Research on PCA dimension reduction with its application in machine learning.Joural of Hunan University of Technology, 2019, 33(1): 80-85
[14]	Zhou Y H, Zhang X W, Wang J M, Gong Y. Research on speaker feature dimension reduction based on CCA and PCA. In: Proceedings of the International Conference on Wireless Communications & Signal Processing (WCSP). Suzhou, China: IEEE, 2010. 1−4
[15]	Sharma N, Saroha K. A novel dimensionality reduction method for cancer dataset using PCA and feature ranking. In: Proceedings of the International Conference on Advances in Computing, Communications and Informatics (ICACCI). Kochi, India: IEEE, 2015. 2261−2264
[16]	刘文博, 梁盛楠, 董小刚. 基于t类加权核函数的主成分分析维度约简算法. 统计与决策, 2022, 38(9): 52-56 Liu Wen-Bo, Liang Sheng-Nan, Dong Xiao-Gang. PCA dimension reduction algorithm based on t class weighted kernel function.Statistics & Decision, 2022, 38(9): 52-56
[17]	Li X H, Jia R C, Zhang R R, Yang S Y, Chen G M. A KPCA-BRANN based data-driven approach to model corrosion degradation of subsea oil pipelines. Reliability Engineering System Safety, 2022, 219: Article No. 108231 doi: 10.1016/j.ress.2021.108231
[18]	张成, 高宪文, 李元. 基于k近邻主元得分差分的故障检测策略. 自动化学报, 2020, 46(10): 2229-2238 Zhang Cheng, Gao Xian-Wen, Li Yuan. Fault detection strategy based on principal component score difference of k nearest neighbors. Acta Automatica Sinica, 2020, 46(10): 2229-2238
[19]	左益宏, 王远亮, 何红丽等. 基于GA-BPNN的自适应抗野值无迹Kalman滤波方法. 空军工程大学学报(自然科学版), 2021, 22(05): 30-36 Zuo Yi-Hong, Wang Yuan-Liang, He Hong-Li. An Adaptive Anti-Outliter Unscented Kalman Filtering Method Based on GA-BPNN.Journal of Air Force Engineering University(Natural Science Edition), 2021, 22(05): 30-36
[20]	常海涛, 蔡静, 温悦, 朱玉梅. 一种基于主成分分析的TDLAS高频噪声滤波. 计量学报, 2022, 43(10): 1285-1290 Chang Hai-Tao, Cai Jing, Wen Yue, Zhu Yu-Mei. A principal component analysis method for TDLAS to remove high frequency noise. Acta Metrologica Sinica, 2022, 43(10): 1285-1290
[21]	Yuan J J, Shao H, Cai Y, Shi X H. Energy efficiency state identification of milling processing based on EEMD-PCA-ICA. Measurement, 2021, 174.
[22]	韩丽黎. 基于非高斯特征提取的复杂工业过程建模与监控方法研究 [硕士学位论文], 中国计量大学, 中国, 2020. Han Li-Li. Research on Modeling and Monitoring of Complex Industrial Processes Based on Non-Gaussian Feature Extraction [Master thesis], China Jiliang University, China, 2020.
[23]	王肖锋, 陆程昊, 郦金祥等. 广义余弦二维主成分分析[J]. 自动化学报, 2022, 48(11): 2836-2851 Wang Xiaofeng, Lu Chenghao, Li Jinxiang, Liu Jun. Generalized cosine two-dimensional principal component analysis. Acta Automatica Sinica, 2022, 48(11): 2836-2851
[24]	马兴亮. 建筑结构表面风压非高斯特性分析方法研究 [博士学位论文], 大连理工大学, 中国, 2019. Ma Xing-Liang. Study on Non-Gaussian Characteristic Analysis Methods of Wind Pressures on Building Surface [Ph.D. dissertation], Dalian University of Technology, China, 2019.
[25]	高山. 海洋工程结构物的非高斯响应极值与疲劳研究 [博士学位论文], 大连理工大学, 中国, 2019. Gao Shan. Non-Gaussian Response Extrema and Fatigue of Marine Stuctures [Ph.D. dissertation], Dalian University of Technology, China, 2019.
[26]	江伟华, 童峰, 王彬, 刘世刚. 采用主分量分析的非合作水声通信信号调制识别. 兵工学报, 2016, 37(9): 1670-1676 Jiang Wei-Hua, Tong Feng, Wang Bin, Liu Shi-Gang. Method of recognition non-cooperation underwater acoustic communication signals using principal component analysis.Acta Armamentarii, 2016, 37 (9): 1670-1676
[27]	Yan X C, Lin Z, Lin Z H, Lin Z Y, Vucetic B. A novel exploitative and explorative GWO-SVM algorithm for smart emotion recognition. IEEE Internet of Things Journal, 2023, 10(11): 9999-10011 doi: 10.1109/JIOT.2023.3235356
[28]	Jain M, Saihjpal V, Singh N, Singh S B. An overview of variants and advancements of PSO algorithm. Applied Sciences, 2022, 12, 17: Article No. 8392 doi: 10.3390/app12178392
[29]	张新明, 姜云, 刘尚旺, 刘国奇, 窦智, 刘艳. 灰狼与郊狼混合优化算法及其聚类优化. 自动化学报, 2022, 48, 11: 2757-2776 Zhang Xin-Ming, Jiang Yun, Liu Shang-Wang, Liu Guo-Qi, Dou Zhi, Liu Yan. Hybrid coyote optimization algorithm with grey wolf optimizer and its application to clustering optimization. Acta Automatica Sinica, 2022, 48(11): 2757-2776
[30]	Gupta S, Deep K. Hybrid grey wolf optimizer with mutation operator. In: Proceedings of the Soft Computing for Problem Solving. Singapore: Springer Singapore, 2019. 961−968
[31]	汤影, 李建平, 吴淮. 一种分离低维信号的ICA快速算法. 自动化学报, 2011, 37(7): 794-799 doi: 10.1016/S1874-1029(11)60210-3 Tang Ying, Li Jian-Ping, Wu Huai. A simple and accurate ICA algorithm for separating mixtures of Up to Four Independent Components. Acta Automatica Sinica, 2011, 37(7): 794-799. doi: 10.1016/S1874-1029(11)60210-3
[32]	Zhang L, Wang L. Optimization of site investigation program for reliability assessment of undrained slope using Spearman rank correlation coefficient[J]. Computers and Geotechnics, 2023, 155: Article No. 105208 doi: 10.1016/j.compgeo.2022.105208
[33]	杨斌. 正态性检验的几种方法比较. 统计与决策, 2015, 14:72-74 Yang Bin.Comparison of Several Methods for Testing Normality. Statistics & Decision, 2015, 14:72-74
[34]	丁勇. 多元正态分布的一个特殊积分和拟合优度检验. 统计与决策, 2020, 36(4): 18-21 Ding Yong. A special integral and goodness-of-fit test for multivariate normal distribution, Statistics & decision, 2020, 36(4): 18-21