基于突触巩固机制的前馈小世界神经网络设计

李文静; 李治港; 乔俊飞

doi:10.16383/j.aas.c220638

基于突触巩固机制的前馈小世界神经网络设计

doi: 10.16383/j.aas.c220638

李文静^{1, 2, 3, 4, 5,},
李治港^{1, 2, 3, 4, 5,},
乔俊飞^{1, 2, 3, 4, 5,}

1.
北京工业大学信息学部北京 100124
2.
北京人工智能研究院北京 100124
3.
智能感知与自主控制教育部工程研究中心北京 100124
4.
计算智能与智能系统北京市重点实验室北京 100124
5.
智慧环保北京实验室北京 100124

基金项目: 国家重点研发计划(2021ZD0112301), 国家自然科学基金(62173008, 62021003, 61890930-5) 资助

详细信息

作者简介:
李文静：北京工业大学信息学部副教授. 主要研究方向为神经网络计算, 污水处理过程智能建模. 本文通信作者. E-mail: wenjing.li@bjut.edu.cn

李治港：北京工业大学信息学部硕士研究生. 主要研究方向为神经网络结构设计与优化, 污水处理过程特征建模. E-mail: lzg551602@emails.bjut.edu.cn

乔俊飞：北京工业大学信息学部教授. 主要研究方向为污水处理过程智能控制, 神经网络结构设计与优化. E-mail: adqiao@bjut.edu.cn

计量
- 文章访问数: 610
- HTML全文浏览量: 80
- PDF下载量: 134
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-11
- 录用日期: 2022-11-12
- 网络出版日期: 2022-12-20
- 刊出日期: 2023-10-24

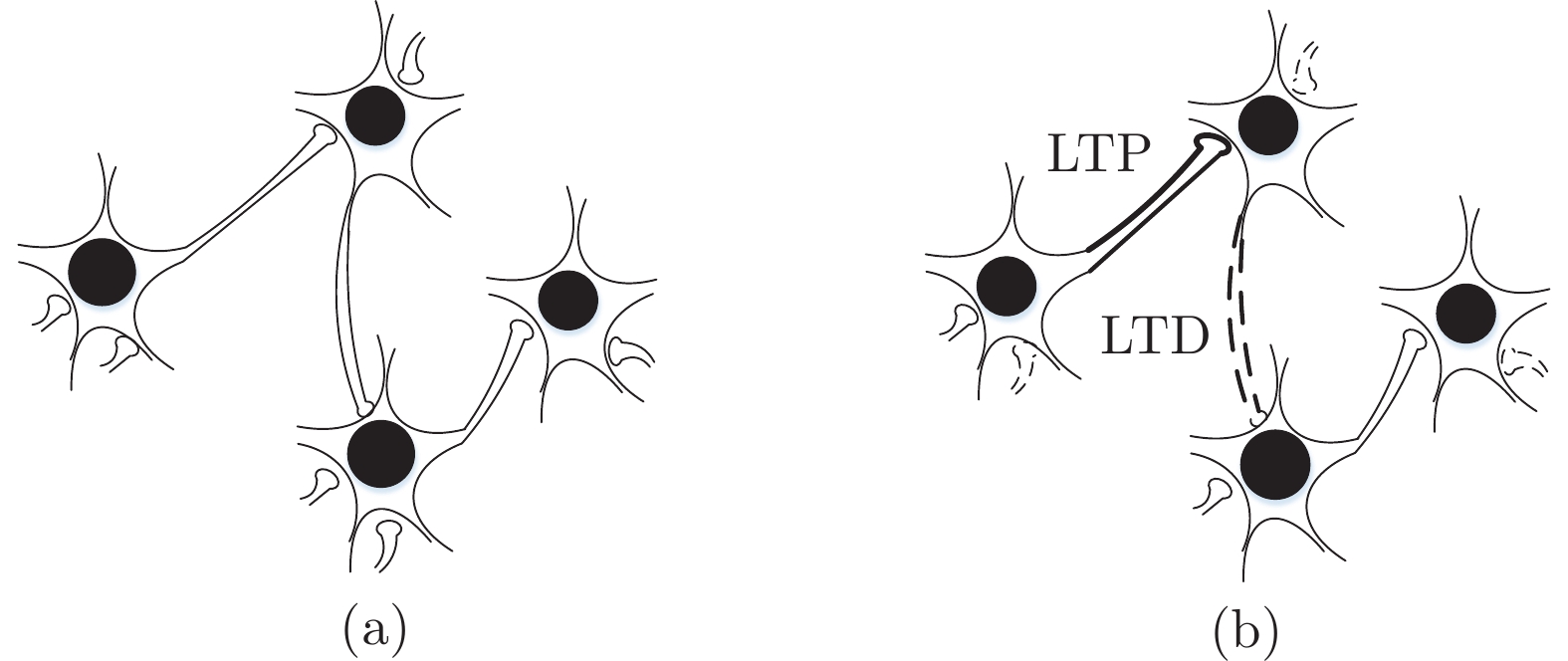
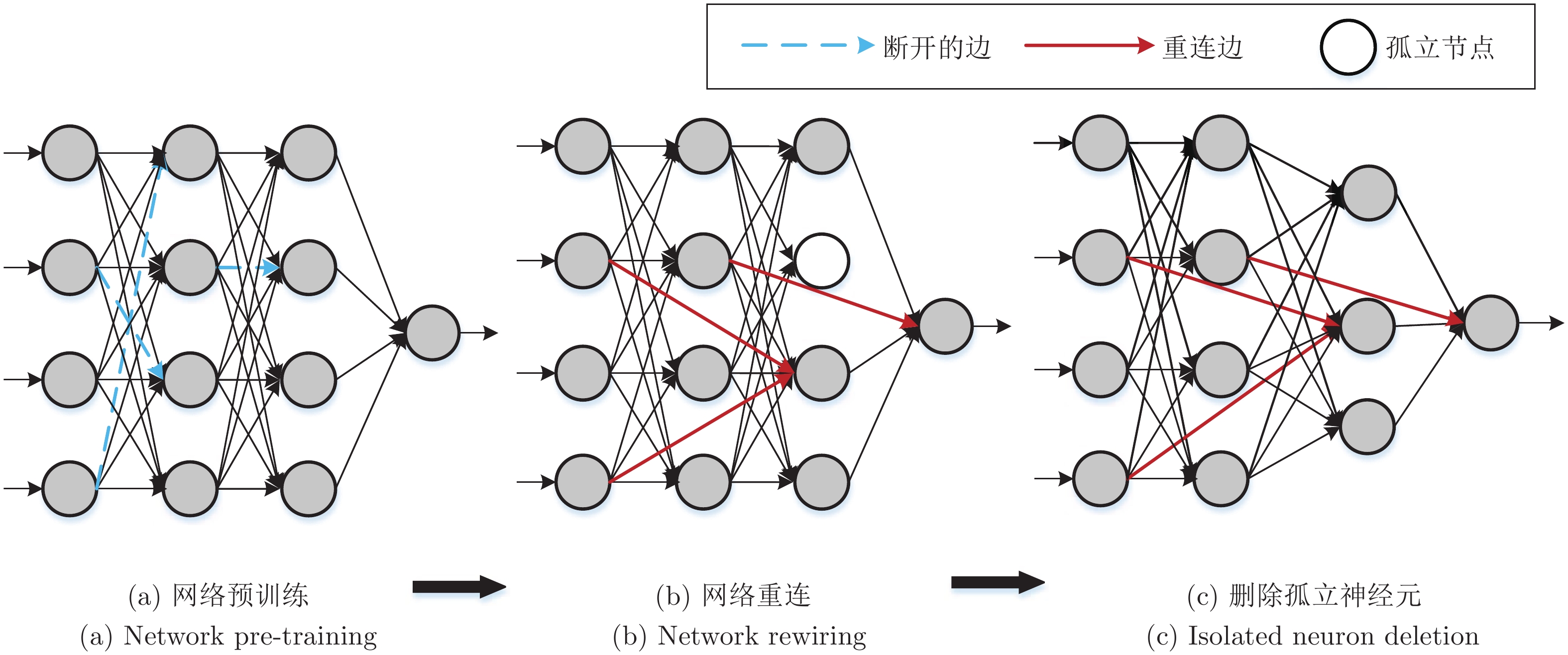
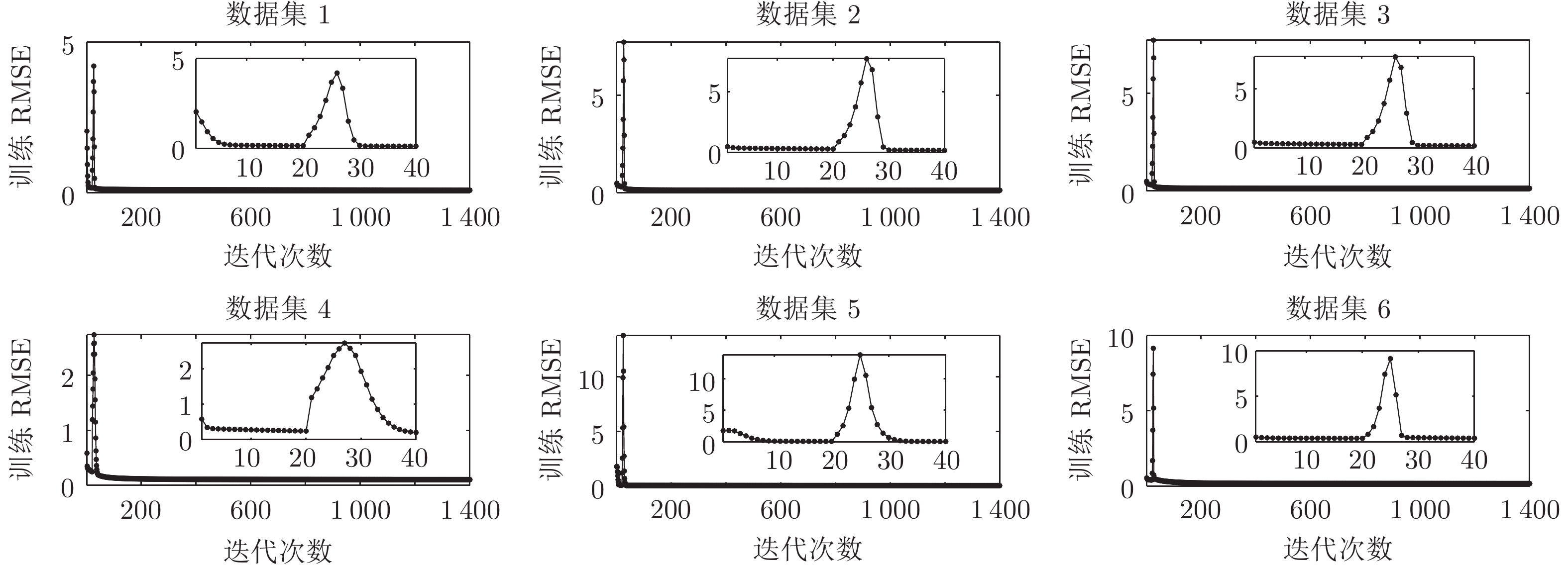
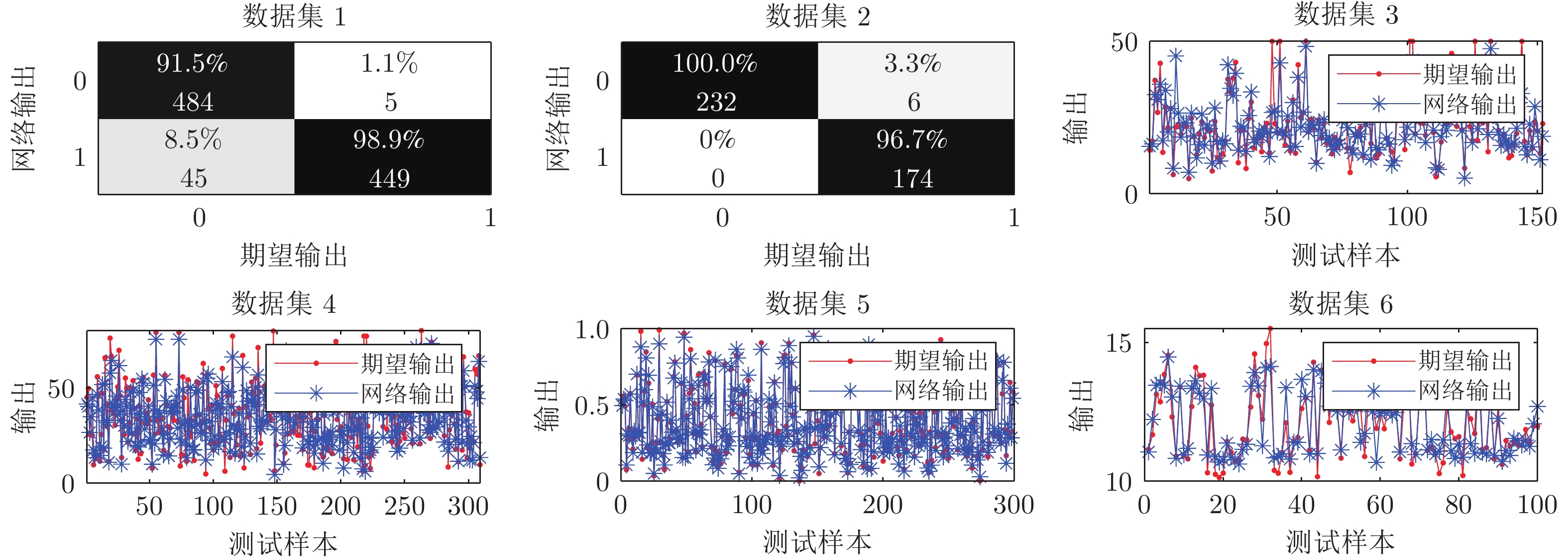
Structure Design for Feedforward Small-world Neural Network Based on Synaptic Consolidation Mechanism

LI Wen-Jing^{1, 2, 3, 4, 5
,},
LI Zhi-Gang^{1, 2, 3, 4, 5
,},
QIAO Jun-Fei^{1, 2, 3, 4, 5
,}

1.
Faculty of Information Technology, Beijing University of Technology, Beijing 100124
2.
Beijing Artificial Intelligence Institute, Beijing 100124
3.
Engineering Research Center of Intelligence Perception and Autonomous Control, Ministry of Education, Beijing 100124
4.
Beijing Key Laboratory of Computational Intelligence and Intelligent System, Beijing 100124
5.
Beijing Laboratory for Intelligent Environmental Protection, Beijing 100124

Funds: Supported by National Key Research and Development Program of China (2021ZD0112301) and National Natural Science Foundation of China (62173008, 62021003, 61890930-5)

More Information

Author Bio:
LI Wen-Jing　Associate professor at the Faculty of Information Technology, Beijing University of Technology. Her research interest covers neural network computation and intelligent modelling in wastewater treatment process. Corresponding author of this paper

LI Zhi-Gang　Master student at the Faculty of Information Technology, Beijing University of Technology. His research interest covers structure design and optimization of neural networks, and feature modelling in wastewater treatment process

QIAO Jun-Fei　Professor at the Faculty of Information Technology, Beijing University of Technology. His research interest covers intelligent control of wastewater treatment process and structure design and optimization of neural networks

摘要

摘要: 小世界神经网络具有较快的收敛速度和优越的容错性, 近年来得到广泛关注. 然而, 在网络构造过程中, 随机重连可能造成重要信息丢失, 进而导致网络精度下降. 针对该问题, 基于Watts-Strogatz (WS) 型小世界神经网络, 提出了一种基于突触巩固机制的前馈小世界神经网络(Feedforward small-world neural network based on synaptic consolidation, FSWNN-SC). 首先, 使用网络正则化方法对规则前馈神经网络进行预训练, 基于突触巩固机制, 断开网络不重要的权值连接, 保留重要的连接权值; 其次, 设计重连规则构造小世界神经网络, 在保证网络小世界属性的同时实现网络稀疏化, 并使用梯度下降算法训练网络; 最后, 通过4个UCI基准数据集和2个真实数据集进行模型性能测试, 并使用Wilcoxon符号秩检验对对比模型进行显著性差异检验. 实验结果表明: 所提出的FSWNN-SC模型在获得紧凑的网络结构的同时, 其精度显著优于规则前馈神经网络及其他WS型小世界神经网络.
- 小世界神经网络 /
- 突触巩固机制 /
- 网络正则化 /
- 重连规则 /
- Wilcoxon符号秩检验
Abstract: Because of faster convergence speed and superior fault tolerance, small-world neural network has attracted wide attention in recent years. However, in the construction process, it may cause the loss of important information due to random reconnection, which may lead to the decline of network accuracy. To solve this problem, derived from the Watts-Strogatz (WS) small-world neural network, a feedforward small-world neural network based on synaptic consolidation (FSWNN-SC) mechanism is proposed in this study. Firstly, the regular feedforward neural network is pre-trained by using the network regularization method. Based on the synaptic consolidation mechanism, the unimportant connection weights of the network are disconnected and the important connection weights are retained. Secondly, the rewiring rules are designed to construct a small-world neural network, which can realize the sparseness of the network while ensuring the small-world properties of the network. The gradient descent algorithm is used to train the network. Finally, four UCI benchmark experiments and two practical experiments are carried out to evaluate the model performance, and the Wilcoxon signed-ranks test is performed to test the significant differences between comparative models. Experimental results show that the FSWNN-SC model proposed in this study not only obtains a compact network structure, but also has significantly better accuracy than regular feedforward neural networks and other WS small-world neural networks.
- Small-world neural networks /
- synaptic consolidation mechanism /
- network regularization /
- rewiring rule /
- Wilcoxon signed-ranks test

HTML全文

图 1 前馈神经网络结构示意图

Fig. 1 The architecture of feedforward neural network

下载: 全尺寸图片幻灯片

图 2 突触巩固

Fig. 2 Synaptic consolidation

下载: 全尺寸图片幻灯片

图 3 基于突触巩固小世界神经网络构造流程

Fig. 3 Construction process of small-world neural network based on synaptic consolidation

下载: 全尺寸图片幻灯片

图 4 FSWNN-SC算法流程图

Fig. 4 The flowchart of FSWNN-SC

下载: 全尺寸图片幻灯片

图 5 网络小世界属性$\eta$与重连概率$P$的关系曲线$(P\text{-}\eta$曲线)

Fig. 5 The curves for the relationship between the small-world property $\eta$ and the rewiring probability $P\;(P\text{-}\eta$ curves)

下载: 全尺寸图片幻灯片

图 6 预训练次数对网络性能的影响

Fig. 6 Influence of pre-training epochs on network performance

下载: 全尺寸图片幻灯片

图 7 训练过程RMSE曲线

Fig. 7 The RMSE curves in the training process

下载: 全尺寸图片幻灯片

图 8 测试集样本拟合与分类效果

Fig. 8 Test set sample fitting and classification effects

下载: 全尺寸图片幻灯片

表 1 实验超参数设置

Table 1 Setting of the hyperparameters in experiments

数据集	网络结构	$\lambda$	$\mu$	$iter_{\mathrm{max}}$	$\mathrm{RMSE}_d$
数据集1	8-15-15-1	$1.0\times10^{-3}$	0.0003	6000	0.001
数据集2	4-15-15-1	$1.0\times10^{-3}$	0.0008	6000	0.001
数据集3	13-20-20-1	$1.0\times10^{-6}$	0.0008	10000	0.001
数据集4	8-20-20-1	$1.0\times10^{-6}$	0.0008	10000	0.001
数据集5	6-20-20-1	$1.0\times10^{-6}$	0.0005	10000	0.001
数据集6	10-20-20-1	$1.0\times10^{-6}$	0.0008	10000	0.001

下载: 导出CSV

表 2 分类实验结果对比

Table 2 Comparison results in classification experiments

分类实验	网络	网络结构	稀疏度SP	测试 Acc		训练时间 (s)
分类实验	网络	网络结构	稀疏度SP	均值	标准差	均值	标准差
数据集1	FSWNN-SC	8-15-12-1	0.8861	0.9472	0.0034	3.9631	0.1936
	PFSWNN-SL	8-15-11-1	0.7511	0.9403	0.0026	5.6645	0.2085
	PFSWNN-Katz	8-12-10-1	0.6056	0.9396	0.0126	4.0555	0.2764
	FSWNN-TO	8-15-15-1	—	0.9392	0.0066	5.4922	0.0147
	FSWNN-WS	8-15-15-1	—	0.9374	0.0073	3.9371	0.1255
	FNN	8-15-15-1	—	0.9195	0.0093	3.7201	0.0609
数据集2	FSWNN-SC	4-15-12-1	0.8950	0.9883	0.0049	2.7552	0.4252
	PFSWNN-SL	4-15-10-1	0.6608	0.9788	0.0081	4.6556	0.2525
	PFSWNN-Katz	4-10-11-1	0.5463	0.9823	0.0054	2.8007	0.1837
	FSWNN-TO	4-15-15-1	—	0.9840	0.0040	3.6596	0.0614
	FSWNN-WS	4-15-15-1	—	0.9782	0.0071	2.3605	0.0419
	FNN	4-15-15-1	—	0.9756	0.0132	2.3402	0.0347

下载: 导出CSV

表 3 回归实验结果对比

Table 3 Comparison results in regression experiments

回归实验	网络	网络结构	稀疏度SP	测试NRMSE		训练时间 (s)
回归实验	网络	网络结构	稀疏度SP	均值	标准差	均值	标准差
数据集3	FSWNN-SC	13-20-13-1	0.7941	0.4331	0.0199	2.9838	0.0978
	PFSWNN-SL	13-20-14-1	0.7265	0.4546	0.0187	6.9352	0.2077
	PFSWNN-Katz	13-15-16-1	0.7563	0.4551	0.0200	4.6810	0.1358
	FSWNN-TO	13-20-20-1	—	0.4476	0.0193	4.3250	0.0267
	FSWNN-WS	13-20-20-1	—	0.4582	0.0232	2.9583	0.0609
	FNN	13-20-20-1	—	0.5728	0.0235	3.1481	0.1228
数据集4	FSWNN-SC	8-20-16-1	0.8865	0.4814	0.0308	4.7431	0.1883
	PFSWNN-SL	8-20-17-1	0.7706	0.5104	0.0275	8.4518	0.3075
	PFSWNN-Katz	8-17-18-1	0.8064	0.5159	0.0234	5.6207	0.5053
	FSWNN-TO	8-20-20-1	—	0.4944	0.0147	5.8352	0.0231
	FSWNN-WS	8-20-20-1	—	0.5142	0.0222	4.6306	0.1288
	FNN	8-20-20-1	—	0.6691	0.0058	4.4024	0.0585
数据集5	FSWNN-SC	6-20-14-1	0.7952	0.1351	0.0017	5.0063	0.2048
	PFSWNN-SL	6-20-14-1	0.6698	0.1405	0.0080	8.3014	0.3069
	PFSWNN-Katz	6-17-14-1	0.6647	0.1371	0.0031	5.2003	0.4510
	FSWNN-TO	6-20-20-1	—	0.1374	0.0032	5.5165	0.1494
	FSWNN-WS	6-20-20-1	—	0.1378	0.0026	4.8520	0.2943
	FNN	6-20-20-1	—	0.1544	0.0084	5.0213	0.4910
数据集6	FSWNN-SC	10-20-16-1	0.8663	0.4055	0.0101	2.7706	0.1334
	PFSWNN-SL	10-20-15-1	0.7298	0.4168	0.0112	6.2909	0.0112
	PFSWNN-Katz	10-15-18-1	0.7649	0.4139	0.0093	3.5227	0.4455
	FSWNN-TO	10-20-20-1	—	0.4124	0.0143	3.2057	0.0388
	FSWNN-WS	10-20-20-1	—	0.4144	0.0102	2.7778	0.0161
	FNN	10-20-20-1	—	0.4309	0.0134	2.7206	0.0132

下载: 导出CSV

表 4 Wilcoxon符号秩检验结果

Table 4 Results of Wilcoxon signed-rank test

实验	模型	${R^+}$	${R^-}$	$Z$	${P_{w}}$
	FSWNN-SC vs. PFSWNN-SL	206	4	−3.7706	0.0002*
	FSWNN-SC vs. PFSWNN-Katz	179	31	−2.7626	0.0058*
数据集1	FSWNN-SC vs. FSWNN-TO	203	7	−3.6586	0.0002*
	FSWNN-SC vs. FSWNN-WS	198.5	11.5	−3.4906	0.0004*
	FSWNN-SC vs. FNN	210	0	−3.9199	0*
	FSWNN-SC vs. PFSWNN-SL	203.5	6.5	−3.6773	0.0002*
	FSWNN-SC vs. PFSWNN-Katz	177	33	−2.6880	0.0074*
数据集2	FSWNN-SC vs. FSWNN-TO	176.5	33.5	−2.6693	0.0076*
	FSWNN-SC vs. FSWNN-WS	199.5	10.5	−3.5279	0.0004*
	FSWNN-SC vs. FNN	206.5	3.5	−3.7893	0.0004*
	FSWNN-SC vs. PFSWNN-SL	187	23	−3.0613	0.0022*
	FSWNN-SC vs. PFSWNN-Katz	207	3	−3.8079	0.0002*
数据集3	FSWNN-SC vs. FSWNN-TO	190	20	−3.1733	0.0016*
	FSWNN-SC vs. FSWNN-WS	209	1	−3.8826	0.0002*
	FSWNN-SC vs. FNN	210	0	−3.9199	0*
	FSWNN-SC vs. PFSWNN-SL	184	26	−2.9493	0.0032*
	FSWNN-SC vs. PFSWNN-Katz	210	0	−3.9199	0.0000*
数据集4	FSWNN-SC vs. FSWNN-TO	159	51	−2.0160	0.0434*
	FSWNN-SC vs. FSWNN-WS	208	2	−3.8453	0.0002*
	FSWNN-SC vs. FNN	210	0	−3.9199	0*
	FSWNN-SC vs. PFSWNN-SL	187	23	−3.0613	0.0022*
	FSWNN-SC vs. PFSWNN-Katz	169	41	−2.3893	0.0168*
数据集5	FSWNN-SC vs. FSWNN-TO	177	33	−2.6880	0.0074*
	FSWNN-SC vs. FSWNN-WS	190	20	−3.1733	0.0016*
	FSWNN-SC vs. FNN	210	0	−3.9199	0*
	FSWNN-SC vs. PFSWNN-SL	171	39	−2.4640	0.0138*
	FSWNN-SC vs. PFSWNN-Katz	160	50	−2.0533	0.0434*
数据集6	FSWNN-SC vs. FSWNN-TO	177	33	−2.6880	0.0074*
	FSWNN-SC vs. FSWNN-WS	172	38	−2.5013	0.0124*
	FSWNN-SC vs. FNN	210	0	−3.9199	0*

下载: 导出CSV

参考文献(46)

[1]	Tran V P, Santoso F, Garrat M A, Anavatti S G. Neural network-based self-learning of an adaptive strictly negative imaginary tracking controller for a quadrotor transporting a cable-suspended payload with minimum swing. IEEE Transactions on Industrial Electronics, 2021, 68(10): 10258-10268 doi: 10.1109/TIE.2020.3026302
[2]	Zhang G H, Li B, Wu J X, Wang R, Lan Y Z, Sun L, et.al. A low-cost and high-speed hardware implementation of spiking neural network. Neurocomputing, 2020, 382: 106-115 doi: 10.1016/j.neucom.2019.11.045
[3]	Lv H, Wen M, Lu R A, Li J. An adversarial attack based on incremental learning techniques for unmanned in 6G scenes. IEEE Transactions on Vehicular Technology, 2021, 70(6): 5254-5264 doi: 10.1109/TVT.2021.3069426
[4]	Li W J, Li M, Zhang J K, Qiao J F. Design of a self-organizing reciprocal modular neural network for nonlinear system modeling. Neurocomputing, 2020, 411: 327-339 doi: 10.1016/j.neucom.2020.06.056
[5]	乔俊飞, 丁海旭, 李文静. 基于WTFMC算法的递归模糊神经网络结构设计. 自动化学报, 2020, 46(11): 2367-2378 doi: 10.16383/j.aas.c180847 Qiao Jun-Fei, Ding Hai-Xu, Li Wen-Jing. Structure design for recurrent fuzzy neural network based on wavelet transform fuzzy markov chain. Acta Automatica Sinica, 2020, 46(11): 2367-2378 doi: 10.16383/j.aas.c180847
[6]	冯永, 陈以刚, 强保华. 融合社交因素和评论文本卷积网络模型的汽车推荐研究. 自动化学报, 2019, 45(3): 518-529 Feng Yong, Chen Yi-Gang, Qiang Bao-Hua. Social and comment text CNN model based automobile recommendation. Acta Automatica Sinica, 2019, 45(3): 518-529
[7]	Wang S, Cao J, Yu P S. Deep learning for spatio-temporal data mining: A survey. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(8): 3681-3700 doi: 10.1109/TKDE.2020.3025580
[8]	陈清江, 张雪. 基于并联卷积神经网络的图像去雾. 自动化学报, 2021, 47(7): 1739-1748 Chen Qing-Jiang, Zhang Xue. Single image dehazing based on multiple convolutional neural networks. Acta Automatica Sinica, 2021, 47(7): 1739-1748
[9]	Jiao Y, Yao H, Xu C. SAN: Selective alignment network for cross-domain pedestrian detection. IEEE Transactions on Image Processing, 2021, 30: 2155-2167 doi: 10.1109/TIP.2021.3049948
[10]	Otter D W, Medina J R, Kalita J K. A Survey of the Use of Deep Learning for Natural Language Processing. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(2): 604-624 doi: 10.1109/TNNLS.2020.2979670
[11]	奚雪峰, 周国栋. 面向自然语言处理的深度学习研究. 自动化学报, 2016, 42(10): 1445-1465 Xi Xue-Feng, Zhou Guo-Dong. A survey on deep learning for natural language processing. Acta Automatica Sinica, 2016, 42(10): 1445-1465
[12]	Watts D J, Strogatz S H. Collective dynamics of small world networks. Nature, 1998, 393(4): 440-442
[13]	Bassett D S, Bullmore E. Small-world brain networks. Neuroscientist, 2006, 12(6): 512-523 doi: 10.1177/1073858406293182
[14]	Strogatz S H. Exploring complex networks. Nature, 2001, 410: 268-276 doi: 10.1038/35065725
[15]	Pessoa L. Understanding brain networks and brain organization. Physics of Life Reviews, 2014, 11(3): 400-435 doi: 10.1016/j.plrev.2014.03.005
[16]	Latora V, Marchiori M. Efficient behavior of small-world networks. Physical Review Letters, 2001, 87(19): Article No. 198701
[17]	Li H, Zhang L. A bilevel learning model and algorithm for self-organizing feed-forward neural networks for pattern classification. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(11): 4901-4915 doi: 10.1109/TNNLS.2020.3026114
[18]	Guliyev N J, Ismailov V E. On the approximation by single hidden layer feedforward neural networks with fixed weights. Neural Networks, 2017, 98: 296-304
[19]	Huang G B, Chen L, Siew C K. Universal approximation using incremental constructive feedforward networks with random hidden nodes. IEEE Transactions on Neural Networks, 2006, 17(4): 879-892 doi: 10.1109/TNN.2006.875977
[20]	Qiao J F, Li F, Yang C L, Li W J, Gu K. A self-organizing RBF neural network based on distance concentration immune algorithm. IEEE/CAA Journal of Automatica Sinica, 2022, 7(1): 276-291
[21]	Yu Q, Song S, Ma C, Wei J, Chen S, Tan K C. Temporal encoding and multispike learning framework for efficient recognition of visual patterns. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(8): 3387-3399 doi: 10.1109/TNNLS.2021.3052804
[22]	Simard D, Nadeau L, Kroger H. Fastest learning in small-world neural networks. Physics Letters A, 2004, 336(1): 8-15
[23]	Li X H, Li X L, Zhang J H, Zhang Y L, Li M L. A new multilayer feedforward small-world neural network with its performances on function approximation. In: Proceedings of the IEEE International Conference on Computer Science and Automation Engineering (CSAE). Shanghai, China: IEEE, 2011. 353−357
[24]	Li X, Xu F, Zhang J, Wang S. A multilayer feed forward small-world neural network controller and its application on electrohydraulic actuation system. Journal of Applied Mathematics, 2013, 21: 1-8
[25]	Dong Z K, Duan S K, Hu X F, Li H. A novel memristive multilayer feedforward small-world neural network with its applications in PID control. The Scientific World Journal, 2014, 14: 1-12
[26]	Wang S X, Zhao X, Wang H, Li M. Small-world neural network and its performance for wind power forecasting. CSEE Journal of Power and Energy Systems, 2020, 6(2): 362-373
[27]	Erkaymaz O, Ozer M. Impact of small-world networktopology on the conventional artificial neural network for the diagnosis of diabetes. Chaos, Solitons & Fractals, 2016, 83: 178-185
[28]	Erkaymaz O, Ozer M, Perc M. Performance of small-world feedforward neural networks for the diagnosis of diabetes. Applied Mathematics and Computation, 2017, 311: 22-28 doi: 10.1016/j.amc.2017.05.010
[29]	Zhang R C, Hu X L. Effluent quality prediction of wastewater treatment system based on small-world ANN. Journal of Computers, 2012, 7(9): 2136-2143
[30]	Li W J, Chu M H, Qiao J F. A pruning feedforward small-world neural network based on Katz centrality for nonlinear system modeling. Neural Networks, 2020, 130: 269-285 doi: 10.1016/j.neunet.2020.07.017
[31]	Newman M E J, Watts D J. Renormalization group analysis of the small-world network model. Physics Letters A, 1999, 263(4): 341-346
[32]	李小虎, 杜海峰, 张进华, 王孙安. 多层前向小世界神经网络及其函数逼近. 控制理论与应用, 2010, 27(7): 836-842 Li Xiao-Hu, Du Hai-Feng, Zhang Jin-Hua, Wang Sun-An. Multilayer feedforward small-world neural networks and its function approximation. Control Theory & Applications, 2010, 27(7): 836-842
[33]	王爽心, 杨成慧. 基于层连优化的新型小世界神经网络. 控制与决策, 2014, 29(1): 77-82 doi: 10.13195/j.kzyjc.2012.1420 Wang Shuang-Xin, Yang Cheng-Hui. Novel small-world neural network based on topology optimization. Control and Decision, 2014, 29(1): 77-82 doi: 10.13195/j.kzyjc.2012.1420
[34]	Guo D, Yang L. Research on trim of multilayer feedforward small world network based on E-exponential information entropy. In: Proceedings of the 9th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC). Hangzhou, China: IEEE, 2017. 155−158
[35]	Grutzendler J, Kasthuri N, Gan W B. Long-term dendritic spine stability in the adult cortex. Nature, 2002, 420: 812-816 doi: 10.1038/nature01276
[36]	Zuo Y, Lin A, Chang P, Gan W B. Development of long-term dendritic spine stability in diverse regions of cerebral cortex. Neuron, 2005, 46: 181-189 doi: 10.1016/j.neuron.2005.04.001
[37]	Demiar J, Schuurmans D. Statistical comparisons of classifiers over multiple data sets. Journal of Machine Learning Research, 2006, 7(1): 1-30
[38]	Humphries M D, Gurney K. Network “Small-world-ness”: A quantitative method for determining canonical network equivalence. Plos One, 2008, 3(4): Article No. e0002051
[39]	Ziegler L, Zenke F, Kastner D B, Gerstner W. Synaptic consolidation: From synapses to behavioral modeling. Journal of Neuroscience, 2015, 35(3): 1319-1334 doi: 10.1523/JNEUROSCI.3989-14.2015
[40]	Bliss T V P, Lømo T. Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path. The Journal of Physiology, 1973, 232(2): 331-356 doi: 10.1113/jphysiol.1973.sp010273
[41]	Dudek S M, Bear M F. Homosynaptic long-term depression in area CA1 of hippocampus and effects of N-methyl-D-aspartate receptor blockade. Proceedings of the National Academy of Sciences, 1992, 89(10): 4363-4367 doi: 10.1073/pnas.89.10.4363
[42]	Rathi N, Panda P, Roy K. STDP-based pruning of connections and weight quantization in spiking neural networks for energy-efficient recognition. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2019, 38(4) : 668-677 doi: 10.1109/TCAD.2018.2819366
[43]	Peng J, Tang B, Jiang H, Li Z, Lin T, Li H F. Overcoming long-term catastrophic forgetting through adversarial neural pruning and synaptic consolidation. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(9): 4243-4256 doi: 10.1109/TNNLS.2021.3056201
[44]	Wang J, Xu C, Yang X, Zurada J M. A novel pruning algorithm for smoothing feedforward neural networks based on group lasso method. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(5): 2012-2024 doi: 10.1109/TNNLS.2017.2748585
[45]	Bache K, Lichman M. UCI machine learning repository [Online], available: https://archive.ics.uci.edu/ml, December 20, 2021
[46]	Papantoni-Kazakos P. Small-sample efficiencies of rank tests. IEEE Transactions on Information Theory, 1975, 21(2): 150-157 doi: 10.1109/TIT.1975.1055361