-
摘要: 针对密集场景中大规模冲突导致多机器人路径规划(Multi-agent path finding, MAPF) 成功率低的问题, 引入讨价还价博弈机制并以层级协作A* (Hierarchical cooperative A*, HCA*) 算法为内核, 提出一种基于讨价还价博弈机制的改进层级协作A* (Bargaining game based improving HCA*, B-IHCA*) 算法. 首先, 在HCA* 算法基础上, 对导致路径无解的冲突双方或多方进行讨价还价博弈. 由高优先级机器人先出价, 当低优先级机器人在该条件下无法求解时, 则其将不接受该出价, 并通过降约束求解方式进行还价. 再由其他冲突方对此做进一步还价, 直至各冲突方都能协调得到可接受的路径方案. 其次, 为避免原始HCA* 算法由于高优先级的阻碍陷于过长或反复无效搜索状态, 在底层A* 搜索环节加入了熔断机制. 通过熔断机制与讨价还价博弈相配合可在提升路径求解成功率的同时兼顾路径代价. 研究结果表明, 所提算法在密集场景大规模机器人路径规划问题上较现有算法求解成功率更高、求解时间更短, 路径代价得到改善, 验证了算法的有效性.Abstract: Large-scale conflict of paths is a reason which can hugely reduce the success rate for multi-agent path finding (MAPF) in dense scenarios. For this problem, a bargaining game based improving hierarchical cooperation A* (B-IHCA*) algorithm is proposed by introducing bargaining game mechanism and taking hierarchical cooperation A* (HCA*) algorithm as the core. Firstly, based on the HCA* algorithm, the bargaining game is performed between the two or more parties that leads to conflicts and the unsolved state. The high-priority agent finds a path and bids first. If the low-priority agent cannot get a path with constraint of the bid, it will does not accept the bid and counter-offer another path by reducing the constraint. And then the other conflicting parties will make further counter-offers until all conflicting parties can coordinate to obtain an acceptable path scheme. Secondly, in order to avoid the state of too long or repeated invalid search of HCA* algorithm due to the obstruction of high-priority agent, a fusing mechanism is added to its bottom A* algorithm. Accordingly, by the cooperation of bargaining game and fusing mechanism, the success rate of the paths finding can be improved while taking into account the path costs. The results show that, compared with the existing algorithms, the proposed algorithm has higher success rate, shorter time consumption and ameliorative path costs for large-scale MAPF problem in dense scenarios, which verifies the effectiveness of the algorithm.
-
Key words:
- Multi-agent /
- path finding /
- bargaining game /
- decoupling /
- cooperation
-
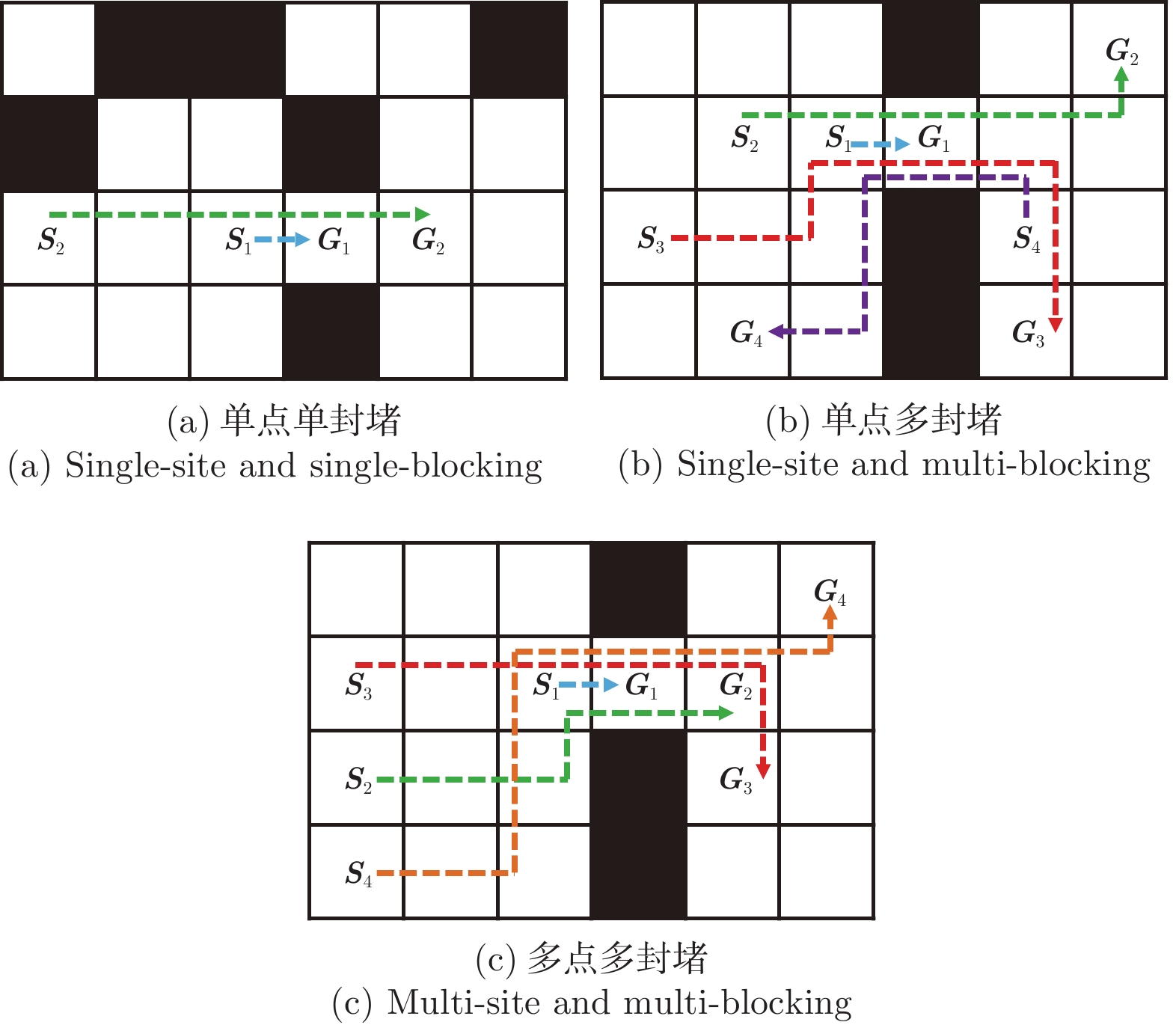
表 1 单点单封堵类型路径规划结果
Table 1 Solution of the single-site and single-blocking
机器人 路径 具体方案 ${a_1}$ ${p_{1, 1} }$ [(3, 2), (3, 2), (3, 1), (3, 2), (4, 2)] ${a_2}$ ${p_{2, 1} }$ [(1, 2), (2, 2), (3, 2), (4, 2), (5, 2)] 表 2 单点多封堵类型路径规划结果
Table 2 Solution of the single-site and multi-blocking
机器人 路径 具体方案 ${a_1}$ ${p_{1, 1} }$ [(3, 3), (3, 2), (3, 3), (3, 2), (3, 3), (3, 3), (3, 3), (3, 3), (3, 4), (3, 3), (4, 3)] ${a_2}$ ${p_{2, 1} }$ [(2, 3), (3, 3), (4, 3), (5, 3), (5, 4), (6, 4)] ${a_3}$ ${p_{3, 1} }$ [(1, 2), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (5, 2), (5, 1)] ${a_4}$ ${p_{4, 1} }$ [(5, 2), (5, 3), (5, 3), (5, 2), (5, 3), (5, 4), (5, 3), (4, 3), (3, 3), (3, 2), (3, 1), (2, 1)] 表 3 多点多封堵类型路径规划结果
Table 3 Solution of the multi-site and multi-blocking
机器人 路径 具体方案 ${a_1}$ ${p_{1, 1} }$ [(3, 3), (3, 3), (3, 4), (3, 4), (3, 4), (3, 4), (3, 3), (4, 3)] ${a_2}$ ${p_{2, 1} }$ [(1, 2), (1, 3), (2, 3), (3, 3), (3, 2), (3, 3), (4, 3), (5, 3)] ${a_3}$ ${p_{3, 1} }$ [(1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (5, 2)] ${a_4}$ ${p_{4, 1} }$ [(1, 1), (1, 2), (1, 3), (2, 3), (3, 3),
(4, 3), (5, 3), (5, 4), (6, 4)]表 4 不同$N_{\rm{robot}}$规模对应的求解限制时间
Table 4 Time limits for different sizes of $N_{\rm{robot}}$
机器人个数 限制时间(s) $0 < {N_{\rm{robot}}} \le 50$ 150 $50 < {N_{\rm{robot}}} \le 100$ 300 ${N_{\rm{robot}}} > 100$ 500 表 5 实验I参数设置
Table 5 Parameters for Experiment I
地图类型 $N_{\rm{robot}}$ $\alpha$ (%) $\beta$ (%) $\omega $ ${R_L}$ $8 \times 8$ grid 10 23.4375 20.4082 3 6000 表 6 实验I求解结果
Table 6 Results of Experiment I
算法 路径总代价 (步) 求解时间 (s) HCA* NA NA CBS NA NA CBS-DS 62 132.0 WdSIPP $(w = 1.01)$ NA NA WdSIPP $(w = 1.75)$ NA NA B-IHCA* 73 0.1 表 7 B-IHCA* 求解过程路径与冲突信息
Table 7 Path and conflict information during the solving process of B-IHCA*
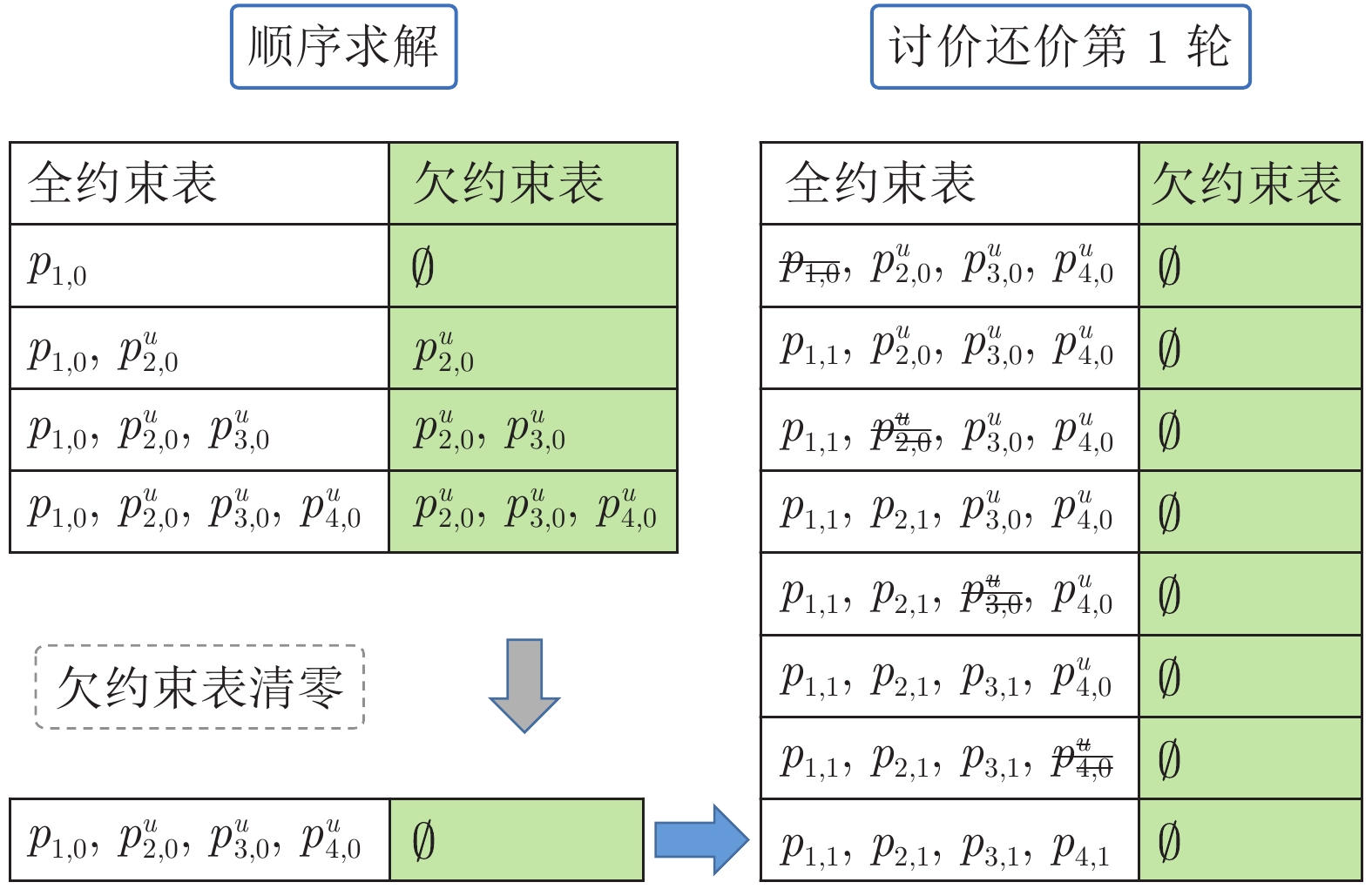
求解阶段 信息类型 信息值 顺序求解 全约束路径 ${p_{1, 0} },{p_{2, 0} },{p_{5,0} },{p_{6,0} },{p_{7, 0} },{p_{9, 0} },{p_{10, 0} }$ 欠约束路径 $p_{3, 0}^u,p_{4, 0}^u,p_{8, 0}^u$ 零约束路径 $\emptyset $ 冲突机器人 $({a_2},{a_3}),({a_2},{a_4}),({a_5},{a_8})$ 全约束路径 ${p_{1, 1}}$, ${p_{2, 1}}$, ${p_{3, 1}}$, ${p_{4, 1}}$, ${p_{5, 1}}$,
${p_{6, 1}}$, ${p_{7, 1}}$, ${p_{8, 1}}$, ${p_{9, 1}}$, ${p_{10, 1}}$讨价还价 欠约束路径 $\emptyset $ 第 1 轮 零约束路径 $\emptyset $ 冲突机器人 $\emptyset $ 表 8 实验II参数设置 (1)
Table 8 The parameters for Experiment II (1)
地图类型 $\alpha $ (%) $R_L$ $20 \times 20$ blocked-10 地图 9.7500 10000 $20 \times 20$ random-15 地图 15.0000 15000 $32 \times 32$ blocked-20 地图 19.9219 15000 $32 \times 32$ room 地图 33.3984 15000 表 9 实验II参数设置 (2)
Table 9 The parameters for Experiment II (2)
$20 \times 20$ blocked-10 地图 $20 \times 20$ random-15 地图 $32 \times 32$ blocked-20 地图 $32 \times 32$ room 地图 $N_{\rm{robot}}$ $\beta $ (%) $\omega $ $N_{\rm{robot}}$ $\beta$ (%) $\omega $ $N_{\rm{robot}}$ $\beta$ (%) $\omega $ $N_{\rm{robot}}$ $\beta$ (%) $\omega $ 20 5.5402 2 15 4.4118 2 30 3.6585 4 10 1.4663 4 40 11.0803 4 30 8.8235 5 50 6.0976 5 20 2.9326 5 60 16.6205 6 45 13.2353 6 70 8.5366 6 30 4.3988 6 80 22.1607 6 60 17.6471 6 90 10.9756 6 40 5.8651 8 100 27.7008 7 75 22.0588 8 110 13.4146 8 50 7.3314 10 120 33.2410 8 90 26.4706 10 130 15.8537 10 60 8.7977 12 表 10 算法路径质量统计
Table 10 Path cost statistics of the tested algorithms
地图类型 $N_{\rm{robot}}$ 公共算例数 平均总代价 (步) 平均求解轮数 CBS CBS-DS HCA* WdSIPP (1.01) WdSIPP (1.75) B-IHCA* 公共算例 非公共算例 $20 \times 20$ blocked-10 20 13 263.1 267.1 273.0 275.8 281.5 267.2 1.54 1.43 40 17 NA NA 603.8 604.9 622.1 591.9 1.41 1.67 60 19 NA NA 933.2 928.2 969.5 926.3 1.32 2.00 80 10 NA NA 1340.9 1347.7 1392.3 1327.8 1.40 2.00 100 6 NA NA 1731.3 1744.2 1820.7 1731.3 1.00 2.62 $20 \times 20$ random-15 15 18 209.1 211.1 219.1 220.1 224.4 213.7 1.50 1.00 30 18 NA NA 473.0 472.8 488.2 470.2 1.33 2.50 45 15 NA NA 745.2 745.1 771.3 737.5 1.27 2.25 60 11 NA NA 1076.8 1072.3 1115.2 1055.9 1.91 2.22 75 9 NA NA 1391.2 1390.4 1437.4 1386.7 1.33 2.09 $32 \times 32$ blocked-20 30 6 — 618.3 626.2 630.0 655.7 623.7 1.17 1.29 50 18 NA NA 1237.2 1342.9 1311.6 1234.0 1.11 1.50 70 17 NA NA 1781.5 1778.6 1881.8 1763.0 1.41 2.50 90 14 NA NA 2396.9 2383.5 2538.5 2368.1 1.64 2.80 110 9 NA NA 3010.3 3008.6 3190.3 2981.8 1.89 2.33 130 6 NA NA 3596.3 3555.5 3757.7 3558.5 1.67 2.70 $32 \times 32$ room 10 17 248.7 249.9 253.1 254.6 264.2 252.5 1.06 1.67 20 6 — 550.5 566.5 563.7 585.8 558.2 1.50 1.62 30 15 NA NA 841.1 838.5 874.7 830.8 1.40 2.00 40 14 NA NA 1188.3 1174.5 1208.9 1175.6 1.43 1.83 50 11 NA NA 1536.3 1528.3 1573.7 1512.4 1.91 2.43 60 6 NA NA 1891.5 1892.8 1949.7 1881.2 1.67 2.83 -
[1] 施伟, 冯旸赫, 程光权, 黄红蓝, 黄金才, 刘忠, 等. 基于深度强化学习的多机协同空战方法研究. 自动化学报, 2021, 47(7): 1610-1623 doi: 10.16383/j.aas.c201059Shi Wei, Feng Yang-He, Cheng Guang-Quan, Huang Hong-Lan, Huang Jin-Cai, Liu Zhong, et al. Research on multi-aircraft cooperative air combat method based on deep reinforcement learning. Acta Automatica Sinica, 2021, 47(7): 1610-1623 doi: 10.16383/j.aas.c201059 [2] Li J Y, Surynek P, Felner A, Ma H, Kumar T K S, Koenig S. Multi-agent path finding for large agents. In: Proceedings of the 33rd AAAI Conference on Artificial Intelligence (AAAI). Hono lulu, USA: AAAI, 2019. 7627−7634 [3] Yu J, LaValle S M. Optimal multi-robot path planning on graphs: Complete algorithms and effective heuristics. IEEE Transactions on Robotics, 2016, 32(5): 1163-1177 doi: 10.1109/TRO.2016.2593448 [4] 李昆鹏, 刘腾博, 阮炎秋. 半导体生产车间智能AGV路径规划与调度. 计算机集成制造系统, 2022, 28(9): 2970-2980Li Kun-Peng, Liu Teng-Bo, Ruan Yan-Qiu. Research on intelligent AGV routing scheduling with applications in semi-conductor production. Computer Integrated Manufacturing Systems, 2022, 28(9): 2970-2980 [5] Morris R, Pasareanu C S, Luckow K, Malik W, Ma H, Kumar T K S, et al. Planning, scheduling and monitoring for airport surface operations. In: Proceedings of the 30th AAAI Conference on Artificial Intelligence (AAAI). Phoenix, USA: AAAI, 2016. 608−614 [6] Yu J J, LaValle S M. Structure and intractability of optimal multi-robot path planning on graphs. In: Proceedings of the 27th AAAI Conference on Artificial Intelligence (AAAI). Bellevue Washington, USA: AAAI, 2013. 1443−1449 [7] Wagner G, Choset H. Subdimensional expansion for multirobot path planning. Artificial Intelligence, 2015, 219: 1-24 doi: 10.1016/j.artint.2014.11.001 [8] Han S D, Rodriguez E J, Yu J J. SEAR: A polynomial-time multi-robot path planning algorithm with expected constant-factor optimality guarantee. In: Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Madrid, Spain: IEEE, 2018. 7967−7974 [9] 段书用, 王启帆, 韩旭, 刘桂荣. 具有确保安全距离的A*路径优化方法. 机械工程学报, 2020, 56(18): 205-215 doi: 10.3901/JME.2020.18.205Duan Shu-Yong, Wang Qi-Fan, Han Xu, Liu Gui-Rong. Improved A-star algorithm for safety insured optimal path with smoothed corner turns. Chinese Journal of Mechanical Engineering, 2020, 56(18): 205-215 doi: 10.3901/JME.2020.18.205 [10] Standley T, Korf R E. Complete algorithms for cooperative pathfinding problems. In: Proceedings of the 22nd International Joint Conference on Artificial Intelligence (IJCAI). Barcelona, Spain: AAAI, 2011. 668−673 [11] Standley T. Finding optimal solutions to cooperative pathfinding problems. In: Proceedings of the 24th AAAI Conference on Artificial Intelligence (AAAI). Atlanta, GA, USA: AAAI, 2010. 173−178 [12] Sharon G, Stern R, Goldenberg M, Felner A. The increasing cost tree search for optimal multi-agent pathfinding. Artificial Intelligence, 2013, 195: 470-495 doi: 10.1016/j.artint.2012.11.006 [13] Sharon G, Stern R, Felner A, Sturtevant N R. Meta-agent conflict-based search for optimal multi-agent path finding. In: Proceedings of the 5th Annual Symposium on Combinatorial Search (SoCS). Niagara Falls, Ontario, Canada: AAAI, 2012. 97−104 [14] Sharon G, Stern R, Felner A, Sturtevant N R. Conflict- based search for optimal multi-agent pathfinding. Artificial Intelligence, 2015, 219: 40-66 doi: 10.1016/j.artint.2014.11.006 [15] Ma H, Harabor D, Stuckey P J, Li J Y, Koenig S. Searching with consistent prioritization for multi-agent path finding. In: Proceedings of the 33rd AAAI Conference on Artificial Intelligence (AAAI). New Orleans, USA: AAAI, 2018. 7643−7650 [16] Li J, Harabor D, Stuckey P J, Ma H, Koenig S. Disjoint splitting for multi-agent path finding with conflict-based search. In: Proceedings of the 29th International Conference on Automated Planning and Scheduling (ICAPS). Berkeley, USA: AAAI, 2019. 279−283 [17] Boyarski E, Felner A, Stern R, Sharon G, Tolpin D, Betzalel O, et al. ICBS: Improved conflict-based search algorithm for multi-agent pathfinding. In: Proceedings of the 24th International Joint Conference on Artificial Intelligence (IJCAI). Buenos Aires, Argentina: AAAI, 2015. 740−746 [18] Andreychuk A, Yakovlev K, Boyarski E, Stern R. Improving continuous-time conflict based search. In: Proceedings of the 35th AAAI Conference on Artificial Intelligence (AAAI). Virtually, USA: AAAI, 2021. 11220−11227 [19] Silver D. Cooperative pathfinding. In: Proceedings of the 1st AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment (AIIDE). California, USA: AAAI, 2005. 117−122 [20] Erdmann M A, Lozano-Pérez T. On multiple moving objects. Algorithmica, 1987, 2: 477-521 doi: 10.1007/BF01840371 [21] Sharon G. Novel Search Techniques for Path Finding in Complex Environment [Ph.D. dissertation], Ben-Gurion University, Israel, 2015 [22] Čáp M, Novák P, Kleiner A, Selecký M. Prioritized planning algorithms for trajectory coordination of multiple mobile robots. IEEE Transactions on Automation Science and Engineering, 2015, 12(3): 835-849 doi: 10.1109/TASE.2015.2445780 [23] Li H, Long T, Xu G T, Wang Y J. Coupling-degree-based heuristic prioritized planning method for UAV swarm path generation. In: Proceedings of the Chinese Automation Congress (CAC). Hangzhou, China: IEEE, 2019. 3636−3641 [24] Wu W Y, Bhattacharya S, Prorok A. Multi-robot path deconfliction through prioritization by path prospects. In: Proceedings of the IEEE International Conference on Robotics and Automation (ICRA). Paris, France: IEEE, 2020. 9809−9815 [25] Yakovlev K, Andreychuk A, Stern R. Revisiting bounded-suboptimal safe interval path planning. In: Proceedings of the 30th International Conference on Automated Planning and Scheduling (ICAPS). Nancy, France, USA: AAAI, 2020. 279−283 [26] 李珣, 南恺恺, 赵征凡, 王晓华, 景军锋. 多智能体博弈的纺织车间搬运机器人任务分配. 纺织学报, 2020, 41(7): 78-87 doi: 10.13475/j.fzxb.20190800210Li Xun, Nan Kai-Kai, Zhao Zheng-Fan, Wang Xiao-Hua, Jing Jun-Feng. Task allocation of handling robot in textile workshop based on multi-agent game theory. Journal of Textile Research, 2020, 41(7): 78-87 doi: 10.13475/j.fzxb.20190800210 [27] Wu H, Shang H. Potential game for dynamic task allocation in multi-agent system. ISA Transactions, 2020, 102: 208-220 doi: 10.1016/j.isatra.2020.03.004 [28] 郑延斌, 王林林, 席鹏雪, 樊文鑫, 韩梦云. 基于蚁群算法及博弈论的多Agent路径规划算法. 计算机应用, 2019, 39(3): 681-687 doi: 10.11772/j.issn.1001-9081.2018071601Zheng Yan-Bin, Wang Lin-Lin, Xi Peng-Xue, Fan Wen-Xin, Han Meng-Yun. Multi-agent path planning algorithm based on ant colony algorithm and game theory. Journal of Computer Applications, 2019, 39(3): 681-687 doi: 10.11772/j.issn.1001-9081.2018071601 [29] Kaduri O, Boyarski E, Stern R. Experimental evaluation of classical multi agent path finding algorithms. In: Proceedings of the 14th International Symposium on Combinatorial Search (SoCS). Guangzhou, China: AAAI, 2021. 126−130 [30] Li J Y, Andrew T, Scott K, Durham J W, Kumar T K S, Koenig S. Lifelong multi-agent path finding in large-scale warehouses. In: Proceedings of the 35th AAAI Conference on Artificial Intelligence (AAAI). Virtually, USA: AAAI, 2021. 11272−11281 [31] 万千. 基于CBS算法的物流分拣多AGV路径规划的研究 [硕士学位论文], 哈尔滨工业大学, 中国, 2018Wan Qian. Research on Multi-AGV Path Planning for Logistics Sorting Based on CBS Algorithm [Master thesis], Harbin Institute of Technology, China, 2018 [32] Ma H. Target Assignment and Path Planning for Navigation Tasks With Teams of Agents [Ph.D. dissertation], University of Southern California, USA, 2020 [33] Sturtevant N R. Benchmarks for grid-based pathfinding. IEEE Transactions on Computational Intelligence and AI in Games, 2012, 4: 144-148 doi: 10.1109/TCIAIG.2012.2197681 -




 下载:
下载: