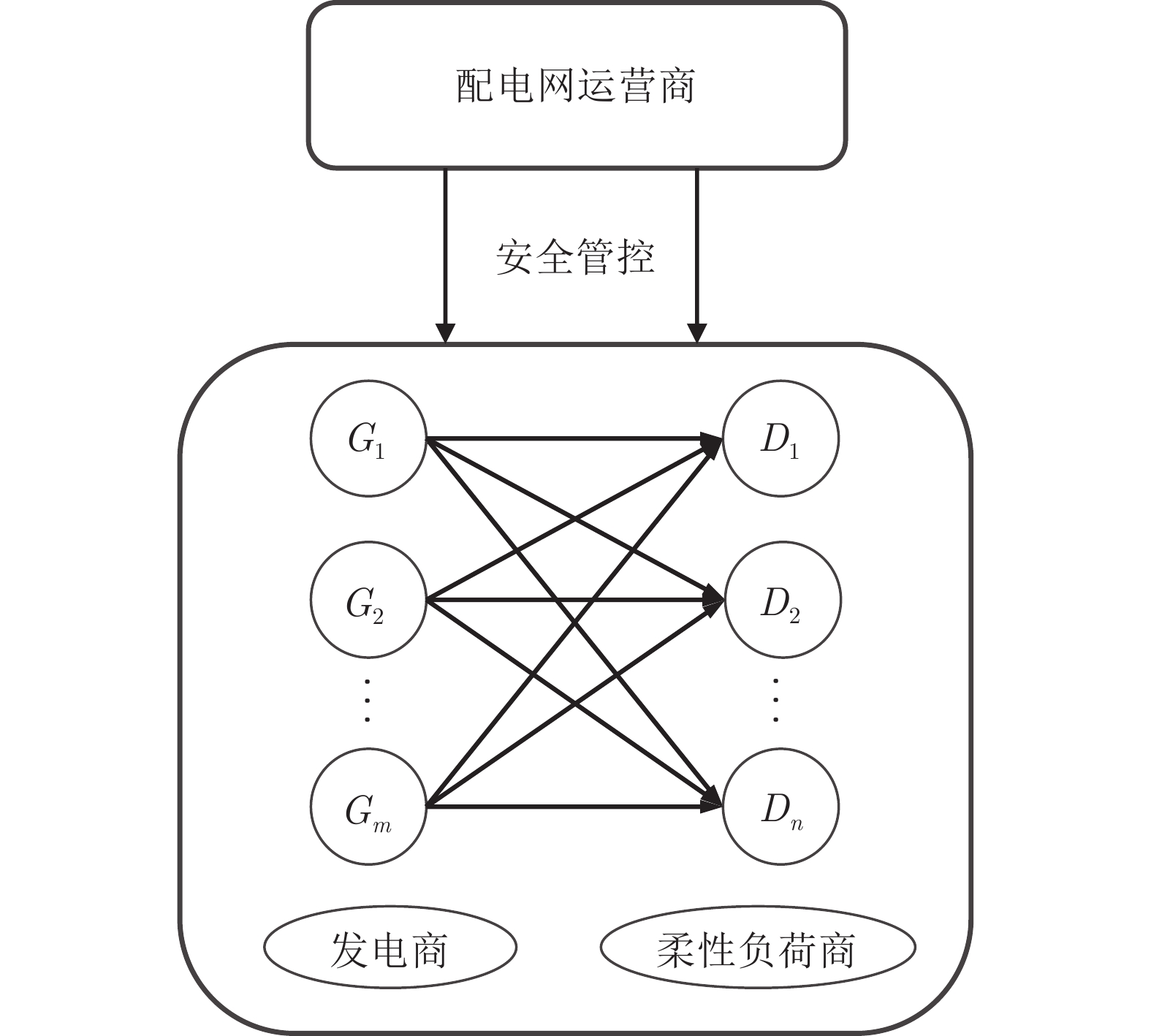
Research on Distributed Power Market Trading Model Based on Grid Line Transmission Security
-
摘要: 电力市场分布式交易模型可有效缓解传统集中模型下市场主体的隐私安全等问题, 但难以在保障市场主体收益和电力系统安全稳定运行的同时, 实现社会福利最大化. 因此, 基于电网线路传输安全, 首先以社会福利最大化为目标, 构建集中式交易模型, 并采用拉格朗日乘子法和对偶定理, 将其等价分解为各市场主体自身利益最大化的分布式交易模型. 在此基础上, 设计2种适用于不同情形的分布式交易方法及其求解算法, 并构造电网安全成本影响市场主体的决策, 从而保证电网线路传输安全. 最后, 基于算例分析, 验证了2种交易方法的有效性.Abstract: The distributed power market trading model can effectively alleviate the problems among market entities such as privacy problem in the traditional centralized trading model. However, there is still a lack of distributed trading models that can maximize social welfare while ensuring the benefits of market entities and the safe and stable operation of the power system. Therefore, a centralized trading model with the objective of maximizing social welfare is constructed, which considers the power grid line transmission security. Then, it is equivalently decomposed into a distributed trading model that maximizes the interests of each market agent using the Lagrange multiplier method and dual duality theorem. On this basis, two distributed trading methods and the corresponding solution algorithms suitable for different scenarios are designed, and the grid security cost is used to influence the decision-making of market entities, thereby ensuring grid line transmission security. Finally, the effectiveness of the two trading methods are verified based on simulation analysis.
-
图 4 2种交易方法求得的社会福利对比
Fig. 4 Comparison of social welfare obtained by the 2 trading methods
图 7 情形1下, 2种算法求得的各发电商的出力
Fig. 7 Power generation of each generator obtained by the 2 algorithms in scenario 1
图 8 情形2下, 2种算法求得各发电商的出力
Fig. 8 Power generation of each generator obtained by the 2 algorithms in scenario 2
图 10 在IEEE 33节点电力系统中, 2种交易方法求解结果的残差
Fig. 10 Residuals of the solution results of the 2 trading models in IEEE 33 bus power system
图 11 情形1下, 2种算法求得的各发电商的出力
Fig. 11 Power generation of each generator obtained by the 2 algorithms in scenario 1
图 12 情形2下, 2种算法求得的各发电商的出力
Fig. 12 Power generation of each generator obtained by the 2 algorithms in scenario 2
图 13 情形1下, 3种算法的迭代求解结果
Fig. 13 The iterative solution results of the 3 algorithms in scenario 1
图 14 情形2下, 3种算法的迭代求解结果
Fig. 14 The iterative solution results of the 3 algorithms in scenario 2
表 1 2种分布式交易情形下, IEEE 9节点电力系统的发电商出力上限和下限(MW)
Table 1 Upper and lower limits on generator output for IEEE 9 bus power system in 2 distributed trading scenarios (MW)
发电商 $G_1$ $G_2$ $G_3$ 情形1 $p_{G,i}^{\max }$ 350 290 400 $p_{G,i}^{\min }$ 10 20 15 情形2 $p_{G,i}^{\max }$ 120 100 140 $p_{G,i}^{\min }$ 10 20 15 
下载: 导出CSV
表 2 2种分布式交易情形下, IEEE 9节点电力系统的柔性负荷商需求上限和下限(MW)
Table 2 Upper and lower limits on flexible loaders＇demand for IEEE 9 bus power system in 2 distributed trading scenarios (MW)
柔性负荷商 ${{D}_{4}}$ ${{D}_{5}}$ ${{D}_{6}}$ ${{D}_{7}}$ ${{D}_{8}}$ ${{D}_{9}}$ 情形1 $p_{D,j}^{\max }$ 150 100 145 140 150 170 $p_{D,j}^{\min }$ 60 50 90 60 50 70 情形2 $p_{D,j}^{\max }$ 150 90 100 140 150 150 $p_{D,j}^{\min }$ 20 15 30 30 15 20
下载: 导出CSV
表 3 IEEE 9节点电力系统线路潮流上限(MW)
Table 3 Upper limit of grid line power flow for IEEE 9 bus power system (MW)
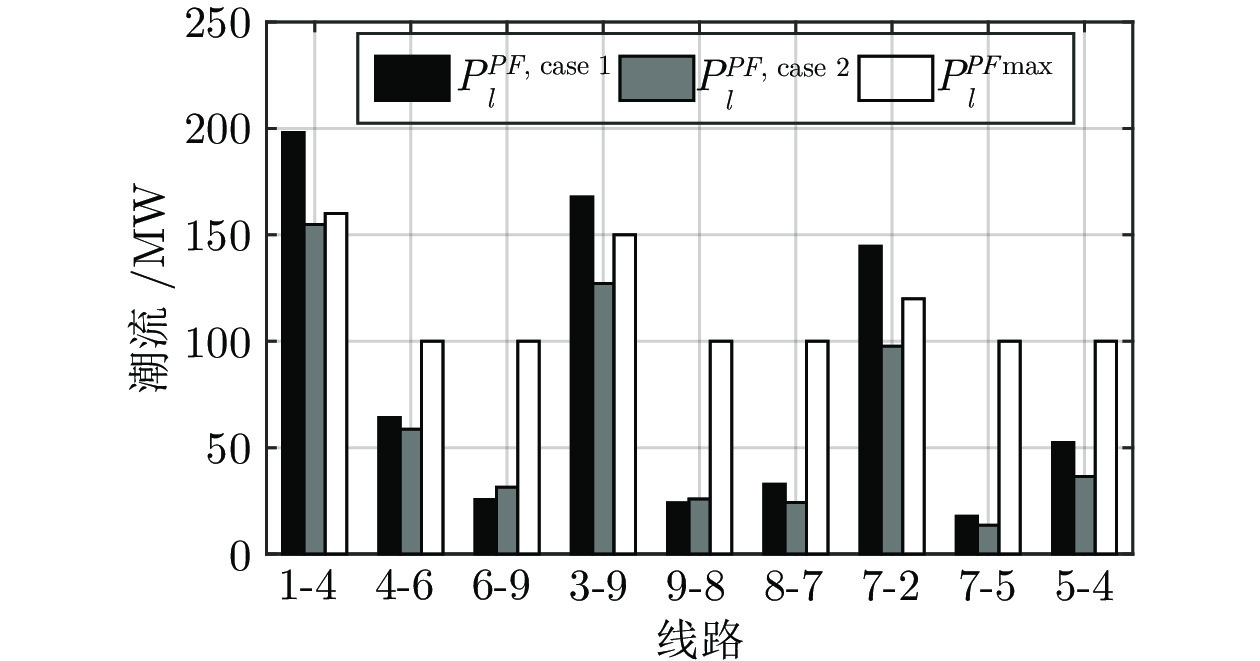
线路 1-4 4-6 6-9 3-9 9-8 8-7 7-2 7-5 5-4 $P_{l}^{PF\max}$ 160 100 100 150 100 100 120 100 100
下载: 导出CSV
表 4 2种交易方法下, 各市场主体交易量对比 (MW)
Table 4 Comparison of the trading volume of market entities obtained by the 2 trading methods (MW)
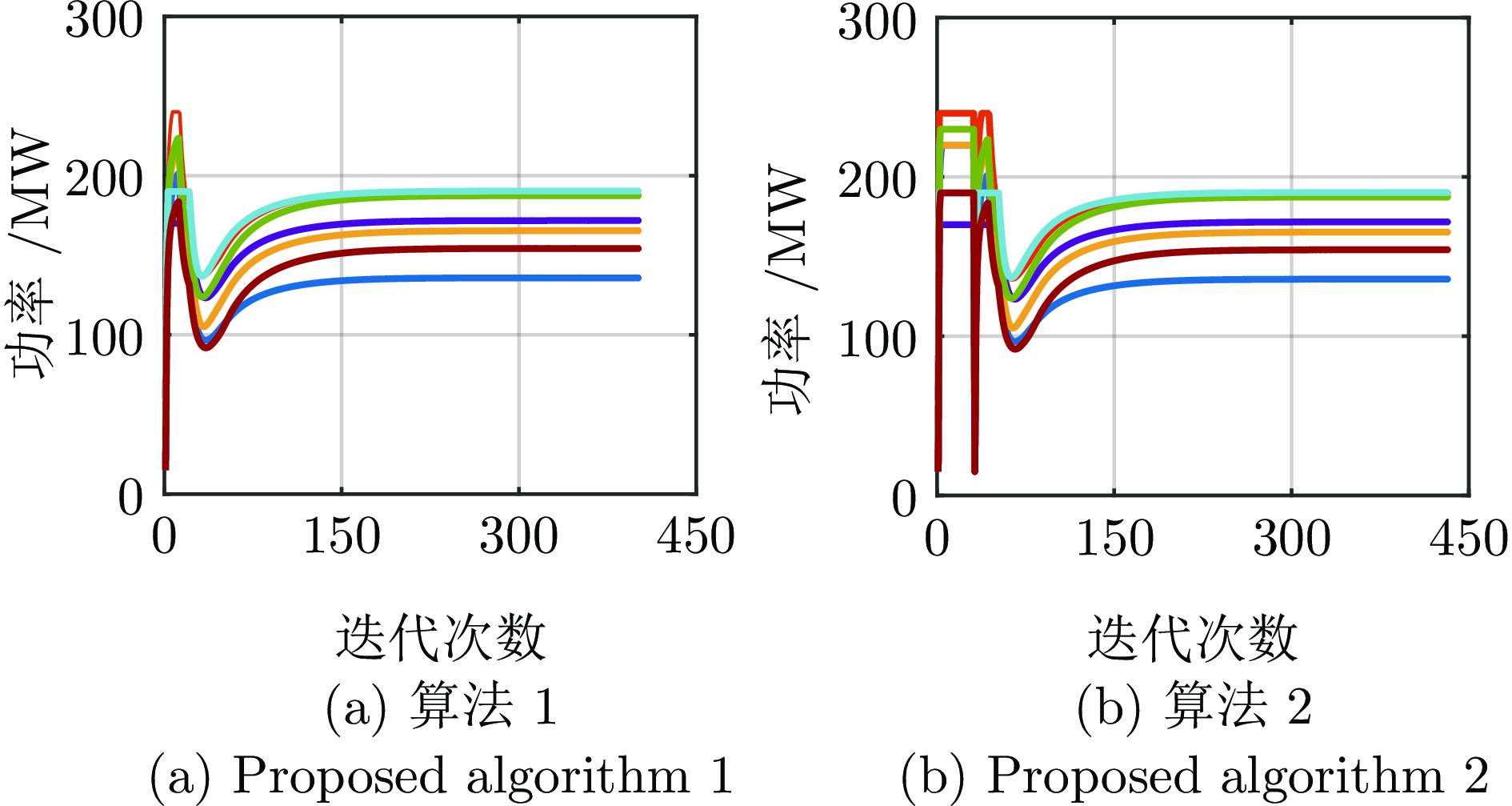
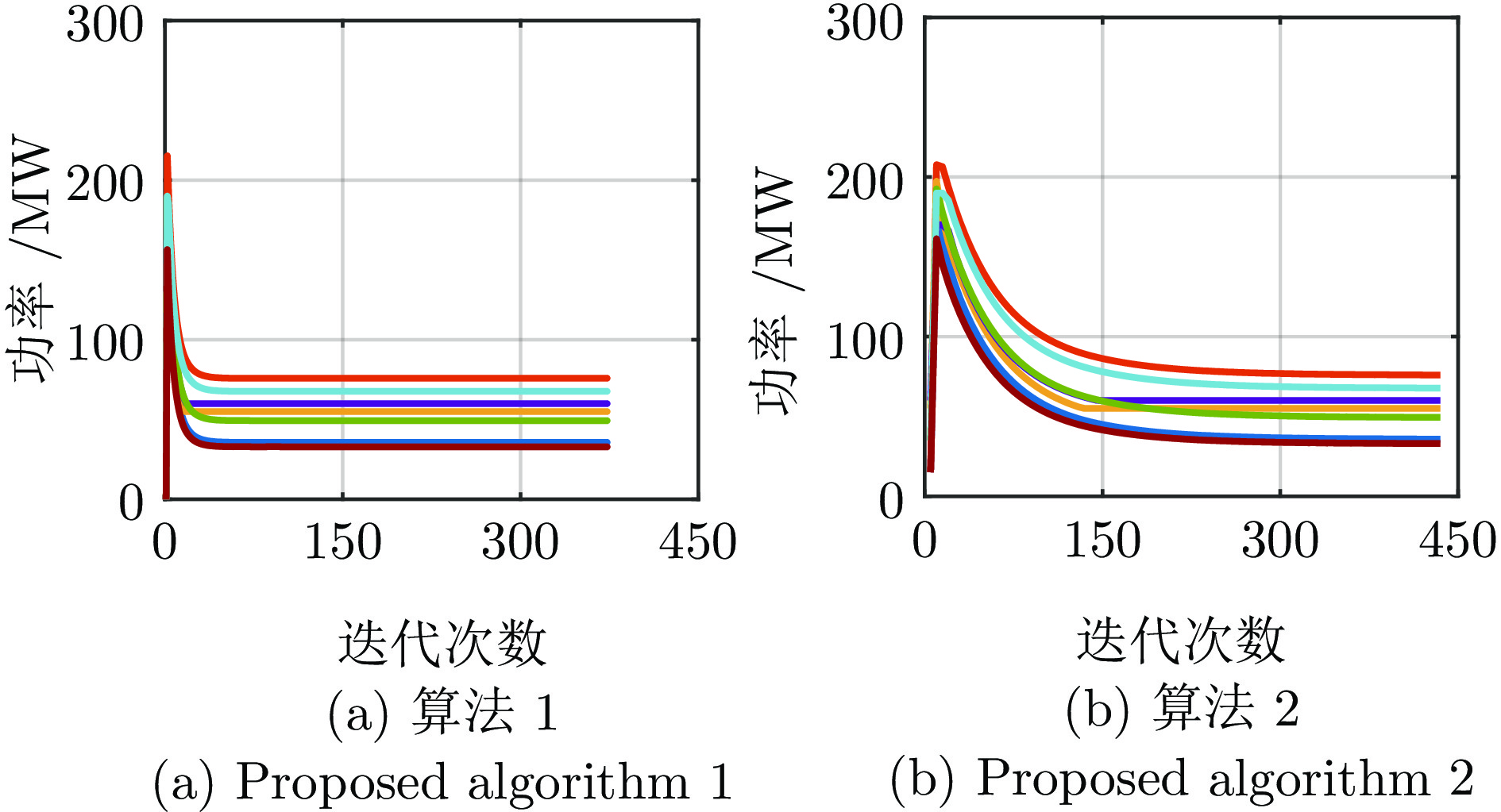
交易量 集中式 分布式 ${{G}_{1}}$ 155.374 155.376 ${{G}_{2}}$ 97.747 97.747 ${{G}_{3}}$ 126.912 126.918 ${{D}_{4}}$ 59.998 60.002 ${{D}_{5}}$ 50.010 50.007 ${{D}_{6}}$ 90.007 90.007 ${{D}_{7}}$ 60.006 60.006 ${{D}_{8}}$ 50.009 50.006 ${{D}_{9}}$ 70.012 70.006
下载: 导出CSV
表 5 IEEE 9节点电力系统下, 2种算法的迭代次数和 计算时间对比
Table 5 Comparison of iterations and computation time of the 2 algorithms in IEEE 9 bus system
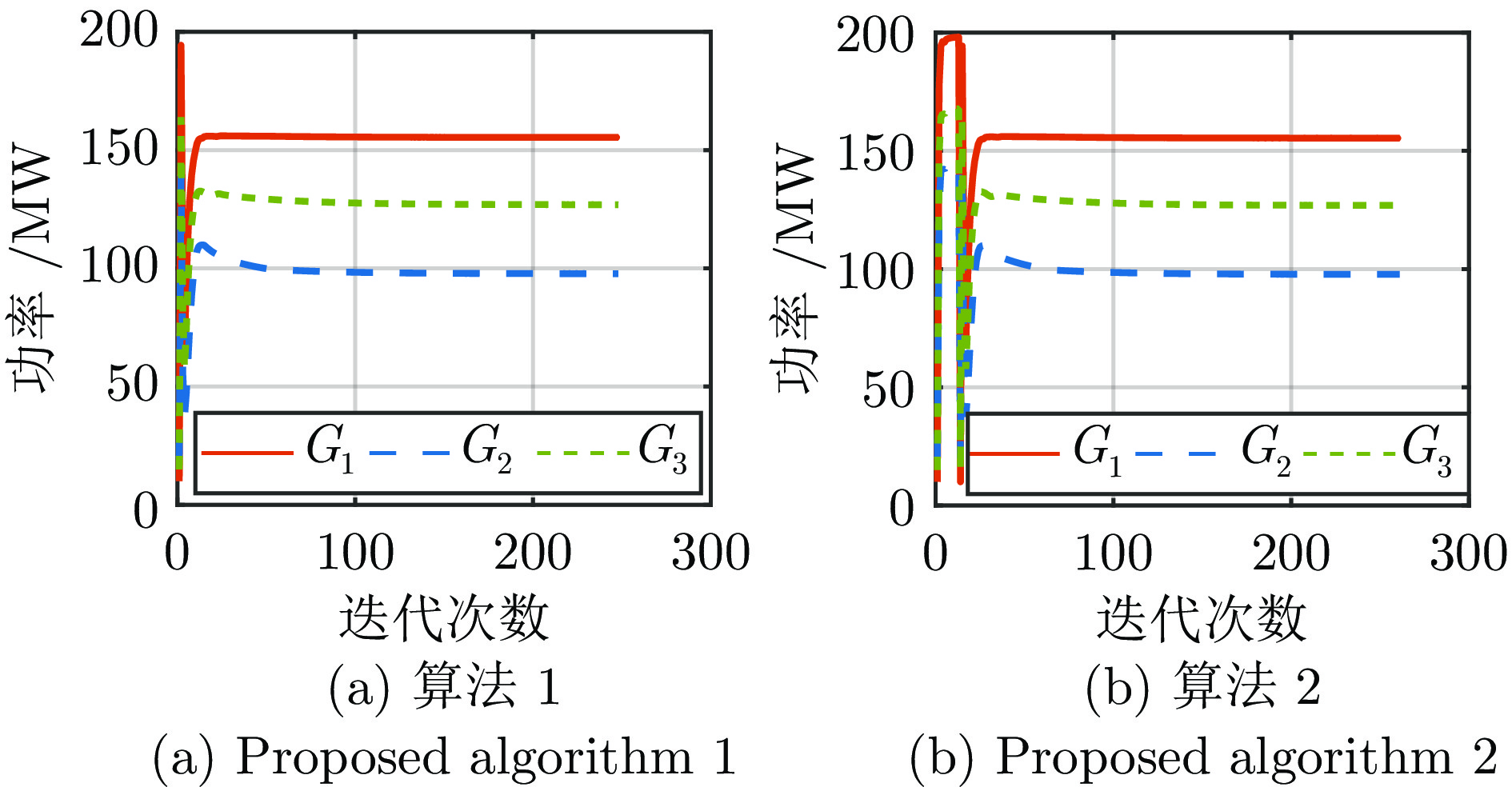
情形 算法1 算法2 迭代次数 计算时间(s) 迭代次数 计算时间(s) 情形1 248 71.5 265 79.8 情形2 216 60.2 52 15.7
下载: 导出CSV
表 6 IEEE 33节点电力系统中, 2个案例的 潮流对比(MW)
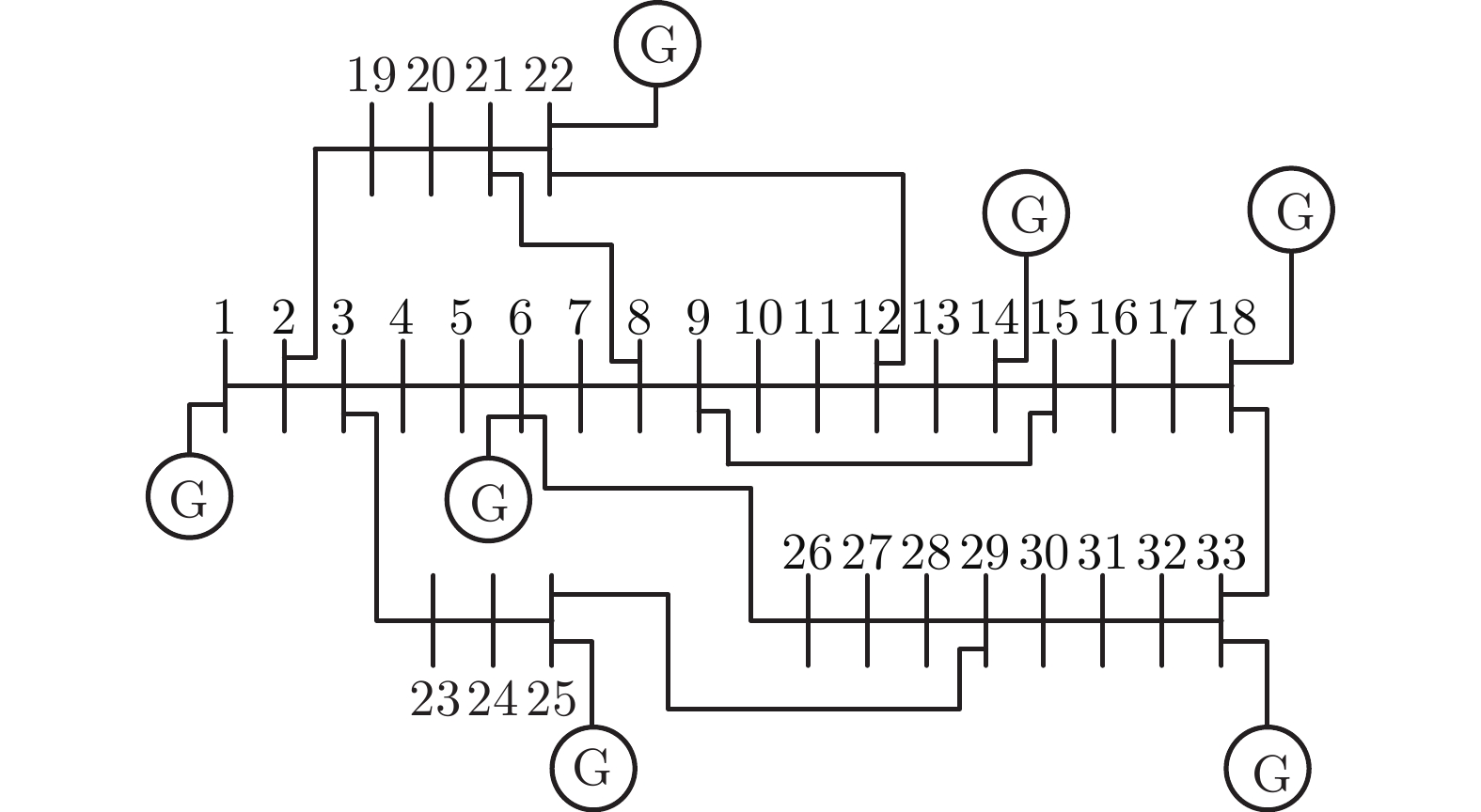
Table 6 Comparison of the power flow in the 2 cases of the IEEE 33 bus power system (MW)
线路 $P_{l}^{PF,\;{\rm{case} }\;1}$ $P_{l}^{PF,\;{\rm{case} }\;2}$ $P_{l}^{PF\max}$ 1-2 189.22 190.36 250 2-3 145.40 78.52 250 3-4 136.56 98.60 150 4-5 58.56 56.30 250 5-6 258.55 168.56 200 6-7 59.87 43.69 250 7-8 25.21 8.96 250 8-9 62.17 56.18 250 9-10 32.74 32.80 250 10-11 62.15 57.71 150 11-12 16.12 15.23 150 12-13 30.06 34.89 200 13-14 51.10 40.55 250 14-15 218.53 188.37 200 15-16 39.89 22.97 150 16-17 101.01 59.95 150 17-18 165.36 137.69 150 2-19 74.80 60.84 150 19-20 95.37 87.90 250 20-21 212.80 183.99 200 21-22 61.00 68.73 150 3-23 58.97 60.04 150 23-24 45.51 37.73 200 24-25 75.72 43.37 250 6-26 145.70 155.01 250 26-27 169.74 125.79 150 27-28 243.25 188.26 200 28-29 135.98 97.89 150 29-30 14.31 32.59 150 30-31 34.64 44.72 250 31-32 43.94 44.88 150 32-33 140.00 122.20 150 21-8 122.87 99.63 150 9-15 87.32 65.97 150 12-22 120.66 156.98 200 18-33 35.62 40.33 200 25-29 158.77 142.65 200
下载: 导出CSV
表 7 IEEE 33节点系统下, 2种算法迭代次数和 计算时间对比
Table 7 Comparison of iterations and computation time of the 2 algorithms in IEEE 33 bus system
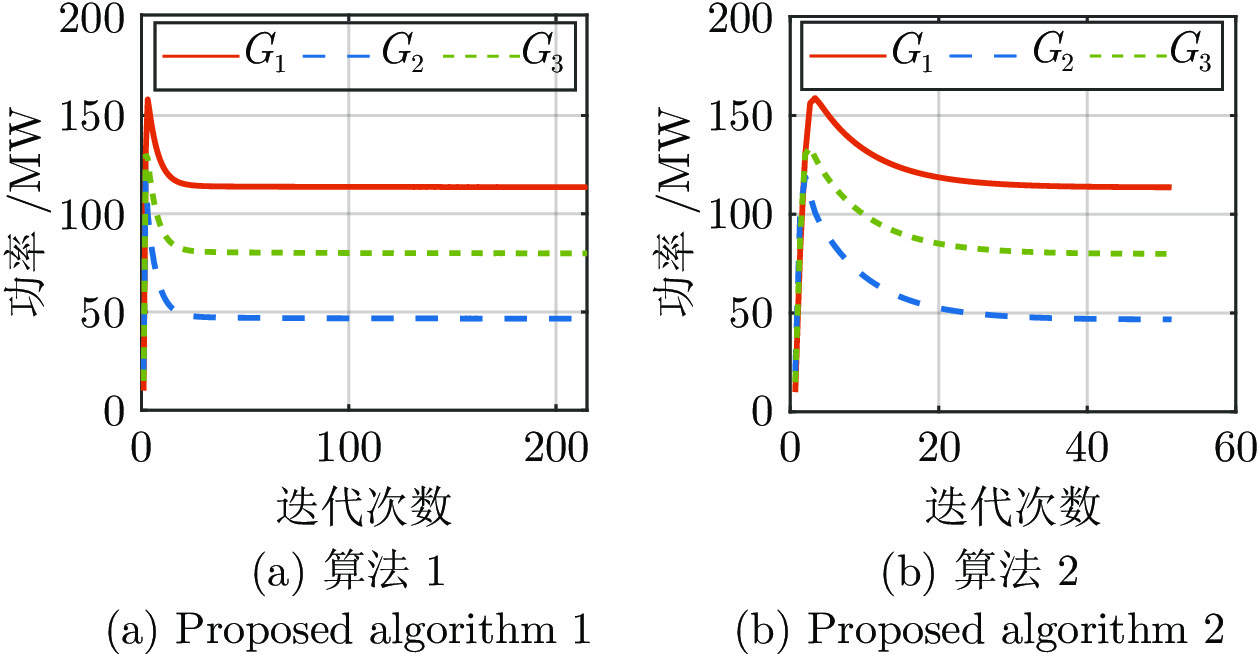
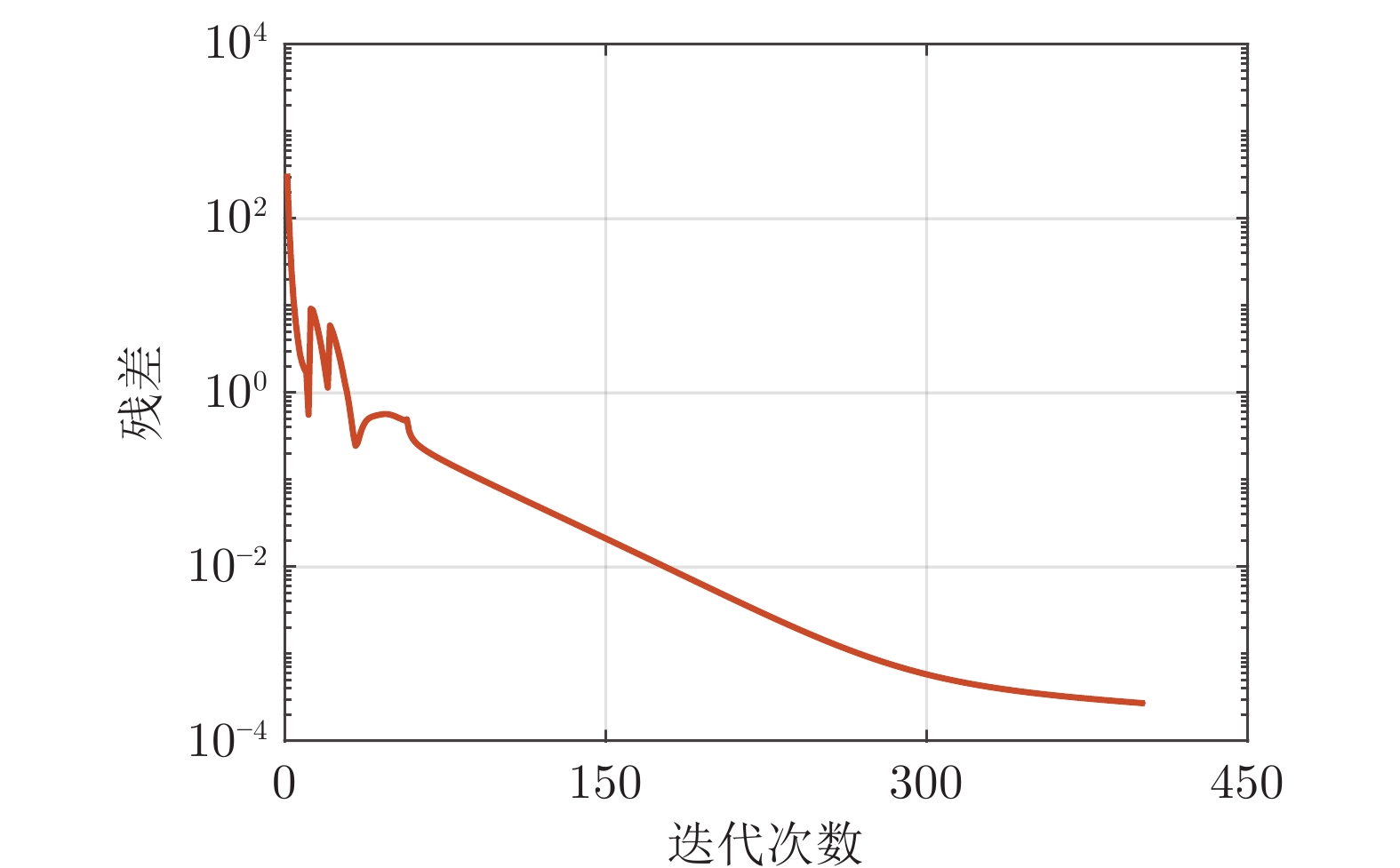
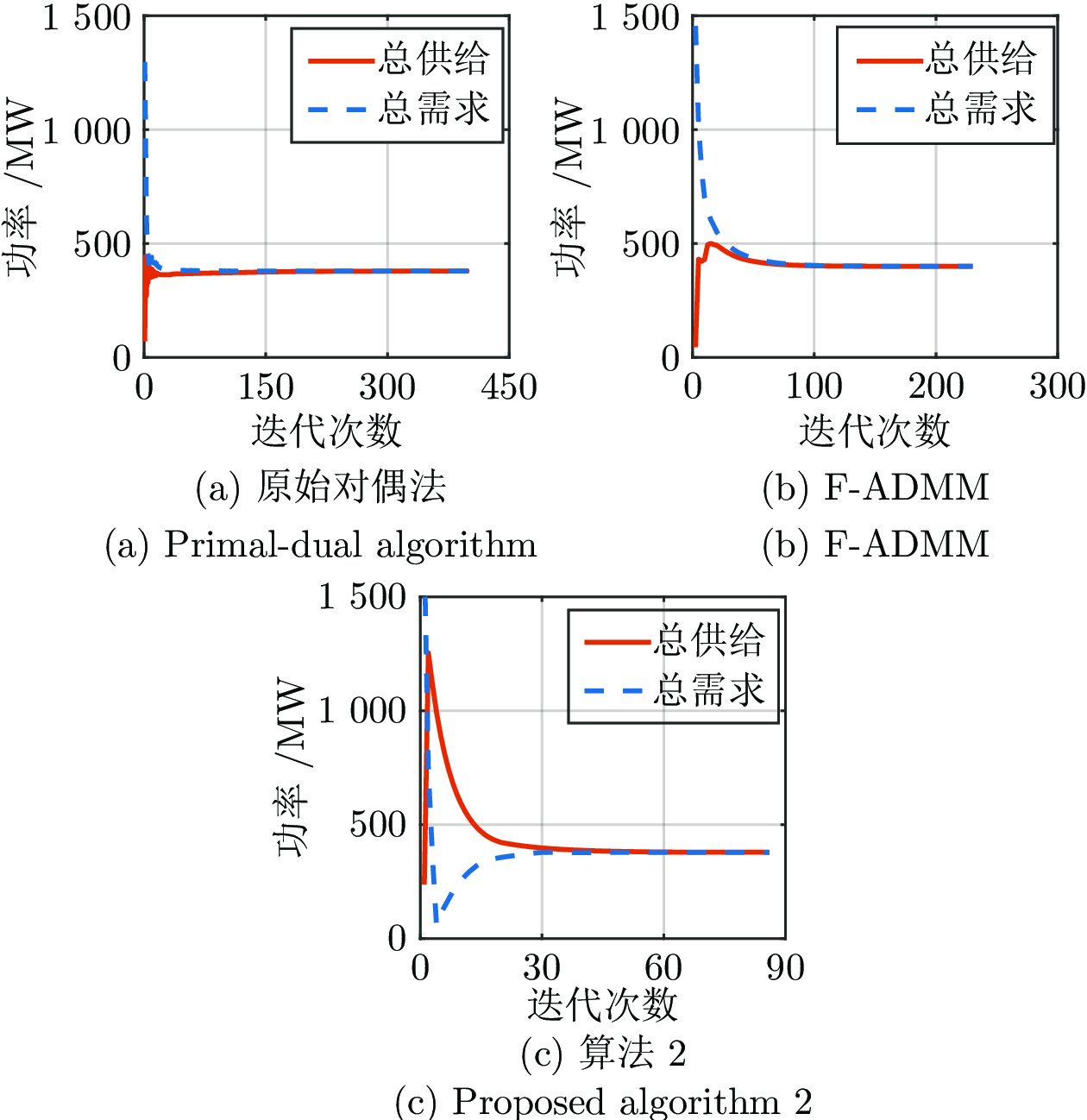
情形 算法1 算法2 迭代次数 计算时间(s) 迭代次数 计算时间(s) 情形1 402 158.3 433 165.9 情形2 374 143.3 86 32.6
下载: 导出CSV
表 8 情形1下, 3种算法的迭代次数和计算时间对比
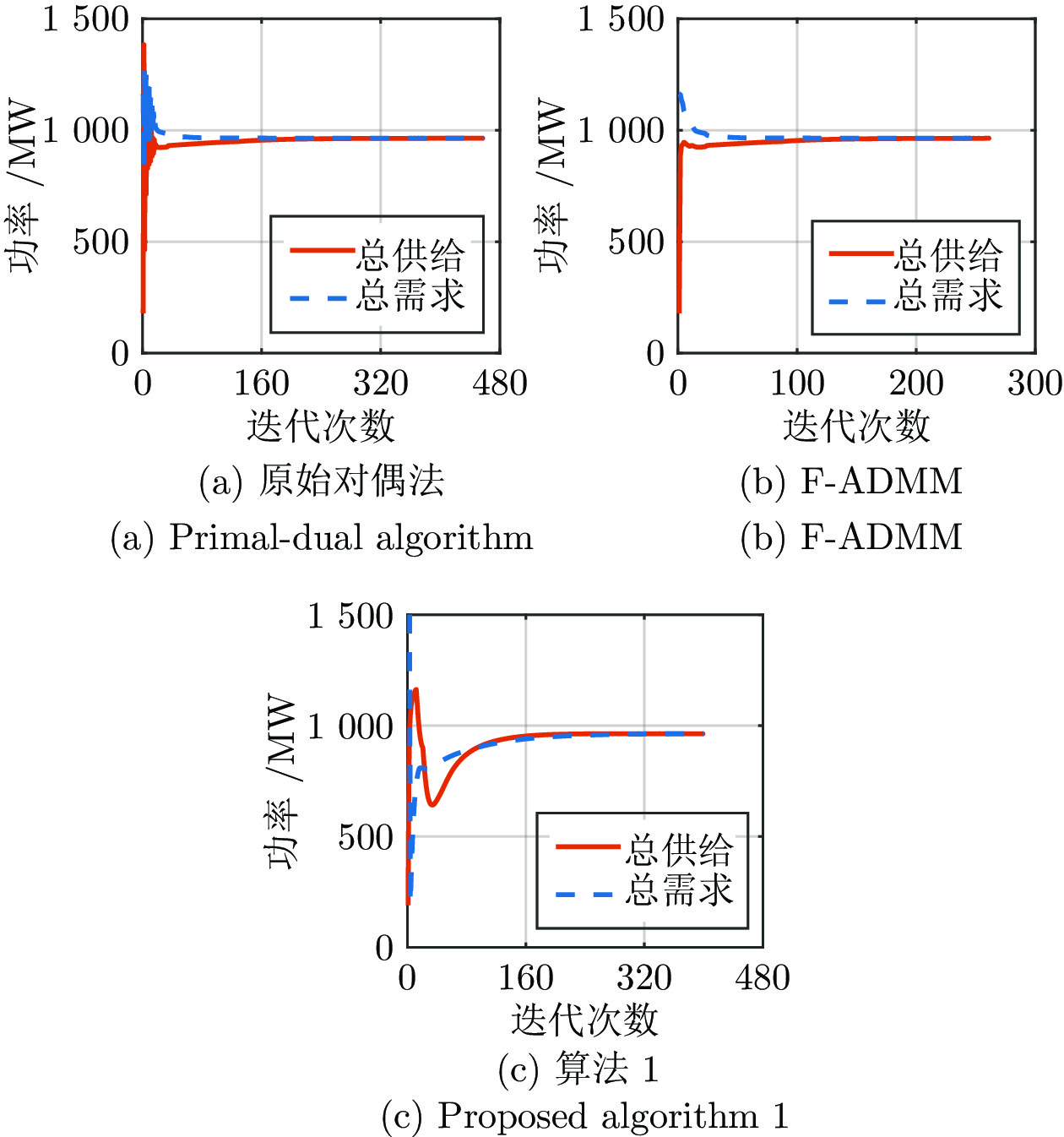
Table 8 Comparison of iterations and computation time of the 3 algorithms in scenario 1
算法名称 迭代次数 计算时间(s) 原始对偶法 458 162.2 F-ADMM 262 96.5 算法1 402 158.3
下载: 导出CSV
表 9 情形2下, 3种算法的迭代次数和计算时间对比
Table 9 Comparison of iterations and computation time of the 3 algorithms in scenario 2
算法名称 迭代次数 计算时间(s) 原始对偶法 395 149.8 F-ADMM 218 80.4 算法2 86 32.6
下载: 导出CSV
-
[1] 孙秋野, 滕菲, 张化光. 能源互联网及其关键控制问题. 自动化学报, 2017, 43(2): 176−194 doi: 10.16383/j.aas.2017.c160390Sun Qiu-Ye, Teng Fei, Zhang Hua-Guang. Energy internet and its key control issues. Acta Automatica Sinica, 2017, 43(2): 176−194 doi: 10.16383/j.aas.2017.c160390 [2] 平作为, 何维, 李俊林, 杨涛. 基于稀疏学习的微电网负载建模. 自动化学报, 2020, 46(9): 1798−1808 doi: 10.16383/j.aas.c200154Ping Zuo-Wei, He Wei, Li Jun-Lin, Yang Tao. Sparse learning for load modeling in microgrids. Acta Automatica Sinica, 2020, 46(9): 1798−1808 doi: 10.16383/j.aas.c200154 [3] 李玉帅, 李天义, 高炜, 高文忠. 基于异步动态事件触发通信策略的综合能源系统分布式协同优化运行方法. 自动化学报, 2020, 46(9): 1831−1843Li Yu-Shuai, Li Tian-Yi, Gao Wei, Gao Wen-Zhong. Distributed collaborative optimization operation approach for integrated energy system based on asynchronous and dynamic event-triggering communication strategy. Acta Automatica Sinica, 2020, 46(9): 1831−1843 [4] Valero S, Ortiz M, Senabre C, Alvarez C, Franco F, Gabaldón A. Methods for customer and demand response policies selection in new electricity markets. IET Generation, Transmission & Distribution, 2007, 1(1): 104−110 [5] 张晓萱, 薛松, 杨素, 屠俊明, 魏哲, 马莉. 售电侧市场放开国际经验及其启示. 电力系统自动化, 2016, 40(9): 1−8 doi: 10.7500/AEPS20151128001Zhang Xiao-Xuan, Xue Song, Yang Su, Tu Jun-Ming, Wei Zhe, Ma Li. International experience and lessons in power sales side market liberalization. Automation of Electric Power Systems, 2016, 40(9): 1−8 doi: 10.7500/AEPS20151128001 [6] 单俊嘉, 胡俊杰, 吴界辰. 面向虚拟电厂能量管理的点对点市场交易机制与模型. 电网技术, 2020, 44(9): 3401−3408Shan Jun-Jia, Hu Jun-Jie, Wu Jie-Chen. Peer-to-peer market trading mechanism and model for virtual power plant energy management. Power System Technology, 2020, 44(9): 3401−3408 [7] Iweh C D, Gyamfi S, Tanyi E, Effah-Donyina E. Distributed generation and renewable energy integration into the grid: Prerequisites, push factors, practical options, issues and merits. Energies, 2021, 14(17): 1−34 [8] Bahrami S, Amini M. A decentralized trading algorithm for an electricity market with generation uncertainty. Applied Energy, 2018, 218: 520−532 doi: 10.1016/j.apenergy.2018.02.157 [9] 田硕. 电动汽车聚合商参与日前市场的运营优化与竞标策略研究 [硕士论文], 华北电力大学, 中国, 2018.Tian Shuo. Operation Optimization and Bidding Strategy of the Electric Vehicle Aggregator Participating in Day-ahead Electricity Markets [Master thesis], North China Electric Power Univ-ersity, China, 2018. [10] 袁晓冬, 费骏韬, 胡波, 张友旺, 葛乐. 资源聚合商模型下的分布式电源、储能与柔性负荷联合调度模型. 电力系统保护与控制, 2019, 47(22): 17−26Yuan Xiao-Dong, Fei Jun-Tao, Hu Bo, Zhang You-Wang, Ge Le. Joint scheduling model of distributed generation, energy storage and flexible load under resource aggregator mode. Power System Protection and Control, 2019, 47(22): 17−26 [11] 林俐, 许冰倩, 王皓怀. 典型分布式发电市场化交易机制分析与建议. 电力系统自动化, 2019, 43(4): 1−8 doi: 10.7500/AEPS20180829001Lin Li, Xu Bing-Qian, Wang Hao-Huai. Analysis and recommendations of typical market-based distributed generation trading mechanisms. Automation of Electric Power Systems, 2019, 43(4): 1−8 doi: 10.7500/AEPS20180829001 [12] 蒋嗣凡. 分布式光伏P2P交易机制和交易策略研究 [硕士论文], 浙江大学, 中国, 2020.Jiang Si-Fan. Research on P2P Trading Mechanism and Strategy of Distributed PV Generation [Master thesis], Zhejiang University, China, 2020. [13] Paudel A, Chaudhari K, Chao L, Gooi H. Peer-to-peer energy trading in a prosumer based community microgrid: A game-theoretic model. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6087−6097 doi: 10.1109/TIE.2018.2874578 [14] Zhang K, Troitzsch S, Hanif S, Hamacher T. Coordinated market design for peer-to-peer energy trade and ancillary services in distribution grids. IEEE Transactions on Smart Grid, 2020, 11(4): 2929−2941 doi: 10.1109/TSG.2020.2966216 [15] Paudel A, Sampath L, Yang J, Gooi H. Peer-to-peer energy trading in smart grid considering power losses and network fees. IEEE Transactions on Smart Grid, 2020, 11(6): 4727−4737 doi: 10.1109/TSG.2020.2997956 [16] Tushar W, Saha T K, Yuen C, Smith D, Poor H V. Peer-to-peer trading in electricity networks: An overview. IEEE Transactions on Smart Grid, 2020, 11(4): 3185−3200 doi: 10.1109/TSG.2020.2969657 [17] 马腾, 刘洋, 刘俊, 蒋拯, 许立雄. 智能合约技术下微电网群电能分布式交易模型. 电力建设, 2021, 42(1): 41−48 doi: 10.12204/j.issn.1000-7229.2021.01.005Ma Teng, Liu Yang, Liu Jun, Jiang Zheng, Xu Li-Xiong. Distributed transaction model of electricity in multi-microgrid applying smart contract technology. Electric Power Construction, 2021, 42(1): 41−48 doi: 10.12204/j.issn.1000-7229.2021.01.005 [18] Guerrero J, Chapman A, Verbi G. Decentralized P2P energy trading under network constraints in a low-voltage network. IEEE Transactions on Smart Grid, 2019, 10(5): 5163−5173 doi: 10.1109/TSG.2018.2878445 [19] Khorasany M, Mishra Y, Ledwich G. A decentralized bilateral energy trading system for peer-to-peer electricity markets. IEEE Transactions on Industrial Electronics, 2020, 67(6): 4646−4657 doi: 10.1109/TIE.2019.2931229 [20] Morstyn T, Teytelboym A, Hepburn C, McCulloch M D. Integrating P2P energy trading with probabilistic distribution locational marginal pricing. IEEE Transactions on Smart Grid, 2020, 11(4): 3095−3106 doi: 10.1109/TSG.2019.2963238 [21] Coffrin C, Knueven B, Holzer J, Vuffary M. The impacts of convex piecewise linear cost formulations on AC optimal power flow. Electric Power Systems Research, 2021, 199(1): 1−11 [22] 王怡, 杨知方, 余娟, 赵唯嘉. 节点电价与对偶乘子的内在关联分析与扩展. 电力系统自动化, 2021, 45(6): 82−91Wang Yi, Yang Zhi-Fang, Yu Juan, Zhao Wei-Jia. Analysis and extension of internet relationship between locational marginal price and dual multiplier. Automation of Electric Power Syste-ms, 2021, 45(6): 82−91 [23] Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine learning, 2011, 3(1): 1−12 [24] Bertsekas D. Nonlinear Programming. Belmont: Athena Scientific, 1999. 234−244, 334 [25] Ullah M H, Park J D. Peer-to-peer energy trading in transactive markets considering physical network constraints. IEEE Transactions on Smart Grid, 2021, 12(4): 3390−3403 doi: 10.1109/TSG.2021.3063960 -
计量
- 文章访问数: 601
- HTML全文浏览量: 161
- PDF下载量: 63
- 被引次数: 0
