-
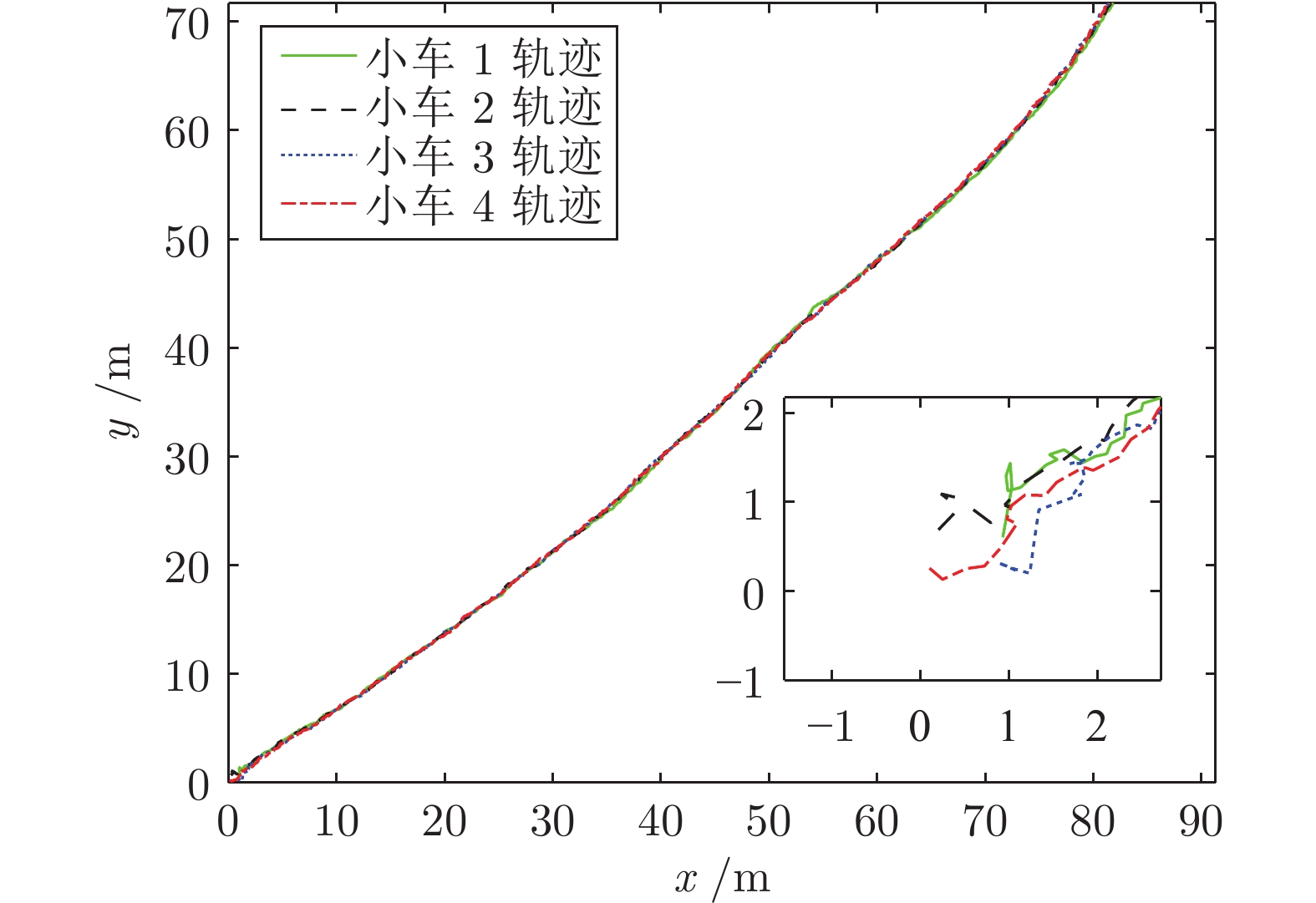
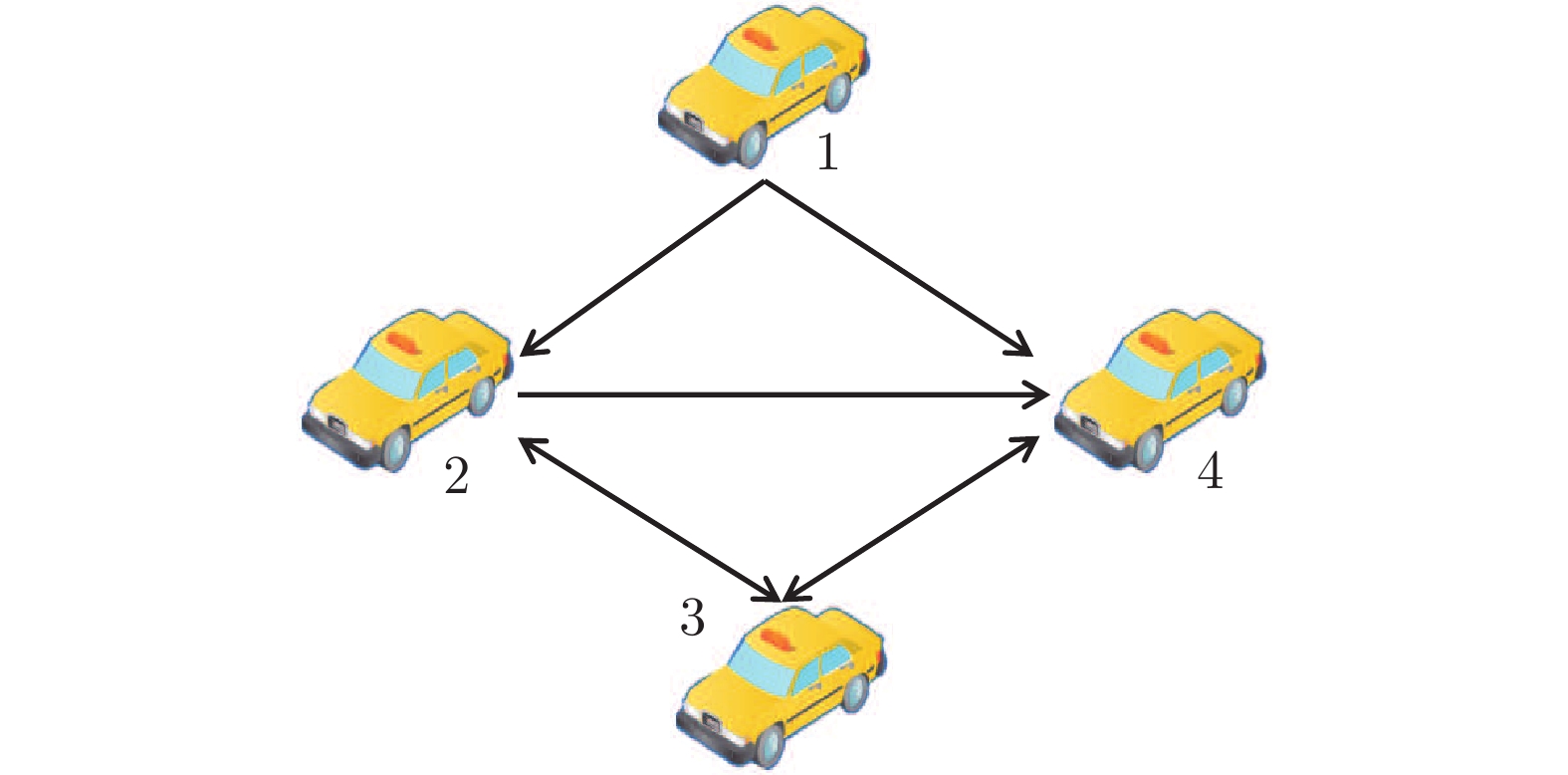
摘要: 研究一类存在一步随机时滞的复杂网络分布式状态估计问题, 采用伯努利随机变量刻画测量值的随机时滞情况. 基于复杂网络模型和不可靠测量值, 分别设计复杂网络的状态预测器和分布式状态估计器, 基于杨氏不等式消除节点之间的耦合项, 通过优化杨氏不等式引进的参数, 优化状态预测协方差. 通过设计估计器增益, 获得状态估计误差协方差, 同时结合预测误差协方差, 获得状态估计误差协方差的迭代公式, 并给出估计误差协方差稳定的充分条件. 最后, 对由小车组成的耦合系统进行数值仿真, 验证所设计估计器的有效性.Abstract: This work addresses the distributed state estimation for complex networks with delayed measurements. The Bernoulli process is employed to describe the measurements with randomly occurred one step delay. The state predictor is derived based on the system mode, and the distributed state estimator is designed by using delayed measurements. The coupling term between nodes is eliminated based on Young's inequality, and the covariance of state prediction is improved by optimizing the parameters introduced by Young's inequality. Furthermore, the optimal state estimation error covariance is achieved by designing the estimator gain. Thanks to the state prediction error covariance, the iterative inequality of the state estimation error covariance is derived, and its sufficient condition for stability is established. Finally, the moving vehicles based coupled system is given to illustrate the effectiveness of the designed estimator.
-
Key words:
- Complex network /
- distributed state estimation /
- delayed measurement /
- stability analysis
-
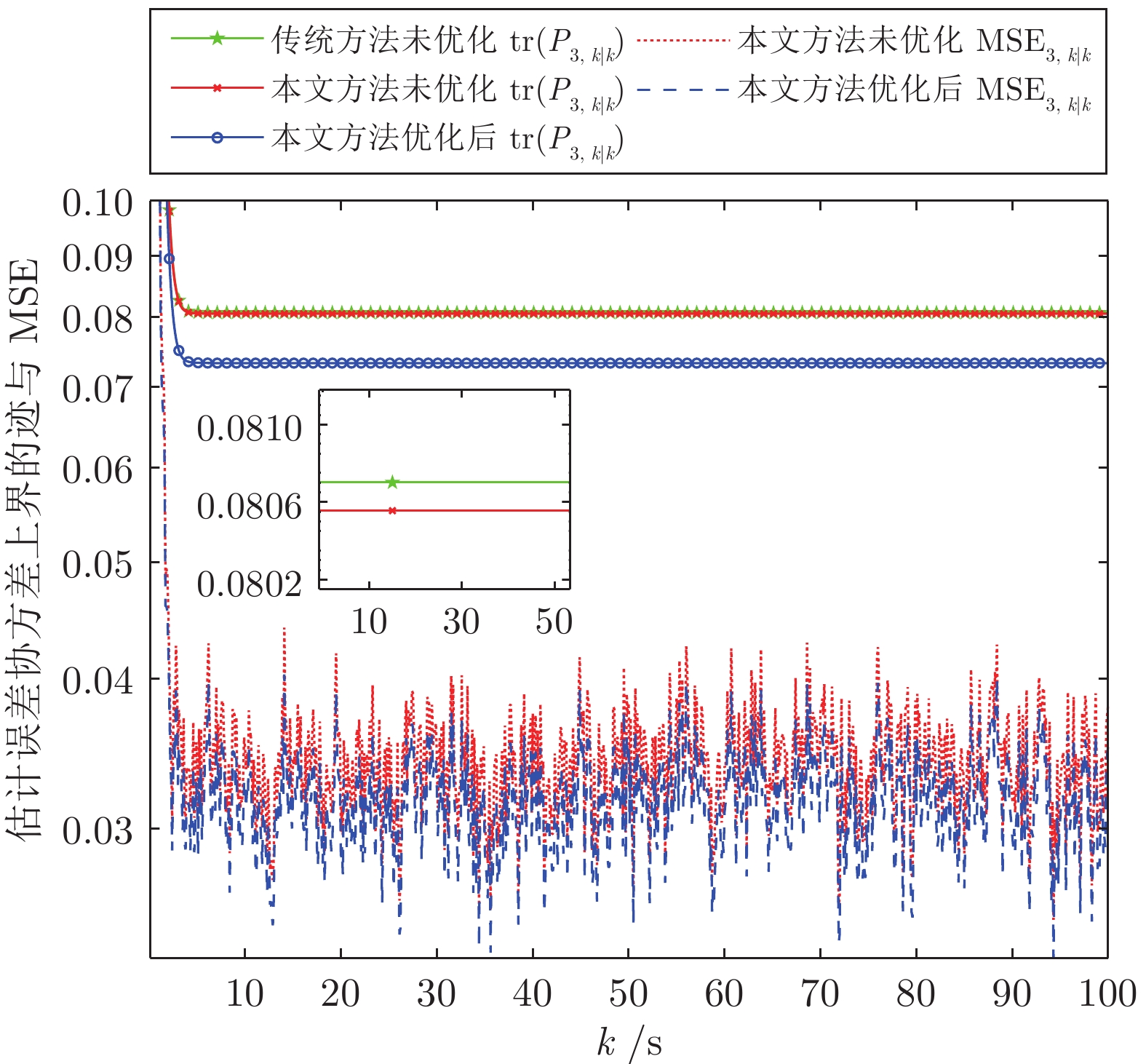
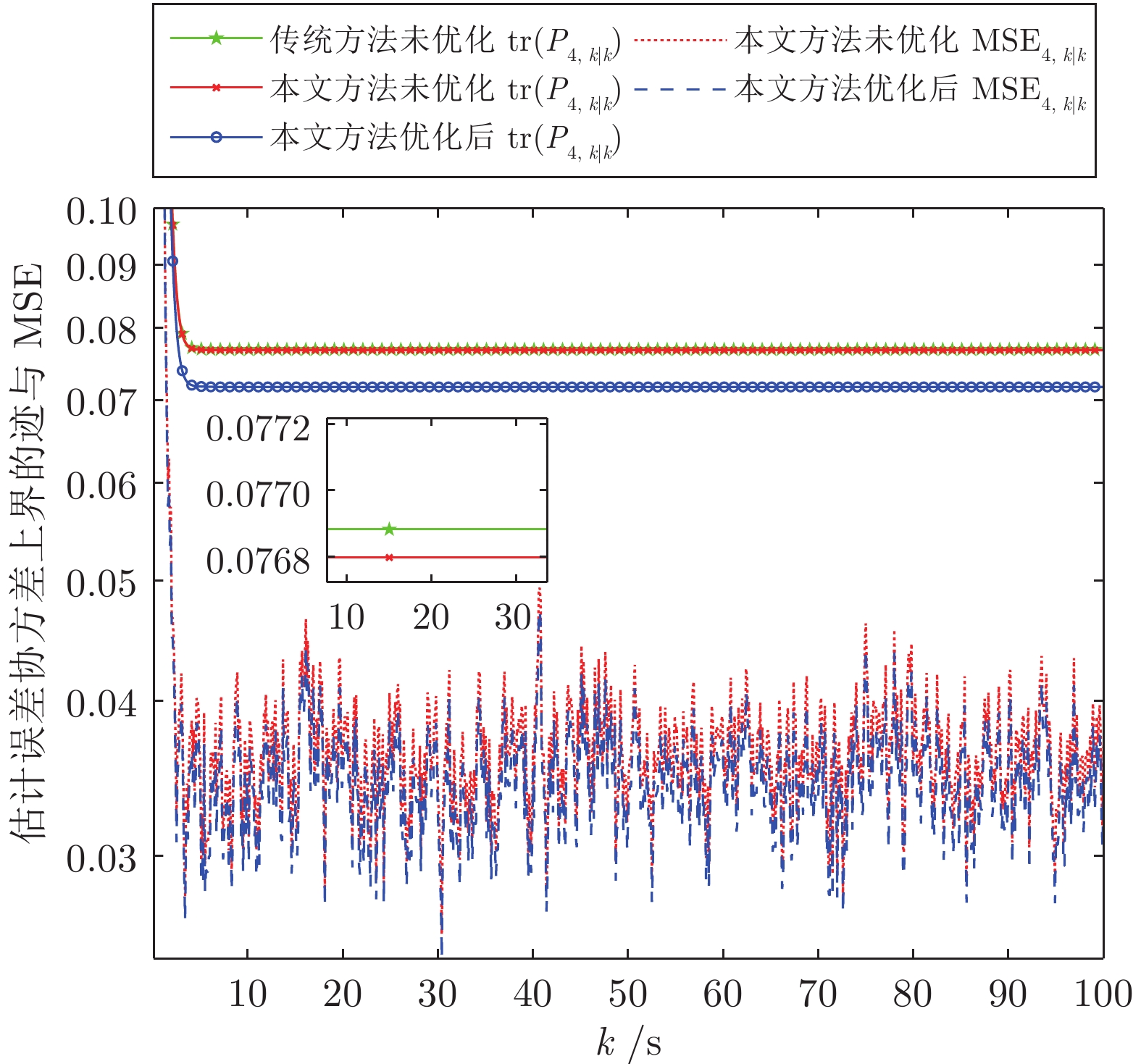
表 1 基于优化和未优化的$\gamma_{1,i,k}$的上界$\rm{tr}(P_{i,k|k})$
Table 1 The upper bound $\rm{tr}(P_{i,k|k})$ based on $\gamma_{1,i,k}$ with and without optimization
节点$i$ 未优化$\rm{tr}(P_{i,k|k})$上界 优化后$\rm{tr}(P_{i,k|k})$上界 优化幅度(%) 1 0.0679 0.0622 8.50 2 0.0686 0.0630 8.23 3 0.0806 0.0733 9.04 4 0.0768 0.0717 6.60 表 2 基于优化和未优化的$\gamma_{1,i,k}$的MSE$_{i,k|k}$
Table 2 The MSE$_{i,k|k}$ based on $\gamma_{1,i,k}$ with and without optimization
节点$i$ 未优化MSE$_{i,k|k}$均值 优化后MSE$_{i,k|k}$均值 优化幅度(%) 1 0.0357 0.0338 5.23 2 0.0364 0.0347 4.82 3 0.0424 0.0400 5.73 4 0.0456 0.0438 3.83 -
[1] Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D U. Complex networks: Structure and dynamics. Physics Reports, 2006, 424(4–5): 175−308 [2] Li W L, Jia Y M, Du J P. Variance-constrained state estimation for nonlinearly coupled complex networks. IEEE Transactions on Cybernetics, 2018, 48(2): 818−824 doi: 10.1109/TCYB.2017.2653242 [3] Rad A, Khadivi A, Hasler M. Information processing in complex networks. IEEE Circuits and Systems Magazine, 2010, 10(3): 26−37 doi: 10.1109/MCAS.2010.937881 [4] 席裕庚. 大系统控制论与复杂网络—探索与思考. 自动化学报, 2013, 39(11): 1758−1768 doi: 10.3724/SP.J.1004.2013.01758Xi Yu-Geng. Large-scale systems control and complex networks—Exploration and thinking. Acta Automatica Sinica, 2013, 39(11): 1758−1768 doi: 10.3724/SP.J.1004.2013.01758 [5] Li X, Chen G R. Synchronization and desynchronization of complex dynamical networks: An engineering viewpoint. IEEE Transactions on Circuits and Systems Part I Fundamental Theory and Applications, 2003, 50(11): 1381−1390 [6] Dorfler F, Bullo F. Synchronization in complex networks of phase oscillators: A survey. Automatica, 2014, 50(6): 1539−1564 doi: 10.1016/j.automatica.2014.04.012 [7] Yi Y H, Zhang Z Z, Patterson S. Scale-free loopy structure is resistant to noise in consensus dynamics in complex networks. IEEE Transactions on Cybernetics, 2020, 50(1): 190−200 doi: 10.1109/TCYB.2018.2868124 [8] Xu Y F, Choi J. Spatial prediction with mobile sensor networks using Gaussian processes with built-in Gaussian Markov random fields. Automatica, 2012, 48(8): 1735−1740 doi: 10.1016/j.automatica.2012.05.029 [9] Li Q, Shen B, Wang Z D, Huang T W, Luo J. Synchronization control for a class of discrete time-delay complex dynamical networks: A dynamic event-triggered approach. IEEE Transactions on Cybernetics, 2018, 49(5): 1979−1986 [10] Meng C, Wang T M, Chou W S, Luan S, Zhang Y R, Tian Z M. Remote surgery case: Robot-assisted teleneurosurgery. IEEE International Conference on Robotics and Automation, 2004, 1: 819−823 [11] Walsh G C, Ye H, Bushnell L G. Stability analysis of networked control systems. IEEE Transactions on Control Systems Technology, 2002, 10(3): 438−446 doi: 10.1109/87.998034 [12] 徐雍, 饶红霞, 王卓, 鲁仁全, 李宗. 带有随机通信时滞的状态估计. 中国科学信息科学, 2022, 52(8): Article No. 1513Xu Yong, Rao Hong-Xia, Wang Zhuo, Lu Ren-Quan, Li Zong. State estimation for networked uncertain nonlinear systems with time-delays. Scientia Sinica Informationis, 2022, 52(8): Article No. 1513 [13] Hespanha J P, Naghshtabrizi P, Xu Y G. A survey of recent results in networked control systems. Proceedings of the IEEE, 2007, 95(1): 138−162 doi: 10.1109/JPROC.2006.887288 [14] Samad T, Bay J S, Godbole D. Network-centric systems for military operations in urban terrain: The role of UAVs. Proceedings of the IEEE, 2007, 95: 92−107 doi: 10.1109/JPROC.2006.887327 [15] Ren W, Xiong J L. Tracking control of nonlinear networked and quantized control systems with communication delays. IEEE Transactions on Automatic Control, 2019, 65(8): 3685−3692 [16] Liu H, Lu J A, Lv J H, Hill D J. Structure identification of uncertain general complex dynamical networks with time delay. Automatica, 2009, 45(8): 1799−1807 doi: 10.1016/j.automatica.2009.03.022 [17] 杨园华, 付敏跃, 张焕水. 带有随机通信时滞的状态估计. 自动化学报, 2013, 39(3): 237−243 doi: 10.1016/S1874-1029(13)60025-7Yang Yuan-Hua, Fu Min-Yue, Zhang Huan-Shui. State estimation subject to random communication delays. Acta Automatica Sinica, 2013, 39(3): 237−243 doi: 10.1016/S1874-1029(13)60025-7 [18] Wang Y, Xiong J L, Ho D W C. Decentralized control scheme for large-scale systems defined over a graph in presence of communication delays and random missing measurements. Automatica, 2018, 98: 190−200 doi: 10.1016/j.automatica.2018.09.023 [19] Xu Y, Zhou J Y, Rao H X, Lu R Q, Xie L H. Reset moving horizon estimation for quantized discrete time systems. IEEE Transactions on Automatic Control, 2021, 66(9): 4199−4205 doi: 10.1109/TAC.2020.3037140 [20] Xu Y, Yang L X, Wang Z, Rao H X, Lu R Q. State estimation for networked systems with Markov driven transmission and buffer constraint. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(12): 7727−7734 doi: 10.1109/TSMC.2020.2980425 [21] Hu J, Wang Z D, Alsaadi F E, Hayat T. Event-based filtering for time-varying nonlinear systems subject to multiple missing measurements with uncertain missing probabilities. Information Fusion, 2017, 38: 74−83 doi: 10.1016/j.inffus.2017.03.003 [22] Hao J, Sun S. Distributed Kalman filtering for sensor networks with random sensor activation, delays, and packet dropouts. International Journal of Systems Science, 2022, 53(3): 575−592 doi: 10.1080/00207721.2021.1963502 [23] Paul A, Kamwa I, Jóos G. Centralized dynamic state estimation using a federation of extended Kalman filters with intermittent PMU data from generator terminals. IEEE Transactions on Power Systems, 2018, 33(6): 6109−6119 doi: 10.1109/TPWRS.2018.2834365 [24] Liu Y, Wang Z D, Zhou D H. Scalable distributed filtering for a class of discrete-time complex networks over time-varying topology. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(8): 2930−2941 doi: 10.1109/TNNLS.2019.2934131 [25] Li W L, Jia Y M, Du J P. State estimation for stochastic complex networks with switching topology. IEEE Transactions on Automatic Control, 2017, 62(12): 6377−6384 doi: 10.1109/TAC.2017.2649878 [26] Liu Y, Wang Z D, Zhou D H. Resilient actuator fault estimation for discrete-time complex networks: A distributed approach. IEEE Transactions on Automatic Control, 2021, 66(9): 4214−4221 doi: 10.1109/TAC.2020.3033710 [27] Duan P H, Duan Z S, Lv Y Z, Chen G R. Distributed finite-horizon extended Kalman filtering for uncertain nonlinear systems. IEEE Transactions on Cybernetics, 2021, 51(2): 512−520 doi: 10.1109/TCYB.2019.2919919 [28] Basu H, Yoon S S. Distributed state estimation by a network of observers under communication and measurement delays. Systems and Control Letters, 2019, 133: 1−10 [29] Anderson B D O, Moore J B. Optimal Filtering. New York: Dover publication, 2012. [30] Sinopoli B, Schenato L, Franceschetti M, Poolla K, Jordan M I, Sastry S S. Kalman filtering with intermittent observations. IEEE Transactions on Automatic Control, 2004, 1(9): 1453−1464 [31] Jin H, Sun S L. Distributed filtering for sensor networks with fading measurements and compensations for transmission delays and losses. Signal Processing, 2022, 190: Article No. 108306 doi: 10.1016/j.sigpro.2021.108306 [32] Peng H, Zeng B R, Yang L X, Xu Y, Lu R Q. Distributed extended state estimation for complex networks with nonlinear uncertainty. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(9): 5952−5960 [33] Huang Z H, Marelli D, Xu Y, Fu M Y. Distributed target tracking using maximum likelihood Kalman filter with non-linear measurements. IEEE Sensors Journal, 2021, 21(24): 27818−27826 doi: 10.1109/JSEN.2021.3125153 [34] Lin Z Y, Wang L L, Han Z M, Fu M Y. Distributed formation control of multi-agent systems using complex laplacian. IEEE Transactions on Automatic Control, 2014, 59(7): 1765−1777 doi: 10.1109/TAC.2014.2309031 [35] Dong X W, Hua Y Z, Zhou Y, Ren Z, Zhong Y S. Theory and experiment on formation-containment control of multiple multirotor unmanned aerial vehicle systems. IEEE Transactions on Automation Science and Engineering, 2019, 16(1): 229−240 doi: 10.1109/TASE.2018.2792327 -




 下载:
下载: