Real-time State Estimation and Feedback Control for n-qubit Stochastic Quantum Systems
-
摘要: 研究了$n $比特随机量子系统实时状态估计及其反馈控制的问题. 对于连续弱测量(Continuous weak measurement, CWM)过程存在高斯噪声的情况, 基于在线交替方向乘子法(Online alternating direction multiplier method, OADM)推导出一种适用于$n $比特随机量子系统的实时量子状态估计算法, 即QSE-OADM (Quantum state estimation based on OADM). 运用李雅普诺夫方法设计控制律, 实现基于实时量子状态估计的反馈控制, 并证明所提控制律的收敛性. 以2比特随机量子系统为例进行数值仿真实验, 通过与基于QST-OADM (Quantum state tomography based on OADM)算法和OPG-ADMM (Online proximal gradient-based alternating direction method of multipliers)算法的量子反馈控制方案的性能对比, 验证了所提控制方案的优越性.Abstract: The problem of real-time state estimation and feedback control of $n{\text{-}}{\rm{qubit}} $ stochastic quantum systems is investigated in this paper. Considering the presence of Gaussian noises in the continuous weak measurement (CWM) process, a real-time quantum state estimation (QSE) algorithm based on the online alternating direction multiplier method (OADM), short for QSE-OADM, is deduced for $ n{\text{-}}{\rm{qubit}} $ stochastic quantum systems. The control law is designed via the Lyapunov-based approach to realize real-time quantum state estimation-based feedback control, and the convergence of the proposed control law is proved. Numerical simulations are carried out for 2-qubit stochastic quantum systems, and the superiority of the proposed control scheme is verified in comparison with the performance of quantum feedback control schemes based on the QST-OADM (quantum state tomography based on the online alternating direction multiplier method) algorithm and the OPG-ADMM (online proximal gradient-based alternating direction method of multipliers) algorithm.
-
图 1 不同外部控制场的作用下的实时状态估计性能
Fig. 1 Real-time state estimation performance under various external control fields
图 2 不同初始测量算符作用下的实时状态估计性能
Fig. 2 Real-time state estimation performance under various initial measurement operators
图 3 不同的相互作用强度作用下的实时状态估计性能
Fig. 3 Real-time state estimation performance under various interaction strengths
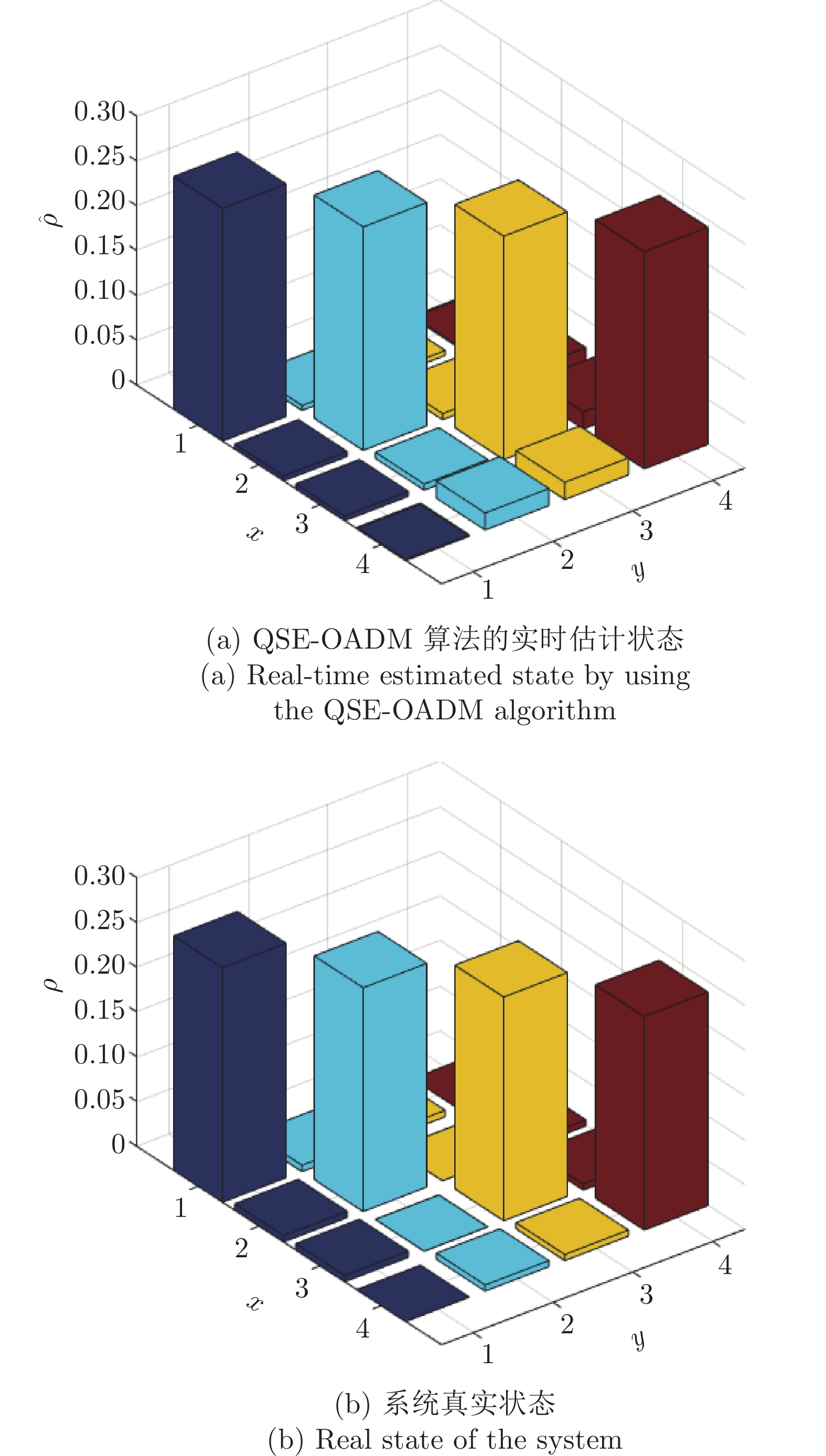
图 4 第30次采样时2比特量子系统估计状态与真实状态比较$( H' = {H_0} + {\;}1\cdot{\sigma _x} $, $ {M_1} = {\sigma _z} \otimes {\sigma _z} $, $ L' = {\;}0.7{\sigma _z}) $
Fig. 4 Comparison between the estimated state and the real state of a 2-qubit system at the 30th sampling time $( H' = {H_0} + {\;}1\cdot{\sigma _x} $, $ {M_1} = {\sigma _z} \otimes {\sigma _z} $, $ L' = {\;}0.7{\sigma _z} )$
图 5 基于实时状态估计的n比特随机量子系统反馈控制方案的框图
Fig. 5 Real-time state estimation-based feedback control scheme for n-qubit stochastic quantum systems
图 7 叠加态反馈控制的仿真结果
Fig. 7 Simulation results on feedback control of a superposition state
表 1 测量值序列的构造方法
Table 1 Construction approach of the measurement record sequence
$y_1$ $y_2$ $ \cdots $ $y_k$ $b_1$ ${\rm{tr}}(M_1^\dagger {\rho _1})$ — $ \cdots $ — $b_2$ ${\rm{tr}}(M_2^\dagger {\rho _2})$ ${\rm{tr}}(M_1^\dagger {\rho _2})$ $ \cdots $ — $\vdots$ $\vdots$ $\vdots$ $\ddots$ $\vdots$ $b_k$ ${\rm{tr}}(M_k^\dagger {\rho _k})$ ${\rm{tr}}(M_{k - 1}^\dagger {\rho _k})$ $\cdots$ ${\rm{tr}}(M_1^\dagger {\rho _k})$ 
下载: 导出CSV
表 2 本征态反馈控制性能指标的对比
Table 2 Comparison of performance indicators of feedback control of an eigenstate
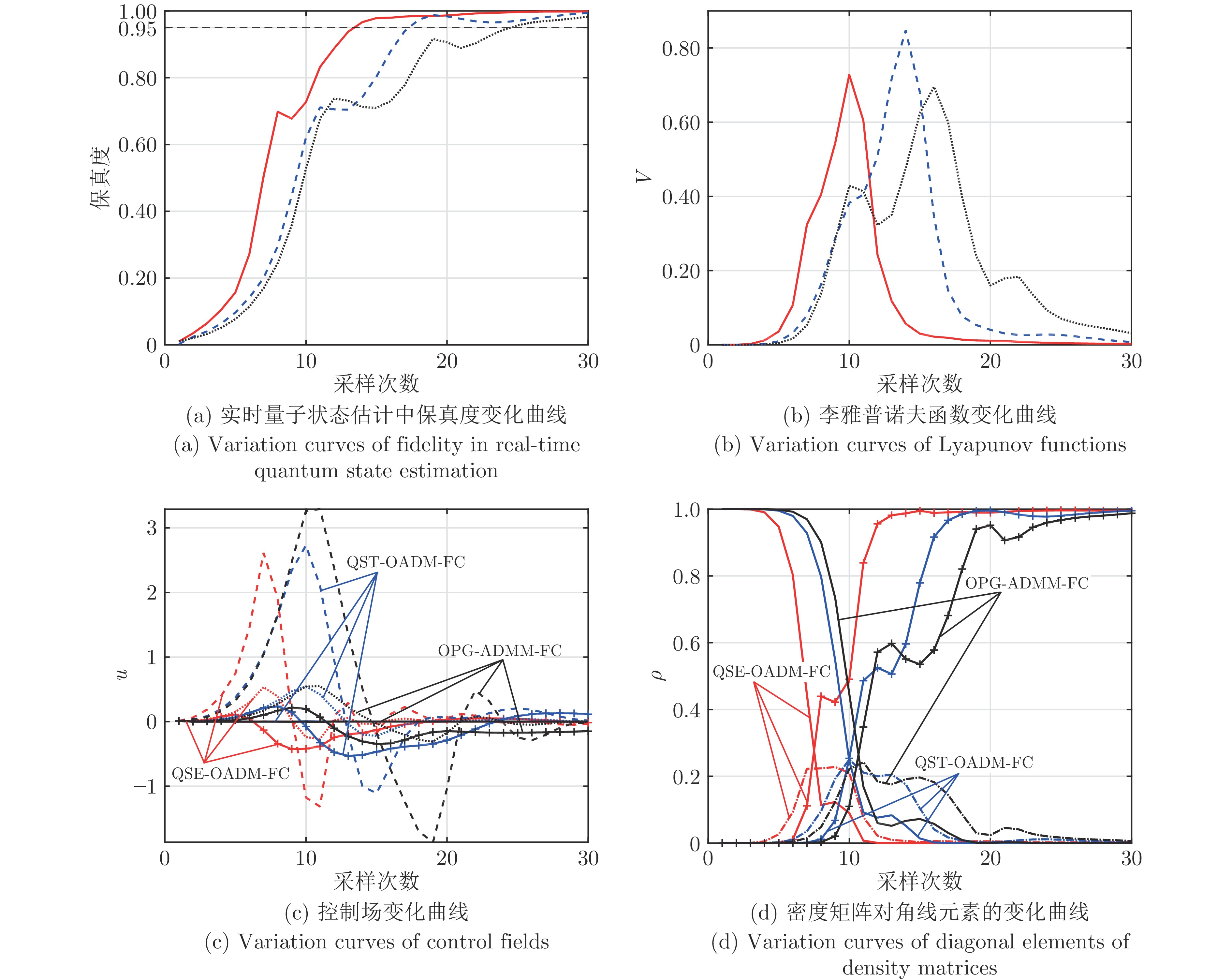
指标 方案 1 方案 2 方案 3 $k_{s1}$ 14 18 25 $k_{s2}$ 15 18 28 $Fidelity(30)$(%) 99.84 99.40 98.29 $V(30)$ $5.399 \times {10^{ - 4}}$ $1.484 \times {10^{ - 3}}$ $6.312 \times {10^{ - 3}}$ $J(30)$ 18.247 28.721 52.112
下载: 导出CSV
表 3 叠加态反馈控制性能指标的对比
Table 3 Comparison of performance indicators of feedback control of a superposition state
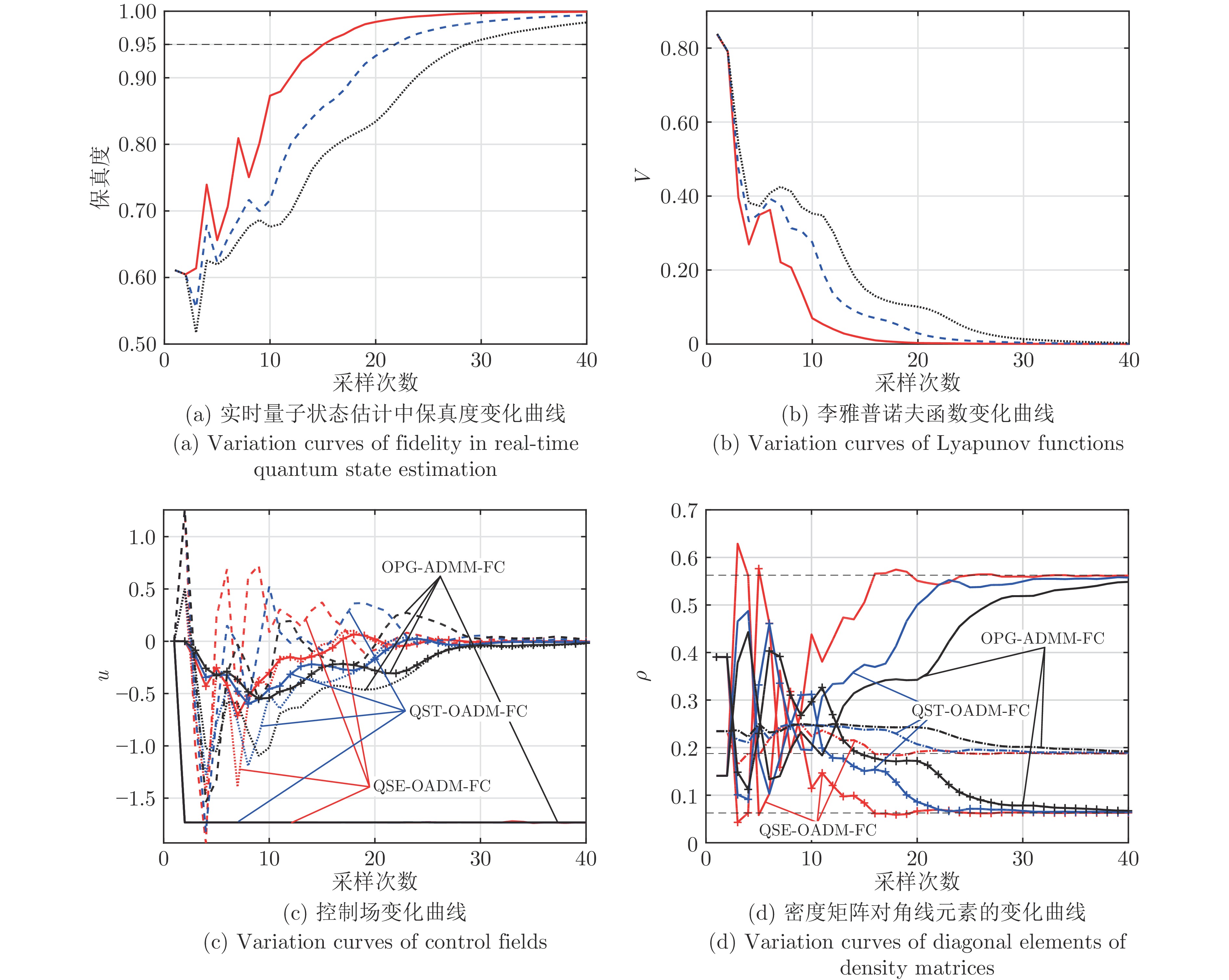
指标 方案 1 方案 2 方案 3 $k_{s1}$ 16 22 29 $k_{s2}$ 16 25 33 $Fidelity(40)$(%) 99.90 99.40 98.30 $V(40)$ $1.651 \times {10^{ - 4}}$ $6.180 \times {10^{ - 4}}$ $2.854 \times {10^{ - 3}}$ $J(40)$ 133.179 133.880 136.223
下载: 导出CSV
-
[1] Huang G M, Tarn T J, Clark J W. On the controllability of quantum-mechanical systems. Journal of Mathematical Physics, 1983, 24(11): 2608-2618 doi: 10.1063/1.525634 [2] Tesch C M, Kurtz L, Vivie-Riedle R D. Applying optimal control theory for elements of quantum computation in molecular systems. Chemical Physics Letters, 2001, 343(5-6): 633-641 doi: 10.1016/S0009-2614(01)00748-5 [3] Nigmatullin R, Schirmer S G. Implementation of fault-tolerant quantum logic gates via optimal control. New Journal of Physics, 2009, 11(10): Article No. 105032 doi: 10.1088/1367-2630/11/10/105032 [4] Nourallah G, Cong S. Preparation of Hadamard gate for open quantum systems by the Lyapunov control method. IEEE/CAA Journal of Automatica Sinica, 2018, 5(3): 733-740 doi: 10.1109/JAS.2018.7511084 [5] Viola L, Lloyd S. Dynamical suppression of decoherence in two-state quantum systems. Physical Review A, 1998, 58(4): 2733-2744 doi: 10.1103/PhysRevA.58.2733 [6] Zhang M, Ou B Q, Dai H Y, Hu D W. Control decoherence by quantum generalized measurement. Acta Automatica Sinica, 2008, 34(4): 433-437 doi: 10.3724/SP.J.1004.2008.00433 [7] Dong D, Petersen I R. Quantum control theory and applications: A survey. IET Control Theory & Applications, 2009, 4(12): 2651-2671 [8] 丛爽. 量子分子动力学中的操纵技术及其系统控制理论. 控制理论与应用, 2010, 27(1): 1-12Cong Shuang. Manipulation technology and system control theory in quantum molecular dynamics. Control Theory & Applications, 2010, 27(1): 1-12 [9] Cong S. Control of Quantum Systems: Theory and Methods. Singapore: Wiley, 2014. [10] Dong W, Wu R, Yuan X, Li C, Tarn T J. The modelling of quantum control systems. Science Bulletin, 2015, 60(17): 1493-1508 doi: 10.1007/s11434-015-0863-3 [11] Zhang J, Liu Y X, Wu R B, Jacobs K, Nori F. Quantum feedback: Theory, experiments, and applications. Physics Reports, 2017, 679: 1-60 doi: 10.1016/j.physrep.2017.02.003 [12] D＇Alessandro D. Introduction to Quantum Control and Dynamics. New York: Chapman & Hall/CRC, 2020. [13] Silberfarb A, Jessen P S, Deutsch I H. Quantum state reconstruction via continuous measurement. Physical Review Letters, 2005, 95(3): Article No. 030402 [14] Smith G A, Silberfarb A, Deutsch I H, Jessen P S. Efficient quantum-state estimation by continuous weak measurement and dynamical control. Physical Review Letters, 2006, 97(18): Article No. 180403 doi: 10.1103/PhysRevLett.97.180403 [15] Ralph J F, Jacobs K, Hill C D. Frequency tracking and parameter estimation for robust quantum state-estimation. Physical Review A, 2011, 84(5): 1398-1405 [16] 唐雅茹, 丛爽, 杨靖北. 单量子比特系统状态的在线估计. 自动化学报, 2020, 46(8): 1592-1599 doi: 10.16383/j.aas.c180752Tang Ya-Ru, Cong Shuang, Yang Jing-Bei. On-line state estimation of one-qubit system. Acta Automatica Sinica, 2020, 46(8): 1592-1599 doi: 10.16383/j.aas.c180752 [17] Harraz S, Cong S, Li K. Online quantum state tomography of N-qubit via continuous weak measurement and compressed sensing. International Journal of Quantum Information, 2020: Article No. 2040006 [18] Zhang K, Cong S, Li K, Wang T. An online optimization algorithm for the real-time quantum state tomography. Quantum Information Processing, 2020, 19(10): Article No. 361 doi: 10.1007/s11128-020-02866-4 [19] Zhang K, Cong S, Tang Y, Freris N M. An efficient online estimation algorithm for evolving quantum states. In: Proceedings of the European Signal Processing Conference (EUSIPCO). Amsterdam, the Netherlands: IEEE, 2020. 2249−2253 [20] Kuang S, Cong S. Lyapunov control methods of closed quantum systems. Automatica, 2008, 44(1): 98-108 doi: 10.1016/j.automatica.2007.05.013 [21] Sayrin C, Dotsenko I, Zhou X, Peaudecerf B, Rybarczyk T, Gleyzes S, et al. Real-time quantum feedback prepares and stabilizes photon number states. Nature, 2011, 477(7362): 73-77 doi: 10.1038/nature10376 [22] Qi B, Guo L. Is measurement-based feedback still better for quantum control systems? Systems & Control Letters, 2010, 59(6): 333-339 [23] Qi B, Pan H, Guo L. Further results on stabilizing control of quantum systems. IEEE Transactions on Automatic Control, 2013, 58(5): 1349-1354 doi: 10.1109/TAC.2012.2224252 [24] Qamar S, Cong S. Observer-based feedback control of two-level open stochastic quantum system. Journal of the Franklin Institute, 2019, 356(11): 5675-5691 doi: 10.1016/j.jfranklin.2019.05.021 [25] Harraz S, Cong S. State transfer via on-line state estimation and Lyapunov-based feedback control for a N-qubit system. Entropy, 2019, 21(8): Article No. 751 doi: 10.3390/e21080751 [26] 丛爽, 胡龙珍, 杨霏, 刘建秀. Non-Markovian开放量子系统的特性分析与状态转移. 自动化学报, 2013, 39(4): 360-370 doi: 10.1016/S1874-1029(13)60035-XCong Shuang, Hu Long-Zhen, Yang Fei, Liu Jian-Xiu. Characteristics analysis and state transfer for Non-Markovian open quantum systems. Acta Automatica Sinica, 2013, 39(4): 360-370 doi: 10.1016/S1874-1029(13)60035-X [27] Bosse J, Rabaste O. Subspace rejection for matching pursuit in the presence of unresolved targets. IEEE Transactions on Signal Processing, 2018, 66(8): 1997-2010 doi: 10.1109/TSP.2018.2795572 [28] 张贤达. 矩阵分析与应用. 北京: 清华大学出版社, 2013.Zhang Xian-Da. Matrix Analysis and Applications. Beijing: Tsinghua University Press, 2013. [29] Ge S S, Vu T L, Hang C C. Non-smooth Lyapunov function-based global stabilization for quantum filters. Automatica, 2012, 48(6): 1031-1044 doi: 10.1016/j.automatica.2012.03.001 -
计量
- 文章访问数: 608
- HTML全文浏览量: 212
- PDF下载量: 148
- 被引次数: 0
