基于混合变分自编码器回归模型的软测量建模方法

崔琳琳; 沈冰冰; 葛志强

doi:10.16383/j.aas.c210035

基于混合变分自编码器回归模型的软测量建模方法

doi: 10.16383/j.aas.c210035

崔琳琳^{1, 2,},
沈冰冰^{1, 2,},
葛志强^{1, 2,}

1.
浙江大学控制科学与工程学院工业控制研究所杭州 310027
2.
浙江大学工业控制技术国家重点实验室杭州 310027

基金项目: 国家自然科学基金(62103362, 92167106), 浙江省自然科学基金(LR18F030001)资助

详细信息

作者简介:
崔琳琳：浙江大学控制科学与工程学院硕士研究生. 主要研究方向为工业软测量. E-mail: linlincui@zju.edu.cn

沈冰冰：浙江大学控制科学与工程学院博士研究生. 主要研究方向为数据驱动建模, 过程数据分析和软测量应用. E-mail: shenbingbing@zju.edu.cn

葛志强：浙江大学教授、博导. 主要研究方向为工业大数据、过程监测与故障诊断、软测量技术、智能系统与知识自动化. 本文通信作者. E-mail: gezhiqiang@zju.edu.cn

计量
- 文章访问数: 2190
- HTML全文浏览量: 723
- PDF下载量: 481
- 被引次数: 0
出版历程
- 收稿日期: 2021-01-13
- 录用日期: 2021-04-16
- 网络出版日期: 2021-05-30
- 刊出日期: 2022-02-18

A Mixture Variational Autoencoder Regression Model for Soft Sensor Application

CUI Lin-Lin^{1, 2
,},
SHEN Bing-Bing^{1, 2
,},
GE Zhi-Qiang^{1, 2
,}

1.
Institute of Industrial Process Control, College of Control Science and Engineering, Zhejiang University, Hangzhou 310027
2.
State Key Laboratory of Industrial Control Technology, Zhejiang University, Hangzhou 310027

Funds: Supported by National Natural Science Foundation of China (62103362, 92167106), the Natural Science Foundation of Zhejiang Province (LR18F030001)

More Information

Author Bio:
CUI Lin-Lin　Master student at the Department of Control Science and Engineering, Zhejiang University. Her research interest covers industrial soft sensor

SHEN Bing-Bing　Ph.D. candidate at the Department of Control Science and Engineering, Zhejiang University. Her research interest covers data-driven modeling, process data analysis and soft sensor applications

GE Zhi-Qiang　Professor and doctoral supervisor at Zhejiang University. His research interest covers industrial big data, process monitoring and fault diagnosis, soft sensor, intelligent system and knowledge automation. Corresponding author of this paper

摘要

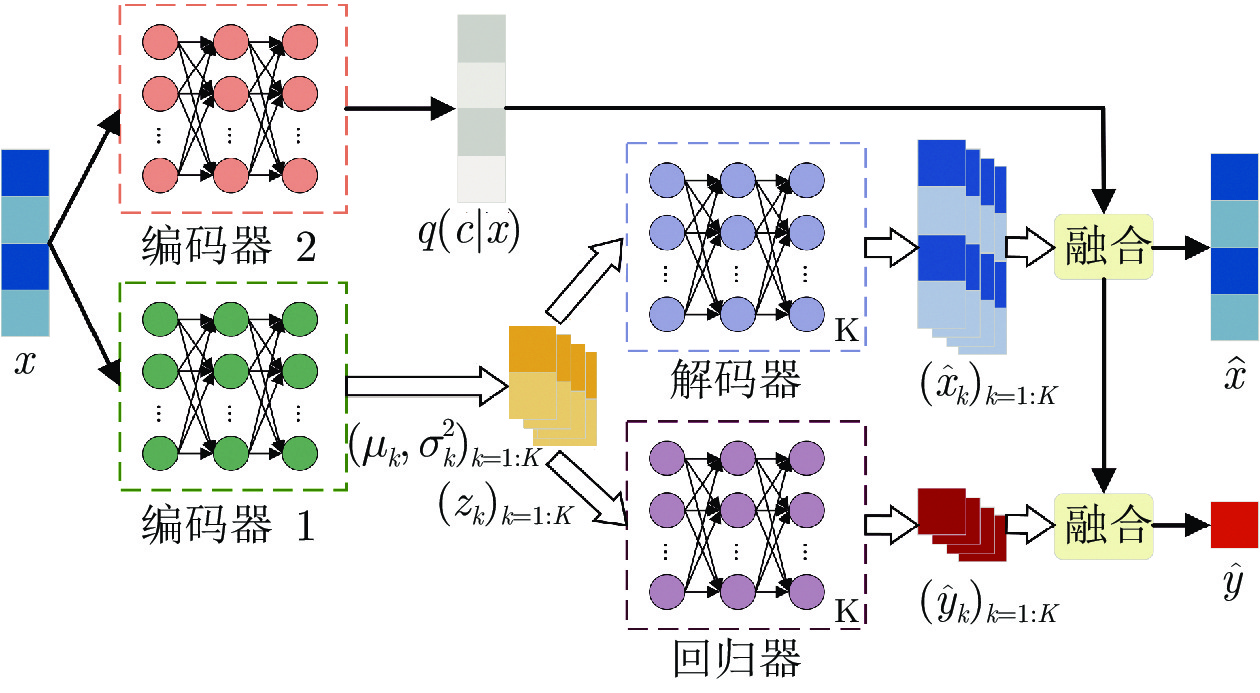
摘要: 近年来, 变分自编码器(Variational auto-encoder, VAE)模型由于在概率数据描述和特征提取能力等方面的优越性, 受到了学术界和工业界的广泛关注, 并被引入到工业过程监测、诊断和软测量建模等应用中. 然而, 传统基于VAE的软测量方法使用高斯分布作为潜在变量的分布, 限制了其对复杂工业过程数据, 尤其是多模态数据的建模能力. 为了解决这一问题, 本论文提出了一种混合变分自编码器回归模型(Mixture variational autoencoder regression, MVAER), 并将其应用于复杂多模态工业过程的软测量建模. 具体来说, 该方法采用高斯混合模型来描述VAE的潜在变量分布, 通过非线性映射将复杂多模态数据映射到潜在空间, 学习各模态下的潜在变量, 获取原始数据的有效特征表示. 同时, 建立潜在特征表示与关键质量变量之间的回归模型, 实现软测量应用. 通过一个数值例子和一个实际工业案例, 对所提模型的性能进行了评估, 验证了该模型的有效性和优越性.
- 软测量 /
- 变分自编码器 /
- 高斯混合模型 /
- 混合变分自编码器回归模型 /
- 多模态工业过程
Abstract: Recently, variational autoencoder (VAE) has caught much attention from academia and industry owing to its superiority in probabilistic data description and feature extraction, and has been introduced into industrial applications such as process monitoring, diagnosis and soft sensor modeling. However, traditional soft sensing methods based on VAE use the Gaussian distribution as the distribution of latent variables, which limits their ability to model complex industrial process data, especially multimode data. To tackle this issue, a mixture variational autoencoder regression (MVAER) model is proposed and applied to soft sensor modeling for complex multimode industrial processes in this paper. Specifically, the proposed model maps multimode data to the latent space by nonlinear mapping and uses the Gaussian mixture model to describe the distribution of latent variables. Thus, the latent variables under each mode are learned to obtain the effective feature representation of the original data. Meanwhile, a regression model between latent features and key quality variables is established for soft sensor application. Case studies including a numerical example and a real-world industrial process are carried out to assess the performance of the MVAER model, which demonstrate the effectiveness and superiority of the proposed approach.
- Soft sensor /
- variational autoencoder /
- Gaussian mixture model /
- mixture variational autoencoder regression model /
- multimode industrial process

HTML全文

图 1 VAE模型结构图

Fig. 1 Model structure of VAE

下载: 全尺寸图片幻灯片

图 2 混合变分自编码器回归模型结构图

Fig. 2 Model structure of the MVAER model

下载: 全尺寸图片幻灯片

图 3 基于MVAER的软测量建模流程图

Fig. 3 Flowchart for soft sensor modeling based on the MVAER model

下载: 全尺寸图片幻灯片

图 4 数值算例的数据模式

Fig. 4 Data pattern of the numerical example

下载: 全尺寸图片幻灯片

图 5 PLS、GMR、AE、VAE和MVAER模型的预测结果图

Fig. 5 Predicted results of PLS, GMR, AE, VAE and MVAER models

下载: 全尺寸图片幻灯片

图 6 预测结果散点图

Fig. 6 The predicted scatter points of different models

下载: 全尺寸图片幻灯片

图 7 一段炉工艺流程图

Fig. 7 Flowchart of the primary reformer

下载: 全尺寸图片幻灯片

图 8 PLS、GMR、VAE和MVAER模型的预测结果图

Fig. 8 Predicted results of PLS, GMR, VAE and MVAER models

下载: 全尺寸图片幻灯片

图 9 预测误差图

Fig. 9 The prediction errors of different models

下载: 全尺寸图片幻灯片

图 10 预测结果散点图

Fig. 10 The predicted scatter points of different models

下载: 全尺寸图片幻灯片

表 1 数值算例的配置

Table 1 Configuration of the numerical example

变量参数	$X({x_1},{x_2})$			$Y({y_1})$关系
变量参数	$\pi$	$\mu$	$\Sigma $	$Y({y_1})$关系
$k = 1$	0.3	[18 12]	$\left[ \begin{aligned} \;\;{7.5}\;\; - 2.5\\{ - 2.5}\;\;\;{4.5}\;\;\end{aligned} \right]$	${y_1} = 5{x_1}\sin {x_2}$
$k = 2$	0.4	[1 10]	$\left[ \begin{aligned} {4.5}\;\;{1.6}\\{1.6}\;\;{6.6}\end{aligned} \right]$	${y_1} = {x_1} + x_2^2$
$k = 3$	0.4	[12 5]	$\left[ \begin{aligned}{8.2}\;\;{ - 2.5}\\{ - 2.5}\;\;\;{6.0}\;\;\end{aligned} \right]$	${y_1} = {x_1}{x_2}$

下载: 导出CSV

表 2 PLS、GMR、AE、VAE和MVAER模型的性能评价指标

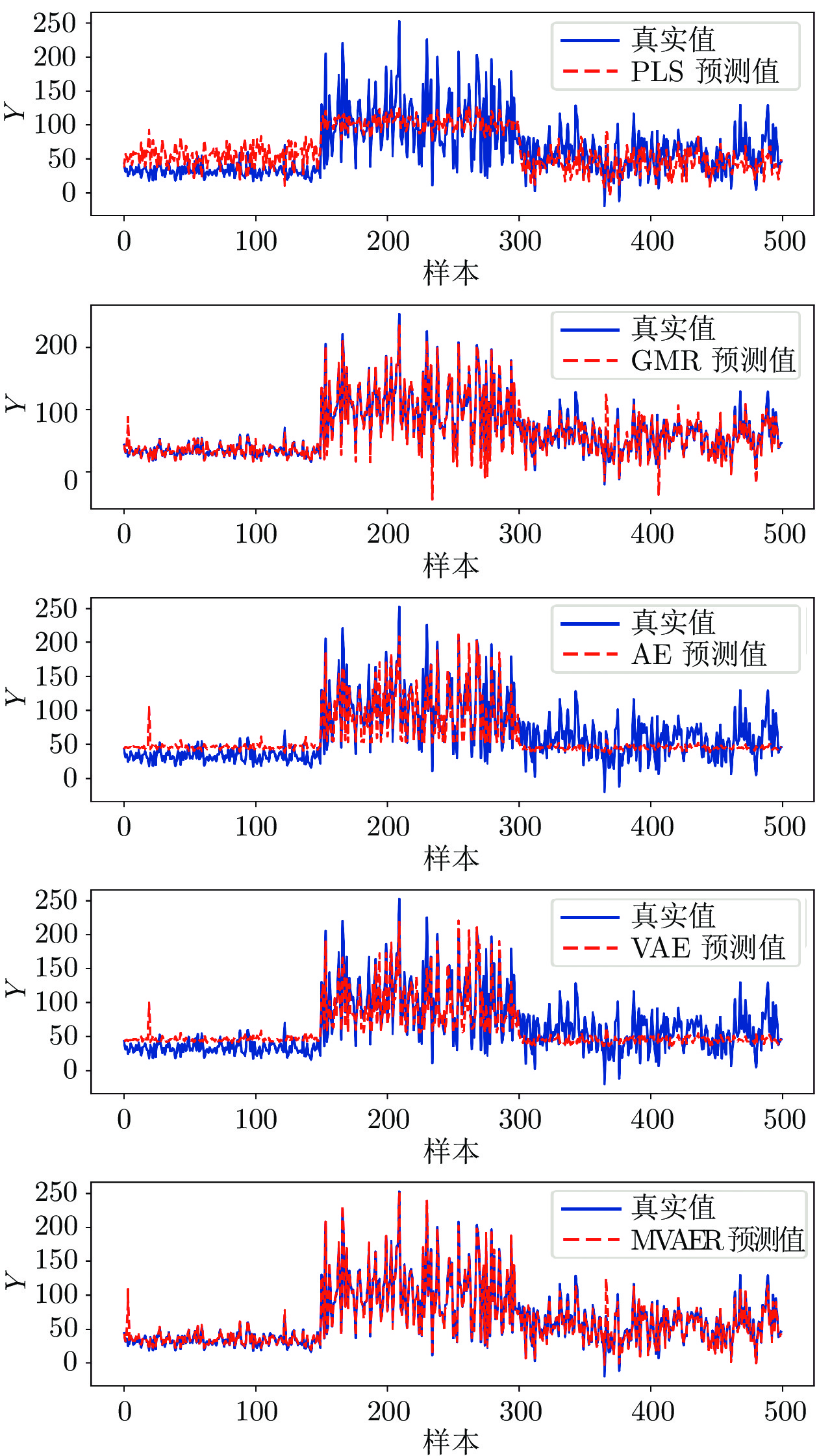
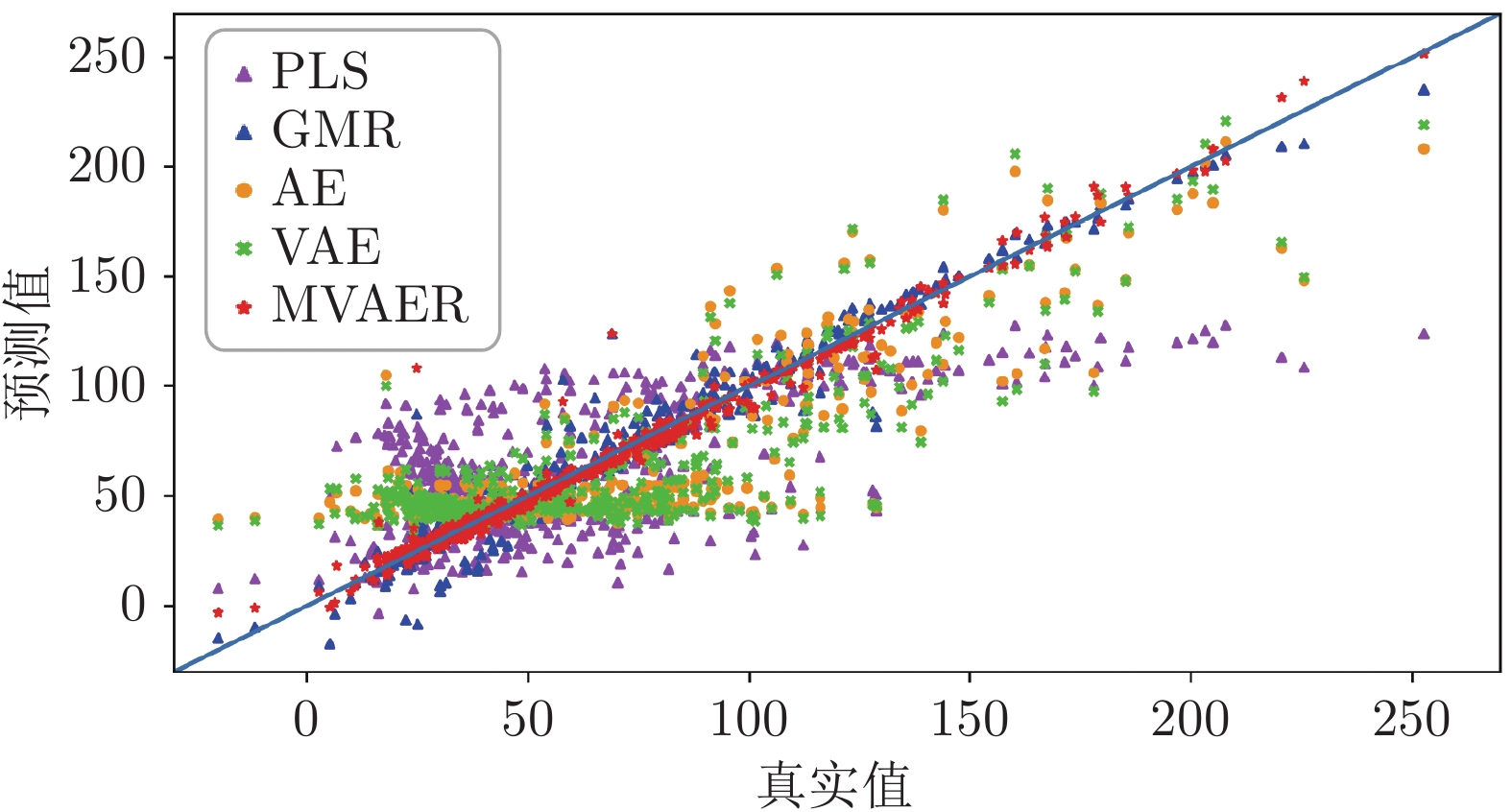
Table 2 Performance evaluation indices of PLS, GMR, AE, VAE and MVAER models

模型	PLS	GMR	AE	VAE	MVAER
RMSE	33.2076	9.2463	25.0299	25.3014	6.1914
R²	0.3964	0.9532	0.6571	0.6496	0.9797

下载: 导出CSV

表 3 一段炉过程变量描述

Table 3 The description of the process instruments in the primary reformer

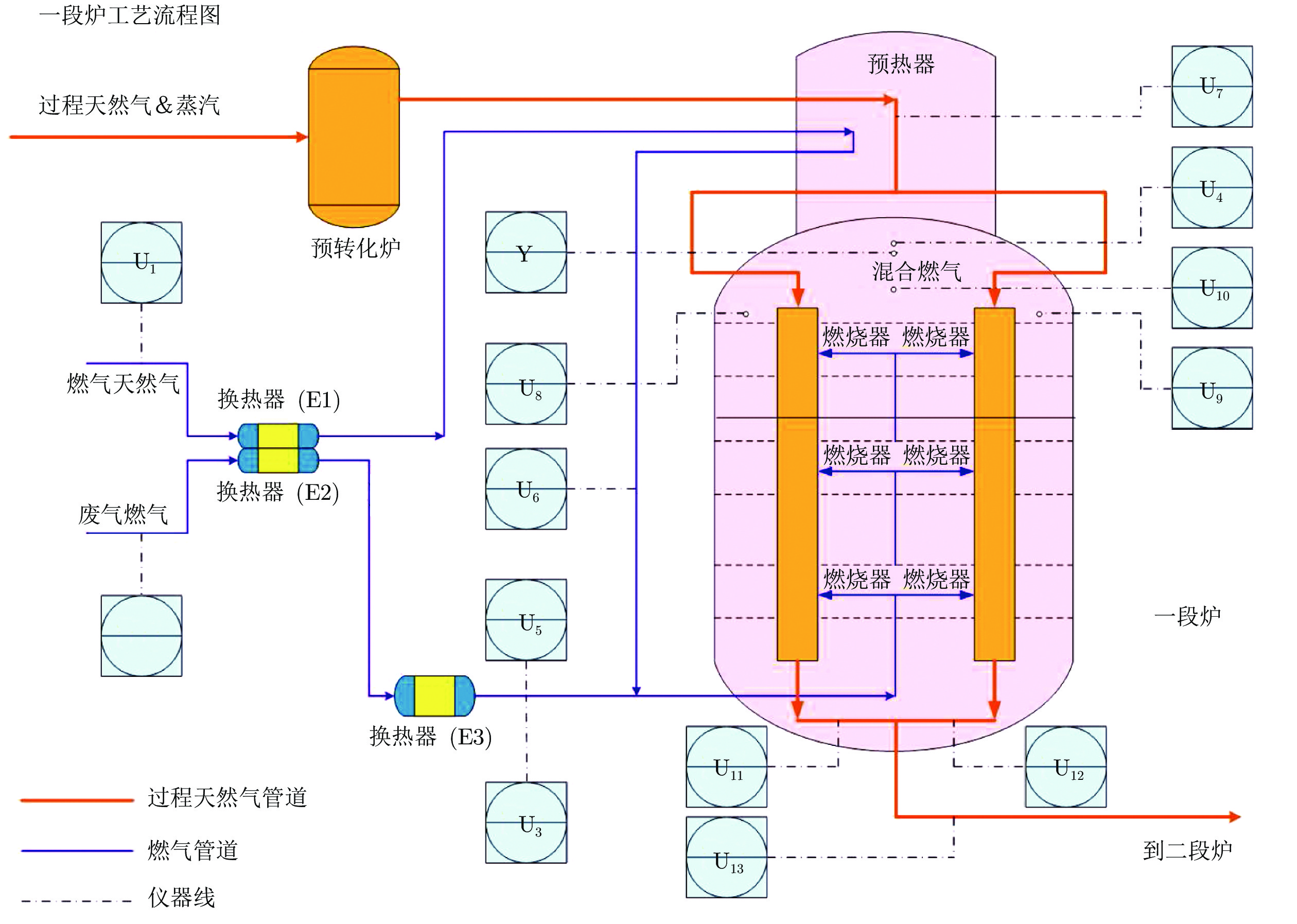
标签	名称
U₁	燃料天然气流量
U₂	燃料尾气流量
U₃	E3 出口燃料天然气压力
U₄	PR 出口炉膛烟气压力
U₅	E3 出口燃料尾气温度
U₆	PH 出口燃料天然气温度
U₇	PR 入口工艺气温度
U₈	PR 顶部左侧炉膛烟气温度
U₉	PR 顶部右侧炉膛烟气温度
U₁₀	PR 顶部混合炉膛烟气温度
U₁₁	PR 出口转换气温度
U₁₂	PR 右侧出口转换气温度
U₁₃	PR 出口转换气温度
Y	炉内顶部氧气含量

下载: 导出CSV

表 4 PLS、GMR、VAE和MVAER模型的性能评价指标

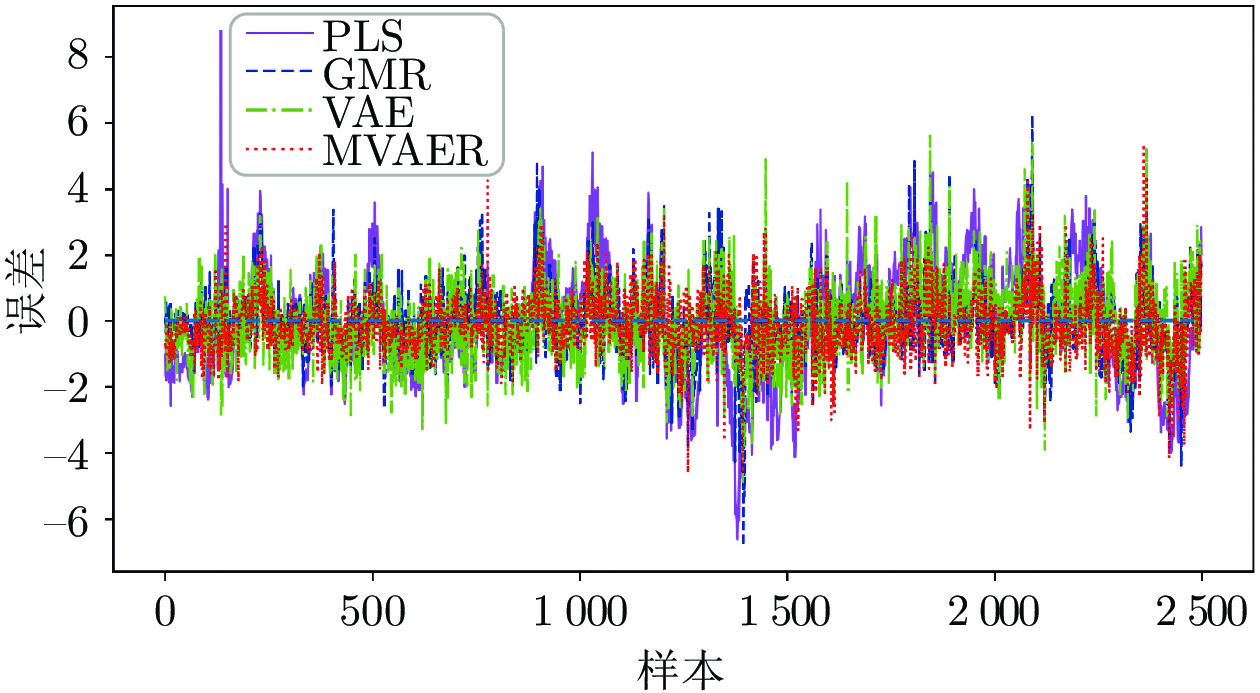
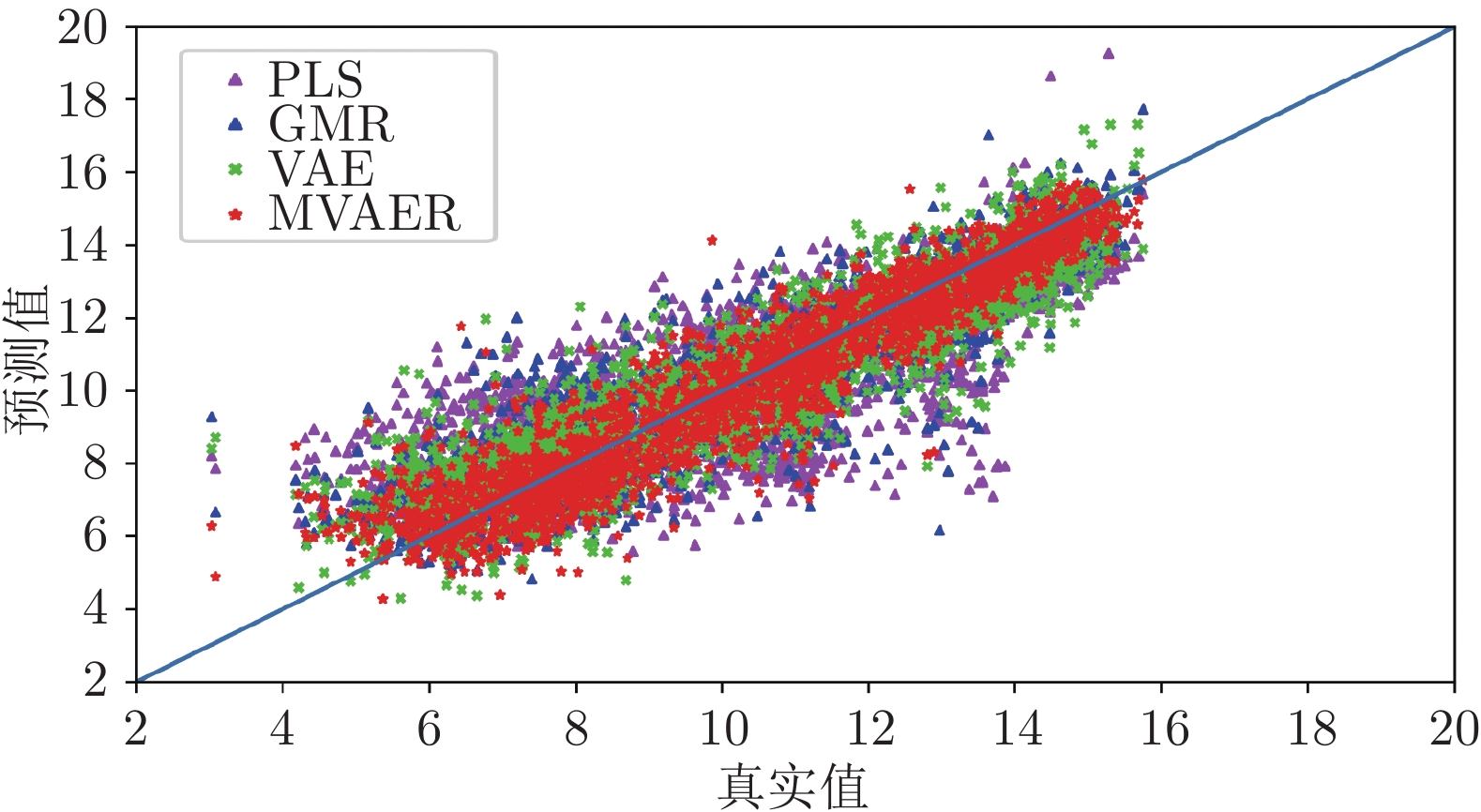
Table 4 Performance evaluation indices of PLS, GMR, VAE and MVAER models

模型	PLS	GMR	VAE	MVAER
RMSE	1.7329	1.0844	1.1379	0.8940
R²	0.6129	0.8484	0.8331	0.8970

下载: 导出CSV

参考文献(39)

[1]	Sun, Q, Ge Z. A survey on deep learning for data-driven soft sensors. IEEE Transactions on Industrial Informatics, 2021, 17(9): 5853-5866 doi: 10.1109/TⅡ.2021.3053128
[2]	Yin S, Li X, Gao H, et al. Data-based techniques focused on modern industry: An overview. IEEE Transactions on Industrial Electronics, 2014, 62(1): 657-667.
[3]	Liu Y, Yang C, Liu K, et al. Domain adaptation transfer learning soft sensor for product quality prediction. Chemometrics and Intelligent Laboratory Systems, 2019, 192: 103813. doi: 10.1016/j.chemolab.2019.103813
[4]	Liu Y, Yang C, Gao Z, et al. Ensemble deep kernel learning with application to quality prediction in industrial polymerization processes. Chemometrics and Intelligent Laboratory Systems, 2018, 174: 15-21. doi: 10.1016/j.chemolab.2018.01.008
[5]	柴天佑. 复杂工业过程运行优化与反馈控制. 自动化学报, 2013, 39(11): 1744-1757 doi: 10.3724/SP.J.1004.2013.01744 Chai Tian-You. Operational optimization and feedback control for complex industrial processes. Acta Automatica Sinica, 2013, 39(11): 1744-1757 doi: 10.3724/SP.J.1004.2013.01744
[6]	Sun, Q, Ge Z. Deep Learning for Industrial KPI Prediction: When Ensemble Learning Meets Semi-Supervised Data.IEEE Transactions on Industrial Informatics, 2021, 17: 260-269. doi: 10.1109/TII.2020.2969709
[7]	Shao W, Tian X, Wang P, et al. Online soft sensor design using local partial least squares models with adaptive process state partition. Chemometrics and Intelligent Laboratory Systems, 2015, 144: 108-121. doi: 10.1016/j.chemolab.2015.04.003
[8]	Yuan X, Ou C, Wang Y, et al. A novel semi-supervised pre-training strategy for deep networks and its application for quality variable prediction in industrial processes. Chemical Engineering Science, 2020, 217: 115509. doi: 10.1016/j.ces.2020.115509
[9]	Zheng W, Liu Y, Gao Z, et al. Just-in-time semi-supervised soft sensor for quality prediction in industrial rubber mixers. Chemometrics and Intelligent Laboratory Systems, 2018, 180: 36-41. doi: 10.1016/j.chemolab.2018.07.002
[10]	Xie R, Hao K, Huang B, et al. Data-Driven Modeling Based on Two-Stream λ Gated Recurrent Unit Network With Soft Sensor Application. IEEE Transactions on Industrial Electronics, 2019, 67(8): 7034-7043.
[11]	Yan W, Tang D, Lin Y. A data-driven soft sensor modeling method based on deep learning and its application. IEEE Transactions on Industrial Electronics, 2016, 64(5): 4237-4245.
[12]	Kadlec P, Gabrys B, Strandt S. Data-driven soft sensors in the process industry. Computers & chemical engineering, 2009, 33(4): 795-814.
[13]	Yuan X, Huang B, Wang Y, et al. Deep learning-based feature representation and its application for soft sensor modeling with variable-wise weighted SAE. IEEE Transactions on Industrial Informatics, 2018, 14(7): 3235-3243. doi: 10.1109/TII.2018.2809730
[14]	Ge Z. Process data analytics via probabilistic latent variable models: A tutorial review. Industrial & Engineering Chemistry Research, 2018, 57(38): 12646-12661.
[15]	Chen N, Dai J, Yuan X, et al. Temperature prediction model for roller kiln by ALD-based double locally weighted kernel principal component regression. IEEE Transactions on Instrumentation and Measurement, 2018, 67(8): 2001-2010. doi: 10.1109/TIM.2018.2810678
[16]	Peng K, Zhang K, You B, et al. Quality-related prediction and monitoring of multi-mode processes using multiple PLS with application to an industrial hot strip mill. Neurocomputing, 2015, 168: 1094-1103. doi: 10.1016/j.neucom.2015.05.014
[17]	Kaneko H, Funatsu K. Database monitoring index for adaptive soft sensors and the application to industrial process. AIChE Journal, 2014, 60(1): 160-169. doi: 10.1002/aic.14260
[18]	Gonzaga J C B, Meleiro L A C, Kiang C, et al. ANN-based soft-sensor for real-time process monitoring and control of an industrial polymerization process. Computers & chemical engineering, 2009, 33(1): 43-49.
[19]	Shang C, Yang F, Huang D, et al. Data-driven soft sensor development based on deep learning technique. Journal of Process Control, 2014, 24(3): 223-233. doi: 10.1016/j.jprocont.2014.01.012
[20]	Yao L, Ge Z. Deep learning of semisupervised process data with hierarchical extreme learning machine and soft sensor application. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1490-1498. doi: 10.1109/TIE.2017.2733448
[21]	Yuan X, Zhou J, Huang B, et al. Hierarchical quality-relevant feature representation for soft sensor modeling: a novel deep learning strategy. IEEE Transactions on Industrial Informatics, 2019, 16(6): 3721-3730.
[22]	Zhang X, Ge Z. Automatic Deep Extraction of Robust Dynamic Features for Industrial Big Data Modeling and Soft Sensor Application. IEEE Transactions on Industrial Informatics, 2020, 16(7): 4456-4467. doi: 10.1109/TII.2019.2945411
[23]	Zheng S, Liu K, Xu Y, et al. Robust soft sensor with deep kernel learning for quality prediction in rubber mixing processes. Sensors, 2020, 20(3): 695. doi: 10.3390/s20030695
[24]	Zhou L, Chen J, Song Z, et al. Probabilistic latent variable regression model for process-quality monitoring. Chemical Engineering Science, 2014, 116: 296-305. doi: 10.1016/j.ces.2014.04.045
[25]	Yuan X, Ge Z, Huang B, et al. A probabilistic just-in-time learning framework for soft sensor development with missing data. IEEE Transactions on Control Systems Technology, 2016, 25(3): 1124-1132.
[26]	Kingma D P, Welling M. Auto-encoding variational bayes. arXiv preprint arXiv: 1312.6114, 2013.
[27]	Wang K, Forbes M G, Gopaluni B, et al. Systematic development of a new variational autoencoder model based on uncertain data for monitoring nonlinear processes. IEEE Access, 2019, 7: 22554-22565. doi: 10.1109/ACCESS.2019.2894764
[28]	Lee S, Kwak M, Tsui K L, et al. Process monitoring using variational autoencoder for high-dimensional nonlinear processes. Engineering Applications of Artificial Intelligence, 2019, 83: 13-27. doi: 10.1016/j.engappai.2019.04.013
[29]	Shen B, Yao L, Ge Z. Nonlinear probabilistic latent variable regression models for soft sensor application: From shallow to deep structure. Control Engineering Practice, 2020, 94: 104198. doi: 10.1016/j.conengprac.2019.104198
[30]	Guo F, Xie R, Huang B. A deep learning just-in-time modeling approach for soft sensor based on variational autoencoder. Chemometrics and Intelligent Laboratory Systems, 2020, 197: 103922. doi: 10.1016/j.chemolab.2019.103922
[31]	Shen B, Ge Z. Supervised nonlinear dynamic system for soft sensor application aided by variational auto-encoder[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(9): 6132-6142.
[32]	Grbić R, Slišković D, Kadlec P. Adaptive soft sensor for online prediction and process monitoring based on a mixture of Gaussian process models. Computers & chemical engineering, 2013, 58: 84-97.
[33]	Souza F A A, Araújo R. Mixture of partial least squares experts and application in prediction settings with multiple operating modes. Chemometrics and Intelligent Laboratory Systems, 2014, 130: 192-202. doi: 10.1016/j.chemolab.2013.11.006
[34]	郭小萍, 刘诗洋, 李元. 基于稀疏残差距离的多工况过程故障检测方法研究. 自动化学报, 2019, 45(3): 617-625 Guo Xiao-Ping, Liu Shi-Yang, Li Yuan. Fault Detection of Multi-mode Processes Employing Sparse Residual Distance. Acta Automatica Sinica, 2019, 45(3): 617-625
[35]	Dilokthanakul N, Mediano P A M, Garnelo M, et al. Deep unsupervised clustering with gaussian mixture variational autoencoders. arXiv preprint arXiv: 1611.02648, 2016.
[36]	Jiang Z, Zheng Y, Tan H, et al. Variational deep embedding: An unsupervised and generative approach to clustering. arXiv preprint arXiv: 1611.05148, 2016.
[37]	Yang L, Cheung N M, Li J, et al. Deep clustering by Gaussian mixture variational autoencoders with graph embedding. In: Proceedings of International Conference on Computer Vision. Seoul, Korea: IEEE, 2019. 6439−6448
[38]	Doersch C. Tutorial on variational autoencoders. arXiv preprint arXiv: 1606.05908, 2016.
[39]	胡铭菲, 左信, 刘建伟. 深度生成模型综述. 自动化学报, 2022, 48(2): 40-74 Hu Ming-Fei, Zuo Xin, Liu Jian-Wei. Survey on deep generative model. Acta Automatica Sinica, 2020, 41(x): 1-34