融合MRI信息的PET图像去噪: 基于图小波的方法

易利群; 盛玉霞; 柴利

doi:10.16383/j.aas.c201036

融合MRI信息的PET图像去噪: 基于图小波的方法

doi: 10.16383/j.aas.c201036

易利群^1,,
盛玉霞^1,,
柴利^{2, 3,}

1.
武汉科技大学信息科学与工程学院武汉 430081
2.
浙江大学工业控制技术全国重点实验室杭州 310027
3.
浙江大学控制科学与工程学院杭州 310027

基金项目: 国家自然科学基金(62173259, 61625305)资助

详细信息

作者简介:
易利群：武汉科技大学信息科学与工程学院硕士研究生. 主要研究方向为医学图像处理, 信号处理. E-mail: ylqgenuine@sina.cn

盛玉霞：武汉科技大学信息科学与工程学院副教授. 2014年获武汉科技大学控制科学与工程专业博士学位. 主要研究方向为图像处理, 图信号处理. 本文通信作者. E-mail: shengyuxia@wust.edu.cn

柴利：浙江大学控制科学与工程学院教授. 2002年获香港科技大学电子工程系博士学位. 主要研究方向为分布式优化, 滤波器组框架, 图信号处理, 网络化控制系统. E-mail: chaili@zju.edu.cn

计量
- 文章访问数: 1445
- HTML全文浏览量: 575
- PDF下载量: 183
- 被引次数: 0
出版历程
- 收稿日期: 2020-12-15
- 录用日期: 2021-04-29
- 网络出版日期: 2021-06-13
- 刊出日期: 2023-12-27

PET Images Denoising With MRI Information: A Graph Wavelet Based Method

YI Li-Qun^1
,,
SHENG Yu-Xia^1
,,
CHAI Li^{2, 3
,}

1.
School of Information Science and Engineering, Wuhan University of Science and Technology, Wuhan 430081
2.
State Key Laboratory of Industrial Control Technology, Zhejiang University, Hangzhou 310027
3.
College of Control Science and Engineering, Zhejiang University, Hangzhou 310027

Funds: Supported by National Natural Science Foundation of China (62173259, 61625305)

More Information

Author Bio:
YI Li-Qun　Master student at the School of Information Science and Engineering, Wuhan University of Science and Technology. Her research interest covers medical image processing and signal processing

SHENG Yu-Xia　Associate professor at the School of Information Science and Engineering, Wuhan University of Science and Technology. She received her Ph.D. degree in control science and engineering from Wuhan University of Science and Technology in 2014. Her research interest covers image processing and graph signal processing. Corresponding author of this paper

CHAI Li　Professor at the College of Control Science and Engineering, Zhejiang University. He received his Ph.D. degree in electrical engineering from Hong Kong University of Science and Technology in 2002. His research interest covers distributed optimization, filter bank frames, graph signal processing, and networked control systems

摘要

摘要: 正电子发射断层成像(Positron emission tomography, PET)是一种强大的核医学功能成像模式, 广泛应用于临床诊断, 但PET图像的空间分辨率低且含有噪声, 有必要对PET图像进行去噪以提升PET图像的质量. 随着PET/MR (Magnetic resonance)等一体化成像设备的出现, 磁共振成像(Magnetic resonance imaging, MRI)的先验信息可用于PET图像去噪, 提高PET图像质量. 针对动态PET图像, 提出了一种融合MRI先验信息的PET图像图小波去噪新方法. 首先构建PET合成图像; 再将PET合成图像与MRI信息通过硬阈值方法进行融合; 接着在融合图像上构造图拉普拉斯矩阵; 最后通过图小波变换(Graph wavelet transfrom, GWT)对动态PET图像去噪. 仿真实验结果表明, 与单独的图滤波、图小波去噪方法以及其他结合MRI的PET图像去噪方法相比, 本文方法有更高的信噪比(Signal-to-noise ratio, SNR), 更好地保留了病灶信息; 本文方法的去噪性能与VGG (Visual Geometry Group)深度神经网络等基于学习的方法相当, 但不需要大量数据的训练, 计算复杂度低.
- 正电子发射断层成像 /
- 磁共振成像 /
- 图小波 /
- 去噪
Abstract: Positron emission tomography (PET) is a powerful nuclear medicine functional imaging modality, which is widely used in clinical diagnosis. However, the PET images have low spatial resolution and contain noise. It is necessary to improve the quality of PET images by denoising. As hybrid imaging devices such as PET/MR (magnetic resonance) have become available, magnetic resonance imaging (MRI) prior information could be used to improve the denoising quality of PET images. For dynamic PET images, this paper presents a novel denoising method based on graph wavelet transform (GWT) with MRI information. Firstly, the composite image is generated by the dynamic PET frames. Then, we fuse the MRI image and the composite image through the hard threshold method to obtain a new fusion image. Next, the graph Laplacian matrix is constructed based on the fusion image. Finally, we perform GWT on the dynamic PET images to denoise. The simulation experiments show that, compared with graph filtering and GWT, and other MRI incorporated methods, the proposed approach has higher SNR (signal-to-noise ratio) while preserving the image lesions details. Compared with VGG (Visual Geometry Group) deep neural network based method, the proposed method has the similar denoising performance, but it does not need a lot of data training and has low computational complexity.
- Positron emission tomography (PET) /
- magnetic resonance imaging (MRI) /
- graph wavelet /
- denoising

HTML全文

图 1 两种图像示例

Fig. 1 Example of two kinds of images

下载: 全尺寸图片幻灯片

图 2 无病灶PET图像去噪结果

Fig. 2 Denoising results of normal PET images

下载: 全尺寸图片幻灯片

图 3 单病灶图像

Fig. 3 Single-lesion images

下载: 全尺寸图片幻灯片

图 4 单病灶PET图像去噪结果

Fig. 4 Denoising results of single-lesion PET images

下载: 全尺寸图片幻灯片

图 5 单病灶PET图像去噪残差图

Fig. 5 Denoising residual map of single-lesion PET images

下载: 全尺寸图片幻灯片

图 6 不同方法病灶点CRC与背景区域STD曲线图

Fig. 6 CRC-STD curves of the different denoising methods for single-lesion PET images

下载: 全尺寸图片幻灯片

表 1 本文方法参数设置

Table 1 Parameter setting in this paper

参数符号	参数设置
n	5
k	11
$\theta $	20
$\eta $	0.0008
J	4
Threshold	0.75

下载: 导出CSV

表 2 无病灶情况下结合MRI的PET图像去噪方法比较

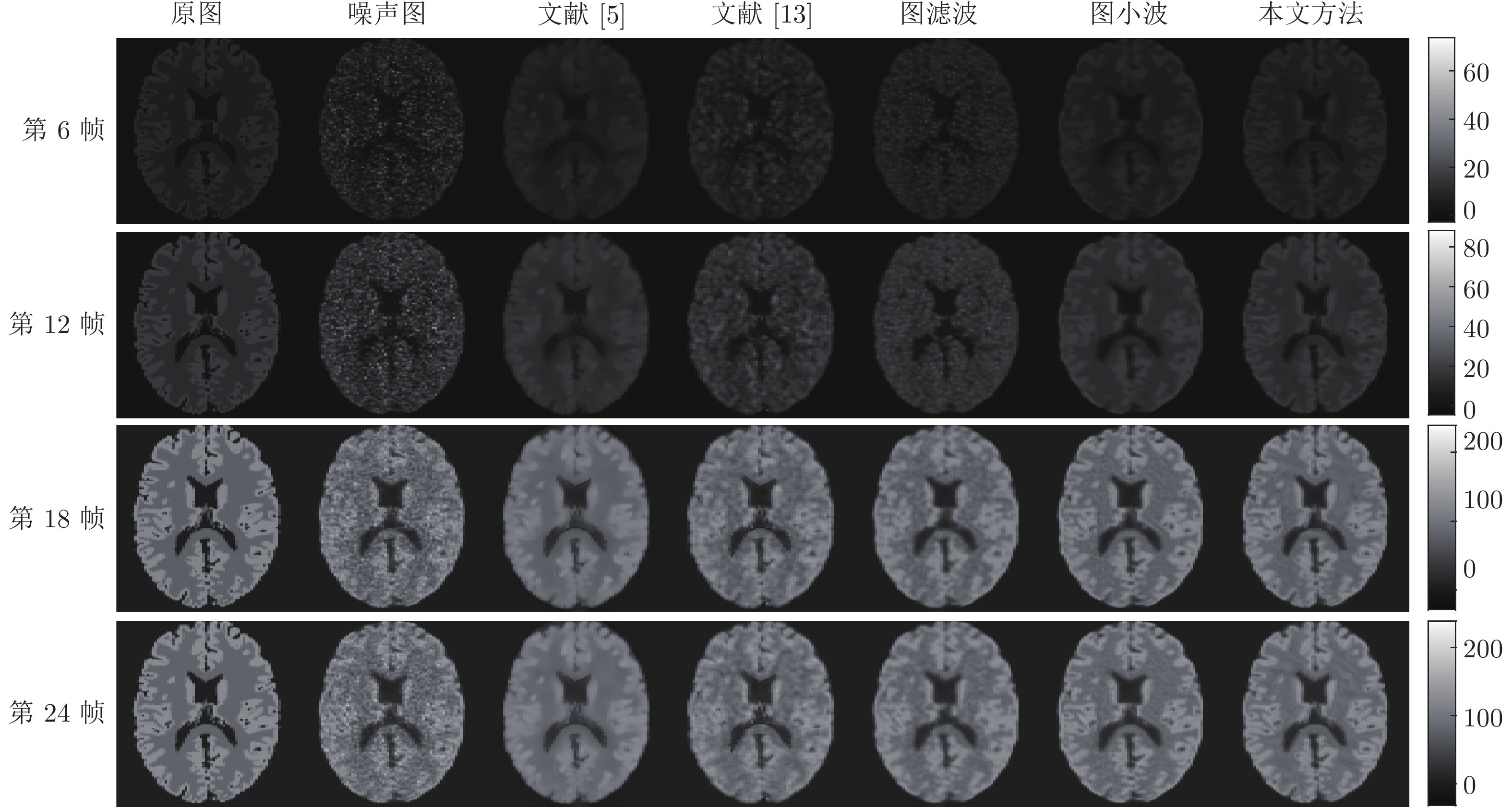
Table 2 Comparison of PET image denoising methods incorporated with MRI on the normal dataset

方法	第6帧		第12帧		第18帧		第24帧
方法	SNR	RMSE	SNR	RMSE	SNR	RMSE	SNR	RMSE
文献[5]	10.4529	1.6572	10.9457	3.0838	11.1680	19.5106	11.0675	20.4923
文献[13]	7.9343	2.2146	9.5184	3.6345	11.6153	18.5312	11.5232	19.4450
本文方法	11.7851	1.4215	12.2803	2.6445	12.6945	16.3661	12.6693	17.0413

下载: 导出CSV

表 3 无病灶情况下由PET合成图像构图的方法与本文方法比较

Table 3 Comparison of the methods of constructing graph by PET composite image with the proposed method on the normal dataset

方法	第6帧		第12帧		第18帧		第24帧
方法	SNR	RMSE	SNR	RMSE	SNR	RMSE	SNR	RMSE
图滤波	7.7670	2.2577	9.7258	3.5488	11.5317	18.7104	11.4831	19.5350
图小波	11.4064	1.4849	11.7967	2.7960	12.5395	16.6608	12.4637	17.4495
本文方法	11.7851	1.4215	12.2803	2.6445	12.6945	16.3661	12.6693	17.0413

下载: 导出CSV

表 4 单病灶情况下结合MRI的PET图像去噪方法比较

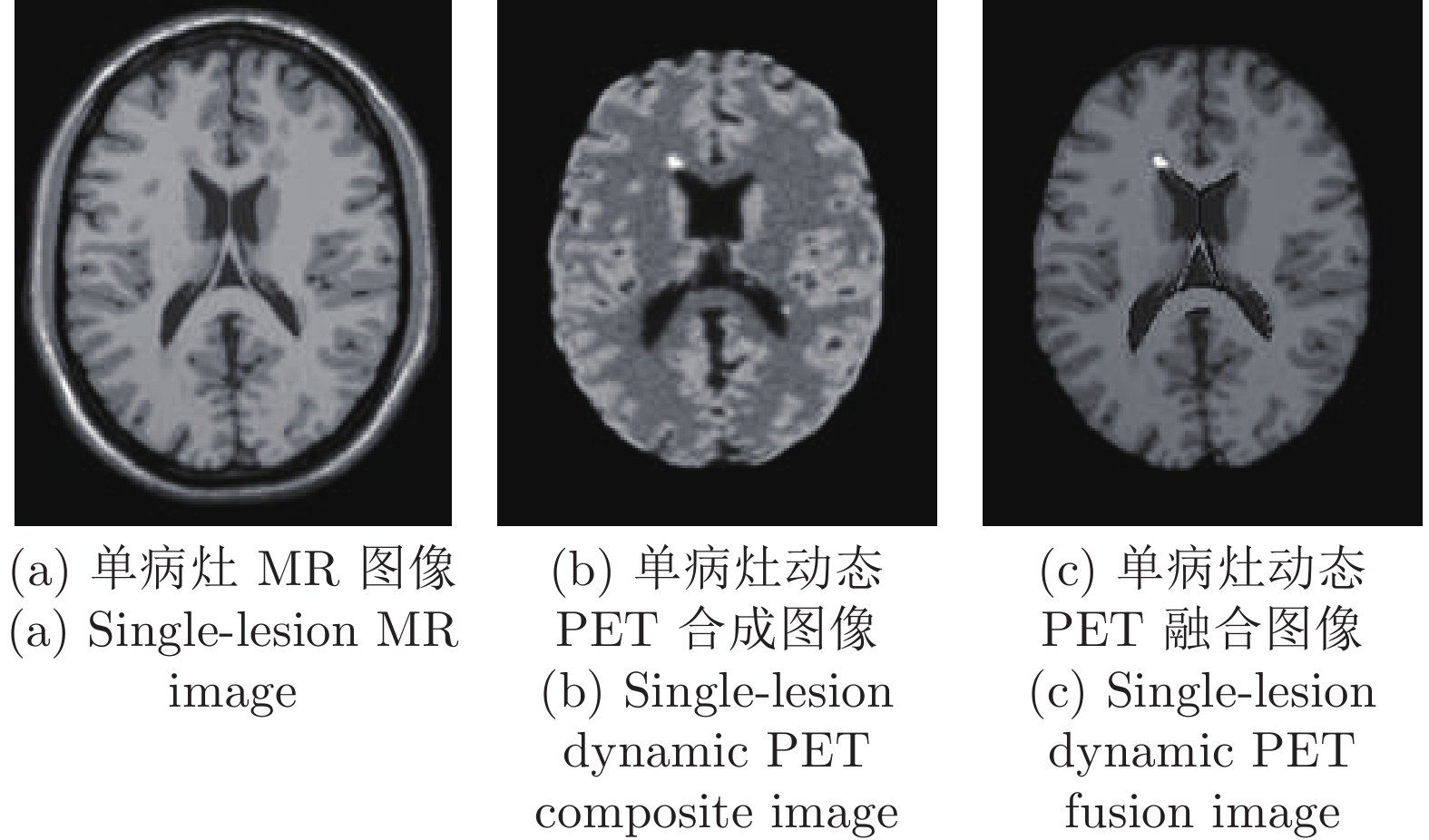
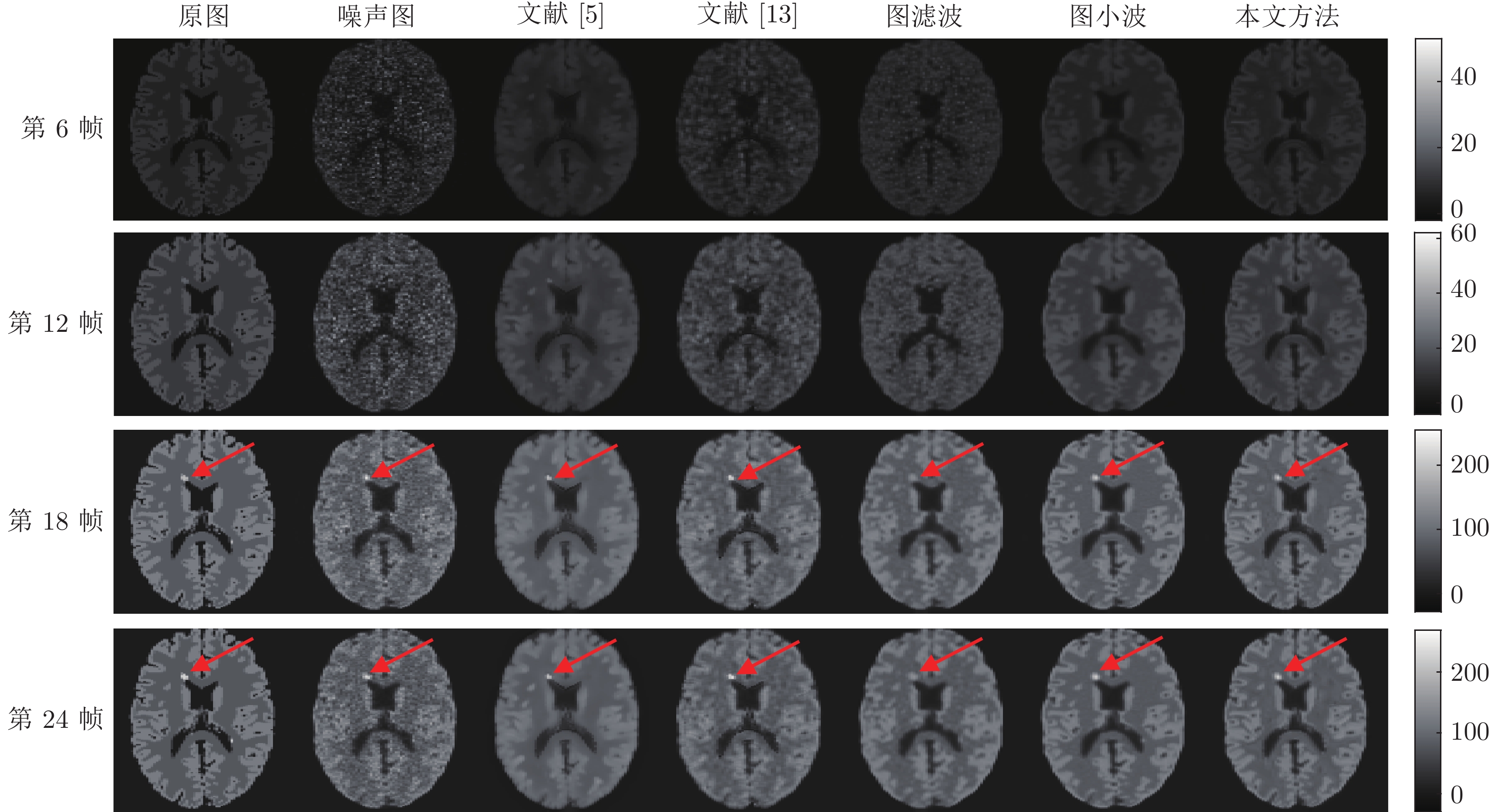
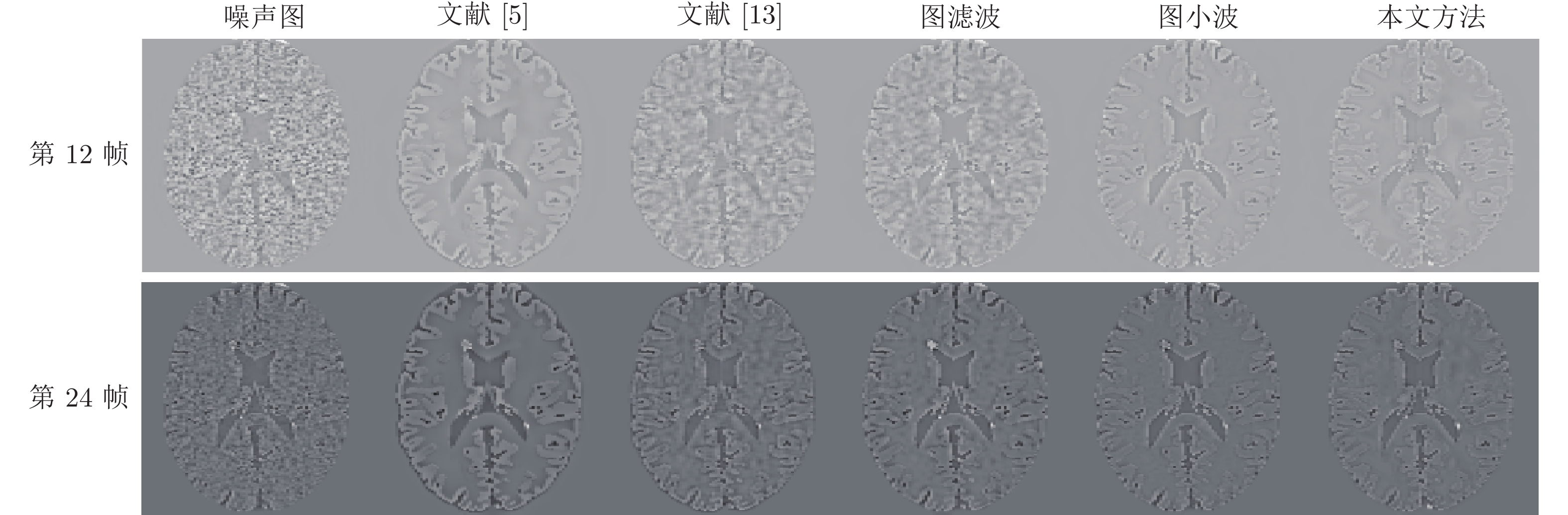
Table 4 Comparison of PET image denoising methods incorporated with MRI on the single-lesion dataset

方法	第6帧		第12帧		第18帧		第24帧
方法	SNR	RMSE	SNR	RMSE	SNR	RMSE	SNR	RMSE
文献[5]	10.4428	1.6614	11.0090	3.0692	11.1229	19.7005	10.9810	20.8295
文献[13]	8.6050	2.0529	10.0760	3.4169	11.6955	18.4437	11.5874	19.4249
本文方法	11.6739	1.4419	12.2405	2.6635	12.7017	16.4262	12.5982	17.2910

下载: 导出CSV

表 5 单病灶情况下由PET合成图像构图的方法与本文方法比较

Table 5 Comparison of the methods of constructing graph by PET composite image with the proposed method on the single-lesion dataset

方法	第6帧		第12帧		第18帧		第24帧
方法	SNR	RMSE	SNR	RMSE	SNR	RMSE	SNR	RMSE
图滤波	8.7456	2.0190	10.2172	3.3621	11.5850	18.6797	11.4849	19.6554
图小波	11.3632	1.4998	11.7036	2.8333	12.5196	16.7742	12.4090	17.6698
本文方法	11.6739	1.4419	12.2405	2.6635	12.7017	16.4262	12.5982	17.2910

下载: 导出CSV

表 6 单病灶PET图像在不同光子数时各种去噪方法比较

Table 6 Comparison of different denoising methods for single-lesion PET images with different photon numbers

方法	光子数$7\times10^8 $/第12帧		光子数$7\times10^8 $/第24帧		光子数$7\times10^9$/第12帧		光子数$7\times10^9$/第24帧
方法	SNR	RMSE	SNR	RMSE	SNR	RMSE	SNR	RMSE
文献[5]	11.4403	2.9205	11.2873	20.1078	11.4398	2.9207	11.2884	20.1053
文献[13]	11.4789	2.9076	11.4751	19.6777	11.4690	2.9109	11.2807	20.1229
图滤波	11.2474	2.9861	11.2387	20.2206	11.6630	2.8466	11.4971	19.6278
图小波	11.3028	2.9671	11.5849	19.4305	11.3609	2.9473	11.8315	18.8866
本文方法	11.9611	2.7506	11.9411	18.6497	11.9734	2.7467	12.0638	18.3881

下载: 导出CSV

参考文献(36)

[1]	Dutta J, Leahy R M, Li Q. Non-local means denoising of dynamic PET images. PloS ONE, 2013, 8(12): e81390. doi: 10.1371/journal.pone.0081390
[2]	Mansoor A, Bagci U, Mollura D J. Optimally stabilized PET image denoising using trilateral filtering. In: Proceedings of the IEEE International Conference on Medical Image Computing and Computer-Assisted Intervention. Boston, USA: 2014. 130–137
[3]	Buades A, Coll B, Morel J M. A non-local algorithm for image denoising. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, USA: IEEE, 2005. 60–65
[4]	Jommaa H, Mabrouk R, Khlifa N, Morain-Nicolier, F. Denoising of dynamic PET images using a multi-scale transform and non-local means filter. Biomedical Signal Processing and Control, 2018, 41: 69–80. doi: 10.1016/j.bspc.2017.11.002
[5]	Yan J, Lim J C S, Townsend D W. MRI-guided brain PET image filtering and partial volume correction. Physics in Medicine and Biology, 2015, 60(3): 961–976. doi: 10.1088/0031-9155/60/3/961
[6]	Song T A, Yang F, Chowdhury S R, Kim K, Johnson K A, Fakhri, G A et al. PET image deblurring and super-resolution with an MR-based joint entropy prior. IEEE Transactions on Computational Imaging, 2019, 5(4): 530–539. doi: 10.1109/TCI.2019.2913287
[7]	Song T A, Chowdhury S R, Yang F, Dutta J. PET image super-resolution using generative adversarial networks. Neural Networks, 2020, 125: 83-91. doi: 10.1016/j.neunet.2020.01.029
[8]	Li T, Jiang C H, Gao J, Yang Y F, Liang D, Liu X, et al. Low-count PET image restoration using sparse representation. Nuclear Instruments and Methods in Physics Research Section A Accelerators Spectrometers Detectors and Associated Equipment, 2018, 888: 222-227. doi: 10.1016/j.nima.2018.01.083
[9]	Wang Y, Ma G, An L, Shi F, Zhang P, Lalush D S, et al. Semisupervised tripled dictionary learning for standard-dose PET image prediction using low-dose PET and multimodal MRI. IEEE Transactions on Biomedical Engineering, 2017, 64(3): 569-579. doi: 10.1109/TBME.2016.2564440
[10]	An L, Zhang P, Adeli E, Wang Y, Ma G K, Shi F, et al. Multi-level canonical correlation analysis for standard-dose PET image estimation. IEEE Transactions Image Process, 2016, 25(7): 3303-3315. doi: 10.1109/TIP.2016.2567072
[11]	Zhang Y, Zhang X. PET-MRI joint reconstruction with common edge weighted total variation regularization. Inverse Problems, 2018, 34(6): 065006. doi: 10.1088/1361-6420/aabce9
[12]	Bergounioux M, Papoutsellis E, Stute S, Tauber C. Infimal convolution spatiotemporal PET reconstruction using total variation based priors [Online], available: https://www.researchgate.net/publication/322918637_Infimal_convolution_spatiotemporal_PET_reconstruction_using_total_variation_based_priors, 26 January, 2018
[13]	Cheng J C K, Matthews J, Boellaard R, Sossi V. A MR guided denoising for PET using IHYPR-LR. In: Proceedings of the IEEE Nuclear Science Symposium and Medical Imaging Conference. Atlanta, USA: IEEE, 2017. 1–3
[14]	Tahaei M S, Reader A J, Collins D L. Two novel PET image restoration methods guided by PET-MR kernels: Application to brain imaging. Medical Physics, 2019, 46(5): 2085-2102. doi: 10.1002/mp.13418
[15]	Gong K, Berg E, Cherry S R, Qi J. Machine learning in PET: From photon detection to quantitative image reconstruction. Proceedings of the IEEE, 2020, 108(1): 51-68. doi: 10.1109/JPROC.2019.2936809
[16]	田娟秀, 刘国才, 谷珊珊, 鞠忠建, 刘劲光, 顾冬冬. 医学图像分析深度学习方法研究与挑战. 自动化学报, 2018, 44(3): 401-424. Tian Juan-Xiu, Liu Guo-Cai, Gu Shan-Shan, Ju Zhong-Jian, Liu Jin-Guang, Gu Dong-Dong. Deep learning in medical image analysis and its challenges. Acta Automatica Sinica, 2018, 44(3): 401-424.
[17]	施俊, 汪琳琳, 王珊珊, 陈艳霞, 王乾, 魏冬铭, 等. 深度学习在医学影像中的应用综述. 中国图象图形学报, 2020, 25(10): 1953-1981. doi: 10.11834/jig.200255 Shi Jun, Wang Lin-Lin, Wang Shan-Shan, Chen Yan-Ming, Wang Qian, Wei Dong-Ming et al. Applications of deep learning in medical imaging: A survey. Journal of Image and Graphics, 2020, 25(10): 1953-1981. doi: 10.11834/jig.200255
[18]	范家伟, 张如如, 陆萌, 何佳雯, 康霄阳, 柴文俊, 等. 深度学习方法在糖尿病视网膜病变诊断中的应用. 自动化学报, 2021, 47(3): 985−1004. Fan Jia-Wei, Zhang Ru-Ru, Lu Meng, He Jia-Wen, Kang Xiao-Yang, Chai Wen-Jun, et al. Applications of deep learning techniques for diabetic retinal diagnosis. Acta Automatica Sinica, 2021, 47(3): 985−1004.
[19]	Reader A J, Corda G, Mehranian A, Costa-Luis C D, Ellis S, Schnabel J A. Deep learning for PET image reconstruction. IEEE Transactions on Radiation and Plasma Medical Sciences, 2020, 5(1): 1-25.
[20]	Gong K, Guan J H, Liu C, Liu C C, Qi J Y. PET image denoising using a deep neural network through fine tuning. IEEE Transactions on Radiation and Plasma Medical Sciences, 2019, 3(2): 153-161. doi: 10.1109/TRPMS.2018.2877644
[21]	Gong Y, Shan H M, Teng Y Y, Zheng H R, Wang G, Wang S S. Deeply-supervised multi-dose prior learning for low-dose PET imaging. In: Proceedings of the 17th IEEE International Symposium on Biomedical Imaging Workshops. Iowa, USA: IEEE, 2020. 1–4
[22]	Gong Y, Shan H M, Teng Y Y, Zheng H R, Wang G, Wang S S. Low-dose PET image restoration with 2D and 3D network prior learning. In: Proceedings of the 17th IEEE International Symposium on Biomedical Imaging Workshops. Iowa, USA: IEEE, 2020. 1–4
[23]	Gong Y, Shan H G, Teng Y Y, Tu N, Li M, Liang G D, et al. Parameter-Transferred Wasserstein Generative Adversarial Network (PT-WGAN) for low-dose PET image denoising. IEEE Transactions on Radiation and Plasma Medical Sciences, 2021, 5(2): 213-223. doi: 10.1109/TRPMS.2020.3025071
[24]	Wang Y, Zhou L P, Yu B T, Wang L, Zu C, Lalush D S, et al. 3D auto-context-based locality adaptive multi-modality GANs for PET synthesis. IEEE Transactions on Medical Imaging, 2019, 38(6): 1328-1339. doi: 10.1109/TMI.2018.2884053
[25]	Shuman D I, Narang S K, Frossard P, Ortega A, Vandergheynst P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Processing Magazine, 2013, 30(3): 83–98. doi: 10.1109/MSP.2012.2235192
[26]	Sandryhaila A F, Moura J M. Big data analysis with signal processing on graphs: Representation and processing of massive data sets with irregular structure. IEEE Signal Processing Magazine, 2014, 31(5): 80–90. doi: 10.1109/MSP.2014.2329213
[27]	杨杰, 赵磊, 郭文彬. 基于图谱域移位的带限图信号重构算法. 自动化学报, 2021, x(x): 1−11. Yang Jie, Zhao Lei, Guo Wen-Bin. Graph band-limited signals reconstruction method based graph spectral domain shifting. Acta Automatica Sinica, 2021, x(x): 1−11.
[28]	Cheung G, Magli E, Tanaka Y, Ng M K. Graph spectral image processing. Proceedings of the IEEE, 2018, 106(5): 907-930. doi: 10.1109/JPROC.2018.2799702
[29]	Guo S Y, Sheng Y X, Chai L, Zhang J X. Graph filtering approach to PET image denoising. In: Proceedings of the 1st International Conference on Industrial Artificial Intelligence. Shenyang, China: IEEE, 2019. 1–6
[30]	Hammond D K, VandergheynstT P, Gribonval R. Wavelets on graphs via spectral graph theory. Applied and Computational Harmonic Analysis, 2011, 30(2): 129–150. doi: 10.1016/j.acha.2010.04.005
[31]	Hammond D K, Vandergheynst P, Gribonval R. The spectral graph wavelet transform: Fundamental theory and fast computation. Vertex-Frequency Analysis of Graph Signals. Springer, 2019. 141–175
[32]	Deutsch S, Ortega A, Medioni G. Manifold denoising based on spectral graph wavelets. In: Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing. Shanghai, China: IEEE, 2016. 4673–4677
[33]	Wang G, Qi J. PET image reconstruction using kernel method. IEEE Transactions on Medical Imaging, 2014, 34(1): 61–71.
[34]	Shepp L A, Vardi Y. Maximum likelihood reconstruction for positron emission tomography. IEEE Transactions on Medical Imaging, 1982, 1(2): 113-122. doi: 10.1109/TMI.1982.4307558
[35]	Aubert-Broche B, Griffin M, Pike G B, Evans A C, Collins D L. Twenty new digital brain phantoms for creation of validation image databases. IEEE Transactions on Medical Imaging, 2006, 25(11): 1410–1416. doi: 10.1109/TMI.2006.883453
[36]	Feng D, Wong K P, Wu C M, Siu W C. A technique for extracting physiological parameters and the equired input function simultaneously from PET image measurements: Theory and simulation study. IEEE Transactions on Information Technology in Biomedicine, 1997, 1(4): 243–254. doi: 10.1109/4233.681168