基于微分博弈的追逃问题最优策略设计

刘坤; 郑晓帅; 林业茗; 韩乐; 夏元清

doi:10.16383/j.aas.c200979

基于微分博弈的追逃问题最优策略设计

doi: 10.16383/j.aas.c200979

刘坤^1,,
郑晓帅^1,,
林业茗^1,,
韩乐^1,,
夏元清^1,

1.
北京理工大学自动化学院复杂系统智能控制与决策国家重点实验室北京 100081

基金项目: 国家自然科学基金(61873034), 北京自然科学基金(4182057), 北京市智能物流系统协同创新中心开放课题(BILSCIC-2019KF-13)资助

详细信息

作者简介:
刘坤：北京理工大学自动化学院研究员. 主要研究方向为网络化控制理论与应用, 复杂网络安全. E-mail: kunliubit@bit.edu.cn

郑晓帅：北京理工大学自动化学院硕士研究生. 主要研究方向为对抗学习, 追逃博弈. E-mail: xiaoshuaizheng@bit.edu.cn

林业茗：北京理工大学自动化学院博士研究生. 主要研究方向为分布式优化, 分布式学习. 本文通信作者. E-mail: yeminglin@bit.edu.cn

韩乐：北京理工大学自动化学院硕士研究生. 主要研究方向为机器学习, 微分博弈, 追逃博弈, 分布式学习, 编队控制, 鲁棒控制, 多智能体系统协同控制与决策. E-mail: lehan@bit.edu.cn

夏元清：北京理工大学自动化学院教授. 主要研究方向为云控制, 云数据中心优化调度管理, 智能交通, 模型预测控制, 自抗扰控制, 鲁棒控制, 复杂网络控制与安全, 网络化控制理论与应用, 飞行器控制和空天地一体化网络协同控制. E-mail: xia_yuanqing@bit.edu.cn

计量
- 文章访问数: 4883
- HTML全文浏览量: 1318
- PDF下载量: 789
- 被引次数: 0
出版历程
- 收稿日期: 2020-11-25
- 录用日期: 2021-03-02
- 网络出版日期: 2021-05-10
- 刊出日期: 2021-08-20

Design of Optimal Strategies for the Pursuit-evasion Problem Based on Differential Game

1.
Key Laboratory of Intelligent Control and Decision of Complex Systems, School of Automation, Beijing Institute of Technology Beijing 100081

Funds: Supported by National Natural Science Foundation of China (61873034), Beijing Natural Science Foundation (4182057), and the Open Subject of Beijing Intelligent Logistics System Collaborative Innovation Center (BILSCIC-2019KF-13)

More Information

Author Bio:
LIU Kun　Professor at the School of Automation, Beijing Institute of Technology. His research interest covers theory and applications of networked control, and security of complex networked systems

ZHENG Xiao-Shuai　Master student at the School of Automation, Beijing Institute of Technology. His research interest covers adversarial learning and pursuit-evasion problem

LIN Ye-Ming　Ph. D. candidate at the School of Automation, Beijing Institute of Technology. His research interest covers distributed optimization and distributed learning. Corresponding author of this paper

HAN Le　Master student at the School of Automation, Beijing Institute of Technology. Her research interest covers machine learning, differential game, pursuit-evasion problem, distributed learning, formation control problem, robust control, cooperative control and decision of multi-agent system

XIA Yuan-Qing　Professor at the School of Automation, Beijing Institute of Technology. His research interest covers cloud control, cloud data center optimization scheduling and management, intelligent transportation, model predictive control, active disturbance rejection control, robust control, control and security of complex networked systems, theory and applications of networked control, flight control and networked cooperative control for integration of space, air and earth

摘要

摘要:
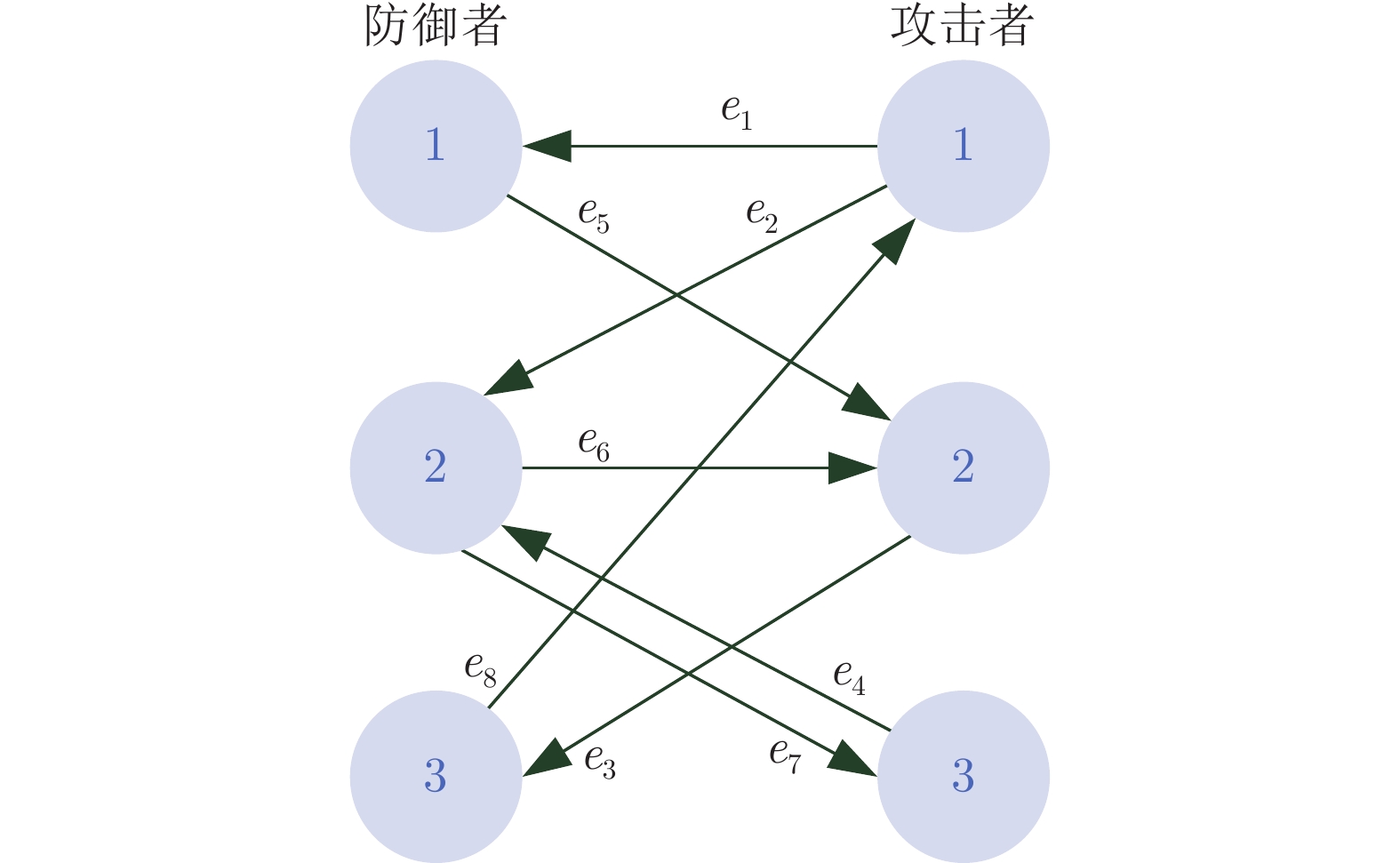
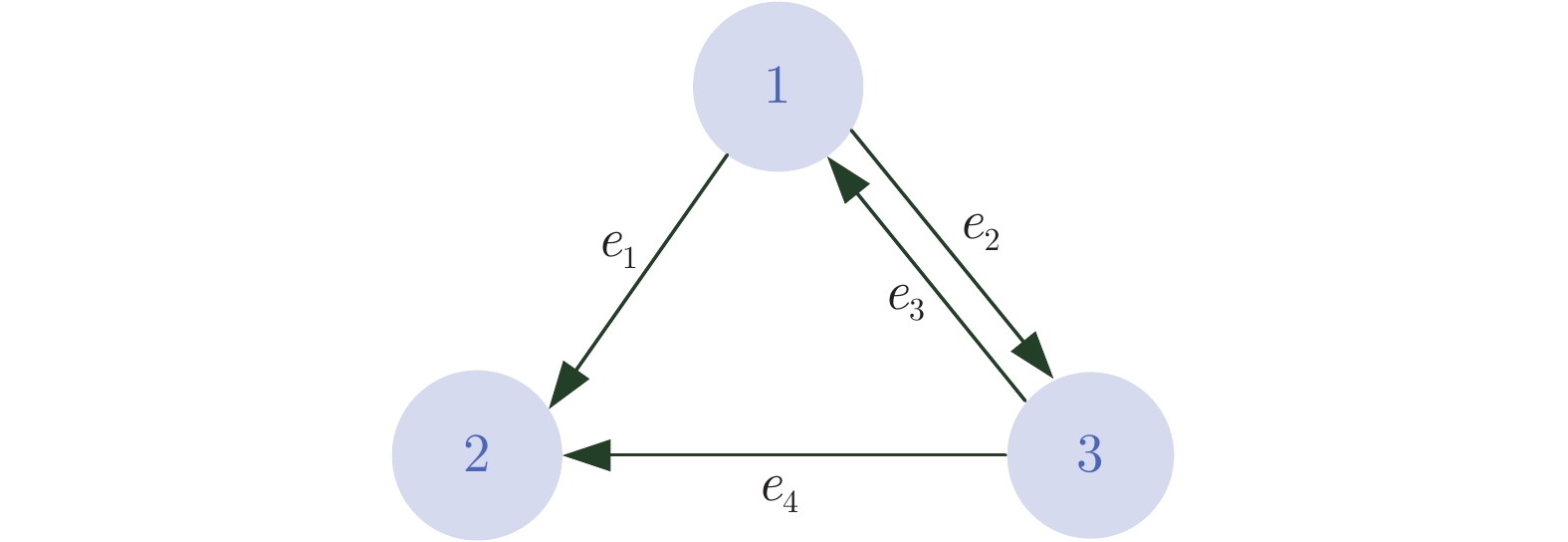
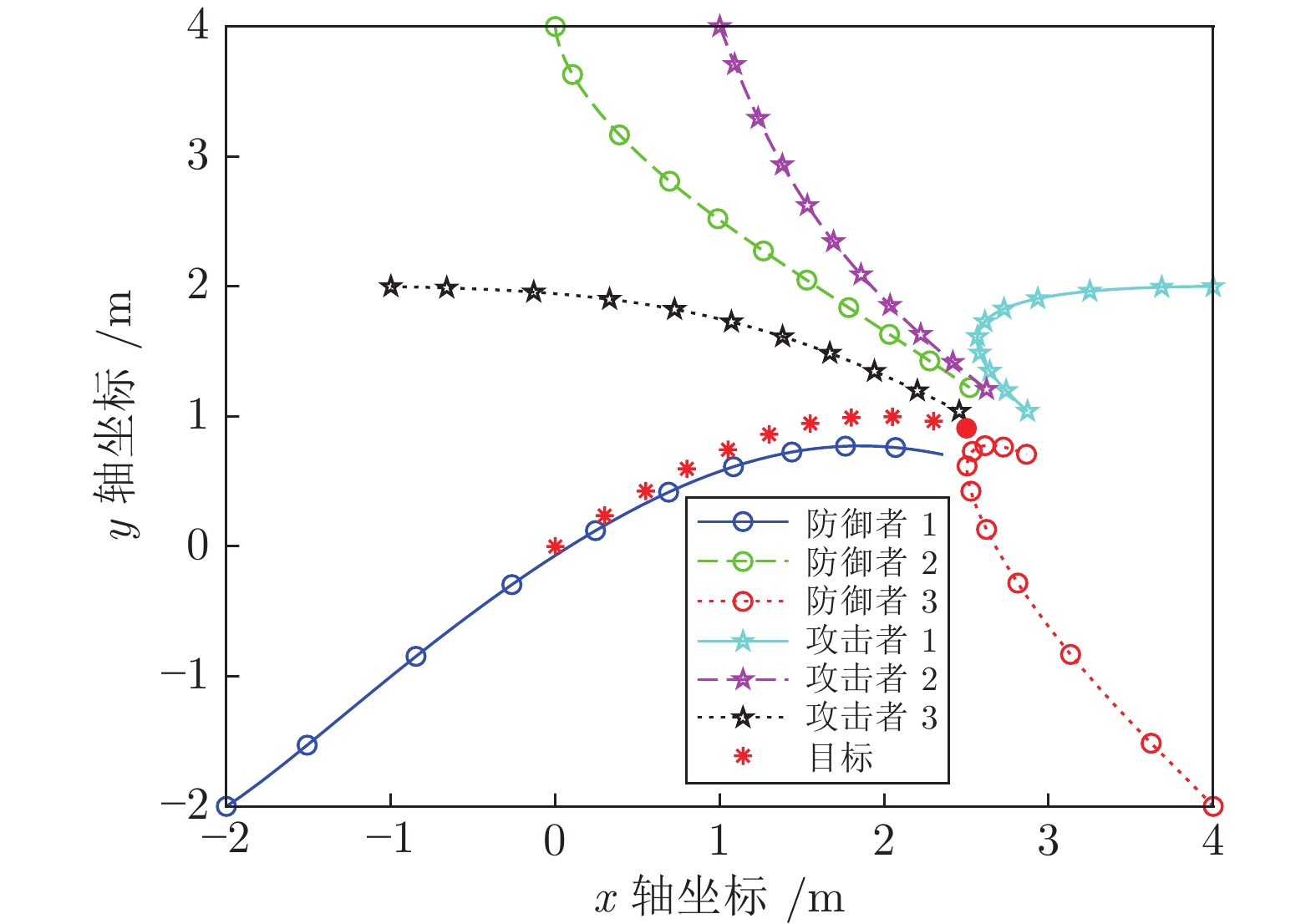
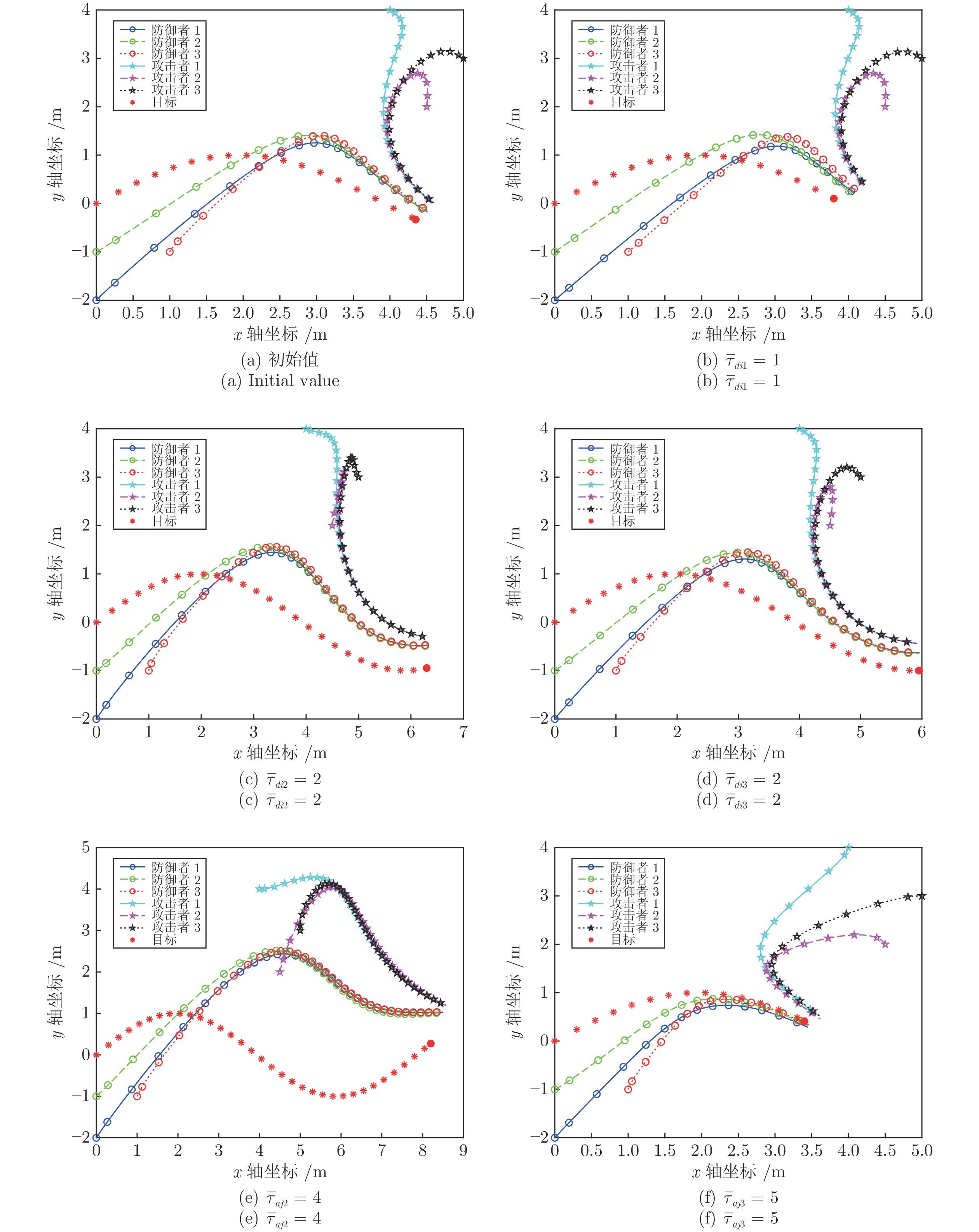
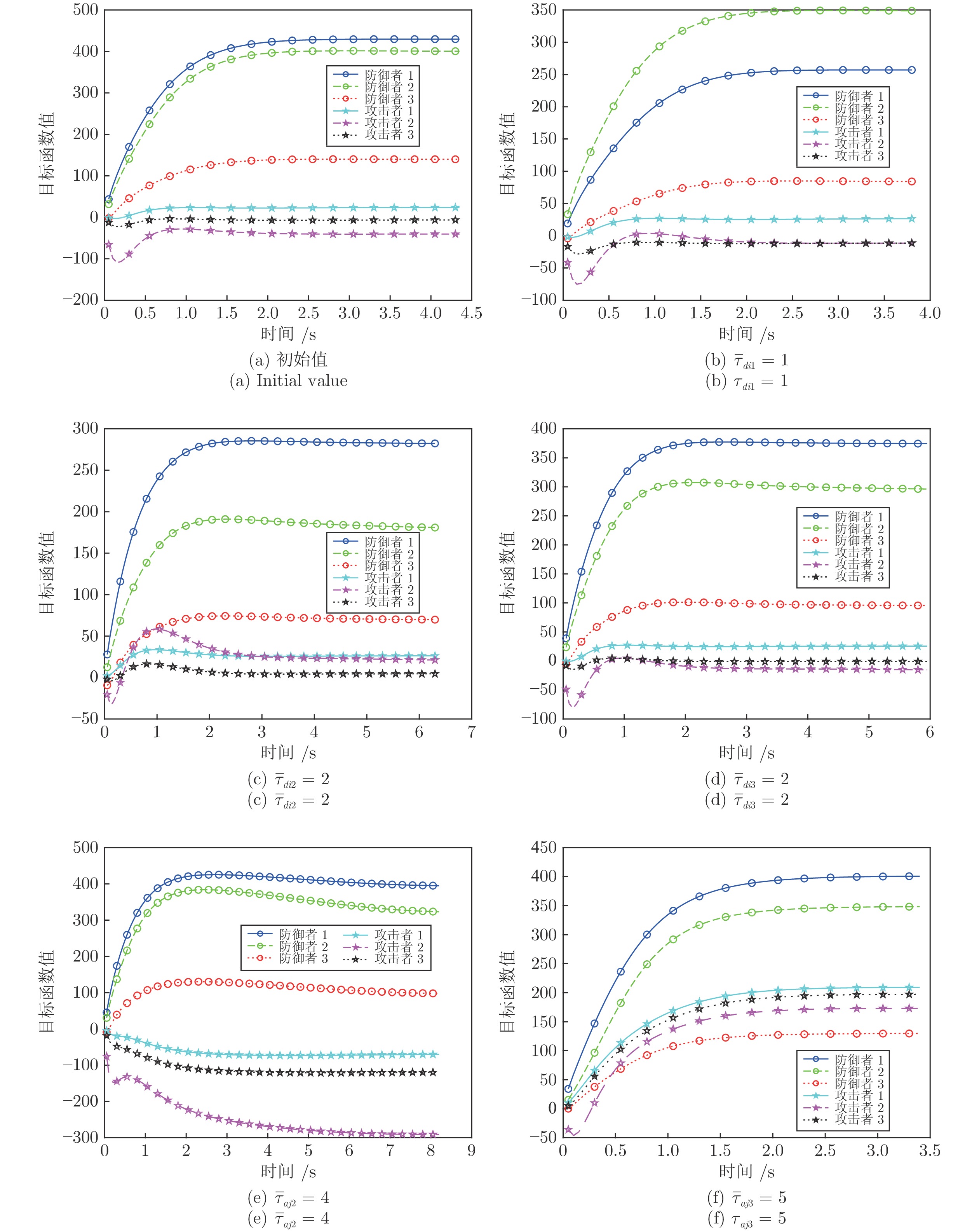
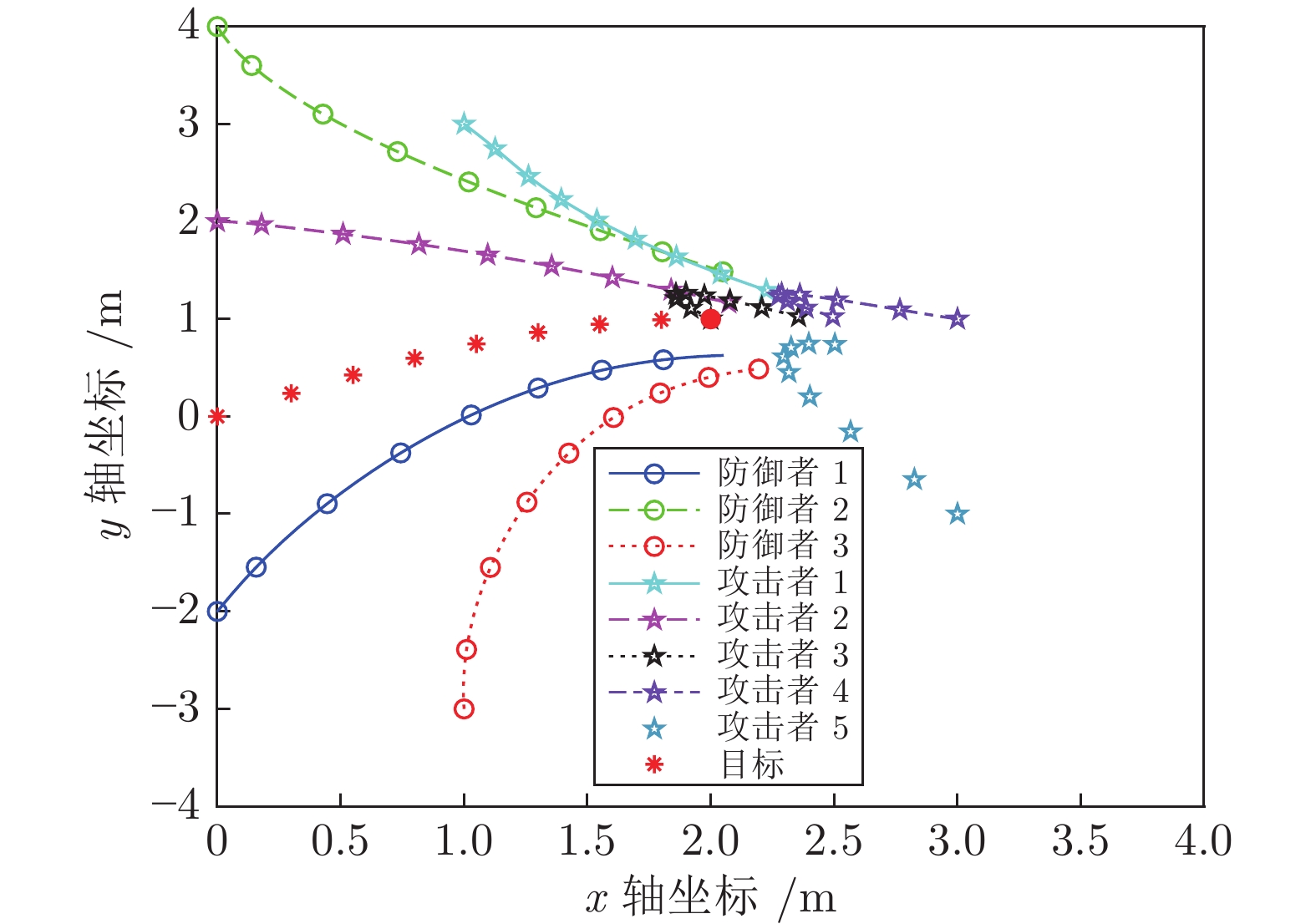
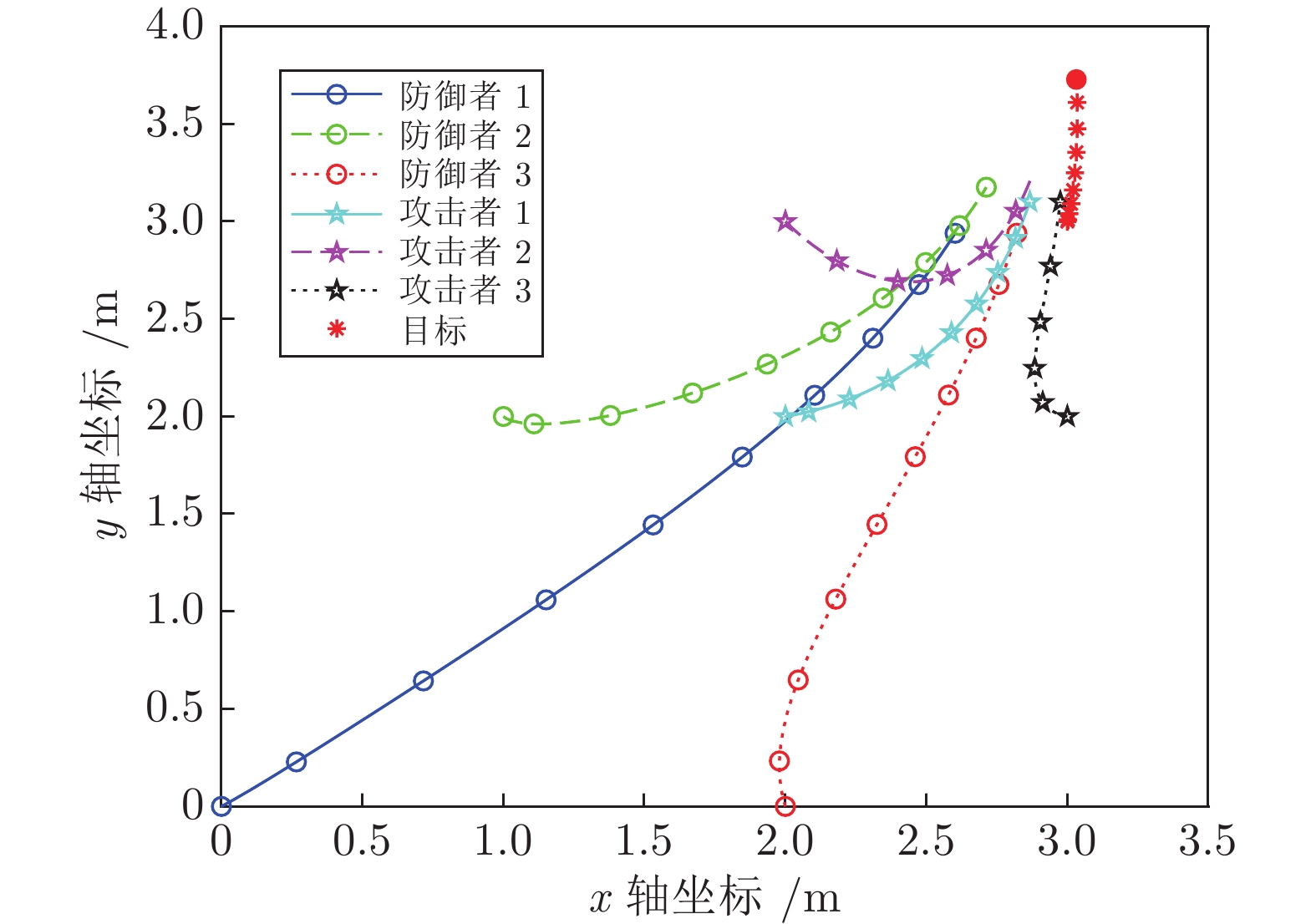
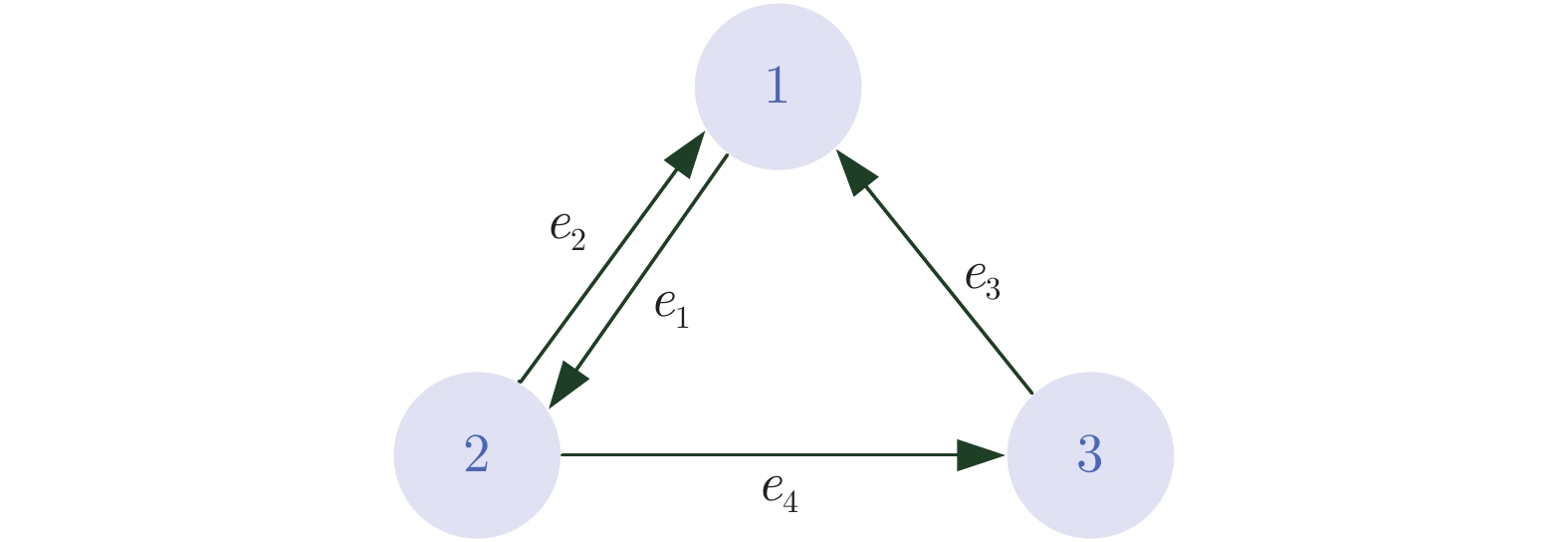
本文设计了基于线性二次型微分博弈的多个攻击者、多个防御者和单个目标的追逃问题最优策略. 首先, 针对攻防双方保持聚合状态的情形, 基于攻击方内部、防御方内部以及双方之间的通信拓扑, 分别给出了目标沿固定轨迹运动和目标采取逃跑时攻防双方的最优策略. 其次, 针对攻防双方保持分散状态的情形, 利用二分图最大匹配算法分配相应的防御者与攻击者, 将多攻击者、多防御者追逃问题转化为多组两人零和微分博弈, 并求解出了攻防双方的最优策略. 最后, 数值仿真验证了所提策略的有效性.
- 微分博弈 /
- 追逃问题 /
- 团队聚合 /
- 线性二次型博弈 /
- 目标–攻击者–防御者
Abstract:
This paper is concerned with the design of optimal strategies for the pursuit-evasion problem with multi-attacker, multi-defender and single target based on the linear quadratic differential game. Firstly, for the case that attackers and defenders maintain their group cohesion, strategies of attackers and defenders are proposed when the target moves with a certain trajectory or the target adopts evasion policy respectively, based on communication graphs among attackers, among defenders, and between attackers and defenders. Secondly, for the case that attackers and defenders stay distributed, the maximum matching algorithm of bipartite graph is used to match attackers for defenders and the multi-attacker multi-defender pursuit-evasion problem is transformed into multi two-person zero-sum differential games, and then optimal strategies of attackers and defenders are proposed. Finally, simulation examples are provided to verify the effectiveness of the proposed strategies.
- Differential game /
- pursuit-evasion problem /
- group cohesion /
- linear quadratic game /
- target-attacker-defender

HTML全文

图 1 防御者通信拓扑

Fig. 1 The communication topology of defendes

下载: 全尺寸图片幻灯片

图 3 防御者与攻击者之间的通信拓扑

Fig. 3 The communication topology between defendes and attackers

下载: 全尺寸图片幻灯片

图 2 攻击者通信拓扑

Fig. 2 The communication topology of attackers

下载: 全尺寸图片幻灯片

图 4 攻击者胜利时目标、攻击者、防御者的运动轨迹

Fig. 4 Trajectories of the target, attackers and defenders when attackers win

下载: 全尺寸图片幻灯片

图 5 防御者胜利时权重系数调整目标、攻击者、防御者的运动轨迹

Fig. 5 Trajectories of the target, attackers and defenders with different weight coefficients when defendes win

下载: 全尺寸图片幻灯片

图 6 防御者胜利时权重系数调整目标、攻击者、防御者的成本函数

Fig. 6 Cost functions of the target, attackers and defenders with different weight coefficients when defendes win

下载: 全尺寸图片幻灯片

图 7 $ m = 3$, $ l = 5$时目标、攻击者、防御者的运动轨迹

Fig. 7 Trajectories of the target, attackers and defenders with $ m = 3$, $ l = 5$

下载: 全尺寸图片幻灯片

图 8 $m = 5,\;l = 3$时目标、攻击者、防御者的运动轨迹

Fig. 8 Trajectories of the target, attackers and defenders with $m = 5,\;l = 3$

下载: 全尺寸图片幻灯片

图 9 目标采取逃跑行动时目标、攻击者、防御者的运动轨迹

Fig. 9 Trajectories of the target, attackers and defenders when the target adopts an escape strategy

下载: 全尺寸图片幻灯片

图 10 防御者、攻击者分散状态下攻击者、防御者的运动轨迹

Fig. 10 Trajectories of attackers and defenders when defenders and attackers stay distributed

下载: 全尺寸图片幻灯片

参考文献(26)

[1]	杜永浩, 邢立宁, 蔡昭权. 无人飞行器集群智能调度技术综述. 自动化学报, 2020, 46(2): 222-241. DU Yong-Hao, XING Li-Ning, CAI Zhao-Quan. Survey on intelligent scheduling technologies for unmanned flying craft clusters. Acta Automatica Sinica, 2020, 46(2): 222-241.
[2]	周宏宇, 王小刚, 单永志, 赵亚丽, 崔乃刚. 基于改进粒子群算法的飞行器协同轨迹规划. 自动化学报, DOI: 10.16383/j.aas.c190865 Zhou Hong-Yu, Wang Xiao-Gang, Shan Yong-Zhi, Zhao Ya-Li, Cui Nai-Gang. Synergistic path planning for multiple vehicles based on an improved particle swarm optimization method. Acta Automatica Sinica, DOI: 10.16383/j.aas.c190865
[3]	Azam M A, Ragi S. Decentralized formation shape control of UAV swarm using dynamic programming. In: Proceedings of Signal Processing, Sensor/Information Fusion, and Target Recognition XXIX. California, USA, 2020. 11423: 114230I
[4]	Zhou Z, Zhang W, Ding J, Huang, H, Stipanovic D M, Tomlin C J. Cooperative pursuit with voronoi partitions. Automatica, 2016, 72: 64-72. doi: 10.1016/j.automatica.2016.05.007
[5]	De Simone D, Scianca N, Ferrari P, Lanari L, Oriolo G. MPC-based humanoid pursuit-evasion in the presence of obstacles. In: Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. 2017. 5245−5250
[6]	Isaacs R. Differential Games: A Mathematical Theory With Applications to Warfare and Pursuit, Control and Optimization. Courier Corporation, 1999.
[7]	Fang B, Pan Q, Hong B, Lei D, Zhong Q B, Zhang Z. Research on high speed evader vs. multi lower speed pursuers in multi pursuit-evasion games. Information Technology Journal, 2012, 11(8): 989-997. doi: 10.3923/itj.2012.989.997
[8]	Lin W, Qu Z, Simaan M A. Nash strategies for pursuit-evasion differential games involving limited observations. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 1347-1356. doi: 10.1109/TAES.2014.130569
[9]	Pachter M, Garcia E, Casbeer D W. Differential game of guarding a target. Journal of Guidance, Control, and Dynamics, 2017, 40(11): 2991-2998. doi: 10.2514/1.G002652
[10]	Venkatesan R H, Sinha N K. The target guarding problem revisited: Some interesting revelations. In: Proceedings of IFAC World Congress. Cape Town, South Africa, 2014. 1556−1561
[11]	Li D, Cruz J B. Defending an asset: A linear quadratic game approach. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1026-1044. doi: 10.1109/TAES.2011.5751240
[12]	Garcia E, Casbeer D W, Pachter M. Design and analysis of state-feedback optimal strategies for the differential game of active defense. IEEE Transactions on Automatic Control, 2018, 64(2): 553-568.
[13]	Liang L, Deng F, Peng Z, Li X, Zha W. A differential game for cooperative target defense. Automatica, 2019, 102: 58-71. doi: 10.1016/j.automatica.2018.12.034
[14]	Casbeer D W, Garcia E, Pachter M. The target differential game with two defenders. Journal of Intelligent & Robotic Systems, 2018, 89(1-2): 87-106.
[15]	Chen M, Zhou Z, Tomlin C J. Multiplayer reach-avoid games via low dimensional solutions and maximum matching. In: Proceedings of American Control Conference. Portland, USA, 2014. 1444−1449
[16]	Coon M, Panagou D. Control strategies for multiplayer target-attacker-defender differential games with double integrator dynamics. In: Proceedings of IEEE Conference on Decision and Control. Melbourne, Australia, 2017. 1496−1502
[17]	Chipade V S, Panagou D. Multiplayer target-attacker-defender differential game: pairing allocations and control strategies for guaranteed intercept. In: Proceedings of AIAA Scitech 2019 Forum. California, USA, 2019. 658−678
[18]	Yan R, Shi Z, Zhong Y. Task assignment for multiplayer reach-avoid games in convex domains via analytical barriers. IEEE Transactions on Robotics, 2019, 36(1): 107-124.
[19]	Garcia E, Casbeer D W, Von Moll A, Pachter M. Multiple Pursuer Multiple Evader Differential Games. IEEE Transactions on Automatic Control, arxiv: 1911. 03806
[20]	Sin E, Arcak M, Packard A, Philbrick D, Seiler P. Optimal assignment of collaborating agents in multi-body asset-guarding games. In: Proceedings of the 2020 American Control Conference (ACC). Denver, Colorado, USA, 2020. 858−864
[21]	Li D X, Cruz J B. Graph-Based Strategies for Multi-Player Pursuit Evasion Games. In: Proceedings of IEEE Conference on Decision and Control. New Orleans, LA, USA, 2007. 4063−4068
[22]	Mejia V G L, Lewis F L, Wan Y, Sanchez E N, Fan L. Solutions for multiagent pursuit-evasion games on communication graphs: Finite-time capture and asymptotic behaviors. IEEE Transactions on Automatic Control, 2019, 65(5): 1911-1923.
[23]	Engwerda J. LQ dynamic optimization and differential games. John Wiley & Sons, 2005.
[24]	Kuhn H. The Hungarian method for the assignment problem. Naval Research Logistics Quarterly, 1955, 2(1-2): 83-97. doi: 10.1002/nav.3800020109
[25]	Amato F, Pironti A. A note on singular zero-sum linear quadratic differential games. In: Proceedings of IEEE Conference on Decision and Control. Lake Buena Vista, USA, 1994. 1533−1535
[26]	夏元清. 云控制系统及其面临的挑战. 自动化学报, 2016, 42(01): 1-12. Xia Yuan-Qing. Cloud control systems and their challenges. Acta Automatica Sinica, 2016, 42(1): 1-12.