Maximal Admissible Mode Decision Delay Under Consistency Constraint in Terminal Guidance System
-
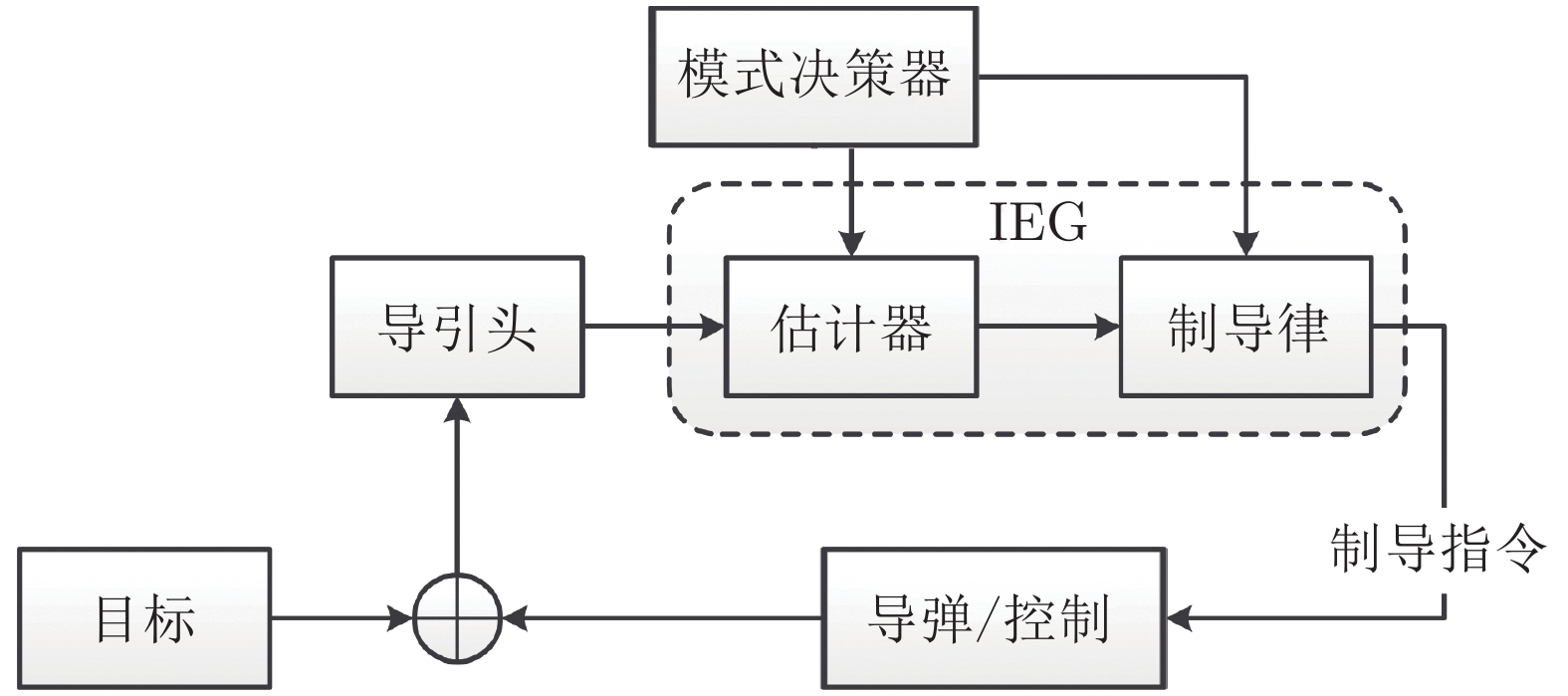
摘要: 对于大机动目标拦截问题, 模式决策器是基于逻辑的集成估计导引系统(Integrated estimation and guidance, IEG)中的一个重要组件. 为了保证系统的估计精度和制导性能, 模式决策器的模式延迟应尽可能小. 本文针对末制导场景, 首先推导了离散时间系统零控脱靶量的估计误差模型, 然后在一致性约束条件下给出了系统最大可容许模式决策延迟的数值计算方法. 本文的研究结果可为IEG系统中模式决策器的设计提供指标参考.Abstract: For highly maneuvering target interception, mode decision-maker is a critical component of the logic-based integrated estimation and guidance (IEG) system. To ensure the estimation accuracy and guidance performance, the mode delay of the mode decision-maker should be as small as possible. For the case of terminal guidance scenario, this paper first derives the estimation error model of the zero-effort miss distance of the discrete-time system, and then gives a numerical computing method of the maximal admissible mode decision delay under consistency constraint. The results provide an index reference for the design of (IEG) mode decision-maker in IEG systems.
-
表 1 符号说明
Table 1 Description of symbols
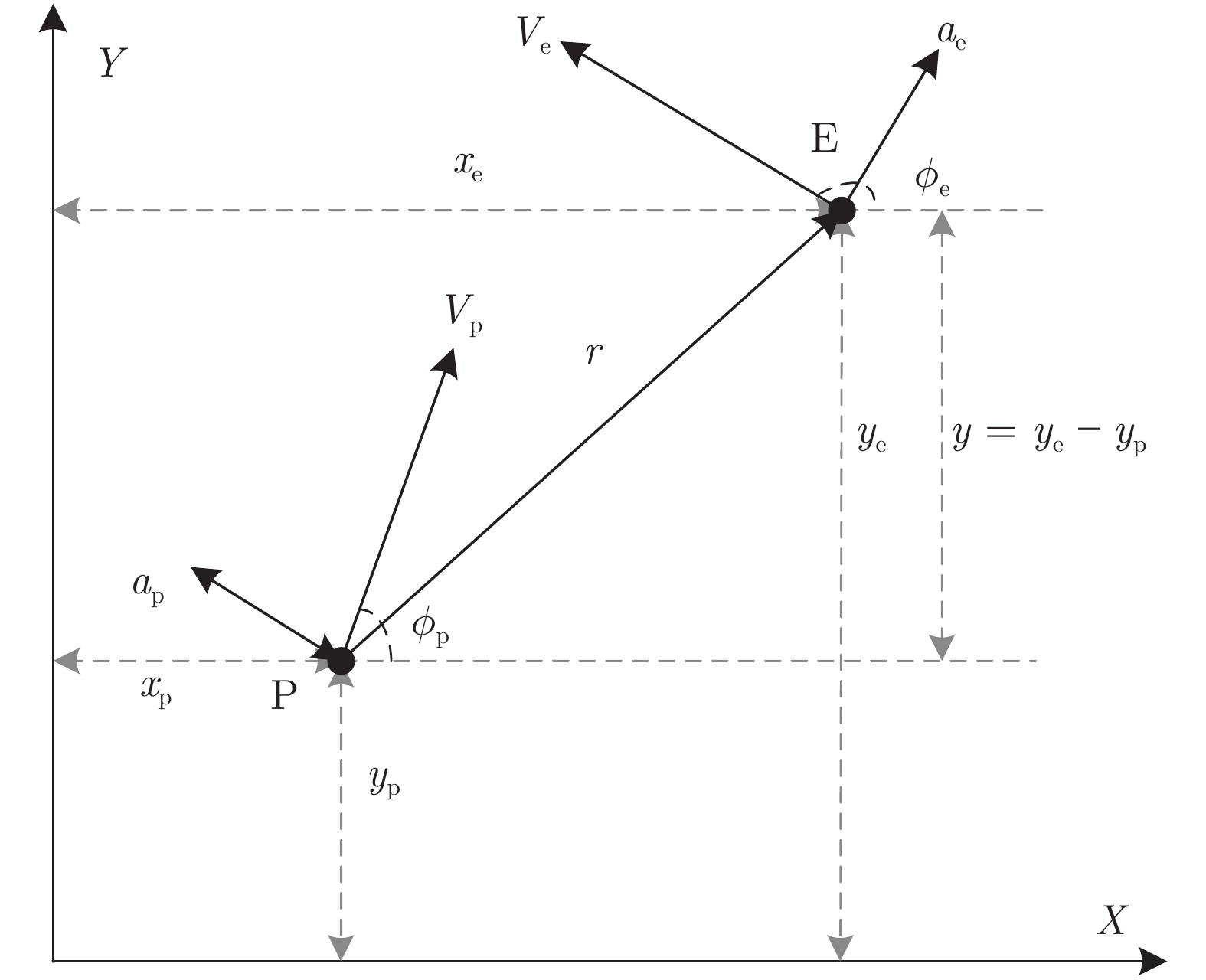
变量名称 变量描述 P 导弹 E 目标 $\tau_{\rm p}$,$\tau_{\rm e}$ 导弹和目标控制系统的时间常数 $a_{\rm p}^{\max},a_{\rm e}^{\max}$ 导弹和目标最大横向加速度 ${V_{\rm p}},{V_{\rm e}}$ 导弹和目标的飞行速度 ${u_{\rm p}},{u_{\rm e}}$ 导弹和目标的横向加速度指令 $r$ 弹目相对距离 ${t_{\rm sw}}$ 目标模式切换时刻 $t$ 仿真时间 ${t_{\rm f}}$ 终止时刻 ${t_{\rm go}}$ 剩余飞行时间 g 重力加速度, $9.8\;{\rm{m} }/{{\rm{s}}^2}$ $m$ 目标的运动模式 ${m_1},{m_2}$ 目标在模式切换时刻前后的运动模式 $\Delta m$ 目标运动模式改变量, $\Delta m = {m_2} - {m_1}$ $T$ 采样时间间隔 ${\sigma _\theta }$ 测角精度 ${\sigma _a}$ 导弹加速度测量精度 ${s_w}$ 目标指令加速度误差的功率谱密度 $\Delta t$ 目标运动模式辨识延迟 ${\boldsymbol{\tilde x}}$ 状态估计误差 ${\boldsymbol{\xi }},{\Sigma}$ 状态估计误差的均值和方差 $\mu ,{\sigma ^2}$ ZEM估计误差的均值和方差 $\chi_k^2$ 检验统计量 表 2 仿真参数
Table 2 Simulation parameters
参数类型 参数名称 单位 值 (范围) 弹目参数 $ {V_{\rm p}} $ m/s 2300 $ {V_{\rm e}} $ m/s 2700 $ a_{\rm p}^{{\max}} $ g 30 $ a_{\rm e}^{{\max}} $ g 15 $ {\tau _{\rm p}} $ s 0.2 $ {\tau _{\rm e}} $ s 0.2 观测参数 $ T $ s 0.01 $ {\sigma _\theta } $ mrad 5 $ {\sigma _a } $ $ {\rm{m}}/{\rm{s}}^2 $ 1 场景参数 $ r_0 $ m 15000 $ {\phi_{\rm p}}(0) $ rad $ \pi/18 $ $ {\phi_{\rm e}}(0) $ rad $ > \pi /2 $且满足碰撞三角形 目标机动方式 — 随机乒乓 估计器参数 $ s_w $ $ {\rm{g}}^2/{\rm{Hz}} $ 1 初估计误差 — $ {{\boldsymbol{\tilde x}}_0} = {[0,0,0,0]^{\rm T}} $ 初估协方差阵 — ${ {{P} }_0} = \left[ \begin{aligned}\;\;0\;\;0\;\;\;\;\;\;0\;\;\;\;\;\;\;\;0\;\;\\\;\;0\;\;0\;\;\;\;\;\;0\;\;\;\;\;\;\;\;0\;\;\\\;\;0\;\;0\,\;\;{ { {(a_{\rm e}^{ {\max} })}^2} }\;\;\;0\;\;\\\;\;0\;\;0\;\;\;\;\;\;0\;\;\;\;\;\;\;\;0\;\; \end{aligned}\right]$ 表 3 两种方法MAMDD对比
Table 3 Comparison of MAMDD with two methods
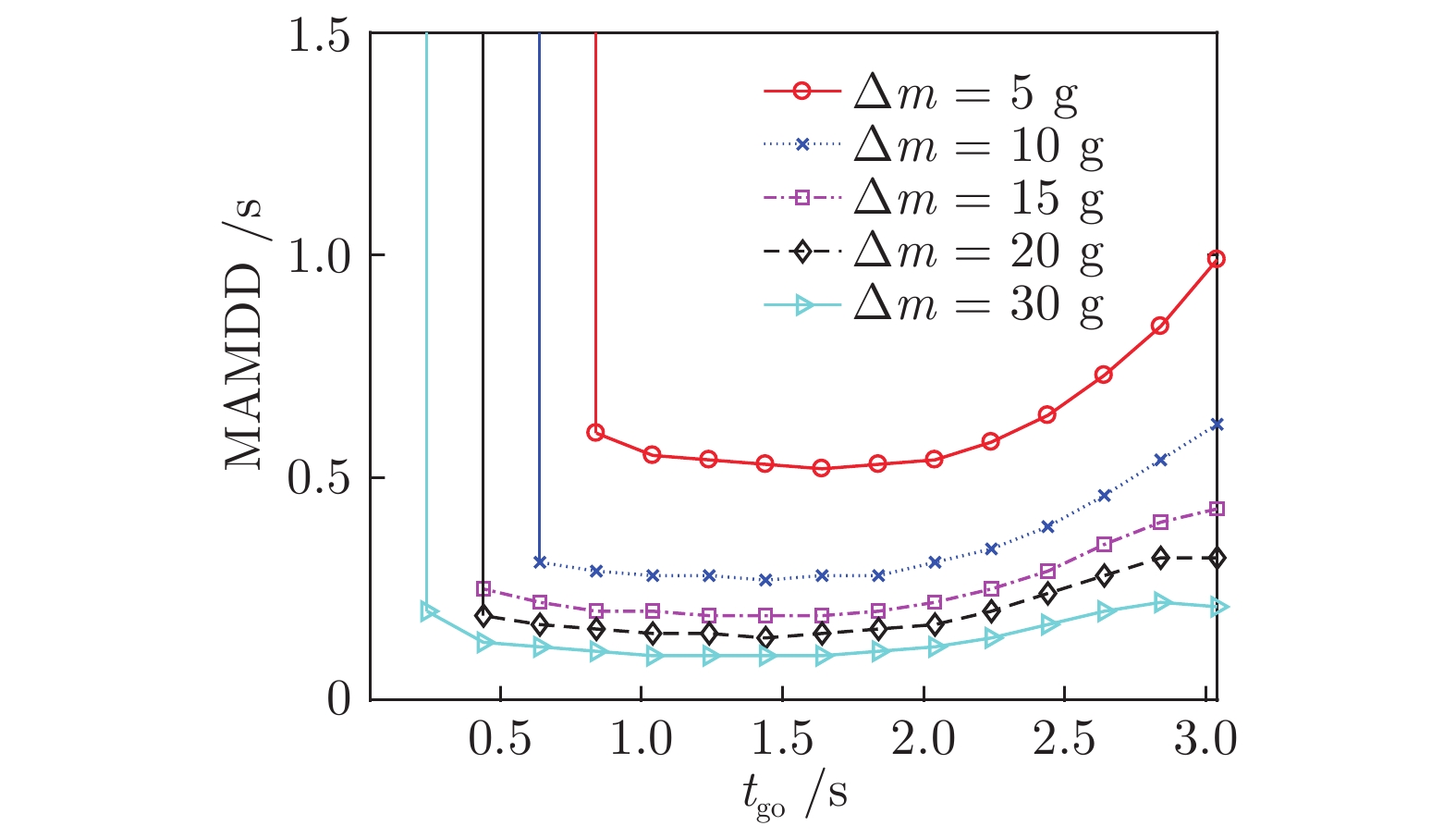
$t_{{\rm{sw}}}$ (s) 捕获区约束MAMDD (s) 一致性约束MAMDD (s) $ \Delta m = 5 \;{\rm{g}}$ 0.6 1.35 0.64 1.2 0.94 0.53 1.8 0.58 0.54 2.2 0.37 0.60 2.6 0.18 $ \infty $ $ \Delta m = 10 \;{\rm{g}}$ 0.6 0.94 0.39 1.2 0.65 0.28 1.8 0.41 0.28 2.2 0.26 0.29 2.6 0.12 $ \infty $ $ \Delta m = 15 \;{\rm{g}}$ 0.6 0.72 0.29 1.2 0.50 0.20 1.8 0.32 0.19 2.2 0.20 0.25 2.6 0.09 $ \infty $ $ \Delta m = 20 \;{\rm{g}}$ 0.6 0.58 0.24 1.2 0.41 0.16 1.8 0.26 0.15 2.2 0.16 0.16 2.6 0.08 0.19 $ \Delta m = 30 \;{\rm{g}}$ 0.6 0.42 0.17 1.2 0.30 0.11 1.8 0.19 0.10 2.2 0.12 0.11 2.6 0.05 0.13 -
[1] Li X R, Jilkov V P. Survey of maneuvering target tracking. Part IV: decision-based methods. In: Proceedings of the 2002 SPIE Conference on Signal and Data Processing of Small Targets, Orlando, USA: SPIE, 2002. 511−534 [2] Li X R, Jilkov V P. Survey of maneuvering target tracking. Part V: Multiple-model methods. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1255-1321 [3] Shinar J, Turetsky V, Glizer V Y. On Estimation in Interception Endgames. Journal of Optimization Theory and Applications, 2013, 157(3): 593-611 [4] Shinar J, Shima T. Non-orthodox guidance law development approach for the interception of maneuvering anti-surface missiles. In: Proceedings of the 2000 AIAA Guidance, Navigation, and Control Conference and Exhibit, Denver, USA: AIAA, 2000. [5] Glizer V Y, Turetsky V. A Linear Differential Game with Bounded Controls and Two Information Delays. Optimal Control Applications and Methods, 2009, 30(2): 135-161 [6] Glizer V Y, Turetsky V, Shinar J. Differential game with linear dynamics and multiple information delays. In: Proceedings of the 13th WSEAS International Conference on Systems, Rodos, Greece: WSEAS Press, 2009.179−184 [7] Shinar J, Turetsky V. What Happens When Certainty Equivalence Is Not Valid? Is There an Optimal Estimator for Terminal Guidance? Annual Reviews in Control, 2003, 27(2): 119-130 [8] Dionne D, Michalska H, Shinar J, Oshman Y. Decision-Directed Adaptive Estimation and Guidance for an Interception Endgame. Journal of Guidance, Control and Dynamics, 2006, 29(4): 970-980 [9] 花文华, 陈兴林, 宋申民. 基于目标机动检测的集成估计与制导方法. 中南大学学报(自然科学版). 2011, 42 (6): 1617-1623.Hua W H, Chen X L, Song S M. Decision-Directed Adaptive Estimation and Guidance for An Interception Endgame. Journal of Central South University, 2011, 42(6): 1617-1623 [10] Kumar G S, Ghose D, Vengadarajan A. A novel IEG strategy for realistically modeled seeker-less interceptors. In: Proceedings of the 2015 AIAA Guidance, Navigation, and Control Conference, Kissimmee, USA: AIAA, 2015. [11] Shinar J, Turetsky V, Oshman Y. Integrated Estimation/Guidance Design Approach for Improved Homing Against Randomly Maneuvering Targets. Journal of Guidance, Control and Dynamics, 2007, 30(1): 154-161 [12] Shinar J, Turetsky V. Three-Dimensional Validation of an Integrated Estimation/Guidance Algorithm Against Randomly Maneuvering Targets. Journal of Guidance, Control and Dynamics, 2009, 32(3): 1034-1039 [13] Su M, Liu L, Wang Y. Integrated Estimation/Guidance Law Against Exoatmo-Spheric Maneuvering Targets. Complexity, 2018, 2018: 1-19 [14] Zhu Y L, Fan H Q, Fan J P, Lu Z Q, Fu, Q. Target Turning Maneuver Detection Using High Resolution Doppler Profile. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 762-779 [15] Fan S J, Xiao H T, Fan H Q, Fan J P. Target Maneuver Discrimination Using ISAR Image in Interception. Eurasip Journal on Advances in Signal Processing, 2016, 24(1): 1-13 [16] Fan H Q, Zhu Y L, Fu Q. Impact of Mode Decision Delay on Estimation Error for Maneuvering Target Interception. IEEE Transactions on Aerospace and Electronic Systems, 2012, 47(1): 702-711 [17] Xiang S W, Fan H Q, Fu Q. Impact of Mode Decision Delay on Estimation Error in Continuous-Time Controlled System. IEEE Access, 2018, 6: 73265-73272 [18] Xiang S W, Li T C, Chen W, Fan H Q, Fu Q. Maximal Admissible Mode Decision Delay in Terminal Guidance. Chinese Journal of Aeronautics, 2019, 32(8): 1959-1966 [19] Xiang S W, Fan H Q, Fu Q. Error distribution of zero-effort miss distance under mode mismatch. International Journal of Control, 2021, 94(3): 643−652 [20] 范红旗. 主动寻的制导中机动目标运动模式辨识技术 [博士学位论文], 国防科技大学, 中国. 2008.Fan Hong-Qi. Technology on Maneuvering Target Motion Model Identification in Active Homing Guidance [Ph.D. dissertation], National University of Defense Technology, China. 2008. [21] 樊世杰. 特征辅助的大机动目标拦截技术研究 [博士学位论文], 国防科技大学, 中国. 2015.Fan Shi-Jie. Research on Feature Aided Highly Maneuvering Target Interception [Ph.D. dissertation], National University of Defense Technology, China. 2015. -




 下载:
下载: