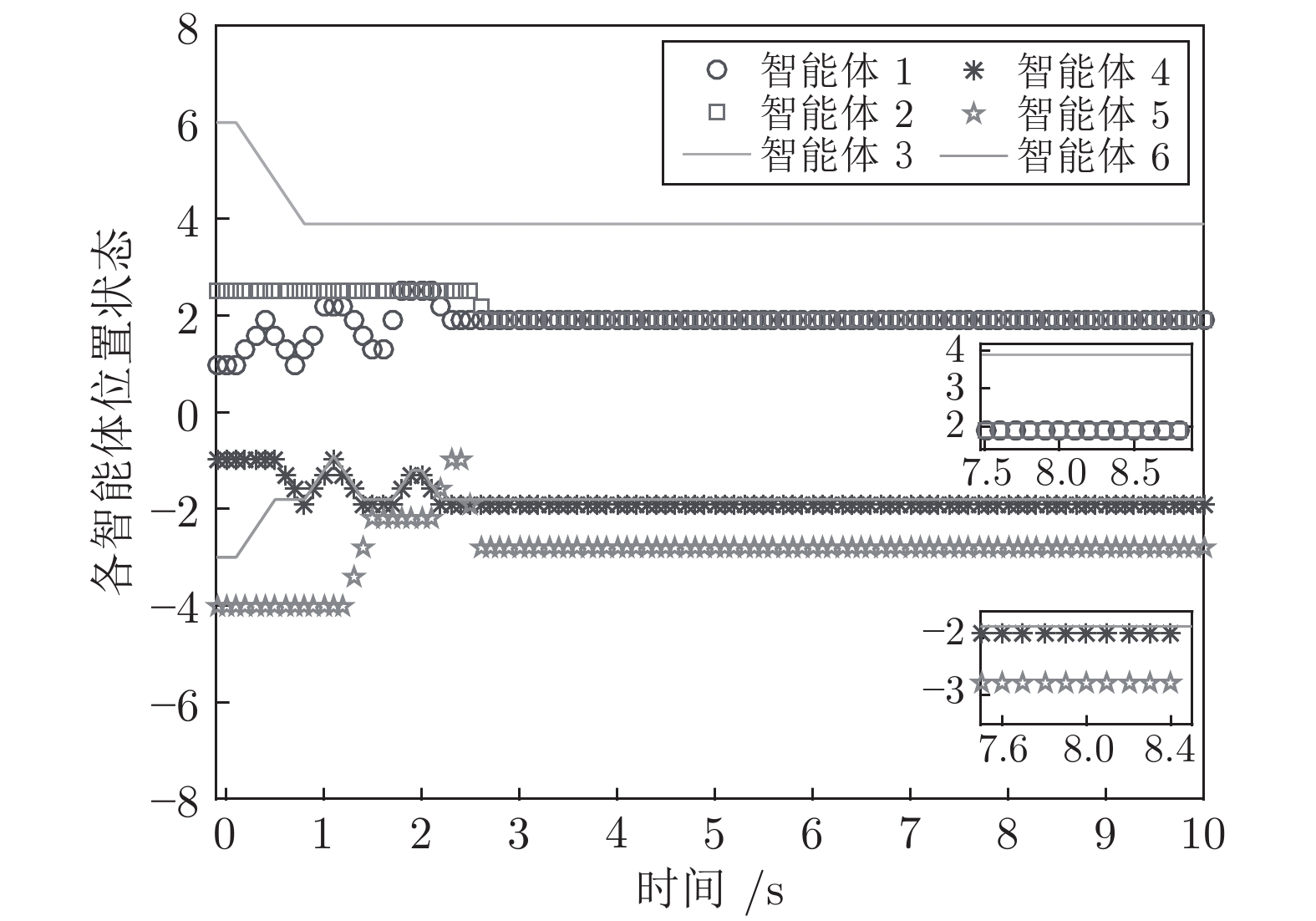
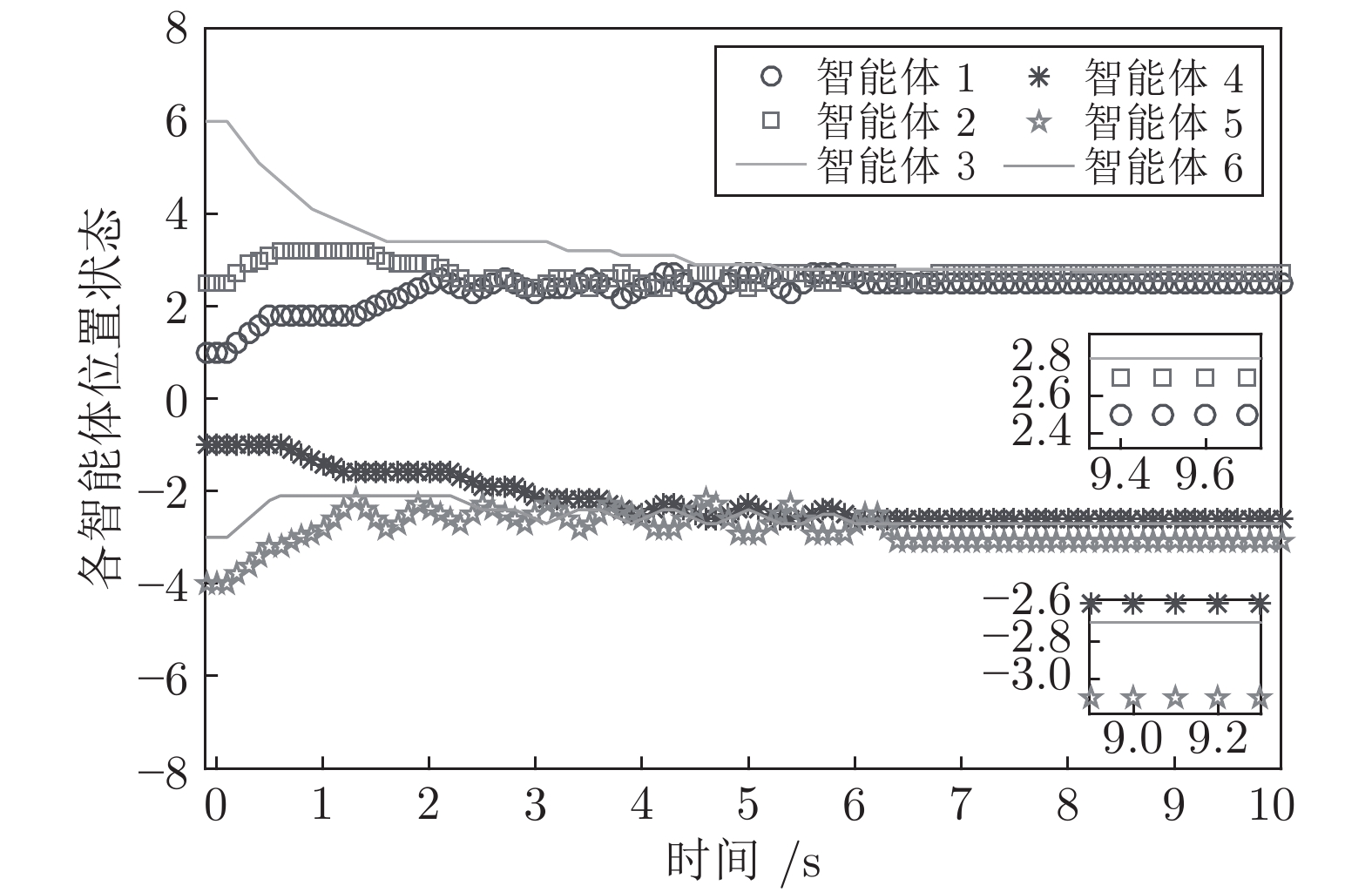
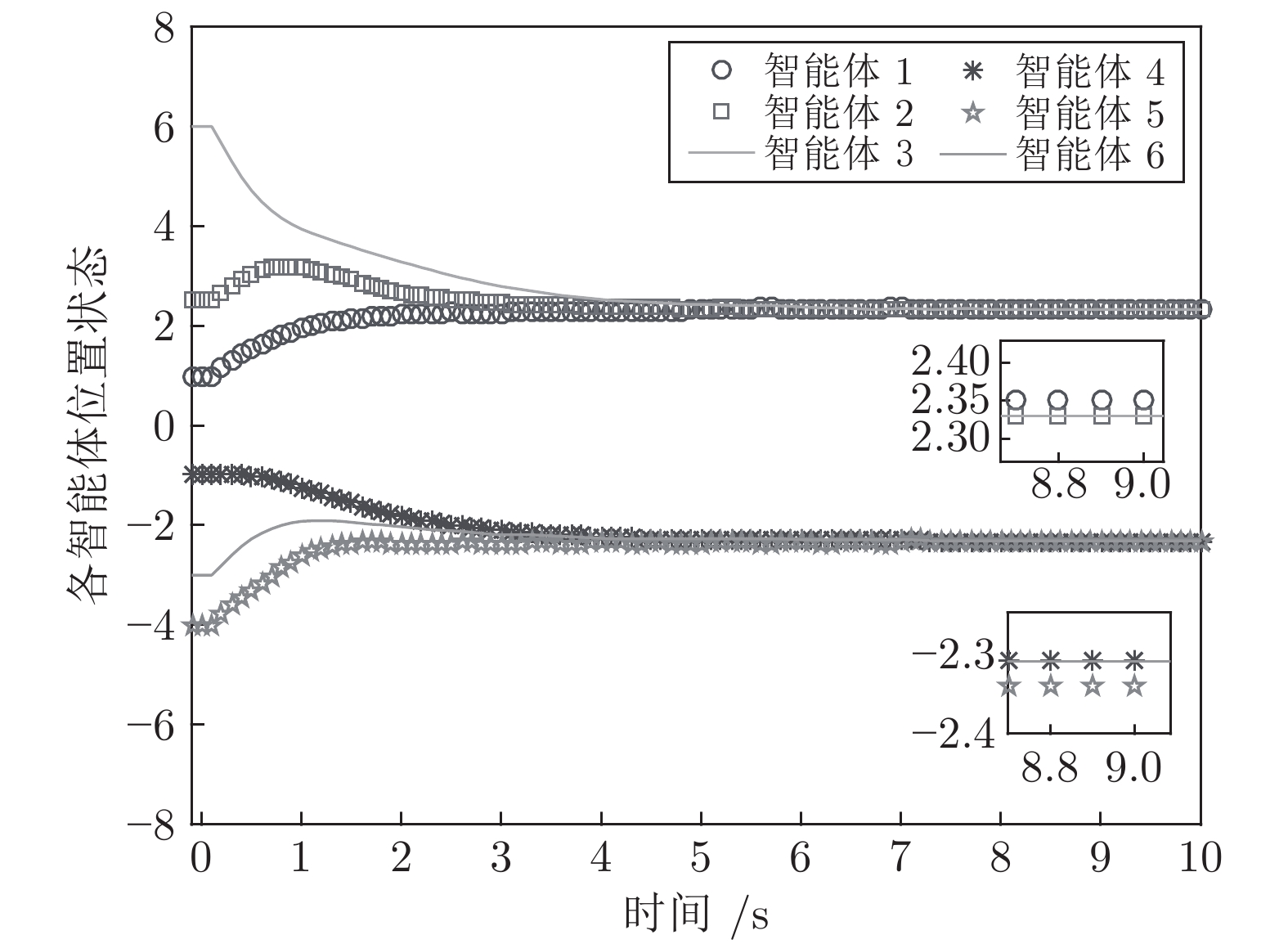
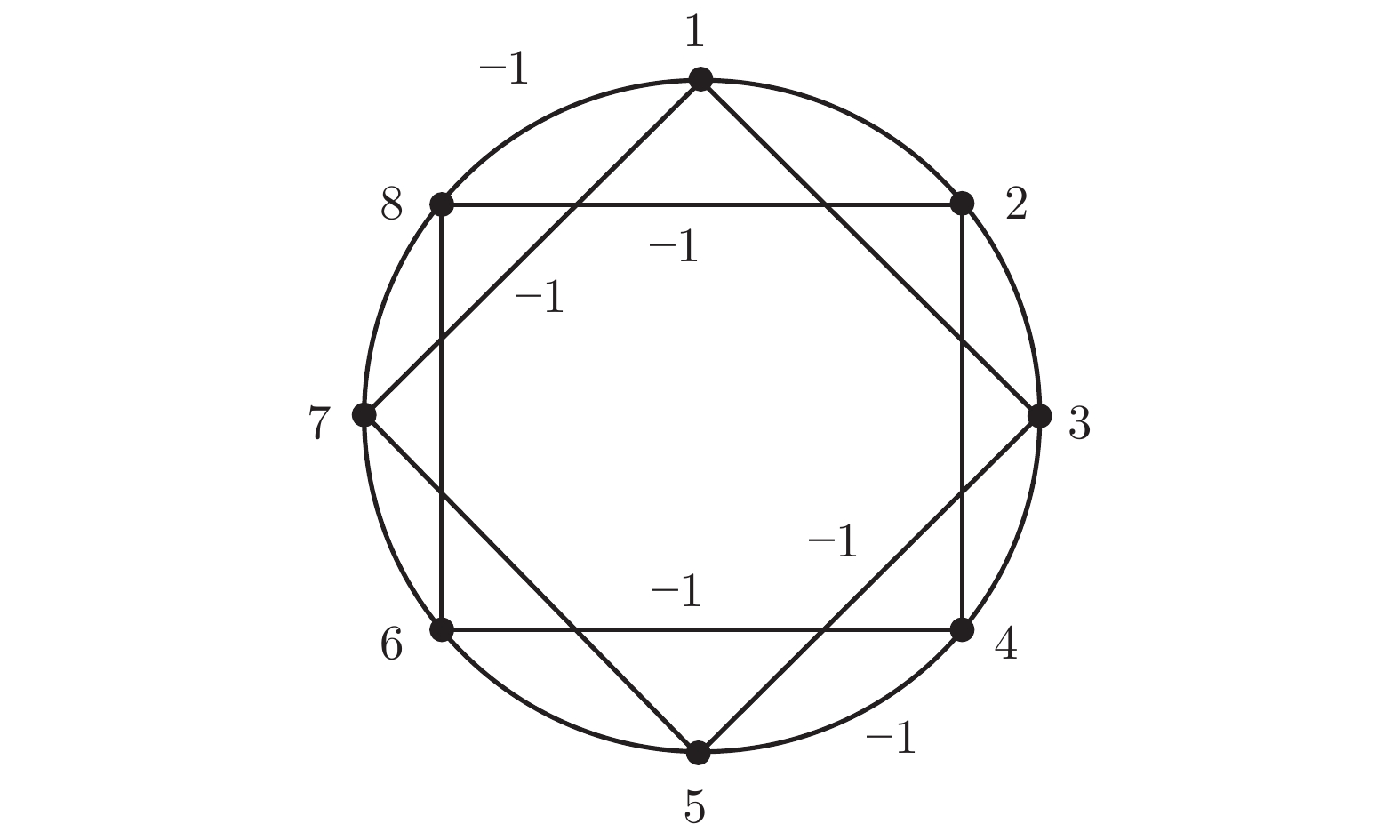
|
[1]
|
Jadbabaie A, Lin J, Morse A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control, 2003, 48(6): 988--1001. doi: 10.1109/TAC.2003.812781
|
|
[2]
|
Forti M, Nistri P, Papini D. Global exponential stability and global convergence in finite time of delayed neural networks with infinite gain[J]. IEEE Transactions on Neural Networks, 2005, 16(6): 1449--1463. doi: 10.1109/TNN.2005.852862
|
|
[3]
|
Yu W W, Chen G R, Cao M. Some necessary and sufficient conditions for second-order consensus in multi-agent dynamical systems[J]. Automatica, 2010, 46(6): 1089--1095. doi: 10.1016/j.automatica.2010.03.006
|
|
[4]
|
陈世明, 化俞新, 祝振敏, 赖强. 邻域交互结构优化的多智能体快速蜂拥控制算法[J]. 自动化学报, 2015, 41(12): 2092--2099.Chen Shi-Ming, Hua Yu-Xin, Zhu Zhen-Min, Lai Qiang. Fast flocking algorithm for multi-agent systems by opti-mizing local interactive topology[J]. Acta Automatica Sinica, 2015, 41(12): 2092--2099.
|
|
[5]
|
Kim J M, Park J B, Choi Y H. Leaderless and leader-following consensus for heterogeneous multi-agent systems with random link failures[J]. Iet Control Theory and Applications, 2014, 8(1): 51--60. doi: 10.1049/iet-cta.2012.0855
|
|
[6]
|
Ma Q, Wang Z, Miao G Y. Second-order group consensus for multi-agent systems via pinning leader-following approach[J]. Journal of The Franklin Institute-engineering and Applied Mathematics, 2014, 351(3): 1288--1300. doi: 10.1016/j.jfranklin.2013.11.002
|
|
[7]
|
Roy S. Scaled consensus[J]. Automatica, 2015: 259--262.
|
|
[8]
|
Zhang Z, Chen S M, Su H S. Scaled Consensus of second-order nonlinear multiagent systems with time-varying delays via aperiodically intermittent control[J]. IEEE Transactions on Cybernetics, 2020, 50(8): 3503--3516. doi: 10.1109/TCYB.2018.2883793
|
|
[9]
|
S. Chen, Z. Zhang and Y. Zheng, "H∞ Scaled Consensus for MASs With Mixed Time Delays and Disturbances via Observer-Based Output Feedback," in IEEE Transactions on Cybernetics, vol. 52, no. 2, pp. 1321-1334, Feb. 2022, doi: 10.1109/TCYB.2020.3001643.
|
|
[10]
|
Wang Z H, Xu J J, Zhang H S. Consensusability of multi-agent systems with time-varying communication delay[J]. Systems & Control Letters, 2014: 37--42.
|
|
[11]
|
Chen Y, Shi Y. Consensus for Linear Multiagent Systems With Time-Varying Delays: A Frequency Domain Perspective[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2017, 47(8): 2143--2150.
|
|
[12]
|
Qiu Z R, Xie L H, Hong Y G. Quantized Leaderless and Leader-Following Consensus of High-Order Multi-Agent Systems With Limited Data Rate[J]. IEEE Transactions on Automatic Control, 2016, 61(9): 2432--2447. doi: 10.1109/TAC.2015.2495579
|
|
[13]
|
Dong X W, Xi J X, Shi Z Y, Zhong Y S. Practical consensus for high-order linear time-invariant swarm systems with interaction uncertainties, time-varying delays ang external disturbances[J]. International Journal of systems Science, 2013, 44(10): 1843--1856. doi: 10.1080/00207721.2012.670296
|
|
[14]
|
Bernuau E, Moulay E, Coirault P, Lsfoula F. Practical consensus of homogeneous sampled-data multiagent systems[J]. IEEE Transactions on Automatic Control, 2019, 64(11): 4691--4697. doi: 10.1109/TAC.2019.2904442
|
|
[15]
|
Ning B, Han Q L, Zuo Z Y. Practical fixed-time consensus for integrator-type multi-agent systems: A time base generator approach[J]. Automatica, 2019, 105(105): 406--414.
|
|
[16]
|
Panteley E, Loria A, Elati A. Practical dynamic consensus of Stuart–Landau oscillators over heterogeneous networks[J]. International Journal of Control, 2020, 93(2): 261--273. doi: 10.1080/00207179.2018.1551618
|
|
[17]
|
张文, 马忠军, 王毅. 带未知耦合权重的领导-跟随多智能体系统的实用一致性[J]. 自动化学报, 2018, 44(12): 2300--2304.Zhang Wen, Ma Zhong-Jun, Wang Yi. Practical consensus of leader-following multi-agent system with unknown coupling weights[J]. Acta Automatica Sinica, 2018, 44(12): 2300--2304.
|
|
[18]
|
Altafini C. Consensus problems on networks with antagonistic interactions[J]. IEEE Transactions on Automatic Control, 2013, 58(4): 935--946. doi: 10.1109/TAC.2012.2224251
|
|
[19]
|
Zhang H, Chen J. Bipartite consensus of multi-agent systems over signed graphs: State feedback and output feedback control approaches[J]. International Journal of Robust and Nonlinear Control, 2017, 27(1): 3--14. doi: 10.1002/rnc.3552
|
|
[20]
|
Jiang Y, Zhang H W, Chen J. Sign-consensus of linear multi-agent systems over signed directed graphs[J]. IEEE Transactions on Industrial Electronics, 2017, 64(6): 5075--5083. doi: 10.1109/TIE.2016.2642878
|
|
[21]
|
Meng D Y, Meng Z Y, Hong Y G. Uniform convergence for signed networks under directed switching topologies[J]. Automatica, 2018, 90: 8--15. doi: 10.1016/j.automatica.2017.12.028
|
|
[22]
|
Pan L, Shao H, Mesbahi M, Li D. Bipartite consensus on matrix-valued weighted networks[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2018, 66(8): 1441--1445.
|
|
[23]
|
Su H S, Chen J H, Yang Y C. The bipartite consensus for multi-agent systems with matrix-weight-based signed network[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2019, 67(10): 2019--2023.
|
|
[24]
|
翟世东, 刘佩, 高辉. 具有对抗关系和时变拓扑的耦合离散系统有界双向同步[J]. 自动化学报, 2020.Zhai Shi-Dong, Liu Pei, Gao Hui. Bounded bipartite synchronization for coupled discrete systems under antagonistic[J]. Acta Automatica Sinica, to be publication. 2020.
|
|
[25]
|
Akshay K, Tamer B, R. Srikant. Quantized consensus[J]. Automatica, 2007, 43: 1192--1203. doi: 10.1016/j.automatica.2007.01.002
|
|
[26]
|
Dimarogonasa D V, Johansson K H. Stability analysis for multi-agent systems using the incidence martrix: Quantized communication and formation control[J]. Automatica, 2010, 46(4): 695--700. doi: 10.1016/j.automatica.2010.01.012
|
|
[27]
|
Ceragioli F, Claudio D P, Paolo F. Discontinuities and hysteresis in quantized average consensus[J]. Automatica, 2011, 47(9): 1916--1928. doi: 10.1016/j.automatica.2011.06.020
|
|
[28]
|
Zhu Y R, Li S L, Ma J Y, Zheng Y S. Bipartite consensus in networks of agents with antagonistic interactions and quantization[J]. IEEE Transactions on circuits and systems-express briefs, 2018, 65(12): 2012--2018. doi: 10.1109/TCSII.2018.2811803
|
|
[29]
|
Wu J, Deng Q, Han T, Yan H C. Distributed bipartite tracking consensus of nonlinear multi-agent systems with quantized communication[J]. Neurocomputing, 2020. 395: 78--85. doi: 10.1016/j.neucom.2020.02.017
|




 下载:
下载: