Broad Siamese Network for Edge Computing Applications
-
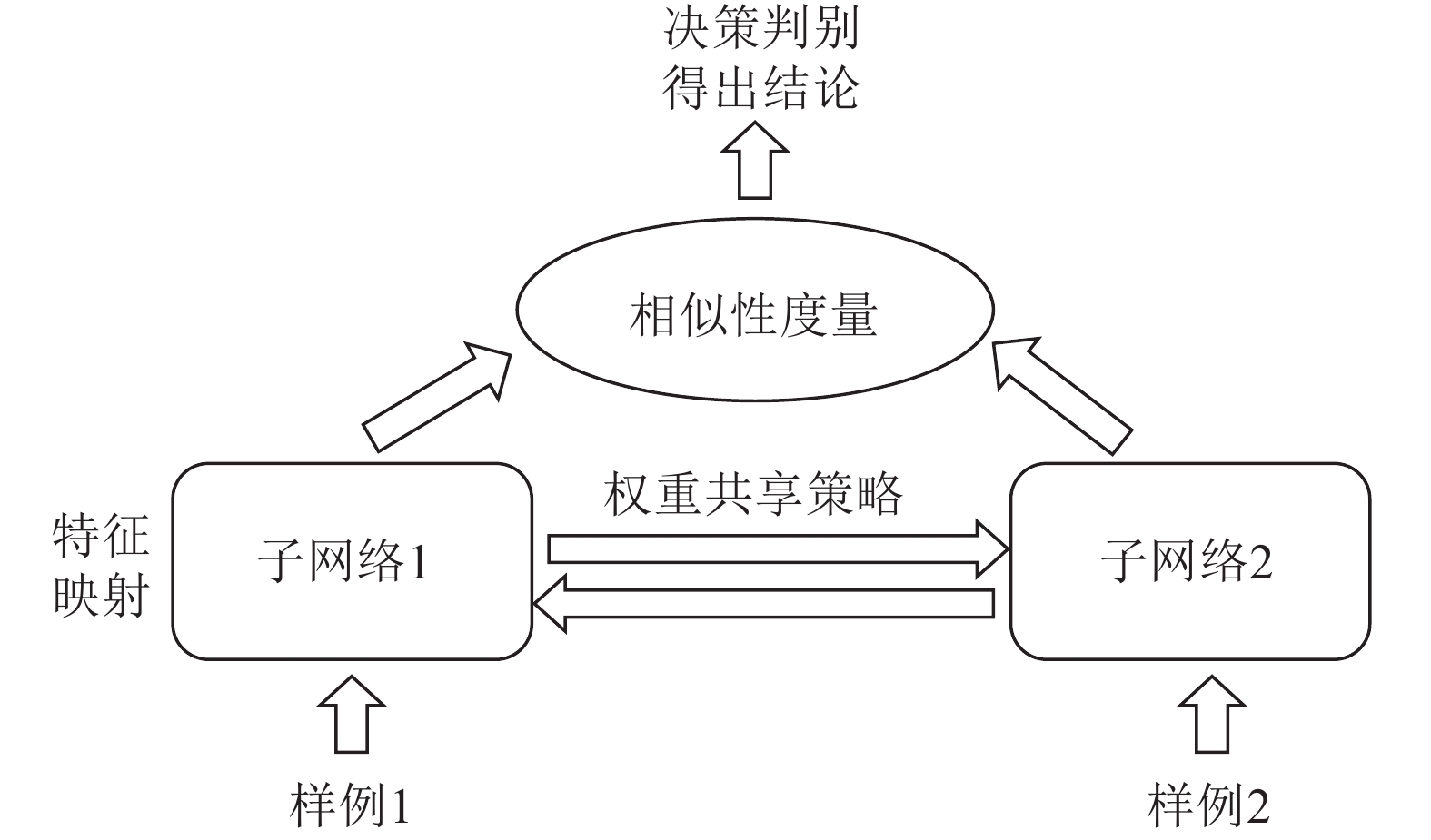
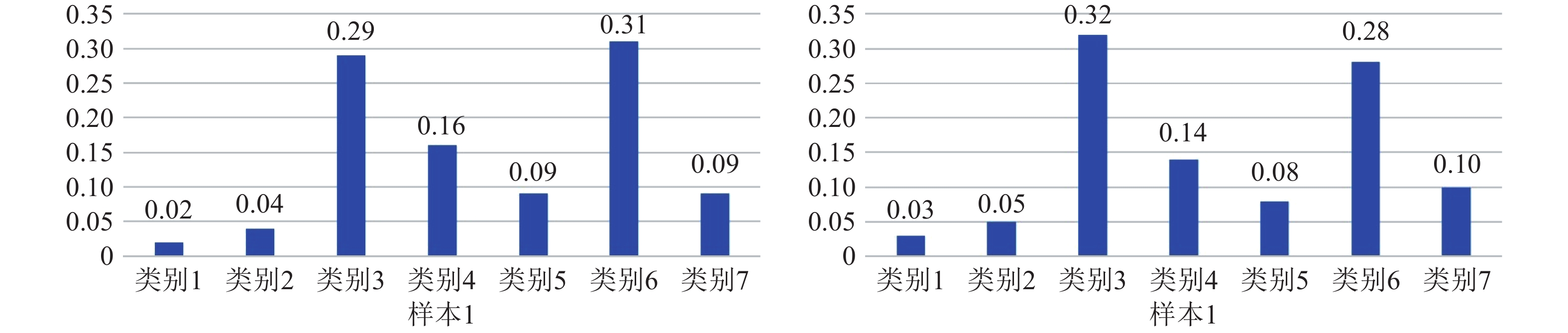
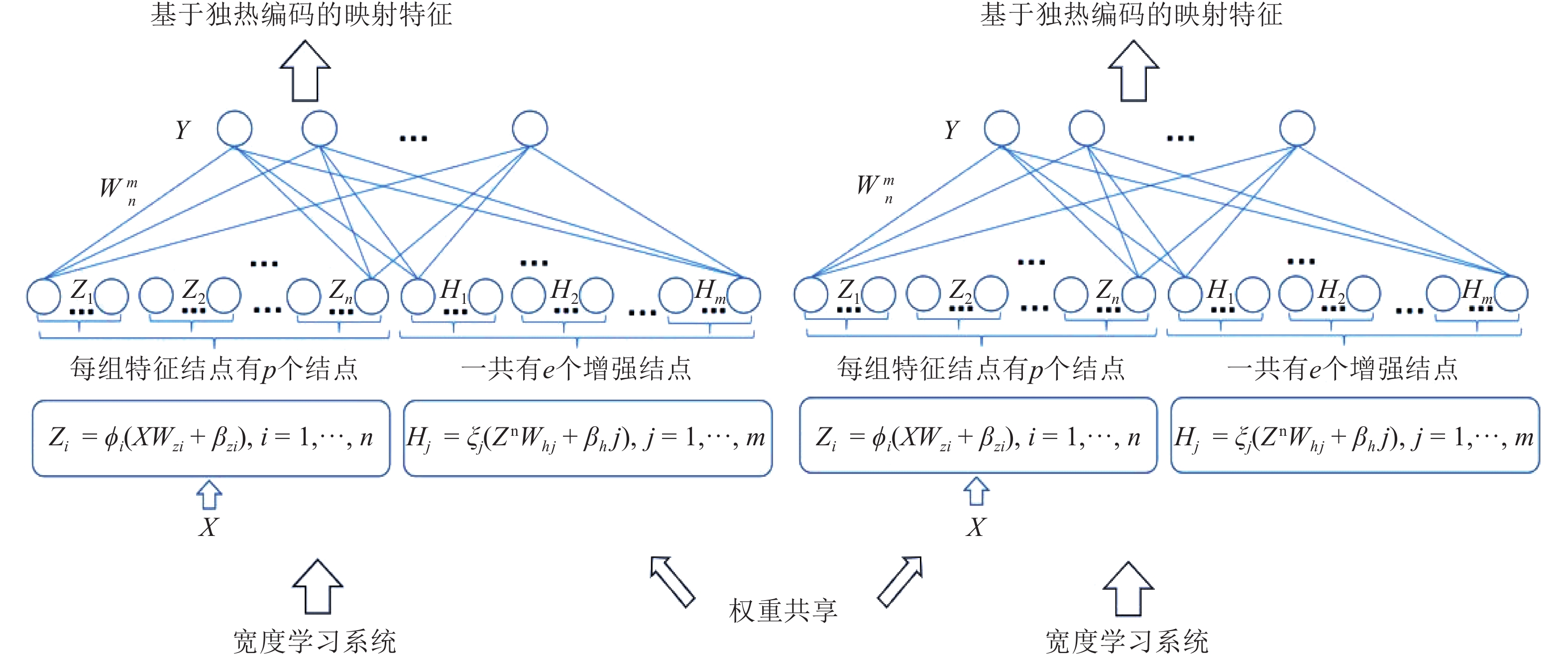
摘要: 边缘计算是将计算、存储、通信等任务分配到网络边缘的计算模式. 它强调在用户终端附近执行数据处理过程, 以达到降低延迟, 减少能耗, 保护用户隐私等目的. 然而网络边缘的计算、存储、能源资源有限, 这给边缘计算应用的推广带来了新的挑战. 随着边缘智能的兴起, 人们更希望将边缘计算应用与人工智能技术结合起来, 为我们的生活带来更多的便利. 许多人工智能方法, 如传统的深度学习方法, 需要消耗大量的计算、存储资源, 并且伴随着巨大的时间开销. 这不利于强调低延迟的边缘计算应用的推广. 为了解决这个问题, 我们提出将宽度学习系统(Broad learning system, BLS)等浅层网络方法应用到边缘计算应用领域, 并且设计了一种宽度孪生网络算法. 我们将宽度学习系统与孪生网络结合起来用于解决分类问题. 实验结果表明我们的方法能够在取得与传统深度学习方法相似精度的情况下降低时间和资源开销, 从而更好地提高边缘计算应用的性能.Abstract: Edge computing is a paradigm that allocates computing, storage, communication tasks to the edge of network. It emphasizes that data processing should be placed in the proximity of user terminals in order to reduce latency and energy consumption while protecting user privacy. However, resources for computation, storage and power at the edge of network are limited, which brings new challenges to edge computing applications. With the emergence of edge intelligence, people prefer to combine edge computing applications with artificial intelligence techniques to bring more convenience to our lives. Many artificial intelligence methods such as traditional deep learning methods, need to consume a lot of computation and storage resources with a huge time consumption. It is not conducive to the popularity of edge computing applications, which always require low latency. In order to resolve such a problem, we propose that shallow network methods such as broad learning system can be applied in edge computing applications and design a broad Siamese network algorithm. We combine broad learning system (BLS) with Siamese network for classification tasks. Experimental results show that our method can reduce the cost of time and resources, while achieving a similar result as deep learning methods, consequently improving the performance of edge computing applications.
-
Key words:
- Broad learning system (BLS) /
- edge computing /
- Siamese network /
- shallow network /
- edge intelligence
-
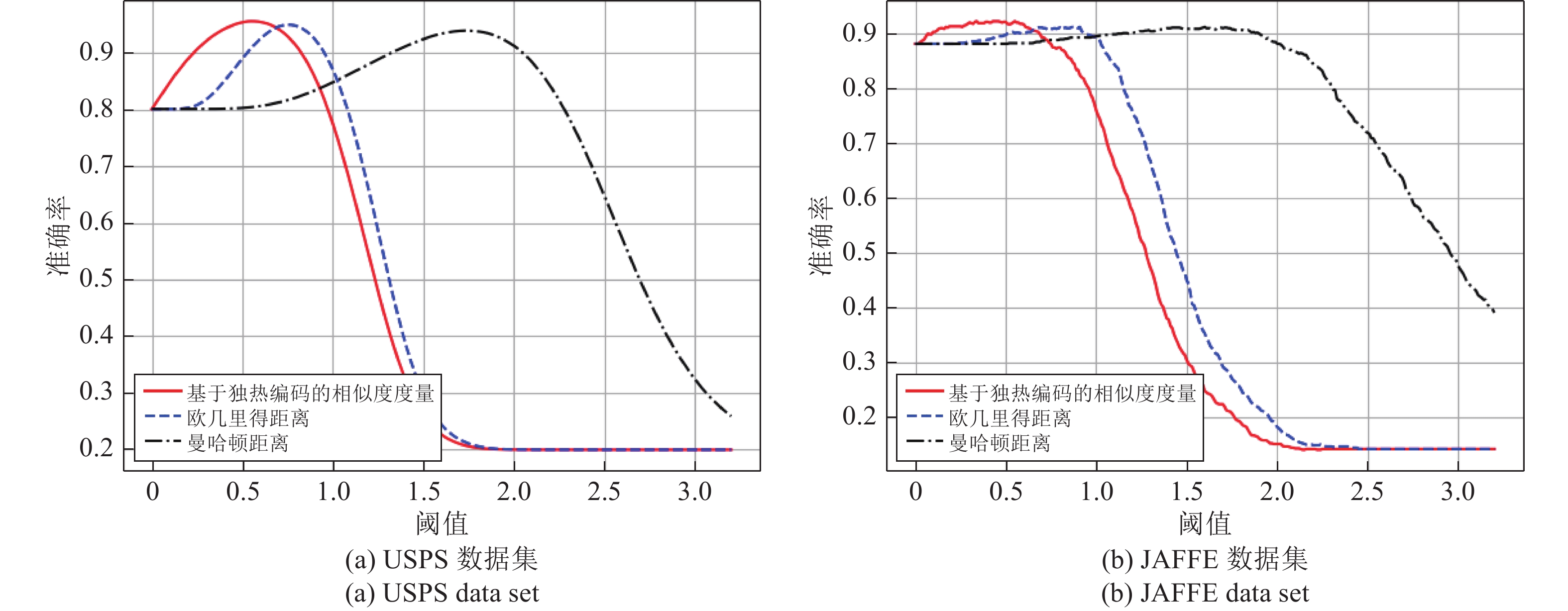
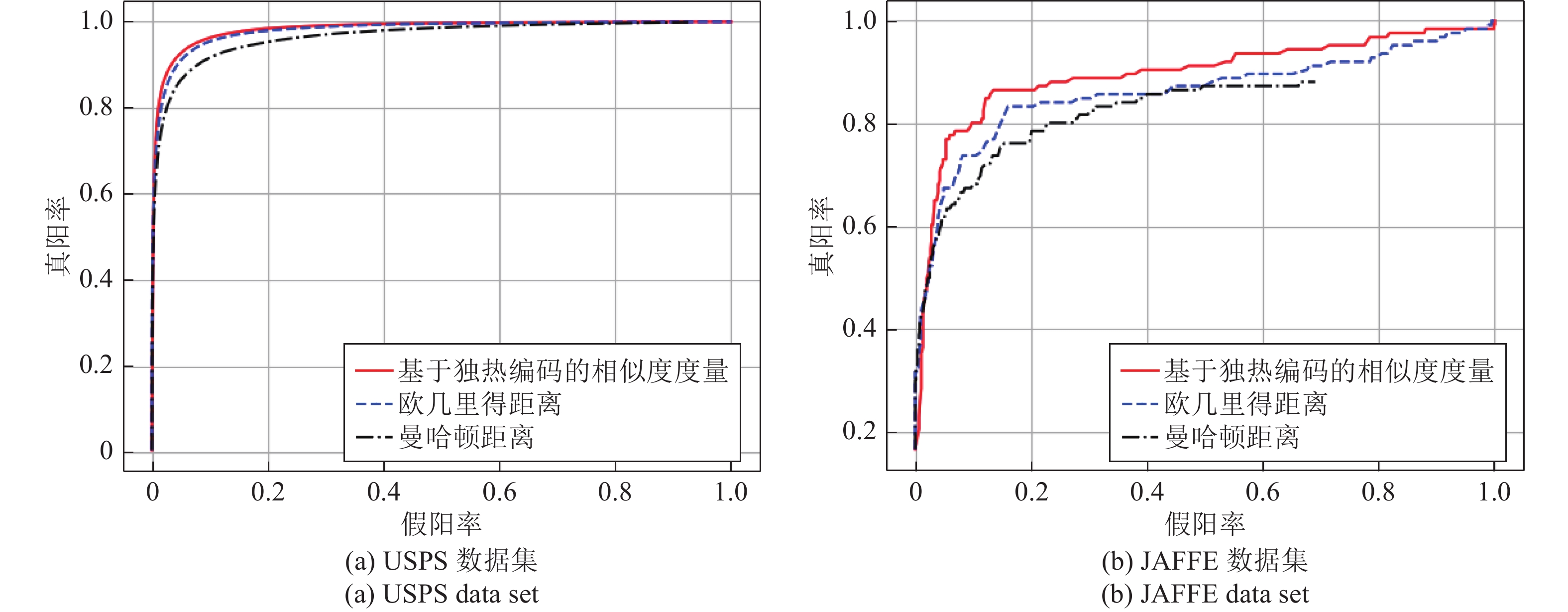
表 1 实验数据集信息表
Table 1 Table of data set for experiments
数据集 样本
规模类别
数量各类别样本数量 特征
维度CK+ 5876 7 (1022, 233, 868, 546, 1331, 547, 1329) 14400 MNIST 70000 10 每个类别近似 7000 样本 784 JAFFE 213 7 (30, 29, 32, 31, 30, 31, 30) 14 400 USPS 20000 10 每个类别 2 000 样本 784 表 2 宽度孪生网络参数设置信息
Table 2 Table of parameters for broad Siamese network
数据集 n p e CK+ 8 10 9000 MNIST 10 10 500 JAFFE 8 10 9000 USPS 10 10 1500 表 3 对比算法中全连接神经网络结点个数设置信息
Table 3 Table of number about nodes in the fully connected network for comparison
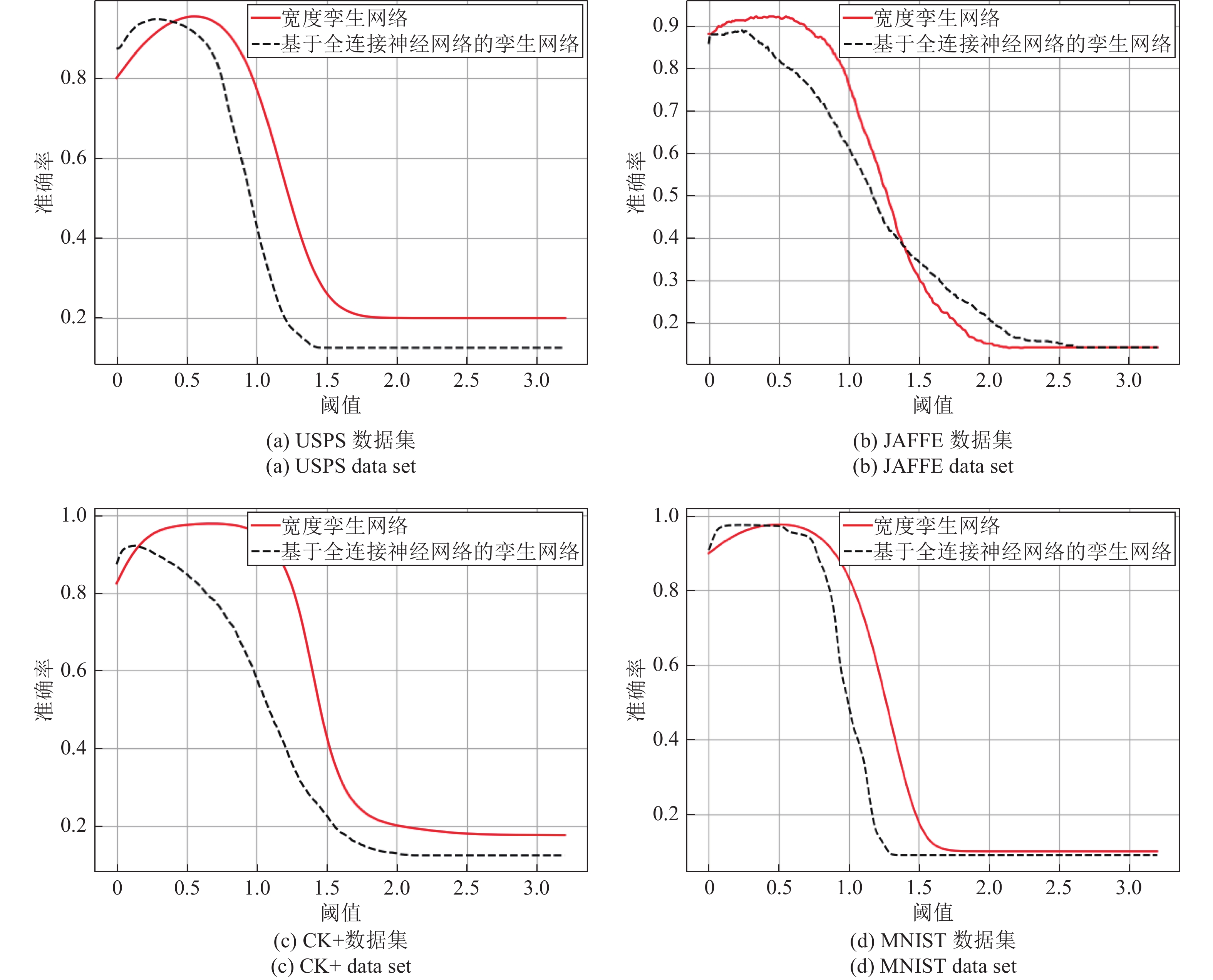
数据集 第一层结点数 第二层结点数 第三层结点数 CK+ 512 128 512 MNIST 16 16 16 JAFFE 1024 128 1024 USPS 128 128 128 表 4 准确率实验结果
Table 4 Table of experiment results about accuracy
数据集 宽度孪生网络 基于全连接神经网络的孪生网络 CK+ 0.9788738 0.9287094 MNIST 0.9798112 0.9777414 JAFFE 0.9217687 0.9206349 USPS 0.9536075 0.9505025 表 5 训练时间实验结果
Table 5 Table of experiment results about training time
数据集 宽度孪生网络 基于全连接神经网络的孪生网络 CK+ 94.140997 567.9896214 MNIST 5.6314652 60.0518959 JAFFE 58.4795067 1105.1385579 USPS 3.0834677 29.8392925 表 6 内存开销实验结果
Table 6 Table of experiment results about memory overhead
数据集 宽度孪生网络 基于全连接神经网络的孪生网络 CK+ 3.3491211 6.0307884 MNIST 2.4598732 2.0554810 JAFFE 0.2893066 5.6162262 USPS 1.2569504 0.8804893 -
[1] Chen C L P , Liu Z. Broad learning system: an effective and efficient incremental learning system without the need for deep architecture. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(1): 10−24 doi: 10.1109/TNNLS.2017.2716952 [2] Peng X, Ota K, Dong M. A broad learning-driven network traffic analysis system based on fog computing paradigm. China Communications, 2020, 17(2): 1−13 doi: 10.23919/JCC.2020.02.001 [3] Zhang T, Liu Z, Wang X, Xing X, Chen C L P, Chen E. Facial expression recognition via broad learning system. In: Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan: IEEE, 2018. 1898−1902 [4] Gao S, Guo G, Huang H, Cheng X, Chen C L P. An end-to-end broad learning system for event-based object classification. IEEE Access, 2020, 8: 45974−45984 doi: 10.1109/ACCESS.2020.2978109 [5] Liu X, Qiu T, Chen C, Ning H, Chen N. An incremental broad learning approach for semi-supervised classification. In: Prceedings of the 2019 IEEE International conference on Dependable, Autonomic and Secure Computing, International conference on Pervasive Intelligence and Computing, International conference on Cloud and Big Data Computing, International conference on Cyber Science and Technology Congress (DASC/PiCom/CBDCom/CyberSciTech), Fukuoka, Japan: IEEE. 2019. 250−254 [6] Wang X, Zhang T, Xu X, Chen L, Xing X, Chen C L P. EEG emotion recognition using dynamical graph convolutional neural networks and broad learning system. In: Proceedings of the 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Madrid, Spain: 2018.1240−1244 [7] Chu F, Liang T, Chen C L P, Wang X, Ma X. Weighted broad learning system and its application in nonlinear industrial process modeling. IEEE Transactions on Neural Networks and Learning Systems. 2020, 31(8): 3017−3031 [8] Bromley J, Guyon I, Lecun Y, et al. Signature verification using a Siamese time delay neural network. In: Proceedings of the Advances in Neural Information Processing Systems 6, 7th NIPS Conference, Denver, Colorado, USA: Morgan Kaufmann Publishers Inc., 1993. [9] Nair V, Hinton G E. Rectified linear units improve restricted boltzmann machines. In: Proceedings of the 27th International Conference on International Conference on Machine Learning (ICML´10). Omnipress, Madison, WI, USA: 2019.807−814 [10] Treible W, Saponaro P, Kambhamettu C. Wildcat: in-the-wild color-and-thermal patch comparison with deep residual pseudo-Siamese networks. In: Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, China: IEEE, 2019. 1307−1311 [11] Baraldi L, Grana C, Cucchiara R. A deep Siamese network for scene detection in broadcast videos. In: Proceedings of the 23rd ACM International Conference on Multimedia (MM'15). Association for Computing Machinery, New York, NY, USA: 1199−1202 [12] Melekhov I, Kannala J, Rahtu E. Siamese network features for image matching. In: Proceedings of the 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico: 2016. 378−383 [13] Bertinetto L , Valmadre J , Henriques J F , et al. Fully-convolutional Siamese networks for object tracking. In: Proceedings of European Conference on Computer Vision (ECCV) Workshops. 2016. 850—865 [14] Zeghidour N, Synnaeve G, Usunier N, et al. Joint learning of speaker and phonetic similarities with siamese networks. In: Proceedings of Interspeech 2016, 2016. 1295−1299 [15] Neculoiu P, Versteegh M, Rotaru M. Learning text similarity with Siamese recurrent networks. In: Proceedings of the 1st Workshop on Representation Learning for NLP. 2016. 148−157 [16] Rahul M V, Ambareesh R, Shobha G. Siamese network for underwater multiple object tracking. In: Proceedings of the 9th International Conference on Machine Learning and Computing (ICMLC 2017). New York, NY, USA: ACM, 2017. 511−516 -





 下载:
下载: