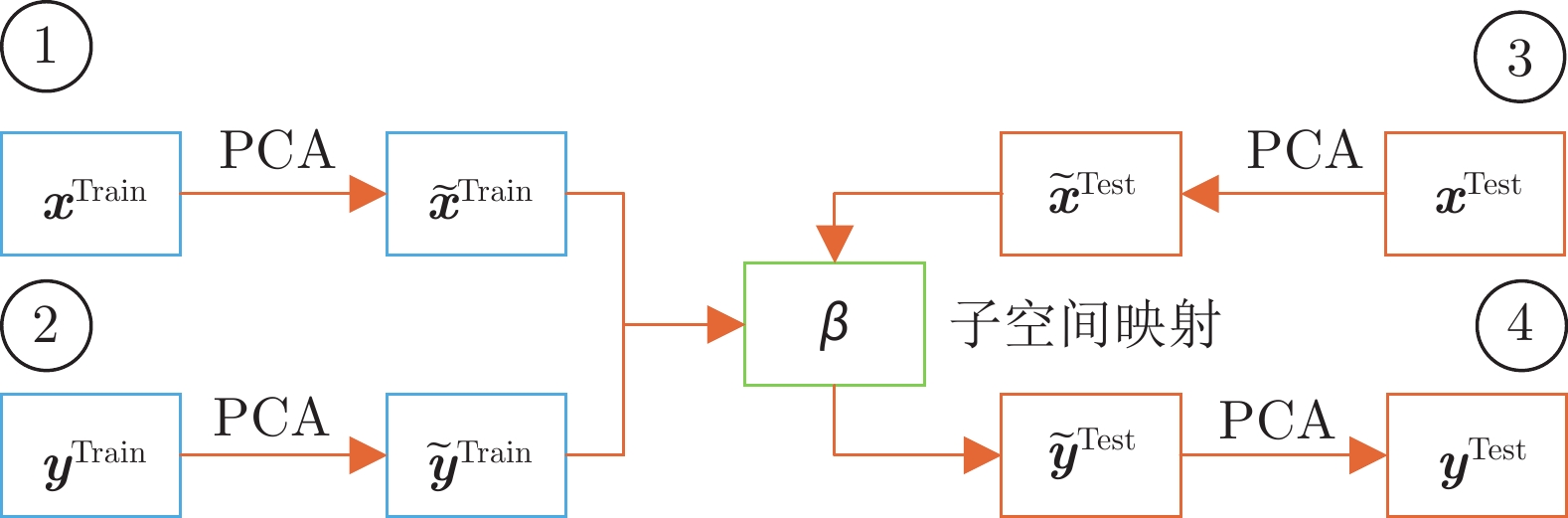
-
摘要: 呼吸会引起体内器官和肿瘤的运动, 这会显著影响放射治疗的过程和效果. 人体内部膈肌和胸腹部外表面是当前两种与呼吸系统高度相关的结构, 本文对其进行系统研究, 提出了一种新的分步子空间映射(Two-step subspace mapping, TSSM)算法, 通过对体外胸腹部表面的测量, 来预测体内膈肌的运动. 首先采用三维图像分割技术对4D CT图像进行分割, 在不使用标记物的情况下, 准确测量体内膈肌和体外胸腹部表面的位移. 为了解决跨空间的预测问题, TSSM首先构造特征子空间, 并将膈肌数据和胸腹外表面数据分别映射到各自的子空间中, 以减少数据的相关性和冗余信息; 然后通过线性岭回归优化过程, 对两个子空间进行二次映射, 从而有效地捕获跨空间数据之间的相关性. 根据训练得到的相关模型, 通过体外胸腹部外表面的运动情况, 对体内膈肌的运动情况进行准确的预测. 为了研究数据之间的非线性关系, 进一步将TSSM推广到了基于核的TSSM (kTSSM)算法. 实验表明, 该方法可以根据腹腔外表面的运动情况, 准确地对体内膈肌位移进行预测, 优于经典的线性模型和ANN模型. 给出了优化算法的解析解, 其运算速度快, 将有助于提高放射治疗中门控技术和跟踪技术的效率和精度.Abstract: Respiratory induced organ and tumor motion has great influence in radiation therapy. Two highly correlated structures with respiratory are comprehensively investigated including internal diaphragm and external thoracoabdominal surface in this paper. A novel two-step subspace mapping (TSSM) algorithm is proposed to predict the diaphragm displacement by markerless thoracoabdominal surface measurement. TSSM first incorporates 3D image segmentation to accurately measure the displacement of the diaphragm and the thoracoabdominal surface without markers on 4D CT images. To solve the cross-domain estimation problem, TSSM first constructs eigenspaces and projects the two organs＇ displacement data into their corresponding subspaces to reduce the redundancy and irrelevance. Then, TSSM makes a mapping between the subspaces by a Ridge regression optimization to effectively characterize their correlation. Based on the trained correlation model, the diaphragm domain can be adapted to the abdominal surface domain, and then the diaphragm displacement can be estimated by the abdominal surface without markers. In order to investigate the non-linear correlation, TSSM is further extended to kernel TSSM (kTSSM). Experiments show the proposed method can accurately predict the displacement of the internal diaphragm by the external thoracoabdominal surface, and outperform the classical linear model and ANN model. The simple closed form for the optimization algorithm leads to an extremely fast algorithm, which has potential for improving the timing accuracy of surface-guided gating and tracking in radiotherapy.
-
Key words:
- Respiratory motion /
- thoracoabdominal surface /
- diaphragm /
- subspace mapping /
- regression model /
- 4D CT
-
图 1 三维图像分割结果横断平面展示图, 背景体素值为0, 身体区域的体素值为1, 肺部体素值为3
Fig. 1 3D segmentation images shown on the axial plane, where the background voxels is set to 0, the voxels of body area to 1, and the voxels of lungs to 3
图 2 三维图像分割结果, 及其对应的肺部区域和身体区域
Fig. 2 A 3D segmentation result and the corresponding separated 3D lungs and body
图 6 膈肌和胸腹部表面的位移, 每一种颜色的曲线对应一个患者的数据
Fig. 6 The displacement of diaphragm and thoracoabdominal surface, where each color corresponds to a specific patient＇s data
图 7 归一化后的膈肌和胸腹部表面的位移, 每一种颜色的曲线对应一个患者的数据
Fig. 7 The displacement of diaphragm and thoracoabdominal surface after normalization, where each color corresponds to a specific patient＇s data
图 8 三个方向的预测结果. 该结果对应于100次运行MSE的中位数值
Fig. 8 Prediction results corresponding the median MSE value in three directions after 100 independent runs
图 9 三个方向各相位预测误差的统计箱图
Fig. 9 Boxplot of the prediction performance on every phase in three directions
图 10 主方向的预测结果, 该结果对应于100次运行MSE的中位数值
Fig. 10 Prediction results corresponding the median MSE values in the principal direction after 100 independent runs
图 11 主方向各相位预测误差的统计箱图
Fig. 11 Boxplot of the prediction performance on every phase in the principal direction
图 13 噪声对主方向预测性能的影响
Fig. 13 Influence of noise on the prediction in principal direction
图 14 PCA中的阈值
$\varepsilon $ 对TSSM预测模型的影响Fig. 14 The influence of
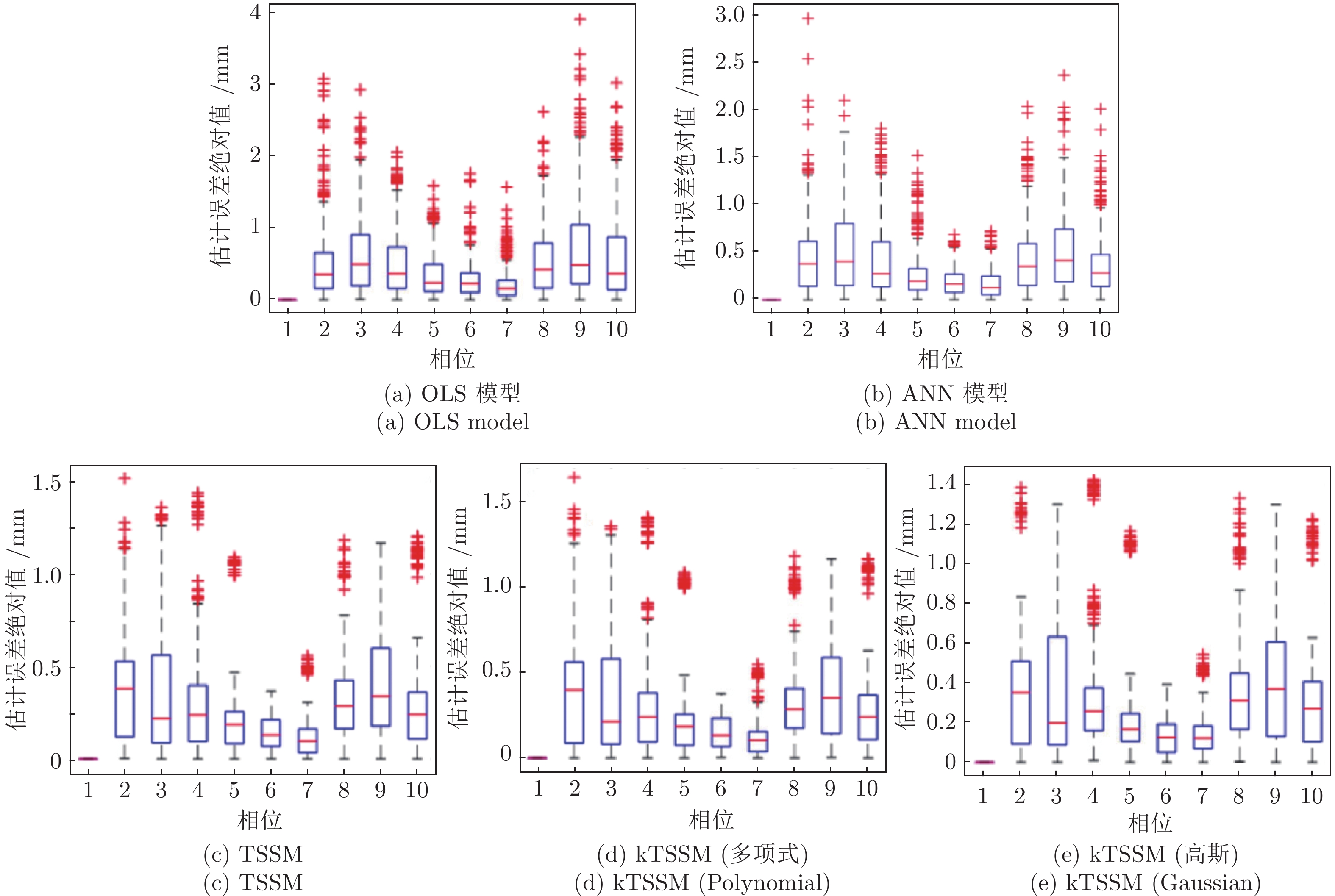
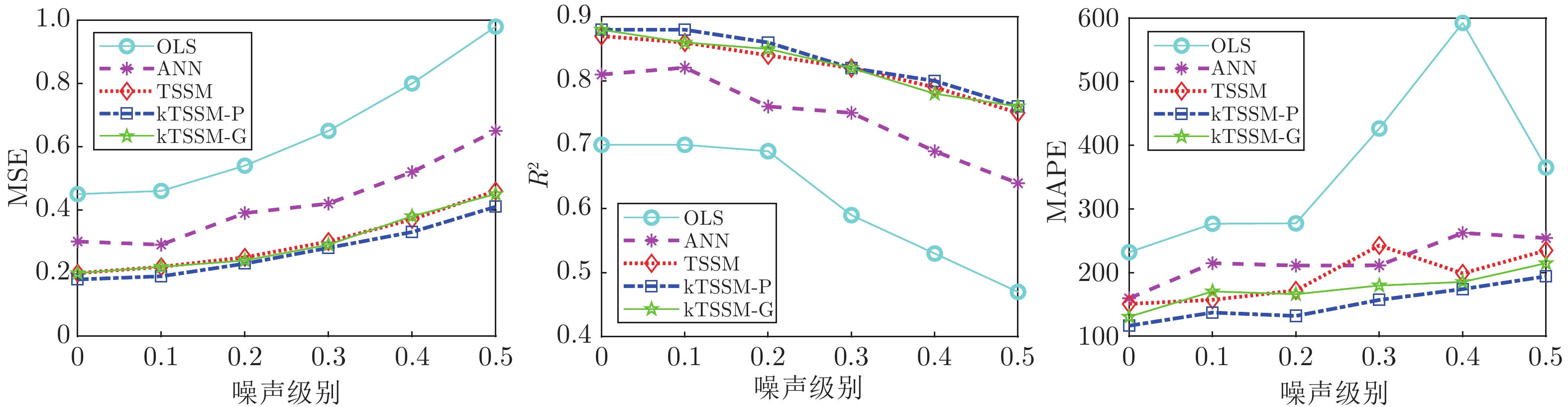
$\varepsilon $ in PCA on the prediction performance of TSSM表 1 在三个方向上的预测结果
Table 1 Prediction results in three directions
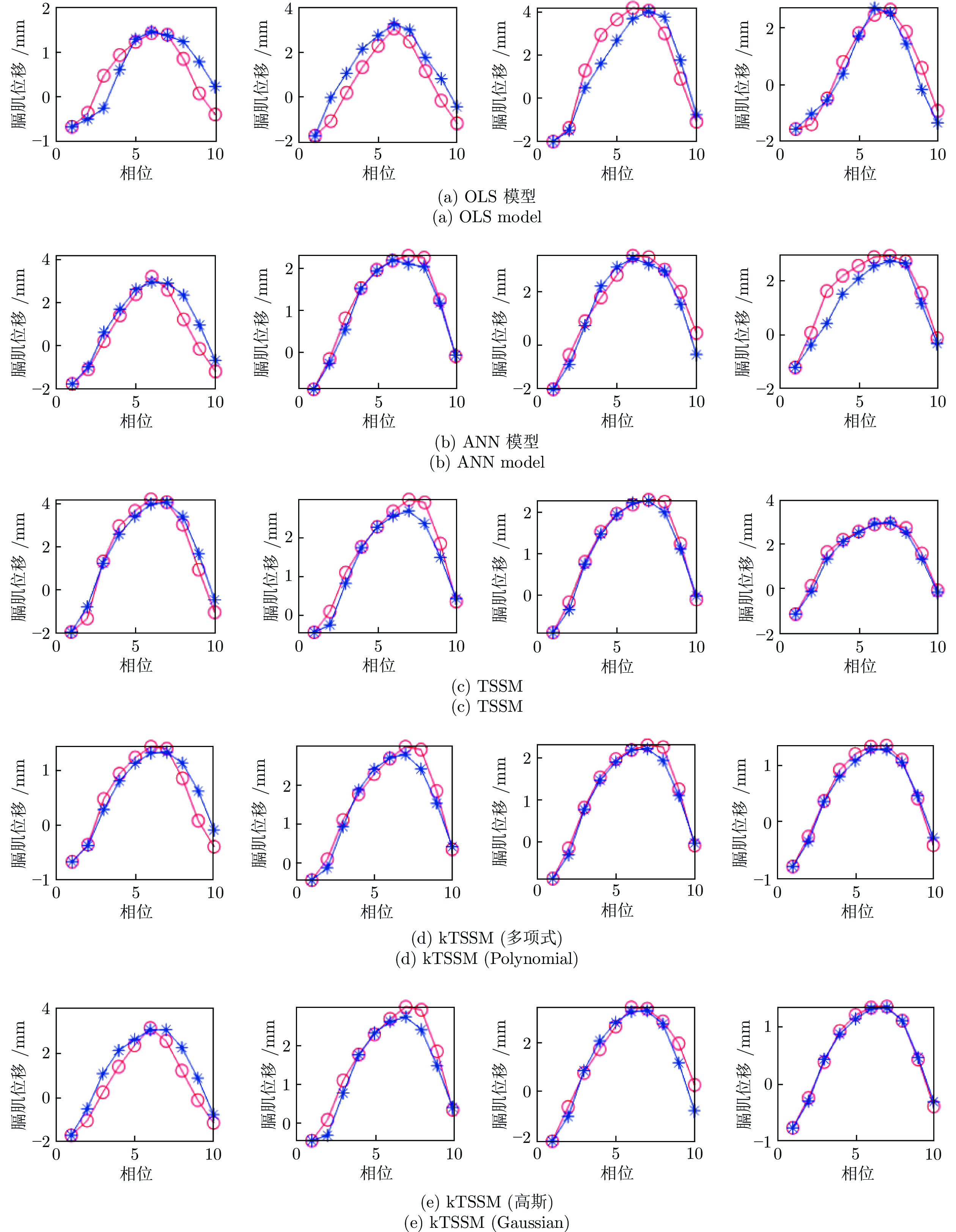
OLS 模型 ANN TSSM (线性) kTSSM (多项式) kTSSM (高斯) 没有噪声 MSE 0.45 (0.23) 0.30 (0.16) 0.20 (0.09) 0.18 (0.08) 0.20 (0.10) R2 0.70 (0.14) 0.81 (0.07) 0.87 (0.05) 0.88 (0.04) 0.88 (0.04) MAPE 232.11 (156.44) 159.60 (112.37) 150.82 (83.98) 116.57 (71.28) 130.69 (87.26) 噪声 ($\sigma =0.1$) MSE 0.46 (0.22) 0.29 (0.15) 0.22 (0.10) 0.19 (0.09) 0.22 (0.09) R2 0.70 (0.15) 0.82 (0.07) 0.86 (0.05) 0.88 (0.04) 0.86 (0.05) MAPE 276.86 (551.10) 214.82 (257.92) 157.28 (117.30) 137.25 (92.36) 170.47 (204.00) 噪声 ($\sigma =0.2$) MSE 0.54 (0.24) 0.39 (0.18) 0.25 (0.11) 0.23 (0.10) 0.24 (0.10) R2 0.69 (0.13) 0.76 (0.10) 0.84 (0.05) 0.86 (0.04) 0.85 (0.06) MAPE 277.42 (348.60) 211.14 (196.70) 172.08 (171.03) 131.98 (78.23) 166.12 (156.08) 噪声 ($\sigma =0.3$) MSE 0.65 (0.25) 0.42 (0.21) 0.30 (0.11) 0.28 (0.11) 0.29 (0.12) R2 0.59 (0.20) 0.75 (0.11) 0.82 (0.05) 0.82 (0.06) 0.82 (0.06) MAPE 426.45 (1371.37) 211.37 (228.00) 242.75 (274.21) 157.12 (94.87) 179.81 (115.10) 噪声 ($\sigma =0.4$) MSE 0.80 (0.28) 0.52 (0.33) 0.37 (0.13) 0.33 (0.13) 0.38 (0.13) R2 0.53 (0.21) 0.69 (0.19) 0.79 (0.07) 0.80 (0.06) 0.78 (0.07) MAPE 592.47 (1687.33) 262.36 (405.00) 198.89 (112.67) 174.14 (116.58) 185.34 (133.87) 噪声 ($\sigma =0.5$) MSE 0.98 (0.33) 0.65 (0.29) 0.46 (0.16) 0.41 (0.15) 0.45 (0.17) R2 0.47 (0.22) 0.64 (0.15) 0.75 (0.08) 0.76 (0.08) 0.76 (0.09) MAPE 365.33 (399.98) 254.35 (291.97) 234.93 (185.28) 194.18 (150.11) 214.82 (260.37) 
下载: 导出CSV
表 2 在主方向上的预测结果
Table 2 Prediction results in principal direction
OLS 模型 ANN TSSM (线性) kTSSM (多项式) kTSSM (高斯) 没有噪声 MSE 0.47 (0.28) 0.27 (0.18) 0.14 (0.07) 0.13 (0.06) 0.15 (0.06) R2 0.73 (0.20) 0.86 (0.08) 0.93 (0.03) 0.93 (0.03) 0.92 (0.03) MAPE 91.07 (38.34) 63.62 (23.72) 47.85 (15.31) 45.17 (14.94) 46.47 (14.39) 噪声 ($\sigma =0.1$) MSE 0.40 (0.26) 0.25 (0.18) 0.15 (0.07) 0.14 (0.06) 0.15 (0.07) R2 0.78 (0.16) 0.86 (0.08) 0.92 (0.04) 0.92 (0.03) 0.91 (0.03) MAPE 143.90 (173.93) 100.38 (136.34) 116.46 (198.17) 68.29 (66.63) 107.08 (145.85) 噪声 ($\sigma =0.2$) MSE 0.43 (0.23) 0.29 (0.12) 0.18 (0.07) 0.17 (0.06) 0.18 (0.07) R2 0.76 (0.14) 0.84 (0.07) 0.90 (0.04) 0.91 (0.04) 0.90 (0.04) MAPE 188.52 (476.86) 138.61 (386.48) 133.32 (129.00) 79.96 (53.09) 82.96 (79.07) 噪声 ($\sigma =0.3$) MSE 0.61 (0.33) 0.38 (0.18) 0.23 (0.10) 0.20 (0.08) 0.24 (0.09) R2 0.64 (0.20) 0.79 (0.11) 0.87 (0.06) 0.87 (0.06) 0.88 (0.05) MAPE 192.18 (223.53) 136.84 (116.74) 134.21 (151.02) 86.07 (64.90) 101.09 (88.78) 噪声 ($\sigma =0.4$) MSE 0.70 (0.31) 0.45 (0.36) 0.30 (0.12) 0.26 (0.09) 0.29 (0.11) R2 0.65 (0.17) 0.77 (0.21) 0.83 (0.07) 0.87 (0.06) 0.85 (0.07) MAPE 221.12 (417.10) 175.31 (342.96) 142.09 (168.43) 94.42 (64.70) 109.11 (116.15) 噪声 ($\sigma =0.5$) MSE 1.01 (0.50) 0.52 (0.28) 0.39 (0.13) 0.32 (0.13) 0.36 (0.14) R2 0.47 (0.35) 0.75 (0.15) 0.80 (0.09) 0.84 (0.07) 0.81 (0.09) MAPE 173.44 (98.15) 193.44 (455.90) 146.14 (212.00) 102.30 (130.34) 116.74 (94.49)
下载: 导出CSV
表 3 TSSM和kTSSM取得最优预测结果时的参数设置
Table 3 Parameter setting of TSSM and kTSSM for optimal results
模型 TSSM (线性) kTSSM (高斯) kTSSM (多项式) 参数 λ λ σkernel λ d c 三个方向的预测 没有噪声 1.0 0.1 0.2 100.0 6.0 9 噪声 ($\sigma =0.1$) 1.0 0.1 0.2 1000.0 3.5 9 噪声 ($\sigma =0.2$) 1.0 0.1 0.1 100.0 2.5 9 噪声 ($\sigma =0.3$) 1.0 0.1 0.1 1.0 0.5 4 噪声 ($\sigma =0.4$) 1.0 0.1 0.1 10.0 1.5 7 噪声 ($\sigma =0.5$) 1.0 1.0 0.1 10.0 1.0 4 主方向的预测 没有噪声 0.1 0.1 0.2 1.0 1.0 5 噪声 ($\sigma =0.1$) 0.1 0.1 0.2 0.1 1.0 7 噪声 ($\sigma =0.2$) 1.0 0.1 0.2 0.1 0.5 4 噪声 ($\sigma =0.3$) 1.0 0.1 0.1 1.0 0.5 3 噪声 ($\sigma =0.4$) 1.0 0.1 0.2 1.0 1.0 4 噪声 ($\sigma =0.5$) 1.0 0.1 0.1 0.1 0.5 7
下载: 导出CSV
-
[1] Malinowski K T, McAvoy T J, George R, Dieterich S, D’Souza W D. Mitigating errors in external respiratory surrogate-based models of tumor position. International Journal of Radiation Oncology* Biology* Physics, 2012, 82(5): e709−e716 [2] Fayad H, Pan T, Roux C, Le Rest C C, Pradier O, Clément J F, et al. A patient specific respiratory model based on 4D CT data and a time of flight camera (TOF). In: Proceedings of the 2009 IEEE Nuclear Science Symposium Conference Record (NSS/MIC). Orlando, USA: IEEE, 2009. 2594−2598 [3] Schwaab J, Prall M, Sarti C, Kaderka R, Bert C, Kurz C, et al. Ultrasound tracking for intra-fractional motion compensation in radiation therapy. Physica Medica: European Journal of Medical Physics, 2014, 30(5): 578−582 doi: 10.1016/j.ejmp.2014.03.003 [4] Ozhasoglu C, Murphy M J. Issues in respiratory motion compensation during external-beam radiotherapy. International Journal of Radiation Oncology* Biology* Physics, 2002, 52(5): 1389−1399 [5] Shimizu S, Shirato H, Kagei K, Nishioka T, Bo X, Dosaka-Akita H, et al. Impact of respiratory movement on the computed tomographic images of small lung tumors in three-dimensional (3D) radiotherapy. International Journal of Radiation Oncology* Biology* Physics, 2000, 46(5): 1127−1133 [6] McClelland J R, Blackall J M, Tarte S, Chandler A C, Hughes S, Ahmad S, et al. A continuous 4D motion model from multiple respiratory cycles for use in lung radiotherapy. Medical Physics, 2006, 33(9): 3348−3358 doi: 10.1118/1.2222079 [7] Torshabi A E, Pella A, Riboldi M, Baroni G. Targeting accuracy in real-time tumor tracking via external surrogates: A comparative study. Technology in Cancer Research & Treatment, 2010, 9(6): 551−561 [8] Paganelli C, Seregni M, Fattori G, Summers P, Bellomi M, Baroni G, et al. Magnetic resonance imaging–guided versus surrogate-based motion tracking in liver radiation therapy: A prospective comparative study. International Journal of Radiation Oncology* Biology* Physics, 2015, 91(4): 840−848 [9] Fayad H, Pan T, Clement J F, Visvikis D. Technical note: Correlation of respiratory motion between external patient surface and internal anatomical landmarks. Medical Physics, 2011, 38(6): 3157−3164 [10] Hanley J, Debois M M, Mah D, Mageras G S, Raben A, Rosenzweig K, et al. Deep inspiration breath-hold technique for lung tumors: The potential value of target immobilization and reduced lung density in dose escalation. International Journal of Radiation Oncology* Biology* Physics, 1999, 45(3): 603−611 [11] Mah D, Hanley J, Rosenzweig K E, Yorke E, Braban L, Ling C C, et al. Technical aspects of the deep inspiration breath-hold technique in the treatment of thoracic cancer. International Journal of Radiation Oncology* Biology* Physics, 2000, 48(4): 1175−1185 [12] Koshani R, Balter J M, Hayman J A, Henning G T, Van Herk M. Short-term and long-term reproducibility of lung tumor position using active breathing control (ABC). International Journal of Radiation Oncology* Biology* Physics, 2006, 65(5): 1553−1559 [13] Lu W G, Ruchala K J, Chen M L, Chen Q, Olivera G H. Real-time respiration monitoring using the radiotherapy treatment beam and four-dimensional computed tomography (4DCT)—a conceptual study. Physics in Medicine & Biology, 2006, 51(18): 4469−4495 [14] Minohara S, Kanai T, Endo M, Noda K, Kanazawa M. Respiratory gated irradiation system for heavy-ion radiotherapy. International Journal of Radiation Oncology* Biology* Physics, 2000, 47(4): 1097−1103 [15] Kubo H D, Hill B C. Respiration gated radiotherapy treatment: A technical study. Physics in Medicine & Biology, 1996, 41(1): 83−91 [16] Seppenwoolde Y, Shirato H, Kitamura K, Shimizu S, Van Herk M, Lebesque J V, et al. Precise and real-time measurement of 3D tumor motion in lung due to breathing and heartbeat, measured during radiotherapy. International Journal of Radiation Oncology* Biology* Physics, 2002, 53(4): 822−834 [17] Shieh C C, Caillet V, Dunbar M, Keall P J, Booth J T, Hardcastle N, et al. A Bayesian approach for three-dimensional markerless tumor tracking using kV imaging during lung radiotherapy. Physics in Medicine & Biology, 2017, 62(8): 3065−3080 [18] Preiswerk F, De Luca V, Arnold P, Celicanin Z, Petrusca L, Tanner C, et al. Model-guided respiratory organ motion prediction of the liver from 2D ultrasound. Medical Image Analysis, 2014, 18(5): 740−751 doi: 10.1016/j.media.2014.03.006 [19] Shimizu S, Shirato H, Ogura S, Akita-Dosaka H, Kitamura K, Nishioka T, et al. Detection of lung tumor movement in real-time tumor-tracking radiotherapy. International Journal of Radiation Oncology* Biology* Physics, 2001, 51(2): 304−310 [20] Vedam S S, Kini V R, Keall P J, Ramakrishnan V, Mostafavi H, Mohan R. Quantifying the predictability of diaphragm motion during respiration with a noninvasive external marker. Medical Physics, 2003, 30(4): 505−513 doi: 10.1118/1.1558675 [21] Berbeco R I, Jiang S B, Sharp G C, Chen G T Y, Mostafavi H, Shirato H. Integrated radiotherapy imaging system (IRIS): design considerations of tumour tracking with linac gantry-mounted diagnostic x-ray systems with flat-panel detectors. Physics in Medicine & Biology, 2004, 49(2): 243−255 [22] Tang X L, Sharp G C, Jiang S B. Fluoroscopic tracking of multiple implanted fiducial markers using multiple object tracking. Physics in Medicine & Biology, 2007, 52(14): 4081−4098 [23] Sharp G C, Jiang S B, Shimizu S, Shirato H. Tracking errors in a prototype real-time tumour tracking system. Physics in Medicine & Biology, 2004, 49(23): 5347−5356 [24] Booth J T, Caillet V, Hardcastle N, O’brien R, Szymura K, Crasta C, et al. The first patient treatment of electromagnetic-guided real time adaptive radiotherapy using MLC tracking for lung SABR. Radiotherapy and Oncology, 2016, 121(1): 19−25 doi: 10.1016/j.radonc.2016.08.025 [25] Kupelian P, Willoughby T, Mahadevan A, Djemil T, Weinstein G, Jani S, et al. Multi-institutional clinical experience with the Calypso System in localization and continuous, real-time monitoring of the prostate gland during external radiotherapy. International Journal of Radiation Oncology* Biology* Physics, 2007, 67(4): 1088−1098 [26] Willoughby T R, Kupelian P A, Pouliot J, Shinohara K, Aubin M, Roach III M, et al. Target localization and real-time tracking using the Calypso 4D localization system in patients with localized prostate cancer. International Journal of Radiation Oncology* Biology* Physics, 2006, 65(2): 528−534 [27] Hoisak J D P, Sixel K E, Tirona R, Cheung P C F, Pignol J P. Correlation of lung tumor motion with external surrogate indicators of respiration. International Journal of Radiation Oncology* Biology* Physics, 2004, 60(4): 1298−1306 [28] Zhang Q H, Pevsner A, Hertanto A, Hu Y C, Rosenzweig K E, Ling C C, et al. A patient-specific respiratory model of anatomical motion for radiation treatment planning. Medical Physics, 2007, 34(12): 4772−4781 doi: 10.1118/1.2804576 [29] Fassi A, Schaerer J, Fernandes M, Riboldi M, Sarrut D, Baroni G. Tumor tracking method based on a deformable 4D CT breathing motion model driven by an external surface surrogate. International Journal of Radiation Oncology* Biology* Physics, 2014, 88(1): 182−188 [30] Vandemeulebroucke J, Kybic J, Clarysse P, Sarrut D. Respiratory motion estimation from cone-beam projections using a prior model. In: Proceedings of the 12th International Conference on Medical Image Computing and Computer-assisted Intervention. London, UK: Springer, 2009. 365−372 [31] Besl P J, McKay N D. A method for registration of 3-D shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239−256 doi: 10.1109/34.121791 [32] Baktashmotlagh M, Harandi M T, Lovell B C, Salzmann M. Unsupervised domain adaptation by domain invariant projection. In: Proceedings of the 2013 IEEE International Conference on Computer Vision. Sydney, Australia: IEEE, 2013. 769−776 [33] Pan S J, Kwok J T, Yang Q. Transfer learning via dimensionality reduction. In: Proceedings of the 23rd AAAI Conference on Artificial Intelligence. Chicago, USA: AAAI, 2008. 677−682 [34] Pan S J, Tsang I W, Kwok J T, Yang Q. Domain adaptation via transfer component analysis. IEEE Transactions on Neural Networks, 2011, 22(2): 199−210 doi: 10.1109/TNN.2010.2091281 -
计量
- 文章访问数: 1262
- HTML全文浏览量: 370
- PDF下载量: 151
- 被引次数: 0
