Distributed Stochastic Variational Inference Based on Diffusion Method
-
摘要:
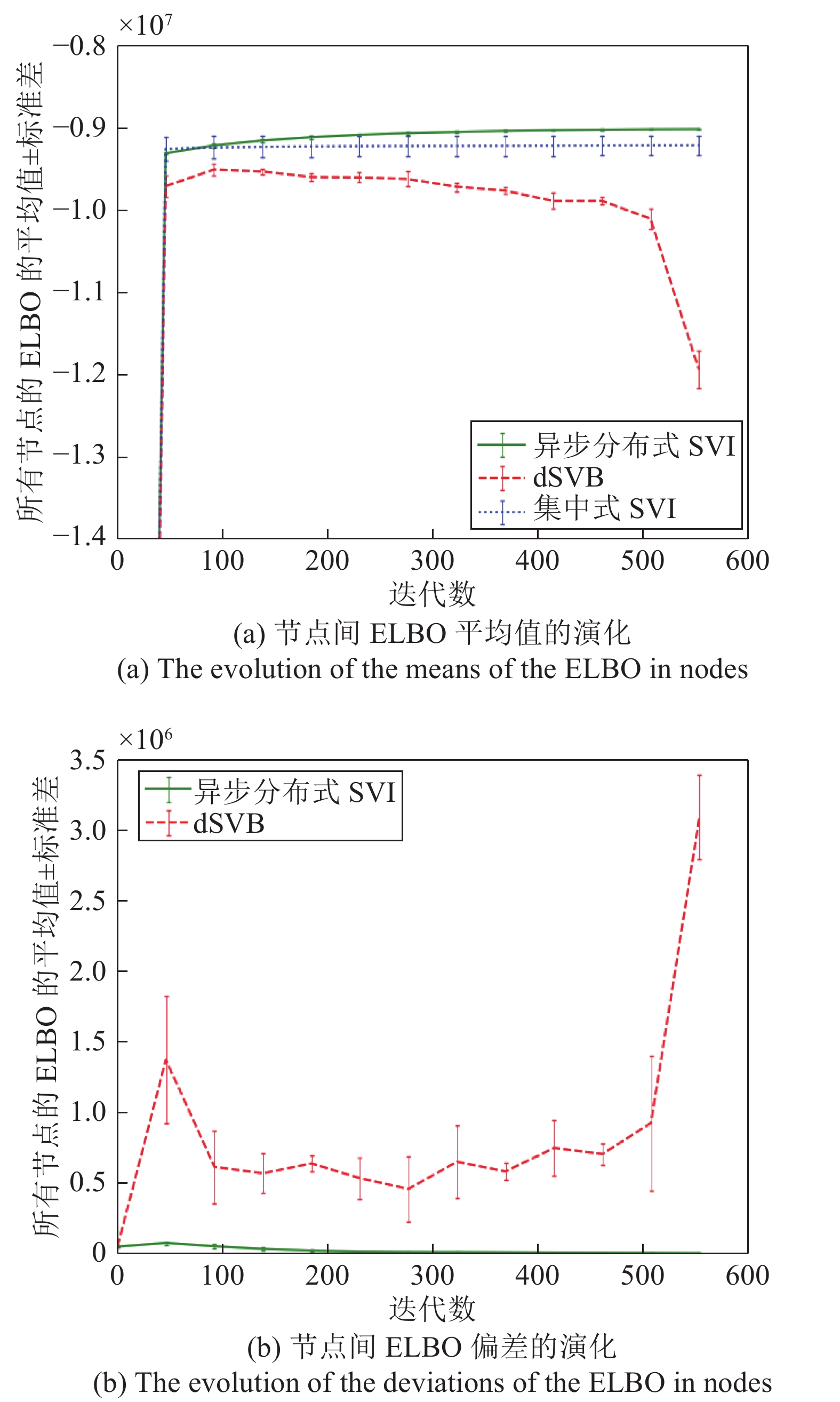
分布式网络上的聚类、估计或推断具有广泛的应用, 因此引起了许多关注. 针对已有的分布式变分贝叶斯(Variational Bayesian, VB)算法效率低, 可扩展性差的问题, 本文借用扩散方法提出了一种新的分布式随机变分推断(Stochastic variational inference, SVI)算法, 其中我们选择自然梯度法进行参数本地更新并选择对称双随机矩阵作为节点间参数融合的系数矩阵. 此外, 我们还为所提出的分布式SVI算法提出了一种对异步网络的适应机制. 最后, 我们在伯努利混合模型(Bernoulli mixture model, BMM)和隐含狄利克雷分布(Latent Dirichlet allocation, LDA)模型上测试所提出的分布式SVI算法的可行性, 实验结果显示其在许多方面的性能优于集中式SVI算法.
Abstract:Clustering, estimation, or inference in distributed networks has received considerable attention due to its broad applications. Considering that existing distributed variational Bayesian (VB) algorithms have the weaknesses of low efficiency and poor scalability, this paper proposes a new distributed stochastic variational inference (SVI) algorithm by borrowing the diffusion method, where the natural gradient method is used for the update of local parameters, and a symmetric and doubly stochastic matrix is applied for the fusion of local parameters. In addition, an adaptation mechanism is introduced in the proposed distributed SVI algorithm for use in asynchronous networks. The feasibility of the proposed distributed SVI algorithm is demonstrated with the Bernoulli mixture model (BMM) and the latent Dirichlet allocation (LDA) model. Experimental results show that the proposed distributed SVI algorithm outperforms the centralized one in many aspects.
-
图 3 异步分布式SVI算法和集中式SVI算法得到的聚类中心
Fig. 3 Cluster centers obtained by the asynchronous distributed SVI and the centralized SVI
图 4 异步分布式SVI算法、dSVB算法、集中式SVI算法的ELBO的平均值和偏差演化
Fig. 4 The evolution of the means and deviations of the ELBO for the asynchronous distributed SVI, the dSVB, and the centralized SVI
图 5 不同
$(\kappa ,\tau )$ 设置下异步分布式SVI和集中式SVI的ELBO的平均值演化Fig. 5 The evolution of the means of the ELBO for the asynchronous distributed SVI and the centralized SVI under different settings of
$(\kappa ,\tau )$ 
图 7 异步分布式SVI、集中式SVI和dSVB在两个数据集上的表现
Fig. 7 Performance of the asynchronous distributed SVI, the centralized SVI, and the dSVB on the two data sets
图 8 异步分布式SVI和集中式SVI在复旦大学中文文本分类数据集上的表现
Fig. 8 Performance of the asynchronous distributed SVI and the centralized SVI on the Chinese text classification data set of Fudan University
图 9 不同超参数设置下异步分布式SVI和集中式SVI在复旦大学中文文本分类数据集上表现
Fig. 9 Performance of the asynchronous distributed SVI and the centralized SVI on the Chinese text classification data set of Fudan University under different hyperparameter settings
表 1 LDA模型变量
Table 1 Variables in LDA model
变量 $\alpha $ $\eta $ $K$ $D$ $N$ ${\theta _d}$ ${y_{d,n}}$ ${w_{d,n}}$ ${\beta _k}$ 类型 固定参数 固定参数 固定参数 输入参数 输入参数 局部隐藏变量 局部隐藏变量 单词向量 全局隐藏变量 描述> 主题数 文档数 单词数 决定文档的主题分布 单词所属的主题 决定主题的单词分布 分布 $Dir({\theta _d}|\alpha )$ $Mult({y_{d,n}}|{\theta _d})$ $Mult({w_{d,n}}|{\beta _k},{y_{d,n}})$ $Dir({\beta _k}|\eta )$ 
下载: 导出CSV
表 2 不同参数设置下异步分布式SVI和集中式SVI收敛的值
Table 2 The convergent values of the asynchronous distributed SVI and the centralized SVI under different parameter settings
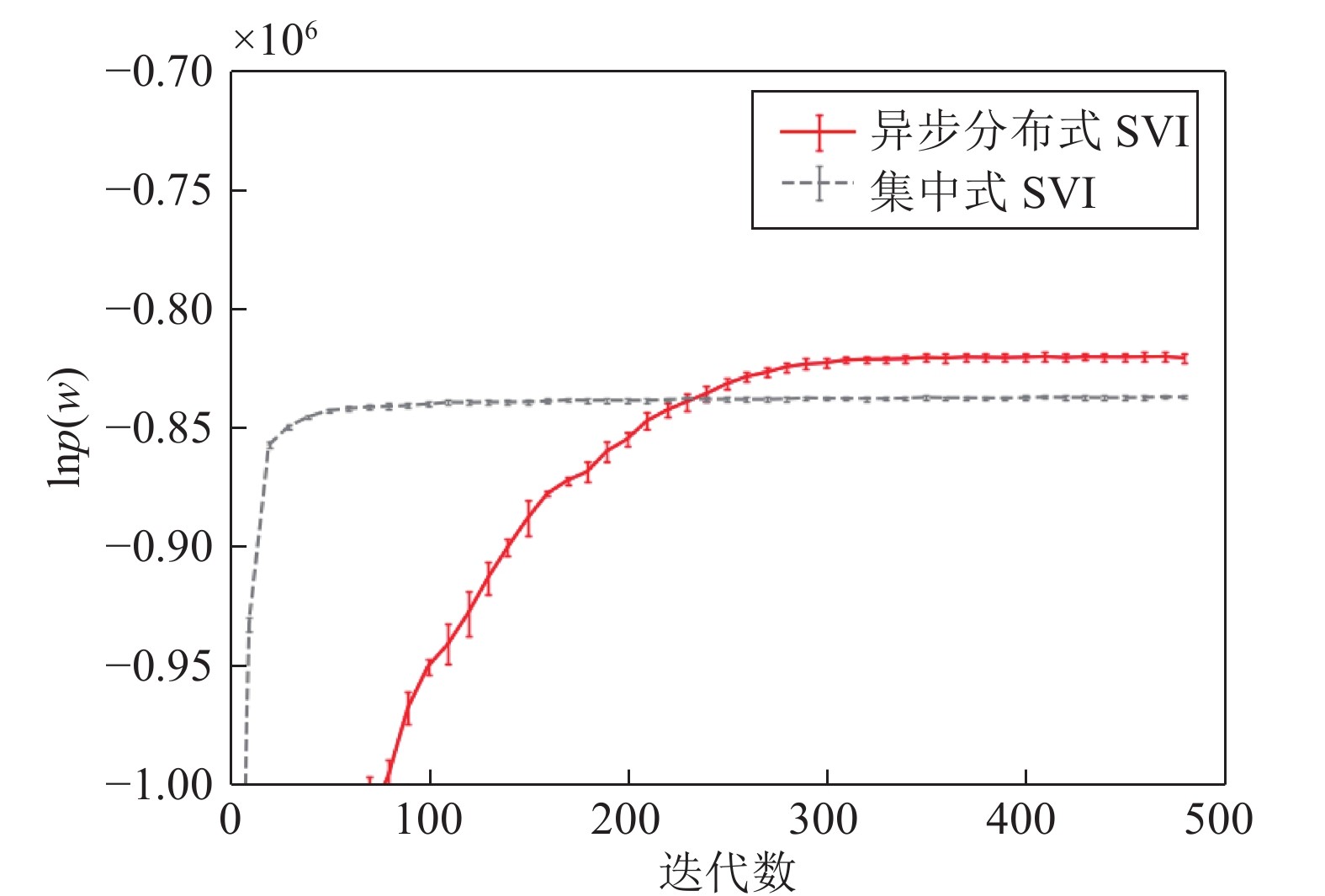
参数设置 $\begin{gathered} \alpha = \eta = 0.4 \\ \kappa = 0.5,\tau = 1 \\ \end{gathered} $ $\begin{gathered} \alpha = \eta = 0.8 \\ \kappa = 0.5,\tau = 1 \\ \end{gathered} $ $\begin{gathered} \alpha = \eta = 0.4 \\ \kappa = 0.7,\tau = 10 \\ \end{gathered} $ $\begin{gathered} \alpha = \eta = 0.8 \\ \kappa = 0.7,\tau = 10 \\ \end{gathered} $ $\begin{gathered} \alpha = \eta = 0.4 \\ \kappa = 1,\tau = 100 \\ \end{gathered} $ $\begin{gathered} \alpha = \eta = 0.8 \\ \kappa = 1,\tau = 100 \\ \end{gathered} $ 异步分布式SVI —53791.33 —55554.12 —54350.50 —56212.30 —57003.45 —57567.67 集中式SVI —54198.30 —56327.50 —54776.18 —56721.87 —57805.78 —58191.39
下载: 导出CSV
表 3 超参数取值表
Table 3 The values of hyperparameters
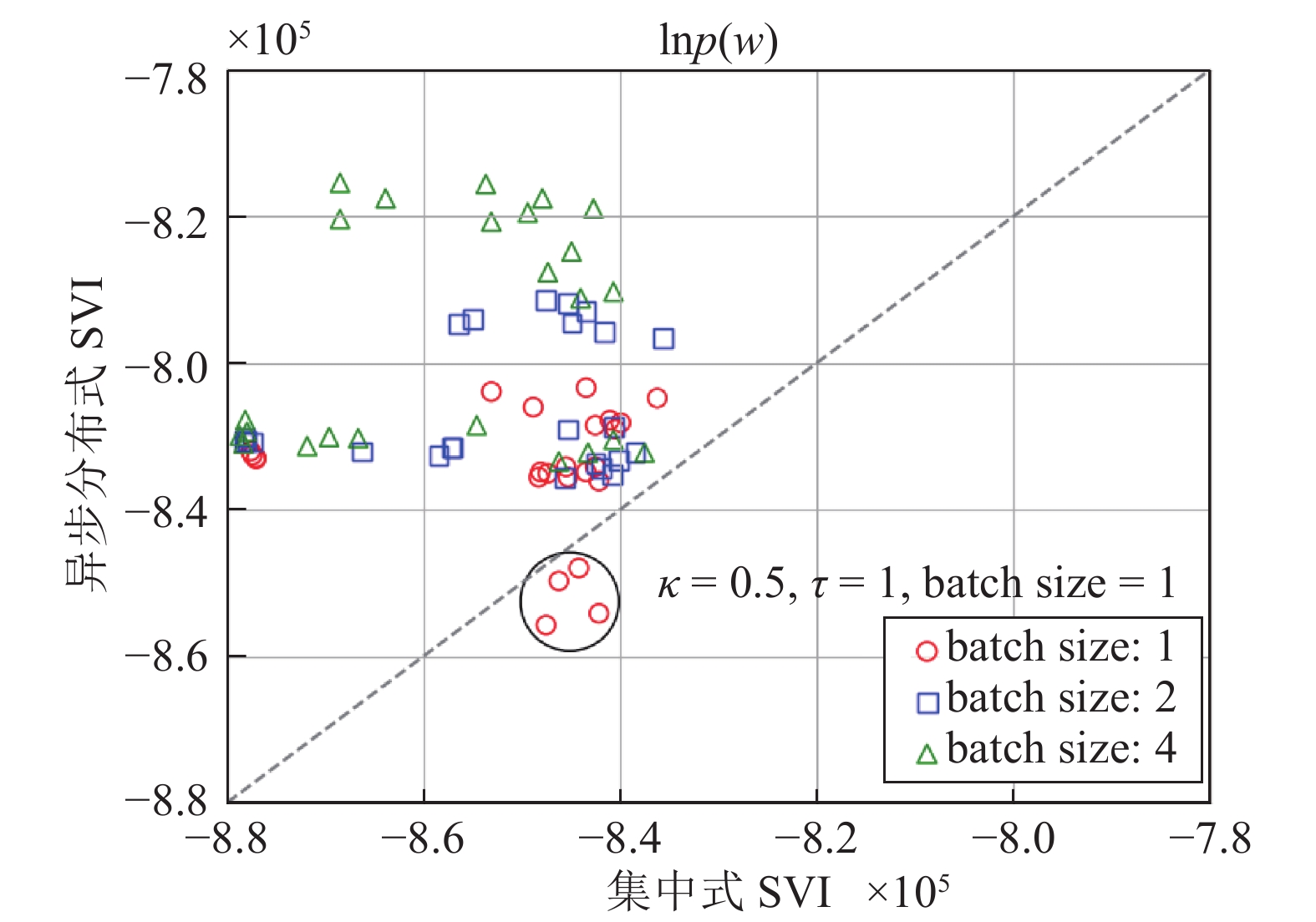
$\kappa $ $\tau $ batch size $\alpha $ $\eta $ 0.5 1 1 0.1 0.1 1.0 10 2 0.2 0.2 — 100 4 — —
下载: 导出CSV
-
[1] Qin J, Fu W, Gao H, Zheng W X. Distributed k-means algorithm and fuzzy c-means algorithm for sensor networks based on multiagent consensus theory. IEEE Transactions on Cybernetics, 2016, 47(3): 772−783 [2] 牛建军, 邓志东, 李超. 无线传感器网络分布式调度方法研究. 自动化学报, 2011, 37(5): 517−528Niu Jian-Jun, Deng Zhi-Dong, Li Chao. Distributed scheduling approaches in wireless sensor network. Acta Automatica Sinica, 2011, 37(5): 517−528 [3] Hua J, Li C. Distributed variational Bayesian algorithms over sensor networks. IEEE Transactions on Signal Processing, 2015, 64(3): 783−798 [4] Corbett J C, Jeffrey D, Michael E, et al. Spanner: Google's globally distributed database. ACM Transactions on Computer Systems, 2013, 31(3): 1−22 doi: 10.1145/2491464 [5] Mehmood A, Natgunanathan I, Xiang Y, Hua G, Guo S. Protection of big data privacy. IEEE Access, 2016, 4: 1821−1834 doi: 10.1109/ACCESS.2016.2558446 [6] Liu S, Pan S J, Ho Q. Distributed multi-task relationship learning. In: Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, Canada, 2017. 937−946 [7] Wang S, Li C. Distributed robust optimization in networked system. IEEE Transactions on Cybernetics, 2016, 47(8): 2321−2333 [8] Hong M, Hajinezhad D, Zhao M M. Prox-PDA: The proximal primal-dual algorithm for fast distributed nonconvex optimization and learning over networks. In: Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 2017. 1529−1538 [9] Scardapane S, Fierimonte R, Di Lorenzo P, Panella M, Uncini A. Distributed semi-supervised support vector machines. Neural Networks, 2016, 80: 43−52 doi: 10.1016/j.neunet.2016.04.007 [10] Aybat N S, Hamedani E Y. A primal-dual method for conic constrained distributed optimization problems. In: Proceedings of Advances in Neural Information Processing Systems, Barcelona, Spain, 2016. 5049−5057 [11] Anwar H, Zhu Q. ADMM-based networked stochastic variational inference [Online], available: https://arxiv.org/abs/1802.10168v1, February 27, 2018. [12] Qin J, Zhu Y, Fu W. Distributed clustering algorithm in sensor networks via normalized information measures. IEEE Transactions on Signal Processing, 2020, 68: 3266−3279 doi: 10.1109/TSP.2020.2995506 [13] 曲寒冰, 陈曦, 王松涛, 于明. 基于变分贝叶斯逼近的前向仿射变换点集匹配方法研究. 自动化学报, 2015, 41(8): 1482−1494 doi: 10.1016/S1874-1029(15)30001-XQu Han-Bing, Chen Xi, Wang Song-Tao, Yu Ming. Forward affine point set matching under variational Bayesian framework. Acta Automatica Sinica, 2015, 41(8): 1482−1494 doi: 10.1016/S1874-1029(15)30001-X [14] Blei D M, Ng A Y, Jordan M I. Latent dirichlet allocation. Journal of Machine Learning Research, 2003, 3(Jan): 993−1022 [15] Hoffman M D, Blei D M, Wang C, Paisley J. Stochastic variational inference. The Journal of Machine Learning Research, 2013, 14(1): 1303−1347 [16] Corduneanu A, Bishop C M. Variational Bayesian model selection for mixture distributions. In: Proceedings of Artificial intelligence and Statistics, Waltham, MA: Morgan Kaufmann, 2001. 27−34 [17] Letham B, Letham L M, Rudin C. Bayesian inference of arrival rate and substitution behavior from sales transaction data with stockouts. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, USA, 2016. 1695−1704 [18] Safarinejadian B, Menhaj M B. Distributed density estimation in sensor networks based on variational approximations. International Journal of Systems Science, 2011, 42(9): 1445−1457 doi: 10.1080/00207721.2011.565380 [19] Safarinejadian B, Estahbanati M E. A novel distributed variational approximation method for density estimation in sensor networks. Measurement, 2016, 89: 78−86 doi: 10.1016/j.measurement.2016.03.074 [20] Mozaffari M, Safarinejadian B. Mobile-agent-based distributed variational Bayesian algorithm for density estimation in sensor networks. IET Science, Measurement and Technology, 2017, 11(7): 861−870 doi: 10.1049/iet-smt.2016.0260 [21] 张宇, 包研科, 邵良杉, 刘威. 面向分布式数据流大数据分类的多变量决策树. 自动化学报, 2018, 44(6): 1115−1127Zhang Yu, Bao Yan-Ke, Shao Liang-Shan, Liu Wei. A multivariate decision tree for big data classification of distributed data streams. Acta Automatica Sinica, 2018, 44(6): 1115−1127 [22] Mohamad S, Bouchachia A, Sayed-Mouchaweh M. Asynchronous stochastic variational inference. In: Proceedings of INNS Big Data and Deep Learning Conference, Sestri Levante, Italy: Springer, 2019. 296−308 [23] Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine learning, 2010, 3(1): 1−122 doi: 10.1561/2200000016 [24] Chen J, Sayed A H. Diffusion adaptation strategies for distributed optimization and learning over networks. IEEE Transactions on Signal Processing, 2012, 60(8): 4289−4305 doi: 10.1109/TSP.2012.2198470 [25] Wainwright M J, Jordan M I. Graphical models, exponential families, and variational inference. Foundations and Trends in Machine Learning, 2008, 1(1−2): 1−305 [26] Wright S J. Coordinate descent algorithms. Mathematical Programming, 2015, 151(1): 3−3 doi: 10.1007/s10107-015-0892-3 -
计量
- 文章访问数: 1101
- HTML全文浏览量: 539
- PDF下载量: 249
- 被引次数: 0
