基于加权矩阵的多维广义特征值并行分解算法

高迎彬; 徐中英

doi:10.16383/j.aas.c200399

基于加权矩阵的多维广义特征值并行分解算法

doi: 10.16383/j.aas.c200399 cstr: 32138.14.j.aas.c200399

高迎彬^{1, 2},
徐中英^1,

1.
火箭军工程大学导弹工程学院西安 710025
2.
中国电子科技集团公司第五十四研究所石家庄 050081

基金项目: 国家自然科学基金(62106242, 62273354)资助

详细信息

作者简介:
高迎彬：中国电子科技集团公司第五十四研究所高级工程师. 主要研究方向为自适应信号处理和神经网络. E-mail: welcome8793@sina.com

徐中英：火箭军工程大学副教授. 主要研究方向为统计信号处理和系统建模. 本文通信作者. E-mail: xuzhy1978@163.com

计量
- 文章访问数: 1277
- HTML全文浏览量: 463
- PDF下载量: 172
- 被引次数: 0
出版历程
- 收稿日期: 2020-06-10
- 修回日期: 2020-09-26
- 网络出版日期: 2020-12-17
- 刊出日期: 2023-12-27

Multiple Generalized Eigenvalue Decomposition Algorithm in Parallel Based on Weighted Matrix

GAO Ying-Bin^{1, 2},
XU Zhong-Ying^1
,

1.
College of Missile Engineering, the Rocket Force University of Engineering, Xi＇an 710025
2.
The 54th Research Institute, China Electronics Technology Group Corporation, Shijiazhuang 050081

Funds: Supported by National Natural Science Foundation of China (62106242, 62273354)

More Information

Author Bio:
GAO Ying-Bin　Senior engineer at the 54th Research Institute, China Electronics Technology Group Corporation. His research interest covers adaptive signal processing and neural networks

XU Zhong-Ying　Associate professor at the Rocket Force University of Engineering. His research interest covers statistical signal processing and system modeling. Corresponding author of this paper

摘要

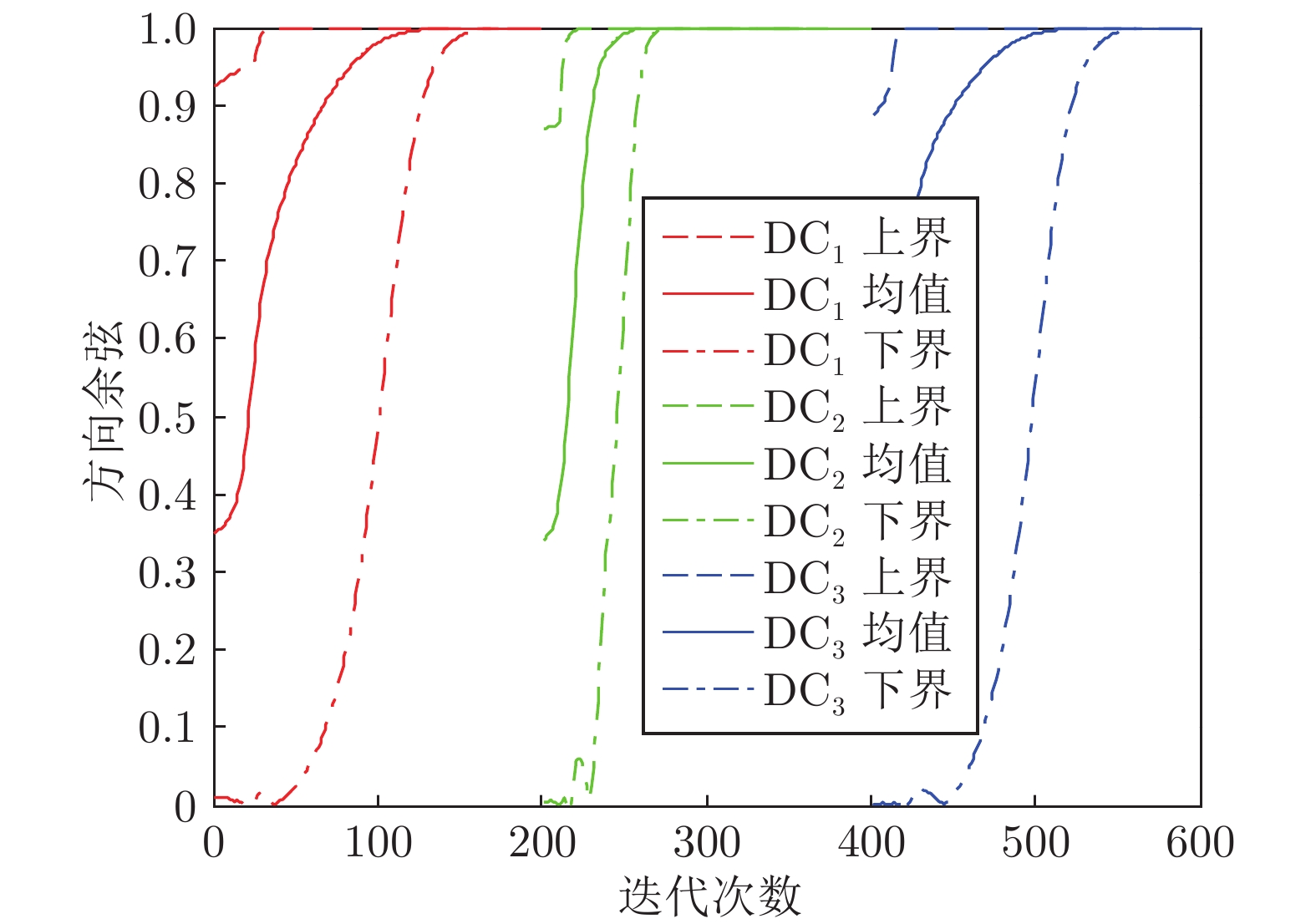
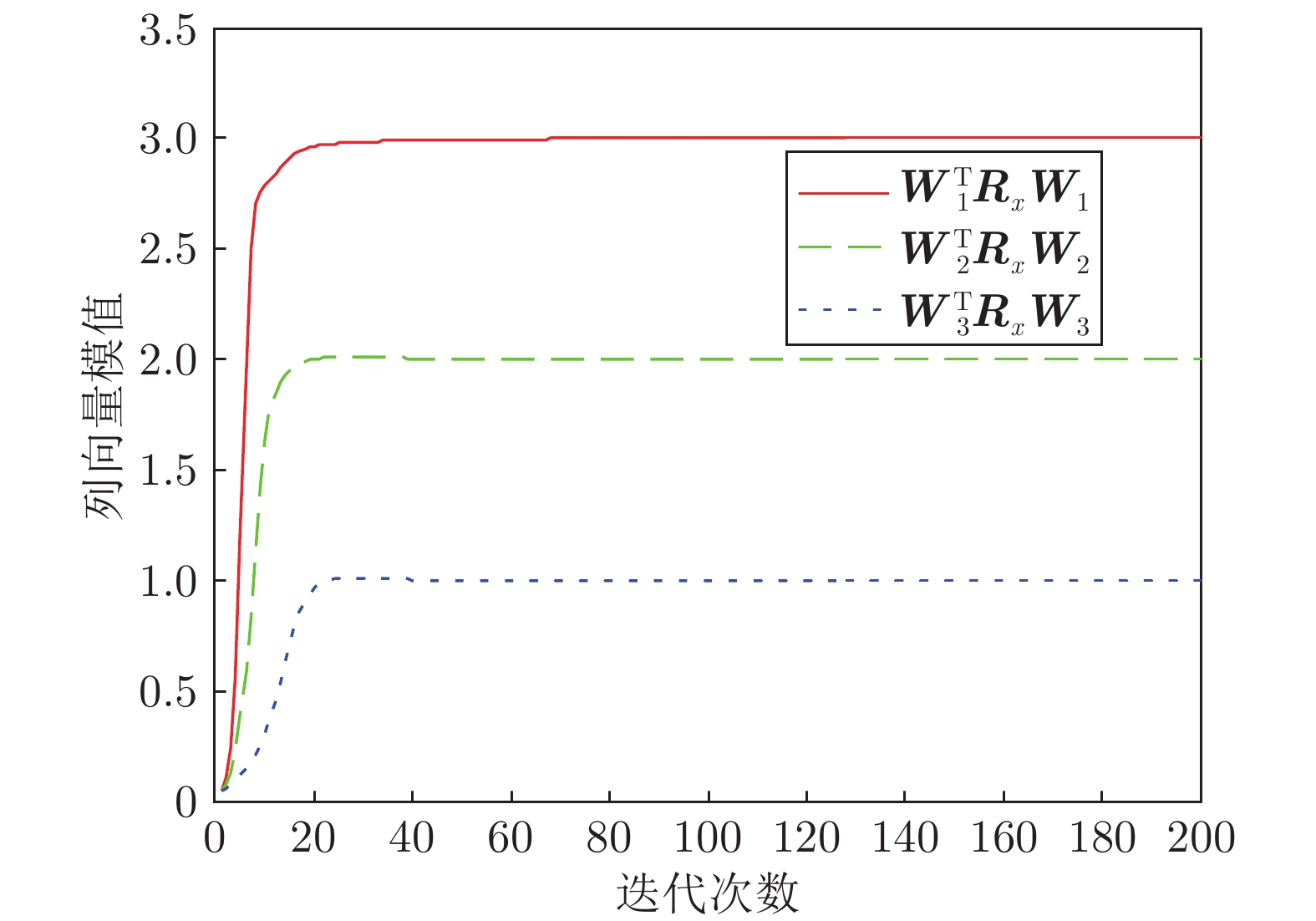
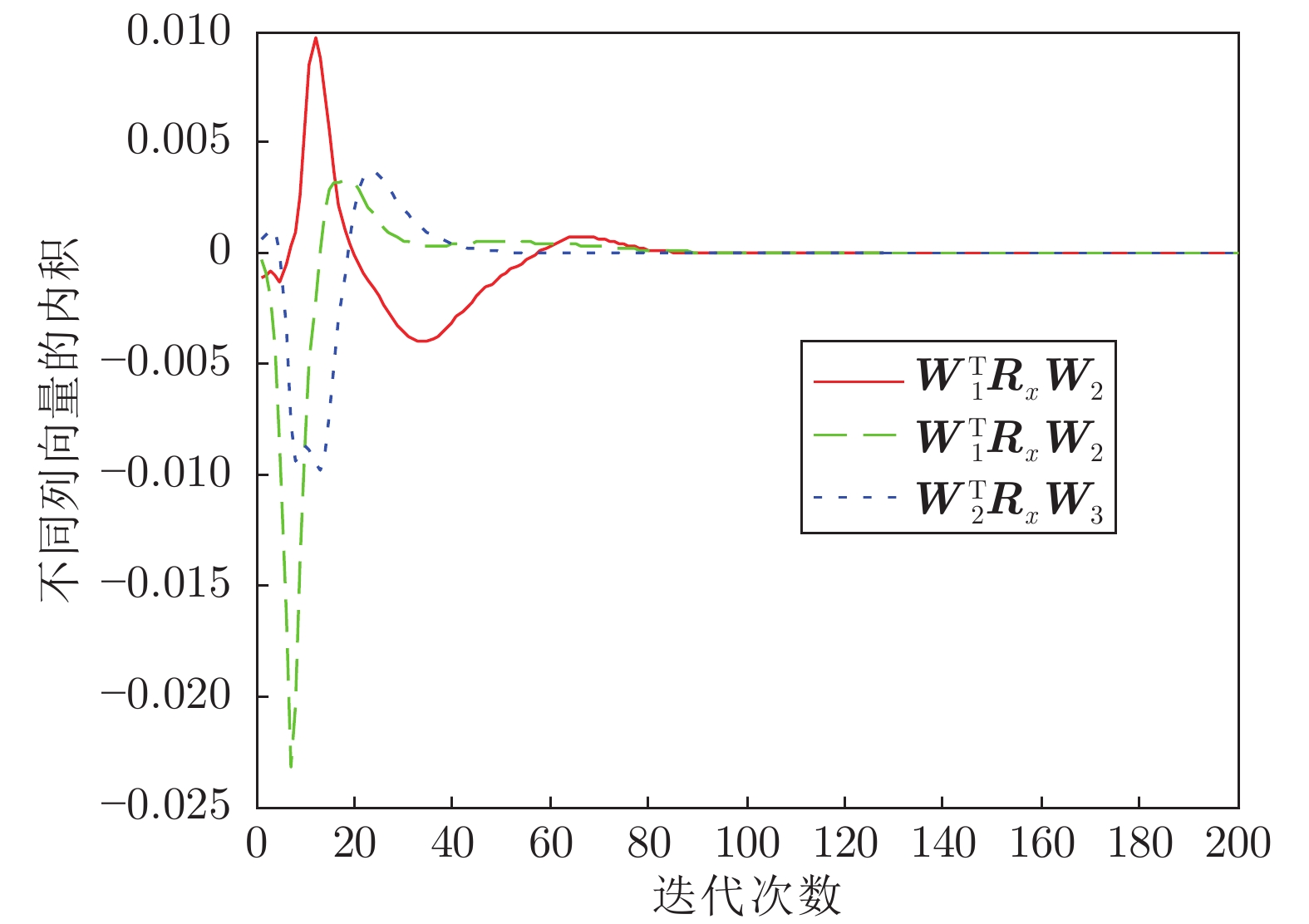
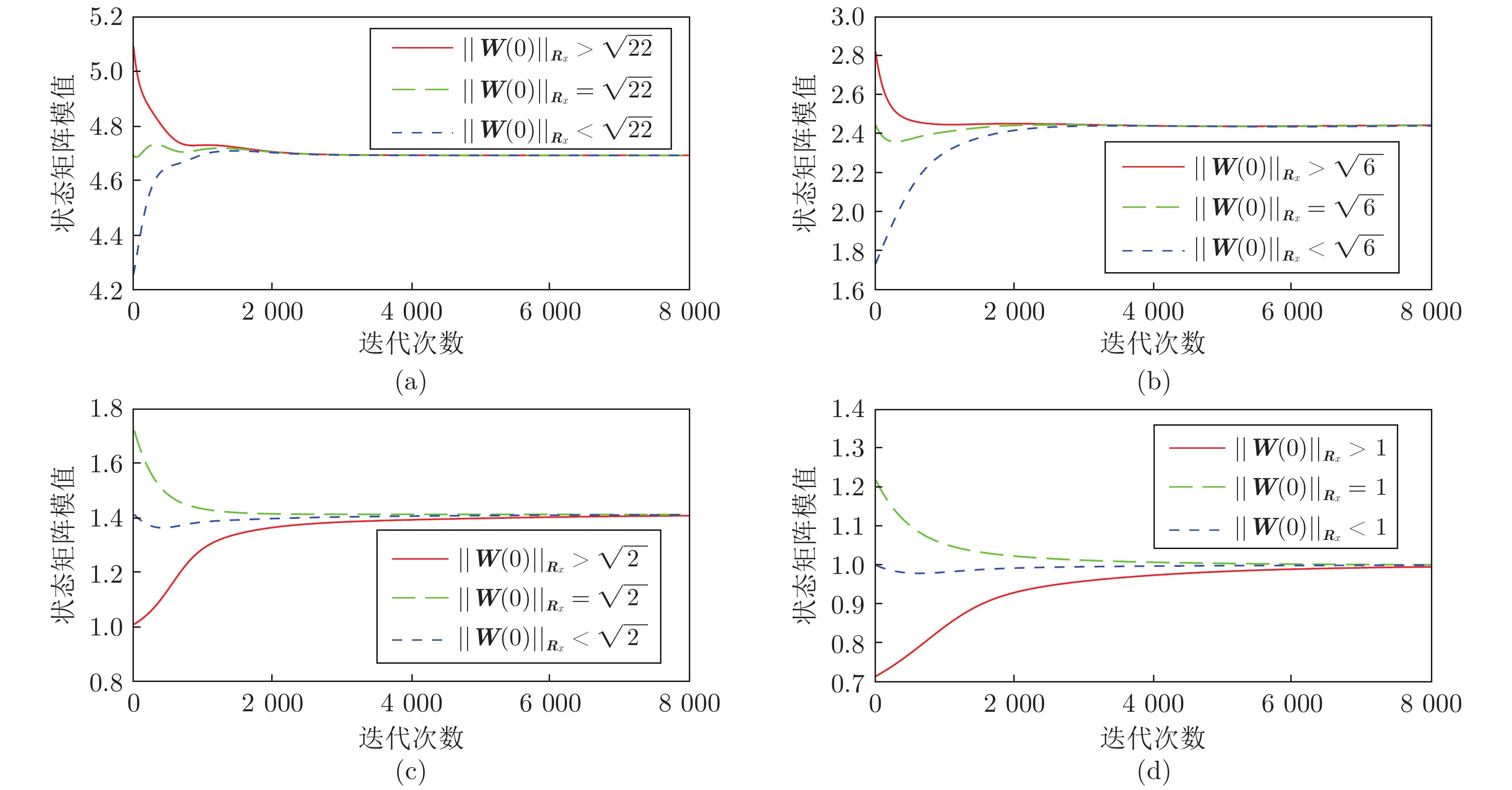
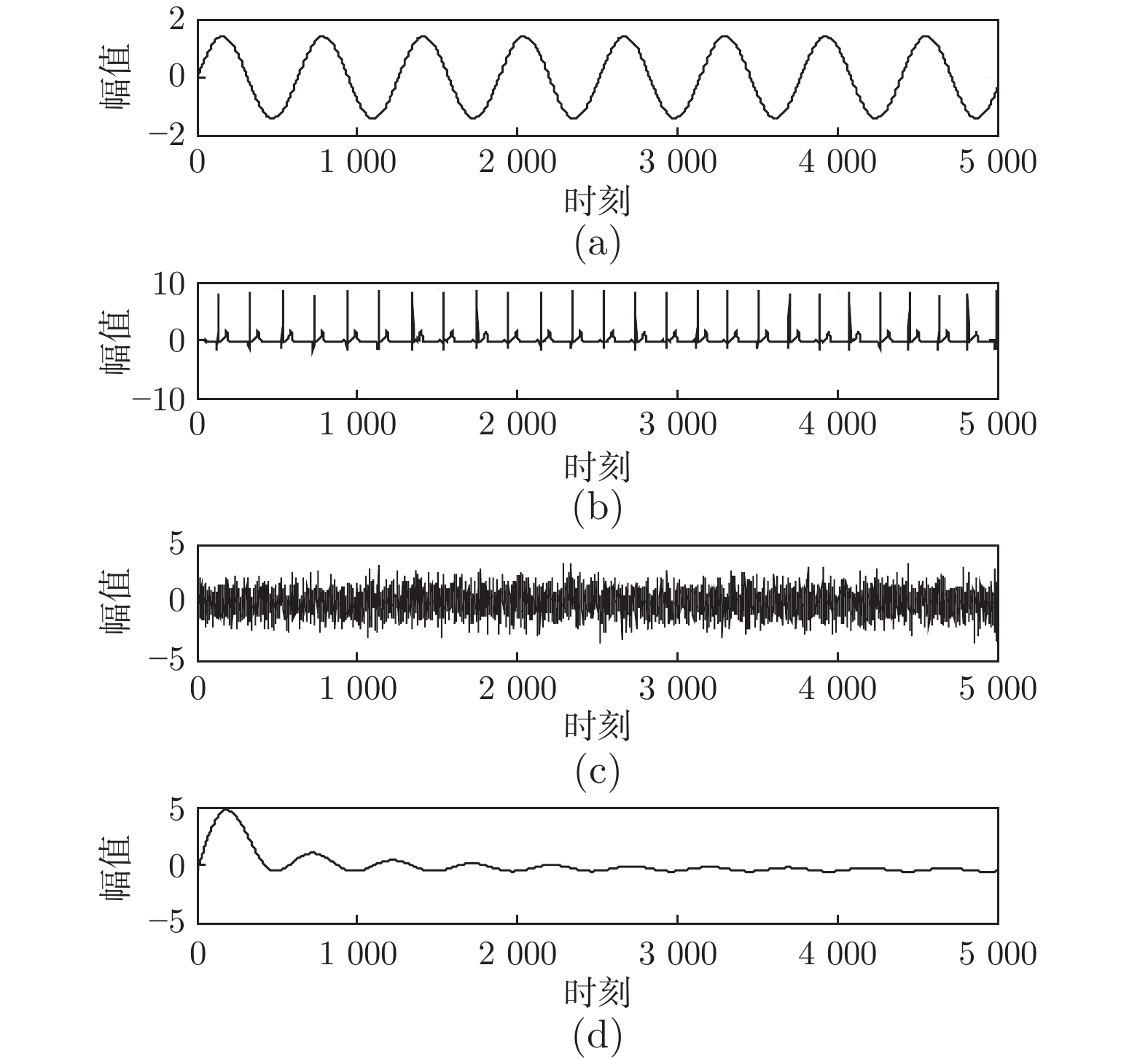
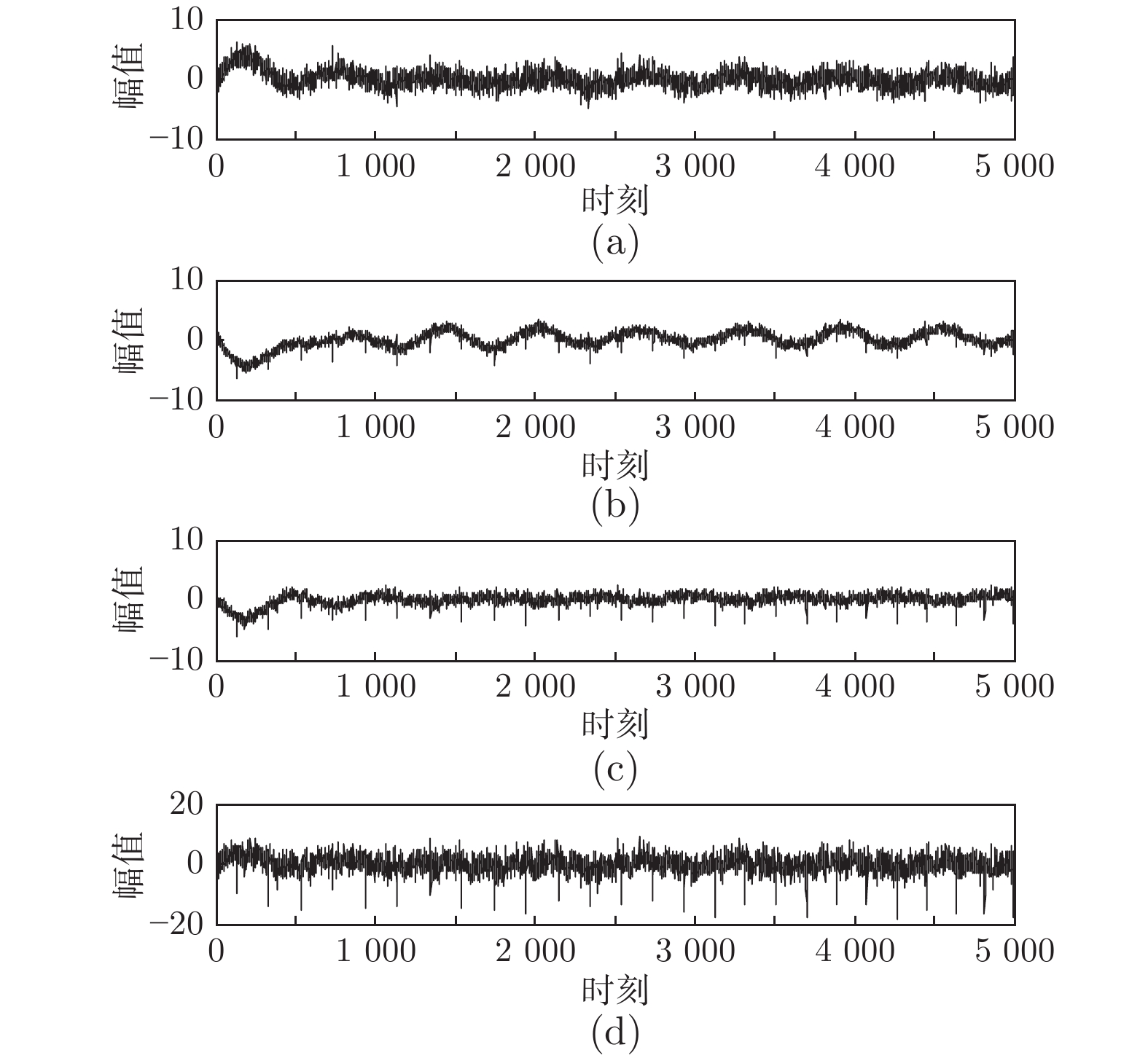
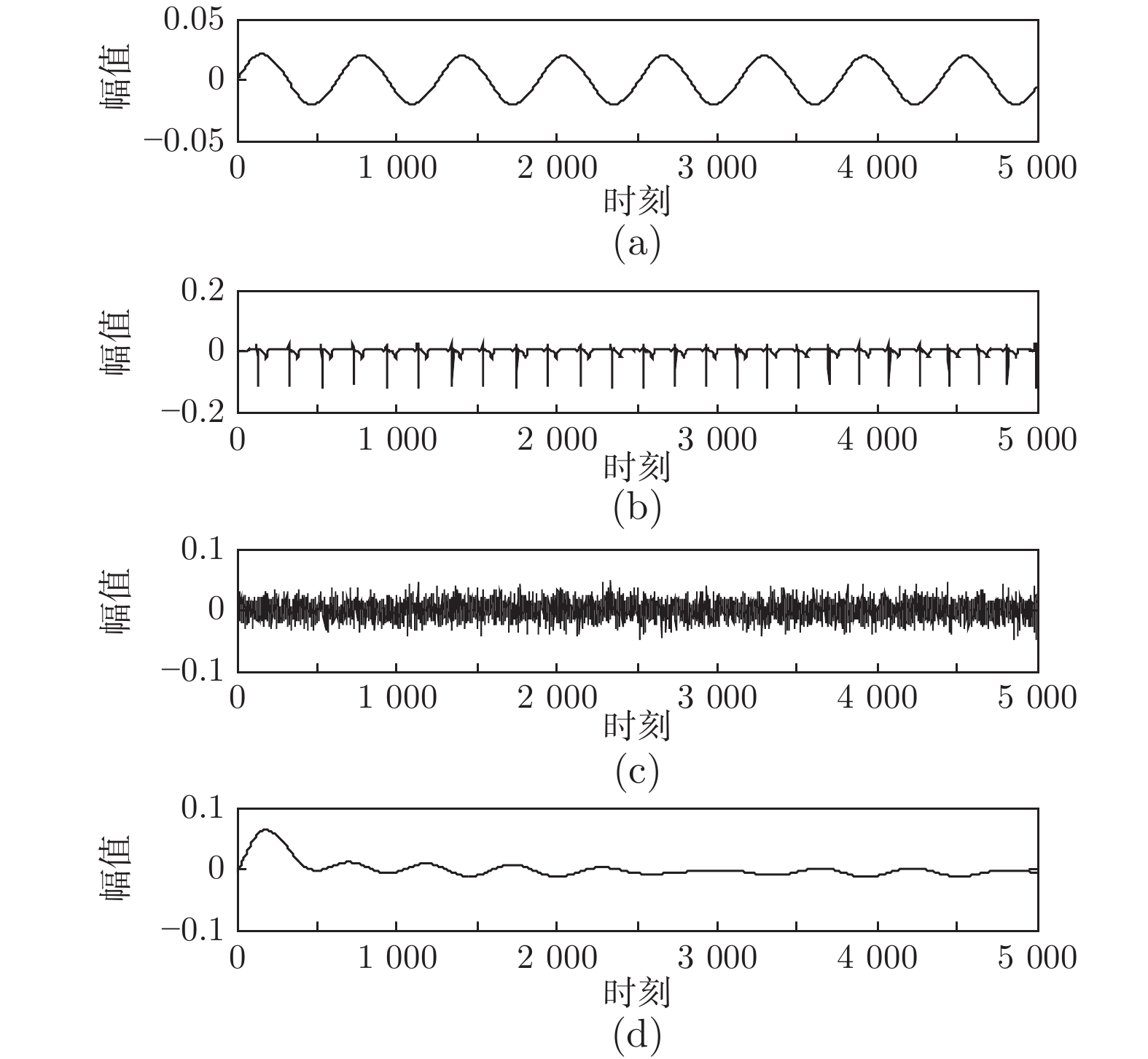
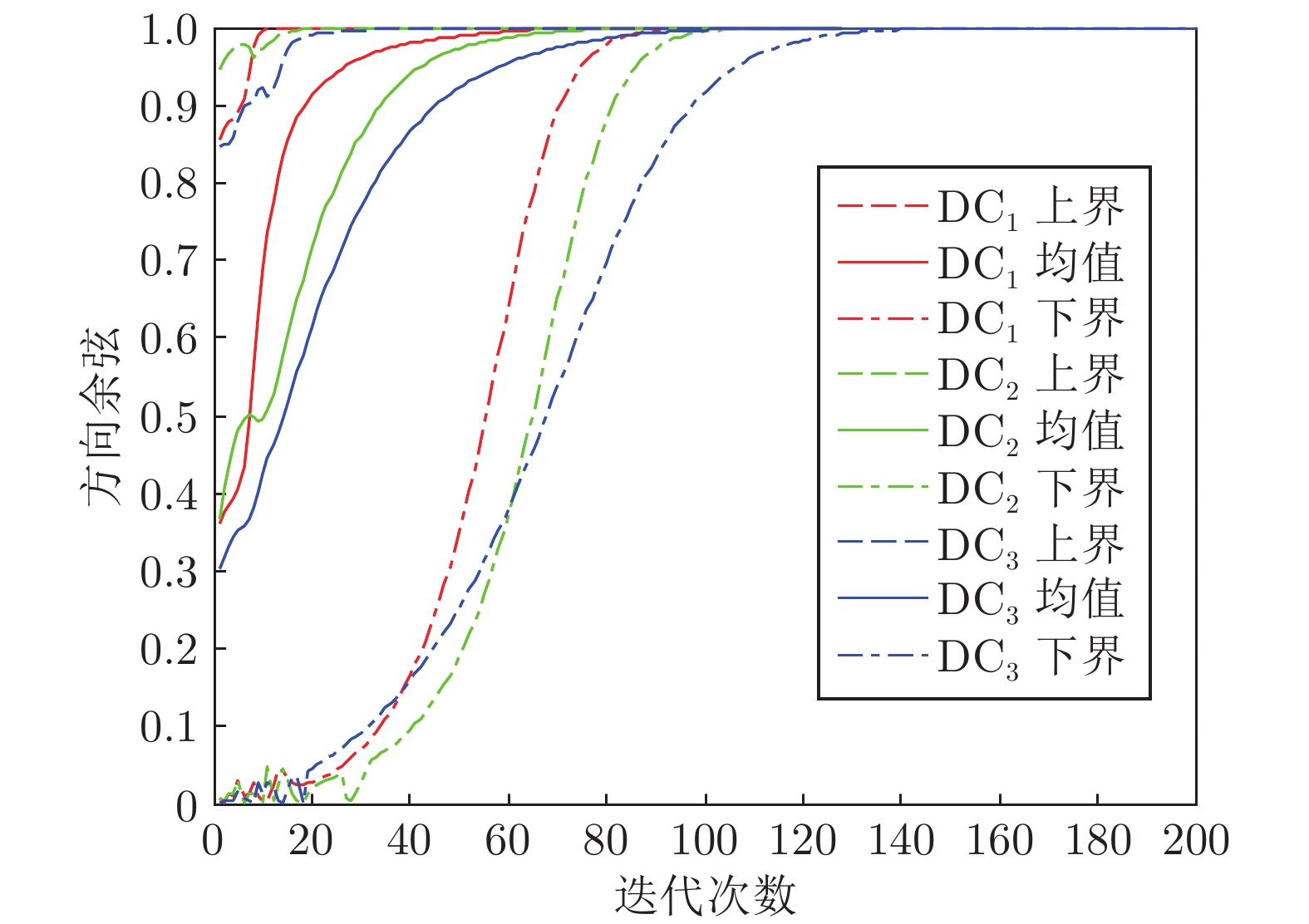
摘要: 针对串行广义特征值分解算法实时性差的缺点, 提出基于加权矩阵的多维广义特征值分解算法. 与串行算法不同, 所提算法能够在一次迭代过程中并行地估计出多维广义特征向量. 平稳点分析表明: 当且仅当算法中状态矩阵等于所需的广义特征向量时, 算法达到收敛状态. 通过对比相邻时刻的状态矩阵模值证明了所提算法的自稳定特性. 所提算法参数选取简单, 实际实施较为容易. 数值仿真和实例应用进一步验证了算法的并行性、自稳定性和实用性.
- 广义特征值分解 /
- 加权矩阵 /
- 并行分解 /
- 多维估计
Abstract: In order to overcome the disadvantages of sequential algorithms, such as poor real time, a multiple generalized eigenvalue decomposition algorithm is proposed based on weighted matrix method. Unlike sequential algorithms, the proposed algorithm is able to estimate multiple generalized eigenvectors in parallel only through one iteration procedure. The stationary point analysis shows that the algorithm reaches convergence state if and only if the state matrix is equal to the desired generalized eigenvectors. The self-stabilization characteristics of the proposed algorithm is proved by comparing the state matrix module values of adjacent moments. The proposed algorithm parameters are simple to select and easy to implement in practice. Numerical simulation and example application further verify the parallelism, self-stability and practicality of the algorithm.
- Generalized eigenvalue decomposition /
- weighted matrix /
- parallel decomposition /
- multiple estimation

HTML全文

图 1 所提算法方向余弦曲线

Fig. 1 The DC curves of the proposed algorithm

下载: 全尺寸图片幻灯片

图 2 GDM算法方向余弦曲线

Fig. 2 The DC curves of the GDM algorithm

下载: 全尺寸图片幻灯片

图 3 列向量模值曲线

Fig. 3 The norm curves of the column vectors

下载: 全尺寸图片幻灯片

图 4 不同列向量内积关系曲线

Fig. 4 The inner product curves of different column vectors

下载: 全尺寸图片幻灯片

图 5 不同对角矩阵下状态矩阵模值曲线

Fig. 5 The norm curves of the state matrix with different diagonal matrices

下载: 全尺寸图片幻灯片

图 6 源信号波形

Fig. 6 The waveform of source signals

下载: 全尺寸图片幻灯片

图 7 观测信号曲线

Fig. 7 The waveform of observed signals

下载: 全尺寸图片幻灯片

图 8 分离信号曲线

Fig. 8 The waveform of separated signals

下载: 全尺寸图片幻灯片

表 1 两种算法的计算时间

Table 1 The time cost of the two algorithms

算法时间 (ms)

所提算法 2.16
GDM算法 14.61

下载: 导出CSV

参考文献(20)

[1]	Kong X Y, Du B Y, Feng X W, Luo J Y. Unified and self-stabilized parallel algorithm for multiple generalized eigenpairs extraction. IEEE Transactions on Signal Processing, 2020, 68: 3644-3659. doi: 10.1109/TSP.2020.2997803
[2]	Rippl M, Lang B, Huckle T. Parallel eigenvalue computation for banded generalized eigenvalue problems. Parallel Computing, 2019, 88: 102542. doi: 10.1016/j.parco.2019.07.002
[3]	Sun S L, Xie X J, Dong C. Multiview learning with generalized eigenvalue proximal support vector machines. IEEE Transactions on Cybernetics, 2019, 49(2): 688-697. doi: 10.1109/TCYB.2017.2786719
[4]	Miyata T. A Riccati-type algorithm for solving generalized Hermitian eigenvalue problems. The Journal of Supercomputing, 2021, 77(2): 2091-2102. doi: 10.1007/s11227-020-03331-w
[5]	郭亚宁, 林伟, 潘泉, 赵春晖, 胡劲文, 马娟娟. 基于推广流形学习的高分辨遥感影像目标分类. 自动化学报, 2019, 45(4): 720-729 doi: 10.16383/j.aas.2017.c170318 Guo Ya-Ning, Lin Wei, Pan Quan, Zhao Chun-Hui, Hu Jin-Wen, Ma Juan-Juan. Generalized manifold learning for high resolution remote sensing image object classification. Acta Automatica Sinica, 2019, 45(4): 720-729 doi: 10.16383/j.aas.2017.c170318
[6]	陈晓云, 廖梦真. 基于稀疏和近邻保持的极限学习机降维. 自动化学报, 2019, 45(2): 325-333 doi: 10.16383/j.aas.2018.c170216 Chen Xiao-Yun, Liao Meng-Zhen. Dimensionality reduction with extreme learning machine based on sparsity and neighborhood preserving. Acta Automatica Sinica, 2019, 45(2): 325-333 doi: 10.16383/j.aas.2018.c170216
[7]	孔祥玉, 冯晓伟, 胡昌华. 广义主成分分析算法及应用. 北京: 国防工业出版社, 2018. Kong Xiang-Yu, Feng Xiao-Wei, Hu Chang-Hua. General Principal Component Analysis and Application. Beijing: National Defense Industry Press, 2018.
[8]	Gao Y B, Kong X Y, Zhang Z X, Hou L A. An adaptive self-stabilizing algorithm for minor generalized eigenvector extraction and its convergence analysis. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(10): 4869-4881 doi: 10.1109/TNNLS.2017.2783360
[9]	Nguyen T D, Takahashi N, Yamada I. An adaptive extraction of generalized eigensubspace by using exact nested orthogonal complement structure. Multidimensional Systems and Signal Processing, 2013, 24(3): 457-483 doi: 10.1007/s11045-012-0172-9
[10]	Li H Z, Du B Y, Kong X Y, Gao Y B, Hu C H, Bian X H. A generalized minor component extraction algorithm and its analysis. IEEE Access, 2018, 6: 36771-36779 doi: 10.1109/ACCESS.2018.2852060
[11]	Kong X Y, Hu C H, Duan Z S. Principal Component Analysis Networks and Algorithms. Singapore: Springer, 2017.
[12]	Liu L J, Shao H M, Nan D. Recurrent neural network model for computing largest and smallest generalized eigenvalue. Neurocomputing, 2008, 71(16-18): 3589-3594 doi: 10.1016/j.neucom.2008.05.005
[13]	Attallah S, Abed-Meraim K. A fast adaptive algorithm for the generalized symmetric eigenvalue problem. IEEE Signal Processing Letters, 2008, 15: 797-800 doi: 10.1109/LSP.2008.2006346
[14]	Nguyen T D, Yamada I. Adaptive normalized quasi-newton algorithms for extraction of generalized Eigen-pairs and their convergence analysis. IEEE Transactions on Signal Processing, 2013, 61(6): 1404-1418 doi: 10.1109/TSP.2012.2234744
[15]	Qiu J L, Wang H, Lu J B, Zhang B B, Du K L. Neural network implementations for PCA and its extensions. International Scholarly Research Notices, 2012, 2012: 847305.
[16]	Lewis D W. Matrix Theory. Singapore: World Scientific, 1991.
[17]	杜柏阳, 孔祥玉, 冯晓伟. 次成分提取信息准则的加权规则方向收敛分析. 通信学报, 2020, 41(3): 25-32 doi: 10.11959/j.issn.1000-436x.2020014 Du Bo-Yang, Kong Xiang-Yu, Feng Xiao-Wei. Direction convergence analysis of weighted rule for minor component extraction information criteria. Journal on Communications, 2020, 41(3): 25-32 doi: 10.11959/j.issn.1000-436x.2020014
[18]	Möller R. Derivation of Coupled PCA and SVD Learning Rules From a Newton Zero-finding Framework, Computer Engineering, Faculty of Technology, Bielefeld University, Berlin, 2017.
[19]	Gao Y B, Kong X Y, Hu C H, Li H Z, Hou L A. A generalized information criterion for generalized minor component extraction. IEEE Transactions on Signal Processing, 2017, 65(4): 947-959 doi: 10.1109/TSP.2016.2631444
[20]	Zhang W T, Lou S T, Feng D Z. Adaptive quasi-newton algorithm for source extraction via CCA approach. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(4): 677-689 doi: 10.1109/TNNLS.2013.2280285