Operating Performance Assessment Based on Granular Clustering forIron Ore Sintering Process
-
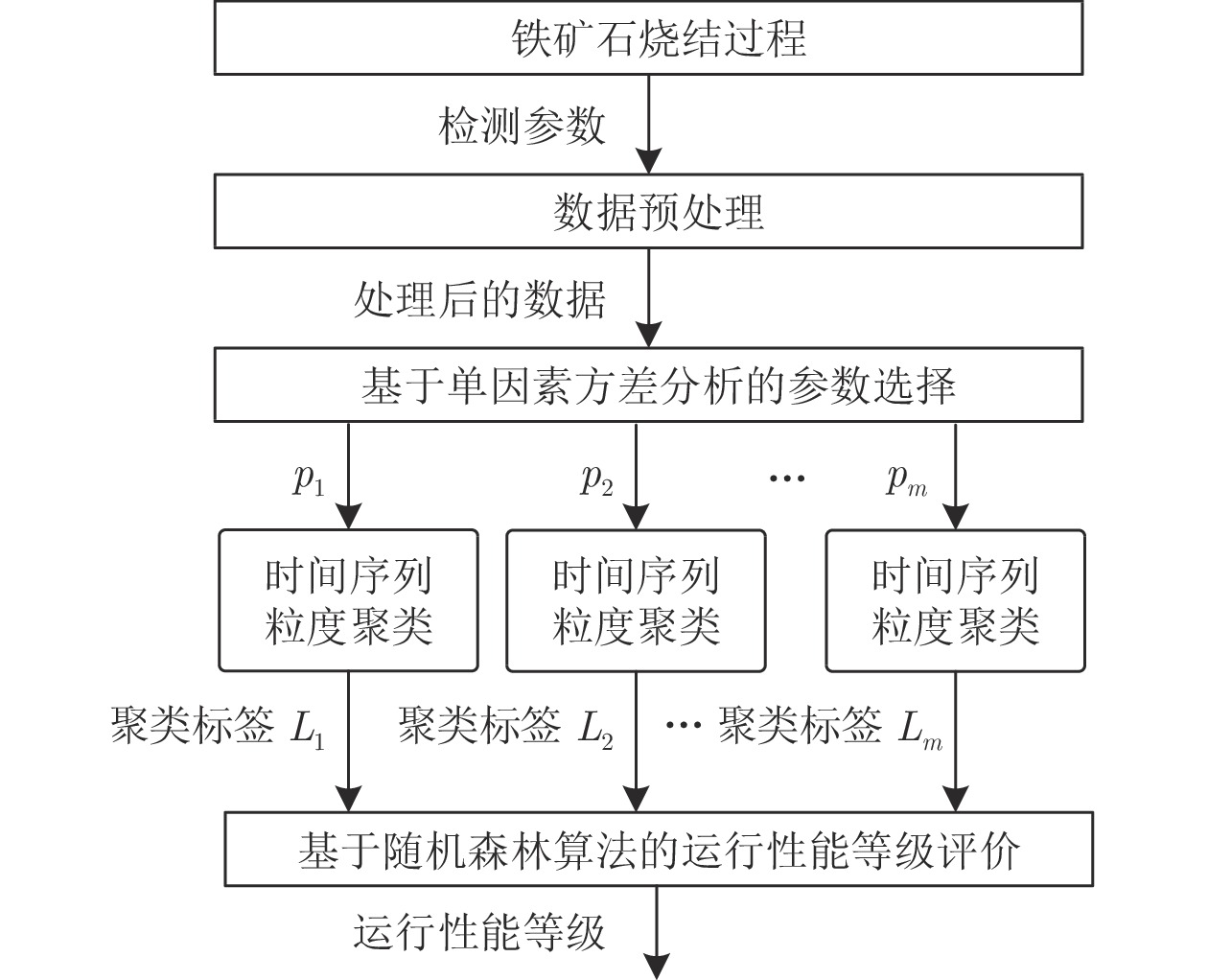
摘要: 烧结过程的运行性能是生产效率和能源利用的综合表现. 运行性能评价是保持烧结过程的运行性能处于最优等级的前提. 考虑到时间序列数据的冗余, 提出一种基于粒度聚类的铁矿石烧结过程运行性能评价方法. 首先, 利用单因素方差分析方法选取影响运行性能等级的检测参数; 然后, 采用多粒度区间信息粒化实现检测参数时间序列数据的降维, 并进行粒度聚类, 得到聚类标签; 最后, 以聚类得到的聚类标签为输入, 利用随机森林算法进行运行性能等级评价. 利用实际钢铁企业的运行数据进行实验, 构建两个对比实验, 分别采用基于时间序列数据聚类(Time series data clustering, TSDC)方法和基于时间序列特征聚类(Time series feature clustering, TSFC)方法. 实验结果表明, 该方法为有效评价烧结过程的运行性能提供了一套可行方案, 为操作人员提升烧结过程运行性能提供了有力的指导.Abstract: The operating performance of the sintering process is about the comprehensive representation of production efficiency and energy utilization. The operating performance assessment is a prerequisite to maintain the operating performance of the sintering process at the optimal grade. By considering the redundancy of time series data, an operating performance assessment method based on granular clustering for the iron ore sintering process is presented in this paper. First, the one-way analysis of variance method is used to select the detection parameters that affect the operating performance grade. Then, the multi-granularity interval information granulation is used to achieve dimensionality reduction of the time series data for the detection parameters, and the granules are clustered to form the clustering labels. Finally, with labels obtained by clustering being the input, the random forest algorithm is used to assess the operating performance grade. Experiments are performed using the actual running data of iron and steel enterprises, and two comparative experiments are constructed using a method based on time series data clustering (TSDC) and a method based on time series feature clustering (TSFC), respectively. Results show that the proposed method provides a feasible scheme to assess the operating performance of the sintering process effectively, and provides powerful guidance for operators to improve the operating performance of the sintering process.
-
Key words:
- Granular clustering /
- sintering process /
- time series /
- operating performance
-
图 1 风箱废气温度和烧结带分布
Fig. 1 Temperature of exhaust gas in bellows andsintering zone distribution
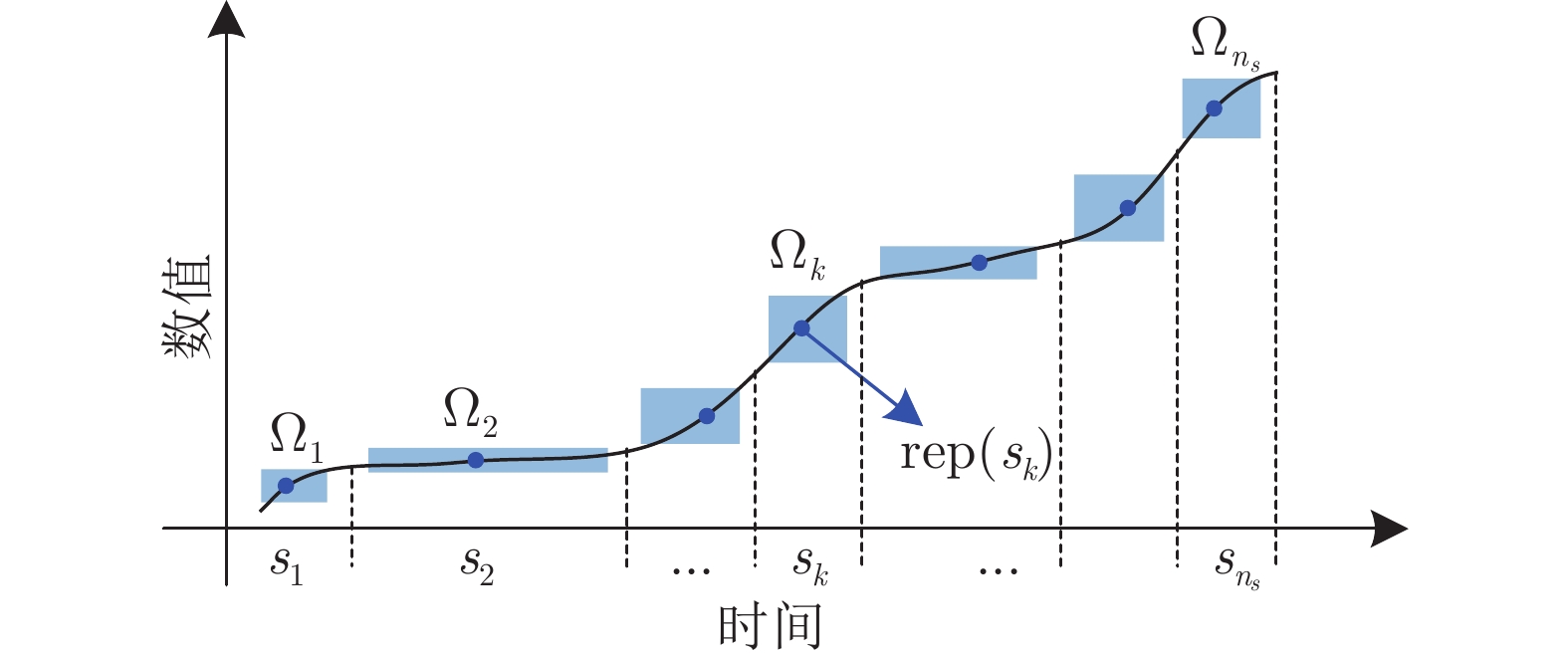
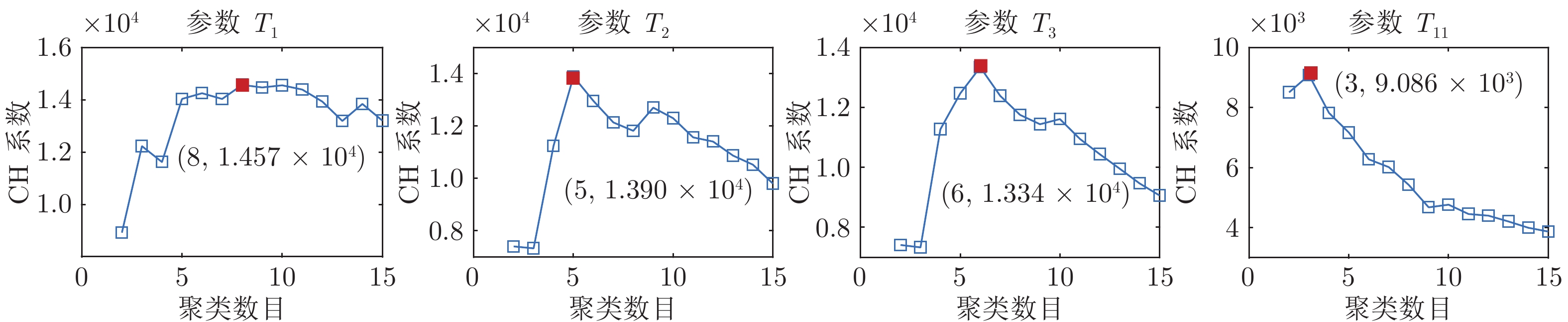
$T_{BTP} $ 烧结终点(Burn-through point, BTP)温度(℃) $L_{BTP} $ 烧结终点位置 $T_{i} $ 第i个风箱废气温度(℃) $P_{N} $ 主风箱负压(kPa) $H_{M} $ 料层厚度(mm) $C_{pm} $ 田口过程能力指数 ${V_T} $ 台车速度 (m/min) $P_i $ 第i个检测参数 $L_i $ 第i个聚类标签 $G_i $ 第i个运行性能等级 $F_T $ 检验统计量 $\rho $ 检验概率 $X $ 时间序列 $s_k $ 第k个时间序列片段 $\Omega_k $ 第k个信息粒 ${\rm{rep}}(s_k) $ $\Omega_k$的数值代表 ${\rm{rep}}(X) $ 粒时间序列 $c $ 聚类数目 $C_i $ 第i个簇的聚类中心 $u_{ij} $ 属于第i个簇的隶属度 $C_H(c) $ Calinski-Harabasz系数 
下载: 导出CSV
表 1 运行性能等级划分
Table 1 Operating performance grade division
运行性能等级 描述 优 (Perfect, Pe) $C_{pm}\geq$ 1.67 良 (Good, Go) 1.67 $>C_{pm}\geq \;$1.33 一般 (General, Ge) 1.33 $>C_{pm}\geq$1.00 差 (Poor, Po) 1.00 $> C_{pm}\geq$ 0.67 不可接受 (Unacceptable, Un) 0.67 $>C_{pm}$
下载: 导出CSV
表 2 单因素方差分析结果
Table 2 Results of one-way analysis of variance
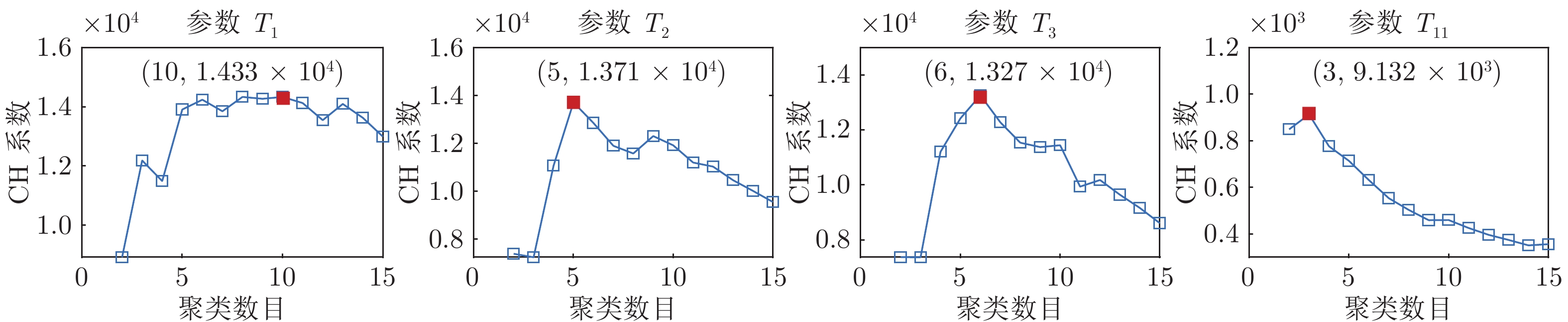
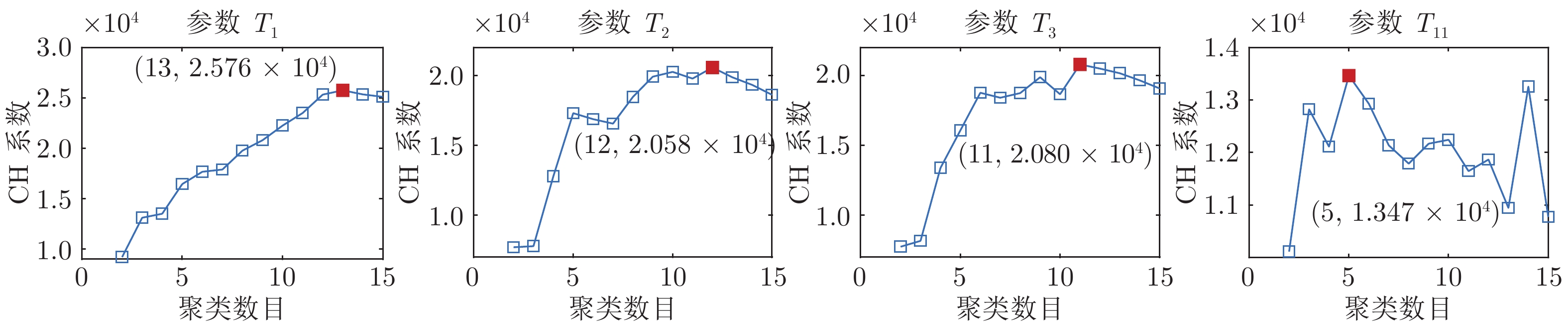
参数 $\rho$ $T_{1}$ 6.76 × 10–8 $T_{2}$ 1.56 × 10–5 $T_{3}$ 8.26 × 10–5 $T_{5}$ 6.40 × 10–2 $T_{7}$ 1.90 × 10–2 $T_{9}$ 4.26 × 10–3 $T_{11}$ 2.47 × 10–25 $T_{13}$ 5.85 × 10–20 $T_{15}$ 6.43 × 10–20 $T_{17}$ 4.17 × 10–15 $~~T_{18}$ 9.39 × 10–25 $T_{19}$ 2.89 × 10–18 $T_{20}$ 1.84 × 10–21 $~~T_{21}$ 6.53 × 10–18 $T_{22}$ 3.59 × 10–20 $T_{23}$ 1.24 × 10–16 $T_{24}$ 2.35 × 10–35 $P_N$ 2.46 × 10–26 $H_M$ 1.46 × 10–13 $V_T$ 6.25 × 10–2
下载: 导出CSV
表 3 运行性能评价结果 (%)
Table 3 Results of operating performance assessment (%)
评估等级 实际等级 精度 Pe Go Ge Po Un TSDC Pe 89.08 7.96 1.20 0.70 1.06 79.70 Go 8.97 75.41 9.21 3.38 3.03 Ge 4.58 8.50 66.45 13.73 6.75 Po 2.29 4.30 14.61 67.34 11.46 Un 1.53 4.81 5.03 8.10 80.53 TSFC Pe 90.08 7.08 1.20 0.64 0.99 80.28 Go 8.84 75.55 8.96 3.90 2.76 Ge 4.43 9.09 67.63 11.31 7.54 Po 1.37 5.75 13.97 66.85 12.05 Un 1.22 4.22 5.22 8.10 81.24 TSGC Pe 94.24 5.04 0.14 0.36 0.22 83.40 Go 8.35 79.52 10.41 1.37 0.34 Ge 0.44 12.66 67.03 12.45 7.42 Po 0 1.15 11.17 74.50 13.18 Un 0 0.54 5.59 11.60 82.28
下载: 导出CSV
-
[1] Chen X, Lan T, Shi X, Tong C. A semi-supervised linear–nonlinear least-square learning network for prediction of carbon efficiency in iron ore sintering process. Control Engineering Practice, 2020, DOI: 10.1016/j.conengprac.2020.104454. [2] Huang X, Fan X, Chen X, Gan M, Zhao X. Soft-measuring models of thermal state in iron ore sintering process. Measurement, 2018, 130: 145-150. doi: 10.1016/j.measurement.2018.07.095 [3] Wang S, Li H, Zhang Y, Zou Z. A hybrid ensemble model based on ELM and improved AdaBoost.RT algorithm for predicting the iron ore sintering characters. Computational Intelligence and Neuroscience, 2019, DOI: 10.1155/2019/4164296. [4] Du S, Wu M, Chen X, Lai X, Cao W. Intelligent coordinating control between burn-through point and mixture bunker level in an iron ore sintering process. Journal of Advanced Computational Intelligence and Intelligent Informatics, 2017, 21(1): 139-147. doi: 10.20965/jaciii.2017.p0139 [5] Chen X, Shi X, Tong C. Multi-time-scale TFe prediction for iron ore sintering process with complex time delay. Control Engineering Practice, 2019, 89: 84-93. doi: 10.1016/j.conengprac.2019.05.012 [6] Liu Y, Wang F, Chang Y, Ma R. Comprehensive economic index prediction based operating optimality assessment and nonoptimal cause identification for multimode processes. Chemical Engineering Research and Design, 2015, 97: 77-90. doi: 10.1016/j.cherd.2015.03.008 [7] Liu Y, Chang Y, Wang F. Online process operating performance assessment and nonoptimal cause identification for industrial processes. Journal of Process Control, 2014, 24(10): 1548-1555. doi: 10.1016/j.jprocont.2014.08.001 [8] 邹筱瑜, 王福利, 常玉清, 王敏, 蔡庆宏. 基于分层分块结构的流程工业过程运行状态评价及非优原因追溯. 自动化学报, 2019, 45(2): 315-324.Zou X, Wang F, Chang Y, Wang M, Cai Q. Plant-wide process operating performance assessment and non-optimal cause identification based on hierarchical multi-block structure. Acta Automatica Sinica, 2019, 45(2): 315-324. [9] 邹筱瑜, 王福利, 常玉清, 郑伟. 基于两层分块GMM-PRS的流程工业过程运行状态评价. 自动化学报, 2019, 45(11): 2071-2081.Zou X, Wang F, Chang Y, Zheng W. Plant-wide process operating performance assessment based on two-level multiblock GMM-PRS. Acta Automatica Sinica, 2019, 45(11): 2071-2081. [10] Zou X, Zhao C. Concurrent assessment of process operating performance with joint static and dynamic analysis. IEEE Transactions on Industrial Informatics, 2020, 16(4): 2776- 2786. doi: 10.1109/TII.2019.2934757 [11] Zou X, Wang F, Chang Y. Assessment of operating performance using cross-domain feature transfer learning. Control Engineering Practice, 2019, 89: 143-153. doi: 10.1016/j.conengprac.2019.05.007 [12] Du S, Wu M, Chen L, Cao W, Pedrycz W. Operating mode recognition of iron ore sintering process based on the clustering of time series data. Control Engineering Practice, 2020, DOI: 10.1016/j.conengprac.2020.104297. [13] Cho H, Choi N, Lee B. Oscillation recognition using a geometric feature extraction process based on periodic timeseries approximation. IEEE Access, 2020, 8: 34375-34386. doi: 10.1109/ACCESS.2020.2974259 [14] Guo H, Wang L, Liu X, Pedrycz W. Information granulation-based fuzzy clustering of time series. IEEE Transactions on Cybernetics, 2020, DOI: 10.1109/TCYB.2020.2970455. [15] Pedrycz W, Bargiela A. Granular clustering: a granular signature of data. IEEE Transactions on Systems, Man, and Cybernetics−Part B: Cybernetics, 2002, 32(2): 212-224. doi: 10.1109/3477.990878 [16] Lu W, Chen X, Pedrycz W, Liu X, Yang J. Using interval information granules to improve forecasting in fuzzy time series. International Journal of Approximate Reasoning, 2015, 57: 1-18. doi: 10.1016/j.ijar.2014.11.002 [17] Boyles R A. The Taguchi capability index. Journal of Quality Technology. 1991, 23(1): 17-26. doi: 10.1080/00224065.1991.11979279 [18] Du S, Wu M, Chen L, Zhou K, Hu J, Cao W, Pedrycz W. A fuzzy control strategy of burn-through point based on the feature extraction of time-series trend for iron ore sintering process. IEEE Transactions on Industrial Informatics, 2020, 16(4): 2357-2368. doi: 10.1109/TII.2019.2935030 [19] Wu C W. An efficient inspection scheme for variables based on Taguchi capability index. European Journal of Operational Research, 2012, 223(1): 116-122. doi: 10.1016/j.ejor.2012.06.023 [20] Booker J M, Raines M, Swift K G. Designing Capable and Reliable Products. Oxford: Butterworth-Heinemann, 2001. [21] 卢伟. 基于粒计算的时间序列分析与建模方法研究 [博士论文], 大连理工大学, 中国, 2015Lu Wei. Time Series Analysis and Modeling Method Research Based on Granular Computing [Ph.D. dissertation], Dalian University of Technology, China, 2015 [22] Wang W, Pedrycz W, Liu X. Time series long-term forecasting model based on information granules and fuzzy clustering. Engineering Applications of Artificial Intelligence. 2015, 41: 17-24. doi: 10.1016/j.engappai.2015.01.006 [23] Bezdek J C, Ehrlich R, Full W. FCM: The fuzzy c-means clustering algorithm. Computers & Geosciences, 1984, 10(2- 3): 191-203. [24] Caliński T, Harabasz J. A dendrite method for cluster analysis. Communications in Statistics-theory and Methods, 1974, 3(1): 1-27. doi: 10.1080/03610927408827109 [25] Chai Z, Zhao C. Enhanced random forest with concurrent analysis of static and dynamic nodes for industrial fault classification. IEEE Transactions on Industrial Informatics, 2020, 16(1): 54-66. doi: 10.1109/TII.2019.2915559 [26] Räsänen T, Kolehmainen M. Feature-based clustering for electricity use time series data. In: Proceedings of the 9th International Conference on Adaptive and Natural Computing Algorithms. Kuopio, Finland: 2009. 401−412 -
图(8) / 表(4)
计量
- 文章访问数: 1928
- HTML全文浏览量: 376
- PDF下载量: 159
- 被引次数: 0
