-
摘要: 深度卷积神经网络显著提升了单图像超分辨率的性能. 通常, 网络越深, 性能越好. 然而加深网络往往会急剧增加参数量和计算负荷, 限制了在资源受限的移动设备上的应用. 提出一个基于轻量级自适应级联的注意力网络的单图像超分辨率方法. 特别地提出了局部像素级注意力模块, 给输入特征的每一个特征通道上的像素点都赋以不同的权值, 从而为重建高质量图像选取更精确的高频信息. 此外, 设计了自适应的级联残差连接, 可以自适应地结合网络产生的层次特征, 能够更好地进行特征重用. 最后, 为了充分利用网络产生的信息, 提出了多尺度全局自适应重建模块. 多尺度全局自适应重建模块使用不同大小的卷积核处理网络在不同深度处产生的信息, 提高了重建质量. 与当前最好的类似方法相比, 该方法的参数量更小, 客观和主观度量显著更好.Abstract: Deep convolutional neural networks have significantly improved the performance of single image super-resolution. Generally, the deeper the network, the better the performance. However, deepening network often increases the number of parameters and computational cost, which limits its application on resource constrained mobile devices. In this paper, we propose a single image super-resolution method based on a lightweight adaptive cascading attention network. In particular, we propose a local pixel-wise attention block, which assigns different weights to pixels on each channel, so as to select high-frequency information for reconstructing high quality image more accurately. In addition, we design an adaptive cascading residual connection, which can adaptively combine hierarchical features and is propitious to reuse feature. Finally, in order to make full use of all hierarchical features, we propose a multi-scale global adaptive reconstruction block. Multi-scale global adaptive reconstruction block uses convolution kernels of different sizes to process different hierarchical features, hence can reconstruct high-resolution image more effectively. Compared with other state-of-the-art methods, our method has fewer parameters and achieves superior performance.
-
Key words:
- Super-resolution /
- lightweight /
- attention mechanism /
- multi-scale reconstruction /
- adaptive parameter
-
图 1 自适应级联的注意力网络架构(ACAN)
Fig. 1 Adaptive cascading attention network architecture (ACAN)
图 6 非线性映射模块中每个HFEB输出特征的可视化结果
Fig. 6 Visual results of each HFEB＇s output feature in non-linear mapping
图 7 包含不同个数的HFEB的ACAN在验证集上的性能比较
Fig. 7 Performance comparison of ACAN on validation set with different numbers of HFEB
图 8 包含不同个数的HFEB的ACAN在Set5测试集上的性能比较
Fig. 8 Performance comparison of ACAN on Set5 testing set with different number of HFEB
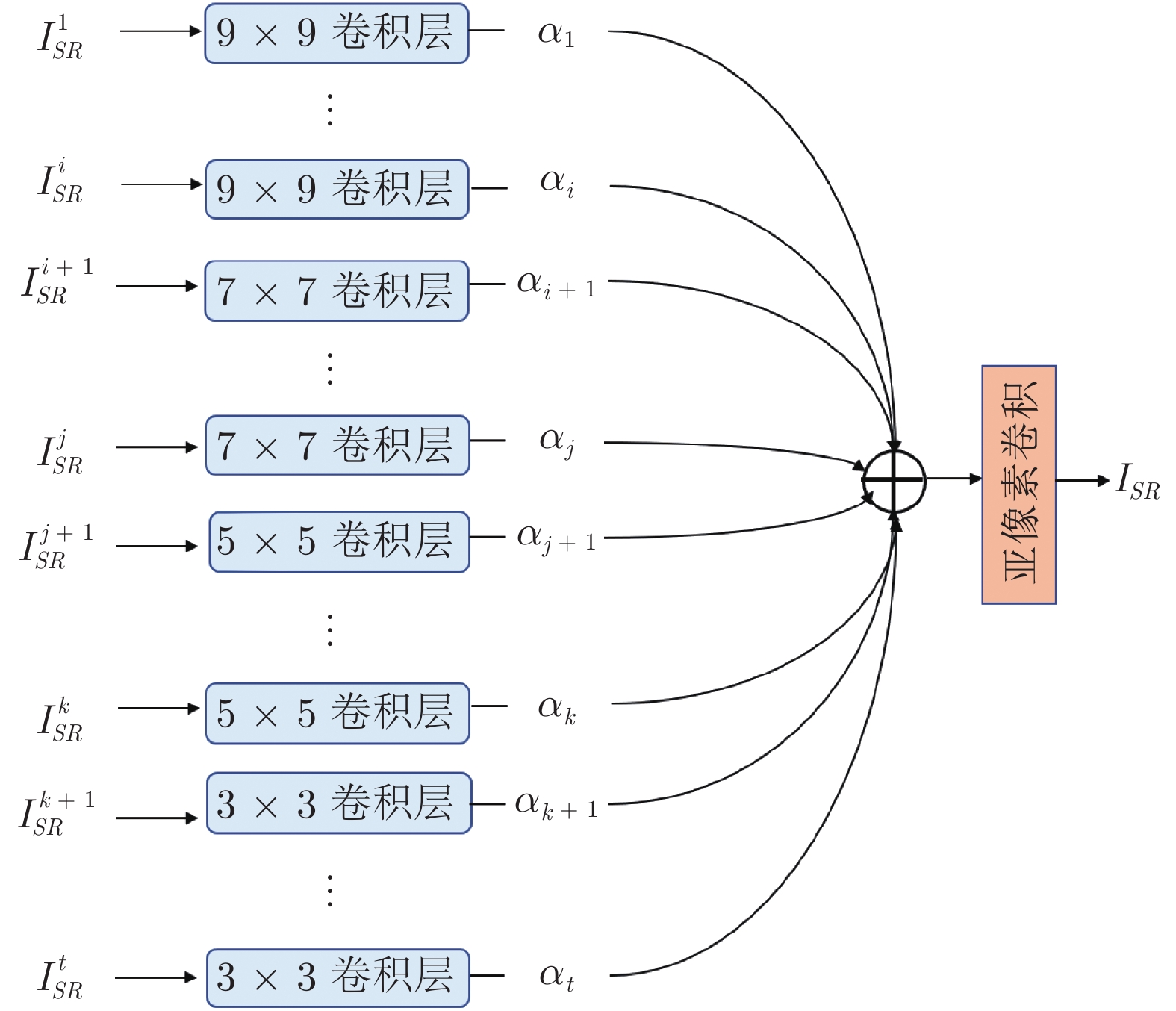
表 1 不同卷积核的排列顺序对重建效果的影响
Table 1 Effect of convolution kernels with different order on reconstruction performance
卷积组排列顺序 9753 3579 3333 9999 PSNR (dB) 35.569 35.514 35.530 35.523 
下载: 导出CSV
表 2 不同层次特征对重建效果的影响
Table 2 Impact of different hierarchical features on reconstruction performance
移除的卷积组大小 3 5 7 9 PSNR (dB) 35.496 35.517 35.541 35.556
下载: 导出CSV
表 3 原始DBPN (O-DBPN)和使用MGAR模块的DBPN (M-DBPN)的客观效果比较
Table 3 Objective comparison between original DBPN (O-DBPN) and DBPN (M-DBPN) using MGAR module
使用不同重建模块的DBPN PSNR (dB) O-DBPN 35.343 M-DBPN 35.399
下载: 导出CSV
表 4 Sigmoid门函数的有无对LPA模块性能的影响
Table 4 Influence of Sigmoid gate function to LPA block
Sigmoid门函数 PSNR (dB) $有$ 35.569 $无$ 35.497
下载: 导出CSV
表 5 不同残差的连接方式对重建效果的影响
Table 5 Effect of different residual connection methods on reconstruction performance
不同种类的残差连接 PSNR (dB) 残差连接 35.515 无残差连接 35.521 带自适应参数的残差连接 35.569
下载: 导出CSV
表 6 使用和未使用LPA模块的客观效果比较
Table 6 Comparison of objective effects of ACAN with and without LPA module
LPA模块 PSNR (dB) $使用$ 35.569 $未使用$ 35.489
下载: 导出CSV
表 7 NLMB使用3种不同连接方式对重建效果的影响
Table 7 Impact of using three different connection methods on NLMB on reconstruction performance
使用的跳跃连接 PSNR (dB) 残差连接 35.542 级联连接 35.502 自适应级联残差连接 35.569
下载: 导出CSV
表 8 不同网络模型深度对重建性能的影响
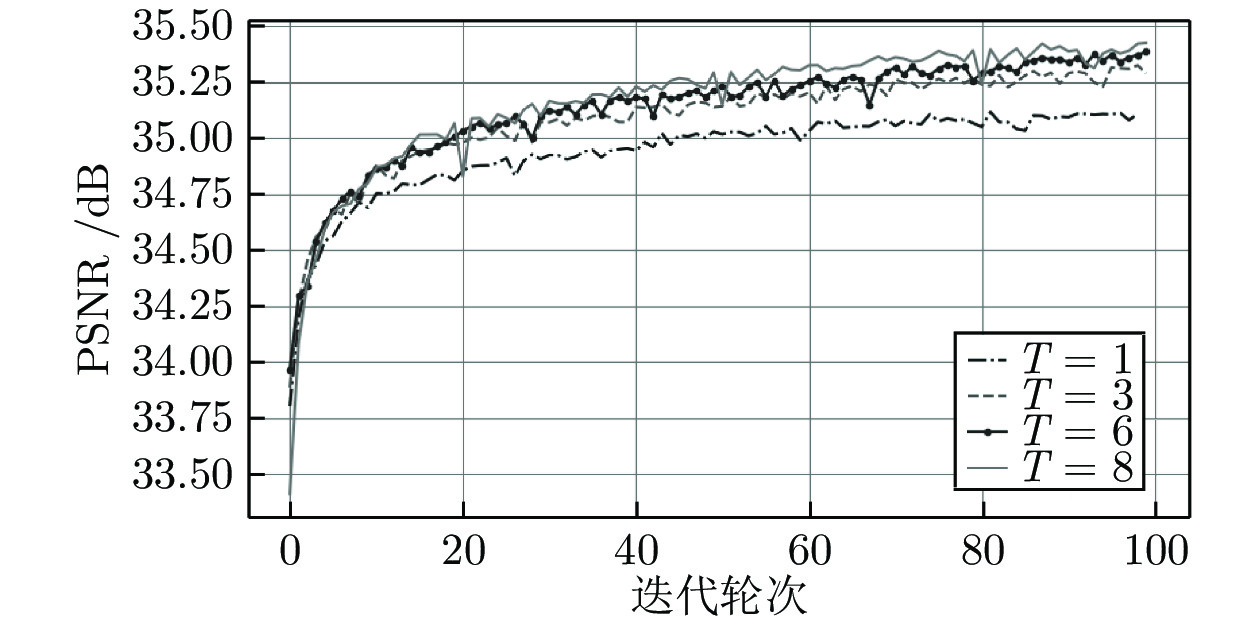
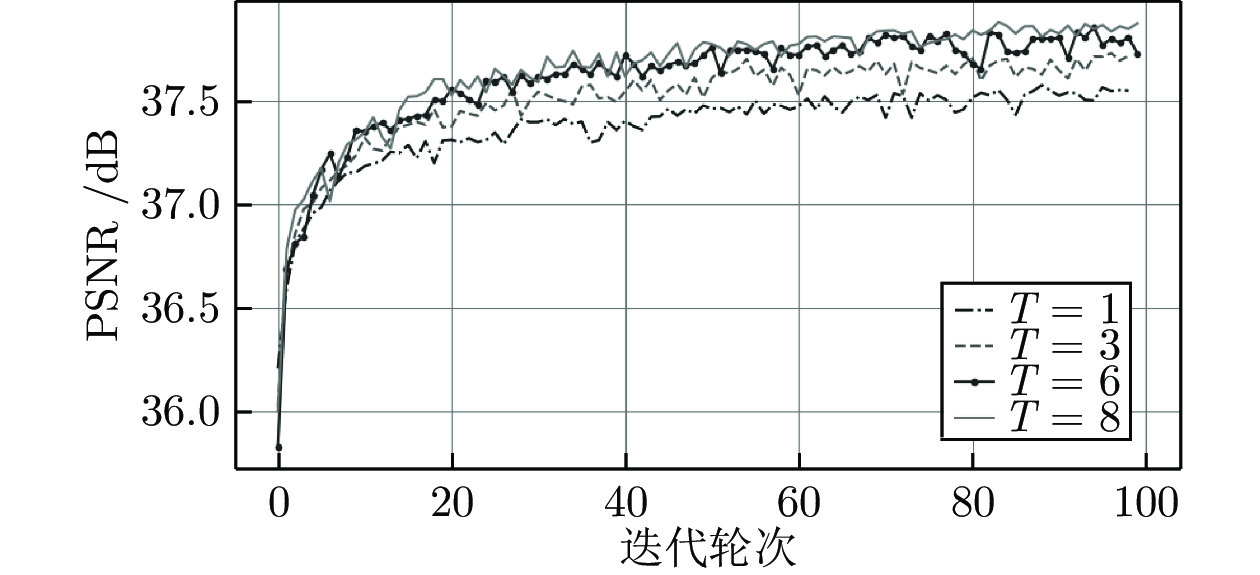
Table 8 Impact of different network depths on reconstruction performance
T 6 7 8 9 PSNR (dB) 35.530 35.538 35.569 35.551
下载: 导出CSV
表 9 各种SISR方法的平均PSNR值与SSIM值
Table 9 Average PSNR/SSIM of various SISR methods
放大倍数 模型 参数量 Set5
PSNR / SSIMSet14
PSNR / SSIMB100
PSNR / SSIMUrban100
PSNR / SSIMManga109
PSNR / SSIM$\times$2 SRCNN 57 K 36.66 / 0.9524 32.42 / 0.9063 31.36 / 0.8879 29.50 / 0.8946 35.74 / 0.9661 FSRCNN 12 K 37.00 / 0.9558 32.63 / 0.9088 31.53 / 0.8920 29.88 / 0.9020 36.67 / 0.9694 VDSR 665 K 37.53 / 0.9587 33.03 / 0.9124 31.90 / 0.8960 30.76 / 0.9140 37.22 / 0.9729 DRCN 1774 K 37.63 / 0.9588 33.04 / 0.9118 31.85 / 0.8942 30.75 / 0.9133 37.63 / 0.9723 LapSRN 813 K 37.52 / 0.9590 33.08 / 0.9130 31.80 / 0.8950 30.41 / 0.9100 37.27 / 0.9740 DRRN 297 K 37.74 / 0.9591 33.23 / 0.9136 32.05 / 0.8973 31.23 / 0.9188 37.92 / 0.9760 MemNet 677 K 37.78 / 0.9597 33.28 / 0.9142 32.08 / 0.8978 31.31 / 0.9195 37.72 / 0.9740 SRMDNF 1513 K 37.79 / 0.9600 33.32 / 0.9150 32.05 / 0.8980 31.33 / 0.9200 38.07 / 0.9761 CARN 1592 K 37.76 / 0.9590 33.52 / 0.9166 32.09 / 0.8978 31.92 / 0.9256 38.36 / 0.9765 SRFBN-S 282K 37.78 / 0.9597 33.35 / 0.9156 32.00 / 0.8970 31.41 / 0.9207 38.06 / 0.9757 本文 ACAN 800 K 38.10 / 0.9608 33.60 / 0.9177 32.21 / 0.9001 32.29 / 0.9297 38.81 / 0.9773 本文 ACAN+ 800 K 38.17 / 0.9611 33.69 / 0.9182 32.26 / 0.9006 32.47 / 0.9315 39.02 / 0.9778 $\times$3 SRCNN 57 K 32.75 / 0.9090 29.28 / 0.8209 28.41 / 0.7863 26.24 / 0.7989 30.59 / 0.9107 FSRCNN 12 K 33.16 / 0.9140 29.43 / 0.8242 28.53 / 0.7910 26.43 / 0.8080 30.98 / 0.9212 VDSR 665 K 33.66 / 0.9213 29.77 / 0.8314 28.82 / 0.7976 27.14 / 0.8279 32.01 / 0.9310 DRCN 1774 K 33.82 / 0.9226 29.76 / 0.8311 28.80 / 0.7963 27.15 / 0.8276 32.31 / 0.9328 DRRN 297 K 34.03 / 0.9244 29.96 / 0.8349 28.95 / 0.8004 27.53 / 0.8378 32.74 / 0.9390 MemNet 677 K 34.09 / 0.9248 30.00 / 0.8350 28.96 / 0.8001 27.56 / 0.8376 32.51 / 0.9369 SRMDNF 1530 K 34.12 / 0.9250 30.04 / 0.8370 28.97 / 0.8030 27.57 / 0.8400 33.00 / 0.9403 CARN 1592 K 34.29 / 0.9255 30.29 / 0.8407 29.06 / 0.8034 27.38 / 0.8404 33.50 / 0.9440 SRFBN-S 376 K 34.20 / 0.9255 30.10 / 0.8372 28.96 / 0.8010 27.66 / 0.8415 33.02 / 0.9404 本文ACAN 1115 K 34.46 / 0.9277 30.39 / 0.8435 29.11 / 0.8055 28.28 / 0.8550 33.61 / 0.9447 本文 ACAN+ 1115 K 34.55 / 0.9283 30.46 / 0.8444 29.16 / 0.8065 28.45 / 0.8577 33.91 / 0.9464 $\times$4 SRCNN 57 K 30.48/0.8628 27.49 / 0.7503 26.90 / 0.7101 24.52 / 0.7221 27.66 / 0.8505 FSRCNN 12 K 30.71 / 0.8657 27.59 / 0.7535 26.98 / 0.7150 24.62 / 0.7280 27.90 / 0.8517 VDSR 665 K 31.35 / 0.8838 28.01 / 0.7674 27.29 / 0.7251 25.18 / 0.7524 28.83 / 0.8809 DRCN 1774 K 31.53 / 0.8854 28.02 / 0.7670 27.23 / 0.7233 25.14 / 0.7510 28.98 / 0.8816 LapSRN 813 K 31.54 / 0.8850 28.19 / 0.7720 27.32 / 0.7280 25.21 / 0.7560 29.09 / 0.8845 DRRN 297 K 31.68 / 0.8888 28.21 / 0.7720 27.38 / 0.7284 25.44 / 0.7638 29.46 / 0.8960 MemNet 677 K 31.74 / 0.8893 28.26 / 0.7723 27.40 / 0.7281 25.50 / 0.7630 29.42 / 0.8942 SRMDNF 1555 K 31.96 / 0.8930 28.35 / 0.7770 27.49 / 0.7340 25.68 / 0.7730 30.09 / 0.9024 CARN 1592 K 32.13 / 0.8937 28.60 / 0.7806 27.58 / 0.7349 26.07 / 0.7837 30.47 / 0.9084 SRFBN-S 483 K 31.98 / 0.8923 28.45 / 0.7779 27.44 / 0.7313 25.71 / 0.7719 29.91 / 0.9008 本文ACAN 1556 K 32.24 / 0.8955 28.62 / 0.7824 27.59 / 0.7366 26.17 / 0.7891 30.53 / 0.9086 本文 ACAN+ 1556 K 32.35 / 0.8969 28.68 / 0.7838 27.65 / 0.7379 26.31 / 0.7922 30.82 / 0.9117
下载: 导出CSV
-
[1] Freeman W T, Pasztor E C, Carmichael O T. Learning lowlevel vision. International Journal of Computer Vision, 2000, 40(1): 25-47 doi: 10.1023/A:1026501619075 [2] PeyréG, Bougleux S, Cohen L. Non-local regularization of inverse problems. In: Proceedings of the European Conference on Computer Vision. Berlin, Germany: Springer, Heidelberg, 2008. 57−68 [3] LeCun Y, Bengio Y, Hinton G. Deep learning. nature, 2015, 521(7553): 436-444 doi: 10.1038/nature14539 [4] Dong C, Loy C C, He K, Tang X. Learning a deep convolutional network for image super-resolution. In: Proceedings of the European Conference on Computer Vision. Zurich, Switzerland: Springer, Cham, 2014. 184−199 [5] Li Z, Yang J, LiuLi Z, Yang J, Liu Z, Yang X, et al. Feedback network for image superresolution. In: Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, USA: IEEE, 2019. 3867−3876 [6] Kim J, Kwon Lee J, Mu Lee K. Deeply-recursive convolutional network for image super-resolution. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA: IEEE, 2016. 1637−1645 [7] Tai Y, Yang J, Liu X. Image super-resolution via deep recursive residual network. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA: IEEE, 2017. 3147−3155 [8] Tai Y, Yang J, Liu X, Xu C. Memnet: A persistent memory network for image restoration. In: Proceedings of the 2017 IEEE International Conference on Computer Vision. Venice, Italy: IEEE, 2017. 4539−4547 [9] Ahn N, Kang B, Sohn K A. Fast, accurate, and lightweight super-resolution with cascading residual network. In: Proceedings of the European Conference on Computer Vision. Zurich, Switzerland: Springer, Cham, 2018. 252−268 [10] Cao C, Liu X, Yang Y, Yu Y, Wang J, Wang Z, et al. Look and think twice: Capturing top-down visual attention with feedback convolutional neural networks. In: Proceedings of the 2015 IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015. 2956−2964 [11] Wang F, Jiang M, Qian C, Yang S, Li C, Zhang H, et al. Residual attention network for image classification. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA: IEEE, 2017. 3156−3164 [12] Hu J, Shen L, Sun G. Squeeze-and-excitation networks. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018. 7132−7141 [13] Li K, Wu Z, Peng K C, Ernst J, Fu Y. Tell me where to look: Guided attention inference network. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018. 9215−9223 [14] Liu Y, Wang Y, Li N, Cheng X, Zhang Y, Huang Y, et al. An attention-based approach for single image super resolution. In: Proceedings of the 2018 24th International Conference on Pattern Recognition. Beijing, China: IEEE, 2018. 2777−2784 [15] Zhang Y, Li K, Li K, Wang L, Zhong B, Fu Y. Image super-resolution using very deep residual channel attention networks. In: Proceedings of the European Conference on Computer Vision. Zurich, Switzerland: Springer, Cham, 2018. 286−301 [16] Kim J, Kwon Lee J, Mu Lee K. Accurate image superresolution using very deep convolutional networks. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA: IEEE, 2016. 1646−1654 [17] Wang Z, Chen J, Hoi S C H. Deep learning for image superresolution: A survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020 [18] Dong C, Loy C C, Tang X. Accelerating the super-resolution convolutional neural network. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Zurich, Switzerland: Springer, Cham, 2016. 391−407 [19] Shi W, Caballero J, Huszár F, Totz J, Aitken A P, Bishop R, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA: IEEE, 2016. 1874−1883 [20] Tong T, Li G, Liu X, Gao Q. Image super-resolution using dense skip connections. In: Proceedings of the 2017 IEEE International Conference on Computer Vision. Venice, Italy: IEEE, 2017. 4799−4807 [21] Li J, Fang F, Mei K, Zhang G. Multi-scale residual network for image super-resolution. In: Proceedings of the European Conference on Computer Vision. Zurich, Switzerland: Springer, Cham, 2018. 517−532 [22] Haris M, Shakhnarovich G, Ukita N. Deep back-projection networks for super-resolution. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA, 2018. 1664−1673 [23] Agustsson E, Timofte R. Ntire 2017 challenge on single image super-resolution: Dataset and study. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu, USA: IEEE, 2017. 126−135 [24] Bevilacqua M, Roumy A, Guillemot C, Alberi-Morel M L. Lowcomplexity single-image super-resolution based on nonnegative neighbor embedding. In: Proceedings of the 23rd British Machine Vision Conference. Guildford, UK: BMVA Press, 2012. (135): 1−10 [25] Zeyde R, Elad M, Protter M. On single image scale-up using sparse-representations. In: Proceedings of International Conference on Curves and Surfaces. Berlin, Germany: Springer, Heidelberg, 2010. 711−730 [26] Huang J B, Singh A, Ahuja N. Single image super-resolution from transformed self-exemplars. In: Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, USA: IEEE, 2015. 5197−5206 [27] Martin D, Fowlkes C, Tal D, Malik J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In: Proceedings of the 2001 International Conference on Computer Vision. Vancouver, Canada: IEEE, 2015. 416−423 [28] Matsui Y, Ito K, Aramaki Y, et al. Sketch-based manga retrieval using manga109 dataset. Multimedia Tools and Applications, 2017, 76(20): 21811-21838 doi: 10.1007/s11042-016-4020-z [29] Kingma D P, Ba J. Adam: A method for stochastic optimization. arXiv preprint, 2014, arXiv: 1412.6980 [30] Lai W S, Huang J B, Ahuja N, Yang M H. Deep laplacian pyramid networks for fast and accurate super-resolution. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA: IEEE, 2017. 5835−5843 [31] Zhang K, Zuo W, Zhang L. Learning a single convolutional super-resolution network for multiple degradations. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018. 3262−3271 [32] Timofte R, Rothe R, Van Gool L. Seven ways to improve example-based single image super resolution. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA: IEEE, 2016. 1865−1873 [33] Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing, 2004, 13(4): 600-612 doi: 10.1109/TIP.2003.819861 [34] Wu H, Zou Z, Gui J, et al. Multi-grained Attention Networks for Single Image Super-Resolution. IEEE Transactions on Circuits and Systems for Video Technology, 2020 -
点击查看大图
计量
- 文章访问数: 1221
- HTML全文浏览量: 367
- PDF下载量: 275
- 被引次数: 0
