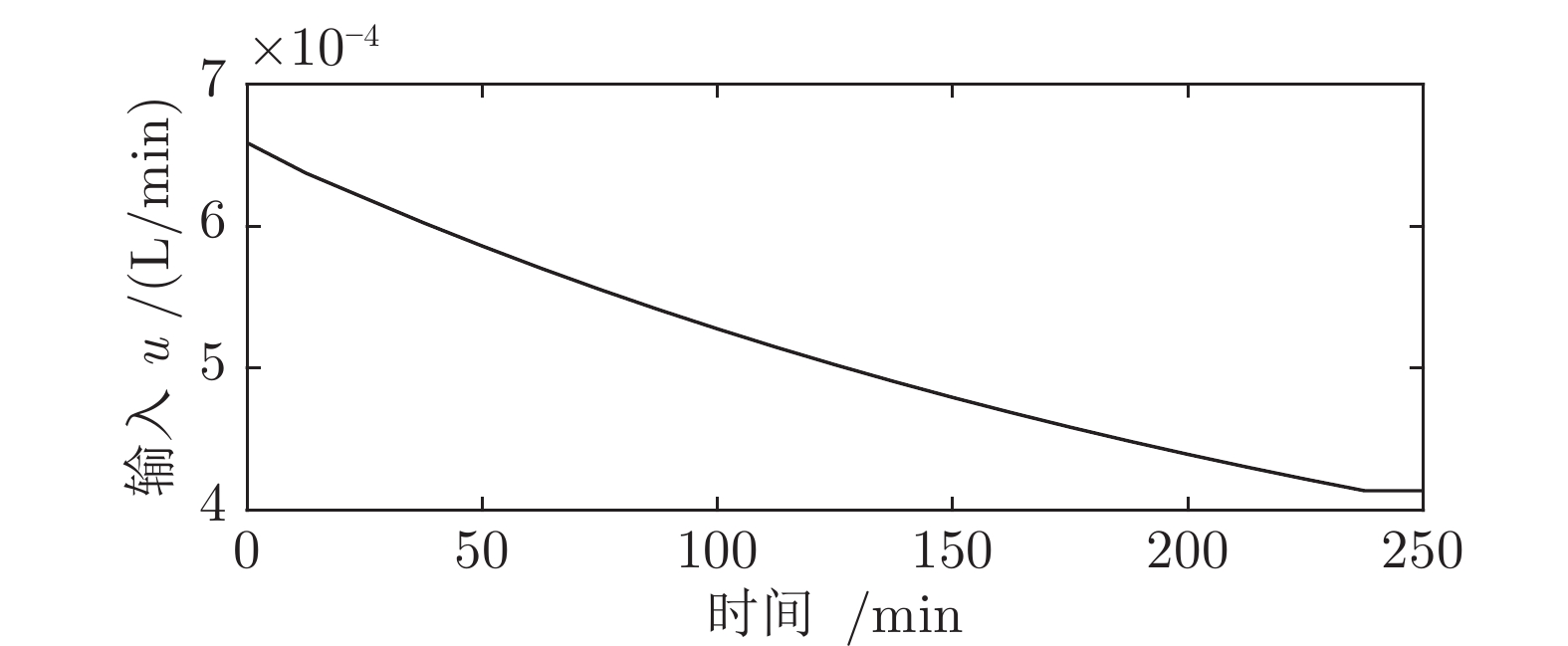
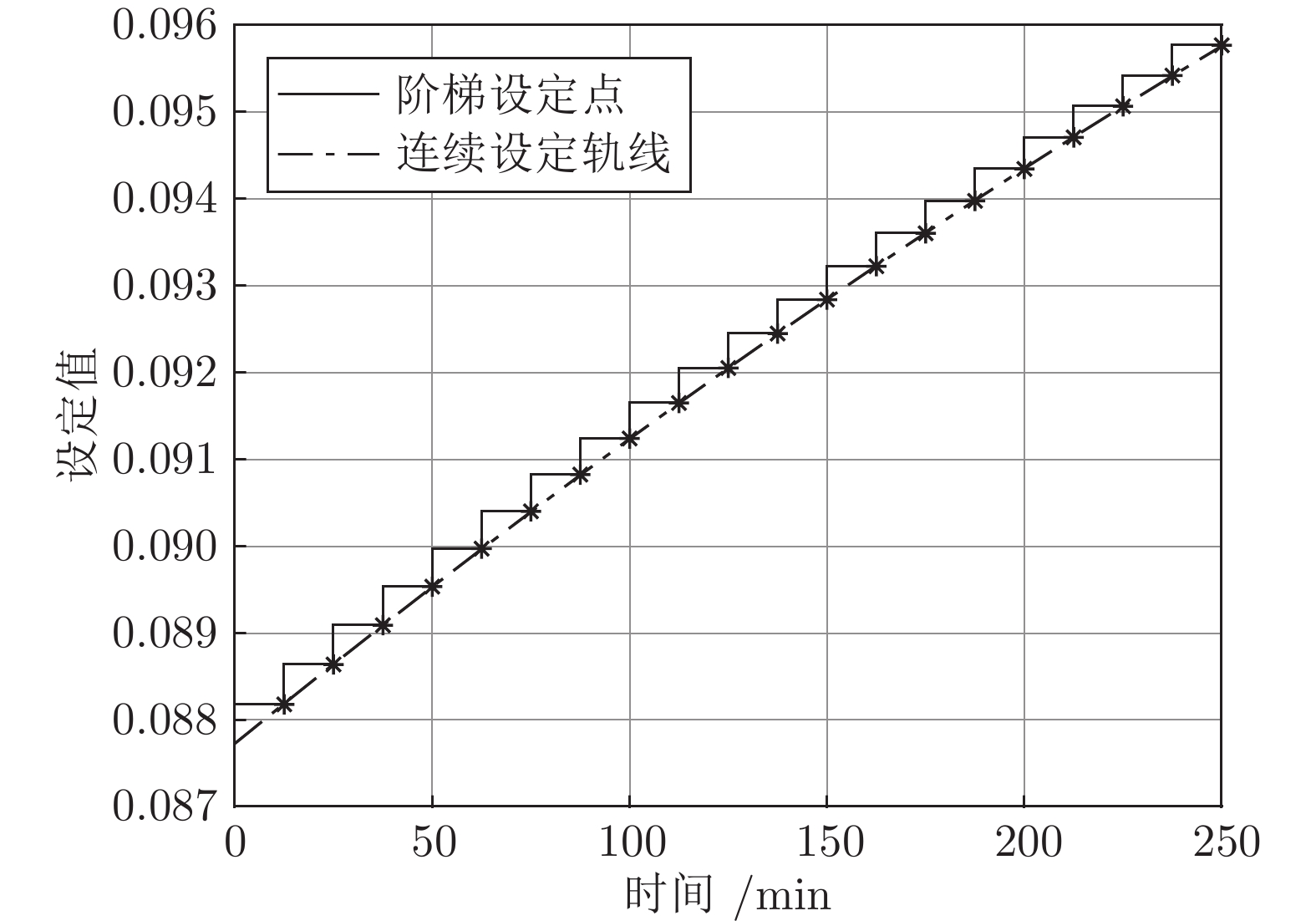
-
摘要: 针对间歇过程的实时优化问题, 提出了一种基于自优化控制的批内优化方法. 以测量变量的线性组合为被控变量, 在单批次内跟踪控制被控变量实现间歇过程的实时优化. 根据是否在间歇过程的不同阶段切换被控变量, 给出了两种自优化控制策略, 对每种策略又分别提出两种设定轨线选取方案. 为求解这些情形下的最优被控变量(组合矩阵), 以最小化平均经济损失为目标, 推导了组合矩阵和经济损失之间的函数关系, 分别将其描述为相应的非线性规划问题. 在此基础上, 进一步引入了扩张组合矩阵, 将这些非线性规划问题归纳为求解扩张组合矩阵的一致形式(扩张组合矩阵具有不同的结构约束), 并推导得到了其中一种方案的解析解计算方法. 以一个间歇反应器为研究对象, 验证了方法的有效性.Abstract: For real-time optimization of uncertain batch processes, a within-batch self-optimizing control (SOC) approach is proposed. In this approach, measurement combinations are selected as controlled variables, which are tracked at time-varying setpoints along batch operations. Regarding whether the controlled variables are switched at different batch phases, two self-optimizing control strategies are given, both of which further contain two schemes in terms of the computation of setpoint trajectory. To solve the optimal controlled variables (combination matrices), the average economic loss is considered as the to-be-minimized cost function, then the nonlinear programming problems are formulated by establishing the relationships between the loss and combination matrices. Based on these results, the extended combination matrix is introduced, then different nonlinear programming problems are uniformed as one problem for solving the optimal extended combination matrix (with different structural constraints). Among these cases, the analytical solution of one option is further derived. A batch reactor is studied to show the effectiveness of the proposed approach.
-
表 1 间歇反应器参数及标称值
Table 1 Parameters for the reactor model and nominal values
符号 物理含义 标称值 $ k_1 $ 主反应的反应常数 0.053 L·mol/min $ k_2 $ 副反应的反应常数 0.128 L·mol/min $ u_L $ $ u $下限 0 L/min $ u_U $ $ u $上限 0.001 L/min $ c_{Bin} $ B 进料浓度 5 mol/L $ c_{Ao} $ A 初始浓度 0.72 mol/L $ c_{Bo} $ B 初始浓度 0.0614 mol/L $ V_o $ V 初始值 1 L $ t_f $ 批次运行时间 250 min 表 2 损失函数
$ L_{\rm{av}} $ Table 2 Loss function
$ L_{\rm{av}} $ 策略及方案 $ N = 2 $ $ N = 20 $ 策略 2 (方案 1) 0.0371 0.0083 策略 2 (方案 2) 0.03423 0.0024 策略 3 (方案 3) 0.0368 0.0069 策略 3 (方案 4) 0.03420 0.0022 表 3 100组随机扰动下的非线性损失统计量
Table 3 Statistics of nonlinear losses for 100 groups of random disturbances
方案 平均损失 最大损失 标准差 标称操作 0.0036 0.0227 0.0068 控制$ c_B $ 0.0042 0.0165 0.0054 策略 2 (方案 1) 0.0026 0.0167 0.0050 策略 2 (方案 2) 0.0007 0.0053 0.0016 -
[1] Chachuat B, Srinivasan B, Bonvin D. Adaptation strategies for real-time optimization. Computers & Chemical Engineering, 2009. 33(10): 1557-1567 [2] 柴天佑. 生产制造全流程优化控制对控制与优化理论方法的挑战. 自动化学报, 2009, 35(6): 641-649 doi: 10.3724/SP.J.1004.2009.00641Chai Tian-You. Challenges of Optimal Control for Plant-wide Production Processes in Terms of Control and Optimization Theories. Acta Automatica Sinica, 2009, 35(6): 641-649 doi: 10.3724/SP.J.1004.2009.00641 [3] Engell S. Feedback control for optimal process operation. Journal of Process Control, 2007, 17(3): 203-219 doi: 10.1016/j.jprocont.2006.10.011 [4] Chen C Y, Joseph B. On-line optimization using a two-phase approach: an application study. Industrial & Engineering Chemistry Research, 1987, 26(9): 1924-1930 [5] Marlin T E, Hrymak A N. Real-time operations optimization of continuous processes. In: AIChE Symposium Series. 1997: New York, NY, USA: American Institute of Chemical Engineers, 1987. 1971−2002 [6] Marchetti A, Chachuat B, Bonvin D. Modifier-Adaptation Methodology for Real-Time Optimization. Industrial & Engineering Chemistry Research, 2009, 48(13): 6022-6033 [7] Marchetti A G, Francois G, Faulwasser T, Bonvin D. Modifier adaptation for real-time optimization—methods and applications. Processes, 2016, 4(4): 55 doi: 10.3390/pr4040055 [8] 代伟, 柴天佑. 数据驱动的复杂磨矿过程运行优化控制方法. 自动化学报, 2014, 40(9): 2005-2014Dai Wei, Chai Tian-You. Data-driven optimal operational control of complex grinding processes. Acta Automatica Sinica, 2014, 40(9): 2005-2014 [9] 李金娜, 高溪泽, 柴天佑, 范家璐. 数据驱动的工业过程运行优化控制. 控制理论与应用, 2016, 33(12): 1584-1592 doi: 10.7641/CTA.2016.60455Li Jin-Na, Gao Xi-Zhe, Chai Tian-You. Data-driven operational optimization control of industrial processes. Control Theory & Applications, 2016, 33(12): 1584-1592 doi: 10.7641/CTA.2016.60455 [10] 代伟, 陆文捷, 付俊, 马小平. 工业过程多速率分层运行优化控制. 自动化学报, 2019, 45(10): 1946-1959Dai Wei, Lu Wen-Jie, Fu Jun, Ma Xiao-Ping. Multi-rate Layered Optimal Operational Control of Industrial Processes. Acta Automatica Sinica, 2019, 45(10): 1946-1959 [11] Skogestad S. Plantwide control: the search for the self-optimizing control structure. Journal of Process Control, 2000. 10(5): p. 487-507 doi: 10.1016/S0959-1524(00)00023-8 [12] Ye L, Cao Y, Yuan X. Global approximation of self-optimizing controlled variables with average loss minimization. Industrial & Engineering Chemistry Research, 2015, 54(48): 12040-12053 [13] Jaschke J, Cao Y, Kariwala V. Self-optimizing control–A survey. Annual Reviews in Control, 2017, 43: 199-223 doi: 10.1016/j.arcontrol.2017.03.001 [14] Ye L, Miao A, Zhang H. Real-Time Optimization of Gold Cyanidation Leaching Process in a Two-Layer Control Architecture Integrating Self-Optimizing Control and Modifier Adaptation. Industrial & Engineering Chemistry Research, 2017, 56(14): 4002-4016 [15] 叶凌箭, 关宏伟. 金氰化浸出过程的自优化控制. 控制与决策, 2017, 32(3): 481-486Ye Ling-Jian, Guan Hong-Wei. Self-optimizing control of gold cyanidation leaching process. Control and Decision, 2017, 32(3): 481-486 [16] Ye L, Cao Y, Yuan X, Zhang H. Retrofit self-optimizing control: A step forward toward real implementation. IEEE Transactions On Industrial Electronics, 2017, 64(6): 4662-4670 doi: 10.1109/TIE.2017.2668991 [17] Francisco M, Skogestad S, Vega P. Model predictive control for the self-optimized operation in wastewater treatment plants: Analysis of dynamic issues. Computers & Chemical Engineering, 2015, 82: 259-272 [18] 卢静宜, 曹志兴, 高福荣. 批次过程控制—回顾与展望. 自动化学报, 2017, 43(6): 933-943Lu Jing-Yi, Cao Zhi-Xing, Gao Fu-Rong. Batch Process Control-Overview and Outlook. Acta Automatica Sinica, 2017, 43(6): 933-943 [19] Lu J, Cao Z, Zhao C, Gao F. 110th Anniversary: An Overview on Learning-Based Model Predictive Control for Batch Processes. Industrial & Engineering Chemistry Research, 2019, 58(37): 17164-17173. [20] 池荣虎, 侯忠生, 黄彪. 间歇过程最优迭代学习控制的发展: 从基于模型到数据驱动. 自动化学报, 2017, 43(6): 917-932CHI Rong-Hu, HOU Zhong-Sheng, HUANG Biao. Optimal Iterative Learning Control of Batch Processes: From Model-based to Data-driven. Acta Automatica Sinica, 2017, 43(6): 917-932 [21] Lu J, Cao Z, Gao F. Multipoint iterative learning model predictive control. IEEE Transactions on Industrial Electronics, 2018, 66(8): 6230-6240 [22] Lu J, Cao Z, Zhang R, Gao F. Nonlinear monotonically convergent iterative learning control for batch processes. IEEE Transactions on Industrial Electronics, 2017, 65(7): 5826-5836 [23] Srinivasan B, Bonvin D, Visser V, Palanki S. Dynamic optimization of batch processes - Ⅱ. Role of measurements in handling uncertainty. Computers & Chemical Engineering, 2003, 27(1): 27-44 [24] Cao Z, Gondhalekar R, Dassau E, Doyle F J. Extremum seeking control for personalized zone adaptation in model predictive control for type 1 diabetes. IEEE Transactions on Biomedical Engineering, 2017, 65(8): 1859-1870. [25] Cao Z, Dürr H B, Ebenbauer C, Allgower F, Gao F. Iterative learning and extremum seeking for repetitive time-varying mappings. IEEE Transactions on Automatic Control, 2016, 62(7): 3339-3353. [26] 史洪岩, 苑明哲, 王天然, 袁德成. 间歇过程动态优化方法综述. 信息与控制, 2012, 41(1): 75-82Shi Hong-yan, Yuan Ming-Zhe, Wang Tian-Ran, Yuan De-Cheng. A suvey on dynamic optimization methods of batch processes. Information and Control, 2012, 41(1): 75-82 [27] Srinivasan B, Palanki S, Bonvin D. Dynamic optimization of batch processes - I. Characterization of the nominal solution. Computers & Chemical Engineering, 2003, 27(1): 1-26 [28] Halvorsen I J, Skogestad S, Morud J C, Alstad V. Optimal selection of controlled variables. Industrial & Engineering Chemistry Research, 2003. 42(14): 3273-3284 [29] Kariwala V. Optimal measurement combination for local self-optimizing control. Industrial & Engineering Chemistry Research, 2007. 46(11): 3629-3634 [30] Alstad V, Skogestad S, Hori E S. Optimal measurement combinations as controlled variables. Journal of Process Control, 2009. 19(1): 138-148 doi: 10.1016/j.jprocont.2008.01.002 [31] Alstad V, Skogestad S. Null space method for selecting optimal measurement combinations as controlled variables. Industrial & Engineering Chemistry Research, 2007. 46(3): 846-853 [32] Francois G, Srinivasan B, Bonvin D. Use of measurements for enforcing the necessary conditions of optimality in the presence of constraints and uncertainty. Journal of Process Control, 2005. 15(6): 701-712 doi: 10.1016/j.jprocont.2004.11.006 [33] 叶凌箭, 宋执环, 马修水. 间歇过程的批间自优化控制. 化工学报, 2015, 66(07): 2573-2580Ye Ling-Jian, Song Zhi-Huan, Ma Xiu-Shui. Batch-to-batch self-optimizing control for batch processes. CIESC Journal, 2015, 66(07): 2573-2580 [34] Ye Ling-Jian, Guan Hong-Wei, Yuan Xiao-Feng, Ma Xiu-Shui. Run-to-run optimization of batch processes with self-optimizing control strategy. The Canadian Journal Of Chemical Engineering, 2017. 95(4): 724-736 doi: 10.1002/cjce.22692 [35] Ye L, Skogestad S. Dynamic self-optimizing control for unconstrained batch processes. Computers & Chemical Engineering, 2018. 117: 451-468 [36] Skogestad S. Control structure design for complete chemical plants. Computers & Chemical Engineering, 2004. 28(1-2): 219-234 [37] Biegler L T, Zavala V M. Large-scale nonlinear programming using IPOPT: An integrating framework for enterprise-wide dynamic optimization. Computers & Chemical Engineering, 2009. 33(3): 575-582 -





 下载:
下载: