Optimal Combination of Image Denoisers Using Multi-channel Shallow Convolutional Neural Network
-
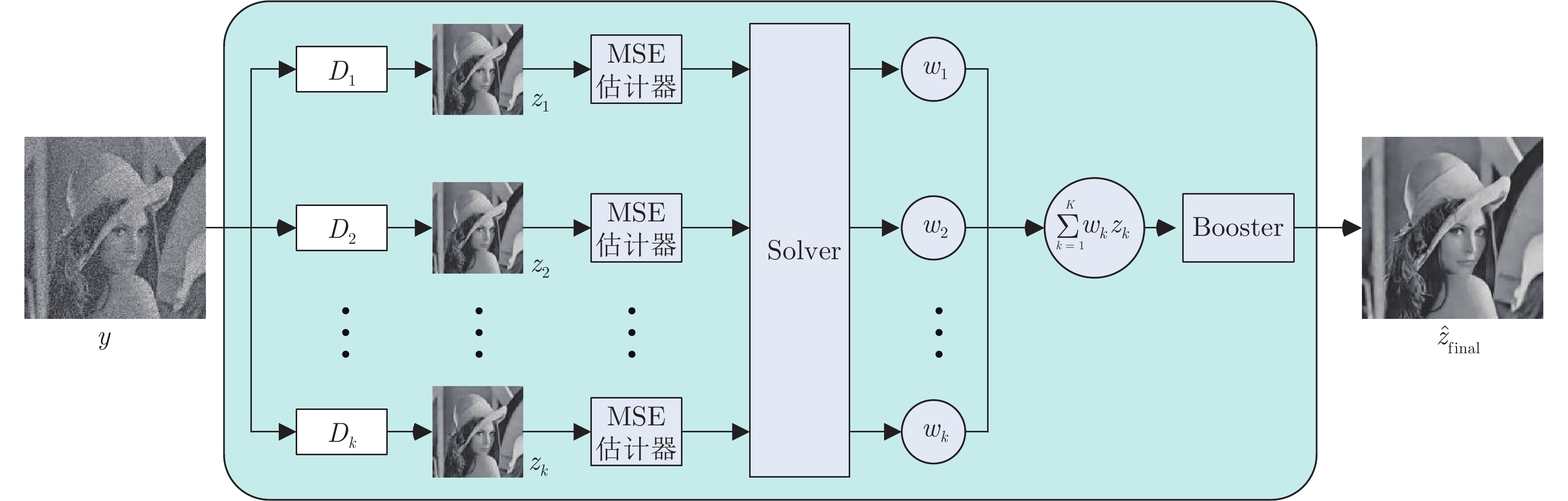
摘要: 现有的一致性神经网络(Consensus neural network, CsNet)利用凸优化和神经网络技术将多个降噪算法(降噪器)输出的图像进行加权组合(融合), 以获得更好的降噪效果, 但该优化模型在降噪效果和执行效率方面仍有较大改进空间. 为此, 提出一种基于轻量型多通道浅层卷积神经网络(Multi-channel shallow convolutional neural network, MSCNN)构建的多降噪器最优组合(Optimal combination of image denoisers, OCID)模型. 该模型采用多通道输入结构直接接收由多个降噪器输出的降噪图像, 并利用残差学习技术合并完成图像融合和图像质量提升两项任务. 具体使用时, 对于给定的一张噪声图像, 先用多个降噪器对其降噪, 并将降噪后图像输入OCID模型获得残差图像, 然后将多个降噪图像的均值图像与残差图像相减, 所得到图像作为优化组合后的降噪图像. 实验结果表明, 与CsNet组合模型相比, 网络结构更为简单的OCID模型以更小的计算代价获得了图像质量更高的降噪图像.
-
关键词:
- 多降噪器最优组合 /
- 一致性神经网络 /
- 多通道浅层卷积神经网络 /
- 降噪效果提升 /
- 执行效率
Abstract: The existing consensus neural network (CsNet) model using the convex optimization and the neural network techniques achieves an optimal combination of the outputs of multiple denoisers for better denoising effect. However, the optimization model still has much room for improvement in noise denoising effect and execution efficiency. To this end, a lightweight multi-channel shallow convolutional neural network (MSCNN)-based model for optimal combination of image denoisers (OCID) was proposed. The OCID model used a multi-channel input structure to receive the outputs of multiple denoisers, and adopted the residual training learning technique to accomplish the task of image combination and quality improvement. For a given noisy image, multiple denoisers were first used to preprocess the given noisy image, and the denoised images were simultaneously fed into the OCID model to obtain a residual image. Then the mean image of the denoised images was subtracted from the residual image to obtain the final optimal denoised image. The experimental results show that, compared with the CsNet model, the images obtained by the OCID model with simpler network structure achieve the better image quality at lower computational cost. -
图 2 多通道神经网络OCID模型架构
Fig. 2 The architecture of OCID model with multi-channel neural network
图 5 各算法在Boat图像上降噪效果对比
Fig. 5 Denoising effect comparison of the competing algorithms on Boat image
表 1 不同网络层数下的MSCNN模型在10张常用图像上的PSNR均值(dB)
Table 1 PSNR performance of different MSCNN models on 10 commonly used images (dB)
噪声水平值 Conv + BN + ReLU 网络层重复的次数 1 3 5 7 9 11 13 15 $\sigma = 20$ 32.52 32.48 32.30 32.34 32.24 32.36 32.42 32.22 $\sigma = 40$ 29.18 29.15 28.91 29.00 28.97 29.15 28.98 29.09 $\sigma = 60$ 27.44 27.48 27.42 27.56 27.25 27.58 27.46 27.42 
下载: 导出CSV
表 2 不同网络层数下的MSCNN模型在10张常用图像上的平均执行时间(s)
Table 2 Execution time performance of different MSCNN models on 10 commonly used images (s)
噪声水平值 Conv + BN + ReLU 网络层重复的次数 1 3 5 7 9 11 13 15 $\sigma = 20$ 0.43 0.93 1.44 1.95 2.43 2.91 3.44 3.97 $\sigma = 40$ 0.42 0.93 1.45 1.94 2.45 2.80 3.48 3.99 $\sigma = 60$ 0.42 0.92 1.44 1.94 2.46 2.79 3.52 3.94
下载: 导出CSV
表 3 2种和3种降噪器组合模式列表
Table 3 List of combination of 2 and 3 denoisers
组合模式 2 种降噪器组合 组合模式 3 种降噪器组合 Case 1 (BM3D + FFDNet) Case 11 (BM3D + DnCNN + NCSR) Case 2 (BM3D + NCSR) Case 12 (BM3D + FFDNet + NCSR) Case 3 (FFDNet + NCSR) Case 13 (BM3D + DnCNN + FFDNet) Case 4 (DnCNN + FFDNet) Case 14 (BM3D + DnCNN + WNNM) Case 5 (DnCNN + NCSR) Case 15 (BM3D + FFDNet + WNNM) Case 6 (BM3D + DnCNN) Case 16 (BM3D + NCSR + WNNM) Case 7 (BM3D + WNNM) Case 17 (DnCNN + FFDNet + NCSR) Case 8 (DnCNN + WNNM) Case 18 (DnCNN + FFDNet + WNNM) Case 9 (FFDNet + WNNM) Case 19 (DnCNN + NCSR + WNNM) Case 10 (NCSR + WNNM) Case 20 (FFDNet + NCSR + WNNM)
下载: 导出CSV
表 4 2种降噪器组合模式在50张纹理图像集上所获得的PSNR均值(dB)
Table 4 Performance comparison of two denoisersin terms of PSNR on 50 texture images (dB)
组合模式 噪声水平值 $\sigma = 10$ $\sigma = 20$ $\sigma = 30$ $\sigma = 40$ $\sigma = 50$ $\sigma = 60$ 均值 Case 1 35.03 30.73 28.51 26.93 26.28 25.49 28.83 Case 2 35.36 31.23 29.12 27.67 26.67 25.92 29.33 Case 3 35.42 31.42 29.38 27.96 26.97 26.18 29.56 Case 4 33.66 30.01 28.12 26.88 26.00 25.27 29.32 Case 5 35.45 31.44 29.36 27.93 26.96 26.12 29.54 Case 6 34.96 30.74 28.68 27.34 26.49 25.78 29.00 Case 7 34.99 30.82 28.71 27.34 26.44 28.73 29.01 Case 8 33.69 30.06 28.16 26.91 26.03 25.30 28.36 Case 9 33.66 29.95 28.08 26.83 25.92 25.23 28.28 Case 10 35.32 31.21 29.15 27.68 26.68 25.86 29.32
下载: 导出CSV
表 5 3种降噪器组合模式的50张纹理图像集上所获得的PSNR均值(dB)
Table 5 Performance comparison of three denoisers on 50 texture images (dB)
组合模式 噪声水平值 $\sigma = 10$ $\sigma = 20$ $\sigma = 30$ $\sigma = 40$ $\sigma = 50$ $\sigma = 60$ 均值 Case 11 36.12 31.76 29.67 28.16 27.08 26.35 29.86 Case 12 36.11 31.75 29.67 28.14 26.99 26.33 29.83 Case 13 34.87 30.66 28.66 27.22 26.40 25.71 28.92 Case 14 34.72 30.51 28.38 27.02 26.09 25.44 28.69 Case 15 34.68 30.38 28.24 26.83 25.92 25.31 28.56 Case 16 36.06 31.71 29.57 28.09 26.95 26.21 29.77 Case 17 35.48 31.47 29.42 27.98 26.99 26.17 29.59 Case 18 33.74 30.10 28.21 26.97 25.37 25.37 28.41 Case 19 35.48 31.47 29.40 27.96 26.98 26.15 29.57 Case 20 35.47 31.47 29.42 27.99 27.01 26.20 29.59
下载: 导出CSV
表 6 2种降噪器融合下的50张纹理图像集上的平均执行时间(s)
Table 6 Execution time of two denoisers on 50 texture images (s)
组合模式 噪声水平值 $\sigma = 10$ $\sigma = 20$ $\sigma = 30$ $\sigma = 40$ $\sigma = 50$ $\sigma = 60$ 均值 Case 1 16.93 17.41 17.10 17.14 17.16 17.21 17.16 Case 2 470.72 818.88 541.01 1049.29 1109.34 822.30 801.92 Case 3 486.92 835.21 557.03 1065.35 1125.38 838.37 818.04 Case 4 21.67 21.76 21.44 21.49 21.47 21.52 21.56 Case 5 475.10 823.23 545.36 1053.64 1113.66 826.61 806.27 Case 6 5.47 5.43 5.43 5.44 5.44 4.45 5.28 Case 7 273.29 276.56 276.99 526.30 399.78 479.47 372.07 Case 8 277.68 280.91 281.34 530.65 404.10 483.78 376.41 Case 9 289.49 292.89 293.01 542.36 415.82 495.54 388.19 Case 10 743.92 1095.36 817.92 1575.51 1508.10 1301.63 1173.74
下载: 导出CSV
表 7 3种降噪器融合下的50张纹理图像集上的平均执行时间(s)
Table 7 Execution time of three denoisers on 50 texture images (s)
组合模式 噪声水平值 $\sigma = 10$ $\sigma = 20$ $\sigma = 30$ $\sigma = 40$ $\sigma = 50$ $\sigma = 60$ 均值 Case 11 475.14 823.27 545.40 1053.69 1113.72 826.68 806.32 Case 12 486.96 835.25 557.07 1065.39 1125.44 838.44 818.09 Case 13 21.92 22.00 21.68 21.73 21.74 21.79 21.81 Case 14 277.72 280.95 281.38 530.694 404.16 483.85 376.46 Case 15 289.54 292.93 293.05 542.40 415.88 495.61 388.24 Case 16 743.97 1095.40 817.96 1575.55 1509.06 1301.70 1173.94 Case 17 491.35 839.60 561.41 1069.74 1129.76 842.76 822.44 Case 18 293.92 297.28 297.39 546.75 420.20 499.92 392.58 Case 19 748.35 1099.75 822.31 1579.90 1513.38 1306.01 1178.28 Case 20 760.17 1111.73 833.98 1591.61 1525.10 1317.77 1190.06
下载: 导出CSV
表 8 各算法在Lena图像上所获得的PSNR值(dB)
Table 8 Performance comparison of the competing algorithms in terms of PSNR on Lena image (dB)
降噪方法 噪声水平值 $\sigma = 10$ $\sigma = 20$ $\sigma = 30$ $\sigma = 40$ $\sigma = 50$ $\sigma = 60$ BM3D 36.55 33.43 31.40 30.05 29.12 28.27 NCSR 36.48 33.26 31.22 30.05 29.11 28.01 WNNM 36.61 33.29 31.62 30.25 29.37 28.51 DnCNN 36.76 33.67 31.78 30.47 29.51 28.62 FFDNet 36.76 33.81 32.05 30.80 29.82 29.02 RedNet 33.82 30.63 29.03 27.95 27.09 28.59 VDNet 36.59 33.69 31.94 30.71 29.75 29.09 TWSC 34.24 30.77 28.95 27.75 26.85 26.11 CsNet 34.05 30.74 29.14 28.04 27.19 28.88 OCID 37.71 34.27 32.50 31.00 30.13 29.35
下载: 导出CSV
表 9 各算法在Lena图像上所获得的SSIM值
Table 9 Performance comparison of the competing algorithms in terms of SSIM on Lena image
降噪方法 噪声水平值 $\sigma = 10$ $\sigma = 20$ $\sigma = 30$ $\sigma = 40$ $\sigma = 50$ $\sigma = 60$ BM3D 0.9251 0.9001 0.8666 0.8369 0.8193 0.7945 NCSR 0.9387 0.9003 0.8683 0.8473 0.8286 0.8044 WNNM 0.9394 0.9002 0.8712 0.8420 0.8266 0.8050 DnCNN 0.9210 0.9026 0.8774 0.8537 0.8341 0.8123 FFDNet 0.9423 0.9102 0.8851 0.8643 0.8459 0.8296 RedNet 0.9073 0.8392 0.7893 0.7506 0.7180 0.8111 VDNet 0.9405 0.9078 0.8825 0.8607 0.8436 0.8298 TWSC 0.9176 0.8438 0.7862 0.7429 0.7083 0.6795 CsNet 0.9113 0.8429 0.7941 0.7556 0.7235 0.8221 OCID 0.9474 0.9135 0.8887 0.8651 0.8486 0.8314
下载: 导出CSV
表 10 各算法在10张常用图像上所获得的PSNR均值(dB)
Table 10 Performance comparison of the competing algorithms in terms of PSNR on 10 commonly used images (dB)
降噪方法 噪声水平值 $\sigma = 10$ $\sigma = 20$ $\sigma = 30$ $\sigma = 40$ $\sigma = 50$ $\sigma = 60$ BM3D 34.82 31.44 29.59 28.13 27.54 26.37 NCSR 34.81 31.38 29.43 28.06 27.02 26.08 WNNM 34.94 31.61 29.80 28.48 27.51 26.68 DnCNN 34.94 31.69 29.83 28.52 27.56 26.65 FFDNet 34.86 31.72 29.95 28.70 27.73 26.92 RedNet 34.25 31.13 29.44 28.23 27.26 26.46 VDNet 34.63 31.53 29.78 28.57 27.64 26.88 TWSC 34.85 31.56 29.73 28.42 27.38 26.51 CsNet 34.62 31.40 29.75 28.55 27.61 26.79 OCID 36.42 32.52 30.61 29.18 28.28 27.44
下载: 导出CSV
表 11 各算法在10张常用图像上所获得的SSIM均值
Table 11 Performance comparison of the competing algorithms in terms of SSIM on 10 commonly used images
降噪方法 噪声水平值 $\sigma = 10$ $\sigma = 20$ $\sigma = 30$ $\sigma = 40$ $\sigma = 50$ $\sigma = 60$ BM3D 0.9296 0.8764 0.8348 0.7968 0.7701 0.7436 NCSR 0.9307 0.8742 0.8289 0.7960 0.7694 0.7428 WNNM 0.9311 0.8773 0.8359 0.8024 0.7823 0.7523 DnCNN 0.9327 0.8829 0.8432 0.8093 0.7437 0.7169 FFDNet 0.9330 0.8855 0.8487 0.8177 0.7908 0.7668 RedNet 0.9197 0.8694 0.8315 0.7986 0.7698 0.7443 VDNet 0.9299 0.8816 0.8449 0.8142 0.7877 0.7651 TWSC 0.9313 0.8787 0.8380 0.8035 0.7727 0.7446 CsNet 0.9251 0.8756 0.8405 0.8100 0.7831 0.7581 OCID 0.9420 0.8943 0.8577 0.8250 0.8012 0.7766
下载: 导出CSV
表 12 各算法在BSD纹理图像集上所获得的PSNR均值(dB)
Table 12 Performance comparison of the competing algorithms in terms of PSNR on BSD database (dB)
降噪方法 噪声水平值 $\sigma = 10$ $\sigma = 20$ $\sigma = 30$ $\sigma = 40$ $\sigma = 50$ $\sigma = 60$ BM3D 33.41 29.56 27.60 26.26 25.40 24.73 NCSR 33.42 29.58 27.60 26.27 25.35 24.59 DnCNN 33.69 30.06 28.14 26.87 25.99 25.23 WNNM 33.53 29.73 27.81 26.54 25.63 24.92 FFDNet 33.61 30.02 28.16 26.93 26.04 25.34 RedNet 33.37 29.51 27.75 26.60 25.75 25.09 VDNet 33.43 29.93 28.08 26.87 25.99 25.31 TWSC 33.48 29.70 27.74 26.46 25.52 24.79 CsNet 33.59 29.67 27.90 26.75 25.91 25.20 OCID 34.96 30.74 28.68 27.34 26.49 25.78
下载: 导出CSV
表 13 各算法DIV2K图像集上所获得的PSNR均值(dB)
Table 13 Performance comparison of the competing algorithms in terms of PSNR on DIV2K database (dB)
降噪方法 噪声水平值 $\sigma = 10$ $\sigma = 20$ $\sigma = 30$ $\sigma = 40$ $\sigma = 50$ $\sigma = 60$ BM3D 33.90 30.08 28.08 26.60 25.69 24.94 NCSR 34.08 30.23 28.14. 26.71 25.69 24.86 WNNM 34.42 30.53 28.47 27.07 26.05 25.25 DnCNN 34.46 30.65 28.57 27.19 26.20 25.34 FFDNet 34.32 30.64 28.66 27.33 26.34 25.56 RedNet 33.97 30.39 28.42 27.09 26.10 25.32 VDNet 33.45 30.21 28.35 27.09 26.15 25.40 TWSC 34.18 30.38 28.44 27.04 25.98 25.13 CsNet 34.30 30.65 28.67 27.33 26.34 25.51 OCID 35.67 31.24 29.17 27.54 26.65 25.89
下载: 导出CSV
表 14 各算法在Waterloo图像集上所获得的PSNR均值(dB)
Table 14 Performance comparison of the competing algorithms in terms of PSNR on Waterloo database (dB)
降噪方法 噪声水平值 $\sigma = 10$ $\sigma = 20$ $\sigma = 30$ $\sigma = 40$ $\sigma = 50$ $\sigma = 60$ BM3D 33.08 29.11 27.02 25.53 24.55 23.80 NCSR 33.14 29.13 27.04 25.54 24.53 23.69 WNNM 33.38 29.39 27.29 25.88 24.84 24.09 DnCNN 33.54 29.64 27.52 26.12 25.12 24.26 FFDNet 33.39 29.63 27.60 26.25 25.24 24.45 RedNet 32.79 29.26 27.29 25.97 24.98 24.20 VDNet 32.86 29.29 27.32 26.01 25.02 24.28 TWSC 33.26 29.35 27.26 25.85 24.81 23.99 CsNet 33.18 29.57 27.59 26.25 25.25 24.42 OCID 34.79 30.25 28.10 26.43 25.54 24.78
下载: 导出CSV
表 15 CsNet与OCID模型在融合阶段的执行时间对比(ms)
Table 15 Execution timein fusion stage of CsNet and OCID model (ms)
模型 噪声水平值 $\sigma = 10$ $\sigma = 20$ $\sigma = 30$ $\sigma = 40$ $\sigma = 50$ $\sigma = 60$ CsNet 3168 3161 3165 3164 3166 3149 OCID 15 12 12 12 12 12
下载: 导出CSV
-
[1] 吴志勇, 丁香乾, 许晓伟, 鞠传香. 基于深度学习和模糊C均值的心电信号分类方法. 自动化学报, 2018, 44(10): 1913-1920.Wu Zhi-Yong, Ding Xiang-Qian, Xu Xiao-Wei, Ju Chuan-Xiang. A method for ECG classification using deep learning and fuzzy C-means. Acta Automatica Sinica, 2018, 44(10): 1913-1920 (in Chinese). [2] Joon H C, Omar A E, Stanley H C. Optimal combination of image denoisers. IEEE Transactions on Image Processing, 2019, 28(8): 4016-4031. doi: 10.1109/TIP.2019.2903321 [3] 刘慧婷, 冷新杨, 王利利, 赵鹏. 联合嵌入式多标签分类算法. 自动化学报, 2019, 45(10): 1969-1982.Liu Hui-Ting, Leng Xin-Yang, Wang Li-Li, Zhao Peng. A joint embedded multi-label classification algorithm. Acta Automatica Sinica, 2019, 45(10): 1969-1982 (in Chinese). [4] 徐少平, 刘婷云, 林珍玉, 张贵珍, 李崇禧. 深度卷积神经网络降噪模型的技术瓶颈与研究展望. 中国图象图形学报, 2019, 24(8): 1207-1214. doi: 10.11834/jig.190165Xu Shao-Ping, LiuTing-Yun, LinZhen-Yu, Zhang Gui-Zhen, Li Chong-Yi. Main bottlenecks and research prospects of the deep convolutional neural network-based denoising model. Journal of Image and Graphics, 2019, 24(8): 1207-1214 (in Chinese). doi: 10.11834/jig.190165 [5] 张红英, 朱恩弘, 吴亚东. 一种基于细节层分离的单曝光HDR图像生成算法. 自动化学报, 2019, 45(11): 2159-2170.Zhang Hong-Ying, Zhu En-Hong, Wu Ya-Dong. High dynamic range image generating algorithm based on detail layer separation of a single exposure image. Acta Automatica Sinica, 2019, 45(11): 2159-2170 (in Chinese). [6] Buades A, Coll B, Morel J M. A non-local algorithm for image denoising. In: Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, CA, USA: IEEE, 2005. 60−65 [7] Dabov K, Foi A, Katkovnik V, Egiazarian K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Transactions on Image Processing, 2007, 16(8): 2080-2095. doi: 10.1109/TIP.2007.901238 [8] Dong W S, Zhang L, Shi G M, Li X. Nonlocally centralized sparse representation for image restoration. IEEE Transactions on Image Processing, 2013, 22(4): 1620-1630. doi: 10.1109/TIP.2012.2235847 [9] Zhang J, Zhao D, Gao W. Group-based sparse representation for image restoration. IEEE Transactions on Image Processing, 2014, 23(8): 3336–3351. doi: 10.1109/TIP.2014.2323127 [10] Xu S P, Yang X H, Jiang S L. A fast nonlocally centralized sparse representation algorithm for image denoising. Signal Processing, 2017, 131: 99-112. doi: 10.1016/j.sigpro.2016.08.006 [11] Gu S H, Zhang L, Zuo W M, Feng X C. Weighted nuclear norm minimization with application to image denoising. In: Proceedings of the 27th IEEE Conference on Computer Vision and Pattern Recognition. Columbus, OH, USA: IEEE, 2014. 2862−2869 [12] Dong W S, Shi G M, Li X. Nonlocal image restoration with bilateral variance estimation: a low-rank approach. IEEE Transactions on Image Processing, 2013, 22(2): 700-711. doi: 10.1109/TIP.2012.2221729 [13] Liu Z, Yu L, Sun H. Image denoising via nonlocal low rank approximation with local structure preserving. IEEE Access, 2019, 7: 7117-7132. doi: 10.1109/ACCESS.2018.2890417 [14] Jin K H, Ye J C. Sparse and low rank decomposition of a Hankel structured matrix for impulse noise removal. IEEE Transactions on Image Processing, 2018, 27(3): 1448-1461. doi: 10.1109/TIP.2017.2771471 [15] Chen J W, Chen J W, Chao H Y, Yang M. Image blind denoising with generative adversarial network based noise modeling. In: Proceedings of the 2018 IEEE Computer Vision and Pattern Recognition. Salt Lake City, UT, USA: IEEE, 2018. 3155−3164 [16] Bae W, Yoo J, Ye J C. Beyond deep residual learning for image restoration: Persistent homology-guided manifold simplification. In: Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu, HI, USA: IEEE, 2017. 1141−1149 [17] Tai Y, Yang J, Liu X M, Xu C Y. MemNet: A persistent memory network for image restoration. In: Proceedings of the 2017 IEEE International Conference on Computer Vision. Venice, Italy: IEEE, 2017. 4549−4557 [18] Chen Y J, Pock T. Trainable nonlinear reaction diffusion: a flexible framework for fast and effective image restoration. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1256-1272. doi: 10.1109/TPAMI.2016.2596743 [19] Du B, Xiong W, Wu J, Zhang L F, Zhang L P, Tao D C. Stacked convolutional denoising auto-encoders for feature representation. IEEE Transactions on Cybernetics, 2017, 47(4): 1017-1027. doi: 10.1109/TCYB.2016.2536638 [20] Jia C C, Shao M, Li S, Zhao H D, Fu Y. Stacked denoising tensor auto-encoder for action recognition with spatiotemporal corruptions. IEEE Transactions on Image Processing, 2018, 27(4): 1878-1887. doi: 10.1109/TIP.2017.2781299 [21] Uwe S, Stefan R. Shrinkage fields for effective image restoration. In: Proceedings of the 27th IEEE Conference on Computer Vision and Pattern Recognition. Columbus, OH, USA: IEEE, 2014. 2774−2781 [22] Zhang K, Zuo WM, Chen Y J, Meng D Y, Zhang L. Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising. IEEE Transactions on Image Processing, 2017, 26(7): 3142-3155. doi: 10.1109/TIP.2017.2662206 [23] Zhang K, Zuo W M, Zhang L. FFDNet: toward a fast and flexible solution for CNN based image denoising. IEEE Transactions on Image Processing, 2018, 27(9): 4608-4622. doi: 10.1109/TIP.2018.2839891 [24] Zhang K, Zuo W M, Gu S H, Zhang L. Learning deep CNN denoiser prior for image restoration. In: Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI, USA: IEEE, 2017. 2808−2817 [25] Lefkimmiatis S. Non-local color image denoising with convolutional neural networks. In: Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI, USA: IEEE, 2017. 5882−5891 [26] Chatterjee P, Milanfar P. Is denoising dead?. IEEE Transactions on Image Processing, 2010, 19(4): 895-911. doi: 10.1109/TIP.2009.2037087 [27] Rawat W, Wang Z H. Deep convolutional neural networks for image classification: a comprehensive review. Neural Computation, 2017, 29(9): 2352-2449. doi: 10.1162/neco_a_00990 [28] Sergey I, Christian S. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In: Proceedings of the 32nd International Conference on Machine Learning. Lille, France: ACM, 2015. 448−456 [29] He K M, Zhang X Y, Ren S Q, Sun J. Deep residual learning for image recognition. In: Proceedings of the 29th IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA: IEEE, 2016. 770−778 [30] Arbeláez P, Maire M, Fowlkes C, Malik, J. Contour detection and hierarchical image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(5): 898-916. doi: 10.1109/TPAMI.2010.161 [31] Dong Y, Jian S. BM3D-Net: a convolutional neural network for transform-domain collaborative filtering. IEEE Signal Processing Letters, 2018, 25(1): 55-59. doi: 10.1109/LSP.2017.2768660 [32] Mao X J, Shen C H, Yang Y B. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections. In: Proceedings of the 2016 Advances in Neural Information Processing Systems. Barcelona, Spain: NIPS, 2016. 2810−2818 [33] Yue Z S, Yong H W, Zhao Q, Zhang L, Meng D Y. Variational denoising network: Toward blind noise modeling and removal [Online], available: http://arxiv.org/abs/1908.11314v1, June 5, 2020 [34] Xu J, Zhang L, Zhang D. A trilateral weighted sparse coding scheme for real-world image denoising. In: Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: Springer Verlag, 2018. 21−38 [35] Eirikur A, Radu T. NTIRE 2017 challenge on single image super-resolution: Dataset and study. In: Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu, HI, USA: IEEE, 2017. 1122−1131 [36] Ma K D, Duanmu Z F, Wu Q B, Wang Z, Yong H W, Li HL, et al. Waterloo exploration database: new challenges for image quality assessment models. IEEE Transactions on Image Processing, 2017, 26(2): 1004-1016. doi: 10.1109/TIP.2016.2631888 -
计量
- 文章访问数: 470
- HTML全文浏览量: 102
- PDF下载量: 282
- 被引次数: 0
