结合全局与局部变化的图像质量评价

高敏娟; 党宏社; 魏立力; 王海龙; 张选德

doi:10.16383/j.aas.c190697

结合全局与局部变化的图像质量评价

doi: 10.16383/j.aas.c190697

1.
陕西科技大学电气与控制工程学院西安 710021
2.
宁夏大学数学统计学院银川 750021
3.
宁夏师范学院数学与计算机科学学院固原 756000
4.
陕西科技大学电子信息与人工智能学院西安 710021

基金项目: 国家自然科学基金(61871260, 61871259), 陕西科技大学人工智能交叉学科PI团队培育专项基金资助

详细信息

作者简介:
高敏娟：陕西科技大学电气与控制工程学院博士研究生. 2010年获得山西大学工学硕士学位. 主要研究方向为图像处理, 图像质量评价.E-mail: gaominjuan1984@163.com

党宏社：陕西科技大学电气与控制工程学院教授. 主要研究方向为工业过程与优化, 计算机控制, 图像处理.E-mail: danghs@sust.edu.cn

魏立力：宁夏大学数学统计学院教授. 主要研究方向为应用统计与数据分析. E-mail: liliwei@nxu.edu.cn

王海龙：宁夏师范学院数学与计算机科学学院讲师. 2011年获得香港公开大学教育硕士学位. 主要研究方向为代数.E-mail: wanghailong7903@163.com

张选德：陕西科技大学电子信息与人工智能学院教授. 2013年获得西安电子科技大学理学博士学位. 主要研究方向为图像恢复, 图像质量评价, 稀疏表示和低秩逼近理论. 本文通信作者.E-mail: zhangxuande@sust.edu.cn

计量
- 文章访问数: 4397
- HTML全文浏览量: 1926
- PDF下载量: 293
- 被引次数: 0
出版历程
- 收稿日期: 2019-10-08
- 录用日期: 2019-12-15
- 网络出版日期: 2020-01-04
- 刊出日期: 2020-12-29

Combining Global and Local Variation for Image Quality Assessment

1.
School of Electrical and Control Engineering, Shaanxi University of Science and Technology, Xi＇ an 710021
2.
School of Mathematics and Statistics, Ningxia University, Yinchuan 750021
3.
School of Mathmatics and Computer Science, Ningxia Normal University, Guyuan 756000
4.
School of Electronic Information and Artificial Intelligence, Shaanxi University of Science and Technology, Xi＇ an 710021

Funds: Supported by National Natural Science Foundation of China (61871260, 61871259) and Shaanxi University of Science and Technology Artificial Intelligence Interdisciplinary PI Team Cultivation Special Project

摘要

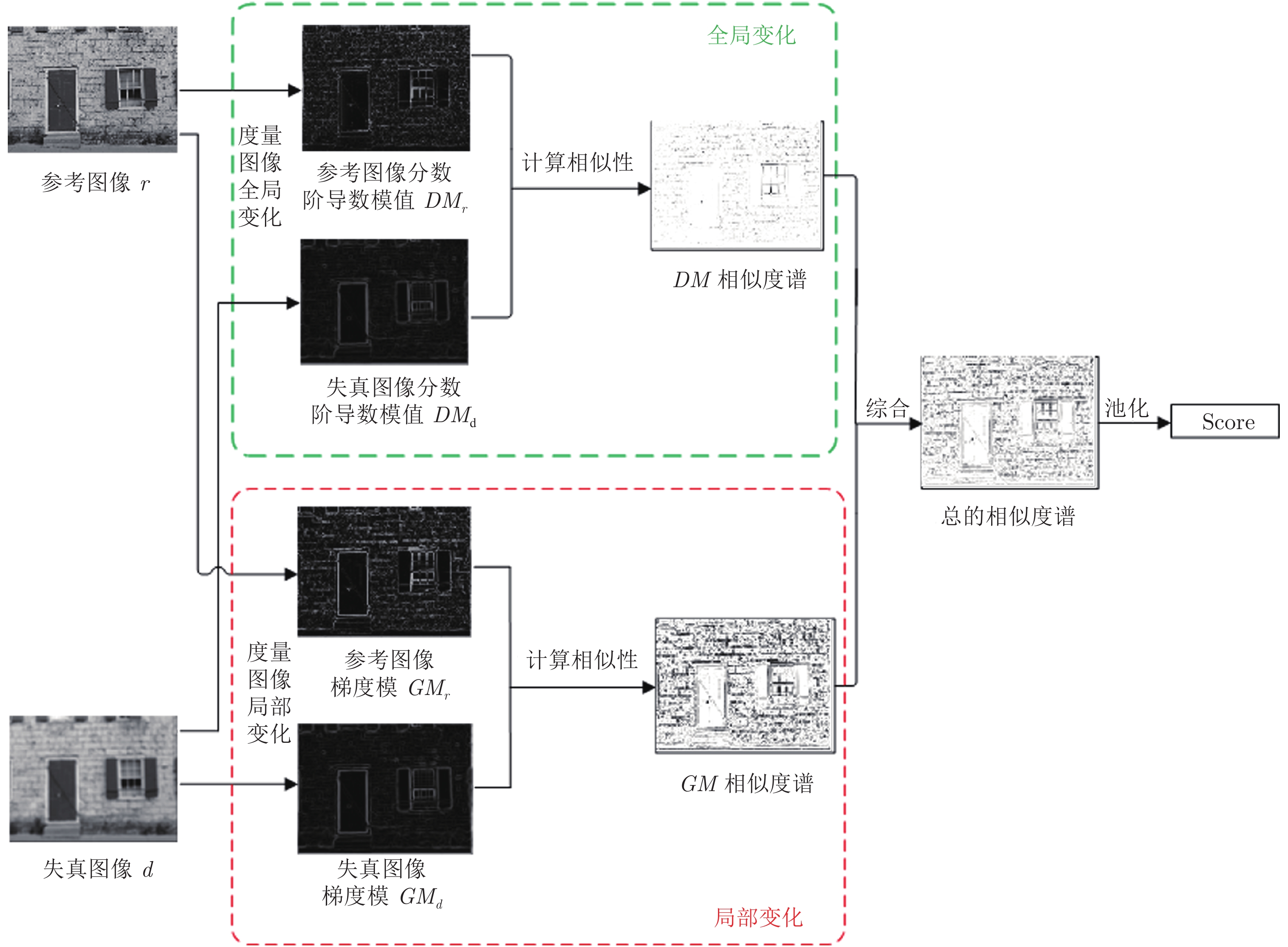
摘要: 图像所包含的信息是通过灰度值在空域的变化呈现的. 梯度是度量变化的基本工具, 这使得梯度成为了目前大多数图像质量评价算法的重要组成部分. 但是梯度只能度量局部变化, 而当人类视觉系统(Human visual system, HVS)感知一幅图像时, 既能感知到局部变化, 也能感知到全局变化. 基于HVS的这一特性, 本文提出了一种结合全局与局部变化的图像质量评价算法(Global and local variation similarity, GLV-SIM). 该算法利用Grünwald-Letnikov分数阶导数来度量图像的全局变化, 利用梯度模来度量图像的局部变化. 然后结合二者计算参考图像和退化图像之间的相似度谱(Similarity map), 进而得到图像的客观评分. 在TID2013、TID2008、CSIQ与LIVE四个数据库上的仿真实验表明, 较之单一度量局部变化的方法, 本文算法能更准确地模拟HVS对图像质量的感知过程, 给出的客观评分与主观评分具有较好的一致性.
- 图像质量评价 /
- 全局与局部 /
- Grünwald-Letnikov分数阶导数 /
- 梯度模
Abstract: The information contained in an image is presented by the changes of gray value in spatial domain. Gradient is the basic tool to measure changes, which makes gradient become an important ingredient of most image quality assessment algorithms. However, gradient can only measure local changes, while when human visual system (HVS) perceives an image, it can perceive both local and global changes. Based on this characteristic of HVS, this paper proposes an image quality assessment algorithm by combining global and local variations similarity (GLV-SIM). The algorithm uses Grünwald-Letnikov fractional derivative to measure the global changes and uses gradient magnitude to measure the local changes of the image. Synthesizing the two aspect changes, similarity map between reference image and distorted image is calculated, and then objective score of the image is obtained. Simulation experiments on four databases TID2013, TID2008, CSIQ and LIVE show that, comparing with the algorithm only considering local changes, the proposed algorithm can more accurately simulate the perception process of HVS on image quality and can obtain better consistency between objective scores and subjective scores.
- Image quality assessment /
- global and local /
- Grünwald-Letnikov fractional derivative /
- gradient magnitude

HTML全文

图 1 Child-swimming图像

Fig. 1 The image of child-swimming

下载: 全尺寸图片幻灯片

图 2 GLV-SIM算法框架

Fig. 2 The framework of GLV-SIM algorithm

下载: 全尺寸图片幻灯片

图 3 参考图像(a)及其不同类型退化图像(b)~(f) (右下角为矩形区域局部放大图)

Fig. 3 Reference image (a) and different types of distorted images (b)~(f)

(The lower right corner is a enlarged view of the rectangular region)

下载: 全尺寸图片幻灯片

图 4 针对图3中各矩形区域对应的$DM$图

Fig. 4 The corresponding $DM$ map for each rectangular region in Fig.3

下载: 全尺寸图片幻灯片

表 1 图3(b)~(f)主观评分和不同算法客观评分

Table 1 Subjective scores and objective scores of different algorithms for Fig. 3(b)~(f)

评价方法	图3(b)	图3(c)	图3(d)	图3(e)	图3(f)
MOS	5.0000	3.8387	4.1875	4.7667	6.2903
PSNR	30.5304	30.5784	26.1303	27.4808	27.3498
VSNR	29.7301	21.1480	20.5342	30.7072	20.2681
IFC	4.7389	3.4351	4.9319	2.9956	11.3746
SSIM	0.9250	0.8461	0.9459	0.9475	0.9568
MS-SSIM	0.9606	0.9159	0.9738	0.9727	0.9821
IW-SSIM	0.9684	0.9075	0.9645	0.9704	0.9661
GSIM	0.9958	0.9888	0.9953	0.9966	0.9979
FSIM	0.9831	0.9462	0.9538	0.9699	0.9707
GLV-SIM	0.9959	0.9845	0.9927	0.9957	0.9961

下载: 导出CSV

表 2 针对表1评分排名

Table 2 The rank of scores on Table 1

评价方法	图3(b)	图3(c)	图3(d)	图3(e)	图3(f)
MOS	2	5	4	3	1
PSNR	2	1	5	3	4
VSNR	2	3	4	1	5
IFC	3	4	2	5	1
SSIM	4	5	3	2	1
MS-SSIM	4	5	2	3	1
IW-SSIM	2	4	5	1	3
GSIM	3	5	4	2	1
FSIM	1	5	4	3	2
GLV-SIM	2	5	4	3	1

下载: 导出CSV

表 3 不同IQA算法在TID2013和TID2008数据库的实验结果比较

Table 3 Comparison the performance results of different IQA algorithms on TID2013 and TID2008 databases

数据库	性能指标	PSNR	VSNR	IFC	SSIM	MS-SSIM	IW-SSIM	GSIM	FSIM	GLV-SIM
TID 2013	SROCC	0.6396	0.6812	0.5389	0.7417	0.7859	0.7779	0.7946	0.8015	0.8068
	KROCC	0.4698	0.5084	0.3939	0.5588	0.6047	0.5977	0.6255	0.6289	0.6381
	PLCC	0.7017	0.7402	0.5538	0.7895	0.8329	0.8319	0.8464	0.8589	0.8580
	RMSE	0.8832	0.8392	1.0322	0.7608	0.6861	0.6880	0.6603	0.6349	0.6368
TID 2008	SROCC	0.5531	0.7046	0.5675	0.7749	0.8542	0.8559	0.8504	0.8805	0.8814
	KROCC	0.4027	0.5340	0.4236	0.5768	0.6568	0.6636	0.6596	0.6946	0.6956
	PLCC	0.5734	0.6820	0.7340	0.7732	0.8451	0.8579	0.8422	0.8738	0.8648
	RMSE	1.0994	0.9815	0.9113	0.8511	0.7173	0.6895	0.7235	0.6525	0.6739

下载: 导出CSV

表 4 不同IQA算法在CSIQ和LIVE数据库的实验结果比较

Table 4 Comparison the performance results of different IQA algorithms on CSIQ and LIVE databases

数据库	性能指标	PSNR	VSNR	IFC	SSIM	MS-SSIM	IW-SSIM	GSIM	FSIM	GLV-SIM
CSIQ	SROCC	0.8058	0.8106	0.7671	0.8756	0.9133	0.9213	0.9108	0.9242	0.9264
	KROCC	0.6084	0.6247	0.5897	0.6907	0.7393	0.7529	0.7374	0.7567	0.7605
	PLCC	0.8000	0.8002	0.8384	0.8613	0.8991	0.9144	0.8964	0.9120	0.9082
	RMSE	0.1575	0.1575	0.1431	0.1334	0.1149	0.1063	0.1164	0.1007	0.1099
LIVE	SROCC	0.8756	0.9274	0.9259	0.9479	0.9513	0.9567	0.9561	0.9634	0.9521
	KROCC	0.6865	0.7616	0.7579	0.7963	0.8045	0.8175	0.8150	0.8337	0.8179
	PLCC	0.8723	0.9231	0.9268	0.9449	0.9489	0.9522	0.9512	0.9597	0.9368
	RMSE	13.359	10.505	10.264	8.9445	8.6188	8.3473	8.4327	7.6780	8.0864

下载: 导出CSV

表 5 不同IQA算法在TID2008数据库单一失真评价性能(SROCC)比较

Table 5 Comparison SROCC for individual distortion of different IQA algorithms on TID2008 database

数据库	失真类型	PSNR	VSNR	IFC	SSIM	MS-SSIM	IW-SSIM	GSIM	FSIM	GLV-SIM
TID 2008	AWN	0.9073	0.7728	0.5806	0.8107	0.8094	0.7869	0.8573	0.8566	0.9125
	ANMC	0.8994	0.7793	0.5460	0.8029	0.8064	0.7920	0.8095	0.8527	0.8979
	SCN	0.9175	0.7665	0.5958	0.8144	0.8195	0.7714	0.8902	0.8483	0.9167
	MN	0.8520	0.7295	0.6732	0.7795	0.8156	0.8087	0.7403	0.8021	0.8087
	HFN	0.9273	0.8811	0.7318	0.8729	0.8685	0.8662	0.8932	0.9093	0.9175
	IMN	0.8725	0.6470	0.5345	0.6732	0.6868	0.6465	0.7721	0.7452	0.7864
	QN	0.8702	0.8271	0.5857	0.8531	0.8537	0.8177	0.8750	0.8564	0.8865
	GB	0.8704	0.9330	0.8559	0.9544	0.9607	0.9636	0.9585	0.9472	0.9587
	DEN	0.9422	0.9286	0.7973	0.9530	0.9571	0.9473	0.9723	0.9603	0.9666
	JPEG	0.8723	0.9174	0.8180	0.9252	0.9348	0.9184	0.9391	0.9279	0.9534
	JP2K	0.8131	0.9515	0.9437	0.9625	0.9736	0.9738	0.9755	0.9773	0.9751
	JGTE	0.7525	0.8056	0.7909	0.8678	0.8736	0.8588	0.8832	0.8708	0.8793
	J2TE	0.8312	0.7909	0.7301	0.8577	0.8522	0.8203	0.8925	0.8544	0.9021
	NEPN	0.5812	0.5716	0.8418	0.7107	0.7336	0.7724	0.7372	0.7491	0.7271
	BLOCK	0.6194	0.1926	0.6770	0.8462	0.7617	0.7623	0.8865	0.8492	0.8960
	MS	0.6966	0.3715	0.4250	0.7231	0.7374	0.7067	0.7174	0.6698	0.6994
	CTC	0.5867	0.4239	0.2713	0.5246	0.6398	0.6301	0.6736	0.6481	0.6689

下载: 导出CSV

参考文献(32)

[1]	Mohammadi P, Ebrahimi-Moghadam A, Shirani S. Subjective and objective quality assessment of image: a survey. Majlesi Journal of Electrical Engineering, 2015, 9(1): 419−423
[2]	Yang X C, Sun Q S, Wang T S. Image quality assessment improvement via local gray-scale fluctuation measurement. Multimedia Tools and Applications, 2018, 77(18): 24185−24202 doi: 10.1007/s11042-018-5740-z
[3]	高敏娟, 党宏社, 魏立力, 张选德. 基于非局部梯度的图像质量评价算法. 电子与信息学报, 2019, 41(5): 1122−1129 doi: 10.11999/JEIT180597 Gao Min-Juan, Dang Hong-She, Wei Li-Li, Zhang Xuan-De. Image quality assessment algorithm based on non-local gradient. Journal of Electronics and Information Technology, 2019, 41(5): 1122−1129 doi: 10.11999/JEIT180597
[4]	许丽娜, 肖奇, 何鲁晓. 考虑人类视觉特征的融合图像评价方法. 武汉大学学报(信息科学版), 2019, 44(4): 546−554 Xu Li-Na, Xiao Qi, He Lu-Xiao. Fused image quality asssessment based on human visual characterisyics. Geomatics and Information Science of Wuhan University, 2019, 44(4): 546−554
[5]	曹清洁, 史再峰, 张嘉平, 李杭原, 高静, 姚素英. 分区域多标准的全参考图像质量评价算法. 天津大学学报(自然科学与工程技术版), 2019, 52(6): 625−630 Cao Qing-Jie, Shi Zai-Feng, Zhang Jia-Ping, Li Hang-Yuan, Gao Jing, Yao Su-Ying. Sub-regional and multiple criteria full-reference image quality assessment. Journal of Tianjin University (Science and Technology), 2019, 52(6): 625−630
[6]	Wang Z, Bovik A C. Mean squared error: love it or leave it? A new look at signal fidelity measures. IEEE Signal Processing Magazine, 2009, 26(1): 98−117 doi: 10.1109/MSP.2008.930649
[7]	Huynh-Thu Q, Ghanbari M. Scope of validity of PSNR in image/video quality assessment. Electronics Letters, 2008, 44(13): 800−801 doi: 10.1049/el:20080522
[8]	Wang Z, Bovik A C, Sheikh H R, Simoncelli E P. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on image processing, 2004, 13(4): 600−612 doi: 10.1109/TIP.2003.819861
[9]	Wang Z, Simoncelli E P, Bovik A C. Multiscale structural similarity for image quality assessment. In: Proceedings of the 37th IEEE Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, USA, 2003. 1398−1402
[10]	Wang Z, Li Q. Information content weighting for perceptual image quality assessment. IEEE Transactions on Image Processing, 2011, 20(5): 1185−1198 doi: 10.1109/TIP.2010.2092435
[11]	Li C F, Bovik A C. Three-component weighted structural similarity index. In: Proceedings of the 2009 SPIE Conference on Image Quality and System Performance, San Jose, California, USA, 2009. 7242: 72420Q−72420Q-9
[12]	刘大瑾, 叶建兵, 刘家骏. SSIM框架下基于SVD的灰度图像质量评价算法研究. 南京师大学报(自然科学版), 2017, 40(1): 73−78 Liu Da-Jin, Ye Jian-Bing, Liu Jia-Jun. SVD-based gray-scale image quality assessmentalgorithms in the SSIM perspective. Journal of Nanjing Normal University (Natural Science Edition), 2017, 40(1): 73−78
[13]	闫乐乐, 李辉, 邱聚能, 梁平. 基于区域对比度和SSIM的图像质量评价方法. 应用光学, 2015, 36(1): 58−63 doi: 10.5768/JAO201536.0102002 Yan Le-Le, Li Hui, Qiu Ju-Neng, Liang Ping. Image qualty assessment method based on regional contrast and structural similarity. Journal of Applied Optics, 2015, 36(1): 58−63 doi: 10.5768/JAO201536.0102002
[14]	Jin X, Jiang G Y, Chen F, Yu M, Shao F, Peng Z J, et al. Adaptive image quality assessment method based on structural similarity. Journal of Optoelectronics. Laser, 2014, 25(2): 378−385
[15]	田浩南, 李素梅. 基于边缘的SSIM图像质量客观评价方法. 光子学报, 2013, 42(1): 110−114 doi: 10.3788/gzxb20134201.0110 Tian Hao-Nan, Li Su-Mei. Objective evaluation method for image quality based on edge structural similarity. Acta Photonica Sinca, 2013, 42(1): 110−114 doi: 10.3788/gzxb20134201.0110
[16]	Zhang L, Zhang L, Mou X Q, Zhang D. FSIM: a feature similarity index for image quality assessment. IEEE Transactions on Image Processing, 2011, 20(8): 2378−2386 doi: 10.1109/TIP.2011.2109730
[17]	Liu A M, Lin W S, Narwaria M. Image quality assessment based on gradient similarity. IEEE Transactions on Image Processing, 2012, 21(4): 1500−1512 doi: 10.1109/TIP.2011.2175935
[18]	Zhang X D, Feng X C, Wang W W, Xue W F. Edge strength similarity for image quality assessment. IEEE Signal Processing Letters, 2013, 20(4): 319−322 doi: 10.1109/LSP.2013.2244081
[19]	Sun W, Liao Q M, Xue J H, Zhou F. SPSIM: a superpixel-based similarity index for full-reference image quality assessment. IEEE Transactions on Image Processing, 2018, 27(9): 4232−4244 doi: 10.1109/TIP.2018.2837341
[20]	Ding L, Huang H, Zang Y. Image quality assessment using directional anisotropy structure measurement. IEEE Transactions on Image Processing, 2017, 26(4): 1799−1809 doi: 10.1109/TIP.2017.2665972
[21]	Xue W F, Zhang L, Mou X Q, Bovik A C. Gradient magnitude similarity deviation: a highly efficient perceptual image quality index. IEEE Transactions on Image Processing, 2014, 23(2): 684−695 doi: 10.1109/TIP.2013.2293423
[22]	Pei S C, Chen L H. Image quality assessment using human visual DOG model fused with random forest. IEEE Transactions on Image Processing, 2015, 24(11): 3282−3292 doi: 10.1109/TIP.2015.2440172
[23]	Reisenhofer R, Bosse S, Kutyniok G, Wiegand T. A haar wavelet-based perceptual similarity index for image quality assessment. Signal Processing: Image Communication, 2018, 61: 33−43 doi: 10.1016/j.image.2017.11.001
[24]	薛定宇. 分数阶微积分学与分数阶控制. 北京: 科学出版社, 2018. 31−72 Xue Ding-Yu. Fractional Calculus and Fractional-order Control. Beijing: Publishing House of Science, 2018. 31−72
[25]	张桂梅, 孙晓旭, 刘建新, 储珺. 基于分数阶微分的TV-L1光流模型的图像配准方法研究. 自动化学报, 2017, 43(12): 2213−2224 Zhang Gui-Mei, Sun Xiao-Xu, Liu Jian-Xin, Chun Jun. Research on TV-L1 optical flow model for image registration based on fractional-order differentiation. Acta Automatica Sinica, 2017, 43(12): 2213−2224
[26]	陈云, 郭宝裕, 马祥园. 基于分数阶微积分正则化的图像处理. 计算数学, 2017, (39): 393−406 Chen Yun, Guo Bao-Yu, Ma Xiang-Yuan. Image processing based on regularization with fractional clculus. Mathematica Numerica Sinica, 2017, (39): 393−406
[27]	Ponomarenko N, Jin L, Ieremeiev O, Lukin V, Egiazarian K, Astola J, et al. Image database TID2013: peculiarities, results and perspectives. Image Communication, 2015, 30(C): 57−77
[28]	Ponomarenko N, Lukin V, Zelensky A, Egiazarian K, Astola J, Carli M, et al. TID2008: a database for evaluation of full-reference visual quality assessment metrics [Online], available: http://www.ponomarenko.info/papers/mre, November 1, 2016
[29]	Larson E C, Chandler D. Categorical subjective image quality (CSIQ) database [Online], available: http://vision.okstate.edu/csiq, November 1, 2016
[30]	Sheikh H R, Wang Z, Bovik A C. Image and video quality assessment research at LIVE. [Online], available: http://live.ece.utexas.edu/rese-arch/quality/, November 1, 2016
[31]	Chandler D M, Hemami S S. VSNR: a wavelet-based visual signal-to-noise ratio for natural images. IEEE Transactions on Image Processing, 2007, 16(9): 2284−2298 doi: 10.1109/TIP.2007.901820
[32]	Sheikh H R, Bovik A C, Veciana G D. An information fidelity criterion for image quality assessment using natural scene statistics. IEEE Transactions on Image Processing, 2005, 14(12): 2117−2128 doi: 10.1109/TIP.2005.859389