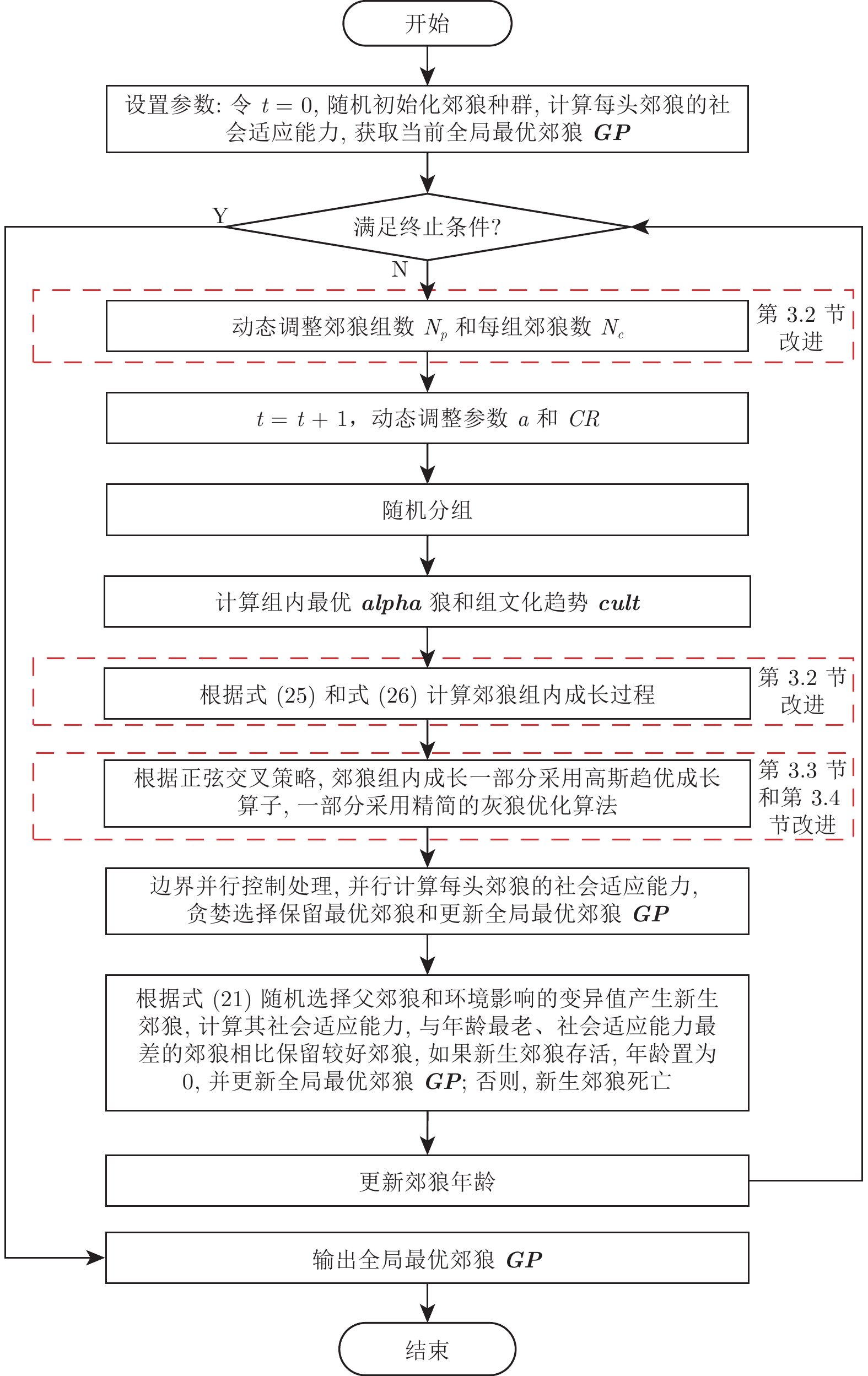
Hybrid Coyote Optimization Algorithm With Grey Wolf Optimizer and Its Application to Clustering Optimization
-
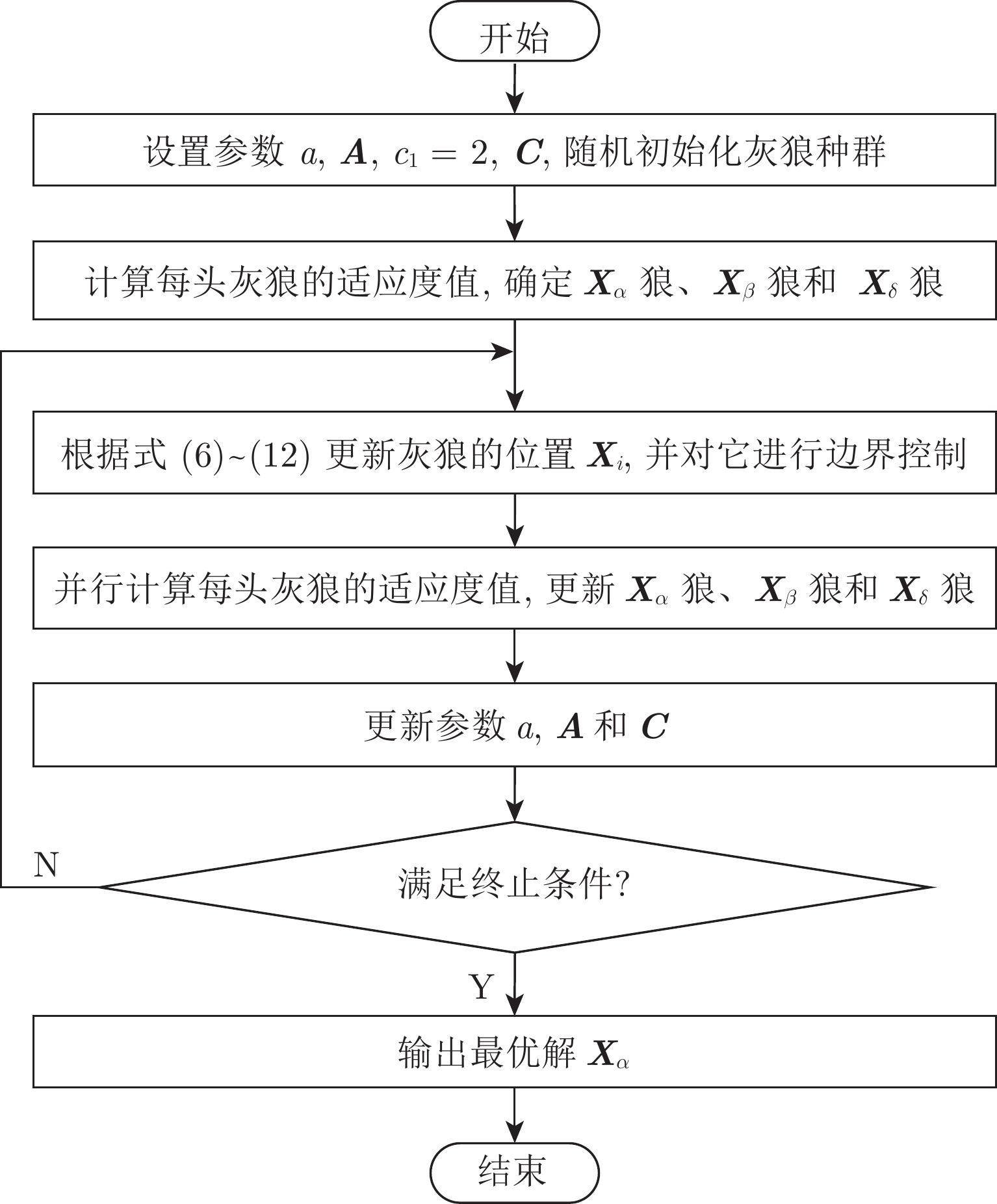
摘要: 郊狼优化算法(Coyote optimization algorithm, COA)是最近提出的一种新颖且具有较大应用潜力的群智能优化算法, 具有独特的搜索机制和能较好解决全局优化问题等优势, 但在处理复杂优化问题时存在搜索效率低、可操作性差和收敛速度慢等不足. 为弥补其不足, 并借鉴灰狼优化算法(Grey wolf optimizer, GWO)的优势, 提出了一种COA与GWO的混合算法(Hybrid COA with GWO, HCOAG). 首先提出了一种改进的COA (Improved COA, ICOA), 即将一种高斯全局趋优成长算子替换原算法的成长算子以提高搜索效率和收敛速度, 并提出一种动态调整组内郊狼数方案, 使得算法的搜索能力和可操作性都得到增强; 然后提出了一种简化操作的GWO (Simplified GWO, SGWO), 以提高算法的可操作性和降低其计算复杂度; 最后采用正弦交叉策略将ICOA与SGWO二者融合, 进一步获得更好的优化性能. 大量的经典函数和CEC2017复杂函数优化以及K-Means聚类优化的实验结果表明, 与COA相比, HCOAG具有更高的搜索效率、更强的可操作性和更快的收敛速度, 与其他先进的对比算法相比, HCOAG具有更好的优化性能, 能更好地解决聚类优化问题.Abstract: Coyote optimization algorithm (COA) is a novel swarm intelligence optimization algorithm with great application potential, which was proposed recently. It has a unique search mechanism and the advantages to solve global optimization problems well and so on. But when dealing with the complex optimization problems, it has some defects, such as low search efficiency, poor operability, slow convergence speed and so on. To make up for COA's disadvantages and utilize the advantages of grey wolf optimizer (GWO), a hybrid COA with GWO (HCOAG) is proposed. Firstly, an improved COA (ICOA) is proposed. A Gaussian global-best growing operator replaces the growing operator of the original algorithm to improve the search efficiency and convergence speed, and a dynamic adjustment scheme of coyote number in each group is proposed to enhance the search ability and operability. Secondly, in order to improve the operability and reduce the computational complexity of the algorithm, a simplified GWO (SGWO) is proposed. Finally, ICOA and SGWO are integrated by a sinusoidal crossover strategy to further get better optimization performance. A large number of experimental results on classical benchmark functions and CEC2017 complex functions and K-Means clustering show that, compared with COA, HCOAG has higher search efficiency, stronger operability and faster convergence speed. Compared with other state-of-the-art comparison algorithms, HCOAG has better optimization performance and can solve clustering optimization problems better.
-
表 1 HCOAG与其不完全算法的结果对比
Table 1 Comparison results of HCOAG and its incomplete algorithms
函数 标准 HCOAG COA GWO HCOAG5 HCOAG10 ICOA SGWO F1 Mean 7.4494×10−4 1.2099×103 1.2813×109 4.1072×10−4 1.9800×10−3 1.0737×102 3.3279×103 Std 1.4801×10−3 1.2998×103 9.6388×108 8.5916×10−4 2.9438×10−3 1.0569×102 4.3271×103 Rank 2 5 7 1 3 4 6 F2 Mean 1.1941×101 2.9013×1021 3.1831×1032 4.8580×103 1.8078×101 8.6764×1015 3.3582×1014 Std 2.4077×101 1.1462×1022 1.5894×1033 3.3985×104 5.0208×101 3.5675×1016 1.3200×1015 Rank 1 6 7 3 2 5 4 F3 Mean 9.5410×10−1 6.0573×104 2.8342×104 7.6972×10−1 1.0995×100 3.3032×104 8.7276×102 Std 1.9288×100 1.0177×104 9.2323×103 9.8032×10−1 1.6794×100 6.8409×103 7.2376×102 Rank 2 7 5 1 3 6 4 F4 Mean 1.8113×101 8.4041×101 2.0825×102 2.0841×101 2.8446×101 4.8248×101 1.0495×102 Std 2.7696×101 8.5306×100 8.4445×101 3.0540×101 3.1826×101 3.3517×101 2.4806×101 Rank 1 5 7 2 3 4 6 F5 Mean 2.8433×101 5.2890×101 9.6116×101 3.5884×101 3.0204×101 3.4844×101 3.1488×101 Std 6.8886×100 1.5025×101 3.2690×101 1.0115×101 8.8983×100 1.0983×101 9.2242×100 Rank 1 6 7 5 2 4 3 F6 Mean 1.7483×10−7 1.6399×10−5 6.3664×100 9.4452×10−7 1.5005×10−6 2.8782×10−4 2.0381×10−2 Std 4.7524×10−7 9.6428×10−6 3.1596×100 2.4080×10−6 5.9643×10−6 1.6254×10−4 2.7102×10−2 Rank 1 4 7 2 3 5 6 F7 Mean 6.1055×101 7.5148×101 1.4460×102 6.7082×101 5.9300×101 6.7675×101 6.4025×101 Std 1.0851×101 1.3762×101 4.6314×101 1.1241×101 9.4998×100 1.1520×101 1.1856×101 Rank 2 6 7 4 1 5 3 F8 Mean 3.2489×101 5.6110×101 8.4662×101 3.6085×101 2.9446×101 3.6138×101 3.1775×101 Std 1.2272×101 1.8774×101 2.5270×101 8.8063×100 7.9048×100 1.0081×101 7.8884×100 Rank 3 6 7 4 1 5 2 F9 Mean 2.7362×10−1 5.6225×10−1 5.5392×102 5.2270×10−1 2.5931×10−1 8.8559×10−2 7.4159×100 Std 4.8298×10−1 1.0209×100 3.2695×102 8.7374×10−1 4.6957×10−1 1.5656×10−1 6.7112×100 Rank 3 5 7 4 2 1 6 F10 Mean 2.2671×103 2.7575×103 3.1862×103 2.5574×103 2.3435×103 2.1380×103 2.1424×103 Std 6.1427×102 4.6685×102 9.7886×102 5.3524×102 6.0670×102 5.6098×102 4.0691×102 Rank 3 6 7 5 4 1 2 F11 Mean 2.1678×101 4.1143×101 4.9771×102 2.9822×101 2.6698×101 2.2685×101 1.0908×102 Std 2.0907×101 2.7367×101 6.4235×102 2.6128×101 2.4059×101 2.0893×101 3.8218×101 Rank 1 5 7 4 3 2 6 F12 Mean 9.8943×103 1.2532×105 4.0285×107 1.2577×104 1.0657×104 1.3660×105 2.0716×105 Std 6.0932×103 1.2555×105 7.3849×107 6.4424×103 6.4606×103 9.3092×104 1.9967×105 Rank 1 4 7 3 2 5 6 F13 Mean 1.9749×103 2.0357×104 2.8073×106 3.0265×103 3.1829×103 3.6293×102 1.3271×104 Std 3.8565×103 2.6333×104 1.6225×107 6.2901×103 8.0719×103 8.9975×101 1.5283×104 Rank 2 6 7 3 4 1 5 F14 Mean 8.6436×101 8.0070×101 1.3112×105 7.7150×101 1.0134×102 5.6726×101 1.4132×104 Std 4.3766×101 1.9915×101 2.3335×105 6.0071×101 9.2585×101 1.4850×101 1.7944×104 Rank 4 3 7 2 5 1 6 F15 Mean 1.8396×103 2.0792×103 3.3658×105 7.1579×102 1.7386×103 6.9111×101 6.6116×103 Std 2.9044×103 7.9984×103 7.9125×105 1.2272×103 2.9477×103 1.9083×101 8.3961×103 Rank 4 5 7 2 3 1 6 F16 Mean 3.0243×102 7.9869×102 8.1416×102 3.3715×102 3.0883×102 4.6416×102 5.0252×102 Std 2.0550×102 2.8651×102 2.6440×102 2.1415×102 1.8878×102 2.6962×102 2.4545×102 Rank 1 6 7 3 2 4 5 F17 Mean 4.7111×101 2.2439×102 2.7004×102 6.4809×101 5.3120×101 3.7365×101 1.3984×102 Std 4.0925×101 1.3518×102 1.3820×102 5.3991×101 4.7801×101 4.0654×101 8.0664×101 Rank 2 6 7 4 3 1 5 F18 Mean 6.1013×104 6.9910×104 7.1643×105 5.1875×104 5.0376×104 3.9930×104 1.8454×105 Std 5.7031×104 1.0210×105 8.2799×105 3.6270×104 3.7592×104 2.0034×104 1.7045×105 Rank 4 5 7 3 2 1 6 F19 Mean 3.4042×101 4.4886×103 4.6400×105 3.4163×101 3.0105×102 2.4678×101 5.4815×103 Std 2.0528×101 1.3325×104 5.4998×105 3.9687×101 1.1322×103 7.1259×100 4.9859×103 Rank 2 5 7 3 4 1 6 F20 Mean 9.6665×101 2.4290×102 3.6059×102 1.0084×102 1.1637×102 1.0389×102 2.0165×102 Std 7.7834×101 1.4995×102 1.0264×102 6.6726×101 7.5890×101 8.7694×101 9.6673×101 Rank 1 6 7 2 4 3 5 F21 Mean 2.3023×102 2.5626×102 2.8298×102 2.3713×102 2.3135×102 2.3724×102 2.3289×102 Std 8.5095×100 1.6800×101 2.5684×101 1.0815×101 9.8453×100 1.1261×101 9.9428×100 Rank 1 6 7 4 2 5 3 F22 Mean 1.0010×102 1.9999×103 8.0434×102 1.0005×102 1.0005×102 1.0005×102 1.2974×102 Std 4.8096×10−1 1.5970×103 1.1113×103 3.4354×10−1 3.4444×10−1 3.4443×10−1 2.0703×102 Rank 4 7 6 1 3 2 5 F23 Mean 3.7755×102 4.1635×102 4.7029×102 3.8706×102 3.7831×102 3.8441×102 3.8854×102 Std 1.0911×101 1.6898×101 2.9324×101 1.3271×101 8.1817×100 1.0543×101 1.3692×101 Rank 1 6 7 4 2 3 5 F24 Mean 4.4827×102 5.4044×102 5.2489×102 4.5484×102 4.4530×102 4.5862×102 4.5671×102 Std 1.0757×101 4.5778×101 3.3902×101 1.1783×101 1.1461×101 1.2203×101 1.1956×101 Rank 2 7 6 3 1 5 4 F25 Mean 3.8777×102 3.8706×102 4.7784×102 3.8747×102 3.8729×102 3.8698×102 4.0239×102 Std 5.4462×100 8.0647×10−1 2.3819×101 1.5625×100 1.2735×100 5.4095×10−1 1.5135×101 Rank 5 2 7 4 3 1 6 F26 Mean 1.2578×103 1.6520×103 2.0116×103 1.3249×103 1.2449×103 1.3138×103 1.5024×103 Std 1.9807×102 1.7070×102 5.7618×102 3.1093×102 3.4947×102 1.9599×102 2.8691×102 Rank 2 6 7 4 1 3 5 F27 Mean 5.1091×102 5.0430×102 5.9279×102 5.1349×102 5.1088×102 5.0560×102 5.3331×102 Std 7.7116×100 8.2707×100 3.8462×101 8.6401×100 8.6837×100 7.3827×100 1.1175×101 Rank 4 1 7 5 3 2 6 F28 Mean 3.3558×102 4.0555×102 5.9941×102 3.2930×102 3.3793×102 3.4828×102 4.5710×102 Std 5.3866×101 3.6156×101 6.9788×101 5.1585×101 5.1950×101 5.3564×101 2.3392×101 Rank 2 5 7 1 3 4 6 F29 Mean 4.5991×102 6.6978×102 8.5036×102 4.8821×102 4.6287×102 4.5683×102 6.2453×102 Std 4.4075×101 1.7459×102 1.8235×102 5.5772×101 4.3839×101 4.4800×101 1.1861×102 Rank 2 6 7 4 3 1 5 F30 Mean 2.9823×103 6.0618×103 4.0643×106 3.1036×103 2.9323×103 1.9586×104 6.1880×103 Std 6.1135×102 4.7022×103 3.1688×106 8.4665×102 5.9332×102 7.3086×103 2.8250×103 Rank 2 4 7 3 1 6 5 Count 10 1 0 4 5 10 0 Ave rank 2.20 5.23 6.87 3.10 2.60 3.07 4.93 Total rank 1 6 7 4 2 3 5 表 2 在6个经典函数上的实验结果对比
Table 2 Comparison results on the 6 classic functions
函数 标准 D = 10 HCOAG COA GWO HFPSO DEBBO f1 Mean 6.0684×10−9 1.7833×102 9.0799×10−15 3.4157×10−5 6.7086×10−2 Std 4.8458×10−9 6.3524×101 2.4849×10−14 2.4485×10−5 3.1056×10−2 Rank 2 5 1 3 4 f2 Mean 8.4133×10−6 2.3737×100 1.3222×10−9 1.3703×10−3 2.8483×10−2 Std 3.7531×10−6 4.0964×10−1 1.1382×10−9 6.5582×10−4 7.0993×10−3 Rank 2 5 1 3 4 f3 Mean 0 1.6180×102 1.0000×10−1 0 0 Std 0 5.0787×101 3.0513×10−1 0 0 Rank 1 5 4 1 1 f4 Mean 1.2498×10−10 4.0253×100 1.5325×10−6 3.5760×10−7 1.8575×10−3 Std 2.0501×10−10 1.6104×100 9.4192×10−7 4.1539×10−7 1.0158×10−3 Rank 1 5 3 2 4 f5 Mean 2.0046×10−8 7.1619×102 2.4093×10−5 4.6770×10−6 2.6132×10−2 Std 5.9686×10−8 1.5819×103 1.4121×10−5 5.6661×10−6 1.0613×10−2 Rank 1 5 3 2 4 f6 Mean 4.1921×10−10 1.7228×100 1.2593×10−2 4.9377×10−7 3.5149×10−3 Std 4.3501×10−10 5.1829×10−1 6.8779×10−2 4.8665×10−7 1.5826×10−3 Rank 1 5 4 2 3 D = 30 f1 Mean 1.3966×10−17 3.2554×101 5.4432×10−41 7.2595×10−9 2.7076×10−4 Std 3.2255×10−17 5.9567×100 7.1605×10−41 7.3446×10−9 1.1010×10−4 Rank 2 5 1 3 4 f2 Mean 2.8862×10−10 1.3998×100 6.0158×10−24 5.3463×10−5 1.3264×10−3 Std 4.6435×10−10 1.9835×10−1 6.2049×10−24 3.9178×10−5 2.3103×10−4 Rank 2 5 1 3 4 f3 Mean 0 3.3700×101 3.3333×10−2 0 0 Std 0 7.9877×100 1.8257×10−1 0 0 Rank 1 5 4 1 1 f4 Mean 1.0451×10−17 3.8002×100 1.5129×10−2 1.7278×10−2 6.4886×10−5 Std 3.0738×10−17 1.3163×100 1.0471×10−2 3.9296×10−2 2.7878×10−5 Rank 1 5 3 4 2 f5 Mean 5.3309×10−17 1.8376×101 1.6587×10−1 3.2962×10−3 5.0150×10−4 Std 1.5184×10−16 5.8919×100 1.1940×10−1 5.1211×10−3 2.1237×10−4 Rank 1 5 4 3 2 f6 Mean 1.2484×10−18 1.8049×100 7.9738×10−1 8.2480×10−3 8.5930×10−5 Std 1.7135×10−18 4.9152×10−1 7.4565×10−1 4.5176×10−2 3.9292×10−5 Rank 1 5 4 3 2 Count 8 0 4 2 2 Ave rank 1.33 5.00 2.75 2.50 2.92 Total rank 1 5 3 2 4 表 3 6个经典函数的情况
Table 3 Details of 6 classical benchmark functions
类型 函数名称 函数表达式 搜索范围 最小值 单峰函数 Sphere ${f_1}(x) = \displaystyle\sum_{i = 1}^D {x_i^2}$ [−100, 100] 0 Schwefel 2.22 ${f_2}(x) = \displaystyle\sum_{i = 1}^D {\left| { {x_i} } \right|} + \prod_{i = 1}^D {\left| { {x_i} } \right|}$ [−10, 10] 0 Step ${f_3}(x) = \displaystyle\sum_{i = 1}^D { { {\left( {\left\lfloor { {x_i} + 0.5} \right\rfloor } \right)}^2} }$ [−100, 100] 0 多峰函数 Penalized 1 ${f_4}(x) = \dfrac{\pi}{D}\bigg\{ {10{ {\sin }^2}\left( {\pi {y_i} } \right)} +$
$\displaystyle\sum_{i = 1}^{D - 1} { { {\left( { {y_i} - 1} \right)}^2}\left[ {1 + 10{ {\sin }^2}\left( {\pi {y_{i + 1} } } \right)} \right]} { + { {\left( { {y_D} - 1} \right)}^2} } \bigg\} +$
$\displaystyle\sum_{i = 1}^D {u\left( { {x_i},10,100,4} \right)}$
${y_i} = 1 + \dfrac{1}{4}\left( { {x_i} + 1} \right)$
$u\left( { {x_i},a,k,m} \right) = $$\left\{ \begin{aligned}&k{\left( { {x_i} - a} \right)^m},\quad\;\; {x_i} > a\\&0, \quad \quad \quad \quad \quad\quad\;\; - a \le {x_i} \le a\\&k{\left( { - {x_i} - a} \right)^m},\quad {x_i} < - a \end{aligned} \right.$[−50, 50] 0 Penalized 2 ${f_5}(x) = 0.1\bigg\{ { { {\sin }^2} } \left( {\pi {x_1} } \right) + \displaystyle\sum_{i = 1}^{D - 1} { { {\left( { {x_i} - 1} \right)}^2} } \left[ {1 + { {\sin }^2}\left( {3\pi {x_{i + 1} } } \right)} \right] +$
$\left( { {x_D} - 1} \right) {\Big[ {1 + { {\sin }^2}\left( {2\pi {x_D} } \right)} \Big]} \bigg\} + \displaystyle\sum_{i = 1}^D {u\left( { {x_i},5,100,4} \right)}$[−50, 50] 0 Levy ${f_6}(x) = \displaystyle\sum_{i = 1}^{D - 1} { { {\left( { {x_i} - 1} \right)}^2} } \left[ {1 + { {\sin }^2}\left( {3\pi {x_{i + 1} } } \right)} \right] +$
${\sin ^2}\left( {3\pi {x_1} } \right) + \left| { {x_D} - 1} \right|\Big[ {1 + { {\sin }^2}\left( {3\pi {x_D} } \right)} \Big]$[−10, 10] 0 表 4 在30维CEC2017复杂函数上的优化结果对比
Table 4 Comparison results on the 30-dimensional complex functions from CEC2017
函数 标准 HCOAG COA GWO MEGWO HFPSO DEBBO SaDE SE04 FWA TLBO F1 Mean 7.4494×10−4 1.2099×103 1.2813×109 4.5517×103 3.9338×103 2.7849×103 3.0714×103 3.2930×103 4.3987×106 2.9846×103 Std 1.4801×10−3 1.2998×103 9.6388×108 1.0677×103 5.3689×103 4.0364×103 3.5072×103 4.2328×103 1.4055×106 3.1471×103 Rank 1 2 10 8 7 3 5 6 9 4 F2 Mean 1.1941×101 2.9013×1021 3.1831×1032 2.8884×108 5.3485×104 1.5057×1017 8.6275×10−1 3.0802×1013 4.1397×1015 1.0448×1016 Std 2.4077×101 1.1462×1022 1.5894×1033 8.0571×108 3.2847×105 3.5179×1017 4.9357×100 1.1694×1014 1.5680×1016 4.7082×1016 Rank 2 9 10 4 3 8 1 5 6 7 F3 Mean 9.5410×10−1 6.0573×104 2.8342×104 2.2633×102 1.5595×10−7 3.6772×104 3.0045×102 9.7974×103 2.4748×104 4.0488×10−4 Std 1.9288×100 1.0177×104 9.2323×103 1.7031×102 2.3334×10−7 5.8394×103 7.3017×102 3.4377×103 6.3467×103 1.6647×10−3 Rank 3 10 8 4 1 9 5 6 7 2 F4 Mean 1.8113×101 8.4041×101 2.0825×102 2.4815×101 6.9386×101 8.4851×101 6.0423×101 8.5881×101 1.1370×102 5.9054×101 Std 2.7696×101 8.5306×100 8.4445×101 2.8995×101 2.1364×101 2.2848×10−1 2.9825×101 1.1251×101 1.7315×101 3.0429×101 Rank 1 6 10 2 5 7 4 8 9 3 F5 Mean 2.8433×101 5.2890×101 9.6116×101 5.6912×101 8.5624×101 5.8216×101 5.6192×101 4.1688×101 1.8456×102 8.5717×101 Std 6.8886×100 1.5025×101 3.2690×101 1.0725×101 1.7427×101 6.5957×100 1.4216×101 8.1545×100 3.3933×101 1.8601×101 Rank 1 3 9 5 7 6 4 2 10 8 F6 Mean 1.7483×10−7 1.6399×10−5 6.3664×100 2.4470×10−1 1.0170×100 1.1369×10−13 8.9317×10−2 7.5481×10−6 5.1770×100 7.2903×100 Std 4.7524×10−7 9.6428×10−6 3.1596×100 8.1620×10−2 2.3644×100 0 1.3955×10−1 3.9880×10−5 3.1351×100 4.4538×100 Rank 2 4 9 6 7 1 5 3 8 10 F7 Mean 6.1055×101 7.5148×101 1.4460×102 8.9106×101 1.0407×102 9.9725×101 9.4945×101 7.2448×101 2.0998×102 1.3661×102 Std 1.0851×101 1.3762×101 4.6314×101 1.0935×101 1.9791×101 6.4285×100 1.9879×101 7.3495×100 4.4817×101 2.4846×101 Rank 1 3 9 4 7 6 5 2 10 8 F8 Mean 3.2489×101 5.6110×101 8.4662×101 5.9398×101 7.2842×101 5.9299×101 5.3942×101 4.4194×101 1.4508×102 7.1339×101 Std 1.2272×101 1.8774×101 2.5270×101 1.0663×101 1.7967×101 6.0788×100 1.2792×101 6.5834×100 2.1470×101 1.4852×101 Rank 1 4 9 6 8 5 3 2 10 7 F9 Mean 2.7362×10−1 5.6225×10−1 5.5392×102 7.8267×100 3.2733×101 4.0125×10−14 8.3556×101 3.0839×10−1 3.5295×103 2.4197×102 Std 4.8298×10−1 1.0209×100 3.2695×102 1.1815×101 1.3249×102 5.4870×10−14 6.2643×101 8.4139×10−1 9.5511×102 1.4491×102 Rank 2 4 9 5 6 1 7 3 10 8 F10 Mean 2.2671×103 2.7575×103 3.1862×103 2.4369×103 2.9908×103 3.2911×103 2.3253×103 2.3267×103 3.7800×103 6.0667×103 Std 6.1427×102 4.6685×102 9.7886×102 4.4542×102 5.9210×102 2.7284×102 4.9247×102 2.8457×102 5.9660×102 1.0625×103 Rank 1 5 7 4 6 8 2 3 9 10 F11 Mean 2.1678×101 4.1143×101 4.9771×102 2.9612×101 1.1553×102 3.7430×101 1.0032×102 4.1343×101 1.6164×102 1.2672×102 Std 2.0907×101 2.7367×101 6.4235×102 1.0347×101 3.9628×101 2.3672×101 4.3101×101 2.7994×101 4.5263×101 4.5717×101 Rank 1 4 10 2 7 3 6 5 9 8 F12 Mean 9.8943×103 1.2532×105 4.0285×107 1.5983×104 9.9670×104 1.3866×105 6.8629×104 1.1143×106 4.6351×106 3.3042×104 Std 6.0932×103 1.2555×105 7.3849×107 4.0434×103 1.0658×105 9.2097×104 3.8252×104 8.1422×105 3.1121×106 2.8646×104 Rank 1 6 10 2 5 7 4 8 9 3 F13 Mean 1.9749×103 2.0357×104 2.8073×106 2.0450×102 3.0927×104 8.1265×103 1.1211×104 4.6063×103 3.7320×104 1.4857×104 Std 3.8565×103 2.6333×104 1.6225×107 2.7028×101 2.7301×104 7.8066×103 1.0535×104 4.8590×103 2.6480×104 1.7072×104 Rank 2 7 10 1 8 4 5 3 9 6 F14 Mean 8.6436×101 8.0070×101 1.3112×105 6.1985×101 6.7377×103 4.9240×103 4.3238×103 7.1204×104 2.6955×105 3.5454×103 Std 4.3766×101 1.9915×101 2.3335×105 8.6647×100 5.5695×103 3.2902×103 5.7159×103 5.9323×104 2.4525×105 4.1276×103 Rank 3 2 9 1 7 6 5 8 10 4 F15 Mean 1.8396×103 2.0792×103 3.3658×105 5.1634×101 9.7487×103 4.9944×103 2.1676×103 2.2013×103 3.2784×103 3.9091×103 Std 2.9044×103 7.9984×103 7.9125×105 1.0713×101 1.2114×104 6.6468×103 3.0178×103 1.9756×103 1.9819×103 4.3347×103 Rank 2 3 10 1 9 8 4 5 6 7 F16 Mean 3.0243×102 7.9869×102 8.1416×102 4.4823×102 7.7229×102 3.9643×102 5.6072×102 4.9392×102 1.2266×103 5.0039×102 Std 2.0550×102 2.8651×102 2.6440×102 1.3443×102 2.2590×102 1.1932×102 2.0850×102 1.7309×102 3.0034×102 2.7575×102 Rank 1 8 9 3 7 2 6 4 10 5 F17 Mean 4.7111×101 2.2439×102 2.7004×102 6.9544×101 2.5591×102 8.1642×101 8.7684×101 1.4116×102 5.5825×102 2.3994×102 Std 4.0925×101 1.3518×102 1.3820×102 1.7296×101 1.2971×102 2.2037×101 9.1289×101 8.5026×101 2.3401×102 8.8703×101 Rank 1 6 9 2 8 3 4 5 10 7 F18 Mean 6.1013×104 6.9910×104 7.1643×105 2.0505×102 1.1409×105 3.2225×105 1.0034×105 2.1361×105 9.8409×105 2.0609×105 Std 5.7031×104 1.0210×105 8.2799×105 4.7536×101 1.1535×105 1.2197×105 1.1019×105 1.3261×105 1.1184×106 1.5131×105 Rank 2 3 9 1 5 8 4 7 10 6 F19 Mean 3.4042×101 4.4886×103 4.6400×105 2.9977×101 8.6631×103 8.3686×103 5.9612×103 2.0723×103 5.2207×103 6.3203×103 Std 2.0528×101 1.3325×104 5.4998×105 3.3897×100 1.9974×104 9.2795×103 7.1112×103 2.1685×103 3.9175×103 1.0793×104 Rank 2 4 10 1 9 8 6 3 5 7 F20 Mean 9.6665×101 2.4290×102 3.6059×102 1.1363×102 2.6516×102 5.5205×101 1.2989×102 1.7303×102 4.6345×102 2.4392×102 Std 7.7834×101 1.4995×102 1.0264×102 5.2411×101 1.1737×102 3.5413×101 7.0970×101 7.2015×101 1.7129×102 8.4432×101 Rank 2 6 9 3 8 1 4 5 10 7 F21 Mean 2.3023×102 2.5626×102 2.8298×102 2.5458×102 2.7446×102 2.5950×102 2.4896×102 2.5047×102 3.7768×102 2.6988×102 Std 8.5095×100 1.6800×101 2.5686×101 3.3247×101 1.9517×101 7.6690×100 1.3195×101 8.4442×100 7.9462×101 1.9589×101 Rank 1 5 9 4 8 6 2 3 10 7 F22 Mean 1.0010×102 1.9999×103 8.0434×102 1.0022×102 1.4532×103 1.0000×102 1.0228×102 1.0211×103 2.1380×103 1.0232×102 Std 4.8096×10−1 1.5970×103 1.1113×103 4.3917×10−2 1.8286×103 2.3100×10−13 3.2279×100 1.2872×103 2.2149×103 4.0114×100 Rank 2 9 6 3 8 1 4 7 10 5 F23 Mean 3.7755×102 4.1635×102 4.7029×102 3.8959×102 4.8447×102 4.0323×102 4.1472×102 4.0247×102 5.8963×102 4.5003×102 Std 1.0911×101 1.6898×101 2.9324×101 6.8787×101 4.4709×101 5.6348×100 1.8742×101 8.1687×100 8.8792×101 3.0546×101 Rank 1 6 8 2 9 4 5 3 10 7 F24 Mean 4.4827×102 5.4044×102 5.2489×102 4.8972×102 5.6079×102 4.7430×102 4.8169×102 4.9840×102 7.9489×102 5.0152×102 Std 1.0757×101 4.5778×101 3.3902×101 1.6597×101 5.7847×101 6.0055×100 2.0610×101 1.3899×101 8.6391×101 2.3700×101 Rank 1 8 7 4 9 2 3 5 10 6 F25 Mean 3.8777×102 3.8706×102 4.7784×102 3.8374×102 3.8818×102 3.8691×102 4.0124×102 3.8779×102 4.1099×102 4.0877×102 Std 5.4462×100 8.0647×10−1 2.3819×101 1.8246×10−1 3.4076×100 7.5524×10−2 1.9489×101 1.1319×100 2.1657×101 2.2401×101 Rank 4 3 10 1 6 2 7 5 9 8 F26 Mean 1.2578×103 1.6520×103 2.0116×103 2.5051×102 1.4922×103 1.4821×103 1.7344×103 1.5337×103 2.2418×103 1.8645×103 Std 1.9807×102 1.7070×102 5.7618×102 4.1112×101 9.6940×102 7.2015×101 7.1347×102 1.9051×102 1.7373×103 1.0276×103 Rank 2 6 9 1 4 3 7 5 10 8 F27 Mean 5.1091×102 5.0430×102 5.9279×102 5.1286×102 5.3523×102 4.9807×102 5.4289×102 5.0744×102 5.7919×102 5.3827×102 Std 7.7116×100 8.2707×100 3.8462×101 6.1632×100 2.1095×101 4.7270×100 1.7086×101 3.6242×100 3.5317×101 1.6907×101 Rank 4 2 10 5 6 1 8 3 9 7 F28 Mean 3.3558×102 4.0555×102 5.9941×102 3.6492×102 3.5331×102 3.2281×102 3.3257×102 4.1364×102 4.6256×102 3.6806×102 Std 5.3866×101 3.6156×101 6.9788×101 3.2477×101 5.9179×101 3.7880×101 5.2165×101 2.5577×101 2.3601×101 5.3388×101 Rank 3 7 10 5 4 1 2 8 9 6 F29 Mean 4.5991×102 6.6978×102 8.5036×102 5.4385×102 6.7006×102 5.1851×102 5.5826×102 5.4778×102 1.0120×103 7.8922×102 Std 4.4075×101 1.7459×102 1.8235×102 5.4241×101 1.4475×102 3.4859×101 1.0040×102 8.1960×101 2.1872×102 1.3560×102 Rank 1 6 9 3 7 2 5 4 10 8 F30 Mean 2.9823×103 6.0618×103 4.0643×106 3.6855×103 1.8733×104 5.9405×103 5.0147×103 4.9671×103 1.5965×104 5.9572×103 Std 6.1135×102 4.7022×103 3.1688×106 3.3042×102 3.4470×104 2.3158×103 1.9712×103 2.0934×103 8.7877×103 3.9139×103 Rank 1 7 10 2 9 5 4 3 8 6 Count 15 0 0 7 1 6 1 0 0 0 Ave rank 1.73 5.27 9.10 3.17 6.67 4.37 4.53 4.63 9.03 6.50 Total rank 1 6 10 2 8 3 4 5 9 7 表 5 在30维CEC2017复杂函数上的上下界结果对比
Table 5 Comparison of upper and lower bounds on the 30-dimensional complex functions from CEC2017
函数 HCOAG COA/DEBBO 下界 上界 下界 上界 F1 3.8942×10-9 7.8898×10-3 3.5001×100 5.0055×103 F5 1.2935×101 4.1788×101 2.6865×101 9.2083×101 F11 4.0954×100 7.5899×101 1.3819×101 8.8108×101 F29 3.7200×102 6.0977×102 4.4500×102 6.2345×102 表 6 Wilcoxon符号秩检验结果
Table 6 Wilcoxon sign rank test results
$p $ $a=0.05 $ $R^+ $ $R^- $ $n/w/t/l $ HCOAG vs COA 1.3039×10−7 YES 453 12 30/27/0/3 HCOAG vs GWO 1.8626×10−9 YES 465 0 30/30/0/0 HCOAG vs MEGWO 2.7741×10−2 YES 339 126 30/23/0/7 HCOAG vs HFPSO 5.5879×10−9 YES 463 2 30/29/0/1 HCOAG vs DEBBO 9.0000×10−6 YES 429 36 30/23/0/7 HCOAG vs SaDE 3.5390×10−8 YES 458 7 30/28/0/2 HCOAG vs SE04 1.3039×10−8 YES 461 4 30/29/0/1 HCOAG vs FWA 1.8626×10−9 YES 465 0 30/30/0/0 HCOAG vs TLBO 3.7253×10−9 YES 464 1 30/29/0/1 表 7 Friedman检验结果
Table 7 Friedman test results
D p HCOAG COA GWO MEGWO HFPSO DEBBO SaDE SE04 FWA TLBO 30 6.3128×10-31 1.73 5.27 9.10 3.17 6.67 4.37 4.53 4.63 9.03 6.50 表 8 6种算法在K-Means聚类优化上的结果对比
Table 8 Comparison results of the 6 algorithms on K-Means clustering optimization
数据集 HCOAG COA MEGWO HFPSO IPSO IGA Wine (178, 13, 3) Mean 88.6271 116.7307 91.5916 93.622 89.8617 89.564 Std 3.4479×10−2 2.9398×100 2.5237×100 6.7353×100 3.9148×100 2.0321×100 Rank 1 6 4 5 3 2 Heart (270, 13, 2) Mean 283.7680 295.3786 284.5731 284.7653 285.0072 284.4112 Std 3.9989×10−3 2.3404×100 2.3896×10−1 2.3804×100 5.2425×100 2.1715×100 Rank 1 6 3 4 5 2 Iris (150, 4, 3) Mean 29.2053 31.0511 29.2659 29.3578 29.3578 29.2607 Std 8.8033×10−2 5.7768×10−1 1.3448×10−1 1.0048×100 1.0048×100 9.2414×10−2 Rank 1 6 3 4 4 2 Glass (214, 9, 6) Mean 55.0255 75.4621 68.8816 62.7114 57.3102 60.8651 Std 2.2242×100 2.1402×100 2.8975×100 3.7975×100 3.5444×100 3.5855×100 Rank 1 6 5 4 2 3 Newthyroid (215, 5, 3) Mean 40.0538 42.0033 40.4736 41.8087 40.8213 41.9155 Std 9.8154×10−3 7.6493×10−1 4.0104×10−1 2.8501×100 2.0086×100 2.8122×100 Rank 1 6 2 4 3 5 Liver disorders (345, 6, 2) Mean 90.3443 93.5344 90.3849 91.0246 90.3365 90.3698 Std 3.8530×10−4 1.0160×100 2.8148×10−2 2.6310×100 2.1424×10−2 2.0447×10−2 Rank 2 6 4 5 1 3 Balance (625, 4, 3) Mean 356.1247 357.6041 356.502 356.0165 356.0802 356.4092 Std 2.3618×10−1 4.0943×10−1 3.3785×10−1 1.5930×10−1 2.0303×10−1 1.4966×10−1 Rank 3 6 5 1 2 4 Count 5 0 0 1 1 0 Ave rank 1.43 6.00 3.71 3.86 2.86 3.00 Total rank 1 6 4 5 2 3 -
[1] 刘三阳, 靳安钊. 求解约束优化问题的协同进化教与学优化算法. 自动化学报, 2018, 44(9): 1690-1697Liu San-Yang, JIN An-Zhao. A Co-evolutionary teaching- learning-based optimization algorithm for constrained optimization problems. Acta Automatica Sinica, 2018, 44(9): 1690-1697 [2] 吕柏权, 张静静, 李占培, 刘廷章. 基于变换函数与填充函数的模糊粒子群优化算法. 自动化学报, 2018, 44(1): 74-86Lv Bai-Quan, Zhang Jing-Jing, Li Zhan-Pei, Liu Ting-Zhang. Fuzzy particle swarm optimization based on filled function and transformation function. Acta Automatica Sinica, 2018, 44(1): 74-86 [3] Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer. Advances in Engineering Software, 2014, 69: 46-61 doi: 10.1016/j.advengsoft.2013.12.007 [4] Pierezan J, Coelho L D S. Coyote optimization algorithm: A new metaheuristic for global optimization problems. In: Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC). Rio de Janeiro, Brazil, USA: IEEE, 2018. [5] 彭喜元, 彭宇, 戴毓丰. 群智能理论及应用. 电子学报, 2003, 12A(31): 1982-1988Peng Xi-yuan, Peng Yu, Dai Yu-feng. Swarm intelligence theory and applications. Acta Electronica Sinica, 2003, 12A(31): 1982-1988 [6] Wolpert D H, Macready W G. No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 67-82 doi: 10.1109/4235.585893 [7] 张新明, 王霞, 康强, 程金凤. GWO与ABC的混合优化算法及其聚类优化. 电子学报, 2018, 46(10): 2430-2442 doi: 10.3969/j.issn.0372-2112.2018.10.017Zhang Xin-ming, Wang Xia, Kang Qiang, Cheng Jin-feng. Hybrid grey wolf optimizer with artificial bee colony and its application to clustering optimization. Acta Electronica Sinica, 2018, 46(10): 2430-2442 doi: 10.3969/j.issn.0372-2112.2018.10.017 [8] Zhang X M, Kang Q, Cheng J F, Wang X. A novel hybrid algorithm based on biogeography-based optimization and grey wolf optimizer. Applied Soft Computing, 2018, 67: 197-214 doi: 10.1016/j.asoc.2018.02.049 [9] Teng Z, Lv J, Guo L. An improved hybrid grey wolf optimization algorithm. Soft Computing, 2019, 23(15): 6617-6631 doi: 10.1007/s00500-018-3310-y [10] Arora S, Singh H, Sharma M, Sharma S, Anand P. A new hybrid algorithm based on grey wolf optimization and crow search algorithm for unconstrained function optimization and feature selection. IEEE Access, 2019, 7: 26343-26361 doi: 10.1109/ACCESS.2019.2897325 [11] 龙文, 伍铁斌, 唐明珠, 徐明, 蔡绍洪. 基于透镜成像学习策略的灰狼优化算法. 自动化学报, 2020, 46(10): 2148−2164Long Wen, Wu Tie-Bin, Tang Ming-Zhu, Xu Ming, Cai Shao-hong. Grey wolf optimizer algorithm based on lens imaging learning strategy. Acta Automatica Sinica, 2020, 46(10): 2148−2164 [12] 张新明, 王豆豆, 陈海燕, 毛文涛, 窦智, 刘尚旺. 强化最优和最差狼的郊狼优化算法及其QAP应用. 计算机应用, 2019, 39(10): 2985-2991Zhang Xin-ming, Wang Dou-dou, Chen Hai-yan, Mao Wen-tao, Dou Zhi, Liu Shang-wang. Best and worst coyotes strengthened coyote optimization algorithm and its application to QAP. Journal of Computer Applications, 2019, 39(10): 2985-2991 [13] Omran M G H, Mahdavi M. Global-best harmony search. Applied Mathematics and Computation, 2008, 198(2): 643-656 doi: 10.1016/j.amc.2007.09.004 [14] Draa A, Bouzoubia S, Boukhalfa I. A sinusoidal differential evolution algorithm for numerical optimization. Applied Soft Computing, 2015, 27: 99-126 doi: 10.1016/j.asoc.2014.11.003 [15] Awad N H, Ali M Z, Liang J J, Qu B Y, Suganthan P N. Problem definitions and evaluation criteria for the CEC 2016 special session and competition on single objective bound constrained real-parameter numerical optimization. In: Computational Intelligence Laboratory, Zhengzhou University, Zhengzhou, China and Technical Report, Nanyang Technological University, Singapore, 2016. [16] Tu Q, Chen X C, Liu X. Multi-strategy ensemble grey wolf optimizer and its application to feature selection. Applied Soft Computing, 2019, 76: 16-30 doi: 10.1016/j.asoc.2018.11.047 [17] Gong W, Cai Z, Ling C. DE/BBO: a hybrid differential evolution with biogeography-based optimization for global numerical optimization. Soft Computing, 2010, 15(4): 645-665 doi: 10.1007/s00500-010-0591-1 [18] Avdilek I B. A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems. Applied Soft Computing, 2018, 66: 232-249 doi: 10.1016/j.asoc.2018.02.025 [19] Qin A K, Huang V L, Suganthan P N. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 398-417 doi: 10.1109/TEVC.2008.927706 [20] Tang D. Spherical evolution for solving continuous optimization problems. Applied Soft Computing, 2019, 81: 1-20 [21] Tan Y, Zhu Y C. Fireworks algorithm for optimization. International Conference in Swarm Intelligence, 2010, 355-364 [22] Rao R V, Savsani V J, Vakharia D P. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Computer-Aided Design, 2011, 43(3): 303-315 doi: 10.1016/j.cad.2010.12.015 [23] 贺毅朝, 王熙照, 刘坤起, 王彦祺. 差分演化的收敛性分析与算法改进. 软件学报, 2010, 21(5): 875-885 doi: 10.3724/SP.J.1001.2010.03486He Yi-chao, Wang Xi-zhao, Liu Kun-qi, Wang Yan-qi. Convergent analysis and algorithmic improvement of differential evolution. Journal of Software, 2010, 21(5): 875-885 doi: 10.3724/SP.J.1001.2010.03486 [24] Derrac J, García S, Molina D, Herrera F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm and Evolutionary Computation, 2011, 1(1): 3-18 doi: 10.1016/j.swevo.2011.02.002 [25] Das P, Das D K, Dey S. A modified bee colony optimization (MBCO) and its hybridization with k-means for an application to data clustering. Applied Soft Computing, 2018, 70: 590-603 doi: 10.1016/j.asoc.2018.05.045 [26] Jain A K. Data clustering: 50 years beyond k-means. Pattern Recognition Letters, 2010, 31(8): 651-666 doi: 10.1016/j.patrec.2009.09.011 [27] 罗可, 李莲, 周博翔. 基于变异精密搜索的蜂群聚类算法. 控制与决策, 2014, 29(5): 838-842Luo Ke, Li Lian, Zhou Bo-xiang. Artificial bee colony rough clustering algorithm based on mutative precision search. Control and Decision, 2014, 29(5): 838-842 -




 下载:
下载: