Belief Rule Base Optimization Method Based on Parallel Multi-population and Redundant Genes Strategy
-
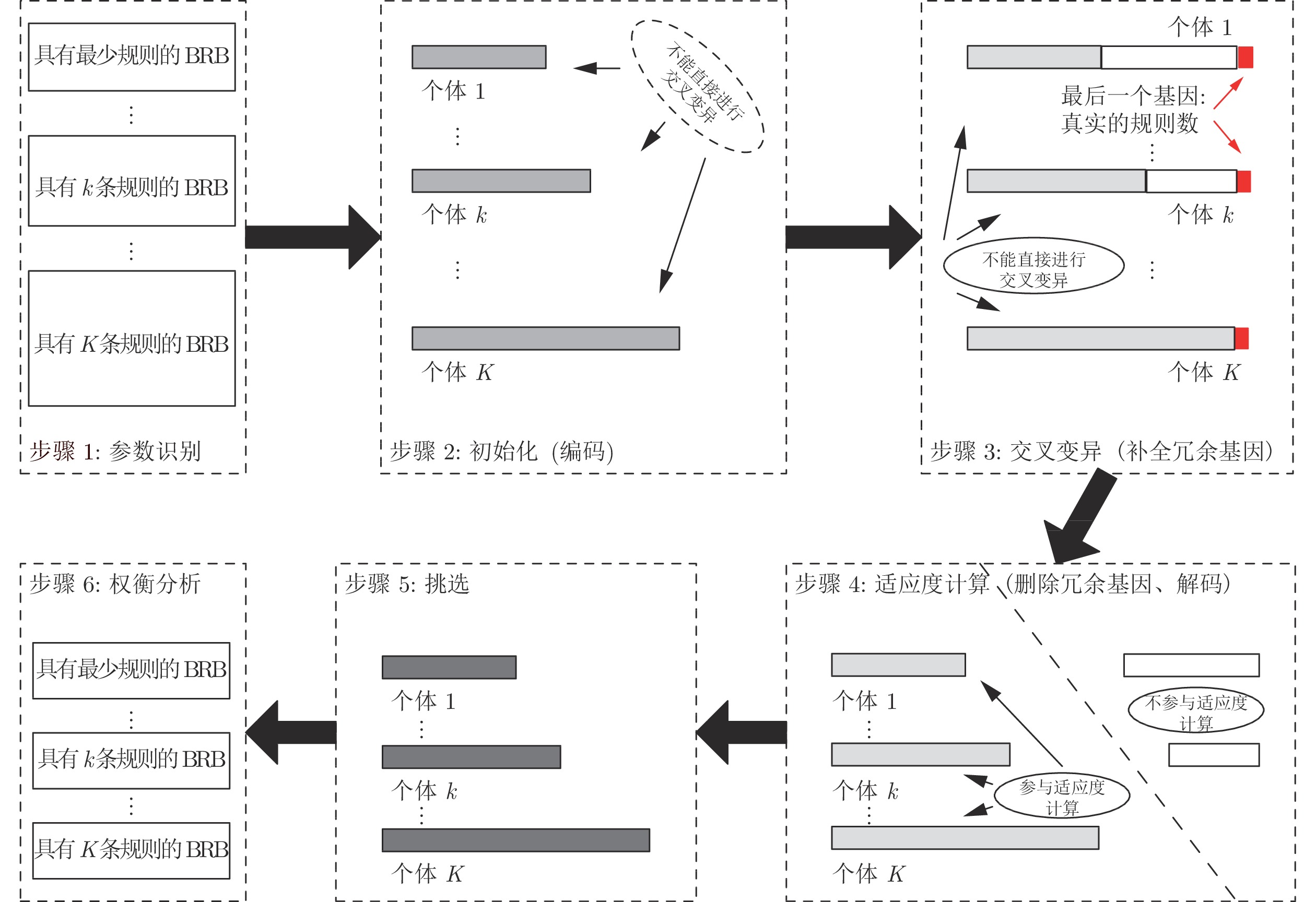
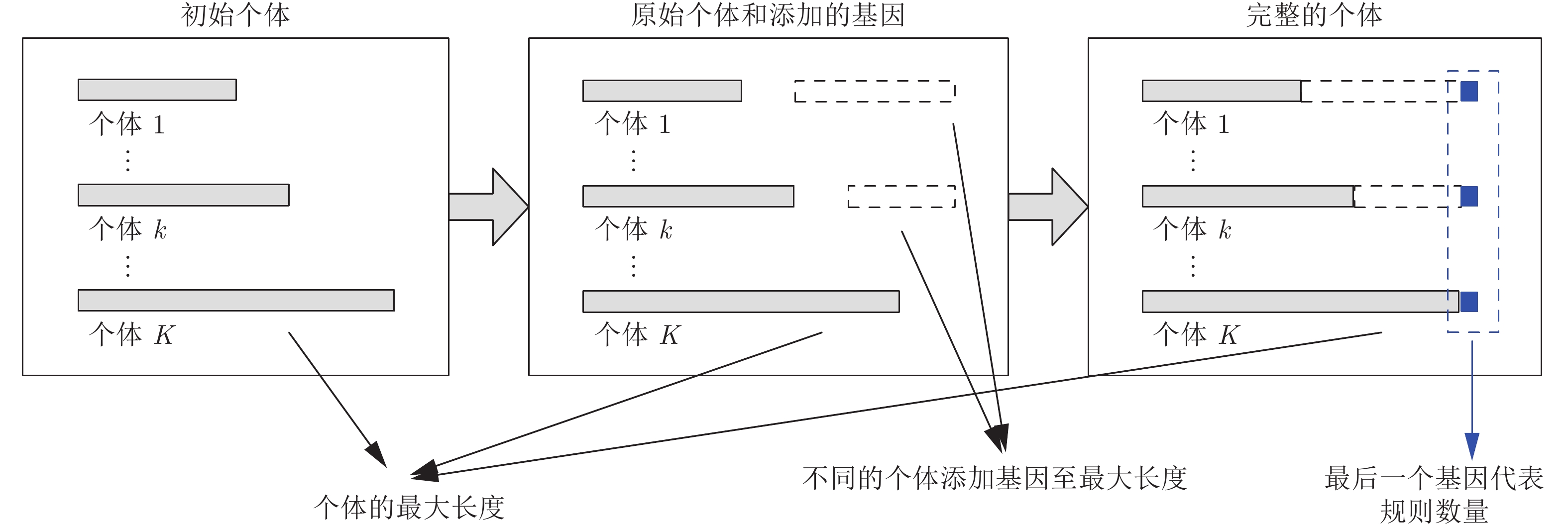
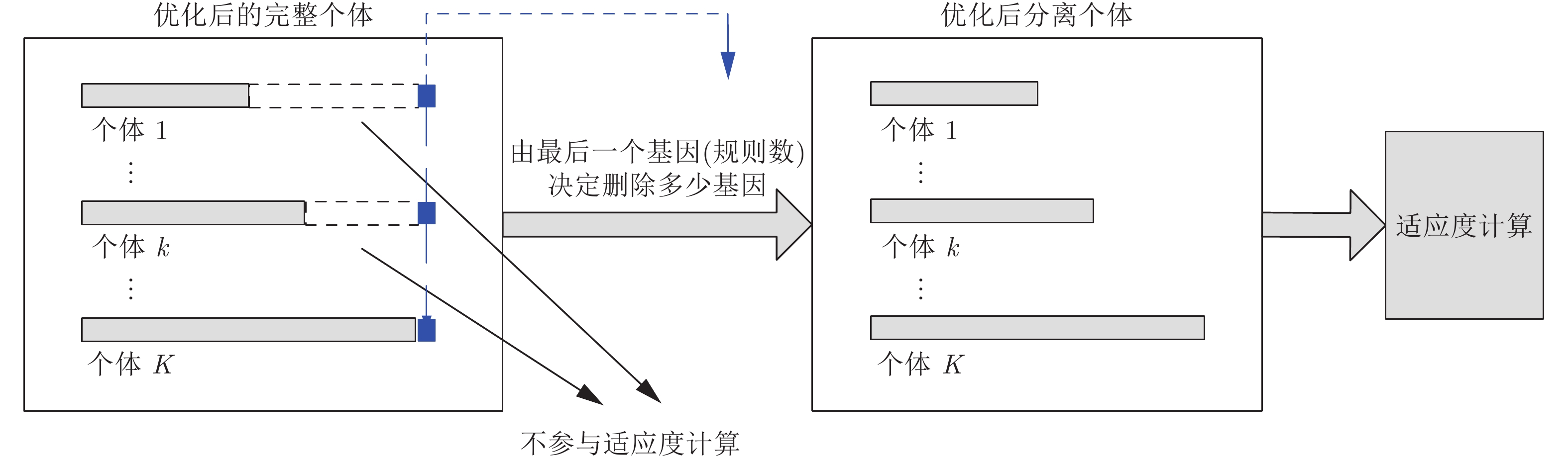
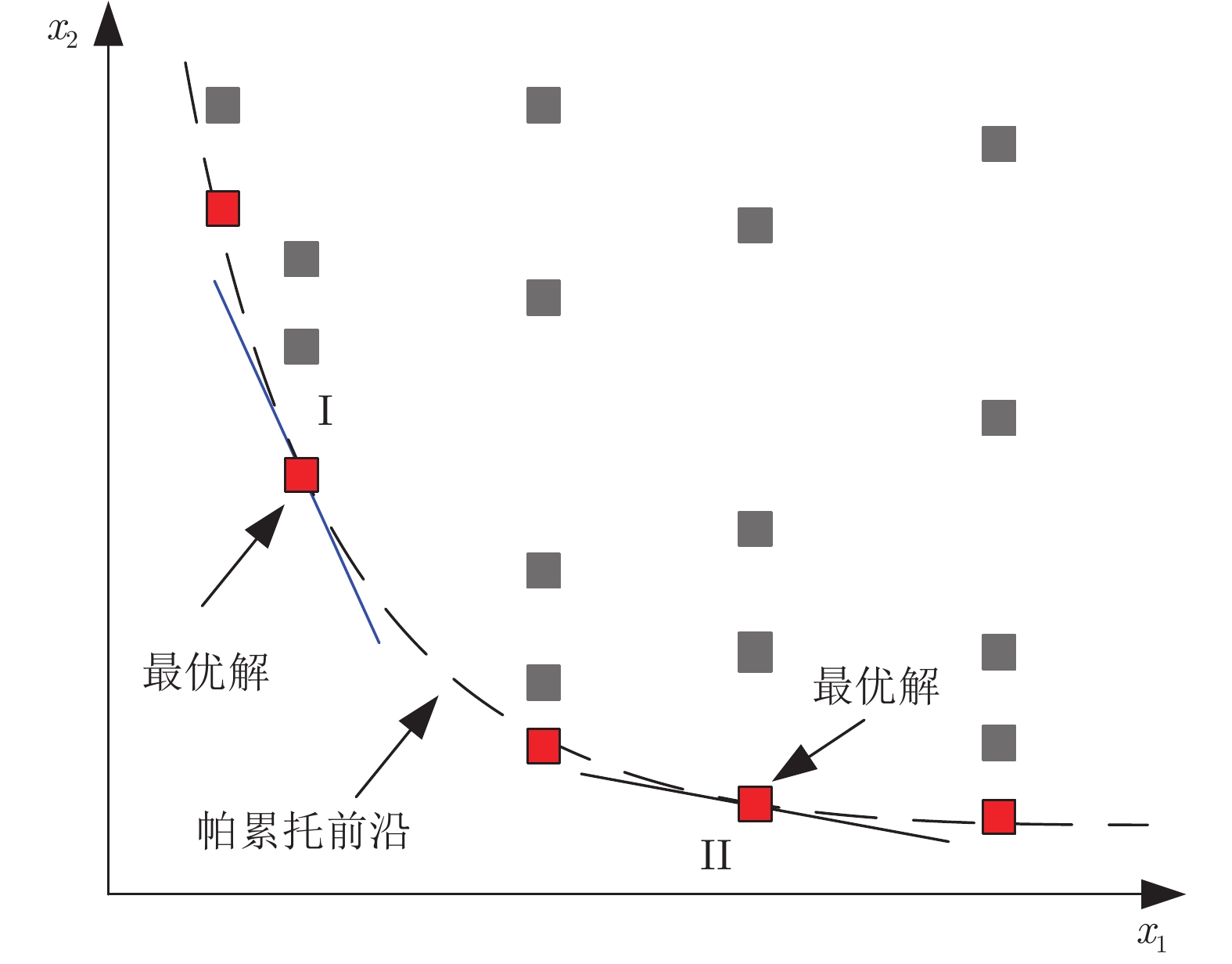
摘要: 置信规则库(Belief rule base, BRB)的参数学习和结构学习共同影响着置信规则库的建模精度和复杂度. 为了提高BRB结构学习和参数学习的优化效率, 本文提出了一种基于平行多种群(Parallel multi-population)策略和冗余基因(Redundant genes)策略的置信规则库优化方法. 该方法采用平行多种群策略以实现对具有不同数量规则BRB同时进行优化的目的, 采用冗余基因策略以确保具有不同数量规则的BRB能够顺利进行(交叉, 变异等)相关优化操作. 最终自动生成具有不同数量规则BRB的最优解, 并得出帕累托前沿(Pareto frontier), 决策者可以根据自身偏好和实际问题需求, 综合权衡并在帕累托前沿中筛选最优解. 最后以某输油管道泄漏检测问题作为示例验证本文提出方法的有效性, 示例分析结果表明本文提出的方法可以一次生成具有多条规则BRB的最优解, 并且可以准确绘制出帕累托前沿, 为综合决策提供较强的决策支持.Abstract: The parameter learning and structure learning of the belief rule base (BRB) affect accuracy and complexity of modeling. In order to improve the optimization efficiency of BRB structure learning and parameter learning, this paper proposes a belief rule base optimization method based on parallel multi-population and redundant genes strategy. This method adopts parallel multi-population strategy to optimize simultaneously BRB with different quantity rules. Redundant genetic strategy is adopted to ensure that BRB with different number of rules can smoothly perform (crossover, mutation, etc.) optimization operations. Then, an optimal solution of BRB with different number of rules is automatically generated, and derived Pareto frontier. Decision maker can comprehensively select the optimal solution based on their own mind and actual problem needs. Finally, this paper presents an example of pipeline leak detection to verity the method proposed. The experimental result shows that the proposed method can generate the optimal solution of BRB with multiple rules at one time and can accurately plot the Pareto frontier which provides strong decision support for decision maker.
-
Key words:
- Parallel population /
- redundant genes /
- belief rule base (BRB) /
- Pareto frontier
-
表 1 运行30次的数据结果
Table 1 Statistics of 30 runs
第 3 条 第 4 条 第 5 条 第 6 条 第 7 条 第 8 条 min ${{4.0389\times10^ {1} } }$ $3.2065\times10^{1}$ ${{2.9210\times10^{1}}}$ $2.9208\times10^{1}$ $2.9200\times10^{1}$ $2.9189\times10^{1}$ avg ${{5.3796\times10^{1}}}$ $3.9717\times10^{1}$ ${{3.7355\times10^{1}}}$ $3.7332\times10^{1}$ $3.6770\times10^{1}$ $4.4892\times10^{1}$ vara ${{9.5350\times10^{2}}}$ $5.2327\times10^{2}$ ${{3.4741\times10^{2}}}$ $3.2595\times10^{2}$ $4.3643\times10^{2}$ $2.4779\times10^{2}$ 表 2 具有5条规则的最优BRB参数
Table 2 Optimal BRB parameters with five rules
序号 权重 前提属性 泄露大小 流量差 压力差 0 2 4 6 8 1 0.8642 $-10.0000$ $-0.002$ 0.3950 0.0692 0.0194 0.0122 0.5042 2 1.0000 $-7.5000$ $-0.0176$ 0.7878 0.2109 0.0001 0.0000 0.0012 3 0.0911 $-1.7830$ 0.0065 0.0101 0.1245 0.0525 0.5794 0.2335 4 0.2838 0.384 5 0.0073 0.2013 0.2072 0.1513 0.2164 0.2238 5 0.2499 2.000 0 0.0400 0.6588 0.0498 0.0929 0.0243 0.1742 表 3 基于不同BRB优化方法的实验结果对比分析
Table 3 Comparative analysis of experimental results based on different BRB optimization methods
序号 方法 描述 MSE (MAE) 尺寸(训练/测试) NOR NOP 1 其他方法 ANFS 0.5073 9 / 2 SVM 0.4219 C = 10, $\delta^2=1$ 3 以前 BRB 学习方法 局部训练[24] 0.4049 500/200 8 56 336 4 在线更新[9] 0.7880 800/200 8 56 336 5 适应性学习[10] 0.3990 500/200 8 56 349 6 动态规则调整[6] 0.5040 900/200 8 14 108 0.4450 6 39 7 双层优化[15] 0.2917 500/200 8 5 36 8 一般并集 BRB 优化[26] 0.3741 500/200 8 3 20 0.2848 5 36 0.2679 12 92 9 本文方法 平行多种群与冗余基因 0.4038 500/200 8 3 240 0.2921 5 注: “NOR”表示规则数量 (Number of rules), “NOP”表示参数数量 (Number of parameters) -
[1] Yang J B, Singh M G. An evidential reasoning approach for multiple-attribute decision making with uncertainty. IEEE Transactions on Systems, Man, and Cybernetics, 1994, 24(1): 1-18 doi: 10.1109/21.259681 [2] Yang J B, Liu J, Wang J, Sii H S, Wang H W. Belief rule-base inference methodology using the evidential reasoning approach-RIMER. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2006, 36(2): 266-285 doi: 10.1109/TSMCA.2005.851270 [3] Hossain M S, Rahaman S, Kor A L, Andersson K, Pattinson C. A belief rule based expert system for datacenter PUE prediction under uncertainty. IEEE Transactions on Sustainable Computing, 2017, 2(2): 140-153 doi: 10.1109/TSUSC.2017.2697768 [4] Yang J B, Xu D L. Nonlinear information aggregation via evidential reasoning in multiattribute decision analysis under uncertainty. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2002, 32(3): 376-393 doi: 10.1109/TSMCA.2002.802809 [5] Chang L L, Zhou Y, Jiang J, Li M J, Zhang X H. Structure learning for belief rule base expert system: A comparative study. Knowledge-Based Systems, 2013, 39: 159-172 doi: 10.1016/j.knosys.2012.10.016 [6] Wang Y M, Yang L H, Fu Y G, Chang L L, Chin K S. Dynamic rule adjustment approach for optimizing belief rule-base expert system. Knowledge-Based Systems, 2016, 96: 40-60 doi: 10.1016/j.knosys.2016.01.003 [7] Li G L, Zhou Z J, Hu C H, Chang L L, Zhou Z G, Zhao F J. A new safety assessment model for complex system based on the conditional generalized minimum variance and the belief rule base. Safety Science, 2017, 93: 108-120 doi: 10.1016/j.ssci.2016.11.011 [8] Yang J B, Liu J, Xu D L, Wang J, Wang H W. Optimization models for training belief-rule-based systems. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2007, 37(4): 569-585 doi: 10.1109/TSMCA.2007.897606 [9] Zhou Z J, Hu C H, Xu D L, Yang J B, Zhou D H. Bayesian reasoning approach based recursive algorithm for online updating belief rule based expert system of pipeline leak detection. Expert Systems With Applications, 2011, 38(4): 3937-3943 doi: 10.1016/j.eswa.2010.09.055 [10] Chen Y W, Yang J B, Xu D L, Zhou Z J, Tang D W. Inference analysis and adaptive training for belief rule based systems. Expert Systems With Applications, 2011, 38(10): 12845-12860 doi: 10.1016/j.eswa.2011.04.077 [11] Savan E E, Yang J B, Xu D L, Chen Y W. A genetic algorithm search heuristic for belief rule-based model-structure validation. In: Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics. Manchester, UK: IEEE, 2013. 1373−1378 [12] Chang L L, Zhou Z J, You Y, Yang L H, Zhou Z G. Belief rule based expert system for classification problems with new rule activation and weight calculation procedures. Information Sciences, 2016, 336: 75-91 doi: 10.1016/j.ins.2015.12.009 [13] 马炫, 李星, 唐荣俊, 刘庆. 一种求解符号回归问题的粒子群优化算法. 自动化学报, 2020, 46(8): 1714-1726 doi: 10.16383/j.aas.c180035Ma Xuan, Li Xing, Tang Rong-Jun, Liu Qing. A particle swarm optimization approach for symbolic regression. Acta Automatica Sinica, 2020, 46(8): 1714-1726 doi: 10.16383/j.aas.c180035 [14] Chang L L, Zhou Z J, Chen Y W, Xu X B, Sun J B, Liao T J, et al. Akaike information criterion-based conjunctive belief rule base learning for complex system modeling. Knowledge-Based Systems, 2018, 161: 47-64 doi: 10.1016/j.knosys.2018.07.029 [15] Chang L L, Zhou Z J, Chen Y W, Liao T J, Hu, Y, et al. Belief Rule Base Structure and parameter joint optimization under disjunctive assumption for nonlinear complex system modeling. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(9): 1542-1554 doi: 10.1109/TSMC.2017.2678607 [16] Yang L H, Wang Y M, Liu J, Martínez L. A joint optimization method on parameter and structure for belief-rule-based systems. Knowledge-Based Systems, 2018, 142: 220-240 doi: 10.1016/j.knosys.2017.11.039 [17] Chen Y, Chen Y W, Xu X B, Pan C C, Yang J B, Yang G K. A data-driven approximate causal inference model using the evidential reasoning rule. Knowledge-Based Systems, 2015, 88: 264-272 doi: 10.1016/j.knosys.2015.07.026 [18] Zhou Z J, Hu C H, Xu D L, Yang J B, Zhou D H. New model for system behavior prediction based on belief rule systems. Information Sciences, 2010, 180(24): 4834-4864 doi: 10.1016/j.ins.2010.08.016 [19] Wu G H, Mallipeddi R, Suganthan P N, Wang R, Chen H K. Differential evolution with multi-population based ensemble of mutation strategies. Information Sciences, 2016, 329: 329-345 doi: 10.1016/j.ins.2015.09.009 [20] Qu B Y, Suganthan P N, Liang J J. Differential evolution with neighborhood mutation for multimodal optimization. IEEE Transactions on Evolutionary Computation, 2012, 16(5): 601-614 doi: 10.1109/TEVC.2011.2161873 [21] Elsayed S, Sarker R, Coello C C. Enhanced multi-operator differential evolution for constrained optimization. In: Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC). Vancouver, Canada: IEEE, 2016. 4191−4198 [22] Toledo C F M, De Oliveira R R R, FrançA P M. A hybrid multi-population genetic algorithm applied to solve the multi-level capacitated lot sizing problem with backlogging. Computers & Operations Research, 2013, 40(4): 910-919 [23] Brown K, Adger W N, Tompkins E, Bacon P, Shim D, Young K. Trade-off analysis for marine protected area management. Ecological Economics, 2001, 37(3): 417-434 doi: 10.1016/S0921-8009(00)00293-7 [24] Xu D L, Liu J, Yang J B, Liu G P, Wang J, Jenkinson I, et al. Inference and learning methodology of belief-rule-based expert system for pipeline leak detection. Expert Systems With Applications, 2007, 32(1): 103-113 doi: 10.1016/j.eswa.2005.11.015 [25] Hancer E, Karaboga D. A comprehensive survey of traditional, merge-split and evolutionary approaches proposed for determination of cluster number. Swarm and Evolutionary Computation, 2017, 32: 49-67 doi: 10.1016/j.swevo.2016.06.004 [26] Chang L L, Zhou Z J, Liao H C, Chen Y W, Tan X, Herrera F. Generic disjunctive belief-rule-base modeling, inferencing, and optimization. IEEE Transactions on Fuzzy Systems, 2019, 27(9): 1866-1880 doi: 10.1109/TFUZZ.2019.2892348 -




 下载:
下载: