A Gait Control Method for Biped Robot on Slope Based on Deep Reinforcement Learning
-
摘要:
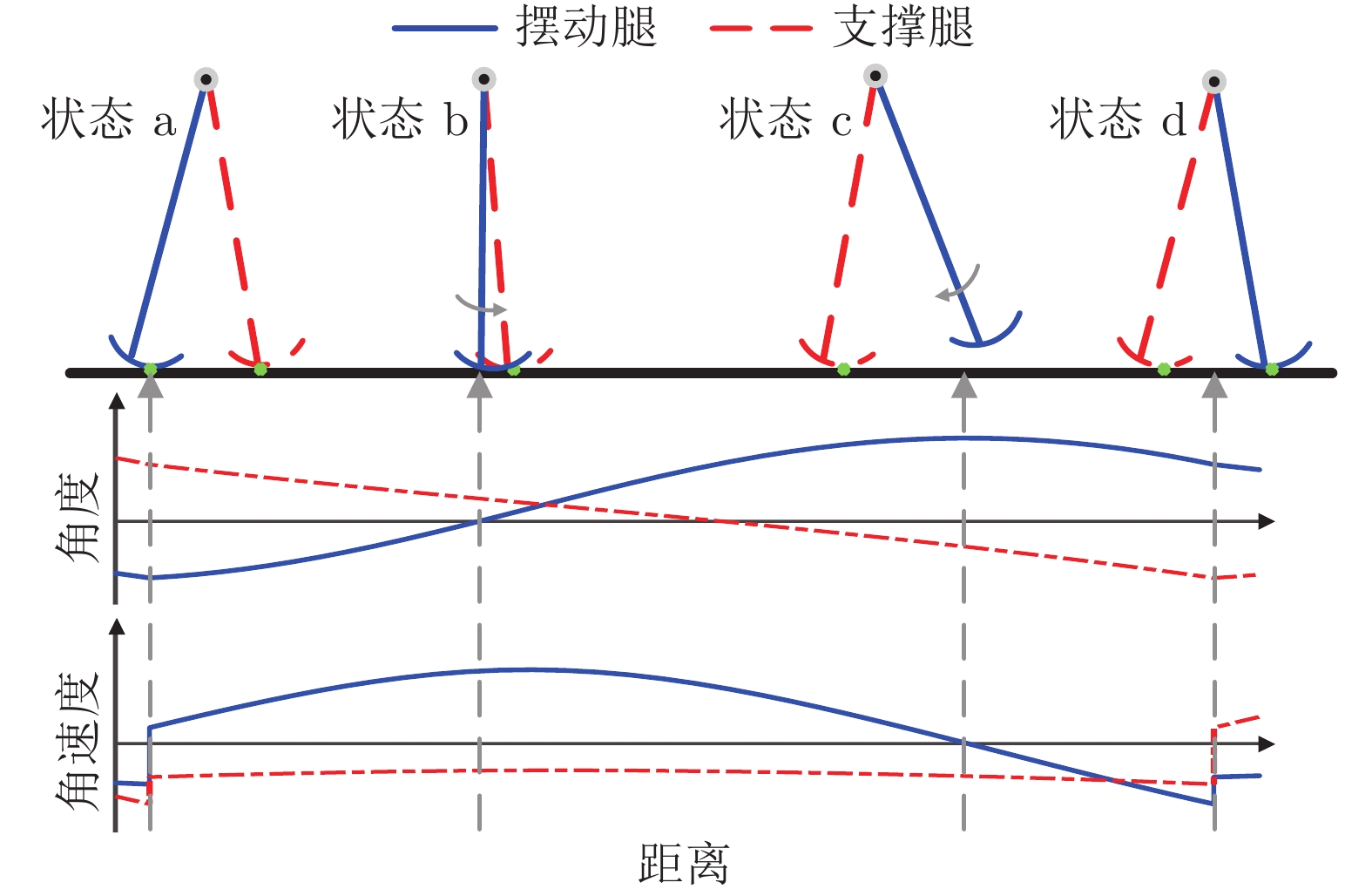
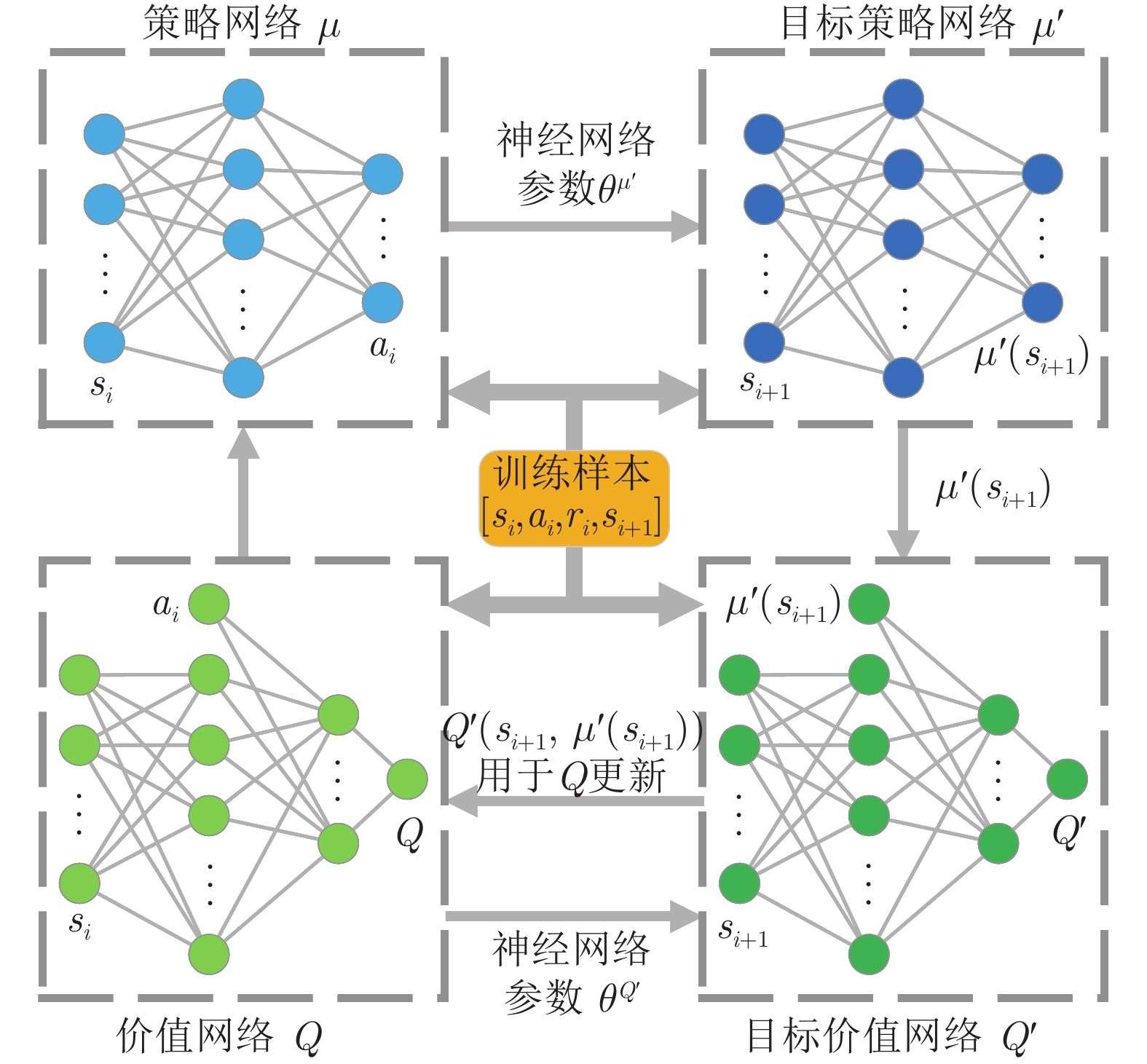
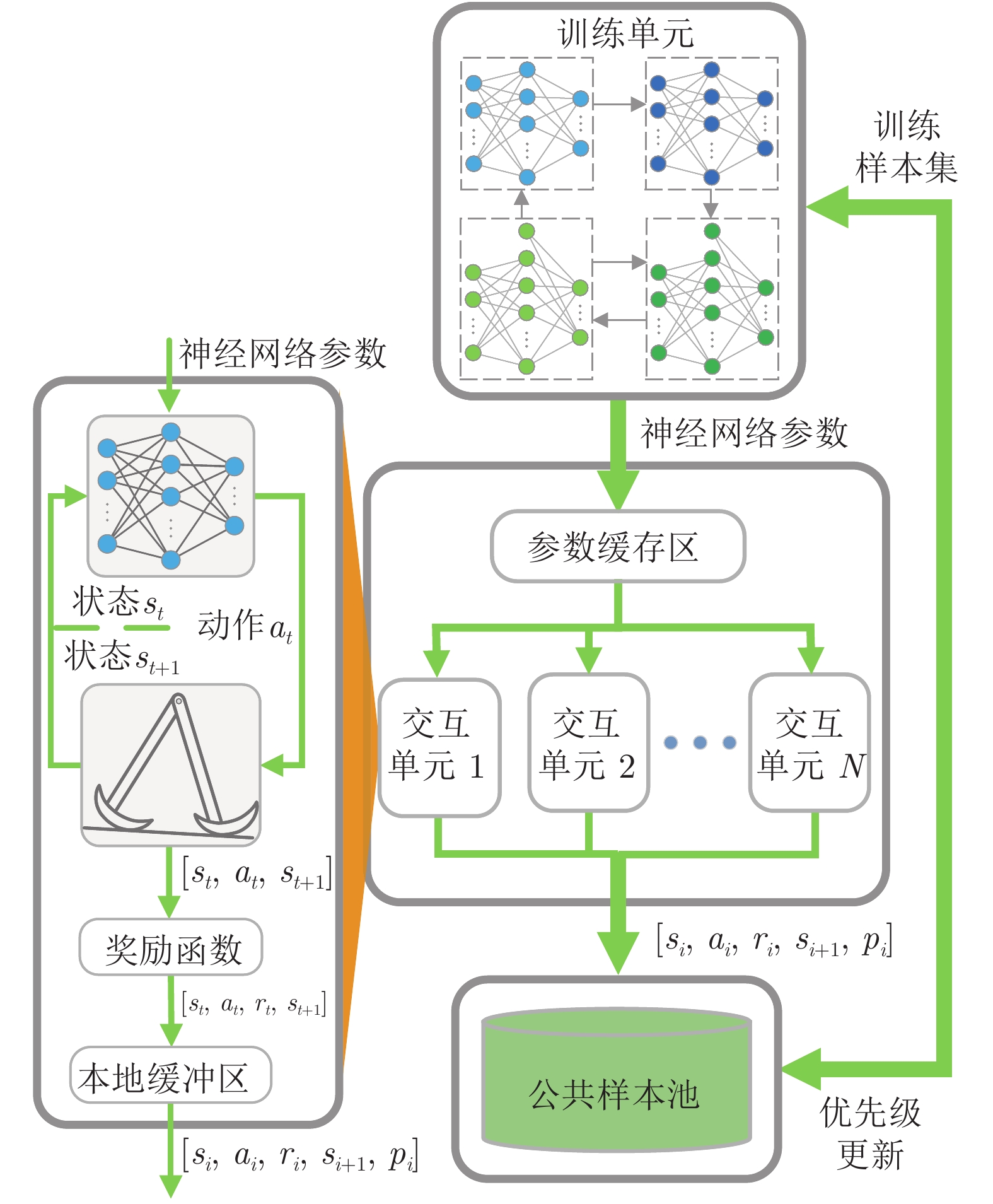
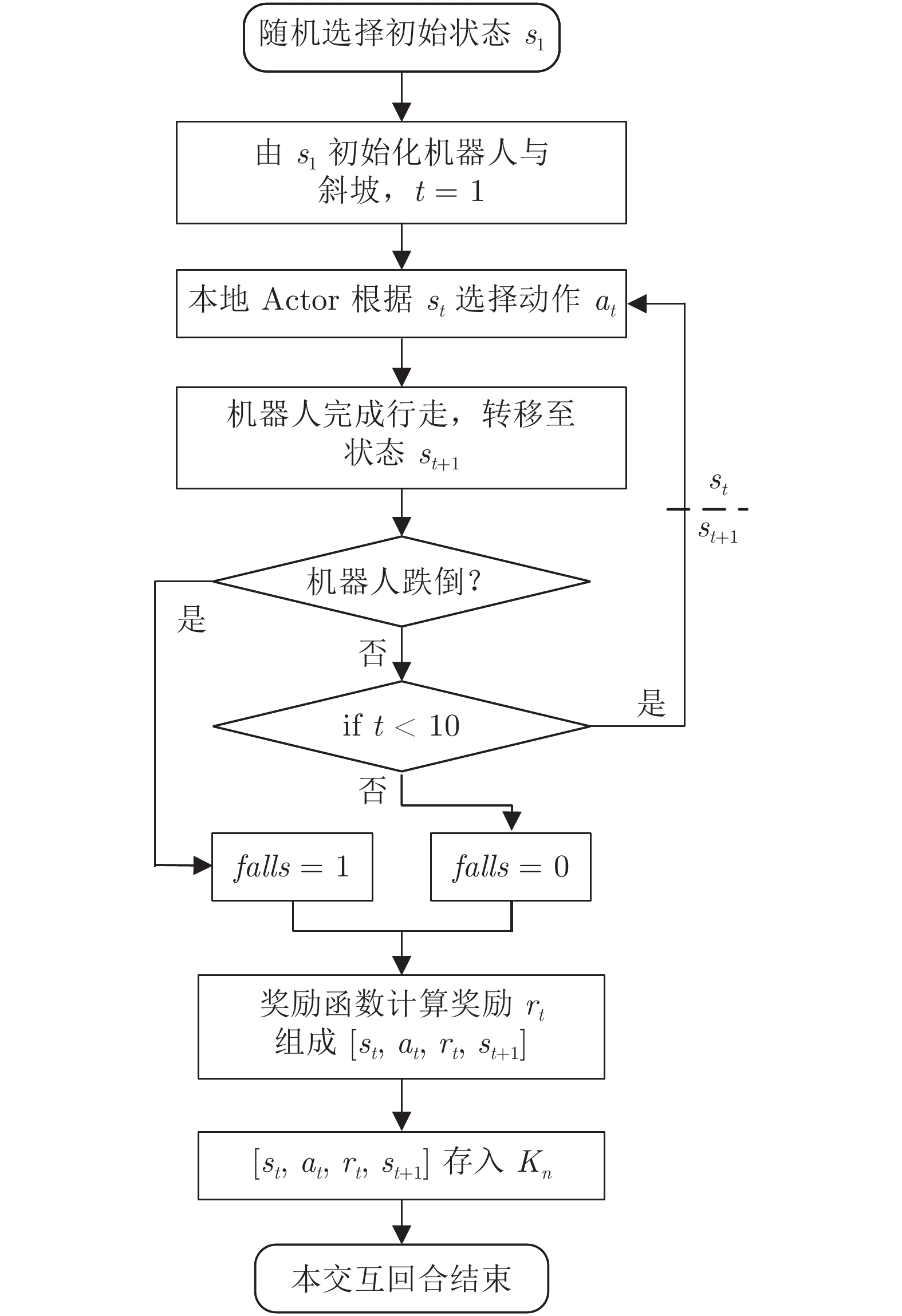
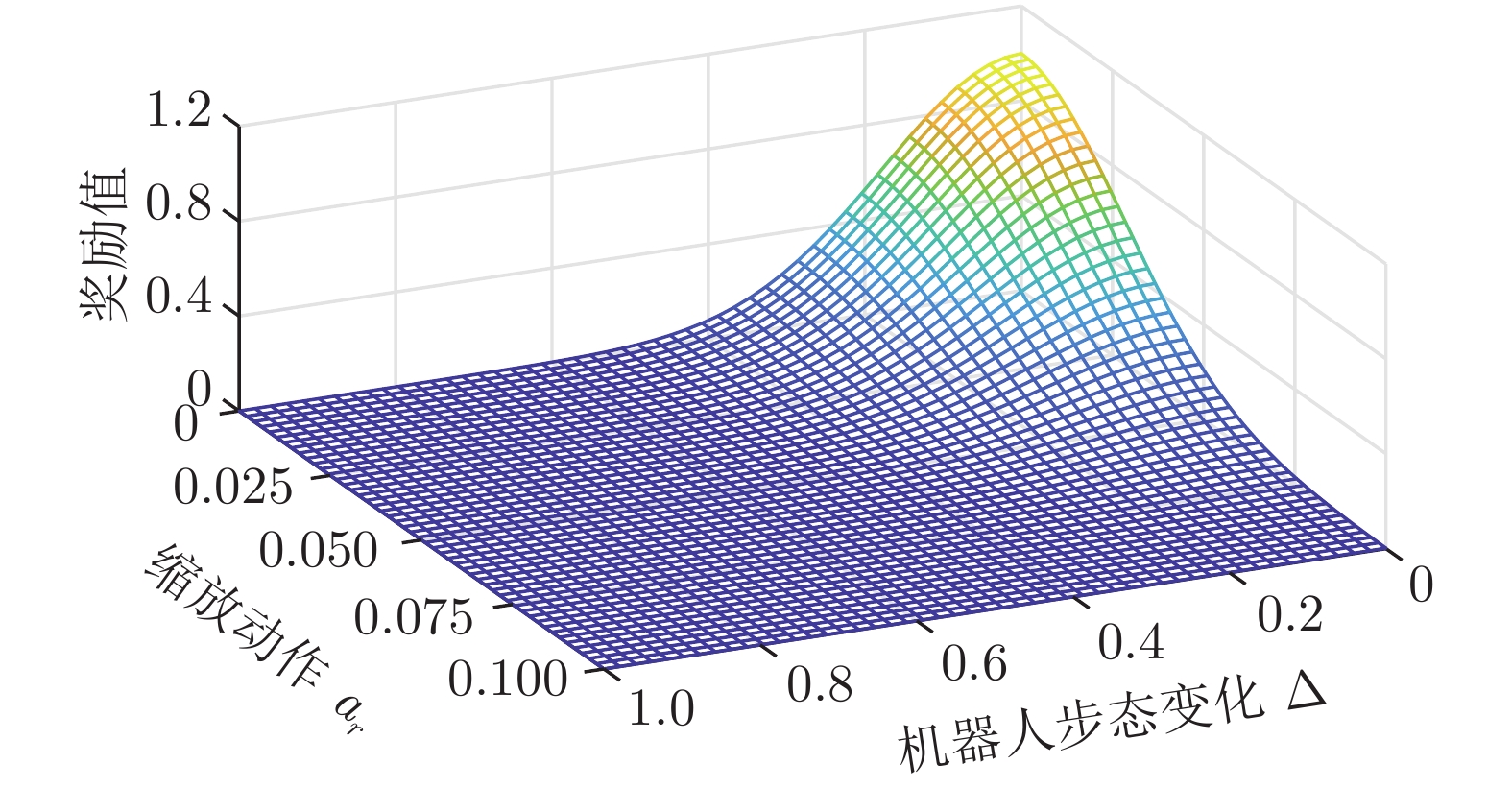
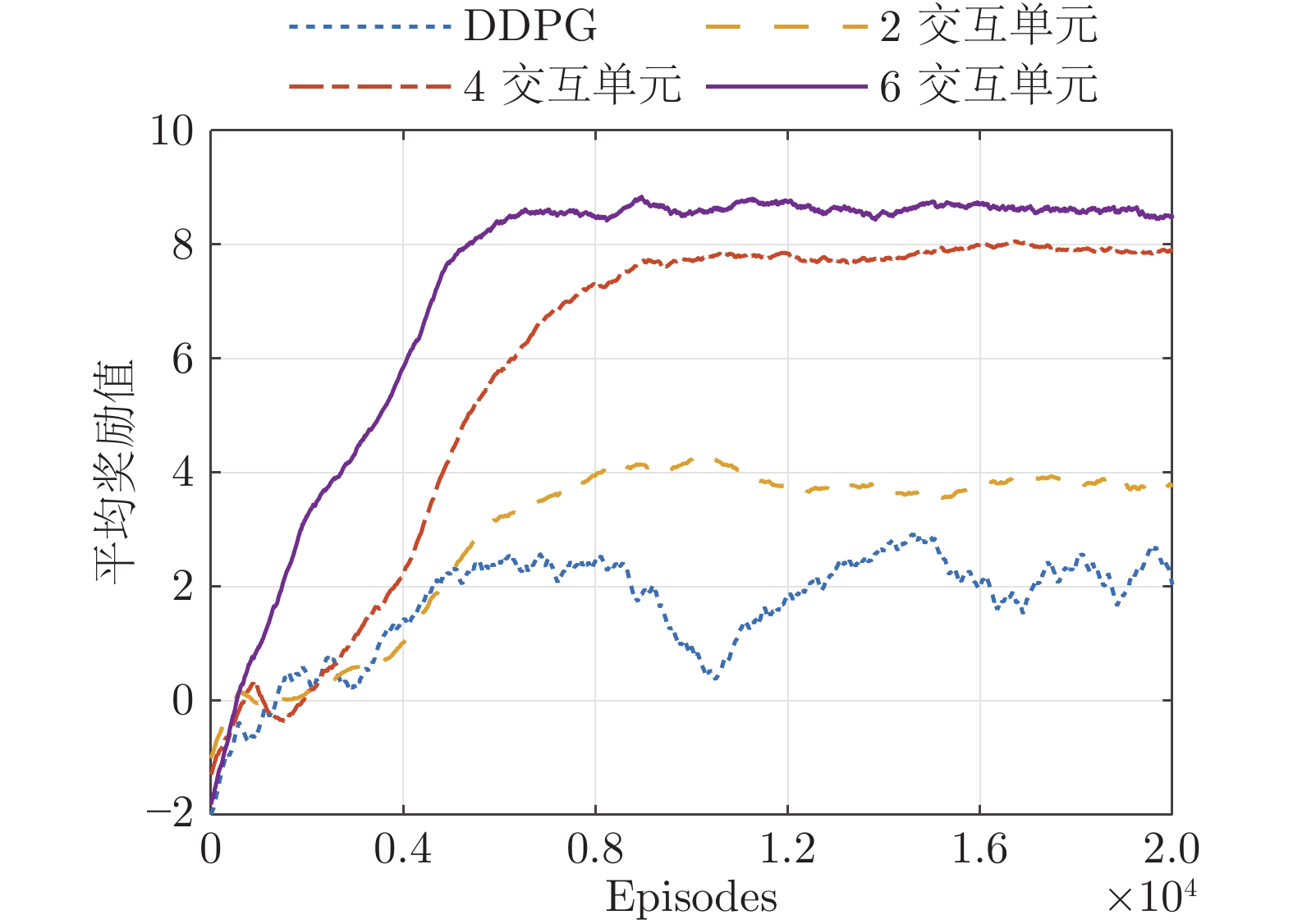
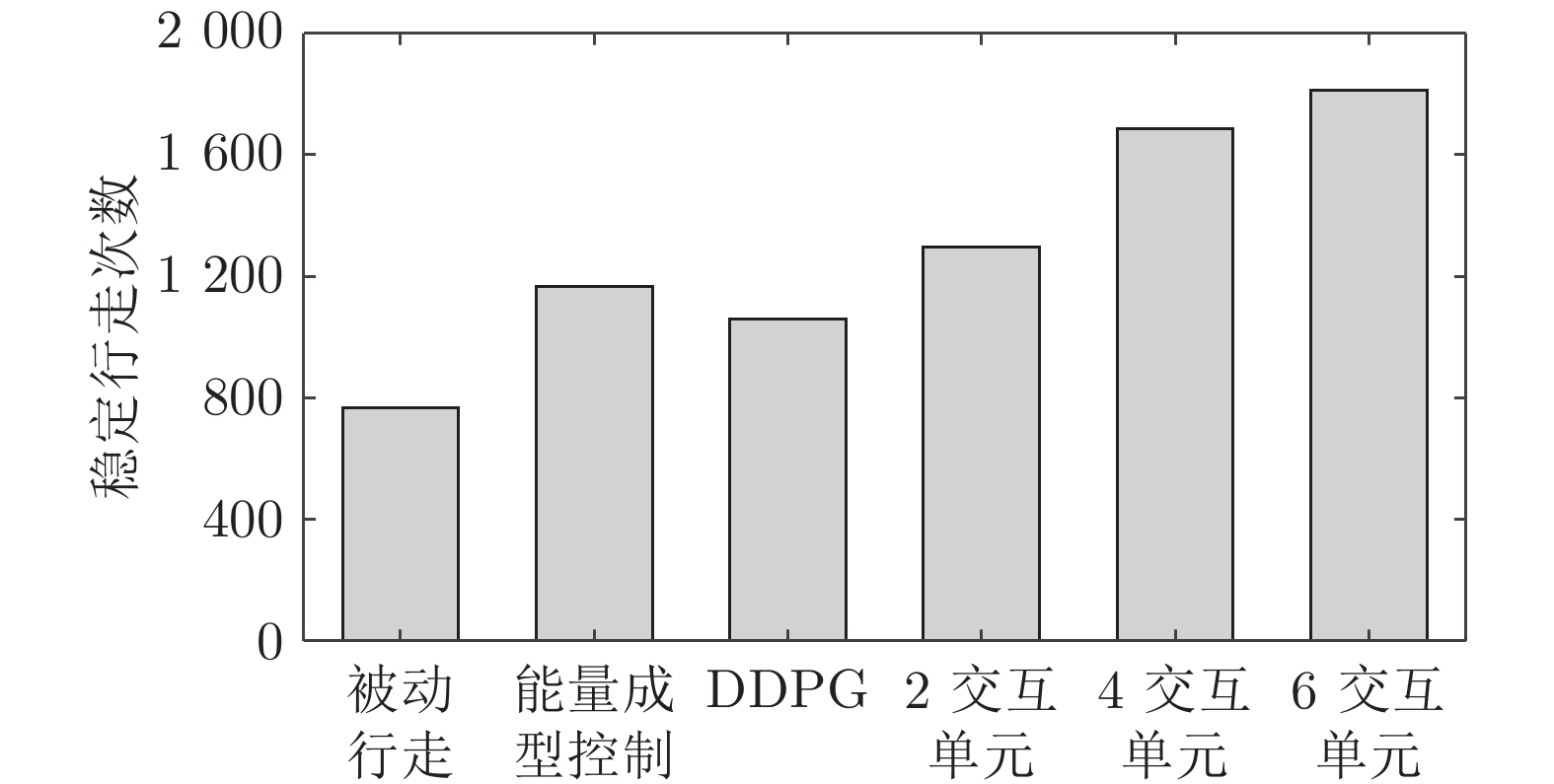
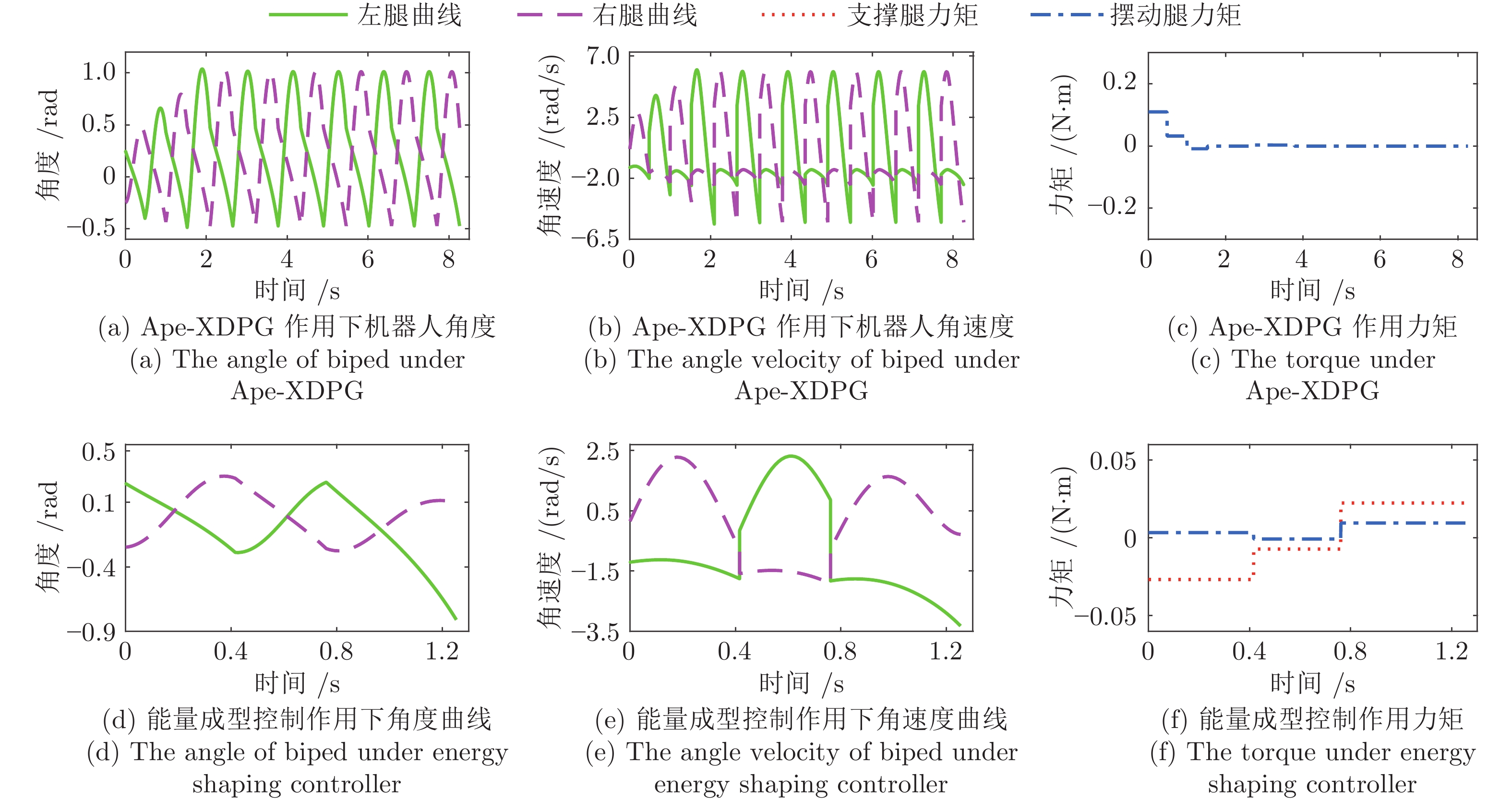
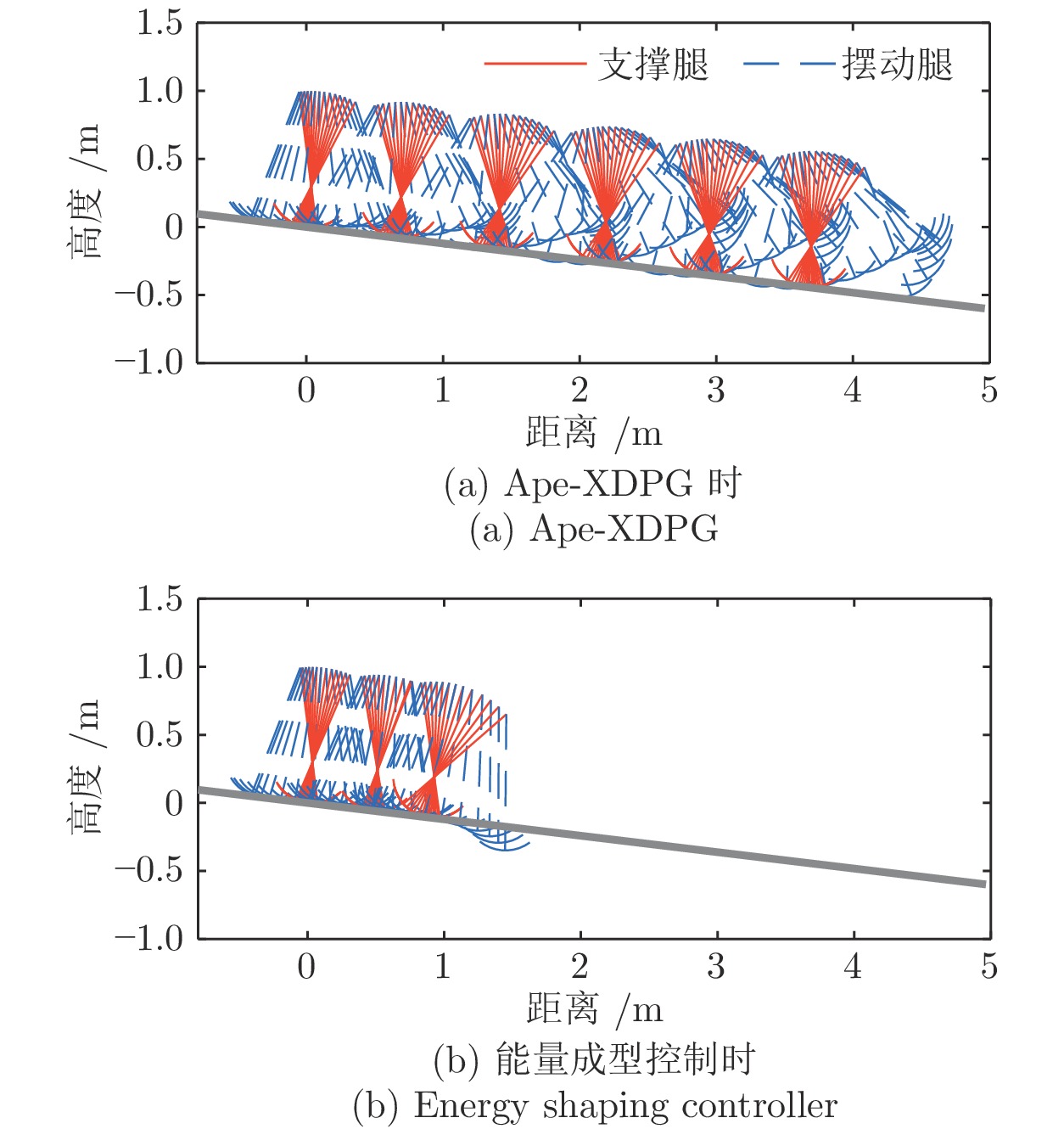
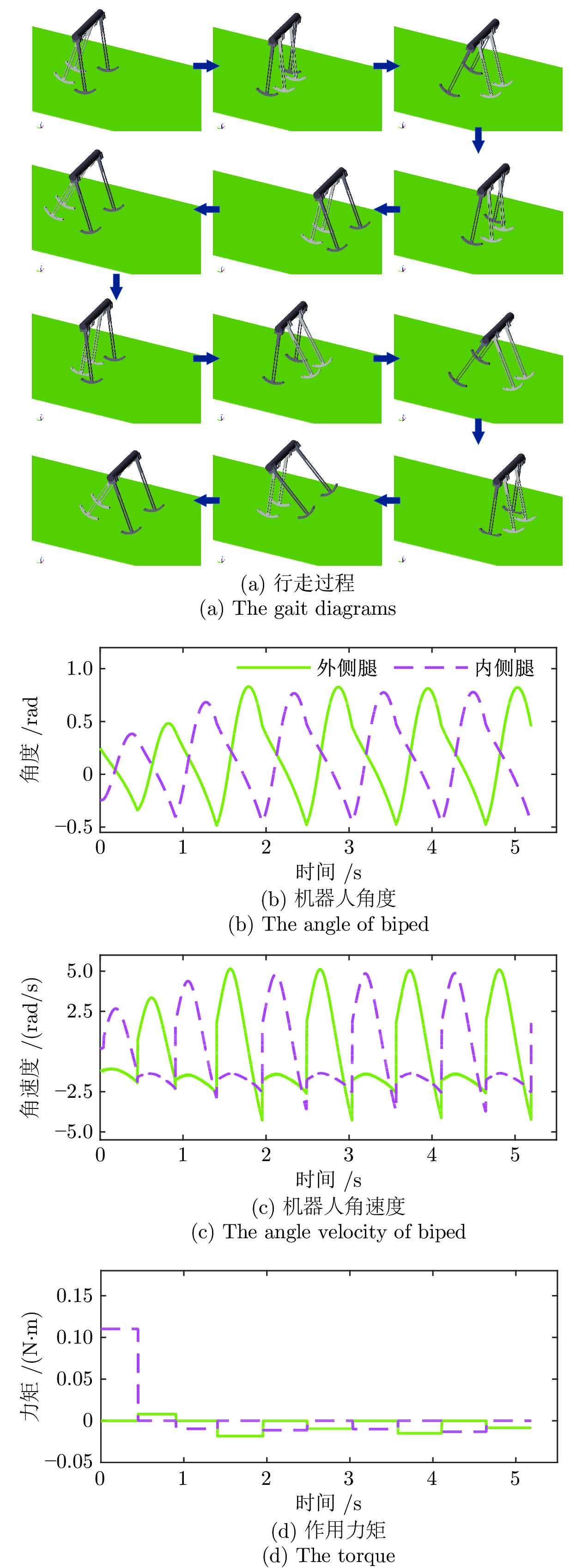
为提高准被动双足机器人斜坡步行稳定性, 本文提出了一种基于深度强化学习的准被动双足机器人步态控制方法. 通过分析准被动双足机器人的混合动力学模型与稳定行走过程, 建立了状态空间、动作空间、episode过程与奖励函数. 在利用基于DDPG改进的Ape-X DPG算法持续学习后, 准被动双足机器人能在较大斜坡范围内实现稳定行走. 仿真实验表明, Ape-X DPG无论是学习能力还是收敛速度均优于基于PER的DDPG. 同时, 相较于能量成型控制, 使用Ape-X DPG的准被动双足机器人步态收敛更迅速、步态收敛域更大, 证明Ape-X DPG可有效提高准被动双足机器人的步行稳定性.
Abstract:In order to improve the walking stability on slope of the quasi-passive biped robot, in this paper, we proposed a gait control method for quasi-passive biped robot based on deep reinforcement learning. By analyzing the hybrid dynamics model and the stable walking process of the quasi-passive biped robot establishing the state space, action space, episode process and reward function. After learning by Ape-X DPG algorithm based on DDPG improvement, quasi-passive biped robot can achieve stable walking in a larger slope range. In the simulation, Ape-X DPG is better than DDPG + PER in both learning ability and convergence speed. Meanwhile, compared with energy shaping controller, the gait convergence of quasi-passive biped robot using Ape-X DPG is more rapid and the basins of attraction is larger, which proves that Ape-X DPG can effectively improve the walking stability of quasi-passive biped robot.
-
近年来, 随着计算能力的显著提升和算法创新的不断涌现, 强化学习(Reinforcement learning, RL)在众多领域取得显著进展, 包括游戏[1]、机器人[2]、自动驾驶等[3]. 尽管已经取得辉煌的成就, RL在实际应用中仍面临一个核心挑战, 即如何提高样本效率. 智能体需要具有从有限的交互中快速学习到有效策略的能力, 尤其是在处理高维观测数据 (如图像)并执行复杂连续控制任务时, 这一挑战显得尤为突出[4]. 在现有的无模型深度强化学习(Deep reinforcement learning, DRL)算法中, 主要分为基于状态输入的学习和基于高维像素输入的学习, 二者在样本效率方面存在显著差异[5]. 这种差异在执行复杂的连续控制任务时尤为明显, 因此, 提高基于视觉的无模型强化学习算法的样本效率, 对于推动视觉强化学习算法的进步及其在现实世界复杂控制任务中的应用至关重要.
在强化学习中, 状态表征是智能体对环境状态的内部特征表示, 它对智能体的学习效率和策略性能有着重要影响[6]. 良好的状态表征应该能够捕捉到环境观测的关键特征, 并排除不相关的噪声, 从而使策略学习变得更加高效. 从强化学习的视角来看, 状态表征学习的目的可以描述为: 如何利用观测序列、智能体的动作以及环境反馈的奖赏等信息, 将观测转化为有效的特征表示[7]. 在先前的研究中, CURL (Contrastive unsupervised representations for reinforcement learning)算法[8]将对比学习引入到强化学习的表征学习中, 从而学习到更具区分度的状态表征. 尽管CURL在多个强化学习任务上显示出优异的性能, 但它也存在一定不足, 如未考虑强化学习数据的时序信息. 近年来的广泛研究表明, 融合时间序列信息的预测任务能够有效学习状态表征, 从而显著提升视觉强化学习的样本效率. CPC (Contrastive predictive coding)算法[9]引入时序信息并通过预测未来的观测来学习有用的状态表征, CPC可以捕捉到时间序列数据中的长期依赖关系, 对于从预测的角度开展RL状态表征学习的研究具有重要意义. 此外, SPR (Self-predictive representation)算法[10]进一步通过自我预测的方式学习状态表征, 通过预测未来的多个时间步来提高状态表征的鲁棒性. 随着掩码重构技术在自然语言处理(Natural language processing, NLP)和计算机视觉(Computer vision, CV)领域的广泛应用, 一些研究通过将掩码引入强化学习预测任务中, 进一步增强了视觉强化学习的样本效率, 其中代表性的工作有M-CURL (Masked contrastive unsupervised representations for reinforcement learning)算法[11], M-CURL通过随机掩码一部分序列状态, 并利用Transformer编码器学习序列状态之间的相关性, 以此来预测完整的序列状态特征. 此外, MLR (Mask-based latent reconstruction)算法[12]在掩码技术上进一步创新, 在时间和空间2个维度同时对序列状态进行掩码, 通过预测被掩码的序列状态促使智能体在学习状态表征时更好地使用上下文信息.
在视觉强化学习的领域, 尽管基于状态表征的研究在提升样本效率问题上取得一定进展, 但这些方法大多集中于Atari游戏等离散动作空间的环境或DMControl的简单任务上, 往往忽视了在具有高维动作空间的复杂控制任务中的应用[13]. 在更为复杂的控制任务, 如类人控制任务时, 仅依靠状态表征很难达到理想的性能水平. 近期研究指出, 动作表征的引入为解决这一问题提供了新的思路[14]. 尽管视觉表征的研究已经较为深入, 动作表征的探索却相对较少. TD7算法[15]通过融合状态和动作信息来学习环境动态, 建模状态与动作之间的微妙互动, 实现有效的状态表征学习. 而TACO (Temporal action-driven contrastive learning)算法[16]则通过最大化当前状态表征与其后续动作序列及未来状态表征之间的互信息, 同时学习状态和动作表征, 理论上能够提供富含控制信息的表征以提升样本效率. 然而, 尽管这些研究为状态−动作表征的学习提供了新的视角, 但大多聚焦于单步的状态−动作对预测, 忽略了强化学习中的时序信息并导致资源的浪费.
在解决高维动作空间的复杂控制任务时, 除了对动作的有效表征, 更精确的状态表征同样扮演着至关重要的角色. 当前的研究大多使用当前状态或结合当前状态和动作来预测未来的状态, 旨在提高表征的有效性[17]. 然而, 强化学习本质上是一个遵循马尔科夫决策过程(Markov decision process, MDP)的序列决策问题, MDP不仅包含状态和动作, 奖赏也是关键元素之一[18]. 当前许多基于预测的无模型强化学习方法忽视了奖赏信息的作用, 未能充分发掘奖赏信息在表征学习中的潜力.
为了提升视觉强化学习中的样本效率, 并更好地应对具有高维动作空间的复杂控制挑战, 本文介绍一种基于Transformer的状态−动作−奖赏预测表征学习框架(Transformer-based state-action-reward prediction representation learning framework, TSAR). TSAR希望通过综合利用状态、动作和奖赏信息来预测未来状态, 从而获得有效的表征. 首先, TSAR引入一个基于Transformer的融合状态−动作−奖赏信息的序列预测任务, 与其他依赖单一状态信息进行预测的方法相比(如图1(a)所示), 该设计通过整合状态、动作及奖赏信息(如图1(b)所示), 加深了对环境动态的理解并促进更有效的表征学习. 此外, 为了提升状态预测模型的鲁棒性, TSAR采用随机掩码技术对序列数据进行处理, 通过最大化掩码序列的预测状态特征与实际目标状态特征之间的互信息, 实现了对状态和动作表征的同步学习. 进一步地, 为了加强状态和动作表征与RL策略的相关性, TSAR引入了动作预测学习和奖赏预测学习作为额外的学习约束以指导状态和动作表征的学习. 与现有的一些方法, 如SPR[10]、MLR[12]和M-CURL[11]相比, TSAR的一个显著区别在于, 它同时将状态表征和动作表征显式地纳入到强化学习的策略训练中, 这种方式显著地增强了表征对策略优化的贡献.
图 1 传统状态预测模型和TSAR的状态预测模型Fig. 1 Traditional stale prediction model and TSAR stale prediction model本文的主要创新点如下:
1) 提出TSAR, 一种基于状态−动作−奖赏的表征学习框架, 通过结合随机掩码技术并在潜空间中预测未来状态, 可以同时学习状态表征和动作表征;
2) 提出一种简单而有效的动作预测学习和奖赏预测学习, 约束并指导模型学会对策略更有帮助的状态和动作表征;
3) 设计一种新的共享表征的形式, 将动作表征与状态表征结合起来共同参与强化学习策略的训练;
4) 在DMControl 9个具有挑战性的困难任务中, TSAR的平均性能相比无模型SOTA (State-of-the-art)算法提高了8.3%, 相比于最新的基于模型的表征学习算法Dreamer-v3提升了30.5%.
1. 相关工作
1.1 视觉表征强化学习
基于视觉信号的强化学习在多个现实世界应用中展现了巨大的潜力, 如机器人和视频游戏AI[19]. 尽管如此, 由于高维观测可能携带大量干扰或冗余信息, RL智能体在学习有效的表征时面临巨大的挑战[20]. 为了应对这一挑战, 许多研究通过设计自监督学习方法来促进强化学习中的状态表征学习. 一种广泛采用的方式是将策略学习目标和辅助目标结合进行联合学习[21]. 辅助目标包括像素重建、奖赏预测[22]、双模拟[23]、动态预测[24]以及基于实例识别的对比学习[25]等. 这些辅助任务通过提供额外的监督信号来帮助智能体更好地理解和表示观测到的环境, 从而提升强化学习的性能和样本效率[26]. 基于模型的方法同样在视觉强化学习问题中得到有效的应用. 这类方法通过学习观测的潜空间状态特征来实现对环境的有效建模, 这种环境模型可以帮助智能体实现更好的决策和规划[27]. 数据增强技术也被证明能够改善学习到的表征或值函数的质量[28], 进而提高学习性能. 通过在训练过程中引入数据增强技术, 可以增加训练数据的多样性, 减少过拟合, 提高模型的泛化能力. 另外, 一种提升表征质量的有效策略是在RL策略学习前对状态编码器进行预训练[29], 以学习原始观测的有效表征. 虽然这种方法可以显著提升状态表征的质量, 但它往往需要额外的离线样本数据[30], 这可能与追求高样本效率的目标不完全一致.
1.2 基于动作表征的强化学习
以往的研究主要集中于状态表征学习, 近年来从动作表征的角度提升强化学习性能的学习引起研究者的广泛关注[14, 31]. 动作表征的研究强调在潜动作空间中学习策略, 并通过潜空间动作到实际动作的转换, 实现对大规模动作集的泛化能力的提升. Chandak等[32]提出一种方法, 通过在潜动作空间上学习策略, 并将这些潜动作转化为实际的动作, 以实现在动作空间上的泛化. Allshire等[33]通过引入变分自编码器(Variational autoencoder, VAE)架构来学习解纠缠的动作表征, 这种方法不仅提高了策略学习的样本效率, 还增强了模型对动作信息的学习和理解. 通过这种方式, 模型能够在保留动作关键信息的同时, 简化策略优化过程. 在基于模型的强化学习领域, Park等[23]提出在学习到的潜动作空间中训练环境模型的策略. 这种方法通过优化潜动作空间中的环境模型, 为基于模型的RL提供了一种有效的策略学习框架. 此外, 动作表征的研究还显示出在多任务学习中的潜力, 潜空间的动作表征可以被多个任务共享, 增强了模型在不同任务间的泛化能力[31]. Zheng等[16]则通过最大化当前状态表征及其后续动作序列与未来状态表征之间的互信息, 以同时学习状态和动作的表征, 理论上能够提供丰富的控制信息, 从而提升样本效率.
1.3 基于对比学习的视觉强化学习
对比学习作为一种强大的学习机制, 在各个领域尤其是计算机视觉中得到了有效的利用[34], 它通过对比相似与不相似的样本来学习有意义的特征嵌入. 在视觉强化学习中, 对比学习主要用于设计自监督辅助任务以改善状态表征的学习质量[35]. 信息噪声对比估计(Information noise contrastive estimation, InfoNCE)[36]损失函数是一种流行的对比学习目标, 能够有效地利用对比损失来提取有效的状态特征[37]. CURL[8]通过将锚点样本的增强状态视作正样本, 序列中其他样本作为负样本来构建自监督对比学习, 但这一方法未充分考虑到马尔科夫决策过程的时间依赖性. 而CPC[9]、ST-DIM (Spatiotemporal DeepInfomax)[38]和ATC (Augmented temporal contrast)[39]等方法则通过最大化当前状态表征与未来状态表征之间的互信息, 将时间维度的信息整合进对比损失中. 尽管这些方法通过学习时序信息获得了更好的表征, 但却忽略了动作表征信息在视觉RL中的作用. 与此同时, Zheng等[16]通过最大化当前状态表征及其随后动作序列与未来状态表征之间的互信息, 实现了状态和动作表征的同时学习. 此外, ADAT (Action-driven auxiliary task)[14]引入一种新的方法, 通过将具有相似策略输出的观测视为正样本, 从而将动作信息直接纳入对比学习过程, 以此来学习动作表征. 这种将动作信息纳入对比学习的做法为动作表征的学习提供了新的视角.
2. 问题描述
强化学习通过与环境的交互直接从像素输入中学习策略[40], 这可以被建模为具有5个元素的标准MDP: $ \left\langle {{\cal{S}},\;{\cal{A}},\;{\cal{P}},\;{\cal{R}},\;\gamma} \right\rangle $. 其中, $ {\cal{S}} $是状态空间, $ s_t \in {\cal{S}} $表示时间$ t $获取的像素图像. $ {\cal{A}} $是动作空间, $ a_t \in {\cal{A}} $表示智能体在时间$ t $所采取的动作. $ {\cal{P}} $表示状态转移动态. $ {\cal{R}} $表示奖赏函数, $ r_t = {\cal{R}}(s_t,\;a_t) $表示在状态$ s_t $采取动作$ a_t $后获得的奖赏. $ \gamma $是一个折扣因子, 用于约束奖赏. 强化学习的目标是训练智能体在每个回合中最大化期望的累积折扣奖赏(又称回报)$ G_t = \sum_{k = 0}^{\infty} \gamma^k r_{t+k+1} $, 其中$ \gamma \in [0,\;1] $.
基于视觉的强化学习问题, 环境状态$ s_t $往往由高维像素数据给出, 智能体需要从像素数据中学习有效的状态表征, 即将一个高维状态$ s_t $映射成一个低维度的特征向量: $ s_t \rightarrow z_t $, 其中, $ z_t $是$ s_t $在低维空间的特征表示. 当遇到更为复杂的具有高维动作空间的视觉强化学习问题时, 为了更好地学习和利用动作信息, 还需要将原始高维动作映射至一个动作表征空间中: $ a_t \rightarrow u_t $, 其中, $ u_t $是$ a_t $的特征表示. 同时学习状态表征和动作表征可以帮助智能体更好地理解环境并在后续的策略学习过程中做出更优的决策.
3. 基于Transformer的状态−动作−奖赏预测表征学习
针对复杂控制任务中视觉强化学习面临的样本效率问题, 本文提出一种基于Transformer的状态−动作−奖赏预测表征学习框架, 称为TSAR. 如图2所示, TSAR包含3种基于预测的辅助任务: 状态预测学习、动作预测学习和奖赏预测学习, 3个任务共同作用以学习状态和动作表征. TSAR与RL策略同步训练, 通过共享在线状态编码器和动作编码器, TSAR可以将学习到的状态表征和动作表征传递给RL算法, 以帮助RL在动作空间维度较大的复杂任务中学习更有效的策略. 本节从基本网络架构、状态预测学习、动作预测学习和奖赏预测学习4个方面详细介绍TSAR的设计和实现.
3.1 基本网络架构
3.1.1 状态编码器和动作编码器
在强化学习中, 智能体利用重放缓冲区中随机采样的轨迹来优化其策略目标, 这种做法有效降低了训练样本间的相关性, 从而稳定了训练过程. 对于一批随机采样的样本, 首先通过随机变换(Random shift)的数据增强技术进行预处理. 接着, 使用这批数据来同时进行基于状态−动作−奖赏的对比表征学习、动作与奖赏预测学习, 以及强化学习策略的学习. 具体来说, 在每次训练迭代中, 对于一个长度为$ K $的经验轨迹批次$ \{s_t,\; a_t,\; r_t,\; \cdots,\; s_{t+K-1}, a_{t+K-1},\; r_{t+K-1}\} $, 对批次中的所有状态应用数据增强技术: $ {s_{t:t+K-1}} \leftarrow \mathrm{Aug}( s_{t:t+K-1} ) $. 用于状态特征提取的在线状态编码器$ f_\theta $由卷积神经网络(Convolutional neural network, CNN)[41]构建, 该编码器将增强后的样本$ s_t $映射到其对应的状态特征, 即
$$ \begin{equation} \begin{split} z_t = f_\theta(s_t) \end{split} \end{equation} $$ (1) 其中, $ \theta $表示在线编码器$ f_\theta $的参数.
为了在高维动作空间中更好地理解动作信息, TSAR利用一个基于CNN的动作编码器来提取动作特征. 为了学习高维动作空间中较为丰富的信息, 动作编码器的输出维度为1.25倍原始动作空间维度. 原始动作$ a_t $经过动作编码器$ g_\alpha $可以被映射为如下的动作特征:
$$ \begin{equation} \begin{split} u_t = g_\alpha(a_t) \end{split} \end{equation} $$ (2) 其中, $ \alpha $表示在线动作编码器$ g_\alpha $的参数. 这些状态特征和动作特征随后用于策略网络$ \pi $和状态预测模型$ \phi $.
遵循之前的研究经验, 例如CURL[8], 引入一个额外的目标状态编码器$ f_{\bar{\theta}} $来计算目标状态的特征, 而不是直接使用在线编码器. 目标状态编码器$ f_{\bar{\theta}} $的参数$ \bar{\theta} $不通过梯度下降更新. 相反, 它们根据在线编码器的参数以及一个衰减率$ \tau \in [0,\;1) $通过指数移动平均(Exponential moving average, EMA)[42]技术进行更新. 更新规则可以表示为
$$ \begin{equation} \begin{split} \bar{\theta} \leftarrow \tau \bar{\theta}+(1-\tau) \theta \end{split} \end{equation} $$ (3) 这样的更新方式使目标编码器的参数能够平滑地跟踪在线编码器参数的变化, 从而在动态环境中保持了对稳定状态表征的学习.
3.1.2 状态预测模型
最近的研究成果已经证明, 时间序列的相关性对于序列表征学习至关重要[11]. TSAR通过充分挖掘潜藏在轨迹中的时间序列相关性, 并借鉴马尔科夫决策过程来实现更有效的表征学习. 受到自然语言处理领域研究的启发, TSAR采用Transformer架构, 通过顺序数据输入, 显式地促使表征学习模型捕捉状态周围的上下文信息. 基于Transformer的状态预测模型$ \phi $的结构设计允许它接收3类输入词符: 1)状态词符, 从状态序列中提取的特征序列$ \left\{z_t,\; \cdots,\; z_{t+K-2}\right\} $, 这些特征由在线状态编码器生成; 2)动作词符, 从动作序列中提取的特征序列$ \left\{u_t,\; u_{t+1},\; \cdots,\; u_{t+K-2}\right\} $, 这些特征由在线动作编码器生成; 3)奖赏词符$ \left\{r_t,\; \cdots,\; r_{t+K-2}\right\} $. 此外, 通过引入相对位置嵌入$ \left\{p_t,\; p_{t+1},\; \cdots,\; p_{t+K-2}\right\} $, 为所有输入词符都添加了空间位置信息, 以便更好地捕捉序列中的时序关系, 这一做法遵循了Transformer模型的标准实践[43]. 值得强调的是, 同一时间步的状态词符、动作词符和奖赏词符共享相同的位置嵌入, 以确保模型能够正确理解状态和动作之间的时序关系.
在状态预测模型$ \phi $中, 采用由$ L $个相同块构成的Transformer模型. 每个块内部包含2个主要的堆叠层: 一个多头自注意力(Multi-headed self-attention, MHSA)层和一个由多层感知机(Multi-layer perceptron, MLP)构成的前馈网络层. 为了提高模型训练过程中的稳定性和加快收敛速度, 每个层的前面均配备了层归一化(Layer normalization, LN)组件. 此外, 为促进更深层次网络的有效训练, 每个层的输出都加上了残差连接, 这有助于防止梯度消失或爆炸问题, 保证信息在网络中的顺畅流动. 状态预测模型$ \phi $的输出可以表示为
$$ \begin{equation} \begin{split} \hat{z}_{t+1:t+K-1} = \phi(z_{t:t+K-2},\; u_{t:t+K-2},\; r_{t:t+K-2}) \end{split} \end{equation} $$ (4) 3.1.3 投影网络
为了避免模型在自监督学习过程中的崩溃问题, 参考BYOL (Bootstrap your own latent)[35]的设计, TSAR采用一种非对称的投影网络架构. 具体来说, 对于状态预测模型输出的目标状态的预测特征$ \hat{z}_{t+1:t+K-1} $, 在线投影网络采用在线投影头$ G_{m_1} $与在线预测头$ H_{m_2} $进行处理, 以得到最终的预测特征, 即
$$ \begin{equation} \begin{split} \tilde{z}_{t+1:t+K-1} = H_{m_2}(G_{m_1}(\hat{z}_{t+1:t+K-1})) \end{split} \end{equation} $$ (5) 对于目标状态$ s_{t+1:t+K-1} $, 仅采用目标投影头$ G_{\bar{m}_1} $来获取最终的特征:
$$ \begin{equation} \begin{split} \bar{z}_{t+1:t+K-1} = G_{\bar{m}_1}(f_{\bar{\theta}}(s_{t+1:t+K-1})) \end{split} \end{equation} $$ (6) 其中, $ m_1 $, $ \bar{m}_1 $, $ m_2 $分别是在线投影头、目标投影头和在线预测头的参数, 目标投影头的参数$ \bar{m}_1 $不参与梯度更新, 而是通过指数移动平均策略, 从在线投影头的参数中继承.
3.1.4 动作预测模型和奖赏预测模型
此外, 为了增强状态表征在未来动作预测中的贡献, TSAR引入动作预测学习作为额外的学习约束. 具体来说, 引入一个由全连接网络组成的动作预测模型$ h_{p_1} $, 输入是当前时刻状态$ s_t $和下一时刻状态$ s_{t+1} $, 输出是当前时刻动作的预测特征$ \tilde{u}_t $, 其中, $ p_1 $是动作预测模型的参数.
为了促进智能体更好地理解其行为可能产生的后果, TSAR引入奖赏预测学习用于约束状态表征和动作表征的学习. 具体来说, 引入一个由全连接网络组成的奖赏预测模型$ l_{p_2} $, 输入是当前时刻状态$ s_t $和一段长度为$ n $的动作序列$ a_{t:t+n-1} $, 输出是未来第$ t+n-1 $时刻的预测奖赏$ \tilde{r}_{t+n-1} $, 其中, $ p_2 $是奖赏预测模型的参数.
3.2 状态预测学习
马尔科夫决策过程是强化学习的理论基础, 它提供一个框架来形式化智能体在某个环境中通过序列决策以最大化累积奖赏的问题. MDP由状态($ {\cal{S}} $)、动作($ {\cal{A}} $)、奖赏($ {\cal{R}} $)、状态转移概率($ {\cal{P}} $) 和折扣因子($ \gamma $) 组成. 在这个框架下, 基于状态、动作和奖赏的预测任务具有重要意义. 将动作表征、奖赏信息与状态表征结合起来, 有助于智能体在学习过程中考虑到更全面的信息. 智能体不仅需要了解环境的当前状态, 还需要理解不同动作和奖赏会如何影响未来状态. 因此, TSAR创新性地提出一种基于状态−动作−奖赏的对比学习用于执行状态预测学习, 如图3所示, 状态预测模型的目标是根据每一个时刻的状态、动作和奖赏信息学习下一时刻的状态特征, 以此来同时学习状态表征和动作表征. 在获得优秀状态表征的基础上, 学习有效的动作表征可以帮助智能体更好地理解动作信息, 促使智能体在具有高维动作空间的复杂控制任务上获得更好的性能和样本效率.
3.2.1 数据预处理
为了提高状态预测学习的鲁棒性, TSAR的状态预测学习引入随机掩码技术, 迫使智能体深入理解序列状态之间的上下文关系. 因此, 用于状态预测学习的批次数据还需执行随机掩码操作.
在一批长度为$ K $的增强样本$ \{s_t,\; s_{t+1},\; \cdots, s_{t+K-2}\} $中, TSAR会在序列中随机选择50%的状态进行掩码. 具体来说, 首先定义一个与$ \{s_t,\; s_{t+1},\; \cdots,\; s_{t+K-2}\} $对应的掩码序列$ M = \{M_t,\; M_{t+1},\; \cdots, M_{t+K-2}\} $, 对于每一个$ M_{t+i} \in [M] $, 有50%的概率$ M_{t+i} = 0 $, 有50%的概率$ M_{t+i} = 1 $. 如果$ M_{t+i} = 1 $, 则$ \left\{s_t,\; s_{t+1},\; \cdots,\; s_{t+K-2}\right\} $中与之对应的状态保持不变. 若$ M_{t+i} = 0 $, 则$ \left\{s_t,\; s_{t+1},\; \cdots,\; s_{t+K-2}\right\} $中与之对应的状态按80%概率被置为零向量, 10%概率置为序列任一其他状态, 10%概率保持不变.
为了方便表示, 将序列中经过随机掩码处理的状态表示为$ s_{mask} $, 其对状态特征的表示为$ z_{mask} $. 则原批次样本可以表示为$ \left\{s_t,\; s_{mask},\; \cdots,\; s_{t+K-2}\right\} $, 其通过在线状态编码器获得的状态特征序列可以表示为: $ \left\{z_t,\; z_{mask},\; \cdots,\; z_{t+K-2}\right\} $. 状态特征序列与动作特征序列$ \left\{u_t,\; u_{t+1},\; \cdots,\; u_{t+K-2}\right\} $和奖赏序列$ \left\{r_t,\; \cdots,\; r_{t+K-2}\right\} $作为3类词符输入基于Transformer的状态预测模型中.
3.2.2 基于状态−动作−奖赏的对比学习
状态预测模型的目标是根据每一个时刻的状态、动作和奖赏信息学习下一时刻的状态特征. 为了明确地模拟强局部关系, TSAR基于“状态−动作−奖赏”对输入词符进行分组, 小组中的每个元素与其他元素都有很强的因果关系. 具体来说, 每个时间步的状态特征$ z_t $、动作特征$ u_t $和奖赏$ r_t $被划分为一个小组, 在状态预测模型的输出端, 对应于这个小组的输出会被求平均值, 以生成对下一时刻状态的预测特征. 通过这种方式, 模型能够基于大量的“状态−动作−奖赏”组合学习到预测的状态表征$ \hat{z}_{t+1:t+K-1} = \phi(z_{t:t+K-2},\; u_{t:t+K-2},\; r_{t:t+K-2}) $. $ \hat{z} $再经过在线投影网络的特征提取和降维, 得到最终的预测特征$ \tilde{z}_{t+1:t+K-1} = H_{m_2}(G_{m_1}(\hat{z}_{t+1:t+K-1})) $.
为了实现更好的表征学习, 状态预测学习使用对比学习进行优化, 通过最大化预测的状态特征$ \tilde{z}_{t+1:t+K-1} $与真实目标状态特征$ \bar{z}_{t+1:t+K-1} = G_{\bar{m}_1}(f_{\bar{\theta}}(s_{t+1:t+K-1})) $之间的互信息, 从而实现对状态−动作表征的同时学习.
对比学习的损失可以定义为
$$ \begin{equation} \begin{split} {\cal{L}}_{\mathrm{s}} = - \frac{1}{K-1} \sum_{i = 1}^{K-1} {\mathrm{ln}} \frac{\exp(q_i^{\mathrm{T}}Wk_+)}{\sum\limits_{j = 1}^{K-1} \exp(q_i^{\mathrm{T}}Wk_j)} \end{split} \end{equation} $$ (7) 其中, $ q_i = \tilde{z}_{t+i} $代表锚点样本的状态特征; $ k_+ = \bar{z}_{t+i} $代表正样本的状态特征; $ k_j = \bar{z}_{t+j} $代表序列中任一样本的状态特征, 包含正样本和负样本. $ W $是一个可学习的参数, 为$ q $和$ k $提供相似性度量的计算空间. 对比学习的目标是让锚点样本的状态特征$ q_i $和正样本的状态特征$ k_+ $相似, 而与序列中的其他负样本的状态特征$ k_j \backslash \{k_+\} $不同.
3.3 动作预测学习
TSAR在常见的状态预测基础上, 进一步引入动作预测学习作为额外的学习约束, 以增强状态表征在未来动作预测中的贡献, 如图4(a)所示. 动作预测学习强制智能体学习状态之间的转换与所采取的动作之间的关系, 这有助于模型更好地理解环境的动态特性, 即哪些动作会导致特定的状态变化. 同时动作预测学习可以约束状态表征的学习方向, 让其朝着更有利于决策的方向前进. 具体来说, 对于任意2个相邻时刻的状态$ s_{t+i} $和$ s_{t+i+1} $, 将其经过在线状态编码器得到的状态特征$ z_{t+i} $和$ z_{t+i+1} $输入到动作预测模型$ h_{p_1} $中, 得到对$ t+i $时刻的动作特征的预测, 即
图 4 动作预测学习和奖赏预测学习框架Fig. 4 The framework of action prediction learning and reward prediction learning$$ \begin{equation} \begin{split} \tilde u_{t+i} = h_{p_1}(z_{t+i},\;z_{t+i+1}) \end{split} \end{equation} $$ (8) 动作预测任务的目标是最小化预测的动作特征$ \tilde u_{t+i} $和真实的动作特征$ u_{t+i} $之间的差异, 其损失函数可以表示为
$$ \begin{equation} \begin{split} {\cal{L}}_{\mathrm{a}} = \sum_{i = 0}^{K-2} \left(\tilde u_{t+i}-u_{t+i}\right)^2 \end{split} \end{equation} $$ (9) 3.4 奖赏预测学习
为了高效地利用每个交互样本, 参考已有工作的成功经验[16], TSAR通过奖赏预测学习促进智能体更好地理解其行为的后果. 如图4(b)所示, 通过对多步动作的奖赏估计, 促使智能体调整其策略以优化长期奖赏. 奖赏预测学习可以作为一种辅助信号, 帮助智能体更快地收敛到更优的策略. 具体来说, 对于任意时刻的状态$ s_{t+i} $和一段长度为$ n $的动作序列$ a_{t+i:t+i+n-1} $, 将其经过在线状态编码器得到的状态特征$ z_{t+i} $和经过动作编码器得到的动作特征$ u_{t+i:t+i+n-1} $输入到奖赏预测模型$ l_{p_2} $中, 得到对$ t+i+n-1 $时刻的预测奖赏, 即
$$ \begin{equation} \begin{split} \tilde r_{t+i+n-1} = l_{p_2}(z_{t+i},\;u_{t+i:t+i+n-1}) \end{split} \end{equation} $$ (10) 奖赏预测任务的目标是最小化预测的奖赏$ \tilde r_{t+i+n-1} $和真实的奖赏$ r_{t+i+n-1} $之间的差异, 其损失函数可以表示为
$$ \begin{equation} \begin{split} {\cal{L}}_{\mathrm{r}} = \sum_{i = 0}^{K-n} \left(\tilde r_{t+i+n-1}-r_{t+i+n-1}\right)^2 \end{split} \end{equation} $$ (11) 3.5 训练过程
TSAR以辅助任务的形式与离策略RL结合, 则总损失可以表示为
$$ \begin{equation} \begin{aligned} {{\cal{L}}_{\mathrm{total}}} = \lambda_1{\cal{L}}_{\mathrm{s}}+\lambda_2{\cal{L}}_{\mathrm{a}}+\lambda_3{\cal{L}}_{\mathrm{r}}+{\cal{L}}_{\mathrm{RL}} \end{aligned} \end{equation} $$ (12) 其中, $ \lambda_1 $, $ \lambda_2 $, $ \lambda_3 $分别控制3种预测损失在总损失中的贡献, $ {\cal{L}}_{\mathrm{RL}} $表示离策略RL的损失, 在本文中, 选择DrQ-v2[22]作为TSAR实现的基准RL算法, 则$ {\cal{L}}_{\mathrm{RL}} $与DrQ-v2损失保持一致. TSAR算法的伪代码如算法1所示.
算法 1. 基于Transformer的状态−动作−奖赏预测表征学习
Require: 将在线状态编码器$ f_{\theta} $、目标状态编码器$ f_{\bar{\theta}} $、动作编码器$ g $、状态预测模型$ \phi $、在线投影头$ G_m $、目标投影头$ G_{\bar{m}} $、在线预测头$ H $, 动作预测模型$ h $, 奖赏预测模型$ l $和策略网络$ \pi $的参数分别表示为$ \theta $, $ \bar{\theta} $, $ \alpha $, $ \psi $, $ m_1 $, $ \bar{m}_1 $, $ m_2 $, $ p_1 $, $ p_2 $和$ \omega $.
1: 初始化经验池$ {\cal{D}}=\emptyset $;
2: 初始化所有网络参数;
3: while 训练 do
4: 运行当前策略并收集交互样本放入经验池
5: $ {\cal{D}} \leftarrow {\cal{D}} \cup\left(s_t,\; a_t,\; r_t,\; s_{t+1}\right) $
6: 从经验池$ {\cal{D}} $中随机采样一批样本
7: $ \left\{s_{t;t+K-1},\; a_{t;t+K-1},\; r_{t;t+K-1}\right\} \sim {\cal{D}} $
8: 所有损失置零
9: 对批次样本执行数据增强和随机掩码
10: 根据式(1)计算批次样本的状态特征:
11: $ z_{t;t+K-1} = f_\theta(s_{t;t+K-1}) $
12: 根据式(2)计算批次样本的动作特征:
13: $ u_{t;t+K-1} = g_\alpha(a_{t;t+K-1}) $
14: 根据式(4)计算目标状态的预测特征:
15: $ \hat{z}_{t+1:t+K-1} = \phi(z_{t:t+K-2},\; u_{t:t+K-2},\; r_{t:t+K-2}) $
16: 根据式(5)计算在线投影网络的预测特征:
17: $ \tilde{z}_{t+1:t+K-1} = H_{m_2}(G_{m_1}(\hat{z}_{t+1:t+K-1})) $
18: 根据式(6)计算目标状态的特征:
19: $ \bar{z}_{t+1:t+K-1} = G_{\bar{m}_1}(f_{\bar{\theta}}(s_{t+1:t+K-1})) $
20: 根据式(7)计算对比学习损失: $ {\cal{L}}_{\mathrm{s}} $
21: 根据式(8)计算动作预测模型预测的特征:
22: $ \tilde u_{t+i} = h(z_{t+i},\;z_{t+i+1}) $
23: 根据式(9)计算动作预测的损失: $ {\cal{L}}_{\mathrm{a}} $
24: 根据式(10)计算奖赏预测模型预测的奖赏:
25: $ \tilde r_{t+i+n-1} = l_{p_2}(z_{t+i},\;u_{t+i:t+i+n-1}) $
26: 根据式(11)计算奖赏预测的损失: $ {\cal{L}}_{\mathrm{r}} $
27: 计算RL的损失: $ {\cal{L}}_{\mathrm{RL}} $
28: 根据式(12)计算总损失:
29: $ {{\cal{L}}_{\mathrm{total}}}=\lambda_1{\cal{L}}_{\mathrm{s}}+\lambda_2{\cal{L}}_{\mathrm{a}}+\lambda_3{\cal{L}}_{\mathrm{r}}+{\cal{L}}_{\mathrm{RL}} $
30: 更新在线网络的参数:
31: $ \left(\theta,\; \alpha,\; \psi,\; m_1,\; m_2,\; p_1,\; p_2,\; \omega\right) $
32: 更新目标网络的参数:
$ \bar{\theta} \leftarrow \tau \bar{\theta}+(1-\tau) \theta $
$ \bar{m}_1 \leftarrow \tau \bar{m}_1+(1-\tau)m_1 $
33: end while
4. 实验与结果分析
在本文中, TSAR选择连续控制平台DMControl作为实验环境. DMControl是由DeepMind开发的一个软件库, 它基于MuJoCo物理引擎, 可以用于机器人运动规划、控制策略开发和测试, 为强化学习算法提供了一个在连续动作空间任务中的实验和测试的平台. 具体来说, 本文在具有挑战性的困难任务: Acrobot Swingup, Cheetah Run, Reacher Hard, Hopper Hop, Finger Turn Hard, Walker Run, 以及具有高维动作空间的困难任务: Quadruped Walk, Quadruped Run和Reach Duplo等9个环境中进行了实验验证. 表1展示了这9个困难环境的基本信息.
表 1 9个困难环境的基本信息Table 1 The fundamental information of nine challenging environments环境 动作空间维度 难易程度 Quadruped Walk 12 困难 Quadruped Run 12 困难 Reach Duplo 9 困难 Walker Run 6 困难 Cheetah Run 6 困难 Hopper Hop 4 困难 Finger Turn Hard 2 困难 Reacher Hard 2 困难 Acrobot Swingup 1 困难 为了验证TSAR的性能和样本效率, 本文设计了以下5组实验:
1) TSAR和对比算法的性能比较;
2) TSAR与相似表征学习目标对比;
3) 状态预测模型的准确性;
4) 动作表征的作用;
5) 关键模块的消融实验.
所有的算法均随机选择5个种子进行实验, 以确保结果的可靠性. 每次性能测试均运行超过30个回合, 并计算平均性能和标准差, 用于结果展示. 此外, 还计算了每个算法在9个环境中的平均性能和中位性能, 从而提供了对它们性能的进一步了解和分析.
4.1 基准算法和超参数设置
本文选择3种无模型视觉强化学习算法进行比较研究. 这些算法包括DrQ-v2[22]、CURL[8]和TACO[16]. 其中DrQ-v2算法是TSAR的基准算法, 其通过数据增强技术和探索策略优化技术, 成为首个在基于视觉的仿人运动任务上取得成效的无模型强化学习算法; CURL作为首个将对比学习与模型无关强化学习结合的方法, 在多个基于视觉的强化学习基准任务上取得了显著的性能提升; TACO[16]是最先进的动作驱动的视觉强化学习算法, 在DMControl连续控制平台的困难环境中均取得了远超基准算法的优异性能.
此外, 本文还比较了用于视觉连续控制的2种最先进的基于模型的强化学习算法: Dreamer-v3[44]和TD-MPC (Temporal difference learning for model predictive control)[27], 其中Dreamer-v3作为Dreamer系列的集大成者, 在潜空间中学习世界模型, 使用预测模型生成学习样本的同时指导智能体学习更有效的表征和策略; TD-MPC将基于模型的预测控制和无模型的时间差分学习结合, 在基于像素的连续控制环境中展现了优秀的样本效率和性能.
实验中所有的算法均可在1张NVIDIA A100显卡中运行, 其中TSAR虽然采用了Transformer架构, 但是由于仅采用2层的Transformer模型进行训练, 因此对资源的消耗并不是很大, 仅需20 G显存即可运行. 所有算法在与环境交互过程中, 默认选择将图像的相邻3帧聚合成单一状态观测. TSAR策略网络的超参数与DrQ-v2原文保持一致, 其表征网络额外的超参数设置如表2所示.
表 2 TSAR额外的超参数Table 2 Additional hyperparameters for TSAR超参数 含义 值 $ \lambda_1 $ 状态预测损失权重 1 $ \lambda_2 $ 动作预测损失权重 1 $ \lambda_3 $ 奖赏预测损失权重 1 batch_size 训练批次大小 256 mask_ratio 掩码比例 50% $ K $ 序列长度 16 $ L $ 注意力层数 2 2: Hopper Hop $ n $ 奖赏预测步长 Reacher Hard 1: 其他 $ \tau $ EMA衰减率 0.95 4.2 对比实验
图5展示了TSAR和基准算法DrQ-v2[22]以及SOTA算法TACO[16]在200万时间步长下的性能表现, 其中, Quadruped Run、Hopper Hop和Walker Run 3个环境因为任务困难导致训练难度更高, 所以统计300万时间步长下的测试结果. 图5中所有算法均收敛或基本收敛, 可以更好地评估算法在困难的连续控制环境中的性能.
表3统计了TSAR和3种无模型的对比算法在100万时间步长时的得分. 此外, 表3统计了TSAR和2种基于模型的对比算法在100万时间步长时的得分. 通过比较100万步长时的性能, 可以更好地评估算法的样本效率. 所有对比算法的成绩均直接引用自原始论文数据, 为了更好地展示算法的性能, 本文统计了所有算法测试结果的平均性能和中位性能. 从这些结果中可以得出以下结论和分析:
表 3 TSAR和对比算法在100万步长时的得分Table 3 Scores achieved by TSAR and comparison algorithms at 1 M time steps环境 TSAR (本文) TACO[16] DrQ-v2[22] CURL[8] Dreamer-v3[44] TD-MPC[27] Quadruped Run 657±25 541±38 407±21 181±14 331±42 397±37 Hopper Hop 293±41 261±52 189±35 152±34 369±21 195±18 Walker Run 699±22 637±11 517±43 387±24 765±32 600±28 Quadruped Walk 837±23 793±8 680±52 123±11 353±27 435±16 Cheetah Run 835±32 821±48 691±42 657±35 728±32 565±61 Finger Turn Hard 636±24 632±75 220±21 215±17 810±58 400±113 Acrobot Swingup 318±19 241±21 128±8 5±1 210±12 224±20 Reacher Hard 937±18 883±63 572±51 400±29 499±51 485±31 Reach Duplo 247±11 234±21 206±32 8±1 119±30 117±12 平均性能 606.6 560.3 226.4 236.4 464.9 379.8 中位性能 657 632 179 181 369 400 注: 加粗字体表示在不同环境下各算法的最优结果. 1) 如图5所示, 在DMControl的连续控制平台的9个具有挑战性的环境中, TSAR算法均展现出超越TACO和DrQ-v2的性能. TSAR能够有如此提升主要原因有两点: a)基于状态−动作−奖赏预测的表征学习可以学习更有效的表征; b) TSAR显式地将动作表征融入到策略训练中, 这对性能的提升十分重要.
2) 与先前的无模型表征强化学习方法相比, TSAR展现出更高的样本效率. 以Reacher Hard这一具有挑战性的环境为例, 如图5(e)所示, 相较于基准算法DrQ-v2, TACO仅需80万步即可达到其最优性能, 而DrQ-v2需要约160万步. 与SOTA算法TACO相较, 尽管二者大约在80万步时均达到最优性能, TSAR却能在仅50万步时实现与TACO相同的最佳性能, 并在80万步时的性能稳定超越TACO.
3) 如表3所示, 在经过100万步长的训练之后, TSAR的平均测试性能相较于基准算法DrQ-v2提升了51.2%, 与SOTA算法TACO相比提升了8.3%. 此外, 在9个挑战性任务中, TSAR在6个任务上的表现超越了最新的基于模型的视觉强化学习算法Dreamer-v3, 其平均测试性能提升了30.5%, 这进一步证明TSAR具有更高的样本效率.
4.3 表征学习目标对比实验
为验证TSAR基于状态−动作−奖赏的表征学习目标的有效性, 本文将TSAR与其他优秀的基于视觉的RL表征学习算法进行比较, 包括M-CURL[11]、SPR[10]和ATC[39]. 这些算法分别采取不同的策略来构建表征学习的目标: M-CURL考虑连续输入间的相关性并设计基于Transformer的预测模型对序列状态进行掩码重建, 构建了一种对比学习目标, 强调序列中各状态的关联性; SPR旨在训练智能体从当前状态的潜空间特征出发, 预测未来多个时刻的状态特征, 采用基于预测的表征学习目标, 以期增强智能体对未来状态变化的预测能力; ATC则通过将轨迹中相邻的观测联系起来, 定义正样本和负样本, 构建对比表征学习目标, 着重于提升状态间的区分能力.
由于SPR最初并非设计用于连续控制任务, 研究中采用DrQ-v2[22]作为基准强化学习算法对其进行了重新实现, 以确保公平比较. 同理, M-CURL和ATC也在DrQ-v2框架下重新实现. 此外, 考虑到TSAR显式地将动作表征融入强化学习策略的训练中, 参与比较的各算法除DrQ-v2和ATC外, 均集成了类似的动作表征融合过程, 以确保比较的重点在于表征学习目标的差异.
实验结果如表4所示, 从这些结果中可以看到, 尽管各对比算法均通过其表征学习目标帮助智能体实现了超越基准算法的性能提升, TSAR在所有9个测试环境中依然展现了超越其他算法的卓越性能. 这一发现进一步证明了TSAR在表征学习目标设计方面的有效性, 能够更全面地学习状态−动作表征, 并为强化学习策略的训练提供显著的增益.
表 4 与不同表征学习目标的对比Table 4 Comparison with other representation learning objectives环境 TSAR (本文) TACO[16] M-CURL[11] SPR[10] ATC[39] DrQ-v2[22] Quadruped Run 657±25 541±38 536±45 448±79 432±54 407±21 Hopper Hop 293±41 261±52 248±61 154±10 112±98 192±41 Walker Run 699±22 637±21 623±39 560±71 502±171 517±43 Quadruped Walk 837±23 793±8 767±29 701±25 718±27 680±52 Cheetah Run 835±32 821±48 794±61 725±49 710±51 691±42 Finger Turn Hard 636±24 632±75 624±102 573±88 526±95 220±21 Acrobot Swingup 318±19 241±21 234±22 198±21 206±61 210±12 Reacher Hard 937±18 883±63 865±72 711±92 863±12 572±51 Reach Duplo 247±11 234±21 229±34 217±25 219±27 206±32 平均性能 606.6 560.3 546.7 476.3 475.4 226.4 中位性能 657 632 623 560 502 179 4.4 状态预测模型的准确性
一般而言, 状态预测模型预测得越准确, 那么其学到的表征越有效且对策略学习更有帮助. 本文通过设计状态预测模型准确性的验证实验, 旨在探究状态预测模型的准确性与其学习到的表征对策略学习的贡献之间的关系. 为此, 选取了基于预测的表征学习算法TACO[16]和M-CURL[11]作为对比算法进行研究, 其中M-CURL[11]是在DrQ-v2[22]框架下重新实现的. 实验中, 从TSAR、TACO和M-CURL 3种算法中提取了经过100万步长训练后的状态预测模型, 目的是通过评估这3个模型的预测准确性来验证上述假设.
实验采用了由训练至收敛的DrQ-v2算法随机采样得到的1千条轨迹, 并将其输入至3种状态预测模型中. 通过计算状态预测模型输出与真实特征之间的互信息, 来衡量预测的准确性. 互信息$ I(X;Y) $的值越大, 表明随机变量$ X $与$ Y $之间的相关性越强. 所有参与比较的算法均通过InfoNCE损失构建其对比学习目标, 该损失函数通过最大化样本 (例如, 状态预测模型的输出) 与其正样本 (例如, 真实特征) 之间的相对相似度, 间接地最大化样本间的互信息. 理论上, 当InfoNCE损失最小化时, 表示的互信息趋向最大化. 因此, 状态预测模型输出与真实特征之间的InfoNCE损失较小, 意味着二者的互信息更强, 预测准确性更高.
1条轨迹在3个状态预测模型中的InfoNCE损失的统计结果和训练100万步长后3种算法的测试性能如表5所展示, 从这些结果中可以看到, TSAR在所有参与实验的5个环境中InfoNCE损失最小, 且明显优于其他两种状态预测模型. 经分析, 本文认为得益于3种预测任务的相互约束和促进, 促使TSAR在这些环境中的预测准确性更高. 与此同时, TSAR在这5个环境中均展现了最佳的性能, 这进一步验证了更准确的状态预测模型能够学习到更优质的表征, 并有效促进RL策略学习的观点.
表 5 状态预测准确性对比Table 5 Comparison of state prediction accuracy环境 TSAR (本文) TACO[16] M-CURL[11] 误差 性能 误差 性能 误差 性能 Quadruped Run 0.097 657±25 0.157 541±38 0.124 536±45 Walker Run 0.081 699±22 0.145 637±21 0.111 623±39 Hopper Hop 0.206 293±41 0.267 261±52 0.245 248±61 Reacher Hard 0.052 937±18 0.142 883±63 0.107 865±72 Acrobot Swingup 0.063 318±19 0.101 241±21 0.082 234±22 4.5 动作表征有效性
TSAR通过基于状态−动作−奖赏的对比表征学习不仅学习到状态表征, 还学到了有效的动作表征. 为了验证学习的动作表征的有效性, 本文在Quadruped Run环境中设计可视化实验验证动作表征是否可以将语义相似的动作聚类在一起. 具体来说, 实验在具有12维动作空间的困难任务Quadruped Run上进行, 首先人为地将Quadruped Run的原始12维动作空间扩充到32维, 其中只有前12维用于与环境交互, 剩余的20维作为随机噪声. 随后, 在这个扩充后的动作空间中进行了TSAR训练, 训练100万步长之后提取动作表征模型.
为了测试动作表征的有效性, 实验中从原始动作空间中随机选择了4种动作, 并对每种动作复制了1份, 再为每份动作添加了从高斯分布独立采样的20维随机噪声, 形成了4组语义上相似的动作样本集. 这4个样本被输入到动作表征模型中, 以获取对应的动作特征. 实验的核心目的是验证TSAR模型能否忽略添加的噪声维度, 而专注于重要的前12维动作信息.
本文选择t-SNE进行可视化展示, 图6展示了原始动作和动作表征的可视化结果. 可视化结果表明, TSAR学习到的动作表征能够根据动作信息有效地对4组样本进行聚类. 这一发现证实了TSAR方法能够从原始动作中提取出有效的动作特征信息, 即使面对高维空间中的随机噪声, TSAR也能准确地识别和利用与环境交互的关键动作维度.
4.6 消融实验
4.6.1 3种预测任务消融实验
TSAR的设计集成了3个关键的预测任务: 状态预测学习、动作预测学习以及奖赏预测学习, 其目标是学习更有效的状态和动作表征, 以更好地促进强化学习的策略学习. 首先, 状态预测学习通过掩码技术和预测任务, 深入学习序列状态间的上下文关系, 致力于提取高质量的状态和动作表征, 这是TSAR最重要的组件; 其次, 动作预测学习作为额外的约束, 目的是引导状态表征的学习向着更有利于决策的方向优化; 最后, 为了进一步提升样本效率, 奖赏预测学习通过预测智能体多步行为后所带来的影响(环境反馈的奖赏), 帮助状态和动作表征向着更有利于策略获得长期奖赏的方向优化.
为了探究这3个预测任务对强化学习策略训练的影响, 本文进行了一系列消融实验, 分别移除了状态预测学习(表示为“TSAR w/o state prediction”)、动作预测学习(表示为“TSAR w/o action prediction”)和奖赏预测学习(表示为“TSAR w/o reward prediction”). 实验在Quadruped Run、Walker Run和Reacher Hard三个环境中进行, 每种算法均在训练了100万步后进行性能测试. 实验结果如图7所示, 由图7可以得出以下结论:
1) 3个预测任务对于强化学习的策略训练均有积极影响. 特别是, 作为TSAR核心的状态预测学习, 不仅能有效地学习深层次的状态和动作表征, 还能显著提升强化学习策略的性能. 在其被移除后, 性能的下降最为显著, 凸显了其在提升算法性能中的关键作用.
2) 在3个环境中, 动作预测学习对算法的提升效果都仅次于对比表征学习. 说明动作预测学习作为对状态表征的额外约束, 可以有效提高智能体的决策性能.
3) 对比表征学习和动作预测学习已经让算法取得了很好的性能, 在此基础上, 奖赏预测学习一方面可以进一步提高现有数据的利用率; 另一方面, 其对多步行为后潜在后果的预测学习可以帮助智能体更好地优化长期奖赏. 从图7中可以看到, 添加了奖赏预测学习后算法性能得到进一步提升.
4.6.2 动作表征消融实验
同时将状态表征和动作表征输入到强化学习策略网络中参与训练是TSAR能够成功的关键因素之一. 为了验证这一设计的有效性, 本文设计了相应的消融实验, 旨在评估动作表征是否参与RL策略学习对性能的影响. 实验中设置了2个版本进行比较: 一个是状态表征和动作表征同时参与RL策略学习的“TSAR”; 另一个是仅有状态表征参与RL策略学习的“TSAR w/o action presentation”. 所有实验均在训练100万步后进行性能测试, 实验结果如图8所示, 可以看到:
图 8 RL策略学习中动作表征的消融实验Fig. 8 Ablation study of action representation in RL policy learning1) 当仅有状态表征参与策略学习时, TSAR算法相比于基准算法依然能够实现有效的性能提升. 这表明状态表征本身对于策略学习具有重要价值, 能够通过提供关于环境状态的深层次信息来促进策略的优化.
2) 动作表征的学习对于TSAR的性能起着至关重要的作用. 当将动作表征融入到RL策略训练中后, 算法的性能得到了明显的提升, 说明动作表征对于策略优化具有重要价值.
4.6.3 状态预测模型输入词符消融实验
TSAR在状态预测学习过程中引入基于状态−动作−奖赏的对比学习框架, 紧扣强化学习的核心, 即马尔科夫决策过程. 其中, 不仅包括状态和动作的信息, 还将奖赏信息作为预测下一状态的重要输入. 这种设计的创新在于, 与传统仅基于状态或状态加动作预测未来状态的方法不同, TSAR通过状态−动作−奖赏的联合输入, 提供了一种更全面的表征学习方式. 为了探究这一设计的有效性, 本文进行了一系列消融实验, 比较了在输入词符中移除奖赏词符 (“TSAR w/o r-tokens”) 和动作词符 (“TSAR w/o a-tokens”) 的影响. 实验结果如图9所示, 由图9可以看到:
图 9 状态预测模型输入词符的消融实验Fig. 9 Ablation study on the input tokens of the state prediction model1) 实验表明, 采用状态−动作−奖赏联合输入的TSAR模型能够在Quadruped Run、Walker Run和Reacher Hard三个环境中获得更优的性能. 这进一步证明了状态−动作−奖赏作为一个整体, 符合马尔科夫决策过程的自然规律, 能够提供更丰富的信息, 促进更准确的未来状态预测和更有效的表征学习.
2) 将移除动作词符和移除奖赏词符进行比较, 结果显示移除动作词符导致性能下降更为明显, 说明动作信息对于状态预测模型的训练和表征学习的贡献大于奖赏信息. 虽然奖赏信息对于强化学习策略的优化有一定帮助, 但在预测下一状态的过程中, 动作信息更为关键. 这可能是因为动作直接决定了环境状态的变化, 而奖赏则更多地提供了对动作效果的评价, 是对当前状态−动作组合的一个补充.
4.6.4 掩码比例消融实验
TSAR在设计状态预测学习时添加了掩码策略, 目的是提高表征学习的性能并提升稳定性. 在最近的图像掩码的工作中, 发现掩码比例对最终的性能有较大的影响. 探索掩码比例对于TSAR性能的影响是理解其表征学习机制和进一步优化算法的关键. 根据实验设置, 本文研究了掩码比例0%, 25%, 50%和75%对算法性能的具体影响. 实验结果如图10所示, 由图10可以看到:
1) 当掩码比例调整至50%时, TSAR的性能达到了最优. 这个掩码比例的选择恰到好处地平衡了两个极端: 一方面, 较低的掩码比例 (如0%或25%) 可能不足以激励模型捕获深层次的、语义丰富的特征, 因为模型可能仅仅通过观察邻近的未掩码内容就能进行有效的预测, 而忽略了对整体内容的深入理解; 另一方面, 较高的掩码比例 (如75%) 可能会导致模型没有足够的上下文信息来进行有效的状态预测, 从而降低了学习效率和性能.
2) 通过在TSAR状态预测模型中引入50%的掩码比例, 可以有效地提升表征学习的性能和稳定性. 这种掩码策略的设计说明在深度强化学习模型中引入适当的挑战 (如信息的部分掩码) 可以促进模型学习到更加鲁棒和有意义的特征表示. 同时, 这一发现与最近图像处理领域内关于掩码模型工作的结论保持一致, 即适当的掩码比例能够显著影响模型的性能.
4.6.5 序列长度消融实验
TSAR通过利用基于Transformer的状态预测模型来捕获状态序列中的时间相关性, 其中序列长度$ K $是影响学习效率和表征能力的因素之一. 为了深入理解不同序列长度对表征学习的影响, 本文在Quadruped Run环境中, 探究了序列长度$ K \in \{4,\;8, {{16}},\;64,\;128\} $对性能的影响. 实验结果如图11所示, 由图11可以得出以下结论:
1) 当序列长度小于16时, 随着序列长度的增加, TSAR的性能也相应提升. 这表明在较短序列长度范围内, 增加序列长度可以帮助模型更好地理解状态之间的时间依赖性, 从而提高表征的质量和策略的性能.
2) 当序列长度大于16时, 性能提升的边际效应减小, 不同序列长度之间的性能差异不大. 这是因为在强化学习的预测问题中预测状态表征所需的有效上下文长度远小于自然语言处理问题中所需的上下文长度 (通常需要数百个词符), 超过一个阈值之后, 算法的性能并不会持续上升, 而是会趋于一个相对稳定的范围内波动, 在M-CURL[11]和MLR[12]中通过实验也发现类似的现象. 因此, 选择序列长度为16不仅能够兼顾表征学习的需要, 也可以在节约训练资源和提高训练效率方面取得好的平衡.
5. 结束语
面对高维视觉输入和高维动作空间的复杂控制任务场景, 强化学习的样本效率面临巨大挑战. 本文介绍了一种基于Transformer的状态−动作−奖赏预测表征学习 (TSAR) 框架. TSAR设计了一种状态预测学习任务, 通过从掩码的序列信息中预测状态特征, 致力于同时学习状态表征和动作表征. 为了进一步增强状态表征和动作表征对策略学习的影响, TSAR引入了动作预测学习和奖赏预测学习作为额外的约束, 提高了模型对环境动态的理解能力. 通过将动作表征和状态表征显式地纳入到强化学习策略的训练中, TSAR能够有效地提升样本效率和策略性能. 在DMControl的9个具有挑战性的困难环境中, TSAR展现出SOTA性能. 其平均性能相较于无模型表征学习的SOTA算法TACO提升了8.3%, 并且相比于最新的基于模型的表征学习算法Dreamer-v3提升了30.5%. 通过对比实验和可视化分析, 发现TSAR之所以表现优异, 得益于其能够更准确地预测状态表征, 以及其对相似语义动作的有效分类能力. 此外, 通过消融实验, 进一步验证了TSAR中各个组成模块设计的有效性. TSAR作为一种新的表征学习框架, 在具有高维动作空间的复杂控制任务中可以帮助视觉强化学习有效提升样本效率.
虽然TSAR在复杂的类人控制任务上取得了可观的性能提升, 但基于状态和动作表征的学习仍然有进一步研究的空间. 首先, 设计更先进的序列对比学习目标, 允许算法在更小的批次数据上进行有效的学习, 这有助于进一步提升算法的样本效率和计算速度; 其次, 利用离线数据进行强化学习也可以很好地解决样本效率问题, 如何将TSAR的学习过程扩展到离线强化学习中, 也是一个值得深度研究的方向.
-
表 1 机器人符号及无量纲参数
Table 1 Symbols and dimensionless default values of biped parameters
参数 符号 数值 腿长 I 1 腿部质心 m1 1 髋关节质心 m2 2 足半径 r 0.3 腿部质心与圆弧足中心距离 I1 0.55 髋关节与圆弧足中心距离 I2 0.7 髋关节到腿部质心距离 c 0.15 腿部转动惯量 J1 0.01 重力加速度 g 9.8 
下载: 导出CSV
表 2 扰动函数N分配与学习耗时
Table 2 Noise function N settings and learning time
算法 高斯扰动 O-U 扰动 网络参数扰动[39] 耗时 DDPG 0 1 0 6.4 h 2 交互单元 1 1 0 4.2 h 4 交互单元 2 1 1 4.2 h 6 交互单元 2 2 2 4.3 h
下载: 导出CSV
表 3 机器人初始状态
Table 3 The initial states of the biped
状态 $\theta_1$ (rad) $\dot\theta_1$ (rad/s) $\dot\theta_2$ (rad/s) $\phi$ a 0.37149 −1.24226 2.97253 0.078 b 0.24678 −1.20521 0.15476 0.121
下载: 导出CSV
-
[1] 田彦涛, 孙中波, 李宏扬, 王静. 动态双足机器人的控制与优化研究进展. 自动化学报, 2016, 42(8): 1142-1157Tian Yan-Tao, Sun Zhong-Bo, Li Hong-Yang, Wang Jing. A review of optimal and control strategies for dynamic walking bipedal robots. Acta Automatica Sinica, 2016, 42(8): 1142-1157 [2] Chin C S, Lin W P. Robust genetic algorithm and fuzzy inference mechanism embedded in a sliding-mode controller for an uncertain underwater robot. IEEE/ASME Transactions on Mechatronics, 2018, 23(2): 655-666 doi: 10.1109/TMECH.2018.2806389 [3] Wang Y, Wang S, Wei Q P, Tan M, Zhou C, Yu J Z. Development of an underwater manipulator and its free-floating autonomous operation. IEEE/ASME Transactions on Mechatronics, 2016, 21(2): 815-824 doi: 10.1109/TMECH.2015.2494068 [4] Wang Y, Wang S, Tan M, Zhou C, Wei Q P. Real-time dynamic Dubins-Helix method for 3-D trajectory smoothing. IEEE Transactions on Control Systems Technology, 2015, 23(2): 730-736 doi: 10.1109/TCST.2014.2325904 [5] Wang Y, Wang S, Tan M. Path generation of autonomous approach to a moving ship for unmanned vehicles. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5619-5629 doi: 10.1109/TIE.2015.2405904 [6] Ma K Y, Chirarattananon P, Wood R J. Design and fabrication of an insect-scale flying robot for control autonomy. In: Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Hamburg, Germany: IEEE, 2015. 1558−1564 [7] McGeer T. Passive dynamic walking. The International Journal of Robotics Research, 1990, 9(2): 62-82 doi: 10.1177/027836499000900206 [8] Bhounsule P A, Cortell J, Ruina A. Design and control of Ranger: An energy-efficient, dynamic walking robot. In: Proceedings of the 15th International Conference on Climbing and Walking Robots and the Support Technologies for Mobile Machines. Baltimore, MD, USA, 2012. 441−448 [9] Kurz M J, Stergiou N. An artificial neural network that utilizes hip joint actuations to control bifurcations and chaos in a passive dynamic bipedal walking model. Biological Cybernetics, 2005, 93(3): 213-221 doi: 10.1007/s00422-005-0579-6 [10] Sun C Y, He W, Ge W L, Chang C. Adaptive neural network control of biped robots. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 47(2): 315-326 [11] Sugimoto Y, Osuka K. Walking control of quasi passive dynamic walking robot "Quartet III" based on continuous delayed feedback control. In: Proceedings of the 2004 IEEE International Conference on Robotics and Biomimetics. Shenyang, China: IEEE, 2004. 606−611 [12] 刘德君, 田彦涛, 张雷. 双足欠驱动机器人能量成型控制. 机械工程学报, 2012, 48(23): 16-22 doi: 10.3901/JME.2012.23.016Liu De-Jun, Tian Yan-Tao, Zhang Lei. Energy shaping control of under-actuated biped robot. Journal of Mechanical Engineering, 2012, 48(23): 16-22 doi: 10.3901/JME.2012.23.016 [13] Spong M W, Holm J K, Lee D. Passivity-based control of bipedal locomotion. IEEE Robotics & Automation Magazine, 2007, 14(2): 30-40 [14] 刘乃军, 鲁涛, 蔡莹皓, 王硕. 机器人操作技能学习方法综述. 自动化学报, 2019, 45(3): 458-470Liu Nai-Jun, Lu Tao, Cai Ying-Hao, Wang Shuo. A review of robot manipulation skills learning methods. Acta Automatica Sinica, 2019, 45(3): 458-470 [15] Tedrake R, Zhang T W, Seung H S. Stochastic policy gradient reinforcement learning on a simple 3D biped. In: Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Sendai, Japan: IEEE, 2004. 2849−2854 [16] Hitomi K, Shibata T, Nakamura Y, Ishii S. Reinforcement learning for quasi-passive dynamic walking of an unstable biped robot. Robotics and Autonomous Systems, 2006, 54(12): 982-988 doi: 10.1016/j.robot.2006.05.014 [17] Ueno T, Nakamura Y, Takuma T, Shibata T, Hosoda K, Ishii S. Fast and stable learning of quasi-passive dynamic walking by an unstable biped robot based on off-policy natural actor-critic. In: Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing, China: IEEE, 2006. 5226−5231 [18] 刘全, 翟建伟, 章宗长, 钟珊, 周倩, 章鹏, 等. 深度强化学习综述. 计算机学报, 2018, 41(1): 1-27 doi: 10.11897/SP.J.1016.2019.00001Liu Quan, Zhai Jian-Wei, Zhang Zong-Zhang, Zhong Shan, Zhou Qian, et al. A survey on deep reinforcement learning. Chinese Journal of Computers, 2018, 41(1): 1-27 doi: 10.11897/SP.J.1016.2019.00001 [19] Kendall A, Hawke J, Janz D, Mazur P, Reda D, Allen J M, et al. Learning to drive in a day [Online], available: https://arxiv.org/abs/1807.00412, July 1, 2018 [20] 王云鹏, 郭戈. 基于深度强化学习的有轨电车信号优先控制. 自动化学报, 2019, 45(12): 2366-2377Wang Yun-Peng, Guo Ge. Signal priority control for trams using deep reinforcement learning. Acta Automatica Sinica, 2019, 45(12): 2366-2377 [21] 张一珂, 张鹏远, 颜永红. 基于对抗训练策略的语言模型数据增强技术. 自动化学报, 2018, 44(5): 891-900Zhang Yi-Ke, Zhang Peng-Yuan, Yan Yong-Hong. Data augmentation for language models via adversarial training. Acta Automatica Sinica, 2018, 44(5): 891-900 [22] Andreas J, Rohrbach M, Darrell T, Klein D. Learning to compose neural networks for question answering. In: Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. San Diego, California, USA: Association for Computational Linguistics, 2016. 1545−1554 [23] Zhang X X, Lapata M. Sentence simplification with deep reinforcement learning. In: Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing. Copenhagen, Denmark: Association for Computational Linguistics, 2017. 584−594 [24] 赵玉婷, 韩宝玲, 罗庆生. 基于deep Q-network双足机器人非平整地面行走稳定性控制方法. 计算机应用, 2018, 38(9): 2459-2463Zhao Yu-Ting, Han Bao-Ling, Luo Qing-Sheng. Walking stability control method based on deep Q-network for biped robot on uneven ground. Journal of Computer Applications, 2018, 38(9): 2459-2463 [25] Mnih V, Kavukcuoglu K, Silver D, Rusu A A, Veness J, Bellemare M G, et al. Human-level control through deep reinforcement learning. Nature, 2015, 518(7540): 529-533 doi: 10.1038/nature14236 [26] Kumar A, Paul N, Omkar S N. Bipedal walking robot using deep deterministic policy gradient. In: Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence. Bengaluru, India: IEEE, 2018. [27] Lillicrap T P, Hunt J J, Pritzel A, Heess N, Erez T, Tassa Y, et al. Continuous control with deep reinforcement learning [Online], available: https://arxiv.org/abs/1509.02971, September 9, 2015 [28] Song D R, Yang C Y, McGreavy C, Li Z B. Recurrent deterministic policy gradient method for bipedal locomotion on rough terrain challenge. In: Proceedings of the 15th International Conference on Control, Automation, Robotics and Vision. Singapore: IEEE, 2018. 311−318 [29] Todorov E, Erez T, Tassa Y. MuJoCo: A physics engine for model-based control. In: Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. Vilamoura-Algarve, Portugal: IEEE. 2012. 5026−5033 [30] Palanisamy P. Hands-On intelligent agents with openai gym: Your guide to developing AI agents using deep reinforcement learning. Birmingham, UK: Packt Publishing Ltd., 2018. [31] Schaul T, Quan J, Antonoglou I, Silver D. Prioritized experience replay. In: Proceedings of the International Conference on Learning Representations 2016. San Juan, Puerto Rico, 2016. 322−355 [32] Horgan D, Quan J, Budden D, Barth-Maron G, Hessel M, van Hasselt H, et al. Distributed prioritized experience replay. In: Proceedings of the International Conference on Learning Representations 2018. Vancouver, Canada, 2018. [33] Zhao J, Wu X G, Zang X Z, Yang J H. Analysis of period doubling bifurcation and chaos mirror of biped passive dynamic robot gait. Chinese Science Bulletin, 2012, 57(14): 1743-1750 doi: 10.1007/s11434-012-5113-3 [34] Silver D, Lever G, Heess N, Degris T, Wierstra D, Riedmiller M. Deterministic policy gradient algorithms. In: Proceedings of the 31st International Conference on International Conference on Machine Learning. Beijing, China, 2014. I-387−I-395 [35] Sutton R S, Barto A G. Reinforcement Learning: An Introduction. Cambridge: MIT Press, 1998. [36] Zhao J, Wu X G, Zhu Y H, Li G. The improved passive dynamic model with high stability. In: Proceedings of the 2009 International Conference on Mechatronics and Automation. Changchun, China: IEEE, 2009. 4687−4692 [37] Abadi M, Barham P, Chen J M, Chen Z F, Davis A, Dean J, et al. TensorFlow: A system for large-scale machine learning. In: Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation. Savannah, USA: USENIX Association, 2016. 265−283 [38] Kingma D P, Ba J. Adam: A method for stochastic optimization. In: Proceedings of the 3rd International Conference for Learning Representations. San Diego, USA, 2015. [39] Plappert M, Houthooft R, Dhariwal P, Sidor S, Chen R Y, Chen X, et al. Parameter space noise for exploration [Online], available: https://arxiv.org/abs/1706.01905, June 6, 2017 [40] Schwab A L, Wisse M. Basin of attraction of the simplest walking model. In: Proceedings of the ASME 2001 Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Pittsburgh, Pennsylvania: ASME, 2001. 531−539 -
下载:
计量
- 文章访问数: 6148
- HTML全文浏览量: 2398
- PDF下载量: 786
- 被引次数: 0
