Multi-robot-multi-task Coordination Framework Based on the Integration of Intelligent Agent and Petri Net
-
摘要:
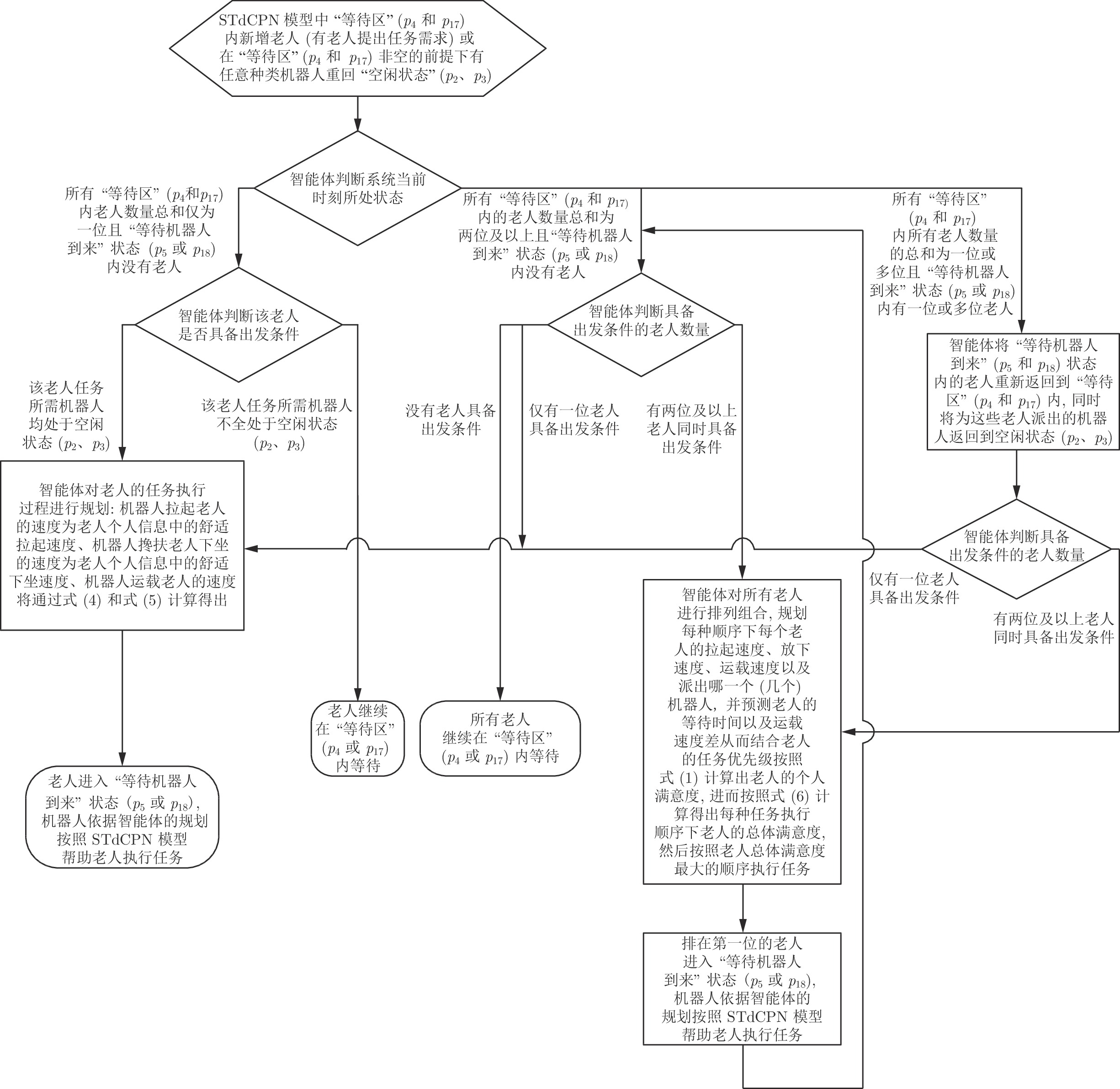
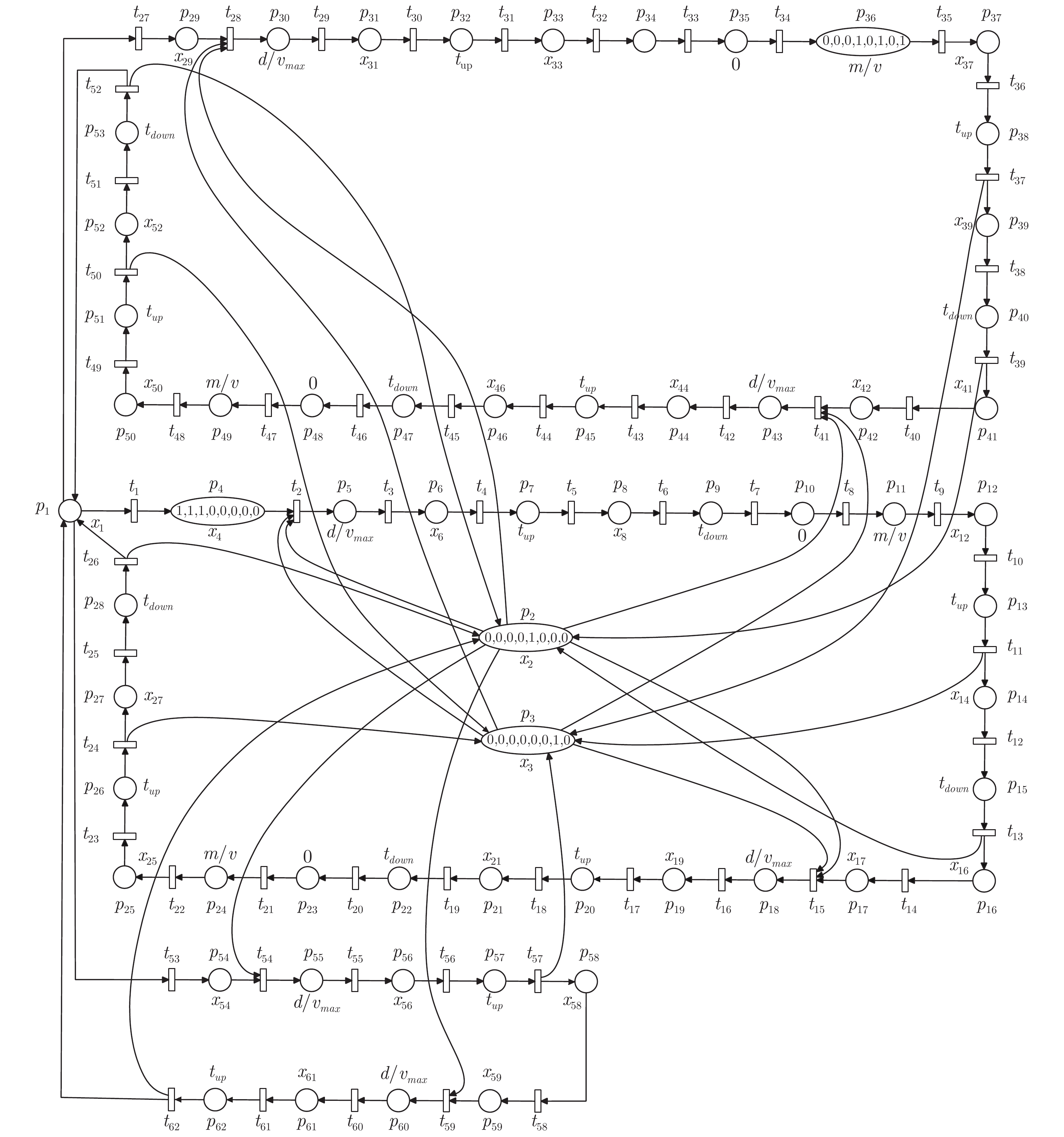
为解决异构的服务机器人团队为多位老人服务时的协调问题以及在此过程中如何最大化老人的总体满意度, 提出了一种服务于多人的多机器人−多任务协调框架. 首先, 结合时延Petri网和颜色Petri网提出了可扩展时延−颜色Petri网(Scalable timed-colored Petri net, STdCPN)对养老院情境下服务机器人照顾老人的过程进行建模. 然后, 将老人的感受和情绪作为机器人照顾老人时的重要指标, 构建了服务对象满意度模型. 最后, 设计智能体来实现该协调框架的调度, 该智能体通过考虑老人“个人因素” 和机器人的实时状态、位置等信息来对任务进行合理的规划调度, 使机器人帮助老人完成任务的同时, 最大化老人总体满意度.
Abstract:In order to solve the coordination problem of heterogeneous service robot team serving multiple elderly people meanwhile to maximize the overall satisfaction of the elders, a multi-robot-multi-task coordination framework for multi-person is proposed. Firstly, scalable timed-colored Petri net (STdCPN) is proposed based on timed Petri net and colored Petri net to model the process of service robots caring for the elders in the context of nursing home. Then the satisfaction model of service object is constructed taking the elders＇ feelings and emotions as important indicators. Finally, an agent is designed to schedule the coordination framework. The agent can plan and schedule tasks reasonably by considering the “personal factors” of the elders and the real-time status and location of the robots, so that the robots can help elders to complete the tasks while maximizing the overall satisfaction.
-
Key words:
- Multi-robot coordination /
- satisfaction /
- Petri net /
- agent
-
图 2 SR和CR协同送老人去卫生间及送回STdCPN模型
Fig. 2 STdCPN model for SR and CR work together to send the elderly to the toilet and return
图 3 基于智能体的考虑人的因素的协调框架结构示意图
Fig. 3 Diagram of coordination framework considering human factors based on intelligent agent
图 4 基于智能体的考虑人的因素的协调框架算法流程图
Fig. 4 Algorithm flow chart of coordination framework considering human factors based on intelligent agent
图 8 案例1中不同任务执行顺序下老人的个人满意度
Fig. 8 Personal satisfaction of the elderly under different task execution sequences in case 1
图 9 案例1中不同任务执行顺序下老人的总体满意度
Fig. 9 Overall satisfaction of the elderly under different task execution sequences in case 1
图 11 案例2中不同任务执行顺序下老人的总体满意度
Fig. 11 Overall satisfaction of the elderly under different task execution sequences in case 2
图 13 案例3中不同任务执行顺序下老人的总体满意度
Fig. 13 Overall satisfaction of the elderly under different task execution sequences in case 3
图 10 案例2中不同任务执行顺序下老人的个人满意度
Fig. 10 Personal satisfaction of the elderly under different task execution sequences in case 2
图 12 案例3中不同任务执行顺序下老人的个人满意度
Fig. 12 Personal satisfaction of the elderly under different task execution sequences in case 3
图 14 案例4中不同任务执行顺序下老人的个人满意度
Fig. 14 Personal satisfaction of the elderly under different task execution sequences in case 4
图 15 案例4中不同任务执行顺序下老人的总体满意度
Fig. 15 Overall satisfaction of the elderly under different task execution sequences in case 4
图 16 案例5中不同任务执行顺序下老人的个人满意度
Fig. 16 Personal satisfaction of the elderly under different task execution sequences in case 5
图 17 案例5中不同任务执行顺序下老人的总体满意度
Fig. 17 Overall satisfaction of the elderly under different task execution sequences in case 5
图 19 案例6中不同任务执行顺序下老人的总体满意度
Fig. 19 Overall satisfaction of the elderly under different task execution sequences in case 6
图 18 案例6中不同任务执行顺序下老人的个人满意度
Fig. 18 Personal satisfaction of the elderly under different task execution sequences in case 6
图 22 案例7中不同任务执行顺序下老人的总体满意度
Fig. 22 Overall satisfaction of the elderly under different task execution sequences in case 7
图 21 案例7中不同任务执行顺序下老人的个人满意度
Fig. 21 Personal satisfaction of the elderly under different task execution sequences in case 7
图 25 案例8中不同任务执行顺序下老人的总体满意度
Fig. 25 Overall satisfaction of the elderly under different task execution sequences in case 8
图 28 案例9中不同任务执行顺序下老人的总体满意度
Fig. 28 Overall satisfaction of the elderly under different task execution sequences in case 9
图 24 案例8中不同任务执行顺序下老人的个人满意度
Fig. 24 Personal satisfaction of the elderly under different task execution sequences in case 8
图 27 案例9中不同任务执行顺序下老人的个人满意度
Fig. 27 Personal satisfaction of the elderly under different task execution sequences in case 9
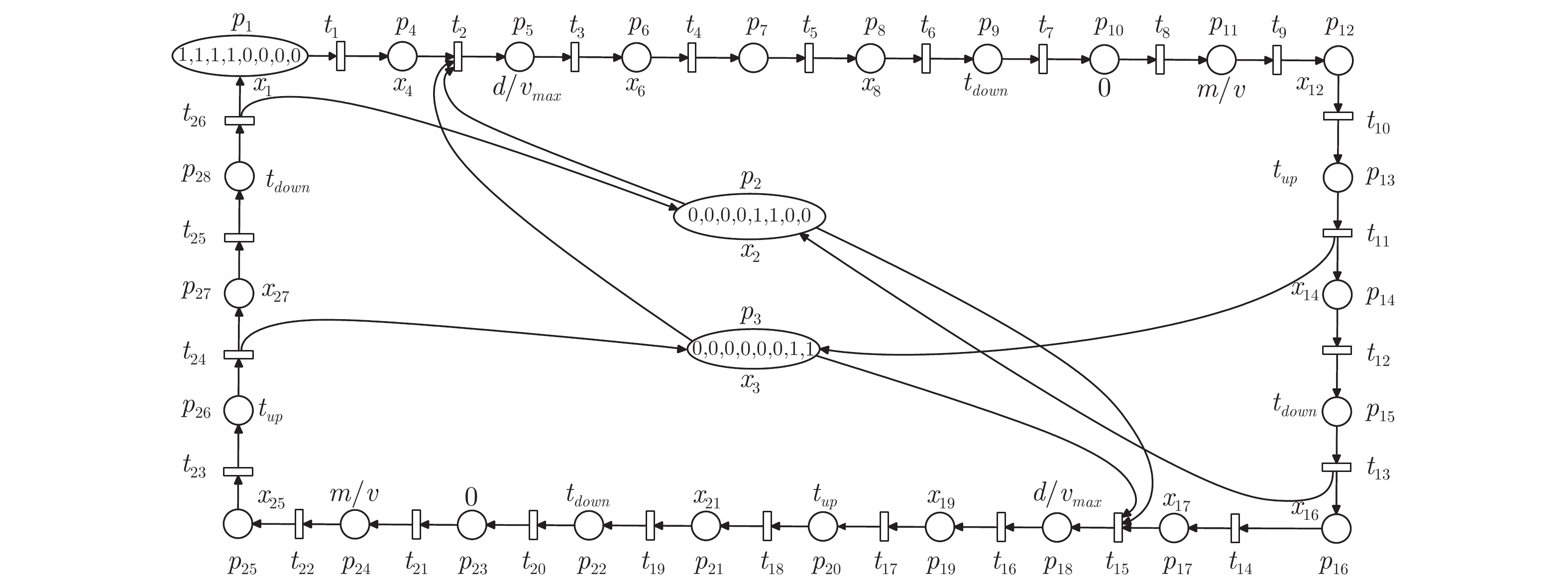
表 1 送老人去卫生间及送回STdCPN模型中库所含义
Table 1 The mean of spaces in the STdCPN model of send the elderly to the toilet and return
库所 含义 $p_1$ 老人在自己的床位上 $p_2$ SR 处于空闲状态 $p_3$ CR 处于空闲状态 $p_4$ 老人在虚拟的“等待区” 内等待,智能体进行任务规划和资源分配 $p_5$ 老人等待 SR 和 CR 到来 $p_6$ 老人被拉起前的准备过程 $p_7$ 老人在 SR 帮助下的站起过程 $p_8$ SR 与 CR 的对接过程 $p_9$ 老人在 SR 帮助下的下坐过程 $p_{10}$ 老人坐在 CR 上 $p_{11}$ CR 载着老人前往卫生间 $p_{12}$ 老人被拉起前的准备过程 $p_{13}$ 老人在 SR 帮助下的站起过程 $p_{14}$ SR 与马桶的对接过程 $p_{15}$ 老人在 SR 帮助下的下坐过程 $p_{16}$ 老人坐在卫生间内的马桶上 $p_{17}$ 老人在虚拟的“等待区” 内等待, 智能体进行任务规划和资源分配 $p_{18}$ 老人等待 SR 和 CR 到来 $p_{19}$ 老人被拉起前的准备过程 $p_{20}$ 老人在 SR 帮助下的站起过程 $p_{21}$ SR 与 CR 的对接过程 $p_{22}$ 老人在 SR 帮助下的下坐过程 $p_{23}$ 老人坐在 CR 上 $p_{24}$ CR 载着老人前往老人的床位 $p_{25}$ 老人被拉起前的准备过程 $p_{26}$ 老人在 SR 帮助下的站起过程 $p_{27}$ SR 与床位的对接过程 $p_{28}$ 老人在 SR 帮助下的下坐过程 
下载: 导出CSV
表 2 送老人去卫生间及送回STdCPN模型中变迁含义
Table 2 The mean of transitions in the STdCPN model of send the elderly to the toilet and return
变迁 含义 $t_1$ 老人提出去卫生间的需求 $t_2$ SR 和 CR 开始前往老人的床位 $t_3$ SR 和 CR 到达老人的床位 $t_4$ 老人已做好站起准备 $t_5$ 老人站起动作完成 $t_6$ SR 与 CR 对接完成 $t_7$ 老人下坐动作完成 $t_8$ CR 开始运载老人前往卫生间 $t_9$ CR 载着老人到达卫生间 $t_{10}$ 老人已做好站起准备 $t_{11}$ 老人站起动作完成 $t_{12}$ SR 与马桶对接完成 $t_{13}$ 老人下坐动作完成 $t_{14}$ 老人提出返回床位的需求 $t_{15}$ SR 和 CR 开始前往老人所在位置 $t_{16}$ SR 和 CR 到达老人所在位置 $t_{17}$ 老人已做好站起准备 $t_{18}$ 老人站起动作完成 $t_{19}$ SR 与 CR 对接完成 $t_{20}$ 老人下坐动作完成 $t_{21}$ CR 开始运载老人前往老人的床位 $t_{22}$ CR 载着老人到达老人的床位 $t_{23}$ 老人已做好站起准备 $t_{24}$ 老人站起动作完成 $t_{25}$ SR 与床位对接完成 $t_{26}$ 老人下坐动作完成
下载: 导出CSV
表 3 任务信息
Table 3 Task information
任务 优先级 拉起次数 放下次数 所需机器人 去卫生间 4 2 2 1 台 SR, 1 台 CR 去餐厅 2 2 2 1 台 SR, 1 台 CR 站起 1 1 0 1 台 SR
下载: 导出CSV
表 5 案例2中老人的个人信息
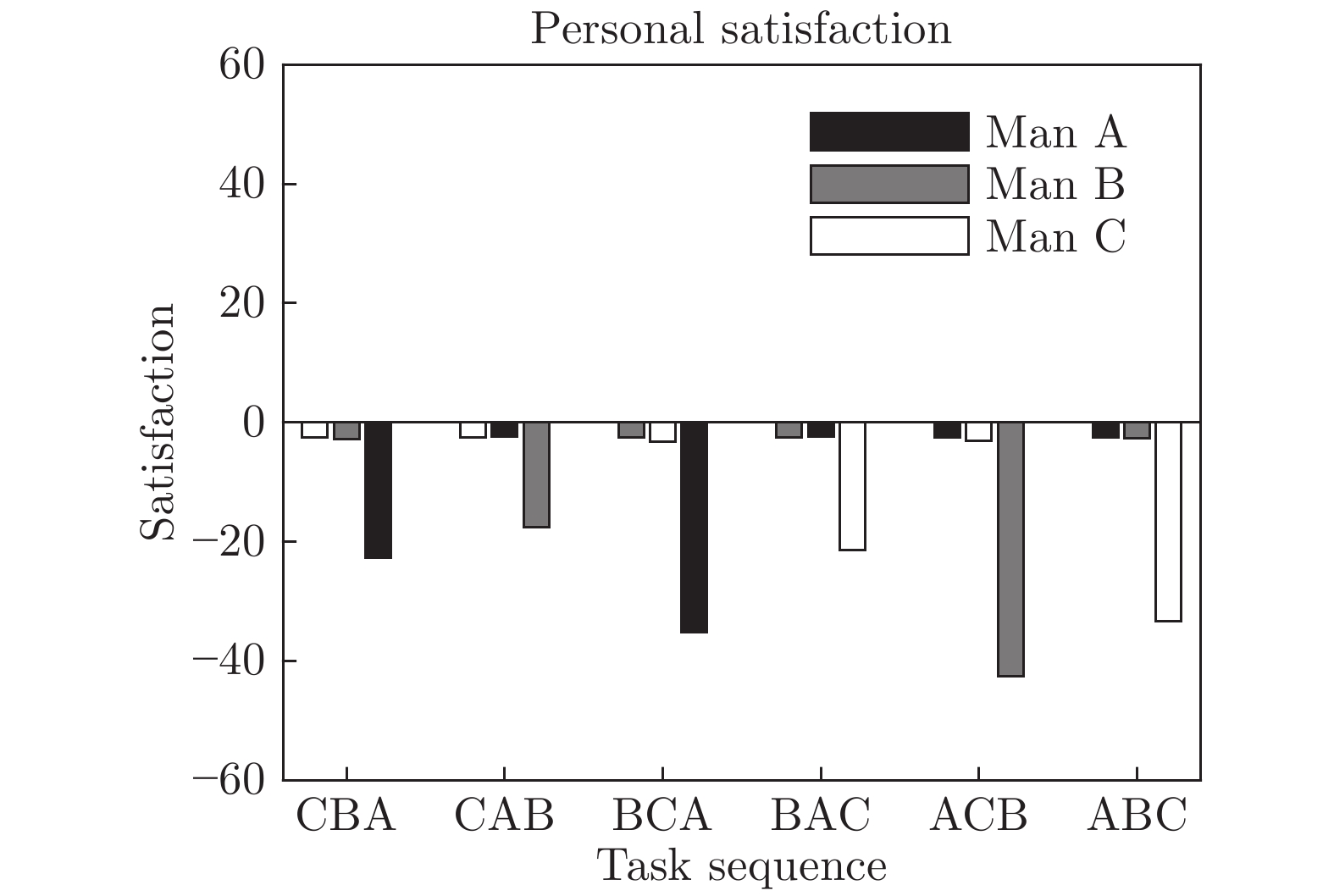
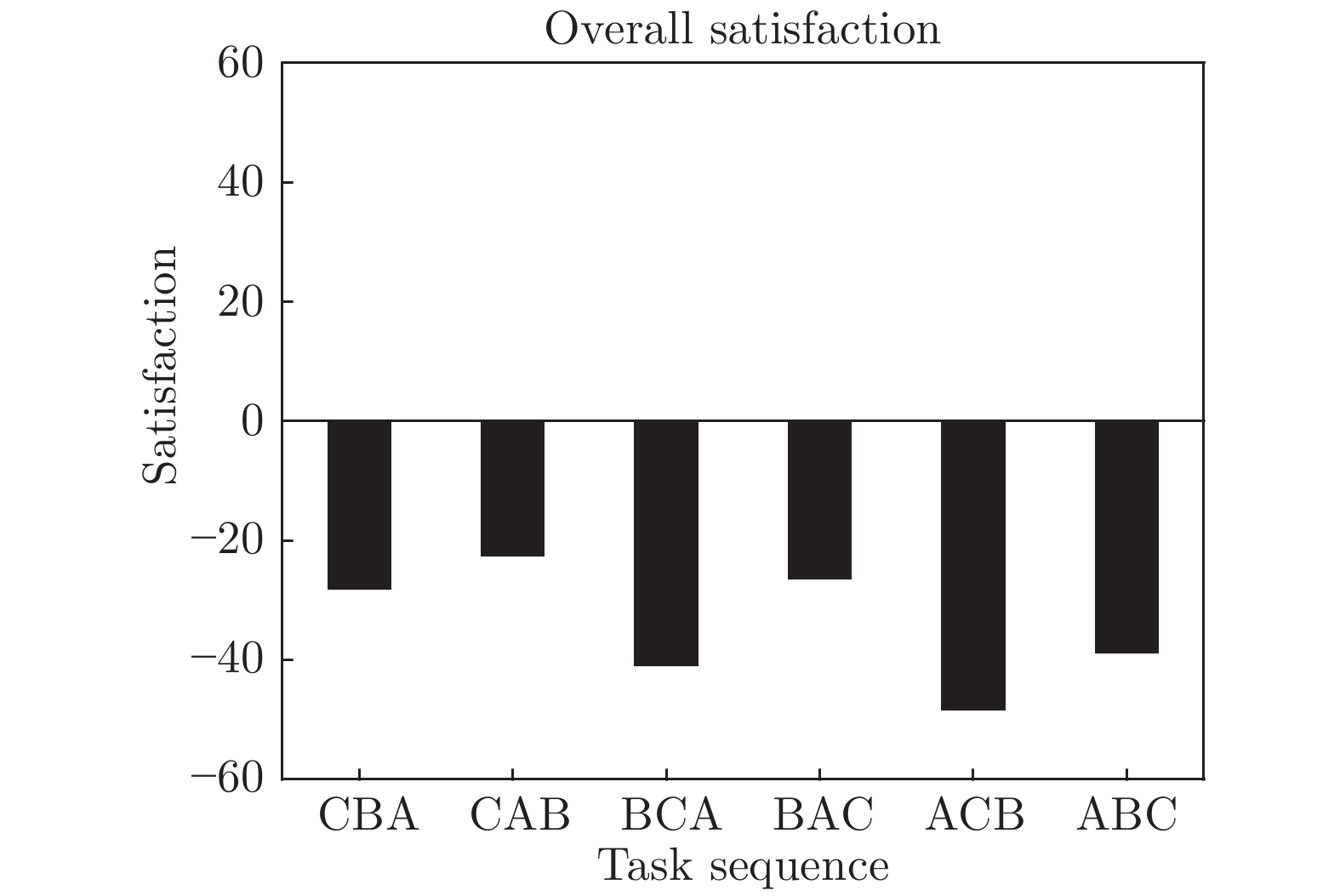
Table 5 Personal information of the elders in case 2
人员 性格急躁
程度舒适运载
速度 (m/s)舒适拉起
时间 (s)舒适下坐
时间 (s)已等待
时间 (s)老人 A 1.1 0.5 3 3 0 老人 B 1.1 0.9 3 3 0 老人 C 1.1 0.5 3 3 0
下载: 导出CSV
表 6 案例3中老人的个人信息
Table 6 Personal information of the elders in case 3
人员 性格急躁
程度舒适运载
速度 (m/s)舒适拉起
时间 (s)舒适下坐
时间 (s)已等待
时间 (s)老人 A 1.4 1.2 1 1 15 老人 B 1.1 0.9 3 3 0 老人 C 1.1 0.5 3 3 0
下载: 导出CSV
表 4 案例1中老人的个人信息
Table 4 Personal information of the elders in case 1
人员 性格急躁
程度舒适运载
速度 (m/s)舒适拉起
时间 (s)舒适下坐
时间 (s)已等待
时间 (s)老人 A 1.1 0.5 3 3 0 老人 B 1.1 0.5 3 3 0 老人 C 1.1 0.5 3 3 0
下载: 导出CSV
表 7 案例4中老人的任务信息
Table 7 Task information of the elders in case 4
人员 所执行任务 老人 A 站起 老人 B 去餐厅 老人 C 去卫生间
下载: 导出CSV
表 8 案例5中老人的任务信息
Table 8 Task information of the elders in case 5
人员 所执行任务 老人 A 去餐厅 老人 B 去卫生间 老人 C 站起
下载: 导出CSV
表 9 案例6中老人的任务信息
Table 9 Task information of the elders in case 6
人员 所执行任务 老人 A 去卫生间 老人 B 站起 老人 C 去餐厅
下载: 导出CSV
表 10 案例7中老人的个人信息
Table 10 Personal information of the elders in case 7
人员 性格急躁
程度舒适运载
速度 (m/s)舒适拉起
时间 (s)舒适下坐
时间 (s)已等待
时间 (s)老人 A 1.0 0.4 2.5 3.5 0 老人 B 1.3 0.3 2.3 2.6 0 老人 C 1.1 0.5 1.7 1.7 2
下载: 导出CSV
表 11 案例7中老人的任务信息
Table 11 Task information of the elders in case 7
人员 所执行任务 老人 A 去卫生间 老人 B 去餐厅 老人 C 去卫生间
下载: 导出CSV
表 12 案例8中老人的个人信息
Table 12 Personal information of the elders in case 8
人员 性格急躁
程度舒适运载
速度 (m/s)舒适拉起
时间 (s)舒适下坐
时间 (s)已等待
时间 (s)老人 A 1.1 0.25 2.4 3.5 7 老人 B 1.0 0.38 2.0 2.3 3 老人 C 1.2 0.42 3.1 2.5 0
下载: 导出CSV
表 13 案例8中老人的任务信息
Table 13 Task information of the elders in case 8
人员 所执行任务 老人 A 去餐厅 老人 B 站起 老人 C 去卫生间
下载: 导出CSV
表 14 案例9中老人的个人信息
Table 14 Personal information of the elders in case 9
人员 性格急躁
程度舒适运载
速度 (m/s)舒适拉起
时间 (s)舒适下坐
时间 (s)已等待
时间 (s)老人 A 1.0 0.65 5.2 4.6 15 老人 B 1.3 0.88 4.8 3.0 0 老人 C 1.2 0.51 4.3 4.4 10
下载: 导出CSV
表 15 案例9中老人的任务信息
Table 15 Task information of the elders in case 9
人员 所执行任务 老人 A 去卫生间 老人 B 站起 老人 C 去餐厅
下载: 导出CSV
-
[1] Bloom D E, Canning D, Lubet A. Global population aging: Facts, challenges, solutions & perspectives. Daedalus, 2015, 144(2): 80−92 doi: 10.1162/DAED_a_00332 [2] Murata T. Petri nets: Properties, analysis and applications. Proceedings of the IEEE, 1989, 77(4): 541−580 doi: 10.1109/5.24143 [3] Joaquin López, Diego Pérez, Zalama E. A framework for building mobile single and multi-robot applications. Robotics and Autonomous Systems, 2011, 59(3−4): 151−162 doi: 10.1016/j.robot.2011.01.004 [4] Ziparo V A, Iocchi L, Lima P U, Nardi D, Palamara P F. Petri net plans. Autonomous Agents and Multi-Agent Systems, 2011, 23(3): 344−383 doi: 10.1007/s10458-010-9146-1 [5] Maza I, Caballero F, Capitán J, Martinez-de-Dios J R, Ollero A. Experimental results in multi-UAV coordination for disaster management and civil security applications. Journal of Intelligent & Robotic Systems, 2011, 61(1−4): 563−585 [6] Farinelli A, Nicoló Boscolo, Zanotto E, Pagello E. Advanced approaches for multi-robot coordination in logistic scenarios. Robotics and Autonomous Systems, 2017, 90: 34−44 doi: 10.1016/j.robot.2016.08.010 [7] Öztürk S, Kuzucuoǧlu A E. A multi-robot coordination approach for autonomous runway foreign object debris (FOD) clearance. Robotics and Autonomous Systems, 2016, 75: 244−259 doi: 10.1016/j.robot.2015.09.022 [8] Jones E G, Dias M B, Stentz A. Time-extended multi-robot coordination for domains with intra-path constraints. Autonomous Robots, 2011, 30(1): 41−56 doi: 10.1007/s10514-010-9202-3 [9] Kala R. Multi-robot path planning using co-evolutionary genetic programming. Expert Systems with Applications, 2012, 39(3): 3817−3831 doi: 10.1016/j.eswa.2011.09.090 [10] Haghighi R, Cheah C C. Multi-group coordination control for robot swarms. Automatica, 2012, 48(10): 2526−2534 doi: 10.1016/j.automatica.2012.03.028 [11] Puig D, García M A, Wu L. A new global optimization strategy for coordinated multi-robot exploration: Development and comparative evaluation. Robotics and Autonomous Systems, 2011, 59(9): 635−653 doi: 10.1016/j.robot.2011.05.004 [12] Nieto-Granda C, Rogers III J G, Christensen H I. Coordination strategies for multi-robot exploration and mapping. The International Journal of Robotics Research, 2014, 33(4): 519−533 doi: 10.1177/0278364913515309 [13] 吴培良, 孔令富, 孔亮. 一种普适机器人系统同时定位、标定与建图方法. 自动化学报, 2012, 38(4): 618−631Wu Pei-Liang, Kong Ling-Fu, Kong Liang. A solution to simultaneous localization, calibration and mapping of ubiquitous robot system. Acta Automatica Sinica, 2012, 38(4): 618−631 [14] Thomas C, Busch F, Kuhlenkoetter B, Deuse J. Enabling Manufacturing Competitiveness and Economic Sustainability. Berlin Heidelberg: Springer-Verlag, 2012. 464−470 [15] Nokata M, Ikuta K, Ishii H. Safety-optimizing method of human-care robot design and control. In: Proceedings of the 2002 IEEE International Conference on Robotics and Automation. Washington DC, USA: IEEE, 2002. 2: 1991−1996 [16] Lu Y, Zeng L, Bone G M. Multisensor system for safer human-robot interaction. In: Proceedings of the 2005 IEEE International Conference on Robotics and Automation. Orlando, FL, USA: IEEE, 2005. 1767−1772 [17] Kulić D, Croft E A. Real-time safety for human-robot interaction. Robotics and Autonomous Systems, 2016, 54(1): 1−12 [18] Gombolay M C, Gutierrez R A, Clarke S G, Sturla G F, Shah J A. Decision-making authority, team efficiency and human worker satisfaction in mixed human-robot teams. Autonomous Robots, 2015, 39(3): 293−312 doi: 10.1007/s10514-015-9457-9 [19] Kim Y C, Yoon W C, Kwon H T, Yoon Y S, Kim H J. A cognitive approach to enhancing human-robot interaction for service robots. In: Proceedings of Symposium on Human Interface and the Management of Information. Berlin Heidelberg: Springer-Verlag, 2007. 858−867 [20] Rosenfeld A, Agmon N, Maksimov O, Kraus S. Intelligent agent supporting human-multi-robot team collaboration. Artificial Intelligence, 2017, 252: 211−231 doi: 10.1016/j.artint.2017.08.005 -
计量
- 文章访问数: 3721
- HTML全文浏览量: 2222
- PDF下载量: 346
- 被引次数: 0
