Trajectory Tracking Control for Connected Vehicle Platoon Considering Car-Following Interactions and Time Delays
-
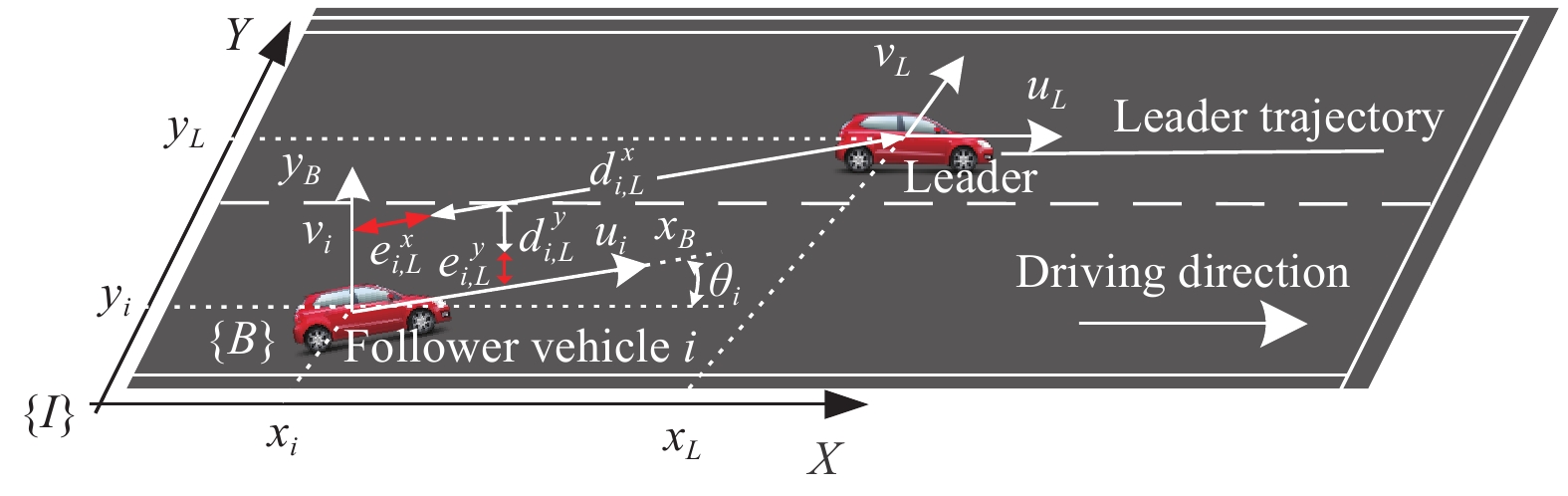
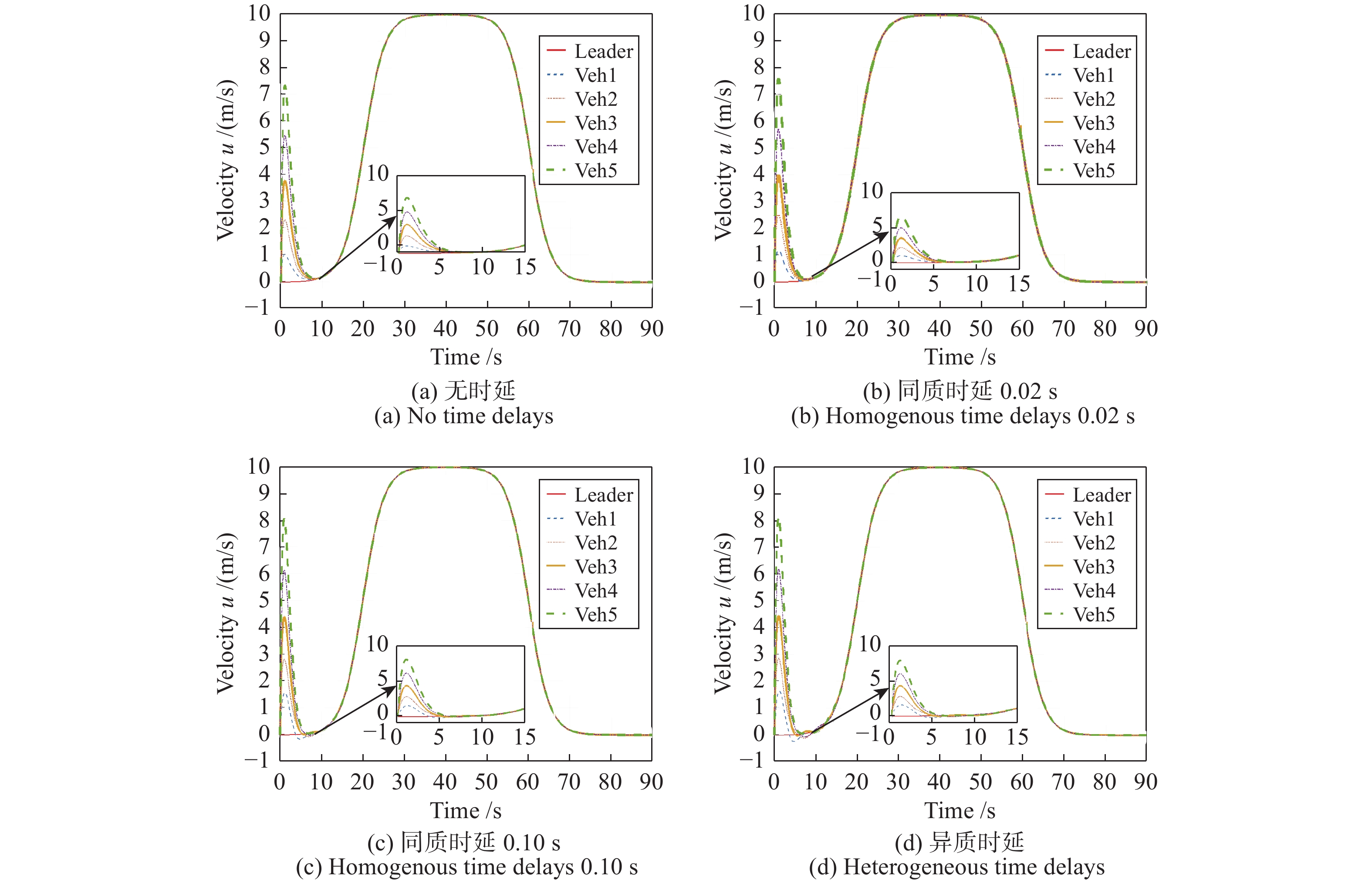
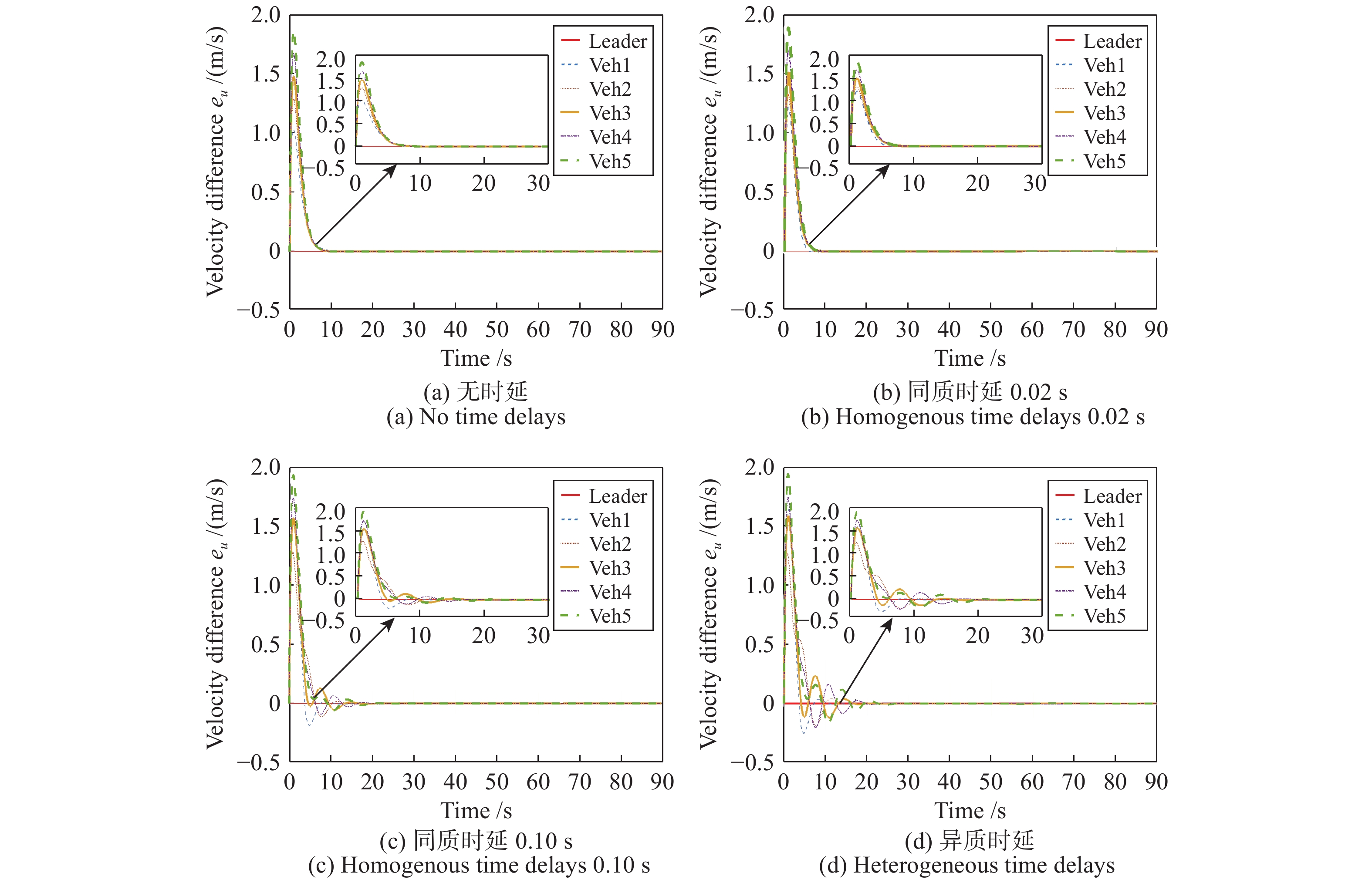
摘要: 针对智能网联车辆轨迹跟踪问题, 本文通过考虑车辆跟驰作用和车车通信过程中存在的通信时延, 提出了一种分布式非线性轨迹跟踪控制器. 具体来讲, 首先, 提出一种双向领导跟随通信拓扑来描述智能网联环境下车辆间的通信连接. 其次, 考虑车辆跟驰作用和通信时延, 设计一种分布式非线性轨迹跟踪控制器. 然后, 使用Lyapunov方法证明了所设计控制器的稳定性. 最后, 考虑速度干扰作用于领导者车辆, 针对无时延、同质时延和异质时延等三种场景进行数值仿真实验. 仿真结果表明: 本文所设计的控制器不仅保证了车辆位置跟踪误差收敛到原点, 而且车辆运动规律符合交通流理论, 即无负位置跟踪误差和负速度现象.Abstract: For the trajectory tracking problem of connected vehicles (CVs), a distributed nonlinear trajectory tracking controller is proposed by incorporating the car-following interactions between vehicles and time delays in this study. In particular, a bidirectional leader-follower communication topology is utilized to characterize the connections among CVs. Then, considering the car-following interactions between vehicles and time delays, a distributed nonlinear trajectory tracking controller for follower vehicles is proposed. Further, the stability of the proposed controller is analyzed using the Lyapunov technique. Finally, simulations are performed for leader with external disturbance and three scenarios: no time delays, homogeneous time delays, and heterogeneous time delays. The simulation results show that the proposed controller in this study not only ensures that position tracking error converges to the origin, but also the vehicle motion is consistent with the traffic flow theory, which means that the negative position tracking error and negative velocity are avoided.
-
表 1 控制器参数
Table 1 Controller parameters
参数 值 单位 ${E}_1$ 7.5 (1,1)T m/s ${E}_2$ 8.79 (1,1)T m/s ${C}_1$ 0.14 (1,1)T m−1 ${C}_2$ 1.74 (1,1)T — $l_c$ 5 m $\kappa$ 0.45 s−1 $\beta$ 2.22 s−1 $J$ 0.047 kg·m2 $k_e$ 1.5 — $g_v$ (1,0)T — $k_z$ 8 — ${ k}_\phi$ 8${\bf I}$ — $d_\upsilon$ 4.5 kg/s $d_\omega$ 0.41 kg·m/s $\delta$ (−0.05,0)T — ${G_\omega }$ 1 — ${B}$ (1,0;0,0.2)T — m 5.5 kg 表 2 不同时延下的性能比较
Table 2 Performance comparisons under different time delays
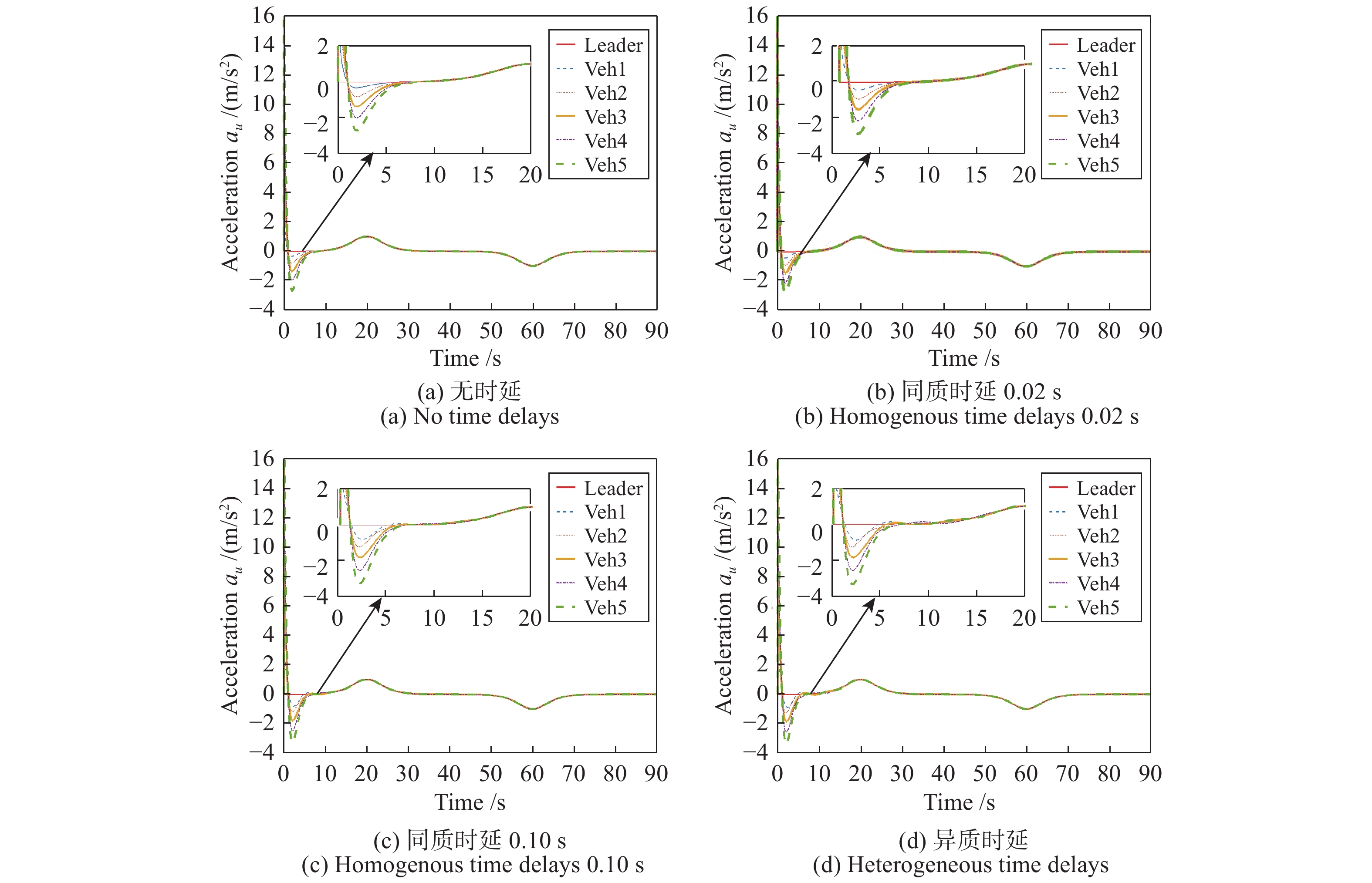
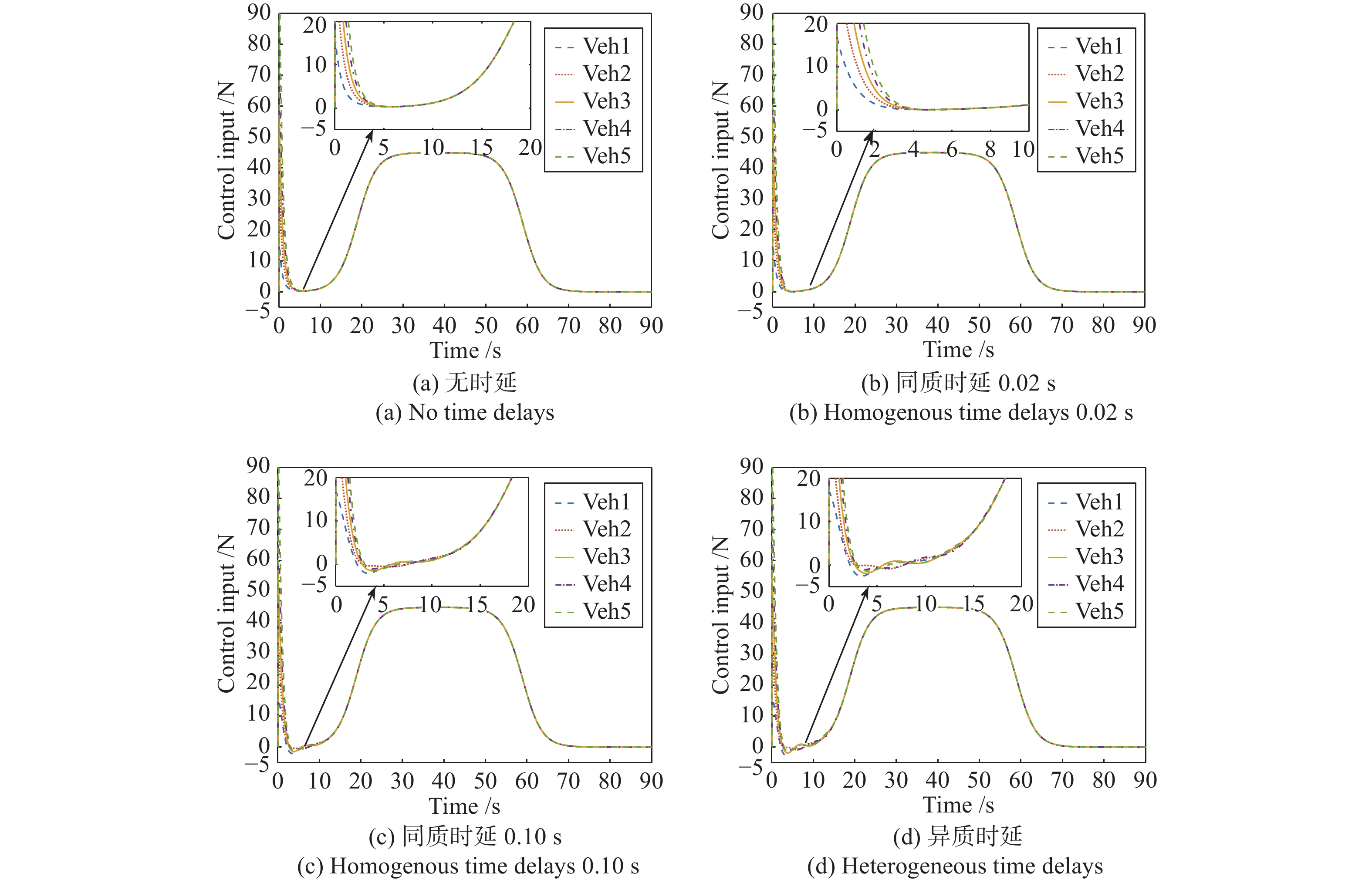
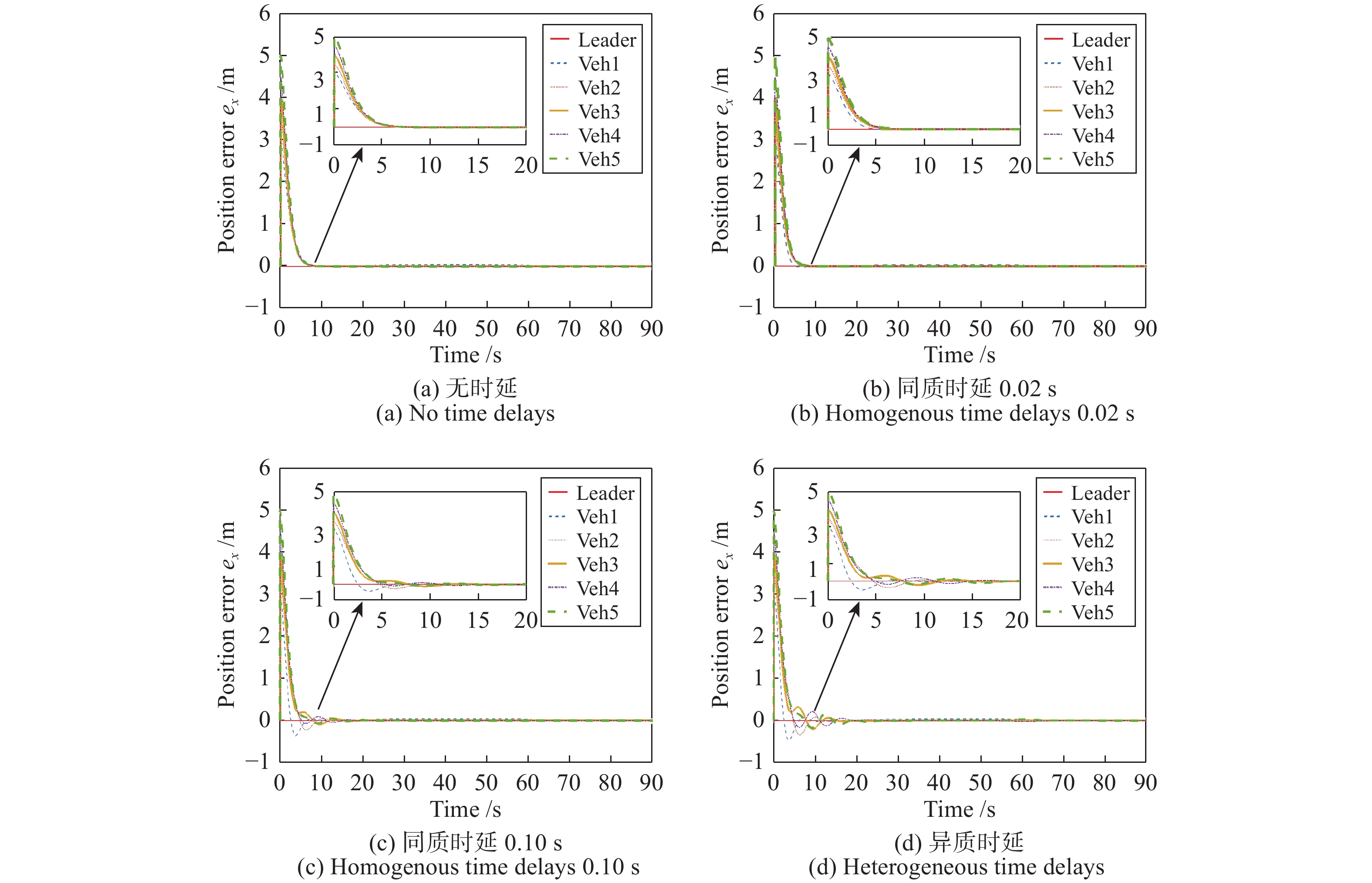
性能 无时延 $\tau=0.02$ s $\tau=0.10$ s 异质时延 控制输入 正 正 负 负 位置跟踪误差 正 正 负 负 速度 正 正 负 负 速度误差振幅 (m/s) 0 0 0.2 0.3 加速度振幅 (m/s2) 2.2 2.3 2.6 2.8 -
[1] Shieh W, Hsu C, Wang T. Vehicle positioning and trajectory tracking by infrared signal-direction discrimination for short-range vehicle-to-infrastructure communication systems. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(2): 368-379. doi: 10.1109/TITS.2017.2697041 [2] Li Y, Tang C, Srinivas P, Wang Y. Integral-sliding-mode braking control for connected vehicle platoon: theory and application. IEEE Transactions on Industrial Electronics. 2019, 66(6): 4618-4628. doi: 10.1109/TIE.2018.2864708 [3] Li Y et al. Consensus-based cooperative control for multiplatoon under the connected vehicles environment. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(6): 2220-2229. doi: 10.1109/TITS.2018.2865575 [4] Li Y et al. Nonlinear consensus-based connected vehicle platoon control incorporating car-following interactions and heterogeneous time delays. IEEE Transactions on Intelligent Transportation Systems. 2019, 20(6): 2209-2219. doi: 10.1109/TITS.2018.2865546 [5] Chatzikomis C et al. Comparison of path tracking and torque-vectoring controllers for autonomous electric vehicles. IEEE Transactions on Intelligent Vehicles, 2018,3(4): 559-570. doi: 10.1109/TIV.2018.2874529 [6] Li Y, Wu C, Srinivas P, Wang Y. Trajectory tracking control for connected vehicle platoon. IFAC-PapersOnLine, 2018, 51(9): 92-97. doi: 10.1016/j.ifacol.2018.07.016 [7] Li Y et al. Nonlinear finite-time consensus-based connected vehicle platoon control under fixed and switching communication topologies. Transportation Research Part C, 2018, 93: 525-543. doi: 10.1016/j.trc.2018.06.013 [8] Li Y et al. Extended-state-observer-based double-loop integral sliding-mode control of electronic throttle valve. IEEE Transactions on Intelligent Transportations Systems, 2015, 16(5): 2501-2510. doi: 10.1109/TITS.2015.2410282 [9] Li Y et al. Nonlane-discipline-based car-following model for electric vehicles in transportation-cyber-physical systems. IEEE Transactions on Intelligent Transportation Systems, 2018,19(1): 38-47. doi: 10.1109/TITS.2017.2691472 [10] Invernizzi D, Lovera M. Trajectory tracking control of thrust-vectoring UAVs. Automatica, 2018, 95: 180-186. doi: 10.1016/j.automatica.2018.05.024 [11] Cai H, Hu G. Distributed tracking control of an interconnected leader-follower multi-agent system. IEEE Transactions on Automatic Control, 2017,62(7): 3494-3501. doi: 10.1109/TAC.2017.2660298 [12] Hong Y, Hu J, Gao L. Tracking control for multi-agent consensus with an active leader and variable topology.Automatica, 2018, 42(7): 1177-1182. [13] Kayacan E, Ramon H, Saeys W. Robust trajectory tracking error model-based predictive control for unmanned ground vehicles. IEEE/ASME Transactions on Mechatronics, 2016,21(2): 806-814. doi: 10.1109/TMECH.2015.2492984 [14] Zhang Q, Lapierre L, Xiang X. Distributed control of cooperative path tracking for networked nonholonomic mobile vehicles.IEEE Transactions on Industrial Informatics, 2013,9(1): 472-484. doi: 10.1109/TII.2012.2219541 [15] 徐杨, 陆丽萍, 褚端峰, 黄子超. 无人车辆轨迹规划与跟踪控制的统一建模方法. 自动化学报, 2019, 45(4): 799-801.Xu Yang, Lu Li-Ping, Chu Duan-Feng, Huang Zi-Chao. Unified modeling method of trajectory planning and tracking for unmanned vehicle.Acta Automatica Sinica, 2019, 45(4): 799-807. [16] Liang Z, Ren Z, Shao X. Decoupling trajectory tracking for gliding reentry vehicles. IEEE/CAA Journal of Automatica Sinica. 2015,2(1): 115-120. doi: 10.1109/JAS.2015.7032913 [17] Aguiar A, Hespanha J. Trajectory-tracking and pathfollowing of underactuated autonomous vehicles with parametric modeling uncertainty. IEEE Transactions on Automatic Control, 2007, 52(8): 1362-1379. doi: 10.1109/TAC.2007.902731 [18] Guo J, Luo Y, Li K. Adaptive non-linear trajectory tracking control for lane change of autonomous four-wheel independently drive electric vehicles. IET Intelligent Transport Systems, 2018, 12(7): 712-720. doi: 10.1049/iet-its.2017.0278 [19] 沈智鹏, 张晓玲. 基于非线性增益递归滑模的船舶轨迹跟踪动态面自适应控制. 自动化学报, 2018, 44(10): 1833-1841.Shen Zhi-Peng, Zhang Xiao-Ling, Recursive sliding-mode dynamic surface adaptive control for ship trajectory tracking with nonlinear gains.Acta Automatica Sinica, 2018, 44(10): 1833-1841. [20] Yu X, Liu L. Target enclosing and trajectory tracking for a mobile robot with input disturbances. IEEE Control Systems Letters, 2017,1(2): 221-226. doi: 10.1109/LCSYS.2017.2712663 [21] Wang J. Distributed coordinated tracking control for a class of uncertain multiagent systems. IEEE Transactions on Automatic Control, 2016,62(7): 3423-3429. [22] Peters A, Middleton H, Mason O. Leader tracking in homogeneous vehicle platoons with broadcast delays. Automatica, 2014, 50: 64-74. doi: 10.1016/j.automatica.2013.09.034 [23] Kim J, Joe H, Yu S, Lee S, Kim M. Time-delay controller design for position control of autonomous underwater vehicle under disturbances. IEEE Transactions on Industrial Electronics. 2016, 63(2): 1052-1061. doi: 10.1109/TIE.2015.2477270 [24] Zhang L, Sun J, Orosz G. Hierarchical design of connected cruise control in the presence of information delays and uncertain vehicle dynamics.IEEE Transactions on Control Systems Technology. 2018,26(1), 7435-7443. [25] Yan Z, Liu X, Zhou J, Wu D. Coordinated target tracking strategy for multiple unmanned underwater vehicles with time delays. IEEE Access, 2018, 6: 10348-10357. doi: 10.1109/ACCESS.2018.2793338 [26] Song D et al. Multi-vehicle tracking with road maps and carfollowing models. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(5), 1375-1386. doi: 10.1109/TITS.2017.2723575 [27] Alasmary W, Zhuang W. The mobility impact in IEEE 802.11p infrastructureless vehicular networks.Ad Hoc Networks, 2012, 10(2), 222-230. doi: 10.1016/j.adhoc.2010.06.006 [28] Ponnusamy S. Series: Convergence and divergence. Foundations of Mathematical Analysis. Birkhäuser, Boston, MA, USA, 2012. -





 下载:
下载: