Sharpness Image of Burden Point Cloud Based on CR Lower Bound Unbiased Energy Estimation
-
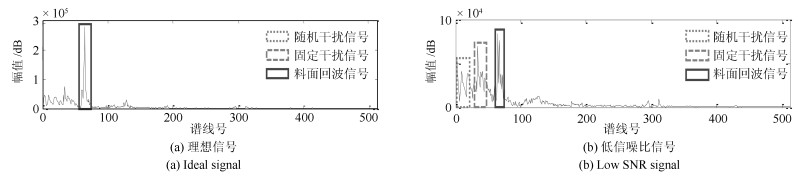
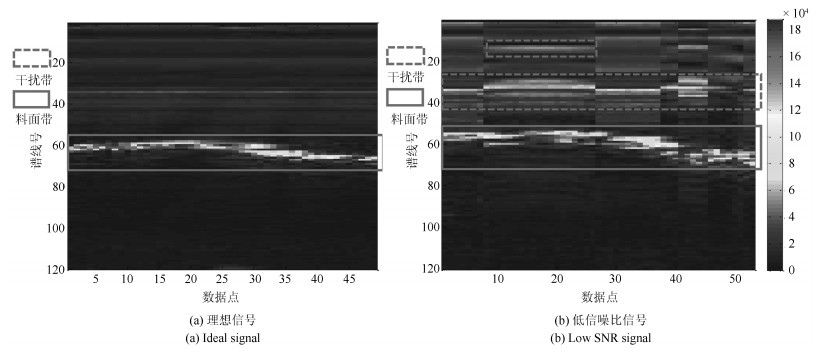
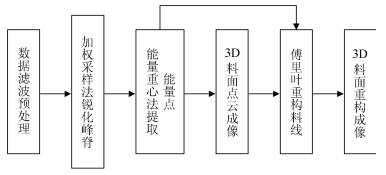
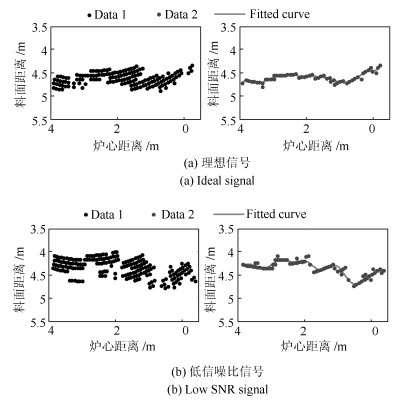
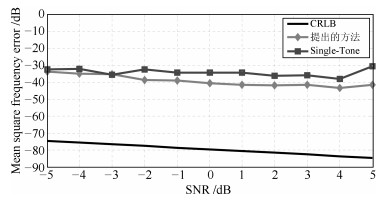
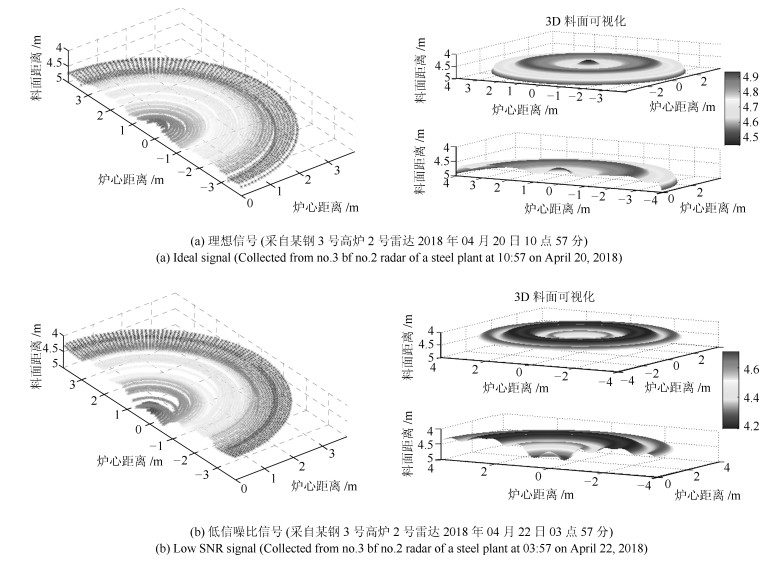
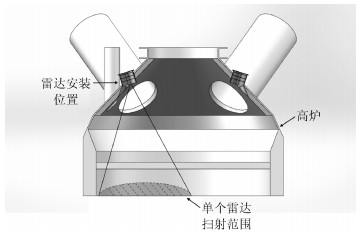
摘要: 高炉雷达获取的料面信息是钢铁冶炼中布料控制的重要参数.但高炉内部环境复杂, 料面具有非均匀流态化特性, 传统信号处理方法难以准确稳定提取料面有效信息, 会导致高炉布料误操作.本文借鉴遥感SAR雷达成像原理, 设计了工业SAR扫描式雷达, 多倍增加料面采样点密度, 提出一种新的料面点云锐化成像算法. 分析了高炉雷达料面回波信号干扰信号特征, 从图像处理角度, 设计多级滤波器对2D频谱图进行去噪处理分离出一条带状的料面回波信号区域. 对料面距离估计问题, 基于克拉美罗下界(Cramer-Rao lower bound, CRLB)提出一种先加权采样锐化料带峰脊再利用能量重心法估测料面距离频率的方法, 生成3D料面点云模型, 并利用CRLB评价本文算法性能.在恶劣条件下, 实测高炉雷达料面回波信号的点云成像验证显示, 本文方法优于传统寻峰法, 能有效处理低信噪比信号, 准确提取料面有效信息.同时料面距离频率估计精度更高, 且相较于其他方法频率估计误差更接近CRLB下界.Abstract: Image information obtained by the radar is an important parameter in the control process of the distribution in iron and steel smelting. The interior of the blast furnace presents high complication. The traditional signal processing method is difficult to extract the effective information accurately and stably, which seriously misleads blast furnace charging operation. Based on the imaging principle of remote sensing SAR radar, this paper designs the industrial SAR scanning radar, which multiplies the density of the sampling points of the surface. We propose a new image forming algorithm of the point cloud surface. In this paper, the characteristics of the echo signal of the surface of the blast furnace radar are analyzed. We design multistage filters for 2D spectrum as a denoising operation in order to isolate a strip of surface echo signal area. To estimate the distance of the blast surface, based on the Cramer-Rao lower bound (CRLB), a new method is proposed to estimate the distance frequency of the blast surface by using energy centrobaric correction method after the weighted sampling of the peak ridge of the sharped surface belt, and the 3D mesh point cloud model is generated, and CRLB is used to evaluate the performance of the algorithm in this paper. In harsh conditions, the point cloud imaging verification of measured echo signal from blast radar shows that proposed method is superior to the traditional peak searching method, and it can effectively process the signal with low signal-to-noise ratio and accurately extract the effective information of the material surface. At the same time, the accuracy of frequency estimation is higher, and the error of frequency estimation is closer to CRLB lower bound than that of other methods.
-
Key words:
- Burden surface /
- iteration threshold filtering /
- ridge peak sharpening /
- energy centrobaric correction method /
- Cramer-Rao lower bound (CRLB)
1) 本文责任编委 徐德 -
图 3 料面径向回波信号2D频谱图对比
Fig. 3 Comparison of 2D spectra of radial echo signal of blast surface
图 4 扇形空间下料面回波信号2D原始频谱图对比
Fig. 4 Comparison of 2D original spectra of fan-shaped space blanking surface echo signal
图 5 三维空间料面回波信号强度峰脊分布
Fig. 5 Peak ridge distribution of echo signal strength in three dimensional space
图 6 高炉料面点云锐化成像算法流程图
Fig. 6 Algorithm flow chart of burden surface point cloud sharpen image processing
图 10 能量点提取与料线拟合(Data1为峰脊锐化后的标志点, Data2为提取的能量点)
Fig. 10 Energy point extraction and material line fitting (Data1 is the mark point after peak ridge sharpening, and Data2 is the energy point extracted)
图 11 不同信噪比下各算法频率估计性能
Fig. 11 The performance of each algorithm under different SNR is estimated
表 1 三种滤波模型
Table 1 Three filtering models
MWATF VITF MWITF 中值法 方差法 中值法 窗函数法 窗函数法 人工阈值法 迭代阈值滤波法 人工阈值法 
下载: 导出CSV
-
[1] 陈先中, 丁爱华, 吴昀. 高炉雷达料面成像系统的设计与实现. 冶金自动化, 2009, 33(2): 52-56 https://www.cnki.com.cn/Article/CJFDTOTAL-YJZH200902012.htmChen Xian-Zhong, Ding Ai-Hua, Wu Yun. Design and implementation of bf radar material surface imaging system. Metallurgical Automation, 2009, 33(2): 52-56 https://www.cnki.com.cn/Article/CJFDTOTAL-YJZH200902012.htm [2] Zankl D, Schuster S, Feger R, et al. BLASTDAR - A Large Radar Sensor Array System for Blast Furnace Burden Surface Imaging. IEEE Sensors Journal, 2015, 15(10): 5893-5909 doi: 10.1109/JSEN.2015.2445494 [3] Zhu Q, Cheng-Long Lü, Yin Y X, et al. Burden Distribution Calculation of Bell-Less Top of Blast Furnace Based on Multi-Radar Data. Journal of Steel Research, 2013, 20(6): 33-37 doi: 10.1016/S1006-706X(13)60108-9 [4] Wei J D, Chen X Z, Kelly J R, et al. Blast furnace stockline measurement using radar. Ironmaking & Steelmaking, 2015, 42(7): 533-541 [5] 赵晓月, 何书睿, 陈先中, 侯庆文. 强干扰环境下高炉雷达信号机器学习算法. 控制理论与应用, 2016, 33(12): 1667-1673 https://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201612013.htmZhao Xiao-Yue, He Shu-Rui, Chen Xian-Zhong, Hou Qing-Wen. Machine learning algorithm for BF radar signal under strong interference environment. Control Theory and Application, 2016, 33(12): 1667-1673 https://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201612013.htm [6] Hawking S W, Penrose R. The Singularities of Gravitational Collapse and Cosmology. Proceedings of the Royal Society of London, 1970, 314(1519): 529-548 [7] Chen Z, Jiang Z, Gui W, et al. A novel device for optical imaging of blast furnace burden surface: parallel low-light-loss backlight high-temperature industrial endoscope. IEEE Sensors Journal, 2016, 16(17): 6703-6717 doi: 10.1109/JSEN.2016.2587729 [8] An J Q, Yang J Y, Wu M, She J H, Terano T. Decoupling control method with fuzzy theory for top pressure of blast furnace. IEEE Transactions on Control Systems Technology, DOI: 10.1109/TCST.2018.2862859 [9] 侯庆文, 陈先中, 王小攀, 尹怡欣, 李晓理. 改进的FMCW信号加权补偿校正相位差法. 仪器仪表学报, 2010, 31(04): 721-726 https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201004001.htmHou Qing-Wen, Chen Xian-Zhong, Wang Xiao-Pan, Yin Yi-Xin, Li Xiao-Li. Improved FMCW signal weighted compensated correction phase difference method. Journal of Instrumentation, 2010, 31(04): 721-726 https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201004001.htm [10] 薛年喜. MATLAB在数字信号处理中的应用. 北京: 清华大学出版社, 2003.Xue Nian-Xi. Application of MATLAB in Digital Signal Processing. Beijing: Tsinghua University Press, 2003. [11] 高云鹏, 滕召胜, 卿柏元. 基于Kaiser窗双谱线插值FFT的谐波分析方法. 仪器仪表学报, 2010, 31(2): 287-292 https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201002011.htmGao Yun-Peng, Teng Zhao-Sheng, Qing Bai-Yuan. Harmonic analysis based on Kaiser window double spectrum line interpolation FFT. Chinese Journal of Scientific Instrument, 2010, 31(2): 287-292 https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201002011.htm [12] L Gupta, B M Klinkhammer, P Boor, D Merhof, M Gadermayr Roychoudhury. Stain independent segmentation of whole slide images: A case study in renal histology. In: Proceedings of IEEE 15th International Symposium on Biomedical Imaging. Washington, USA: IEEE, 2018. 1360-1364 [13] Blumensath T, Davies M E. Iterative hard thresholding for compressed sensing. Applied & Computational Harmonic Analysis, 2009, 27(3): 265-274 http://www.sciencedirect.com/science/article/pii/S1063520309000384 [14] Florescu A, Chouzenoux E, Pesquet J C, et al. Cramer-Rao bound for a sparse complex model. In: Proceedings of International Conference on Communications. Sydney, Australia: IEEE, 2014. 1-4 [15] Peleg S, Porat B. The Cramer-Rao lower bound for signals with constant amplitude and polynomial phase. IEEE Transactions on Signal Processing, 1991, 39(3): 749-752 doi: 10.1109/78.80864 [16] Peleg S, Porat B. The Cramer-Rao lower bound for signals with constant amplitude and polynomial phase. IEEE Press, 1991. [17] Kay S M. Fundamentals of statistical signal processing: estimation theory. PTR Prentice Hall, 1993. [18] 张军华, 藏胜涛, 周振晓, 等. 地震资料信噪比定量计算及方法比较. 石油地球物理勘探, 2009, 44(4): 481-486 doi: 10.3321/j.issn:1000-7210.2009.04.018Zhang Jun-Hua, Zang Sheng-Tao, Zhou Zhen-Xiao, et al. Quantitative calculation and comparison of SNR of seismic data. Petroleum Geophysical Exploration, 2009, 44(4): 481-486 doi: 10.3321/j.issn:1000-7210.2009.04.018 [19] 陈智强, 王作伟, 方龙伟, 菅凤增, 吴毅红, 李硕, 何晖光. 基于机器学习和几何变换的实时2D/3D脊椎配准. 自动化学报, 2018, 44(7): 1183-1194 doi: 10.16383/j.aas.2017.c160711Chen Zhi-Qiang, Wang Zuo-Wei, Fang Long-Wei, Jian Feng-Zeng, Wu Yi-Hong, Li Shou, He Hui-Guang. Real-time 2D/3D Registration of Vertebra via Machine Learning and Geometric Transformation. Journal of Automation, 2018, 44(7): 1183-1194 doi: 10.16383/j.aas.2017.c160711 [20] 丁康, 郑春松, 杨志坚. 离散频谱能量重心法频率校正精度分析及改进. 机械工程学报, 2010, 46(5): 43-48Ding Kang, Zheng Chun-Song, Yang Zhi-Jian. Precision analysis and improvement of frequency correction by the center of gravity method of discrete spectrum energy. Journal of Mechanical Engineering, 2010, 46(5): 43-48 [21] Zheng C S, Ding K, Yang Z J. Noise influence on frequency estimation accuracy from energy centrobaric correction method for discrete spectrum. In: Proceedings of International Conference on Information and Automation. Zhuhai, China: IEEE, 2009: 1477-1481 [22] Riviere C N, Rader R S, Thakor N V. Adaptive cancelling of physiological tremor for improved precision in microsurgery. IEEE Transactions on Biomedical Engineering, 1998, 45(7): 839-846 doi: 10.1109/10.686791 [23] Zhivomirov H, Nedelchev I, Vasilev R. A method for single-tone frequency estimation. Romanian Journal of Acoustics & Vibration, 2016, 13(1): 20-24 http://www.researchgate.net/publication/312455522_A_method_for_single-tone_frequency_estimation -
图(12) / 表(1)
计量
- 文章访问数: 986
- HTML全文浏览量: 163
- PDF下载量: 98
- 被引次数: 0
