A Regional Local Search Strategy for NSGA II Algorithm
-
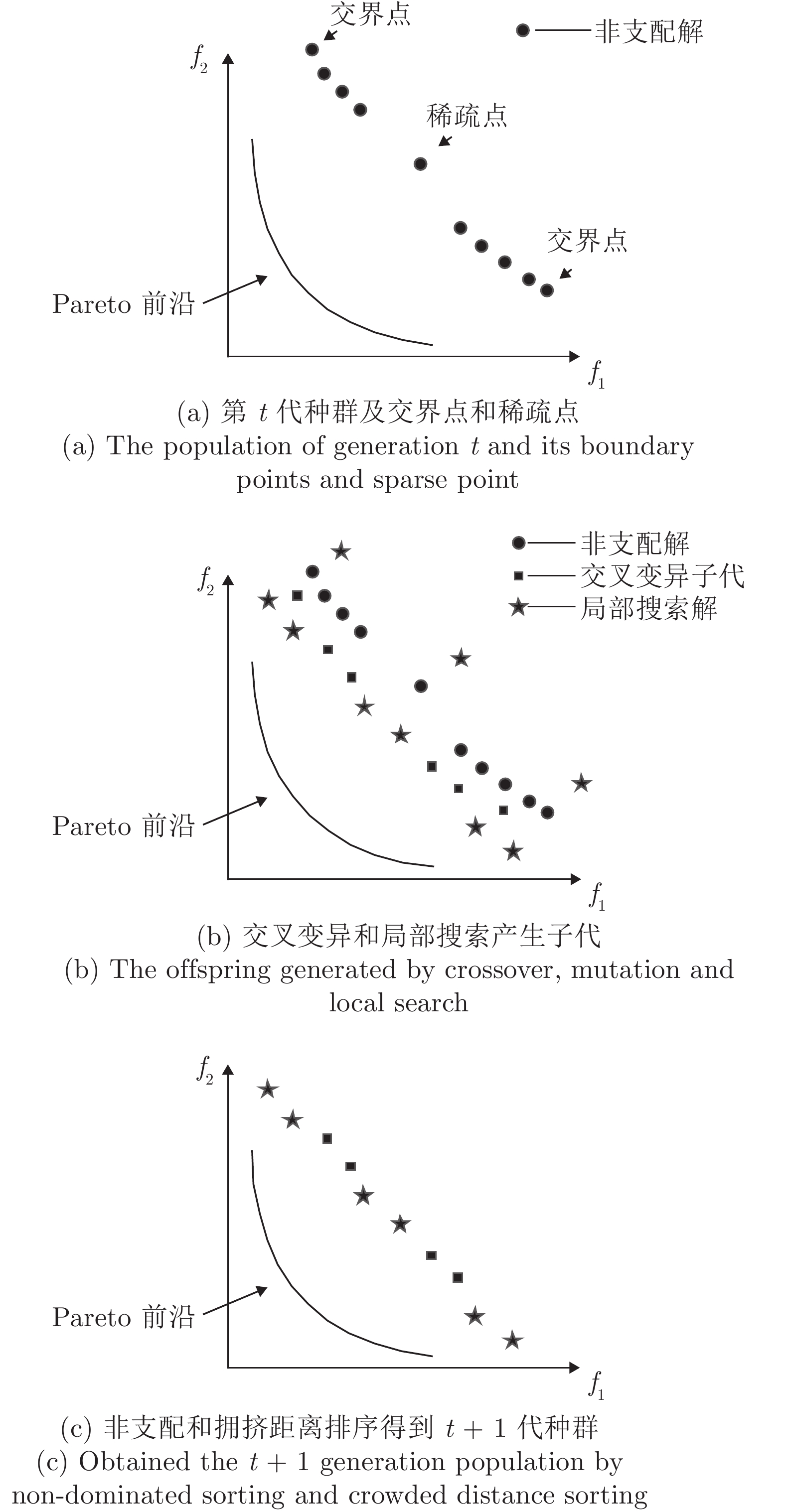
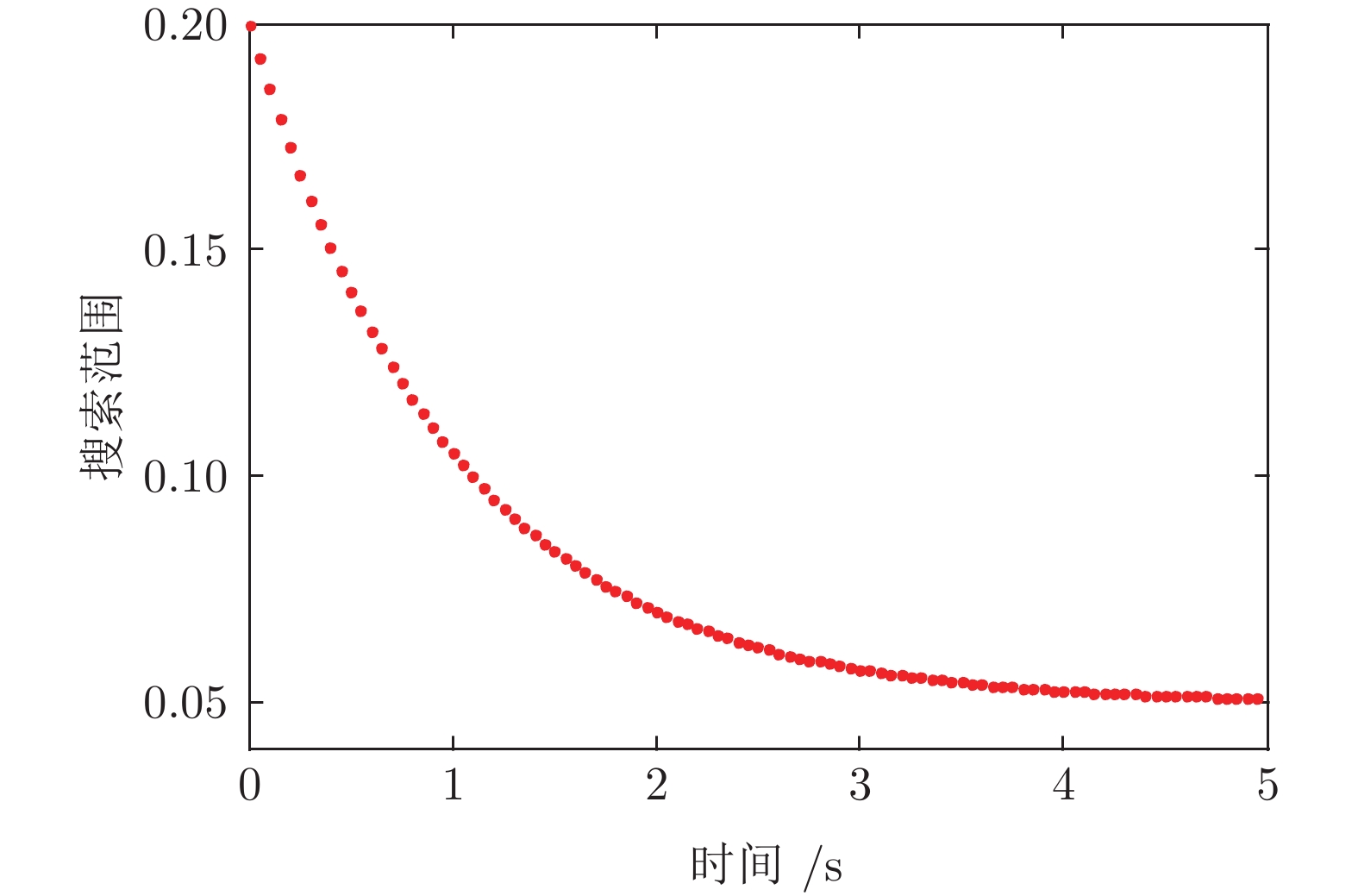
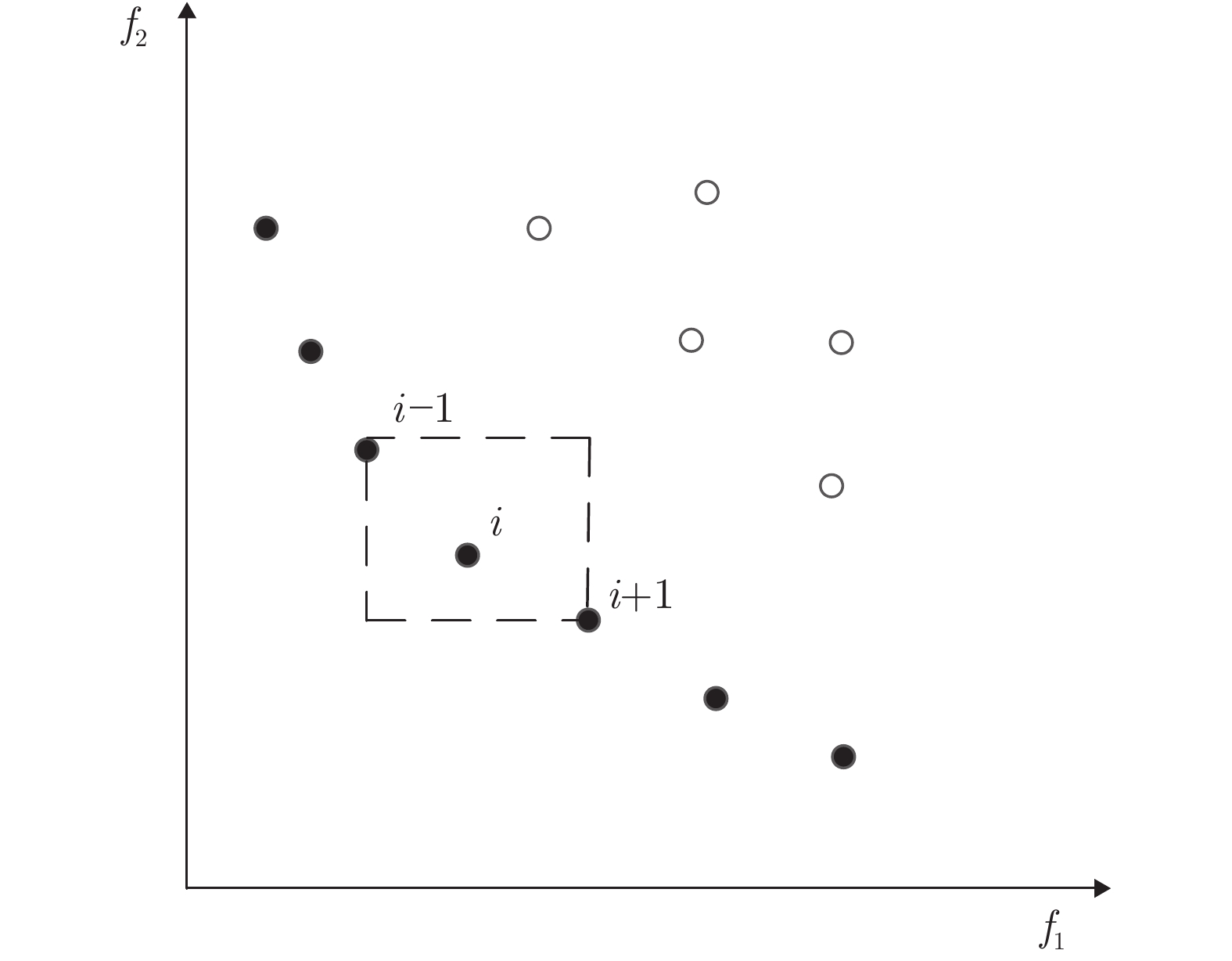
摘要: 针对局部搜索类非支配排序遗传算法 (Nondominated sorting genetic algorithms, NSGA II)计算量大的问题, 提出一种基于区域局部搜索的NSGA II算法(NSGA II based on regional local search, NSGA II-RLS). 首先对当前所有种群进行非支配排序, 根据排序结果获得交界点和稀疏点, 将其定义为交界区域和稀疏区域中心; 其次, 围绕交界点和稀疏点进行局部搜索. 在局部搜索过程中, 同时采用极限优化策略和随机搜索策略以提高解的质量和收敛速度, 并设计自适应参数动态调节局部搜索范围. 通过ZDT和DTLZ系列基准函数对NSGA II-RLS算法进行验证, 并将结果与其他局部搜索类算法进行对比, 实验结果表明NSGA II-RLS算法在较短时间内收敛速度和解的质量方面均优于所对比算法.Abstract: In order to reduce the amount of calculation and keep the advantage of local search strategy simultaneously, this paper proposed a kind of nondominated sorting genetic algorithms (NSGA II) algorithm based on regional local search (NSGA II-RLS). Firstly, get corner points and sparse point according to the results of non-dominated sorting of current populations, define those points as the centers of border areas and sparse area respectively; secondly, search around the corner points and sparse point locally during every genetic process; NSGA II-RLS adopts extreme optimization strategy and random search strategy simultaneously to improve the quality of solutions and convergence rate; adaptive parameter is designed to adjust local search scope dynamically. ZDT and DTLZ functions are used to test the effectiveness of NSGA II-RLS, the performance is compared with four other reported local search algorithms. Results show that: the solution quality of NSGA II-RLS is better than the other methods within limited time; the time complexity of NSGA II-RLS needed to achieve the set IGD value is less than the other methods.
-
图 3
$ T_{\rm{max}} $ 为5 s时$ \gamma $ 的变化曲线Fig. 3 the change curve of
$ \gamma $ when$ T_{\rm{max}} $ is set to be 5 s
图 4
$ T_{\rm{max}} $ 为1 000 s时$ \gamma $ 的变化曲线Fig. 4 the change curve of
$ \gamma $ when$ T_{\rm{max}} $ is set to be 1 000 s表 1 测试函数参数
Table 1 Paramter setting of the test functions
函数 Pareto前沿特征 决策变量维度 目标维度 种群规模 ZDT1 凸 30 2 1 000 ZDT2 凹 30 2 1 000 ZDT4 凸 10 2 1 000 ZDT6 凹 10 2 1 000 DTLZ1 非凸非凹 7 3 2 500 DTLZ2 凹 7 3 4 096 DTLZ3 凹 7 3 4 096 DTLZ4 凹 12 3 4 096 
下载: 导出CSV
表 2 ZDT系列函数IGD值达到0.01时对比算法的总时间复杂度与进化代数 (连续10次实验求平均)
Table 2 For ZDT series function the comparison of total time complexity and the evolution algebra of different algorithms when IGD value reaches 0.01 (mean value of ten consecutive experimental results)
算法 ZDT1 ZDT2 ZDT3 ZDT4 复杂度 代数 复杂度 代数 复杂度 代数 复杂度 代数 NSGA II-RLS 2 100 15 2 380 17 1 960 14 1 400 10 NSGA II-DLS[17] 46 440 (+) 43 34 560 (+) 32 31 320 (+) 29 32 400 (+) 30 ED-LS[9] 2 569 450 (+) 59 1 698 450 (+) 39 168 350 (+) 37 163 800 (+) 36 MOILS[10] 1 419 250 (+) 35 1 135 400 (+) 28 327 050 (+) 31 232 100 (+) 22 DirLS[15] 1 312 500 (+) 30 1 137 500 (+) 26 156 750 (+) 33 114 000 (+) 24 注: (+) 表示NSGA II-RLS的结果明显优于相应的算法
下载: 导出CSV
表 3 DTLZ系列函数IGD值达到0.1时对比算法的总时间复杂度与进化代数 (连续10次实验求平均)
Table 3 For DTLZ series function the comparison of total time complexity and the evolution algebra of different algorithms when IGD value reaches 0.1 (mean value of ten consecutive experimental results)
算法 DTLZ1 DTLZ2 DTLZ3 DTLZ4 复杂度 代数 复杂度 代数 复杂度 代数 复杂度 代数 NSGA II-RLS 29 920 88 17 340 19 33 660 99 27 540 41 NSGA II-DLS[17] 378 000 (+) 175 99 360 (+) 46 416 880 (+) 193 192 240 (+) 89 ED-LS[9] 369 800 (+) 86 116 100 (+) 27 460 100(+) 107 545 300 (+) 41 MOILS[10] 883 300 (+) 73 254 100 (+) 21 1 028 500 (+) 85 1 084 000 (+) 40 DirLS [15] 385 400 (+) 82 159 800 (+) 34 451 200 (+) 96 671 300 (+) 49 注: (+) 表示NSGA II-RLS的结果明显优于相应的算法
下载: 导出CSV
表 4 设定时间内NSGA2-RLS与其他局部搜索算法的ZDT和DTLZ系列实验IGD结果(连续10次实验)
Table 4 The IGD results of NSGA2-RLS and other local search algorithms in the ZDT and DTLZ series experiments within the set time (ten consecutive experimental results)
算法 NSGA II-RLS NSGA II-DLS[17] ED-LS[9] MOILS[10] DirLS[15] ZDT1 最大值 0.0048 0.0144 0.5686 0.2267 0.6891 最小值 0.0042 0.0047 0.3710 0.1549 0.0060 平均值 0.0045 0.0069 (+) 0.4934 (+) 0.1917 (+) 0.3517 (+) 标准差 1.8129 × 10−4 0.0033 0.0734 0.0214 0.2209 ZDT2 最大值 0.0050 0.1047 1.1891 0.8932 1.0808 最小值 0.0045 0.0045 0.5394 0.2294 0.0812 平均值 0.0048 0.0161 (+) 0.8197 (+) 0.5875 (+) 0.4839 (+) 标准差 1.6269 × 10−4 0.0332 0.2337 0.2122 0.3171 ZDT4 最大值 0.0046 0.3231 0.5547 0.8858 1.2584 最小值 0.0042 0.0044 0.1976 0.2982 0.0052 平均值 0.0043 0.0482 (+) 0.3296 (+) 0.5206 (+) 0.3552 (+) 标准差 1.2738 × 10−4 0.1059 0.0967 0.1738 0.4822 ZDT6 最大值 0.0050 0.0638 0.0161 0.0370 0.0617 最小值 0.0029 0.0029 0.0067 0.0081 0.0028 平均值 0.0038 0.0160 (+) 0.0106 (+) 0.0193 (+) 0.0096 (+) 标准差 7.2131 × 10−4 0.0212 0.0028 0.0101 0.0183 DTLZ1 最大值 0.0268 0.5428 0.4200 0.6859 0.4782 最小值 0.0199 0.0203 0.0258 0.0379 0.0278 平均值 0.0218 0.1128 (+) 0.1434 (+) 0.2823 (+) 0.1411 (+) 标准差 0.0025 0.1296 0.1136 0.1865 0.1724 DTLZ2 最大值 0.0648 0.0984 0.0638 0.0789 0.1212 最小值 0.0549 0.0695 0.0477 0.0583 0.0515 平均值 0.0611 0.0833 (+) 0.0597 0.0669 (=) 0.0751 (+) 标准差 0.0040 0.0120 0.0021 0.0075 0.0089 DTLZ3 最大值 0.0628 0.1690 0.2869 0.9678 0.3185 最小值 0.0536 0.0574 0.0682 0.1036 0.0819 平均值 0.0562 0.0778 (+) 0.0813 (+) 0.5109 (+) 0.1345 (+) 标准差 0.0033 0.0335 0.0679 0.3234 0.0850 DTLZ3 最大值 0.0830 0.3515 0.1735 0.2695 0.2701 最小值 0.0715 0.0897 0.1079 0.1616 0.0706 平均值 0.0755 0.1223 (+) 0.1335 (+) 0.2085 (+) 0.1659 (+) 标准差 0.0047 0.0973 0.0179 0.0393 0.0293 注: (+) 表示NSGA II-RLS的结果明显优于相应的算法,
(=) 表示NSGA II-RLS的结果与相应的算法没有显著差异性
下载: 导出CSV
表 5 设定时间内NSGA2-RLS与其他局部搜索算法的DTLZ系列实验I结果(连续10次实验)
Table 5 The I results of NSGA2-RLS and other local search algorithms in the DTLZ series experiments within the set time (ten consecutive experimental results)
算法 NSGA II-RLS NSGA II-DLS[17] ED-LS[9] MOILS[10] DirLS[15] DTLZ1 最大值 0.8066 0.9644 0.8068 1.1246 1.4509 最小值 0.7221 0.7270 0.7484 0.7027 0.9524 平均值 0.7847 0.8217 (+) 0.7879 (=) 0.8269 (+) 1.2380 (+) 标准差 0.0201 0.1267 0.0337 0.2303 0.2571 DTLZ2 最大值 0.7905 1.0426 0.7718 0.8194 1.0250 最小值 0.7008 0.7422 0.7187 0.7243 0.8206 平均值 0.7279 0.8345 (+) 0.7108 0.7443 (+) 0.9314 (+) 标准差 0.0319 0.1247 0.0371 0.0578 0.0786 DTLZ3 最大值 0.7486 0.9972 0.7478 0.8824 0.8185 最小值 0.6793 0.6912 0.7057 0.6866 0.6984 平均值 0.7090 0.8685 (+) 0.7205 (+) 0.7298 (+) 0.7529 (+) 标准差 0.0261 0.1163 0.0294 0.0876 0.0542 DTLZ3 最大值 0.8283 0.8599 1.1197 1.2498 1.3799 最小值 0.7377 0.7965 0.8392 1.0581 0.7823 平均值 0.7907 0.8036 (+) 0.8575 (+) 1.1614 (+) 1.0613 (+) 标准差 0.0449 0.0497 0.0684 0.0856 0.1516 注: (+) 表示NSGA II-RLS的结果明显优于相应的算法,
(=) 表示NSGA II-RLS的结果与相应的算法没有显著差异性
下载: 导出CSV
表 6 设定时间内不同搜索范围的局部搜索算法的DTLZ系列实验IGD结果(连续10次实验求均值)
Table 6 DTLZ series experiments IGD comparison of local search algorithms with different search ranges within the set time (mean value of ten consecutive experimental results)
时刻 NSGA II-RLS NSGA II-RLS1 NSGA II-RLS2 DTLZ1 0.25$T_{\rm{max}}$ 0.4491 0.4787 (=) 2.1773 (+) 0.5$T_{\rm{max}}$ 0.0413 0.0782 (+) 0.5583 (+) 0.75$T_{\rm{max}}$ 0.0265 0.0387 (+) 0.2104 (+) $T_{\rm{max}}$ 0.0218 0.0298 (+) 0.0234 (+) DTLZ2 0.25$T_{\rm{max}}$ 0.1299 0.1278 0.1678 (+) 0.5$T_{\rm{max}}$ 0.0891 0.0986 (+) 0.1288 (+) 0.75$T_{\rm{max}}$ 0.0710 0.0804 (+) 0.1113 (+) $T_{\rm{max}}$ 0.0611 0.0719 (+) 0 0970 (+) DTLZ3 0.25$T_{\rm{max}}$ 0.8229 0.5186 2.0068 (+) 0.5$T_{\rm{max}}$ 0.0902 0.1762 (+) 0.5997 (+) 0.75$T_{\rm{max}}$ 0.0589 0.1090 (+) 0.1820 (+) $T_{\rm{max}}$ 0.0562 0.0811 (+) 0.0952 (+) DTLZ4 0.25$T_{\rm{max}}$ 0.1418 0.1733 (=) 0.1804 (+) 0.5$T_{\rm{max}}$ 0.0967 0.1070 (+) 0.1158 (+) 0.75$T_{\rm{max}}$ 0.0799 0.0880 (+) 0.0829 (=) $T_{\rm{max}}$ 0.0755 0.0819 (+) 0.0717 注: (+) 表示NSGA II-RLS的结果明显优于相应的算法,
(=) 表示NSGA II-RLS的结果与相应的算法没有显著差异性
下载: 导出CSV
-
[1] Yang S, Cao D, Lo K. Analyzing and optimizing the impact of economic restructuring on Shanghai's carbon emissions using STIRPAT and NSGA-II. Sustainable Cities and Society, 2018, 40: 44−53 [2] Maity S, Roy A, Maiti M. A rough multi-objective genetic algorithm for uncertain constrained multi-objective solid travelling salesman problem. Granular Computing, 2018, 46: 1−18 [3] Wang H F, Fu Y P, Huang M, George Q, Wang J W. A NSGA-II based memetic algorithm for multiobjective parallel flowshop scheduling problem. Computers and Industrial Engineering, 2017, 113: 185−194 [4] Ahmadi A. Memory-based adaptive partitioning (MAP) of search space for the enhancement of convergence in pareto-based multi-objective evolutionary algorithms. Applied Soft Computing, 2016, 41: 400−417 doi: 10.1016/j.asoc.2016.01.029 [5] Palar P S, Tsuchiya T, Parks G. Comparison of scalarization functions within a local surrogate assisted multi-objective memetic algorithm framework for expensive problems. IEEE Transactions on Evolutionary Computation, 2015: 862−869 [6] Lust T, Teghem J. Two-phase pareto local search for the biobjective traveling salesman problem. Journal of Heuristics, 2010, 16(3): 475−510 doi: 10.1007/s10732-009-9103-9 [7] Alsheddy A, Tsang E E P K. Guided Pareto local search based frameworks for biobjective optimization, In: Proceedings of 2010 IEEE Congress on Evolutionary Computation. Barcelona, Spain: IEEE, 2010. 1−8. [8] Ozkis A, Babalik A. A novel metaheuristic for multi-objective optimization problems: The multi-objective vortex search algorithm. Information Sciences, 2017, 402: 124−148 doi: 10.1016/j.ins.2017.03.026 [9] Michalak K. ED-LS — A heuristic local search for the multiobjective firefighter problem. Applied Soft Computing, 2017, 59: 389−404 doi: 10.1016/j.asoc.2017.05.049 [10] Xu J Y, Wu C C, Yin Y Q, Lin W C. An iterated local search for the multi-objective permutation flowshop scheduling problem with sequence-dependent setup times. Applied Soft Computing, 2017, 52: 39−47 doi: 10.1016/j.asoc.2016.11.031 [11] Lin Q Z, Hu B S, Tang Y, Zhang L Y, Chen J Y, Wang X M, Ming Z. A local search enhanced differential evolutionary algorithm for sparse recovery. Applied Soft Computing, 2017, 57: 144−163 doi: 10.1016/j.asoc.2017.03.034 [12] Capitanescu F, Marvuglia A, Benetto E, Ahmadi A, Tiruta-Barna L. Linear programming-based directed local search for expensive multi-objective optimization problems: application to drinking water production plants. European Journal of Operational Research, 2017, 262(1): 322−334 doi: 10.1016/j.ejor.2017.03.057 [13] Lara A, Sanchez G, Coello C A C, Schutze O. HCS: A new local search strategy for memetic multiobjective evolutionary algorithms. IEEE Transactions on Evolutionary Computation, 2010, 14(1): 112−132 doi: 10.1109/TEVC.2009.2024143 [14] Kim H, Liou M S. Adaptive directional local search strategy for hybrid evolutionary multiobjective optimization. Applied Soft Computing Journal, 2014, 19(6): 290−311 [15] Michalak K. Evolutionary algorithm with a directional local search for multiobjective optimization in combinatorial problems. Optimization Methods and Software, 2016, 31(2): 392−404 [16] Palar P S, Tsuchiya T, Parks G T. A comparative study of local search within a surrogate-assisted multi-objective memetic algorithm framework for expensive problems. Applied Soft Computing, 2016, 43: 1−19 doi: 10.1016/j.asoc.2015.12.039 [17] Zeng G Q, Chen J, Li L M, Chen M R, Wu L, Dai Y X, Zheng C W. An improved multi-objective population-based extremal optimization algorithm with polynomial mutation. Information Sciences, 2016, 330: 49−73 doi: 10.1016/j.ins.2015.10.010 [18] 栗三一, 李文静, 乔俊飞. 一种基于密度的局部搜索NSGA2算法. 控制与决策, 2018, (1): 60−66Li San-Yi, Li Wen-Jing, Qiao Jun-Fei. A local search strategy based on density for NSGA2 algorithm. Control and Decision, 2018, (1): 60−66 [19] Yang S X. Genetic algorithms with memory- and elitism-based immigrants in dynamic environments. Evolutionary Computation, 2014, 16(3): 385−416 [20] Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182−197 doi: 10.1109/4235.996017 [21] Kumar M, Guria C. The elitist non-dominated sorting genetic algorithm with inheritance (i-NSGA-II) and its jumping gene adaptations for multi-objective optimization. Information Sciences, 2017, 382−383: 15−37 doi: 10.1016/j.ins.2016.12.003 [22] Brownlee A E I, Wright J A. Constrained, mixed-integer and multi-objective optimisation of building designs by NSGA-II with fitness approximation. Applied Soft Computing, 2015, 33: 114−126 doi: 10.1016/j.asoc.2015.04.010 [23] Chan F T S, Jha A, Tiwari M K. Bi-objective optimization of three echelon supply chain involving truck selection and loading using NSGA-II with heuristics algorithm. Applied Soft Computing Journal, 2016, 38: 978−987 doi: 10.1016/j.asoc.2015.10.067 [24] Sindhya K, Miettinen K, Deb K. A hybrid framework for evolutionary multi-objective optimization. IEEE Transactions on Evolutionary Computation, 2013, 17(4): 495−511 doi: 10.1109/TEVC.2012.2204403 -
图(4) / 表(6)
计量
- 文章访问数: 1179
- HTML全文浏览量: 524
- PDF下载量: 249
- 被引次数: 0
