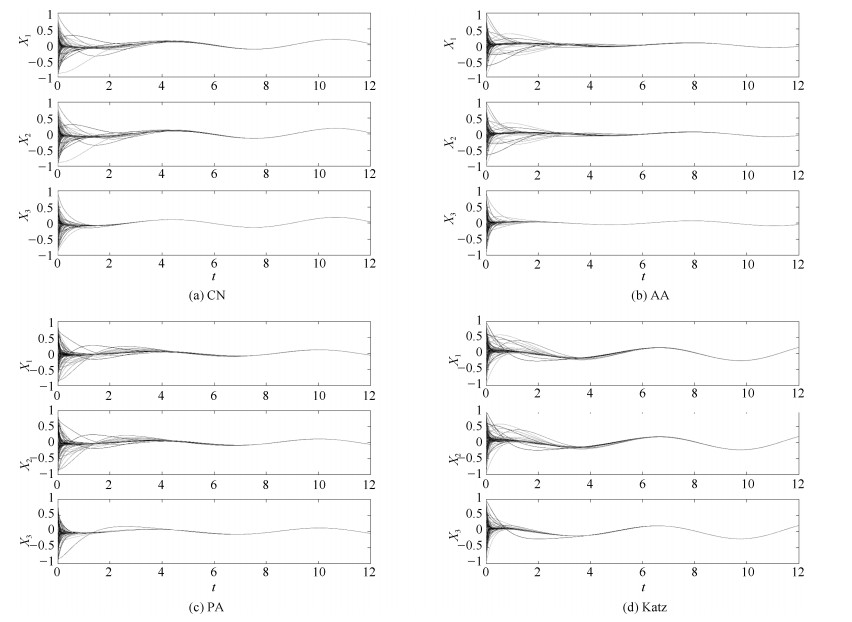
-
摘要: 链路预测是研究复杂网络结构演化趋势的重要组成部分, 用于预测网络丢失的连边和未来可能出现的连边, 具有极大的理论和应用价值.当前链路预测研究成果主要基于网络结构特征对连边进行预测, 具体分析其连边机理的研究较少.网络同步的研究能够深刻反映节点的动力学演化行为与网络结构之间的内在机理.本文针对链路预测考虑的静态网络引入节点动力学模型构成动态网络, 通过分析链路预测连边与动态网络模型同步之间的关系, 对链路预测连边机理进行分析研究.通过实验与理论分析总结发现了链路预测连边具有同步能力稳定性的规律.进一步讨论了链路预测连边的动力学机理, 并揭示了链路预测连边机理与真实网络演化的差别.Abstract: Link prediction is an important part of the study of the evolutionary trend of complex network structure. It is used to predict the missing links and future links of network, and has great theoretical and practical value. The current link prediction researches are mainly based on the characteristics of the network structure. The study of network synchronization can profoundly reflect the internal mechanism between the node's dynamic evolution behavior and network structure. In this paper, we introduce a node dynamic model for link prediction research. By analyzing the relationship between the link prediction and the synchronization of the dynamic network model, we analyze the link prediction mechanism. Furthermore, we discuss the dynamic mechanism of link prediction, and reveal the difference between link prediction mechanism and real network evolution.
-
Key words:
- Complex network /
- link prediction /
- synchronization /
- master stability function
1) 本文责任编委 陈积明 -
表 1 网络的拓扑特征参数
Table 1 Topological characteristic parameters of the network
网络 $ N$ $M$ $k $ $ L $ $C $ Jazz 198 2 742 27.697 2.235 0.6175 USair 332 2 126 12.807 2.738 0.6252 PB 1 222 16 714 27.355 2.738 0.3203 Yeast 2 375 11 693 9.848 5.096 0.3057 FWFB 128 2 075 32.422 1.776 0.3346 表 2 演化网络同步能力增长率(%)
Table 2 Growth rate of evolutionary network synchronizability (%)
$G_{\rm CN}$ $G_{AA}$ $G_{\rm PA}$ $G_{\rm Katz}$ $G_{\rm rd}$ NW 2.74 2.98 1.92 2.51 19.95 Jazz 0.09 0.10 0.51 0.07 402.73 USair 0.04 0.04 0.45 0.04 599.47 PB 0 0 0 0 183.85 Yeast 0 0 0.01 0 1 277.52 FWEB 0 0 0.27 0.08 491.64 表 3 CN演化网络同步能力增长率(%)
Table 3 Growth rate of CN evolutionary network synchronizability (%)
1 2 3 5 7 10 NW 0.11 0.22 0.31 0.82 1.03 2.74 Jazz 0 0 0.02 0.04 0.07 0.09 USair 0 0 0 0.01 0.02 0.04 PB 0 0 0 0 0 0 Yeast 0 0 0 0 0 0 FWEB 0 0 0 0 0 0 表 4 AA演化网络同步能力增长率(%)
Table 4 Growth rate of AA evolutionary network synchronizability (%)
1 2 3 5 7 10 NW 0.10 0.23 0.30 0.93 1.34 2.98 Jazz 0 0 0.02 0.05 0.08 0.10 USair 0 0 0 0 0.02 0.04 PB 0 0 0 0 0 0 Yeast 0 0 0 0 0 0 FWEB 0 0 0 0 0 0 表 5 PA演化网络同步能力增长率(%)
Table 5 Growth rate of PA evolutionary network synchronizability (%)
1 2 3 5 7 10 NW 0.07 0.29 0.31 0.72 1.06 1.92 Jazz 0.09 0.10 0.13 0.21 0.42 0.51 USair 0.03 0.04 0.06 0.20 0.32 0.45 PB 0 0 0 0 0 0 Yeast 0 0 0 0 0 0.01 FWEB 0 0 0 0.05 0.12 0.27 表 6 Katz演化网络同步能力增长率(%)
Table 6 Growth rate of Katz evolutionary network synchronizability (%)
1 2 3 5 7 10 NW 0.15 0.32 0.39 0.94 1.12 2.51 Jazz 0 0 0.02 0.04 0.06 0.07 USair 0 0 0 0.01 0.02 0.04 PB 0 0 0 0 0 0 Yeast 0 0 0 0 0 0 FWEB 0 0 0 0 0.03 0.08 -
[1] Lv L, Zhou T. Link prediction in complex networks: a survey. Physica A Statistical Mechanics and Its Applications, 2011, 390(6): 1150-1170 doi: 10.1016/j.physa.2010.11.027 [2] Mitzenmacher M. A brief history of generative models for power law and lognormal distributions. Internet Mathematics, 2004, 1(2): 226-251 doi: 10.1080/15427951.2004.10129088 [3] Adamic L A, Adar E. Friends and neighbors on the web. Social Networks, 2003, 25(3): 211-230 doi: 10.1016/S0378-8733(03)00009-1 [4] Zhou T, Lv L, Zhang Y C. Predicting missing links via local information. European Physical Journal B, 2009, 71(4): 623 -630 doi: 10.1140/epjb/e2009-00335-8 [5] Xie Y B, Zhou T, Wang B H. Scale-free networks without growth. Physica A Statistical Mechanics and Its Applications, 2005, 387(7): 1683-1688 http://www.sciencedirect.com/science/article/pii/S0378437107012046 [6] Liu S, Ji X, Liu C, Bai Y. Extended resource allocation index for link prediction of complex network. Physica A Statistical Mechanics and Its Applications, 2017, 479: 174-183 doi: 10.1016/j.physa.2017.02.078 [7] Fouss F, Pirotte A, Renders J M, Saerens M. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation. In: Proceedings of the 2007 IEEE Transactions on Knowledge and Data Engineering, 2007, 19(3): 355-369 [8] Tong H, Faloutsos C, Pan J Y. Fast random walk with restart and its applications. In: Proceedings of the 2006 International Conference on Data Mining. IEEE Computer Society, 2006: 613-622 [9] Clauset A, Moore C, Newman M E. Hierarchical structure and the prediction of missing links in networks. Nature, 2008, 453(7191): 98-98 doi: 10.1038/nature06830 [10] Airoldi E M, Blei D M, Fienberg S E, Xing E P. Mixed membership stochastic blockmodels. Journal of Machine Learning Research, 2008, 9(5): 1981-1981 http://dl.acm.org/citation.cfm?id=2981785 [11] Pan L, Zhou T, Linyuan L, Hu C K. Predicting missing links and identifying spurious links via likelihood analysis. Scientific Reports, 2016, 6: 22955-22955 doi: 10.1038/srep22955 [12] He Y L, Liu J N K, Hu Y X, Wang X Z. OWA operator based link prediction ensemble for social network. Expert Systems with Applications, 2015, 42(1): 21-50 doi: 10.1016/j.eswa.2014.07.018 [13] 吴祖峰, 梁棋, 刘峤, 秦志光.基于AdaBoost的链路预测优化算法.通信学报, 2014, 35(3): 116-123 http://d.wanfangdata.com.cn/Periodical/txxb201403013Wu Zu-Feng, Liang Qi, Liu Qiao, Qin Zhi-Guang. Modified link prediction algorithm based on AdaBoost. Journal on Communications, 2014, 35(3): 116-123 http://d.wanfangdata.com.cn/Periodical/txxb201403013 [14] Yu H T, Wang S H, Ma Q Q. Link prediction algorithm based on the Choquet fuzzy integral. Intelligent Data Analysis, 2016, 20(4): 809-824 doi: 10.3233/IDA-160833 [15] 陆君安, 刘慧, 陈娟.复杂动态网络的同步.北京:高等教育出版社2016. 47-47Lu Jun-An, Liu Hui, Chen Juan. Synchronization in Complex Dynamical Networks. Beijing: Higher Education Press, 2016. 47-47 [16] Pecora L M, Carroll T L. Master stability functions for synchronized chaos in arrays of oscillators. Physical Review Letters, 1998, 80: 2109-2112 doi: 10.1103/PhysRevLett.80.2109 [17] Liu H, Chen J, Lu J A, Cao M Generalized synchronization in complex dynamical networks via adaptive couplings. Physica A, 389: 1759-1770 doi: 10.1016/j.physa.2009.12.035 [18] Lu W, Liu B, Chen T. Cluster synchronization in networks of coupled nonidentical dynamical systems. Chaos an Interdisciplinary Journal of Nonlinear Science, 2010, 20(1): 175- 175 doi: 10.1063/1.3329367 [19] Chen L, Lu J A, Chi K T. Synchronization: an obstacle to identification of network topology. IEEE Transactions on Circuits and Systems Ⅱ Express Briefs, 2009, 56(4): 310- 314 doi: 10.1109/TCSII.2009.2015381 [20] Suykens J A K, Osipov G V. Introduction to focus issue: synchronization in complex networks. Chaos an Interdisciplinary Journal of Nonlinear Science, 2008, 18(3): 268-268 http://europepmc.org/abstract/MED/19045475 [21] Arenas A, Díaz-Guilera A, Kurths J, Moreno Y, Zhou C. Synchronization in complex networks. Physics Reports, 2008, 469(3): 93-153 doi: 10.1016/j.physrep.2008.09.002 [22] Wu W, Chen T. Global synchronization criteria of linearly coupled neural network systems with time-varying coupling. IEEE Transactions on Neural Networks, 2008, 19(2): 319- 332 doi: 10.1109/TNN.2007.908639 [23] Han X P, Lu J A, Wu X Q. Synchronization of impulsively coupled systems. International Journal of Bifurcation and Chaos, 2008, 18(5): 1539-1549 doi: 10.1142/S0218127408021154 [24] Zhou J, Lu J A, Lv J. Pinning adaptive synchronization of a general complex dynamical network. Automatica, 2009, 45(2): 598-599 doi: 10.1016/j.automatica.2008.11.001 [25] Liu Q, Fang J Q, Li Y. Synchronization and control of halo-chaos in beam transport network with small world topology. Communications in Theoretical Physics, 2007, 47(4): 752- 758 doi: 10.1088/0253-6102/47/4/040 [26] Xin B L, Xiao F W, Jin Q F. Topological transition features and synchronizability of a weighted hybrid preferential network. Physica A Statistical Mechanics and Its Applications, 2006, 371(2): 841-850 doi: 10.1016/j.physa.2006.03.032 [27] Lu W, Chen T, Chen G. Synchronization analysis of linearly coupled systems described by differential equations with a coupling delay. Physica D Nonlinear Phenomena, 2006, 221(2): 118-134 doi: 10.1016/j.physd.2006.07.020 [28] Barahona M, Pecora L M. Synchronization in small-world systems. Physical Review Letters, 2002, 89(5): 054101- 054101 doi: 10.1103/PhysRevLett.89.054101 [29] 徐明明, 陆君安, 周进.两层星形网络的特征值谱及同步能力.物理学报, 2016, 65(2): 383-395 http://d.wanfangdata.com.cn/Periodical/wlxb201602049Xu Ming-Ming, Lu Jun-An, Zhou Jin. Synchronizability and eigenvalues of two-layer star networks. Acta Physica Sinica, 2016, 65(2): 383-395 http://d.wanfangdata.com.cn/Periodical/wlxb201602049 [30] Aguirre J, Sevilla-Escoboza R, Gutiérrez R, Papo D, Buldú J. Synchronization of interconnected networks: the role of connector nodes. Physical Review Letters, 2014, 112(24): 248701-248701 doi: 10.1103/PhysRevLett.112.248701 [31] Um J, Minnhagen P, Kim B J. Synchronization in interdependent networks. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2011, 21: 5712-5712 http://nsr.oxfordjournals.org/external-ref?access_num=10.1063/1.3596698&link_type=DOI [32] Lu R, Yu W, Lu J, Xue A. Synchronization on complex networks of networks. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(11): 2110-2118 doi: 10.1109/TNNLS.2014.2305443 [33] 陆君安, 刘慧, 陈娟.复杂动态网络的同步.北京:高等教育出版社2016. 81-81Lu Jun-An, Liu Hui, Chen Juan. Synchronization in Complex Dynamical Networks. Beijing: Higher Education Press, 2016. 81-81 [34] Belykh V N, Belykh I V, Hasler M. Connection graph stability method for synchronized coupled chaotic systems. Physica D Nonlinear Phenomena, 2004, 195(1): 159-187 http://www.sciencedirect.com/science/article/pii/S0167278904001599 [35] Schaer J. Generalized connection graph method for synchronization in asymmetrical networks. Physica D Nonlinear Phenomena, 2006, 224(1): 42-51 http://www.sciencedirect.com/science/article/pii/S0167278906003745 [36] Liu H, Cao M, Wu C W. Coupling strength allocation for synchronization in complex networks using spectral graph theory. IEEE Transactions on Circuits and Systems Ⅰ Regular Papers, 2017, 61(5): 1520-1530 http://ieeexplore.ieee.org/document/6684596 [37] Liu H, Cao M, Wu C W, Lu J A, Chi K T. Synchronization in directed complex networks using graph comparison tools. IEEE Transactions on Circuits and Systems Ⅰ Regular Papers, 2017, 62(4): 1185-1194 http://ieeexplore.ieee.org/document/7070888 [38] Zhou J, Lu J A. Topology identification of weighted complex dynamical networks. Physica A Statistical Mechanics and Its Applications, 2007, 386(1): 481-491 doi: 10.1016/j.physa.2007.07.050 [39] Zhan C, Chen G, Yeung L F. On the distributions of laplacian eigenvalues versus node degrees in complex networks. Physica A Statistical Mechanics and Its Applications, 2010, 389(8): 1779-1788 doi: 10.1016/j.physa.2009.12.005 -




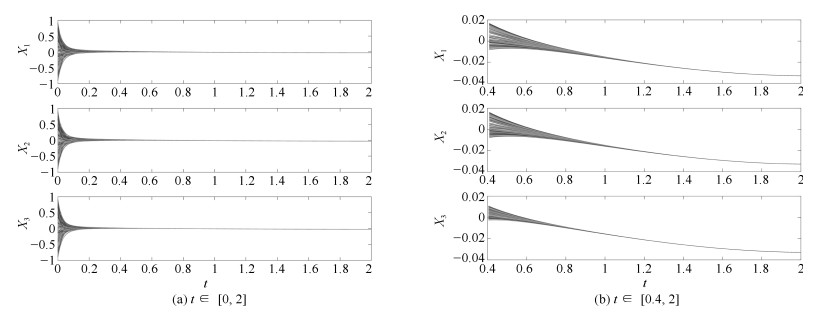
 下载:
下载: