Sea Surface Target Detection for RD Images of HFSWR Based on Optimized Error Self-adjustment Extreme Learning Machine
-
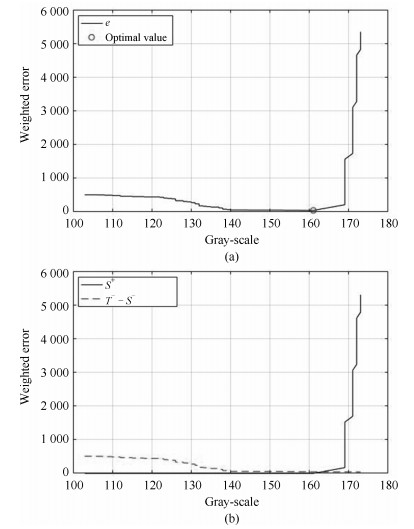
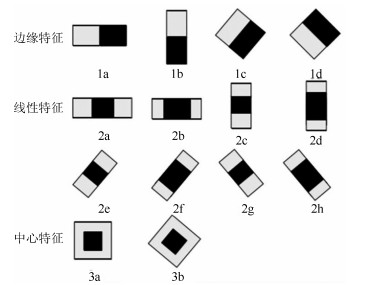
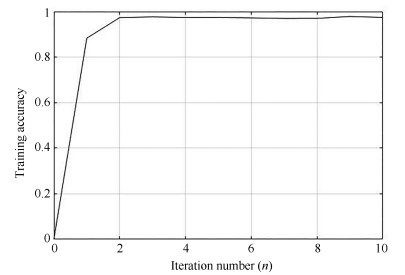
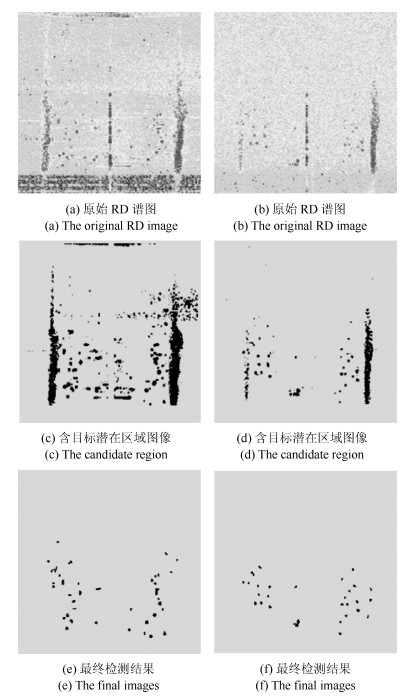
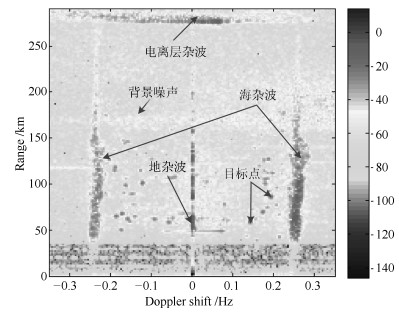
摘要: 高频地波雷达(High-frequency surface wave radar, HFSWR)在超视距舰船目标检测跟踪中有广泛应用.然而, HFSWR工作频段的电磁环境十分复杂, 舰船目标信号往往被淹没在各种噪声中.本文提出一种基于最优误差自校正极限学习机(Optimized error self-adjustment extreme learning machine, OES-ELM)的HFSWR海面目标识别算法.该算法利用二级级联分类策略, 可以显著提高目标的检测效率.首先利用灰度特征和线性分类器快速找出目标的潜在区域.然后利用Haar-like特征和OES-ELM分类器进一步辨识目标和海杂波.在OES-ELM中, 首先利用$L_{1/2}$正则算子裁剪隐层中的"微弱"神经元, 以得到隐层神经元的最优个数; 其次, 通过网络误差回传至隐含层使网络的隐层权值和输出层权值迭代更新至最优状态.实验结果表明:和标准ELM相比, 提出的OES-ELM网络具有更好的性能; 此外, 基于OES-ELM的HFSWR目标检测方法具有良好的实时性和目标检测性能.Abstract: High-frequency surface wave radar (HFSWR) has been widely applied in ship targets detection and tracking beyond the line-of-sight limitation. However, the detection background of HFSWR is completely complex, in which the ship targets usually polluted by all kinds of noises. In this paper, a novel ship target detection method based on optimized error self-adjustment extreme learning machine (OES-ELM) for RD images of HFSWR is presented. Through the application of two-stage cascade classification strategy, the proposed approach can impressively increase the detection efficiency in real time. Firstly, gray-scale feature and a linear classifier are adopted to obtain the target candidate areas. Then, Haar-like features and a optimized ELM are proposed to identify ship targets from precisely. In the proposed OES-ELM, the sparse solution of output weights is found by $L_{1/2}$ regularizer process, in which the optimal hidden neurons can be obtained by pruning the "weak" nodes. In addition, both the output and hidden weights are updated to optimal value by pulling back the output error to the hidden layer. Experimental results show that the proposed OES-ELM has better generalization performance. Furthermore, the proposed method has favorable real time and target detection performance.
-
Key words:
- High frequency surface wave radar (HFSWR) /
- extreme learning machine (ELM) /
- target detection /
- RD image
1) 本文责任编委 黄庆明 -
图 3 线性分类器的权重误差$e$, $S^+$, $ {T^–}-{S^-}$和灰度级间关系曲线
Fig. 3 The weighted error $e$, $S^+$ and $ {T^–}-{S^-}$, when training linear classifier on RD image data set, where the x-axis show the different gray-value
图 6 系数比和隐层神经元数目间关系曲线
Fig. 6 Performance of ratio of the first $l$ accumulation coefficients to the sum coefficients
图 7 训练误差和迭代次数关系曲线
Fig. 7 performance of training accuracy with respect to iteration $n$
表 1 分类数据集的具体信息
Table 1 The detail of classification datasets
数据集 属性数 训练集 测试集 Hill-Valley 101 606 606 Iris 4 60 90 BCW(Original) 10 300 399 Covtype.binary 54 300 000 281 012 Wine 13 90 88 Gisette 5 000 6 000 1 000 Leukemia 7 129 38 34 
下载: 导出CSV
表 2 回归数据集的具体信息
Table 2 The detail of regression datasets
数据集 属性数 训练集 测试集 Forest Fires 13 239 278 Wine Quality 12 2 898 2 000 Abalone 8 3 000 1 477 CPUsmall 12 5 000 4 192 Facebook Metrics 9 300 200
下载: 导出CSV
表 3 不同网络在不同数据集下性能对比
Table 3 Generalization performance comparision
数据集 方法 Tr_acc Te_acc 神经元 Hill-Valley ELM 81.36 % 79.44 % 300 ES-ELM 81.36 % 98.94 % 4 (2m) OES-ELM($ L_1 $) 98.63 % 97.57 % 189 OES-ELM 97.36 % 98.66 % 184 Iris ELM 92.02 % 82.59 % 30 ES-ELM 89.16 % 89.17 % 6(2m) OES-ELM($ L_1 $) 92.23 % 89.16 % 23 OES-ELM 91.79 % 90.27 % 23 BCW (Original) ELM 92.66 % 87.41 % 300 ES-ELM 98.67 % 98.50 % 4(2m) OES-ELM($ L_1 $) 97.01 % 96.47 % 137 OES-ELM 98.37 % 98.96 % 123 Covtype. binary ELM 77.29% 79.28 % 500 ES-ELM 79.83 % 78.15 % 14(2m) OES-ELM($ L_1 $) 76.11 % 78.27 % 867 OES-ELM 79.94 % 78.41 % 899 Wine ELM 98.77 % 84.88 % 300 ES-ELM 99.44 % 98.86 % 6(2m) OES-ELM($ L_1 $) 95.59 % 98.40 % 42 OES-ELM 95.61 % 98.91 % 40 Gisette ELM 92.20 % 86.49 % 5 000 ES-ELM 95.68 % 84.77 % 4(2m) OES-ELM($ L_1 $) 97.99 % 96.09 % 1 355 OES-ELM 98.01 % 96.74 % 1 205 Leukemia ELM 71.60 % 74.36 % 5 000 ES-ELM 84.10 % 69.91 % 4(2m) OES-ELM($ L_1 $) 94.12 % 86.91 % 34 OES-ELM 93.89 % 87.14 % 34
下载: 导出CSV
表 4 不同网络在不同数据集下性能对比
Table 4 Generalization performance comparision
数据集 方法 $ Tr\_RMSE $ $ Te\_RMSE $ 神经元 Forest Fires ELM 0.1568 0.1958 200 OES-ELM($ L_1 $) 0.1467 0.1365 163 OES-ELM 0.1480 0.1374 161 Wine Quality ELM 0.2547 0.1799 200 OES-ELM($ L_1 $) 0.1863 0.1977 244 OES-ELM 0.1845 0.1921 168 Abalone ELM 0.0412 0.0816 200 OES-ELM($ L_1 $) 0.0601 0.0659 108 OES-ELM 0.0592 0.0647 115 CPUsmall ELM 0.2550 0.2497 500 OES-ELM($ L_1 $) 0.2235 0.2226 163 OES-ELM 0.2021 0.2217 159 Facebook Metrics ELM 0.3659 0.2185 200 OES-ELM($ L_1 $) 0.0350 0.0459 27 OES-ELM 0.0417 0.0458 27
下载: 导出CSV
表 5 ELM和OES-ELM在不同正则系数下$ Te\_RMSE $比较
Table 5 The comparision of ELM and OES-ELM with respect to $ Te\_RMSE $
C Forest Fires Wine Quality Abalone CPUsmall Facebook Metrics ELM OES-ELM ELM OES-ELM ELM OES-ELM ELM OES-ELM ELM OES-ELM $ C = 2^{-2} $ 0.1920 0.1286 0.1534 0.2015 0.1065 0.0742 0.2338 0.2285 0.0956 0.0542 $ C = 2^{0} $ 0.1957 0.1204 0.2148 0.2159 0.1895 0.0638 0.2398 0.2227 0.1386 0.0499 $ C = 2^{2} $ 0.1491 0.1245 0.1649 0.1958 0.1099 0.0626 0.2345 0.2218 0.1477 0.0612 $ C = 2^{4} $ 0.2048 0.1367 0.2493 0.2226 0.2201 0.0628 0.2561 0.2214 0.1602 0.0418
下载: 导出CSV
表 6 两个数据集的详细信息
Table 6 The detail of two designed datasets
数据集 样本数 输入 输出 维数 特征 维数 类别 $ X_1 $ 1 274 1 灰度值 2 是否背景 $ X_2 $ 576 49 Haar-like 2 是否目标
下载: 导出CSV
表 7 三种算法的性能对比(时间:平均测试时间(秒))
Table 7 The performance of These three algorithms (Time: Average testing time (second))
方法 $ P_d $ $ P_f $ $ M_r $ $ E_r $ 时间 OES-ELM 92 % 6 % 8 % 14 % 3.65 改进CFAR 85 % 13 % 15 % 28 % 4.90 自适应小波 90 % 8 % 10 % 18 % 6.14
下载: 导出CSV
-
[1] Wait J R. Theory of HF ground wave backscatter from sea waves. Journal of Geophysical Research, 1966, 71(20): 4839-4842 doi: 10.1029/JZ071i020p04839 [2] Conte E, Di Bisceglie M, Lops M. Clutter-map CFAR detection for range-spread targets in non-Gaussian clutter. Ⅱ. Performance assessment. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(2): 444-455 doi: 10.1109/7.575879 [3] Rohling H. Radar CFAR thresholding in clutter and multiple target situations. IEEE Transactions on Aerospace and Electronic Systems, 1983, AES-19(4): 608-621 doi: 10.1109/TAES.1983.309350 [4] 何友, Rohling H.一种新的基于有序统计的恒虚警处理器.系统工程与电子技术, 1994, (4): 17-23 doi: 10.3321/j.issn:1001-506X.1994.04.003He You, Rohling H. A new CFAR processor based on ordered statistoc. Systems Engineering and Electronics, 1994, (4): 17-23 doi: 10.3321/j.issn:1001-506X.1994.04.003 [5] 桂任舟.利用二维恒虚警进行非均匀噪声背景下的目标检测.武汉大学学报(信息科学版), 2012, 37(3): 354-357 https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH201203025.htmGui Ren-Zhou. Detecting target located in nonstationary background based on two-dimensions constant false alarm rate. Geomatics and Information Science of Wuhan University, 2012, 37(3): 354-357 https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH201203025.htm [6] 梁建.高频地波雷达目标二维CFAR检测及软件实现[硕士学位论文], 中国海洋大学, 中国, 2014.Liang Jian. Target CFAR Detection Method and Software Implementation with Two-dimension Data for HFSWR[Master thesis], Ocean University of China, China, 2014. [7] Grosdidier S, Baussard A. Ship detection based on morphological component analysis of high-frequency surface wave radar images. IET Radar, Sonar & Navigation, 2012, 6(9): 813-821 [8] Jangal F, Saillant S, Helier M. Wavelet contribution to remote sensing of the sea and target detection for a high-frequency surface wave radar. IEEE Geoscience and Remote Sensing Letters, 2008, 5(3): 552-556 doi: 10.1109/LGRS.2008.923211 [9] Jangal F, Saillant S, Helier M. Wavelets: a versatile tool for the high frequency surface wave radar. In: Proceedings of 2007 Radar Conference. Boston, USA: IEEE, 2007. 497-502 [10] Li Q Z, Zhang W D, Li M, Niu J, Wu Q M J. Automatic detection of ship targets based on wavelet transform for HF surface wavelet radar. IEEE Geoscience and Remote Sensing Letters, 2017, 14(5): 714-718 doi: 10.1109/LGRS.2017.2673806 [11] Wang Y M, Mao X P, Zhang J, Ji Y G. Ship target detection in sea clutter of HFSWR based on spatial blind filtering. In: Proceedings of IET International Radar Conference 2015. Hangzhou, China: IET, 2015. [12] Zhang L, Zeng L P, Li M, Wang H D. Weak target detection based on complex duffing oscillator for HFSWR. In: Proceedings of the 35th Chinese Control Conference (CCC). Chengdu, China: IEEE, 2016. 4982-4987 [13] Dakovic M, Thayaparan T, Stankovic L. Time-frequency-based detection of fast manoeuvring targets. IET Signal Processing, 2010, 4(3): 287-297 doi: 10.1049/iet-spr.2009.0078 [14] Liang N Y, Huang G B, Saratchandran P, Sundararajan N. A fast and accurate online sequential learning algorithm for feedforward networks. IEEE Transactions on Neural Networks, 2006, 17(6): 1411-1423 doi: 10.1109/TNN.2006.880583 [15] Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: theory and applications. Neurocomputing, 2007, 70(1-3): 489-501 [16] Huang G, Song S J, Gupta J N D, Wu C. Semi-supervised and unsupervised extreme learning machines. IEEE Transactions on Cybernetics, 2014, 44(12): 2405-2417 doi: 10.1109/TCYB.2014.2307349 [17] Bai Z, Huang G B, Wang D W, Wang H, Westover M B. Sparse extreme learning machine for classification. IEEE Transactions on Cybernetics, 2014, 44(10): 1858-1870 doi: 10.1109/TCYB.2014.2298235 [18] Bauer F, Lukas M A. Comparingparameter choice methods for regularization of ill-posed problems. Mathematics and Computers in Simulation, 2011, 81(9): 1795-1841 doi: 10.1016/j.matcom.2011.01.016 [19] Dienstfrey A, Hale P D. Colored noise and regularization parameter selection for waveform metrology. IEEE Transactions on Instrumentation and Measurement, 2014, 63(7): 1769-1778 doi: 10.1109/TIM.2013.2297631 [20] Kurzyński. On the multistage Bayes classifier. Pattern Recognition, 1988, 21(4): 355-365 doi: 10.1016/0031-3203(88)90049-0 [21] Giusti N, Sperduti A. Theoretical and experimental analysis of a two-stage system for classification. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(7): 893-904 doi: 10.1109/TPAMI.2002.1017617 [22] Papageorgiou C P, Oren M, Poggio T. A general framework for object detection. In: Proceedings of the 6th International Conference on Computer Vision (IEEE Cat. No.98CH36271). Bombay, India: IEEE, 2002. 555-562 [23] Schwegmann C P, Kleynhans W, Salmon B P. Synthetic aperture radar ship detection using haar-like features. IEEE Geoscience and Remote Sensing Letters, 2017, 14(2): 154-158 doi: 10.1109/LGRS.2016.2631638 [24] Ma S Y, Bai L. A face detection algorithm based on Adaboost and new Haar-Like feature. In: Proceedings of the 7th IEEE International Conference on Software Engineering and Service Science (ICSESS). Beijing, China: IEEE, 2017. 651-654 [25] Yang Y M, Wu Q M J. Extreme learning machine with subnetwork hidden nodes for regression and classification. IEEE Transactions on Cybernetics, 2016, 46(12): 2885-2898 doi: 10.1109/TCYB.2015.2492468 [26] Yang Y M, Wang Y N, Yuan X F. Bidirectional extreme learning machine for regression problem and its learning effectiveness. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(9): 1498-1505 doi: 10.1109/TNNLS.2012.2202289 [27] Huang G B, Chen L. Convex incremental extreme learning machine. Neurocomputing, 2007, 70(16-18): 3056-3062 doi: 10.1016/j.neucom.2007.02.009 [28] Feng G R, Huang G B, Lin Q P, Gay R. Error minimized extreme learning machine with growth of hidden nodes and incremental learning. IEEE Transactions on Neural Networks, 2009, 20(8): 1352-1357 doi: 10.1109/TNN.2009.2024147 [29] Chen X, Peng Z, Jing W. Sparse kernel logistic regression based on $L_1/2$ regularization. Science China Information Sciences, 2013, 56(4): 1-16 [30] Qi A Z. Neural network optimization algorithm model combining L1/2 regularization and extreme learning machine. In: Proceedings of the 3rd International Workshop on Materials Engineering and Computer Sciences (IWMECS 2018). Jinan, China: Atlantis Press, 2018. [31] He B, Sun T, Yan T, et al. A pruning ensemble model of extreme learning machine with $L_1/2$ regularizer. Proceedings of ELM-2015 Volume 2: Theory, Algorithms and Applications (Ⅱ). Cham: Springer International Publishing, 2016. 1-19 [32] Liang Y, Chai H, Liu X Y, Xu Z B, Zhang H, Leung K S. Cancer survival analysis using semi-supervised learning method based on Cox and AFT models with $L_1/2$ regularization. BMC Medical Genomics, 2016, 9: Article No.11 [33] Yang D K, Liu Y. $L_1/2$ regularization learning for smoothing interval neural networks: algorithms and convergence analysis. Neurocomputing, 2018, 272: 122-129 doi: 10.1016/j.neucom.2017.06.061 [34] Huang G B, Chen L, Siew C K. Universal approximation using incremental constructive feedforward networks with random hidden nodes. IEEE Transactions on Neural Networks, 2006, 17(4): 879-892 doi: 10.1109/TNN.2006.875977 -
图(8) / 表(7)
计量
- 文章访问数: 1005
- HTML全文浏览量: 297
- PDF下载量: 202
- 被引次数: 0
