Acupuncture Sequential Scheming Method With Hybrid Knowledge and MCTS
-
摘要: 传统的序列决策方法旨在对决策过程与决策步骤进行建模, 以求解得到最优的决策序列. 然而, 序列决策建模过程对目标函数的确定性要求高, 且序列搜索的算法多以深度优先或广度优先等遍历搜索为主, 鲜有考虑搜索过程的随机性. 蒙特卡洛树搜索算法(Monte Carlo tree search, MCTS)虽然适合求解随机序列搜索问题, 但目前仅应用于博弈型搜索过程, 鲜有探讨需要专家参与的知识约束序列决策的搜索策略, 另外, 传统MCTS算法往往存在搜索范围过大、收敛不及时等问题. 为此, 提出一种融合群决策经验型知识和部分确定型决策序列片段的混合知识约束的MCTS 序列决策方法, 并给出了详细的求解流程. 最后, 将所提方法应用于一类中风后吞咽功能障碍针灸穴位排序方案制订问题, 给出了融合混合知识与MCTS的针灸排序方案设定方法, 并与其他方法进行对比, 验证了所提方法的可行性和有效性, 为年轻医师的针灸方案制订技能的标准化培训工作奠定了方法基础.Abstract: The traditional method of sequential decision-making aims to establish the decision-making processes model and decision-making steps to obtain the optimal decision-making sequence. However, the decision-making process of sequence decision-making is highly deterministic for objective function, the depth first or breadth first algorithms are always employed in the sequence searching, suffering the randomness of search process. Although Monte Carlo tree search algorithm (MCTS) is suitable for solving the random sequence search problem, it is only used to the game-type search process at present, and rarely applied in the sequence decision problem of knowledge constraint with expert participation, as well as, the traditional MCTS algorithms often have problems such as: too large search scope and poor convergence. In response, this paper proposes an MCTS sequence decision-making method based on hybrid knowledge constrained empirical knowledge of group decision-making and partially deterministic decision sequence segments, along with the detailed steps. Finally, the proposed method is employed in a kind of post-stroke dysphagia dysfunction acupuncture point sorting problem, then, we gave the acupuncture sequential scheming method with hybrid knowledge and MCTS. Comparing with other methods, the feasibility and effectiveness of the proposed method is verified, formulating the standardization training skills for the young doctor's acupuncture program, laying the foundation for the method.
-
图 4 基于混合知识的UCT-max算法的序列决策流程图
Fig. 4 Sequential decision flow chart of UCT-max algorithm based on mixed knowledge
图 6 基于GA算法的5次针灸排序序列搜索的数据图
Fig. 6 The data flowchart of acupuncture sequence searching in five times based on GA
表 1 针灸治疗脑卒中后吞咽障碍腧穴运用频次统计
Table 1 Acupuncture treatment of dysphagia after stroke
序号 腧穴名 频次 频率 (%) 1 廉泉 221 11.16 2 风池 219 11.06 3 翳风 131 6.61 4 金津 112 5.65 5 玉液 111 5.60 6 完骨 82 4.14 7 内关 76 3.84 8 风府 71 3.58 9 人中 61 3.08 10 人迎 58 2.93 11 三阴交 53 2.68 12 合谷 53 2.68 13 旁廉泉 49 2.47 $\vdots$ $\vdots$ $\vdots$ $\vdots$ 
下载: 导出CSV
表 2 针灸序列长度为5的不同分割方式
Table 2 Different segmentation patterns of acupuncture sequence in depth of 5
序列长度 序列分割方式 1维×5 a1, a2, a3, a4, a5 1维×3+2维×1 a1, a2, a3, a4a5; a1, a2, a3a4, a5
a1, a2a3, a4, a5; a1a2, a3, a4, a51维×1+2维×2 a1, a2a3, a4a5; a1a2, a3, a4a5
a1a2, a3a4, a52维×1+3维×1 a1a2, a3a4a5; a1a2a3, a4a5 1维×2+3维×1 a1, a2, a3a4a5; a1, a2a3a4, a5
a1a2a3, a4, a51维×1+4维×1 a1, a2a3a4a5; a1a2a3a4, a5 5维×1 a1a2a3a4a5
下载: 导出CSV
表 3 长度为5的序列优先度量化表
Table 3 Sequence priority quantization table with sequence length 5
序列长度 序列分割方式 序列优先度 1维×5 a1,a2,a3,a4,a5 (a1+0.08)(a2+0.06)×
(a3+0.04)(a4+0.02)(a5)1维×3+
2维×1a1,a2,a3,a4a5 (a1+0.075)(a2+0.05)(a3+0.025)(a4a5) a1,a2,a3a4,a5 (a1+0.075)(a2+0.05)(a3a4+0.025)(a5) a1,a2a3,a4,a5 (a1+0.075)(a2a3+0.05)(a4+0.025)(a5) a1a2,a3,a4,a5 (a1a2+0.075)(a3+0.05)(a4+0.025)(a5) 1维×1+
2维×2a1,a2a3,a4a5 (a1+0.067)a2a3+0.033)(a4a5) a1a2,a3,a4a5 (a1a2+0.067)(a3+0.033)(a4a5) a1a2,a3a4,a5 (a1a2+0.067)(a3a4+0.033)(a5) 2维×1+
3维×1a1a2,a3a4a5 (a1a2+0.05)(a3a4a5) a1a2a3,a4a5 (a1a2a3+0.05)(a4a5) 1维×2+
3维×1a1,a2,a3a4a5 (a1+0.067)(a2+0.033)(a3a4a5) a1,a2a3a4,a5 (a1+0.067)(a2a3a4+0.033)(a5) a1a2a3,a4,a5 (a1a2a3+0.067)(a4+0.033)(a5) 1维×1+
4维×1a1,a2a3a4a5 (a1+0.05)(a2a3a4aa5) a1a2a3a4,a5 (a1a2a3a4+0.05)(a5) 5维×1 a1a2a3a4a5 (a1a2a3a4a5)
下载: 导出CSV
表 4 各层节点的评价值及访问次数
Table 4 Evaluation value and visiting numbers of nodes in each layer
层次 节点编号 评价值 访问次数 第1层 1 0.88 12 550 2 0.83 10 050 $\vdots $ $\vdots $ $\vdots $ 76 0.09 50 77 0.12 50 第2层 $\vdots $ $\vdots $ $\vdots $ $\vdots $ $\vdots $ $\vdots $ $\vdots $ 第5层 6 117.92 50 7 3.03 50 $\vdots $ $\vdots $ $\vdots $ 76 3.03 50 77 1.52 50
下载: 导出CSV
表 5 针灸治疗次序(方案)的优异性验证数据
Table 5 Acupuncture treatment order (plan) superiority verification data
跟踪治疗时机 例数 痊愈数 优异数 非优异数 3周以内 35 10 6 4 6周以内 25 6 17 2 3个月以内 9 5 2 2 6个月以内 7 1 2 4
下载: 导出CSV
表 6 算法对比汇总
Table 6 Comparison between four algorithms
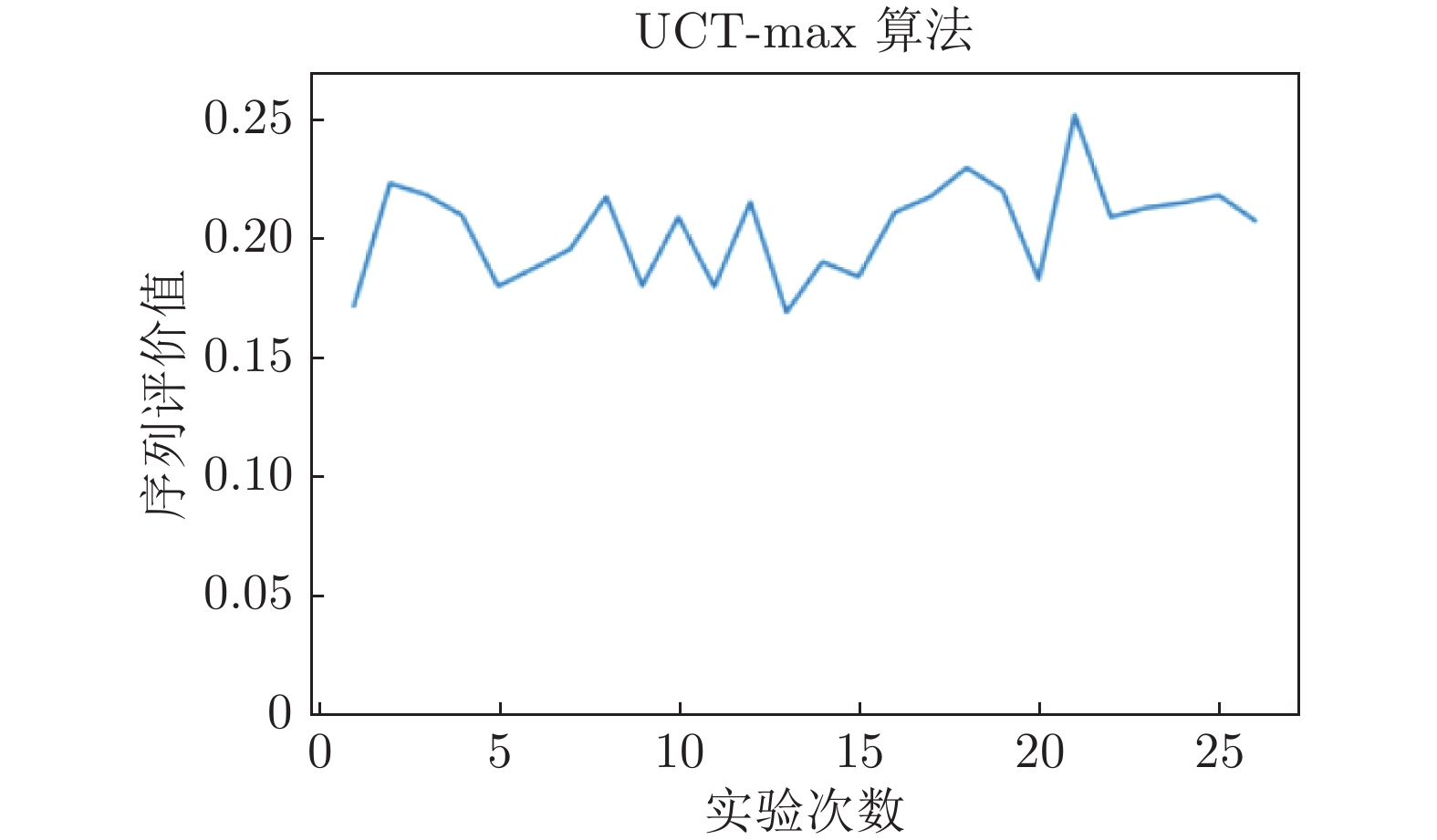
评价 算法复杂度 实验100次得分 评价率 (%) 传统MCTS 12 500 17.130 68.14 基于混合知识的MCTS-max 12 500 21.623 86.01 基于混合知识的遗传算法 120 000 11.468 48.51 基于混合知识的贪心算法 500 21.249 84.52
下载: 导出CSV
表 B.1 吞咽障碍针刺穴位统计表
Table B.1 Statistical table of acupuncture points for dysphagia
出现次数 出现频率 归一化处理 穴位序号 单个穴位的优先度 (java) 最终评价值 廉泉 221 0.11156 1 a1 0.7834 0.8917 风池 219 0.11055 0.99090909 a2 0.7001 0.845504545 翳风 131 0.066128 0.59090909 a3 0 0.590909091 金津 112 0.056537 0.50454545 a4 0.5056 0.505072727 玉液 111 0.056032 0.5 a5 0 0.5 完骨 82 0.041393 0.36818182 a6 0.339 0.353590909 风府 71 0.03584 0.31818182 a7 0.426 0.372090909 人中 61 0.030793 0.27272727 a8 0.2834 0.278063636 人迎 58 0.029278 0.25909091 a9 0.7279 0.493495455 旁廉泉 49 0.024735 0.21818182 a10 0.7556 0.486890909 天突 45 0.022716 0.2 a11 0.6723 0.43615 百会 43 0.021706 0.19090909 a12 0 0.190909091 上廉泉 34 0.017163 0.15 a13 0 0.15 天柱 30 0.015144 0.13181818 a14 0.4298 0.280809091 外玉液 27 0.013629 0.11818182 a15 0 0.118181818 外金津 27 0.013629 0.11818182 a16 0 0.118181818 哑门 25 0.01262 0.10909091 a17 0.3668 0.237945455 翳明 20 0.010096 0.08636364 a18 0 0.086363636 吞咽 17 0.008582 0.07272727 a19 0 0.072727273 地仓 16 0.008077 0.06818182 a20 0 0.068181818 $\vdots $ $\vdots $ $\vdots $ $\vdots $ $\vdots $ $\vdots $ $\vdots $ 三阴交 53 0.026754 0.2363664 a74 0 0.236363636 足三里 27 0.013629 0.11818182 a75 0 0.118181818 照海 24 0.012115 0.10454545 a76 0 0.104545455 太冲 23 0.01161 0.1 a77 0 0.1 丰隆 19 0.009591 0.08181818 a78 0 0.081818182 太溪 13 0.006562 0.05454545 a79 0 0.054545455 委中 5 0.002524 0.01818182 a80 0 0.018181818 公孙 5 0.002524 0.01818182 a81 0 0.018181818 然谷 3 0.001514 0.00909091 a82 0 0.009090909 下巨虚 3 0.001514 0.00909091 a83 0 0.009090909 上巨虚 3 0.001514 0.00909091 a84 0 0.009090909 血海 2 0.00101 0.00454545 a85 0 0.004545455 足临泣 1 0.000505 0 a86 0 0 阳陵泉 1 0.000505 0 a87 0 0 地机 1 0.000505 0 a88 0 0 大抒 3 0.001514 0.00909091 a89 0 0.009090909 心俞 2 0.00101 0.00454545 a90 0 0.004545455 脾俞 1 0.000505 0 a91 0 0 膈俞 1 0.000505 0 a92 0 0 膻中穴 3 0.001514 0.00909091 a93 0 0.009090909 关元 2 0.00101 0.00454545 a94 0 0.004545455 神阙 1 0.000505 0 a95 0 0
下载: 导出CSV
表 D.1 混合知识库
Table D.1 Hybrid knowledge base
(穴位代号, 评价值) (1, 0.891700000) (34, 0.013636364) (67, 0.054545455) (11011, 0.088440506) (2, 0.845504545) (35, 0.013636364) (68, 0.018181818) (90102, 0.139526954) (3, 0.590909091) (36, 0.238168182) (69, 0.018181818) (100902, 0.15563375) (4, 0.505072727) (37, 0.013636364) (70, 0.009090909) (90111, 0.074267505) (5, 0.5000000) (38, 0.013636364) (71, 0.009090909) (21001, 0.13419066) (6, 0.353590909) (39, 0.013636364) (72, 0.009090909) (20901, 0.095735074) (7, 0.372090909) (40, 0.013636364) (73, 0.004545455) (100109, 0.173870168) (8, 0.278063636) (41, 0.013636364) (74, 0.009090909) (20110, 0.175216481) (9, 0.493495455) (42, 0.009090909) (75, 0.004545455) (20109, 0.112918919) (10, 0.486890909) (43, 0.292045455) (76, 0.009090909) (100209, 0.099847447) (11, 0.436150000) (44, 0.009090909) (77, 0.004545455) (10910, 0.119356742) (12, 0.190909091) (45, 0.009090909) (110, 0.419621) (10902, 0.158522203) (13, 0.150000000) (46, 0.009090909) (1001, 0.405419) (91001, 0.143002889) (14, 0.280809091) (47, 0.004545455) (109, 0.391218) (11002, 0.185644285) (15, 0.118181818) (48, 0.281772727) (102, 0.37572) (100111, 0.080705328) (16, 0.118181818) (49, 0.004545455) (201, 0.364057) (91101, 0.067829683) (17, 0.237945455) (50, 0.278072727) (210, 0.357253) (90110, 0.161165872) (18, 0.086363636) (51, 0.004545455) (1009, 0.328796) (100901, 0.105697788) (19, 0.072727273) (52, 0.639200000) (1002, 0.327662) (2011009, 0.131238458) (20, 0.068181818) (53, 0.340909091) (111, 0.306954) (1090211, 0.06947019) (21, 0.068181818) (54, 0.273781818) (1011, 0.291753) (1100902, 0.148610784) (22, 0.050000000) (55, 0.172727273) (901, 0.277497) (1100211, 0.092690625) (23, 0.045454545) (56, 0.081818182) (910, 0.263296) (9020110, 0.139915065) (24, 0.040909091) (57, 0.040909091) (209, 0.24823) (1100911, 0.109088265) (25, 0.036363636) (58, 0.031818182) (211, 0.236621) (2011011, 0.092747959) (26, 0.031818182) (59, 0.004545455) (902, 0.220691) (2090110, 0.114630591) (27, 0.027272727) (60, 0.004545455) (1110, 0.20649) (9011002, 0.121701835) (28, 0.022727273) (61, 0.004545455) (1101, 0.192288) (9100211, 0.053053438) (29, 0.022727273) (62, 0.236363636) (1102, 0.17679) (2110110, 0.079102370) (30, 0.018181818) (63, 0.118181818) (911, 0.157189) (2090111, 0.063698526) (31, 0.018181818) (64, 0.104545455) (1109, 0.160267) (32, 0.018181818) (65, 0.100000000) (11009, 0.188802) (33, 0.312590909) (66, 0.081818182) (10210, 0.125794565)
下载: 导出CSV
表 C.1 穴位组合评价值
Table C.1 Acupoint combination evaluation value
两个穴位 排序优先度 最终评价值 三个穴位 排序优先度 最终评价值 四个穴位 排序优先度 最终评价值 a10a1 0.7508 0.405419 a1a10a9 0.7713 0.188802 a1a10a9a2 0.7776 0.148611 a1a9 0.7245 0.391218 a1a9a10 0.7584 0.185644 a1a2a9a10 0.7321 0.139915 a1a2 0.6958 0.37572 a1a2a9 0.7158 0.175216 a1a2a10a9 0.6867 0.131238 a2a1 0.6742 0.364057 a1a2a10 0.7103 0.17387 a2a1a9a10 0.6368 0.121702 a1a11 0.6616 0.357253 a1a9a2 0.6584 0.161166 a2a1a10a9 0.5998 0.114631 a9a1 0.6089 0.328796 a1a10a2 0.6476 0.158522 a1a9a2a10 0.5708 0.109088 a9a10 0.6068 0.327662 a2a1a9 0.6358 0.155634 a1a9a10a2 0.4853 0.092748 a2a9 0.5666 0.305954 a2a1a10 0.5842 0.143003 a2a9a1a10 0.485 0.092691 a2a11 0.5403 0.291753 a2a9a1 0.57 0.139527 a2a9a10a1 0.4139 0.079102 a2a10 0.5139 0.277497 a2a9a10 0.5482 0.134191 a9a1a2a10 0.3635 0.06947 a11a1 0.4876 0.263296 a2a10a11 0.5139 0.125795 a9a2a1a10 0.3333 0.063699 a10a2 0.4597 0.24823 a1a11a2 0.4876 0.119357 a10a1a2a9 0.2776 0.053053 a9a2 0.4382 0.236621 a9a10a11 0.4613 0.112919 a10a9 0.4087 0.220691 a2a11a1 0.4318 0.105698 a10a1 0.3824 0.20649 a2a11a10 0.3911 0.095735 a11a2 0.3561 0.192288 a9a1a2 0.4079 0.099847 a9a11 0.3274 0.17679 a9a2a1 0.3613 0.088441 a11a10 0.2911 0.157189 a10a11a1 0.3034 0.074268 a10a11 0.2968 0.160267 a10a1a11 0.2771 0.06783
下载: 导出CSV
-
[1] Arnold T, Wooders M H. Dynamic club formation with coordination. Journal of Dynamics and Games, 2017, 2(3–4): 341−361 [2] L Zhang. Artificial neural network model design and topology analysis for FPGA implementation of Lorenz Chaotic generator. In: Proceedings of the 30th IEEE Canadaian Conference on Electrical and Computer Engineering, Windsor, ON, Canada: IEEE, 2017. 1−4 [3] Chen M, Zhou R Q, Zhang R, Zhu X Z. Application of artificial neural network to failure diagnosis on process industry equipments. In: Proceedings of the 6th International Conference on Natural Computation, Yantai, China IEEE, 2010. 1190−1193 [4] 孔令智, 高迎彬, 李红增, 张华鹏. 一种快速的多个主成分并行提取算法. 自动化学报, 2017, 43(5): 835−842Kong Ling-Zhi, Gao Ying-Bin, Li Hong-Zeng, Zhang Hua-Peng. A fast algorithm that extracts multiple principle components in parallel. Acta Automatica Sinica, 2017, 43(5): 835−842 [5] Tan S F, Mavrovouniotis M L. Reducing data dimensionality through optimizing neural network inputs. Aiche Journal, 1995, 41(6): 1471−1480 doi: 10.1002/(ISSN)1547-5905 [6] Hnida M, Idrissi M K, Bennani S. Adaptive teaching learning sequence based on Instructional design and evolutionary computation. In: Proceedings of the 15th International Conference on Information Technology Based Higher Education and Training, Intanbul,Turkey: IEEE, 2016. 1−6 [7] Zhang W, Shi J W, Tang G F, Wu W J, Yue X, Li D F. Predicting small RNAs in bacteria via sequence learning ensemble method. In: Proceedings of the 2017 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Denver-Broomfield, CO, USA: IEEE, 2017. 643−647 [8] Reed M, Yiannakou A, Evering R. An ant colony algorithm for the multi-compartment vehicle routing problem. Elsevier Science Publishers B.V., 2014, 15(2): 169−176 [9] Novoaab C. An approximate dynamic programming approach for the vehicle routing problem with stochastic demands. European Journal of Operational Research, 2009, 196(2): 509−515 doi: 10.1016/j.ejor.2008.03.023 [10] 肖云涛, 欧林林, 俞立. 基于线性时序逻辑的最优巡回路径规划. 自动化学报, 2014, 40(10): 2126−2133Xiao Yun-Tao, Ou Lin-Lin, Yu Li. Optimal patrolling path planning via linear temporal logic. Acta Automatica Sinica, 2014, 40(10): 2126−2133 [11] Bosansky B, Lisy V, Lanctot M, Cermak J, Winands M H M. Algorithms for computing strategies in two player simultaneous move games. Artificial Intelligence, 2016, 237: 1−40 doi: 10.1016/j.artint.2016.03.005 [12] Conway R. T. Sangaline E. W. A Monte Carlo simulation approach for quantitatively evaluating keyboard layouts for gesture input. International Journal of Human-Computer Studies, 2017, 99: 37−47 [13] Kato H, Takaya M, Yamamura A. Analysis of a Monte Carlo tree search in Knight-Amazons. Procedia Computer Science, 2015, 62: 31−38 doi: 10.1016/j.procs.2015.08.406 [14] Powley E J, Cowling P I, Whitehouse D. Information capture and reuse strategies in Monte Carlo tree search with applications to games of hidden information. Artificial Intelligence, 2014, 217(C): 92−116 [15] Gelly S, Wang Y. Exploration exploitation in go. UCT for Monte-Carlo go, 2006, 1−8 [16] Chaslot J B, Winands M H M, Herik H J V D, Uiterwijk J W H M, Bouzy B. Progressive strategies for Monte-Carlo tree search. New Mathematics and Natural Computation, 2008, 4(3): 343−357 doi: 10.1142/S1793005708001094 [17] 田渊栋. 阿法狗围棋系统的简要分析. 自动化学报, 2016, 42(5): 671−675Tian Yuan-Dong. A simple analysis of AlphaGo. Acta Automatica Sinica, 2016, 42(5): 671−675 [18] Kocsis L, Szepesvári C. Bandit based Monte-Carlo planning. In: Proceedings of the 2006 European Conference on Machine Learning Bertin, Heidetberg, Germany: Springer-Vertag, 2006. 4212: 282−293 [19] Mandai Y, Kaneko T. Lin-UCB applied to Monte Carlo tree search. Theoretical Computer Science, 2016, 644: 114−126 doi: 10.1016/j.tcs.2016.06.035 [20] Browne C B, Powley E, Whitehouse D, Lucas S M, Cowling P I. A survey of Monte Carlo tree search methods. IEEE Transactions on Computational Intelligence and AI in Games, 2012, 4(1): 1−43 doi: 10.1109/TCIAIG.2012.2186810 [21] Lorentz R. Using evaluation functions in Monte-Carlo tree search. Theoretical Computer Science, 2016, 644(1): 106−113 [22] Ohmoto Y, Kataoka M, Nishida T. Extended methods to dynamically estimate emphasizing points for group decision-making and their evaluation. Procedia–Social and Behavioral Sciences, 2013, 97: 147−155 doi: 10.1016/j.sbspro.2013.10.215 [23] Meng F Y, Zhang Q. Induced continuous Choquet integral operators and their application to group decision making. Computers and Industrial Engineering, 2014, 68(1): 42−53 [24] Xu Z S, Cai X Q. Dynamic intuitionistic fuzzy multi-attribute decision making. International Journal of Approximate Reasoning, 2008, 48(1): 246−262 doi: 10.1016/j.ijar.2007.08.008 [25] Wilson R D, Howe E C. A cost-effectiveness analysis of screening methods for dysphagia after stroke. PM & R, 2012, 4(4): 273−282 [26] 黄伟新. 针灸联合康复训练治疗卒中后吞咽障碍的文献及临床研究[博士学位论文]. 广州中医药大学, 中国, 2016.Huang Wei–Xin. The Study of Literature and Clinical Research on Acupuncture Treatment Combined with Rehabilitation Training of Dysphagia after Stroke [Ph.D. dissertation]. Guangzhou University of Chinese Medicine, China, 2016. [27] Huang W T, Chen P S, Liu J J, Chen Y R, Chen Y H. Dynamic configuration scheduling problem for stochastic medical resources. Journal of Biomedical Informaticsl, 2018, 4(80): 96−105 [28] Chen P S, Lin Y J, Peng N C. A two-stage method to determine the allocation and scheduling of medical staff in uncertain environments. Computer and Inolustrial Engineering, 2016, 99: 174−188 [29] 刘惊雷, 张伟, 童向荣, 张振荣. 一种O(2.983n)时间复杂度的最优联盟结构生成算法. 软件学报, 2011, 22(5): 938−950Liu Jing-Lei, Zhang Wei, Tong Xiang-Rong, Zhang Zhen-Rong. O(2.983n) time complexity algorithm for optimal coalition structure generation. Journal of Software, 2011, 22(5): 938−950 [30] 张新良, 石纯一. 多Agent联盟结构动态生成算法. 软件学报, 2007, 18(3): 574−581Zhang Xin-Liang, Shi Chun-Yi. A dynamic formation algorithm of multi-agent coalition structure. Journal of Software, 2007, 18(3): 574−581 [31] Michalak T, Rahwan T, Elkind E, Wooldridge M, Jennings N R. A hybrid exact algorithm for complete set partitioning. Artificial Intelligence, 2016, 230(C): 14−50 [32] Aurangzeb M, Lewis F L. Internal structure of coalitions in competitive and altruistic graphical coalitional games. Automatica, 2014, 50(2): 335−348 doi: 10.1016/j.automatica.2013.11.002 [33] 时恩早, 张先哲. 基于直觉模糊偏好关系的多属性群决策方法. 控制工程, 2017, 24(7): 1352−1358Shi En-Zao, Zhang Xian-Zhe. Intuitionist fuzzy preference relations and their applications to multi-attribute decision making. Control Engineering of China, 2017, 24(7): 1352−1358 [34] Liu P D, Chen S M. Multiattribute group decision making based on intuitionistic 2-tuple linguistic information. Information Sciences, 2018, 430: 599−619 [35] Graf T, Platzner M. Adaptive playouts for online learning of policies during Monte Carlo tree search. Theoretical Computer Science, 2016, 644: 53−62 doi: 10.1016/j.tcs.2016.06.029 [36] 倪延延, 张晋昕. 向量自回归模型拟合与预测效果评价. 中国卫生统计, 2014, 31(1): 53−56Ni Yan-Yan, Zhang Jin-Xin. Modeling and forecasting for multivariate time series using a vector autoregression model. Chinese Journal of Health Statistics, 2014, 31(1): 53−56 [37] Xu B, Peng Z P, Yu J P, Ke W D. Quantum coding genetic algorithm based on frog leaping. Engineering Sciences, 2014, 16(3): 108−112 -
图(6) / 表(9)
计量
- 文章访问数: 1419
- HTML全文浏览量: 234
- PDF下载量: 78
- 被引次数: 0
