Improved Differential Evolution Parameter Control and Bidirectional Scheduling Algorithm for the Resource-constrained Project
-
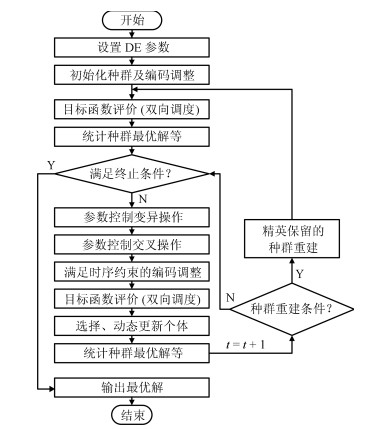
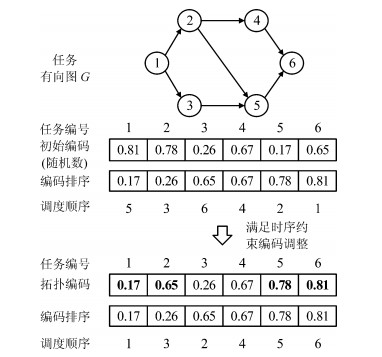
摘要: 针对资源约束项目调度组合优化难题, 提出一种改进的动态差分进化参数控制及双向调度算法.通过参数时变衰减与个体优劣评价, 自适应控制个体进化参数, 提高算法的收敛性能、勘探与开发最优解的能力; 基于动态差分进化(Dynamic differential evolution, DDE), 提出一种双向调度算法, 使用满足任务时序约束的优先数编码、交替正向反向调度, 结合标准化编码调整与精英保留的种群随机重建策略, 建立了一种高效稳健的双向编码调整机制.通过著名的项目调度问题库(Project scheduling problem library, PSPLIB)中实例集测试, 并与其他文献算法比较最优解平均偏差率, 验证了所提算法的有效性与优越性.Abstract: Aiming at the resource-constrained project scheduling problem (RCPSP) which is one of the most intractable combinatorial optimization problems, an improved dynamic differential evolution parameter control method and a bidirectional scheduling algorithm are proposed. Through parameters time-varying attenuation and individual objective evaluation, evolution parameters are adaptively controlled to improve the convergence performance of the algorithm and the ability of exploring and exploiting the optimal solution. Based on the dynamic differential evolution, a bidirectional scheduling algorithm, which uses time precedence constrained activity coding, alternating forward-backward scheduling and combinatorial strategies of standardized coding adjustment and elitist reserved population random reconstruction, is designed to establish an efficient and robust bidirectional coding adjustment mechanism. Through testing the instance set of the wellknown project scheduling problem library (PSPLIB) and comparing the average deviation rate with those of other algorithms, the proposed algorithm shows its effectiveness and superior performance.
-
Key words:
- Resource-constrained project /
- dynamic differential evolution /
- parameter control /
- bidirectional scheduling
1) 本文责任编委 付俊 -
表 1 J30系列不同测试方案结果比较
Table 1 Comparison of the results by different test schemes for J30
方案 DE类型 参数控制 调度算法 避免局部最优 标准化编码 平均偏差率
$av\_dev\, (\%)$ bh成功率
$success\, (\%)$平均代数
$av\_gen$平均CPU时间
$CPUTime$ (s)平均值 标准差 1 DE 固定 正向 0.143 0.013 92.40 109 4.59 2 DDE 固定 正向 0.143 0.021 92.42 90 2.54 3 DDE 正态分布[21] 正向 0.142 0.015 92.46 89 2.62 4 DDE 自适应 正向 0.050 0.011 96.94 53 1.56 5 DDE 自适应 双向 0.027 0.005 98.25 27 2.22 6 DDE 自适应 双向 是 0.065 0.013 96.00 44 1.14 7 DDE 自适应 双向 是 0.016 0.005 98.90 22 1.91 8 DDE 自适应 双向 是 是 0.008 0.003 99.35 13 0.93 表 2 显著性水平($\alpha=0.05)$下平均偏差率双总体t检验
Table 2 Paired-sample t-test of the average deviation rate at the significance level of 0.05
1 2 3 4 5 6 7 8 1 1 2 $\textbf{0.983}$ 1 3 $\textbf{0.939}$ $\textbf{0.937}$ 1 4 1.34$\, \times 10^{-12}$ 3.83$\, \times 10^{-10}$ 4.66$\, \times 10^{-12}$ 1 5 6.69$\, \times 10^{-16}$ 1.98$\, \times 10^{-12}$ 4.33$\, \times 10^{-15}$ 1.38$\, \times 10^{-5}$ 1 6 8.97$\, \times 10^{-11}$ 1.16$\, \times 10^{-8}$ 2.63$\, \times 10^{-10}$ 1.18$\, \times 10^{-2}$ 8.02$\, \times 10^{-8}$ 1 7 1.30$\, \times 10^{-16}$ 4.06$\, \times 10^{-13}$ 8.40$\, \times 10^{-16}$ 5.81$\, \times 10^{-8}$ 3.64$\, \times 10^{-5}$ 1.50$\, \times 10^{-9}$ 1 8 $ {\bf{2}}.{\bf{83}}\times {\bf{1}}{{\bf{0}}^{ - {\bf{17}}}}$ $ {\bf{1}}.{\bf{25}} \times {\bf{1}}{{\bf{0}}^{ - {\bf{13}}}}$ $ {\bf{2}}.{\bf{03}} \times {\bf{1}}{{\bf{0}}^{ - {\bf{16}}}}$ $ {\bf{1}}.{\bf{53}} \times {\bf{1}}{{\bf{0}}^{ - {\bf{9}}}}$ ${\bf{4}}.{\bf{69}} \times {\bf{1}}{{\bf{0}}^{ - {\bf{9}}}}$ $ {\bf{9}}.{\bf{62}} \times {\bf{1}}{{\bf{0}}^{ - {\bf{11}}}}$ $ {\bf{5}}.{\bf{62}} \times {\bf{1}}{{\bf{0}}^{ - {\bf{4}}}}$ 1 表 3 方案5与方案7性能比较
Table 3 Comparison between scheme 5 and scheme 7
Ⅰ类(36个实例) Ⅱ类(444个实例) 平均偏差率 平均代数 平均偏差率 平均代数 $av\_dev~(\%)$ $av\_gen$ $av\_dev~(\%)$ $av\_gen$ 方案5 0.346 285 0.001 6 方案7 0.194 238 0.001 5 表 4 ADDE-BS算法结果
Table 4 Results of ADDE-BS algorithm
最大调度次数 5 000 50 000 实例集 J30 J60 J90 J120 J30 J60 J90 J120 $av\_dev~(\%)$ 0.04 1.32 2.88 25.37 $\textbf{0.01}$ 1.03 2.62 24.43 $success~(\%)$ 97.44 79.58 76.67 30.00 $\textbf{99.35}$ 83.75 77.50 31.50 $CPUTime$ (s) 0.40 6.78 16.24 86.92 $\textbf{0.93}$ 66.55 179.89 1 004.36 表 5 与其他文献算法平均偏差率(%)比较
Table 5 Comparison of average deviation rate (%) with art-of-state algorithms
J30 J60 J90 J120 5 000 50 000 5 000 50 000 5 000 50 000 5 000 50 000 本文ADDE-BS $\textbf{0.04}$ $\textbf{0.01}$ $\textbf{1.32}$ $\textbf{1.03}$ $\textbf{2.88}$ $\textbf{2.62}$ $\textbf{25.37}$ $\textbf{24.43}$ DE[18] 2016 0.00 0.00 0.98 2.07 4.04 8.81 19.62 31.68 ACO CRO[6] 2017 - - 11.40 11.40 12.21 12.21 26.53 26.51 COAs[14] 2017 0.00 0.00 10.77 10.58 - - 32.35 31.23 GA-Part[9] 2017 0.07 0.01 11.08 10.71 - - 33.36 31.81 Heuristic[24] 2017 0.09 0.03 11.31 10.91 - - 34.08 32.52 ReVNS[10] 2016 0.01 0.00 11.10 10.88 - - 33.36 32.21 H-RPSO[7] 2016 0.03 0.01 10.23 10.11 - - 31.94 30.25 GA-MBX[25] 2013 0.04 0.00 10.94 10.65 - - 32.89 31.30 MAOA[26] 2015 0.06 0.01 10.84 10.64 - - 32.64 31.02 PSO-HH[13] 2014 0.04 0.01 11.13 10.68 - - 32.59 31.23 HGA[27] 2013 0.07 0.01 11.14 10.63 - - 32.75 30.66 ASH[27] 2013 0.11 0.03 11.33 10.85 - - 33.54 31.97 -
[1] Kolisch R, Hartmann S. Experimental investigation of heuristics for resource-constrained project scheduling: an update. European Journal of Operational Research, 2006, 174(1): 23-37 doi: 10.1016/j.ejor.2005.01.065 [2] Kolish R, Sprecher A. PSPLIB-A project scheduling problem library. European Journal of Operational Research, 1997, 96(1): 205-216 doi: 10.1016/S0377-2217(96)00170-1 [3] Hartmann S. A self-adapting genetic algorithm for project scheduling under resource constraints. Naval Research Logistics, 2002, 49(5): 433-448 doi: 10.1002/nav.10029 [4] 邓林义, 林焰, 金朝光.采用优先规则的粒子群算法求解RCPSP.计算机工程与应用, 2009, 45(10): 40-44 doi: 10.3778/j.issn.1002-8331.2009.10.013Deng Lin-Yi, Lin Yan, Jin Chao-Guang. Priority rule-based particle swarm optimization for RCPSP. Computer Engineering and Applications, 2009, 45(10): 40-44 doi: 10.3778/j.issn.1002-8331.2009.10.013 [5] 戴月明, 汤继涛, 纪志成.协同震荡搜索混沌粒子群求解资源受限项目调度问题.计算机应用, 2014, 34(6): 1798-1802 http://d.old.wanfangdata.com.cn/Periodical/jsjyy201406060Dai Yue-Ming, Tang Ji-Tao, Ji Zhi-Cheng. Cooperative shock search particle swarm optimization with chaos for resource-constrained project scheduling problems. Journal of Computer Applications, 2014, 34(6): 1798-1802 http://d.old.wanfangdata.com.cn/Periodical/jsjyy201406060 [6] Gonzalez-Pardo A, Del Ser J, Camacho D. Comparative study of pheromone control heuristics in ACO algorithms for solving RCPSP problems. Applied Soft Computing, 2017, 60: 241-255 doi: 10.1016/j.asoc.2017.06.042 [7] Munlin M, Anantathanavit M. Hybrid radius particle swarm optimization. In: Proceedings of the 2016 IEEE Region 10 Conference (TENCON). Singapore: IEEE, 2016. 2180-2184 [8] Valls V, Ballestín F, Quintanilla S. Justification and RCPSP: a technique that pays. European Journal of Operational Research, 2005, 165(2): 375-386 doi: 10.1016/j.ejor.2004.04.008 [9] Zamani R. An evolutionary implicit enumeration procedure for solving the resource-constrained project scheduling problem. International Transactions in Operational Research, 2017, 24(6): 1525-1547 doi: 10.1111/itor.12196 [10] Paraskevopoulos D C, Tarantilis C D, Ioannou G. An adaptive memory programming framework for the resource-constrained project scheduling problem. International Journal of Production Research, 2016, 54(16): 4938-4956 doi: 10.1080/00207543.2016.1145814 [11] 黄志宇.具有资源约束的项目调度问题中的量子进化算法.计算机集成制造系统, 2009, 15(9): 1779-1787, 1822 http://d.old.wanfangdata.com.cn/Periodical/jsjjczzxt200909016Huang Zhi-Yu. Quantum-inspired evolutionary algorithm for resources constrainted project scheduling problem. Computer Integrated Manufacturing Systems, 2009, 15(9): 1779-1787, 1822 http://d.old.wanfangdata.com.cn/Periodical/jsjjczzxt200909016 [12] 陆志强, 刘欣仪.考虑资源转移时间的资源受限项目调度问题的算法.自动化学报, 2018, 44(6): 1028-1036 doi: 10.16383/j.aas.2017.c160834Lu Zhi-Qiang, Liu Xin-Yi. Algorithm for resource-constrained project scheduling problem with resource transfer time. Acta Automatica Sinica, 2018, 44(6): 1028-1036 doi: 10.16383/j.aas.2017.c160834 [13] Koulinas G, Kotsikas L, Anagnostopoulos K. A particle swarm optimization based hyper-heuristic algorithm for the classic resource constrained project scheduling problem. Information Sciences, 2014, 277: 680-693 doi: 10.1016/j.ins.2014.02.155 [14] Elsayed S, Sarker R, Ray T, Coello C C. Consolidated optimization algorithm for resource-constrained project scheduling problems. Information Sciences, 2017, 418-419: 346-362 doi: 10.1016/j.ins.2017.08.023 [15] 吴亮红, 王耀南.动态差分进化算法及其应用.北京:科学出版社, 2014. 1-7Wu Liang-Hong, Wang Yao-Nan. Dynamic Differential Evolution Algorithm and Its Applications. Beijing: Science Press, 2014. 1-7 [16] Das S, Mullick S S, Suganthan P N. Recent advances in differential evolution-an updated survey. Swarm and Evolutionary Computation, 2016, 27: 1-30 [17] Cheng M Y, Tran D H, Wu Y W. Using a fuzzy clustering chaotic-based differential evolution with serial method to solve resource-constrained project scheduling problems. Automation in Construction, 2014, 37: 88-97 doi: 10.1016/j.autcon.2013.10.002 [18] Ali I M, Elsayed S M, Ray T, Sarker R A. A differential evolution algorithm for solving resource constrained project scheduling problems. In: Artificial Life and Computational Intelligence. Lecture Notes in Computer Science, Vol. 9592. Cham: Springer, 2016. 209-220 [19] Ciupe A, Meza S, Orza B. Heuristic optimization for the resource constrained Project Scheduling Problem: a systematic mapping. In: Proceedings of the 2016 Federated Conference on Computer Science and Information Systems. Gdansk, Poland: IEEE, 2016. 619-626 [20] Brest J, Greiner S, Boskovic B, Mernik M, Zumer V. Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems. IEEE Transactions on Evolutionary Computation, 2006, 10(6): 646-657 doi: 10.1109/TEVC.2006.872133 [21] Qin A K, Huang V L, Suganthan P N. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 398-417 doi: 10.1109/TEVC.2008.927706 [22] Zhang J Q, Sanderson A C. JADE: adaptive differential evolution with optional external archive. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945-958 doi: 10.1109/TEVC.2009.2014613 [23] Qing A Y. Dynamic differential evolution strategy and applications in electromagnetic inverse scattering problems. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(1): 116-125 [24] Chand S, Singh H K, Ray T. A heuristic algorithm for solving resource constrained project scheduling problems. In: Proceedings of IEEE Congress on Evolutionary Computation. San Sebastian, Spain: IEEE, 2017. 225-232 [25] Zamani R. A competitive magnet-based genetic algorithm for solving the resource-constrained project scheduling problem. European Journal of Operational Research, 2013, 229(2): 552-559 doi: 10.1016/j.ejor.2013.03.005 [26] Zheng X L, Wang L. A multi-agent optimization algorithm for resource constrained project scheduling problem. Expert Systems with Applications, 2015, 42(15-16): 6039-6049 doi: 10.1016/j.eswa.2015.04.009 [27] Lim A, Ma H, Rodrigues B, Tan S T, Xiao F. New meta-heuristics for the resource-constrained project scheduling problem. Flexible Services and Manufacturing Journal, 2013, 25(1-2): 48-73 doi: 10.1007/s10696-011-9133-0 -




 下载:
下载: